人教版九年级数学上册24.1 圆的基本性质同步练习含答案【2020编选】

合集下载

人教版九年级数学上册24.1.1《圆》圆的有关性质同步测试及答案

圆 24.1__圆的有关性质__24．1.1 圆 [见B 本P36]1．下列命题正确的有( C )(1)半圆是弧；(2)弦是圆上两点之间的部分；(3)半径是弦；(4)直径是最长的弦；(5)在同一平面内，到定点的距离等于定长的点都在同一个圆上．A ．1个B ．2个C ．3个D ．4个【解析】 (1)弧是圆上任意两点间的部分；任意一条直径的两个端点在圆上把圆分成两条弧，每一条弧叫做半圆，因此(1)是正确的命题．(2)弦是连接圆上任意两点的线段，不是圆上两点之间的部分，因此(2)是错误的命题．(3)半径是连接圆心与圆上任意一点的线段，不是弦．因此(3)是假命题．(4)直径是过圆心的弦，也是最长的弦．如图所示，AB 是⊙O 的直径，CD 是任意一条不过圆心的弦，连接OC ，OD ，在△OCD 中，OC ＋OD >CD ，而AB ＝OC ＋OD ，则AB >CD ，因此直径是最长的弦．(5)圆心为O ，半径为r 的圆可以看成由所有到定点O 的距离等于定长r 的点组成的图形，因此(5)正确．所以(1)，(4)，(5)正确，选C.2．如图24－1－1所示，⊙O 中点A ，O ，D 以及点B ，O ，C 分别在同一直线上，图中弦的条数为( A )A ．2B ．3C ．4D ．5图24－1－1图24－1－2图24－1－33．如图24－1－2，P 是⊙O 内的一点，P 到⊙O 的最小距离为4 cm ，最大距离为9 cm ，则该⊙O 的直径为( C )A ．6.5 cmB ．2.5 cmC ．13 cmD ．不可求【解析】过O ，P 作直径AB ，则AB ＝P A ＋PB ＝4＋9＝13(cm)，故选C.4．图24－1－3中，__AC __是⊙O 的直径；弦有__AB ，BC ，AC __；劣弧有__AB ︵，BC ︵__；优弧有__BAC ︵，BCA ︵__．5．如图24－1－4所示，已知∠AOB ＝60°，则△AOB 是__等边__三角形．图24－1－4图24－1－56．如图24－1－5，AB 是⊙O 的直径，AC 是弦，若∠ACO ＝22°，则∠COB 的度数等于__44°__．【解析】 ∵OA ＝OC ，∴∠A ＝∠C ＝22°，∴∠BOC ＝∠A ＋∠C ＝22°×2＝44°.7．如图24－1－6，以O 为圆心的两个同心圆⊙O ，大圆O 的半径OC ，OD 分别交小圆O 于A ，B 两点，求证：AB ∥CD .证明：∵OA ＝OB ，OC ＝OD ，∴∠OAB ＝12(180°－∠O )＝∠C ，∴AB ∥CD .图24－1－6图24－1－78．如图24－1－7，在⊙O 中，D ，E 分别为半径OA ，OB 上的点，且AD ＝BE ，点C 为弧AB 上一点，连接CD ，CE ，CO ，∠AOC ＝∠BOC .求证：CD ＝CE .证明：∵OA ＝OB ，AD ＝BE ，∴OA －AD ＝OB －BE ，即OD ＝OE .在△ODC 和△OEC 中，⎩⎪⎨⎪⎧OD ＝OE ，∠DOC ＝∠EOC ，OC ＝OC ，∴△ODC ≌△OEC ，∴CD ＝CE .9．如图24－1－8所示，已知⊙O 中，直径MN ＝10ABCD 的四个顶点分别在半径OM ，OP 以及⊙O 上，并且∠POM ＝45°，则AB 的长为__5__．【解析】连接OA ，构造Rt △OAB ，利用勾股定理，求出AB 的长．设正方形ABCD 的边长为x ，则AB ＝BC ＝CD ＝x ，又∠POM ＝45°，∠DCO ＝90°，∴∠ODC ＝∠POM ＝45°，∴DC ＝OC ＝x ，∴OB ＝2x .在Rt △OAB 中，AB 2＋OB 2＝OA 2，OA ＝12MN ＝5，即x 2＋(2x )2＝52，∴x ＝ 5.图24－1－810．如图24－1－9，AB ，AC 为⊙O 的弦，连接CO ，BO 并延长分别交弦AB ，AC 于点E ，F ，∠B ＝∠C .求证：CE ＝BF .证明：∵OB ，OC 是⊙O 的半径，∴OB ＝OC .又∵∠B ＝∠C ，∠BOE ＝∠COF ，∴△EOB ≌△FOC ，∴OE ＝OF ，∴CE ＝BF .11．如图24－1－10，半圆O 的直径AB ＝8，半径OC ⊥AB ，D 为弧AC 上一点，DE ⊥OC ，DF ⊥OA ，垂足分别为E ，F ，求EF 的长．图24－1－10解：连接OD .∵OC ⊥AB ，DE ⊥OC ，DF ⊥OA ，∴∠AOC ＝∠DEO ＝∠DFO ＝90°， ∴四边形DEOF 是矩形，∴EF ＝OD .∵OD ＝OA ，∴EF ＝OA ＝4.12．如图24－1－11，AB ，CD 是⊙O 的直径，DF ，BE 是⊙O 的弦，且弦DF ＝BE .求证：∠B ＝∠D .图24－1－11【解析】连接OF ，OE ，证明△DOF ≌△BOE .证明：如图，连接OE ，OF .在△DOF 和△BOE 中，⎩⎪⎨⎪⎧OF ＝OE ，OD ＝OB ，DF ＝BE ，∴△DOF ≌△BOE (SSS)．∴∠B ＝∠D .13．如图24－1－12所示，已知CD 是⊙O 的直径，∠EOD ＝51°，AE 交⊙O 于点B ，且AB ＝OC ，求∠A 的度数．图24－1－12【解析】已知∠EOD＝51°，与未知∠A构成了内、外角关系，而∠E也未知，且AB＝OC这一条件不能直接使用，因此想到同圆的半径相等，需连接半径OB，从而得到OB＝AB.解：如图所示，连接OB.∵AB＝OC，OB＝OC，∴AB＝OB，∴∠A＝∠1.又∵OB＝OE，∴∠E＝∠2＝∠1＋∠A＝2∠A，∴∠DOE＝∠E＋∠A＝3∠A.而∠DOE＝51°，∴3∠A＝51°，∴∠A＝17°.。

人教版九年级数学上册 24.1 圆的有关性质同步培优(含答案)

人教版九年级数学上册24.1 圆的有关性质同步培优一、选择题1. 下列四个命题:①直径所对的圆周角是直角;②圆既是轴对称图形，又是中心对称图形;③在同圆中，相等的圆周角所对的弦相等;④三点确定一个圆.其中正确命题的个数为 ()A.1B.2C.3D.42. 如图，在⊙O中，点A，O，D以及点B，O，C分别在一条直线上，则图中的弦有()A．2条B．3条C．4条D．5条3. 与圆心的距离不大于半径的所有点组成的图形是()A．圆的外部(包括边界) B．圆的内部(不包括边界)C．圆D．圆的内部(包括边界)4. 2019·赤峰如图，AB是⊙O的弦，OC⊥AB交⊙O于点C，D是⊙O上一点，∠ADC＝30°，则∠BOC的度数为()A．30°B．40°C．50°D．60°5. 如图，将半径为2的圆形纸片折叠后，圆弧恰好经过圆心O，则折痕AB的长为()A. 5 B．2 5 C．3 D．2 36. 2020·武汉模拟小名同学响应学习号召，在实际生活中发现问题，并利用所学的数学知识解决问题，他将汽车轮胎如图放置在地面台阶直角处，他测量了台阶高a为160 mm，直角顶点A到轮胎与地面接触点B的距离AB为320 mm，请帮小名同学计算轮胎的直径为()A．350 mm B．700 mmC．800 mm D．400 mm7. 如图，⊙O的半径为8 cm，把劣弧AB沿AB折叠，使劣弧AB经过圆心O，再把劣弧CD沿CD折叠，使劣弧CD经过AB的中点E，则折痕CD的长为()A．8 cm B．8 3 cm C．27 cm D．47 cm8. 2019·武汉京山期中在圆柱形油槽内装有一些油，油槽直径MN为10分米．截面如图，油面宽AB为6分米，如果再注入一些油后，油面宽变为8分米，则油面AB上升()A．1分米B．4分米C．3分米D．1分米或7分米二、填空题9. 如图，AC 是圆内接四边形ABCD 的一条对角线，点D 关于AC 的对称点E 在边BC 上，连接AE ，若∠ABC=64°，则∠BAE 的度数为 .10. 如图，△ABC内接于⊙O ，AC 是⊙O 的直径，∠ACB ＝50°，点D 是BAC ︵上一点，则∠D ＝________．11. 如图，AB 是⊙O的直径，弦CD ⊥AB 于点E ，若AB ＝8，CD ＝6，则BE ＝________．12. 如图，一下水管道横截面为圆形，直径为100 cm ，下雨前水面宽为60 cm ，一场大雨过后，水面宽为80 cm ，则水位上升了 cm.13. 如图所示，动点C 在⊙O 的弦AB 上运动，AB ＝23，连接OC ，过点C 作CD ⊥OC 交⊙O 于点D ，则CD 的最大值为________．14. 如图所示，在半圆O 中，AB为直径，P 为AB ︵的中点，分别在AP ︵和PB ︵上取其中点A 1和B 1，再在P A ︵1和PB ︵1上分别取其中点A 2和B 2.若一直这样取下去，则∠A n OB n ＝________°.15. 只用圆规测量∠XOY 的度数，方法是：以顶点O 为圆心任意画一个圆，与角的两边分别交于点A ，B(如图)，在这个圆上顺次截取AB ︵＝BC ︵＝CD ︵＝DE ︵＝EF ︵＝…，这样绕着圆一周一周地截下去，直到绕第n 周时，终于使第m(m ＞n)次截得的弧的末端恰好与点A 重合，那么∠XOY 的度数等于________．16. 如图，定长弦CD 在以AB 为直径的⊙O 上滑动(点C ，D 与点A ，B 不重合)，M 是CD 的中点，过点C 作CP ⊥AB 于点P.若CD ＝3，AB ＝8，PM ＝l ，则l 的最大值是________．三、解答题 17. 2019·十堰改编如图，四边形ABCD 内接于⊙O ，AE ⊥CB 交CB 的延长线于点E .若BA 平分∠DBE ，AD ＝5，CE ＝13，求AE 的长度．18. 如图，直线AB经过⊙O的圆心，与⊙O相交于点A，B，点C在⊙O上，且∠AOC＝30°，P是直线AB上的一个动点(与点O不重合)，直线PC与⊙O相交于点Q.在直线AB上使QP＝QO成立的点P共有几个？请相应地求出∠OCP的度数．19. 如图，四边形OBCD中的三个顶点在⊙O上，A是优弧BAD上的一个动点(不与点B，D重合)．(1)当圆心O在∠BAD的内部时，若∠BOD＝120°，则∠OBA＋∠ODA＝________°.(2)若四边形OBCD为平行四边形．①当圆心O在∠BAD的内部时，求∠OBA＋∠ODA的度数；②当圆心O在∠BAD的外部时，请画出图形并直接写出∠OBA与∠ODA的数量关系．20. 如图，已知△ABC内接于⊙O，点C在劣弧AB上(不与点A，B重合)，点D 为弦BC的中点，DE⊥BC，DE与AC的延长线交于点E.射线AO与射线EB交于点F，与⊙O交于点G.设∠GAB＝α，∠ACB＝β，∠EAG＋∠EBA＝γ.(1)点点同学通过画图和测量得到以下近似数据α30°40°50°60°β120°130°140°150°γ150°140°130°120°猜想：β关于α(2)若γ＝135°，CD＝3，△ABE的面积为△ABC的面积的4倍，求⊙O半径的长．人教版九年级数学上册24.1 圆的有关性质同步培优-答案一、选择题1. 【答案】C2. 【答案】B3. 【答案】D4. 【答案】D5. 【答案】D[解析] 如图，过点O作OD⊥AB于点D，连接OA.根据题意，得OD＝12OA＝1.再根据勾股定理，得AD＝ 3.根据垂径定理，得AB＝2 3.6. 【答案】C7. 【答案】D[解析] 如图，作CD关于AB对称的弦C′D′，连接OE并延长，交CD于点F，交C′D′于点F′.由题意可得OF′⊥C′D′，且OF′＝34×8＝6(cm)，所以C′F′＝OC′2－OF′2＝ 2 7 cm，所以CD＝C′D′＝2C′F′＝4 7 cm.8. 【答案】D二、填空题9. 【答案】52° [解析]∵圆内接四边形对角互补，∴∠B +∠D=180°，∵∠B=64°，∴∠D=116°.∵点D 关于AC 的对称点是点E ，∴∠D=∠AEC=116°. ∵∠AEC=∠B +∠BAE ，∴∠BAE=52°.10. 【答案】40°【解析】AC 是⊙O 的直径⇒∠ABC ＝90°⇒⎭⎪⎬⎪⎫ ∠A ＝90°－50°＝40°∠A 和∠D 都是BC ︵所对的圆周角 ⇒∠D ＝∠A ＝40°.11. 【答案】 4－7 【解析】如解图，连接OC ，∵AB 是⊙O 的直径，CD ⊥AB ，AB ＝8，CD ＝6，∴CE ＝DE ＝3，OC ＝OB ＝4. 在Rt △OCE 中，OE ＝42－32＝7，∴BE ＝OB －OE ＝4－7.12. 【答案】10或70 [解析]作OD ⊥AB 于C ，OD 交☉O 于点D ，连接OB.由垂径定理得:BC=AB=30 cm . 在Rt △OBC 中，OC==40(cm).当水位上升到圆心以下且水面宽80 cm 时，圆心到水面距离==30(cm)，水面上升的高度为:40-30=10(cm).当水位上升到圆心以上且水面宽80 cm 时，水面上升的高度为:40+30=70(cm). 综上可得，水面上升的高度为10 cm 或70 cm . 故答案为10或70.13. 【答案】3 [解析] 如图，连接OD ，过点O 作OH ⊥AB 于点H ，则AH ＝BH＝12AB ＝ 3.∵CD ⊥OC ，∴CD ＝OD 2－OC 2.∵OD 为⊙O 的半径，∴当OC 最小时，CD 最大．当点C 运动到点H 时，OC 最小，此时CD ＝BH ＝3，即CD 的最大值为 3.14. 【答案】(902n －1) [解析] 当n ＝1时，∠A 1OB 1＝90°；当n ＝2时，∠A 2OB 2＝90°2＝45……所以∠A n OB n ＝(902n －1)°.15. 【答案】⎝ ⎛⎭⎪⎫360n m ° [解析] 设∠XOY 的度数为x ，则mx ＝n ×360°，所以x ＝⎝ ⎛⎭⎪⎫360n m °.16. 【答案】34 [解析] 如图，当CD ∥AB 时，PM 的长最大，连接OM ，OC .∵CD ∥AB ，CP ⊥AB ， ∴CP ⊥CD .∵M 为CD 的中点，OM 过点O ， ∴OM ⊥CD ，∴∠OMC ＝∠PCD ＝∠CPO ＝90°， ∴四边形CPOM 是矩形， ∴PM ＝OC .∵⊙O 的直径AB ＝8， ∴半径OC ＝4，∴PM ＝4.三、解答题17. 【答案】解：连接AC，如图．∵BA平分∠DBE，∴∠1＝∠2.∵∠1＋∠ABC＝180°，∠ABC＋∠CDA＝180°，∴∠1＝∠CDA.又∵∠2＝∠3，∴∠3＝∠CDA，∴AC＝AD＝5.∵AE⊥CB，∴∠AEC＝90°，∴AE＝AC2－CE2＝52－（13）2＝2 3.18. 【答案】解：在直线AB上使QP＝QO成立的点P共有3个．(1)如图①.在△QOC中，OC＝OQ，∴∠OQC＝∠OCQ.在△OPQ中，QP＝QO，∴∠QOP＝∠QPO.又∵∠QPO＝∠OCQ＋∠AOC，且∠AOC＝30°，∠QOP＋∠QPO＋∠OQC＝180°，∴3∠OCQ＝120°，∴∠OCQ＝40°.即∠OCP＝40°.(2)如图②.∵QO＝QP，∴∠QPO＝∠QOP.设∠QPO＝x，则∠OQC＝∠QPO＋∠QOP＝2x.又∵OC＝OQ，∴∠OCQ＝∠OQC＝2x，∴∠AOC＝∠OPC＋∠OCP＝x＋2x＝3x.∵∠AOC＝30°，∴3x＝30°，解得x＝10°，∴∠OCP＝2x＝20°.(3)如图③.∵QO＝QP，∴∠QOP＝∠QPO.∵OC＝OQ，∴∠OQC＝∠OCQ.设∠QPO＝y，则∠OQC＝∠OCQ＝∠QPO＋∠AOC＝y＋30°，∴在△OPQ中，有y＋y＋y＋30°＝180°，解得y＝50°，∴∠OCP＝180°－50°－30°＝100°.综上所述，在直线AB上使QP＝QO成立的点P共有3个，∠OCP的度数分别为40°，20°，100°.19. 【答案】52解：(1)60(2)①如图(a)．∵四边形OBCD为平行四边形，∴∠BOD＝∠BCD，∠OBC＝∠ODC.又∵∠BAD＋∠BCD＝180°，∠BAD＝12∠BOD，∴12∠BOD＋∠BOD＝180°，解得∠BOD＝120°，∴∠BAD＝12∠BOD＝12×120°＝60°，∠OBC＝∠ODC＝180°－∠BOD＝180°－120°＝60°.又∵∠ABC＋∠ADC＝180°，∴∠OBA＋∠ODA＝∠ABC＋∠ADC－(∠OBC＋∠ODC)＝180°－(60°＋60°)＝60°.②如图(b)所示，连接AO.∵OA＝OB，∴∠OBA＝∠OAB.∵OA＝OD，∴∠OAD＝∠ODA.∵∠OAB＝∠OAD＋∠BAD，∴∠OBA＝∠ODA＋∠BAD＝∠ODA＋60°.如图(c)，同理可得∠ODA＝∠OBA＋60°.20. 【答案】【思维教练】(1)观察表格可猜想β＝90°＋α，γ＝180°－α.连接BG，由直径所对的圆周角为90°和圆内接四边形的对角和为180°即可得出β＝90°＋α；由题干条件易知△EBD≌△EGD，∠EBC＝∠ECB，再由三角形的外角和定理和β＝90°＋α，利用角度之间的转化即可得出结论；(2)由(1)的结论可以得出α＝∠BAG＝45°，β＝∠ACB＝135°，∴∠ECB＝45°，∠CEB＝90°，△ECD、△BEC、△ABG 都是等腰直角三角形，由CD的长，可得出BE和CE的长，再由题干条件△ABE 的面积是△ABC的面积的4倍可得出AC的长，利用勾股定理在△ABE中求出AB的长，再利用勾股定理在△ABG求出AG的长，即可求出半径长．①(1)①β＝90°＋α，γ＝180°－α证明：如解图①，连接BG，∵AG是⊙O的直径，∴∠ABG＝90°，∴α＋∠BGA＝90°，(1分)又∵四边形ACBG内接于⊙O，∴β＋∠BGA＝180°，∴β－α＝90°，即β＝90°＋α；(3分)②∵D是BC的中点，且DE⊥BC，∴△EBD≌△ECD，∴∠EBC＝∠ECB，∵∠EAG＋∠EBA＝γ，∴∠EAB＋α＋∠EBC＋∠CBA＝γ，∵∠EAB＋∠CBA＝∠ECB，∴2∠ECB＋α＝γ，(4分)∴2(180°－β )＋α＝γ，由①β＝90°＋α代入后化简得，γ＝180°－α；(6分)(2)如解图②，连接BG，②∵γ＝135°，γ＝180°－α，∴α＝45°，β＝135°，∴∠AGB＝∠ECB＝45°，(8分)∴△ECD和△ABG都是等腰直角三角形，又∵△ABE的面积是△ABC的面积的4倍，∴AE＝4AC，∴EC＝3AC，(9分)∵CD＝3，∴CE＝32，AC＝2，∴AE＝42，(10分)∵∠BEA＝90°，∴由勾股定理得，AB＝BE2＋AE2＝（32）2＋（42）2＝50＝52，(11分)∴AG＝2AB＝2×52＝10，∴r＝5.(12分)。

九年级数学上册第二十四章圆 24.1 圆的有关性质 24.1.4 圆周角同步检测(含解析)(新版)新人教版

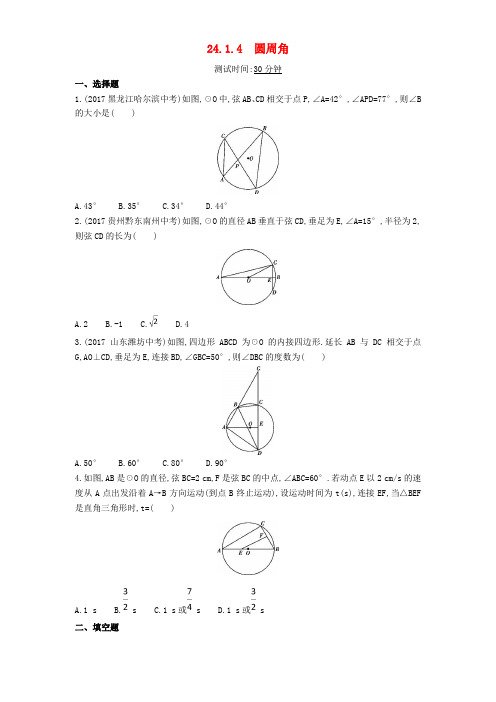
24.1.4 圆周角测试时间:30分钟一、选择题1.(2017黑龙江哈尔滨中考)如图,☉O中,弦AB、CD相交于点P,∠A=42°,∠APD=77°,则∠B 的大小是( )A.43°B.35°C.34°D.44°2.(2017贵州黔东南州中考)如图,☉O的直径AB垂直于弦CD,垂足为E,∠A=15°,半径为2,则弦CD的长为( )A.2B.-1C.D.43.(2017山东潍坊中考)如图,四边形ABCD为☉O的内接四边形.延长AB与DC相交于点G,AO⊥CD,垂足为E,连接BD,∠GBC=50°,则∠DBC的度数为( )A.50°B.60°C.80°D.90°4.如图,AB是☉O的直径,弦BC=2 cm,F是弦BC的中点,∠ABC=60°.若动点E以2 cm/s的速度从A点出发沿着A→B方向运动(到点B终止运动),设运动时间为t(s),连接EF,当△BEF 是直角三角形时,t=( )A.1 sB. sC.1 s或 sD.1 s或 s二、填空题2 25.(2017浙江绍兴中考)如图,一块含45°角的直角三角板,它的一个锐角顶点A 在☉O 上,边AB,AC 分别与☉O 交于点D,E,则∠DOE 的度数为 .6.如图,A 、B 、C 、D 四点都在☉O 上,AD 是☉O 的直径,且AD=6 cm,若∠ABC=∠CAD,则弦AC 的长为 .三、解答题7.(2018湖北黄石大冶月考)已知:如图,△ABC 内接于☉O,AF 是☉O 的弦,AF⊥BC,垂足为D,点E 为弧BF 上一点,且BE=CF. (1)求证:AE 是☉O 的直径; (2)若∠ABC=∠EAC,AE=8,求AC 的长.8.如图,在△ABC 中,AB=AC,以AC 为直径的☉O 交AB 于点D,交BC 于点E. (1)求证:BE=CE;(2)若∠B=70°,求的度数; (3)若BD=2,BE=3,求AC 的长.24.1.4 圆周角一、选择题1.答案 B ∵∠D=∠A=42°,∠APD=77°,∴∠B=∠APD -∠D=35°,故选B.2.答案 A ∵☉O 的直径AB 垂直于弦CD,∴CE=DE,∠CEO=90°,∵∠A=15°,∴∠COE=30°,∵OC=2,∴CE=OC=1,∴CD=2CE=2,故选A.3.答案 C 如图,∵A、B、D、C四点共圆,∠GBC=50°,∴∠GBC=∠ADC=50°,∵AE⊥CD,∴∠AED=90°,∴∠EAD=90°-50°=40°,延长AE交☉O于点M,∵AO⊥CD,∴=,∴∠DBC=2∠EAD=80°.故选C.4.答案 C ∵AB是☉O的直径,∴∠ACB=90°,∵∠ABC=60°,BC=2 cm,∴AB=2BC=4 cm,∵F 是弦BC的中点,∴BF=BC=1 cm.当∠BFE=90°时,∠B=60°,则BE=2BF=2 cm,则AE=AB-BE=2 cm,此时t==1(s);当∠BEF=90°时,∠B=60°,则BE=BF= cm,则AE=AB-BE= cm,此时t==(s).综上所述,t=1 s 或 s.故选C.二、填空题5.答案90°解析∵∠A=45°,∴∠DOE=2∠A=90°.6.答案3 cm解析如图,连接CD,∵∠ABC=∠CAD,∴AC=CD,∵AD是☉O的直径,∴∠ACD=90°.∵AD=6 cm,∴AC2+CD2=36,∴AC=3cm.三、解答题7.解析(1)证明:∵BE=CF,∴=,∴∠BAE=∠CAF.34 4∵AF⊥BC, ∴∠ADC=90°, ∴∠FAC+∠ACD=90°. ∵∠E=∠ACD, ∴∠E+∠BAE=90°, ∴∠ABE=90°, ∴AE 是☉O 的直径. (2)如图,连接OC,∵∠AOC=2∠ABC,∠ABC=∠CAE, ∴∠AOC=2∠CAE. 又∵OA=OC,∴∠CAO=∠ACO=∠AOC, ∴△AOC 是等腰直角三角形. ∵AE=8,∴AO=CO=4, ∴AC=4.8.解析 (1)证明:如图,连接AE, ∵AC 为☉O 的直径,∴∠AEC=90°, ∴AE⊥BC,∵AB=AC, ∴BE=CE.(2)如图,连接OD 、OE,在Rt△ABE 中,∠BAE=90°-∠B=90°-70°=20°, ∴∠DOE=2∠DAE=40°, ∴的度数为40°. (3)如图,连接CD,BC=2BE=6, 设AC=x,∵AB=AC,BD=2,∴AD=x -2, ∵AC 为☉O 的直径, ∴∠ADC=90°,在Rt△BCD 中,CD 2=BC 2-BD 2=62-22=32, 在Rt△ADC 中,AD 2+CD 2=AC 2, ∴(x -2)2+32=x 2,解得x=9, 即AC 的长为9.5。

人教版九年级数学上学期(第一学期)第24章《圆的基本性质》同步练习及答案(3).docx

24.1 圆（第四课时）--------圆周角知识点1、圆周角定义：顶点在，并且两边都和圆的角叫圆周角。

2、圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角，都等于这条弧所对的圆心角的。

推论1、在同圆或等圆中，如果两个圆周角，那么它们所对的弧。

推论2、半圆（或直径）所对的圆周角是； 900的圆周角所对的弦是。

3、圆内接四边形：定义：如果一个多边形的所有顶点都在圆上，这个多边形叫做，这个圆叫做。

性质：圆内接四边形的对角一、选择题1.如图，在⊙O 中，若C 是BD 的中点，则图中与∠BAC 相等的角有（）A.1个B.2 个C.3个D.4个2.如图，△ABC 内接于⊙O ，∠A=40°，则∠BOC 的度数为（）A. 20°B. 40°C. 60°D.80°C · BD OA3.如图，AB是⊙O的直径，点C在⊙O上，若∠A=40 º，则∠B的度数为（）A．80 ºB．60 ºC．50 ºD．40 º4.如图，在△ABC中，AB为⊙O的直径，∠B=60°，∠BOD=100°，则∠C的度数为（）A．50°B．60°C．70°D．80°5.如图，AB、CD是⊙O的两条弦，连接AD、BC，若∠BAD=60°，则∠BCD的度数为（）A.40°B.50°C.60°D.70°A CBO6.如图，⊙C过原点，且与两坐标轴分别交于点A，点B，点A的坐标为（0，3），M是第三象限内⊙C上一点，∠BMO=120°，则⊙C的半径为（）A．6 B．5 C．3 D．327、如图，⊙O是△ABC的外接圆，∠B=60°，OP⊥AC于点P，OP=23，则⊙O的半径为（）A．43B．63C．8 D．128、如图，DC 是⊙O直径，弦AB⊥CD于F，连接BC，DB，则下列结论错误的是（）B．A F=BF C．O F=CF D．∠DBC=90°A.AD BD二、填空题1．如图，点A、B、C在⊙O上，∠AOC=60°，则∠ABC的度数是．2．如图，点A、B、C、D在⊙O上，OB⊥AC，若∠BOC=56°，则∠ADB= 度．3.已知如图，四边形ABCD内接于⊙O，若∠A＝60°，则∠DCE＝ .4.如图，⊙O的弦CD与直径AB相交，若∠BAD＝50°，则∠ACD＝ ..5、如图，AB是⊙O的直径，点C是圆上一点，∠BAC=70°，则∠OCB= ．6、如图，若AB是⊙O的直径，AB=10cm，∠CAB=30°，则BC= cm．7、如图所示⊙O中，已知∠BAC=∠CDA=20°，则∠ABO的度数为．8、如图，△ABC内接于⊙O，∠BAC=120°，AB=AC，BD为⊙O的直径，AD=6，则DC= ．9、如图，圆心角∠AOB=30°，弦CA∥OB，延长CO与圆交于点D，则∠BOD= ．10、如图，量角器的直径与直角三角板ABC的斜边AB重合，其中量角器0刻度线的端点N与点A重合，射线CP从CA处出发沿顺时针方向以每秒3度的速度旋转，CP与量角器的半圆弧交于点E，第24秒，点E在量角器上对应的读数是度．A BC D O三、解答题1、如图，⊙O 的直径AB 为10cm ，弦AC 为6cm ，∠ACB 的平分线交⊙O 于D ，求BC ，AD ，BD 的长.2．如图，AB 是⊙O 的直径，C 是BD 的中点，CE ⊥AB 于 E ，BD 交CE 于点F ．（1）求证：CF ﹦BF ；（2）若CD ﹦6， AC ﹦8，则⊙O 的半径为，CE 的长是．3、如图，A ，P ，B ，C 是半径为8的⊙O 上的四点，且满足∠BAC=∠APC=60°，（1）求证：△ABC 是等边三角形； A CBDE FO（2）求圆心O到BC的距离OD．4、如图，⊙O是△ABC的外接圆，AB是⊙O的直径，D为⊙O上一点，OD⊥AC，垂足为E，连接BD（1）求证：BD平分∠ABC；（2）当∠ODB=30°时，求证：BC=OD．5、如图，AB为⊙O的直径，点C在⊙O上，延长BC至点D，使DC=CB，延长DA与⊙O的另一个交点为E，连接AC，CE．（1）求证：∠B=∠D；（2）若AB=4，BC﹣AC=2，求CE的长．24.1 圆（第四课时）--------圆周角知识点1.圆上相交2.相等一半相等一定相等直角直径3.圆内接多边形这个多边形的外接圆互补一、选择题1.C2.D3.C4.C5. C6.C7、A8、C二、填空题1．150°2．25°3.60°4. 40° .5、20°6、57、50° 8.239、30°10、144°三、解答题1、A B CD O2222222BC AB AC 1068cm CD ACBACD BCD 45AD BDAD BDBD AB 100100AD BD 52cm 2∴∠∠︒∴=-=-=∠∴∠=∠=︒∴=∴=+==∴===解：AB 是O 的直径ACB=ADB=90在Rt ABC 中,AB=10cm,AC=6cm,平分在Rt ADC 中,AB=10cmAD 2．解：(1) 证明：∵AB 是⊙O 的直径，∴∠ACB ﹦90° 又∵CE ⊥AB ， ∴∠CEB ﹦90° ∴∠2﹦90°－∠A ﹦∠1又∵C 是弧BD 的中点，∴∠1﹦∠A ∴∠1﹦∠2,∴ CF ﹦BF ﹒(2) ⊙O 的半径为5 ， CE 的长是524﹒3、解：（1）在△ABC 中，∵∠BAC=∠APC=60°，又∵∠APC=∠ABC ，∴∠ABC=60°， ACB D E FO 1 2∴△ABC是等边三角形；（2）∵△ABC为等边三角形，⊙O为其外接圆，∴O为△ABC的外心，∴BO平分∠ABC，∴∠OBD=30°，∴OD=8×12=4．4、证明：（1）∵OD⊥AC OD为半径，∴CD AD，∴∠CBD=∠ABD，∴BD平分∠ABC；（2）∵OB=OD，∴∠OBD=∠0DB=30°，∴∠AOD=∠OBD+∠ODB=30°+30°=60°，又∵OD⊥AC于E，∴∠OEA=90°，又∵AB为⊙O的直径，∴∠ACB=90°，在Rt△ACB中，BC=12 AB，∵OD=CD ADAB，∴BC=OD．5、（1）证明：∵AB为⊙O的直径，∴∠ACB=90°，∴AC⊥BC，∵DC=CB，∴AD=AB，∴∠B=∠D；（2）解：设BC=x，则AC=x﹣2，在Rt△ABC中，AC2+BC2=AB2，∴（x﹣2）2+x2=42，解得：x1=1+，x2=1﹣（舍去），∵∠B=∠E，∠B=∠D，∴∠D=∠E，∴CD=CE，∵CD=CB，∴CE=CB=1+．。

人教版九年级数学上册24.1.1《圆》圆的有关性质同步测试及答案【新】

人教版九年级数学上册 24.1.1 圆同步练习题(含答案)

人教版九年级数学上册第24章 24.1.1 圆同步练习题一、选择题1．下列条件中，能确定唯一一个圆的是(C)A ．以点O 为圆心B ．以2 cm 长为半径C ．以点O 为圆心，5 cm 长为半径D ．半径为2 cm ，且经过点A 2．已知⊙O 中最长的弦为8 cm ，则⊙O 的半径为(B)A ．2 cmB ．4 cmC ．8 cmD ．16 cm 3．下列命题中正确的有(A)①弦是圆上任意两点之间的部分；②半径是弦；③直径相等的两个圆是等圆；④弧是半圆，半圆是弧；⑤长度相等的两条弧是等弧．A ．1个B ．2个C ．3个D ．4个4．如图所示，以坐标原点O 为圆心的圆与y 轴交于点A ，B ，且OA ＝1，则点B 的坐标是(B)A ．(0，1)B ．(0，－1)C ．(1，0)D ．(－1，0) 5．如图所示，MN 为⊙O 的弦，∠N ＝52°，则∠MON 的度数为(C)A ．38°B ．52°C ．76°D ．104°6.如图所示，AB ，MN 是⊙O 中两条互相垂直的直径，点P 在AM ︵上，且不与点A ，M 重合，过点P 作AB ，MN 的垂线，垂足分别是D ，C.当点P 在AM ︵上移动时，矩形PCOD 的形状、大小随之变化，则PC 2＋PD 2的值(C)A ．逐渐变大B ．逐渐变小C ．不变D ．不能确定二、填空题7．到点O 的距离等于8 cm 的点的集合是以点O 为圆心，以8cm 长为半径的圆． 8．如图，在⊙O 中，弦有AC ，AB ，直径是AB ，优弧有ABC ︵，CAB ︵，劣弧有AC ︵，BC ︵．9．如图，在△ABC 中，∠ACB ＝90°，∠A ＝20°，以点C 为圆心、CB 为半径的圆交AB 于点D ，则∠ACD ＝50°．10．已知A ，B 是半径为6的圆上的两个不同的点，则弦长AB 的取值范围是0<AB ≤12． 11．如图，在Rt △ABC 中，∠ACB ＝90°，∠A ＝30°，BC ＝1，以边AC 上一点O 为圆心，OA为半径的⊙O 经过点B ，则⊙O 312.如图，AB是⊙O的直径，D是圆上的一点，∠DOB＝75°，DC交BA的延长线于点E，交圆于点C，且CE＝AO，则∠E＝25°．13.如图，点D，E在△ABC的边BC，AB上，过A，C，D三点的圆的圆心为点E，以点D为圆心的圆过点B，E.如果∠A＝57°，那么∠B＝22°．14.如图所示，将半径为1的⊙A向右平移2个单位长度至⊙B，两圆相交于C，D两点，则CD＝2．15．如图，C是以点O为圆心，AB为直径的半圆上一点，且CO⊥AB，在OC两侧分别作矩形OGHI和正方形ODEF，且点I，F在OC上，点H，E在半圆上，可证：IG＝FD.小云发现连接图中已知点得到两条线段，便可证明IG＝FD.请回答：小云所作的两条线段分别是OH和OE．16．如图，正方形ABCD和正方形CEFG，点A，F在半圆O上，B，C，E在半圆O的直径上，AB＝5，FE＝4，则OA三、解答题17.矩形ABCD 的对角线AC ，BD 相交于点O .求证：A ，B ，C ，D 四个点在以点O 为圆心的同一个圆上．证明：∵四边形ABCD 为矩形，∴OA ＝OC ＝12AC ，OB ＝OD ＝12BD ，AC ＝BD .∴OA ＝OC ＝OB ＝OD .∴A ，B ，C ，D 四个点在以点O 为圆心，OA 为半径的圆上(如图)．18．如图，AB ，AC 为⊙O 的弦，连接CO ，BO 并延长，分别交弦AB ，AC 于点E ，F ，∠B ＝∠C.求证：CE ＝BF.证明：∵OB ，OC 是⊙O 的半径， ∴OB ＝OC.又∵∠B ＝∠C ，∠BOE ＝∠COF ， ∴△EOB ≌△FOC(ASA)． ∴OE ＝OF.∴OE ＋OC ＝OF ＋OB ，即CE ＝BF.19．如图所示，AB 是⊙O 的弦，半径OC ，OD 分别交AB 于点E ，F ，且AE ＝BF ，请写出线段OE 与OF 的数量关系，并给予证明．解：OE ＝OF. 证明：连接OA ，OB. ∵OA ，OB 是⊙O 的半径， ∴OA ＝OB. ∴∠OAB ＝∠OBA. 又∵AE ＝BF ，∴△OAE ≌△OBF(SAS)． ∴OE ＝OF.20．如图，BD ，CE 是△ABC 的高，M 为BC 的中点．试说明点B ，C ，D ，E 在以点M 为圆心的同一个圆上．证明：连接ME ，MD.∵BD ，CE 分别是△ABC 的高，M 为BC 的中点， ∴ME ＝MD ＝MC ＝MB ＝12BC.∴点B ，C ，D ，E 在以点M 为圆心的同一个圆上．。

人教版九年级数学上24.1圆的有关性质同步检测试卷含答案

（）
A．14° B．28° C．56° D．84° 3．如图，⊙O 的直径 CD 过弦 EF 的中点 G，∠DCF=20°，则∠EOD 等于（）
A．10° B．20° C．40° D．80° 4．如图，已知点 C，D 是半圆上的三等分点，连接 AC，BC，CD，OD，BC 和 OD 相交于点 E．则下列结论： ①∠CBA=30°，②OD⊥BC，③OE= AC，④四边形 AODC 是菱形．正确的个数是（）
24．如图，P 是⊙O 外一点，A、B、C 是⊙O 上的三点，∠AOB=60°，PA、PB 分别交 N 两点，则∠APB 的范围是______．
于 M、
第 5 页（共 8 页）
A．AD=AB B．∠BOC=2∠D C．∠D+∠BOC=90° D．∠D=∠B
第 3 页（共 8 页）
14．如图，在⊙O 中，∠CBO=45°，∠CAO=15°，则∠AOB 的度数是（）
A．75° B．60° C．45° D．30° 15．如图，⊙O 是△ABC 的外接圆，∠OCB=40°，则∠A 的度数是（）
A． B．2 C．2 D．4 11．如图，在⊙O 中，已知∠OAB=22.5°，则∠C 的度数为（）
A．135° B．122.5° C．115.5° D．112.5° 12．如图，已知⊙O 是△ABD 的外接圆，AB 是⊙O 的直径，CD 是⊙O 的弦，∠ABD=58°，则∠ BCD 等于（）
A．116° B．32° C．58° D．64° 13．如图，在⊙O 中，直径 CD⊥弦 AB，则下列结论中正确的是（）
圆的有关性质
一、选择题（共 16 小题） 1．如图，△ABC 内接于⊙O，AB=BC，∠ABC=120°，AD 为⊙O 的直径，AD=6，那么 AB 的值为（）

人教版九年级上《24.1圆的有关性质》同步练习含答案(共4份)

24．1.1圆知识点1圆的定义1．圆的形成定义：在一个平面内，线段绕它固定的一个端点旋转________，另一个端点所形成的图形叫做圆．圆的集合定义：圆心为O、半径为r的圆可以看成是所有到定点O 的距离等于________的点的集合．2．下列条件中，能确定圆的是()A．以已知点O为圆心B．以1 cm长为半径C．经过已知点A，且半径为2 cmD．以点O为圆心，1 cm长为半径3．如图24－1－1所示，以坐标原点O为圆心的圆与y轴交于点A，B，且OA＝1，则点B的坐标是()图24－1－1A．(0，1) B．(0，－1)C．(1，0) D．(－1，0)4．如图24－1－2所示，若BD，CE都是△ABC的高．求证：B，C，D，E四点在同一个圆上．图24－1－2知识点2与圆有关的概念5．如图24－1－3所示，在⊙O中，________是直径，________是弦，劣弧有________，优弧有________．图24－1－36．如图24－1－4，在⊙O中，点A，O，D以及点B，O，C分别在一条直线上，图中弦的条数是()图24－1－4A．2 B．3 C．4 D．57．下列命题中是真命题的有()①两个端点能够重合的弧是等弧；②圆的任意一条弦把圆分成优弧和劣弧两部分；③长度相等的弧是等弧；④半径相等的两个圆是等圆；⑤直径是圆中最长的弦．A．2个B．3个C．4个D．5个8．若圆的半径为3，则弦AB的长度的取值范围是__________．9．已知：如图24－1－5，OA，OB为⊙O的半径，C，D分别为OA，OB的中点．求证：AD＝BC.图24－1－510．已知：如图24－1－6，在⊙O中，AB为弦，C，D两点在弦AB上，且AC＝BD.求证：△OAC≌△OBD.图24－1－611．如图24－1－7，AB 是⊙O 的直径，点D ，C 在⊙O 上，AD ∥OC ，∠DAB ＝60°，连接AC ，则∠DAC 等于( )图24－1－7A ．15°B ．30°C ．45°D ．60°12．如图24－1－8所示，AB ，MN 是⊙O 中两条互相垂直的直径，点P 在AM ︵上，且不与点A ，M 重合，过点P 作AB ，MN 的垂线，垂足分别是D ，C.当点P 在AM ︵上移动时，矩形PCOD 的形状、大小随之变化，则PC 2＋PD 2的值( )图24－1－8A ．逐渐变大B ．逐渐变小C ．不变D ．不能确定13．如图24－1－9，已知P 是⊙O 外一点，Q 是⊙O 上的动点，线段PQ 的中点为M ，连接OP ，OM.若⊙O 的半径为2，OP ＝4，则线段OM 的最小值是( )图24－1－9A ．0B ．1C ．2D ．314．如图24－1－10，在Rt △ABC 中，以点C 为圆心，BC 长为半径的圆交AB 于点D ，交AC 于点E ，∠BCD ＝40°，则∠A ＝________°.图24－1－1015．如图24－1－11，C 是以点O 为圆心，AB 为直径的半圆上一点，且CO ⊥AB ，在OC 两侧分别作矩形OGHI 和正方形ODEF ，且点I ，F 在OC 上，点H ，E 在半圆上，可证：IG ＝FD.小云发现连接图中已知点得到两条线段，便可证明IG ＝FD.请回答：小云所作的两条线段分别是________和________．图24－1－1116．⊙O 1与⊙O 2的半径分别是r 1，r 2，且r 1和r 2是关于x 的方程x 2－ax ＋14＝0的两个根．若⊙O 1与⊙O 2是等圆，则a 2019的值为________．17．如图24－1－12所示，AB 是⊙O 的弦，半径OC ，OD 分别交AB 于点E ，F ，且AE ＝BF ，请你指出线段OE 与OF 的数量关系，并给予证明．图24－1－1218．在⊙O中，直径AB＝6，BC是弦，∠ABC＝30°，点P在BC上，点Q在⊙O上，且OP⊥PQ.(1)如图24－1－13①，当PQ∥AB时，求PQ的长；(2)如图24－1－13②，当点P在BC上移动时，求PQ长的最大值．图24－1－13教师详解详析1．一周定长r2．D [解析]∵圆心和半径都确定后才可以确定圆，只有D 选项中具备这两个条件， ∴D 选项正确．3．B [解析]∵圆的半径都相等，∴OB ＝OA ＝1， ∴点B 的坐标是(0，－1)．故选B .4．证明：如图，取BC 的中点F ，连接DF ，EF.∵BD ，CE 都是△ABC 的高， ∴△BCD 和△BCE 都是直角三角形，∴DF ，EF 分别是Rt △BCD 和Rt △BCE 斜边上的中线， ∴DF ＝EF ＝BF ＝CF ，∴B ，C ，D ，E 四点在以点F 为圆心，BF 的长为半径的圆上． 5．AD AD ，AC AC ︵，CD ︵ ADC ︵，CAD ︵6．B [解析] 图中的弦有AB ，BC ，CE ，共3条．7．A [解析] 等弧是完全重合的弧，故①③错误；直径把圆分成两条相等的弧，即两个半圆，故②错误；半径相等的圆可以完全重合，是等圆，故④正确；直径是圆中最长的弦，故⑤正确．故选A .8．0＜AB ≤69．证明：∵OA ，OB 为⊙O 的半径，∴OA ＝OB. ∵C ，D 分别为OA ，OB 的中点， ∴OC ＝OD.在△AOD 和△BOC 中，∵⎩⎨⎧OA ＝OB ，∠O ＝∠O ，OD ＝OC ，∴△AOD ≌△BOC(SAS )， ∴AD ＝BC.10．证明：∵OA ＝OB ， ∴∠A ＝∠B.在△OAC 和△OBD 中，∵⎩⎨⎧OA ＝OB ，∠A ＝∠B ，AC ＝BD ，∴△OAC ≌△OBD(SAS )． 11．B [解析]∵OA ＝OC ， ∴∠CAO ＝∠ACO.∵AD ∥OC ，∴∠DAC ＝∠ACO ， ∴∠DAC ＝∠CAO.∵∠DAB ＝60°，∴∠DAC ＝12∠DAB ＝30°.12．C [解析] 连接OP.∵四边形PCOD 是矩形，∴PC ＝OD ，∴PC 2＋PD 2＝OD 2＋PD 2＝OP 2，为一定值．故选C .13．B [解析] 设OP 与⊙O 交于点N ，连接MN ，OQ ，如图．∵OP ＝4，ON ＝2，∴N 是OP 的中点．又∵M 是PQ 的中点， ∴MN 为△POQ 的中位线， ∴MN ＝12OQ ＝12×2＝1，∴点M 在以点N 为圆心，1为半径的圆上， ∴当点M 在ON 上时，OM 的值最小，最小值为1. 故选B .14．20 [解析]∵CB ＝CD ，∴∠B ＝∠CDB. ∵∠B ＋∠CDB ＋∠BCD ＝180°，∴∠B ＝12(180°－∠BCD)＝12(180°－40°)＝70°.又∵∠ACB ＝90°，∴∠A ＝90°－∠B ＝20°.15．OH OE [解析] 连接OH ，OE ，如图所示．∵在矩形OGHI 和正方形ODEF 中，IG ＝OH ，OE ＝FD ，又∵OH ＝OE ， ∴IG ＝FD.16．1 [解析]∵⊙O 1与⊙O 2是等圆，∴r 1＝r 2，即方程x 2－ax ＋14＝0有两个相等的实数根，∴Δ＝b 2－4ac ＝a 2－4×14＝0，即a 2＝1，∴a ＝±1.又∵r 1＝r 2>0，a ＝r 1＋r 2，∴a ＝1， ∴a 2019＝12019＝1.17．解：OE ＝OF.证明：连接OA ，OB. ∵OA ＝OB ，∴∠A ＝∠B. 又∵AE ＝BF ， ∴△OAE ≌△OBF ， ∴OE ＝OF.18．解：(1)连接OQ.∵PQ ∥AB ，PQ ⊥OP ，∴OP ⊥AB. ∵AB ＝6，∴OB ＝3. ∵∠ABC ＝30°， ∴PB ＝2OP.在Rt △PBO 中，由勾股定理，得PB 2＝OP 2＋OB 2. 设OP ＝x ，则PB ＝2x ，则(2x)2＝x 2＋32，解得x ＝3(负值已舍去)，∴OP ＝ 3.在Rt △OPQ 中，由勾股定理，得PQ ＝OQ 2－OP 2＝32－（3）2＝ 6. (2)连接OQ ，由勾股定理得 PQ ＝OQ 2－OP 2＝9－OP 2.要使PQ 取最大值，需OP 取最小值，此时OP ⊥BC. ∵∠ABC ＝30°， ∴OP ＝12OB ＝32，此时PQ 最大值＝9－94＝323.24.1.2 垂直于弦的直径知识点 1 圆的对称性1．下列说法中，不正确的是( ) A ．圆既是轴对称图形，又是中心对称图形 B ．圆绕着它的圆心旋转任意角度，都会与自身重合 C ．圆的对称轴有无数条，对称中心只有一个 D ．圆的每一条直径都是它的对称轴知识点 2 垂径定理2．如图24－1－14，AB 是⊙O 的直径，弦CD ⊥AB ，垂足为M ，下列结论不成立的是( )图24－1－14A ．CM ＝DM B.CB ︵＝DB ︵C ．∠ACD ＝∠ADC D ．OM ＝MB3．如图24－1－15所示，⊙O 的半径为13，弦AB 的长度是24，ON ⊥AB ，垂足为N ，则ON 的长度为( )图24－1－15A ．5B ．7C ．9D ．114．2017·泸州如图24－1－16，AB 是⊙O 的直径，弦CD ⊥AB 于点E ，若AB ＝8，AE＝1，则弦CD的长是()图24－1－16A.7B．27C．6 D．85．2017·金华如图24－1－17，在半径为13 cm的圆形铁片上切下一块高为8 cm的弓形铁片，则弓形弦AB的长为()图24－1－17A．10 cm B．16 cm C．24 cm D．26 cm6．2017·长沙如图24－1－18，AB为⊙O的直径，弦CD⊥AB于点E，已知CD＝6，EB＝1，则⊙O的半径为________．图24－1－187．2016·宿迁如图24－1－19，在△ABC中，已知∠ACB＝130°，∠BAC＝20°，BC ＝2，以点C为圆心，CB为半径的圆交AB于点D，则BD的长为________．图24－1－198．如图24－1－20，两个圆都以点O为圆心，大圆的弦AB交小圆于C，D两点．求证：AC＝BD.图24－1－209．如图24－1－21，已知AB，CD是⊙O的两条弦，OE⊥AB于点E，OF⊥CD于点F，OE＝OF.求证：AB＝CD.图24－1－21知识点3垂径定理的推论10．下列说法正确的是()A．垂直于弦的直线平分弦所对的两条弧B．平分弦的直径垂直于弦C．垂直于直径的弦平分这条直径D．弦的垂直平分线经过圆心11．如图24－1－22所示，⊙O的直径CD＝10 cm，AB是⊙O的弦，AM＝BM，OM∶OC＝3∶5，则AB的长为()图24－1－22A．8 cm B.91cmC．6 cm D．2 cm12．如图24－1－23所示，AB是⊙O的直径，∠BAC＝42°，D是弦AC的中点，则∠DOC＝________°.图24－1－2313．2017·西宁如图24－1－24，AB是⊙O的直径，弦CD交AB于点P，AP＝2，BP ＝6，∠APC＝30°，则CD的长为()图24－1－24A.15B．2 5C．2 15D．814．已知⊙O的半径为13 cm，弦AB∥CD，AB＝24 cm，CD＝10 cm，则AB与CD之间的距离为()A．17 cm B．7 cmC．12 cm D．17 cm或7 cm15．如图24－1－25，AB是⊙O的弦，AB的长为8，P是⊙O上一个动点(不与点A，B重合)，过点O作OC⊥AP于点C，OD⊥PB于点D，则CD的长为________．图24－1－2516．如图24－1－26，⊙O的直径为10 cm，弦AB＝8 cm，P是弦AB上的一个动点，则OP长的取值范围是________________．图24－1－2617．如图24－1－27，点A，B，C，D在⊙O上，AB是⊙O的直径，BE＝CE.(1)请写出四个不同类型的正确结论；(2)若BE＝4，AC＝6，求DE的长．图24－1－2718．如图24－1－28，一条公路的转弯处是一段圆弧AB ︵.(1)用直尺和圆规作出AB ︵所在圆的圆心O (要求保留作图痕迹，不写作法)； (2)若AB ︵的中点C 到弦AB 的距离为20 m ，AB ＝80 m ，求AB ︵所在圆的半径．图24－1－2819．有一石拱桥的桥拱是圆弧形，如图24－1－29所示，正常水位下水面宽AB＝60 m，水面到拱顶距离CD＝18 m，当洪水泛滥，水面到拱顶距离为3.5 m时需要采取紧急措施，当水面宽MN＝32 m时，是否需要采取紧急措施？请说明理由．图24－1－29教师详解详析1．D2．D [解析]∵AB 是⊙O 的直径，弦CD ⊥AB ，垂足为M ，∴M 为CD 的中点，即CM ＝DM ，选项A 成立．由已知得B 为CD ︵的中点，即CB ︵＝DB ︵，选项B 成立．在△ACM 和△ADM 中，∵AM ＝AM ，∠AMC ＝∠AMD ＝90°，CM ＝DM ，∴△ACM ≌△ADM ，∴∠ACD ＝∠ADC ，选项C 成立．而OM 与MB 不一定相等，选项D 不成立．故选D .3．A [解析] 因为ON ⊥AB ，所以AN ＝12AB ＝12×24＝12，∠ANO ＝90°.在Rt △AON中，由勾股定理，得ON ＝OA 2－AN 2＝132－122＝5.故选A .4．B [解析] 连接OC ，则OC ＝4，OE ＝3，在Rt △OCE 中，CE ＝OC 2－OE 2＝42－32＝7.因为CD ⊥AB ，所以CD ＝2CE ＝2 7.5．C [解析] 如图，过点O 作OD ⊥AB 于点C ，交⊙O 于点D. ∵CD ＝8 cm ，OD ＝13 cm ， ∴OC ＝5 cm . 又∵OB ＝13 cm ，在Rt △BCO 中，根据勾股定理，得BC ＝OB 2－OC 2＝132－52＝12(cm ) .∵OC ⊥AB ， ∴AB ＝2BC ＝24 cm .6．5 [解析] 如图，连接OC ， ∵AB 为⊙O 的直径，CD ⊥AB ，∴CE ＝DE ＝12CD ＝12×6＝3.设⊙O 的半径为x ，则OC ＝x ，OE ＝OB －BE ＝x －1. 在Rt △OCE 中，OC 2＝OE 2＋CE 2，即x 2＝(x －1)2＋32，解得x ＝5， ∴⊙O 的半径为5.7．2 3 [解析] 如图，作CE ⊥AB 于点E.∠B ＝180°－∠BAC －∠ACB ＝180°－20°－130°＝30°.在Rt △BCE 中，∵∠CEB ＝90°，∠B ＝30°，BC ＝2， ∴CE ＝12BC ＝1，BE ＝BC 2－CE 2＝ 3.∵CE ⊥BD ，∴BD ＝2BE ＝2 3.8．证明：过点O 作OH ⊥AB 于点H ，如图，则AH ＝BH ，CH ＝DH ，∴AH －CH ＝BH －DH ，即AC ＝BD.9．证明：∵OE ⊥AB ，OF ⊥CD ， ∴AE ＝BE ，CF ＝DF.在Rt △OBE 与Rt △ODF 中，∵⎩⎨⎧OB ＝OD ，OE ＝OF ，∴Rt △OBE ≌Rt △ODF(HL )，∴BE ＝DF ，∴2BE ＝2DF ，即AB ＝CD. 10．D11．A [解析] 如图所示，连接OA. ∵⊙O 的直径CD ＝10 cm ，∴⊙O 的半径为5 cm ，即OA ＝OC ＝5 cm . ∵OM ∶OC ＝3∶5，∴OM ＝3 cm . ∵AM ＝BM ，∴AB ⊥CD.在Rt △AOM 中，AM ＝52－32＝4(cm )， ∴AB ＝2AM ＝2×4＝8(cm )．故选A .12．48 [解析]∵AD ＝CD ，∴OD ⊥AC. ∴∠CDO ＝90°，∴∠DOC ＋∠ACO ＝90°. ∵OA ＝OC ，∴∠ACO ＝∠A ＝42°， ∴∠DOC ＝90°－∠ACO ＝48°.13．C [解析] 作OH ⊥CD 于点H ，连接OC ，如图， ∵OH ⊥CD ，∴HC ＝HD.∵AP ＝2，BP ＝6，∴AB ＝8，∴OA ＝4， ∴OP ＝OA －AP ＝2.在Rt △OPH 中，∵∠OPH ＝30°， ∴OH ＝12OP ＝1.在Rt △OHC 中，∵OC ＝OA ＝4，OH ＝1， ∴CH ＝OC 2－OH 2＝15， ∴CD ＝2CH ＝2 15.14．D [解析]①当弦AB 和CD 的位置如图①所示时，过点O 作OE ⊥AB 于点E ，延长OE 交CD 于点F ，则OF ⊥CD. ∵AB ＝24 cm ，CD ＝10 cm ， ∴AE ＝12 cm ，CF ＝5 cm . ∵OA ＝OC ＝13 cm ， ∴OE ＝5 cm ，OF ＝12 cm ， ∴EF ＝12－5＝7(cm )．②当弦AB 和CD 的位置如图②所示时，过点O 作OE ⊥AB 于点E ，延长EO 交CD 于点F ，则OF ⊥CD.∵AB ＝24 cm ，CD ＝10 cm ， ∴AE ＝12 cm ，CF ＝5 cm . ∵OA ＝OC ＝13 cm ， ∴OE ＝5 cm ，OF ＝12 cm ， ∴EF ＝OF ＋OE ＝17(cm )．∴AB 与CD 之间的距离为7 cm 或17 cm . 15. 4 [解析]∵OC ⊥AP ，OD ⊥PB ， ∴AC ＝PC ，PD ＝BD ， ∴CD 是△ABP 的中位线． ∵AB 的长为8， ∴CD ＝12AB ＝4.16．3 cm ≤OP ≤5 cm [解析] 作直径MN ⊥弦AB ，垂足为D.由垂径定理，得AD ＝DB ＝12AB ＝4 cm .由⊙O 的直径为10 cm ，连接OA ，可得OA ＝5 cm . 由勾股定理，得OD ＝OA 2－AD 2＝3 cm . ∵垂线段最短，半径最长，∴OP 长的取值范围是3 cm ≤OP ≤5 cm .17．解：(1)不同类型的正确结论有：BE ＝12BC ，BD ︵＝CD ︵，BD ＝CD ，OD ⊥BC ，△BOD是等腰三角形，△BDE ≌△CDE ，OB 2＝OE 2＋BE 2等(答案不唯一，合理即可)．(2)∵AB 是⊙O 的直径，∴OA ＝OB.∵BE ＝CE ，∴OD ⊥BC ，OE 为△ABC 的中位线， ∴OE ＝12AC ＝12×6＝3.在Rt △OBE 中，由勾股定理，得 OB ＝OE 2＋BE 2＝32＋42＝5， ∴OD ＝OB ＝5，∴DE ＝OD －OE ＝5－3＝2.18．解：(1)如图①，连接AC ，BC ，作线段AC ，BC 的垂直平分线交于点O ，点O 即为所求．(2)如图②，连接OA ，AB ，OC ，OC 交AB 于点D.∵C 为AB ︵的中点，∴OC ⊥AB ， ∴AD ＝BD ＝12AB ＝40 m .设⊙O 的半径为r m ，则OA ＝r m ，OD ＝OC －CD ＝(r －20)m . 在Rt △OAD 中，∵OA 2＝OD 2＋AD 2， ∴r 2＝(r －20)2＋402，解得r ＝50. 即AB ︵所在圆的半径是50 m .19．解：不需要采取紧急措施．理由：∵CD 为弓形的高，∴AB ︵所在圆的圆心在直线CD 上．设圆心为O ，连接OA ，OC ，OM.设OA ＝R m ，在Rt △AOC 中，AC ＝12AB ＝30 m ，OC ＝OD －CD ＝(R －18)m ，∴R 2＝302＋(R －18)2，解得R ＝34.设CD 交MN 于点E ，DE ＝x m ，在Rt △MOE 中，ME ＝12MN ＝16 m ，OE ＝OD －DE＝(34－x)m ，∴342＝162＋(34－x)2，即x 2－68x ＋256＝0，解得x 1＝4，x 2＝64(不合题意，舍去)， ∴DE ＝4 m ．∵4 m ＞3.5 m ， ∴不需要采取紧急措施．24.1.3 弧、弦、圆心角知识点 1 圆心角的概念及其计算1．下面四个图中的角，是圆心角的是( )图24－1－302．如图24－1－31，已知AB 为⊙O 的直径，点D 为半圆周上的一点，且AD ︵所对圆心角的度数是BD ︵所对圆心角度数的2倍，则圆心角∠BOD ＝________°.图24－1－313．在半径为2的⊙O 中，弦AB 的长为2，则弦AB 所对的圆心角的度数为________．知识点 2 弧、弦、圆心角之间的关系4．如图24－1－32，AB ，CD 是⊙O 的两条弦． (1)∵∠AOB ＝∠COD ，∴________，________． (2)∵AB ︵＝CD ︵，∴____________，____________． (3)∵AB ＝CD ，∴____________，____________．图24－1－325．已知：如图24－1－33，AB 是⊙O 的直径，C ，D 是BE ︵的三等分点，∠AOE ＝60°，则∠COE 等于( )图24－1－33A ．40°B ．60°C ．80°D ．120°6．如图24－1－34，AB 是⊙O 的直径，BC ，CD ，DA 是⊙O 的弦，且BC ＝CD ＝DA ，则∠B 等于( )图24－1－34A ．50°B ．60°C ．70°D ．80°7．如图24－1－35，在⊙O 中，C 是AB ︵的中点，∠A ＝50°，则∠BOC ＝________°.图24－1－358．如图24－1－36所示，在⊙O 中，弦AB 与弦CD 相等．求证：AD ︵＝BC ︵.图24－1－369．已知：如图24－1－37，在⊙O 中，AB ︵＝CD ︵，则下列结论：①AB ＝CD ；②AC ＝BD ；③∠AOC ＝∠BOD ；④AC ︵＝BD ︵.其中正确的有( )图24－1－37A ．1个B ．2个C ．3个D ．4个10．如图24－1－38所示，在⊙O 中，如果AB ︵＝2AC ︵，那么( )图24－1－38A ．AB ＝AC B ．AB ＝2AC C ．AB <2ACD ．AB >2AC11．如图24－1－39，已知在△ABC 中，∠ACB ＝90°，∠B ＝35°，以点C 为圆心，CA 长为半径的圆交AB 于点D ，则AD ︵所对的圆心角为________度．图24－1－3912．如图24－1－40所示，A ，B 是半径为3的⊙O 上的两点，若∠AOB ＝120°，C 是AB ︵的中点，则四边形AOBC 的周长等于________．图24－1－4013．2017·牡丹江如图24－1－41，在⊙O 中，AC ︵＝CB ︵，CD ⊥OA 于点D ，CE ⊥OB 于点E .求证：AD ＝BE .图24－1－4114．如图24－1－42，AB，CD是⊙O的两条直径，过点A作AE∥CD交⊙O于点E，连接BD，DE.求证：BD＝DE.图24－1－4215．已知：如图24－1－43，在⊙O 中，M ，N 分别是半径OA ，OB 的中点，且CM ⊥OA ，DN ⊥OB .求证：AC ︵＝BD ︵.图24－1－4316．如图24－1－44所示，∠AOB ＝90°，C ，D 是AB ︵的三等分点，AB 与OC ，OD 分别交于点E ，F .求证：AE ＝BF ＝CD .图24－1－44教师详解详析1．D [解析]∵圆心角的顶点必须在圆心， ∴选项A ，B ，C 均不对．故选D . 2．603．60° [解析] 如图，连接OA ，OB.∵OA ＝OB ＝AB ＝2，∴△OAB 是等边三角形，∴∠AOB ＝60°. 故弦AB 所对的圆心角的度数为60°. 4．(1)AB ︵＝CD ︵AB ＝CD (2)∠AOB ＝∠COD AB ＝CD (3)∠AOB ＝∠COD AB ︵＝CD ︵5．C [解析]∵C ，D 是BE ︵的三等分点， ∴BC ︵＝CD ︵＝DE ︵，∴∠BOC ＝∠COD ＝∠DOE.∵∠AOE ＝60°，∴∠BOC ＝∠COD ＝∠DOE ＝13(180°－∠AOE)＝13(180°－60°)＝40°，∴∠COE ＝80°.6．B [解析] 连接OC ，OD.∵BC ＝CD ＝DA ，∴∠BOC ＝∠COD ＝∠AOD ＝13×180°＝60°，∴△OBC ，△OCD ，△AOD 都是等边三角形，∴∠B ＝60°.7．40 [解析]∵在⊙O 中，OA ＝OB ，∠A ＝50°，∴∠B ＝50°， ∴∠AOB ＝180°－∠A －∠B ＝80°.∵C 是AB ︵的中点， ∴∠BOC ＝12∠AOB ＝40°.8．证明：∵AB ＝CD ，∴AB ︵＝CD ︵， ∴AB ︵－DB ︵＝CD ︵－DB ︵，即AD ︵＝BC ︵.9．D [解析]∵AB ︵＝CD ︵，根据同弧所对的弦相等，∴AB ＝CD ，故①正确．∵AB ︵－CB ︵＝CD ︵－CB ︵，∴AC ︵＝BD ︵，故④正确．根据同弧所对的弦、圆心角都相等，得②③正确．10．C [解析] 取AB ︵的中点D ，连接AD ，BD ，则AD ︵＝BD ︵＝AC ︵，∴AD ＝BD ＝AC.又∵在△ABD 中，AB ＜AD ＋BD ，∴AB ＜2AC.11．7012．12 [解析]∵C 是AB ︵的中点，∴∠AOC ＝∠BOC.又∵∠AOB ＝120°，∴∠AOC ＝∠BOC ＝60°，∴△AOC 和△BOC 都是等边三角形，∴OA ＝OB ＝CA ＝CB ＝3，∴四边形AOBC 的周长等于12.13．证明：连接OC ，∵AC ︵＝CB ︵， ∴∠AOC ＝∠BOC.∵CD ⊥OA 于点D ，CE ⊥OB 于点E ， ∴∠CDO ＝∠CEO ＝90°. 在△COD 与△COE 中，∵⎩⎨⎧∠DOC ＝∠EOC ，∠CDO ＝∠CEO ，CO ＝CO ，∴△COD ≌△COE(AAS )， ∴OD ＝OE. ∵AO ＝BO ，∴AO －OD ＝BO －OE ，即AD ＝BE. 14．证明：如图，连接OE.∵OA ＝OE ，∴∠A ＝∠OEA. ∵AE ∥CD ，∴∠BOD ＝∠A ，∠DOE ＝∠OEA ， ∴∠BOD ＝∠DOE ，∴BD ＝DE. 15．证明：连接OC ，OD ，则OC ＝OD.∵M ，N 分别是半径OA ，OB 的中点， ∴OM ＝ON.∵CM ⊥OA ，DN ⊥OB ， ∴∠OMC ＝∠OND ＝90°. 在Rt △OMC 和Rt △OND 中，⎩⎨⎧OM ＝ON ，OC ＝OD ，∴Rt △OMC ≌Rt △OND(HL )， ∴∠MOC ＝∠NOD ，∴AC ︵＝BD ︵. 16．证明：连接AC ，BD. ∵C ，D 是AB ︵的三等分点，∴AC ＝CD ＝BD ，且∠AOC ＝13×90°＝30°.∵OA ＝OC ，∴∠OAC ＝∠OCA ＝75°. ∵∠AOB ＝90°，OA ＝OB ， ∴∠OAE ＝∠OBF ＝45°，∴∠AEC ＝∠OAE ＋∠AOC ＝45°＋30°＝75°， ∴AE ＝AC.同理可证BF ＝BD ，∴AE ＝BF ＝CD.24.1.4 圆周角知识点 1 圆周角的概念1．下列四个图中，∠α是圆周角的是( )图24－1－452．如图24－1－46，图中有多少个圆周角？BC ︵所对的圆周角有几个？CD ︵所对的圆周角有几个？图24－1－46知识点 2 圆周角定理3．2017·徐州如图24－1－47，点A ，B ，C 在⊙O 上，∠AOB ＝72°，则∠ACB 等于( )图24－1－47A ．28°B ．54°C ．18°D ．36°4．如图24－1－48所示，把一个量角器放置在△ABC 的上面，根据量角器的读数可得∠BAC 的度数是( )图24－1－48A ．60°B ．30°C ．20°D ．15°5．如图24－1－49，A ，B ，P 是半径为2的⊙O 上的三点，∠APB ＝45°，则弦AB 的长为( )图24－1－49A.2B ．2 C ．2 2D ．46．2017·义乌如图24－1－50，一块含45°角的三角尺，它的一个锐角顶点A 在⊙O 上，边AB ，AC 分别与⊙O 交于点D ，E ，则∠EOD ＝________°.图24－1－50知识点 3 圆周角定理的推论7．如图24－1－51，在⊙O 中，AB ︵＝AC ︵，∠BAC ＝50°，则∠AEC 的度数为( )图24－1－51A ．50°B ．55°C ．65°D ．75°8．如图24－1－52，已知AB 是⊙O 的直径，点C 在⊙O 上，若∠CAB ＝40°，则∠ABC ＝________°.图24－1－529．2017·湖州如图24－1－53，已知在△ABC 中，AB ＝AC .以AB 为直径作半圆O ，交BC 于点D .若∠BAC ＝40°，则AD ︵的度数是________度．图24－1－5310．如图24－1－54所示，已知四边形ABCD 的四个顶点均在⊙O 上，AB ＝BC ，BD 交AC 于点E .求证：DB 平分∠ADC .图24－1－54知识点4圆内接多边形11．2017·淮安如图24－1－55，在圆内接四边形ABCD中，若∠A，∠B，∠C的度数之比为4∶3∶5，则∠D的度数是________°.图24－1－5512．如图24－1－56所示，四边形ABCD内接于⊙O，∠B＝50°，∠ACD＝25°，∠BAD＝65°.求证：(1)AD＝CD；(2)AB是⊙O的直径．图24－1－5613．2017·云南如图24－1－57，B，C是⊙A上的两点，AB的垂直平分线与⊙A交于E，F两点，与线段AC交于点D.若∠BFC＝20°，则∠DBC＝()图24－1－57A．30°B．29°C．28°D．20°14．2017·西宁如图24－1－58，四边形ABCD内接于⊙O，点E在BC的延长线上，若∠BOD＝120°，则∠DCE＝________°.图24－1－5815．如图24－1－59，一块三角尺ABC的斜边AB与量角器的直径恰好重合，点D对应的刻度是58°，则∠ACD＝________°.图24－1－5916．已知：如图24－1－60，AB为⊙O的直径，AB＝AC，BC交⊙O于点D，AC交⊙O 于点E，∠BAC＝45°.(1)求∠EBC的度数；(2)求证：BD＝CD.图24－1－6017．如图24－1－61，AB 是⊙O 的直径，C 为AE ︵的中点，CD ⊥AB 于点D ，交AE 于点F ，连接AC .求证：AF ＝CF .图24－1－6118．2017·六盘水如图24－1－62，MN 是⊙O 的直径，MN ＝4，点A 在⊙O 上，∠AMN＝30°，B 为AN ︵的中点，P 是直径MN 上一动点．(1)利用尺规作图，确定当P A ＋PB 最小时点P 的位置(不写作法，但要保留作图痕迹)； (2)求P A ＋PB 的最小值．图24－1－62教师详解详析1．C [解析] 根据圆周角的定义，顶点在圆上，可排除选项D .根据两边都与圆相交可排除选项A ，B .故选C .2．解：图中有8个圆周角，BC ︵所对的圆周角有1个，是∠BDC ；CD ︵所对的圆周角有2个，分别是∠CBD ，∠CAD.3．D [解析] 根据同弧所对的圆周角等于圆心角的一半，得∠ACB ＝12∠AOB ＝12×72°＝36°.4．D5．C [解析] 如图，连接OA ，OB.因为∠APB 和∠AOB 分别是AB ︵所对的圆周角和圆心角，所以∠AOB ＝2∠APB ＝2×45°＝90°.在Rt △AOB 中，OA ＝OB ＝2，由勾股定理，得AB ＝2 2.故选C .6．90 [解析]∠EOD ＝2∠A ＝2×45°＝90°.7．C [解析]∵AB ︵＝AC ︵，∴AB ＝AC.∵∠BAC ＝50°，∴∠ABC ＝12(180°－50°)＝65°，∴∠AEC ＝∠ABC ＝65°.故选C .8．50 [解析]∵AB 是⊙O 的直径，∴∠ACB ＝90°，∴∠ABC ＝90°－∠CAB ＝90°－40°＝50°.9．140 [解析] 连接AD ，OD.∵AB 为圆的直径，∴∠ADB ＝90°.又∵AB ＝AC ，∠BAC ＝40°，根据“等腰三角形三线合一”得到AD 平分∠BAC ，∴∠OAD ＝20°.又∵OA ＝OD ，∴∠BOD ＝2∠OAD ＝40°，∴∠AOD ＝140°.即AD ︵的度数是140度．10．证明：∵AB ＝BC ，∴AB ︵＝BC ︵，∴∠ADB ＝∠BDC ，即DB 平分∠ADC.11．120 [解析] 因为四边形ABCD 是⊙O 的内接四边形，所以∠A ＋∠C ＝∠B ＋∠D ＝180°.因为∠A ，∠B ，∠C 的度数之比为4∶3∶5，所以∠A ，∠B ，∠C ，∠D 的度数之比为4∶3∶5∶6，所以∠D ＝63＋6×180°＝120°.12．证明：(1)∵四边形ABCD 内接于⊙O ， ∴∠D ＝180°－∠B ＝130°. 又∵∠ACD ＝25°，∴∠DAC ＝180°－∠D －∠ACD ＝180°－130°－25°＝25°， ∴∠DAC ＝∠ACD ，∴AD ＝CD.(2)∵∠BAC ＝∠BAD －∠DAC ＝65°－25°＝40°，∠B ＝50°， ∴∠ACB ＝180°－∠B －∠BAC ＝180°－50°－40°＝90°， ∴AB 是⊙O 的直径．13．A [解析]∵∠BFC ＝20°， ∴∠BAC ＝2∠BFC ＝40°. ∵AB ＝AC ，∴∠ABC ＝∠ACB ＝180°－40°2＝70°.又∵EF 是线段AB 的垂直平分线， ∴AD ＝BD ，∴∠A ＝∠ABD ＝40°，∴∠DBC ＝∠ABC －∠ABD ＝70°－40°＝30°. 故选A .14．60 [解析]∵∠BOD ＝120°，∴∠BAD ＝60°.又∵∠BAD ＋∠BCD ＝180°，∠DCE ＋∠BCD ＝180°，∴∠DCE ＝∠BAD ＝60°.15．61 [解析] 设AB 的中点为O ，连接OD.∵三角尺ABC 的斜边AB 与量角器的直径恰好重合，∴点C 在以AB 为直径的圆上．∵点D 对应的刻度是58°，∴∠DCB ＝12×58°＝29°，∴∠ACD ＝90°－29°＝61°.16．解：(1)∵AB 是⊙O 的直径， ∴∠AEB ＝90°.又∵∠BAC ＝45°，∴∠ABE ＝45°. ∵AB ＝AC ，∴∠ABC ＝∠C ＝67.5°，∴∠EBC ＝∠ABC －∠ABE ＝67.5°－45°＝22.5°. (2)证明：连接AD. ∵AB 是⊙O 的直径， ∴∠ADB ＝90°，∴AD ⊥BC. 又∵AB ＝AC ， ∴BD ＝CD.17．证明：如图，连接BC.∵AB 是⊙O 的直径， ∴∠ACB ＝90°，即∠ACF ＋∠BCD ＝90°.∵CD ⊥AB ，∴∠B ＋∠BCD ＝90°， ∴∠ACF ＝∠B. ∵C 为AE ︵的中点，∴AC ︵＝CE ︵， ∴∠B ＝∠CAE ， ∴∠ACF ＝∠CAE ， ∴AF ＝CF.18．[解析] (1)画出点A 关于MN 的对称点A′，连接A′B ，与MN 的交点即为点P. (2)利用∠AMN ＝30°得∠AON ＝∠A′ON ＝60°，又由B 为AN ︵的中点，可得∠BON ＝30°，∴∠A ′OB ＝90°，再由勾股定理求得PA ＋PB 的最小值为2 2.解：(1)如图，点P 即为所求．(2)如图，连接OA ，OA ′，OB.由(1)可得，PA ＋PB 的最小值即为线段A′B 的长．∵点A′和点A 关于MN 对称且∠AMN ＝30°，∴∠AON ＝∠A′ON ＝2∠AMN ＝60°.又∵B 为AN ︵的中点，∴∠BON ＝12∠AON ＝30°，∴∠A ′OB ＝90°.∵MN ＝4，∴OB ＝OA ′＝2.在Rt △A ′OB 中，由勾股定理得A ′B ＝22＋22＝2 2.∴PA ＋PB 的最小值是2 2.。

人教版九年级数学上册第24章24.1《圆的基本性质》同步练习及答案(2).docx

初中数学试卷桑水出品24.1 圆（第三课时）--------- 弧、弦、圆心角知识点1、圆心角定义：顶点在的角叫做圆心角2、定理：在同圆或等圆中，两个圆心角、两条弧、两条弦中有一组量，它们所对应的其余各组量也分别。

一、选择题1．如果两个圆心角相等，那么（）A ．这两个圆心角所对的弦相等;B ．这两个圆心角所对的弧相等C ．这两个圆心角所对的弦的弦心距相等;D ．以上说法都不对2.下列语句中不正确的有（）①相等的圆心角所对的弧相等 ②平分弦的直径垂直于弦 ③圆是轴对称图形，任何一条直径所在直线都是它的对称轴 ④长度相等的两条弧是等弧A.3个B.2个C.1个D.以上都不对3.已知、是同圆的两段弧，且=2，则弦AB 与CD 之间的关系为（）A.AB=2CDB.AB<2CDC.AB>2CDD.不能确定4. 如图，AB 是 ⊙O 的直径，C ，D 是»BE上的三等分点，∠AOE=60°，则∠COE 是（） A ． 40° B. 60° C. 80° D. 120 °OED C B A5、如图，半圆O 的直径AB=10cm ，弦AC=6cm ，AD 平分∠BAC ，则AD 的长为（）A ． cmB ． cmC ． cmD ． 4cmA.4B.82C.24D.16 二、填空题 1.已知圆O 的半径为5,弦AB 的长为5,则弦AB 所对的圆心角∠AOB = .2. 如图，AB 是 ⊙O 的直径，BC⌒ =BD ⌒ ,∠A=25°，则∠BOD= . OD CBA3.在⊙O 中，弦AB 所对的劣弧为圆周的41，圆的半径等于12，则圆心角∠AOB ＝；弦AB 的长为 . 4.如图，在⊙O 中，»»AB AC ，∠B =70°，则∠A 等于．CB AO5．如图，AB 和DE 是⊙O 的直径，弦AC ∥DE ，若弦BE=3，则弦CE=___ _____．O BACE D6. 等腰△ABC 的顶角∠A ＝120°，腰AB ＝AC ＝10，△ABC 的外接圆半径等于 .CO BA三、解答题1、如图，在⊙O 中 ,AB =AC ,∠ACB=60°，求证∠AOB ＝∠BOC ＝∠AOC .2、如图，在⊙O中，AB、CD是两条弦，OE⊥AB，OF⊥CD，垂足分别为EF．（1）如果∠AOB=∠COD，那么OE与OF的大小有什么关系？为什么？（2）如果OE=OF，那么»AB与»CD的大小有什么关系？AB与CD的大小有什么关系？为什么？∠AOB与∠COD呢？D3．如图，在⊙O中，C、D是直径AB上两点，且AC=BD，MC⊥AB，ND⊥AB，M、N•在⊙O上．（1）求证：¼AM=»BN；（2）若C、D分别为OA、OB中点，则¼¼»AM MN NB==成立吗？BA4．如图，∠AOB=90°，C、D是AB三等分点，AB分别交OC、OD于点E、F，求证：AE=BF=CD．OFE DC5、如图，以⊙O的直径BC为一边作等边△ABC,AB、AC交⊙O于D、E,求证：BD=DE=EC24.1 圆（第三课时）--------- 弧、弦、圆心角知识点1.圆心2.相等相等一、选择题1．D2.C 下列语句中不正确的有（）①相等的圆心角所对的弧相等 ②平分弦的直径垂直于弦 ③圆是轴对称图形，任何一条直径所在直线都是它的对称轴 ④长度相等的两条弧是等弧A.3个B.2个C.1个D.以上都不对3.B 已知、是同圆的两段弧，且=2，则弦AB 与CD 之间的关系为（）A.AB=2CDB.AB<2CDC.AB>2CDD.不能确定4. C 如图，AB 是 ⊙O 的直径，C ，D 是»BE上的三等分点，∠AOE=60°，则∠COE 是（） A ． 40° B. 60° C. 80° D. 120 °O E D C B A5、A6.B 二、填空题1. 60°2.50°3.90°, 122 .4. 40° ．5．36. 10三、解答题1∠︒∴∴∴∠∠∠Q V 、证明：AB=AC,ACB=60ABC 是等边三角形AB=AC=BCAOB=AOC=BOC2、D解：（1）如果∠AOB=∠COD ，那么OE=OF理由是：∵∠AOB=∠COD∴AB=CD∵OE ⊥AB ，OF ⊥CD∴AE=12AB ，CF=12CD ∴AE=CF又∵OA=OC∴Rt △OAE ≌Rt △OCF∴OE=OF（2）如果OE=OF ，那么AB=CD ，»AB =»CD ，∠AOB=∠COD 理由是：∵OA=OC ，OE=OF∴Rt △OAE ≌Rt △OCF∴AE=CF又∵OE ⊥AB ，OF ⊥CD∴AE=12AB ，CF=12CD ∴AB=2AE ，CD=2CF∴AB=CD∴»AB =»CD ，∠AOB=∠COD3．（1）连结OM 、ON ，在Rt △OCM 和Rt △ODN 中OM=ON ，OA=OB ，∵AC=DB ，∴OC=OD ，∴Rt △OCM ≌Rt △ODN ，∴∠AOM=∠BON ，∴¼»AM NB =（2）¼¼»AM MN NB ==BA4．AOFE DC连结AC 、BD ，∵C 、D 是»AB 三等分点， ∴AC=CD=DB ，且∠AOC=13×90°=30°， ∵OA=OC ，∴∠OAC=∠OCA=75°，又∠AEC=∠OAE+∠AOE=45°+30°=75°， ∴AE=AC ，同理可证BF=BD ，∴AE=BF=CD5,OEC ∴∠∠︒∴∴∠︒∠︒∴∠︒∠∠︒∴∠∠∠∴Q V Q V V 、证明：连接OD 、OEABC 是等边三角形B=C=60OB=OD,OE=OCOBD 是等边三角形是等边三角形BOD=60,EOC=60DOE=180-BOD-EOC=60BOD=DOE=EOCBD=DE=EC。

人教版九年级数学上册 24.1 圆的有关性质同步训练(含答案)

人教版九年级数学上册 24.1 圆的有关性质同步训练一、选择题 1. 2019·葫芦岛如图，在⊙O 中，∠BAC ＝15°，∠ADC ＝20°，则∠ABO 的度数为( )A ．70°B ．55°C ．45°D ．35°2. 如图，四边形ABCD 内接于⊙O ，F 是CD ︵上一点，且DF ︵＝BC ︵，连接CF 并延长交AD 的延长线于点E ，连接AC ，若∠ABC ＝105°，∠BAC ＝25°，则∠E 的度数为( )A . 45°B . 50°C . 55°D . 60°3. 与圆心的距离不大于半径的所有点组成的图形是()A ．圆的外部(包括边界)B ．圆的内部(不包括边界)C ．圆D ．圆的内部(包括边界)4. (2019•贵港)如图，AD 是O 的直径，AB CD =，若40AOB ∠=︒，则圆周角BPC ∠的度数是A ．40︒B ．50︒C ．60︒D ．70︒5. 如图，将半径为2的圆形纸片折叠后，圆弧恰好经过圆心O ，则折痕AB 的长为( )A. 5 B ．2 5 C ．3 D ．2 36. 2019·聊城如图，BC 是半圆O 的直径，D ，E 是BC ︵上的两点，连接BD ，CE并延长交于点A ，连接OD ，OE .如果∠A ＝70°，那么∠DOE 的度数为( )A ．35°B ．38°C ．40°D ．42°7. 如图，从A 地到B 地有两条路可走，一条路是大半圆，另一条路是4个小半圆．有一天，一只猫和一只老鼠同时从A 地到B 地．老鼠见猫沿着大半圆行走，它不敢与猫同行(怕被猫吃掉)，就沿着4个小半圆行走．假设猫和老鼠行走的速度相同，那么下列结论正确的是( )A ．猫先到达B 地 B ．老鼠先到达B 地C ．猫和老鼠同时到达B 地D ．无法确定8. 如图，已知⊙O 的半径为5，弦AB ，CD 所对的圆心角分别是∠AOB ，∠COD ，若∠AOB与∠COD 互补，弦CD ＝6，则弦AB 的长为( )A ．6B ．8C ．5 2D ．5 3二、填空题9. 如图，一下水管道横截面为圆形，直径为100 cm ，下雨前水面宽为60 cm ，一场大雨过后，水面宽为80 cm ，则水位上升了 cm .10. 2018·毕节如图，AB 是⊙O 的直径，C ，D 为半圆的三等分点，CE ⊥AB 于点E ，则∠ACE 的度数为________．11. 如图，已知等腰三角形ABC 中，∠ACB ＝120°且AC ＝BC ＝4，在平面内任作∠APB ＝60°，则BP 的最大值为________．12. (2019•娄底)如图，C 、D 两点在以AB 为直径的圆上，2AB =，30ACD ∠=︒，则AD =__________．13. 如图，以△ABC 的边BC 为直径的⊙O 分别交AB ，AC 于点D ，E ，连接OD ，OE .若∠A ＝65°，则∠DOE ＝________°.14. 如图，AB ，CD是半径为5的⊙O 的两条弦，AB ＝8，CD ＝6，MN 是⊙O 的直径，AB ⊥MN 于点E ，CD ⊥MN 于点F ，P 为EF 上的任意一点，则PA ＋PC 的最小值为________．15. 如图所示，在半圆O 中，AB为直径，P 为AB ︵的中点，分别在AP ︵和PB ︵上取其中点A 1和B 1，再在P A ︵1和PB ︵1上分别取其中点A 2和B 2.若一直这样取下去，则∠A n OB n ＝________°.16. 如图，定长弦CD 在以AB 为直径的⊙O 上滑动(点C ，D 与点A ，B 不重合)，M 是CD 的中点，过点C 作CP ⊥AB 于点P.若CD ＝3，AB ＝8，PM ＝l ，则l 的最大值是________．三、解答题17. 如图，AB 是⊙O 的直径，AC 是弦，将劣弧AC 沿弦AC 翻折与AB 的交点恰好是圆心O ，作OD ⊥AC ，垂足为E ，交⊙O 于点D ，连接BC ，CD .求证：四边形BCDO 是菱形．18. 如图，AB 为O 的直径，点C 在O 上．(1)尺规作图：作BAC 的平分线，与O 交于点D ；连接OD ，交BC 于点E (不写作法，只保留作图痕迹，且用黑色墨水笔将作图痕迹加黑)； (2)探究OE 与AC 的位置及数量关系，并证明你的结论．19. 如图，在⊙O 中，M ，N分别是半径OA ，OB 的中点，且CM ⊥OA 交⊙O 于点C ，DN ⊥OB 交⊙O 于点D .求证：AC ︵＝BD ︵.20. 2019·十堰改编如图，四边形ABCD 内接于⊙O ，AE ⊥CB 交CB 的延长线于点E .若BA 平分∠DBE ，AD ＝5，CE ＝13，求AE 的长度．21. 如图，已知△ABC内接于⊙O，点C在劣弧AB上(不与点A，B重合)，点D 为弦BC的中点，DE⊥BC，DE与AC的延长线交于点E.射线AO与射线EB交于点F，与⊙O交于点G.设∠GAB＝α，∠ACB＝β，∠EAG＋∠EBA＝γ.(1)点点同学通过画图和测量得到以下近似数据α30°40°50°60°β120°130°140°150°γ150°140°130°120°猜想：β关于α(2)若γ＝135°，CD＝3，△ABE的面积为△ABC的面积的4倍，求⊙O半径的长．人教版九年级数学上册 24.1 圆的有关性质同步训练-答案一、选择题 1. 【答案】B2. 【答案】B 【解析】∵四边形ABCD 是圆内接四边形，∠ABC ＝105°，∴∠ADC＝75°，∵＝，∴∠BAC ＝∠DCF ＝25°，∴∠E ＝∠ADC －∠DCF ＝50°.3. 【答案】D4. 【答案】B【解析】∵AB CD =，40AOB ∠=︒，∴40COD AOB ∠=∠=︒， ∵180AOB BOC COD ∠+∠+∠=︒，∴100BOC ∠=︒，∴1502BPC BOC ∠=∠=︒，故选B ．5. 【答案】D[解析] 如图，过点O 作OD ⊥AB 于点D ，连接OA .根据题意，得OD ＝12OA ＝1.再根据勾股定理，得AD ＝ 3.根据垂径定理，得AB ＝2 3.6. 【答案】C7. 【答案】C8. 【答案】B [解析] 如图，延长AO 交⊙O 于点E ，连接BE ，则∠AOB ＋∠BOE ＝180°. 又∵∠AOB ＋∠COD ＝180°， ∴∠BOE ＝∠COD ， ∴BE ＝CD ＝6.∵AE 为⊙O 的直径，∴∠ABE ＝90°， ∴AB ＝AE 2－BE 2＝8.二、填空题9. 【答案】10或70 [解析]作OD ⊥AB 于C ，OD 交☉O 于点D ，连接OB.由垂径定理得:BC=AB=30 cm . 在Rt △OBC 中，OC==40(cm).当水位上升到圆心以下且水面宽80 cm 时，圆心到水面距离==30(cm)，水面上升的高度为:40-30=10(cm).当水位上升到圆心以上且水面宽80 cm 时，水面上升的高度为:40+30=70(cm). 综上可得，水面上升的高度为10 cm 或70 cm . 故答案为10或70.10. 【答案】30°[解析] 如图，连接OC .∵AB 是⊙O 的直径，AC ︵＝CD ︵＝BD ︵，∴∠AOC ＝∠COD ＝∠DOB ＝60°. ∵OA ＝OC ，∴△AOC 是等边三角形， ∴∠A ＝60°.∵CE ⊥OA ，∴∠AEC ＝90°， ∴∠ACE ＝90°－60°＝30°.11. 【答案】8[解析] 由题意可得A ，P ，B ，C 在同一个圆上，所以当BP 为圆的直径时，BP 最大，此时∠P AB ＝90°.过点C 作CD ⊥AB 于点D ，可求得AB＝4 3，进而可求得BP 的最大值为8.12. 【答案】1【解析】∵AB 为直径，∴90ADB ∠=︒，∵30B ACD ∠=∠=︒，∴112122AD AB ==⨯=．故答案为：1．13. 【答案】50[解析] 由三角形的内角和定理，得∠B ＋∠C ＝180°－∠A .再由OB ＝OD ＝OC ＝OE ，得到∠BDO ＝∠B ，∠CEO ＝∠C .在等腰三角形BOD 和等腰三角形COE 中，∠DOB ＋∠EOC ＝180°－2∠B ＋180°－2∠C ＝360°－2(∠B ＋∠C )＝360°－2(180°－∠A )＝2∠A ，所以∠DOE ＝180°－2∠A ＝50°.14. 【答案】72 [解析] 如图，连接OB ，OC ，BC ，则BC 的长即为P A ＋PC的最小值．过点C 作CH ⊥AB 于点H ，则四边形EFCH 为矩形， ∴CH ＝EF ，EH ＝CF .根据垂径定理，得BE ＝12AB ＝4，CF ＝12CD ＝3， ∴OE ＝OB 2－BE 2＝52－42＝3，OF ＝OC 2－CF 2＝52－32＝4， ∴CH ＝EF ＝OE ＋OF ＝3＋4＝7，BH ＝BE ＋EH ＝BE ＋CF ＝4＋3＝7. 在Rt △BCH 中，由勾股定理，得BC ＝7 2，则P A ＋PC 的最小值为7 2.15. 【答案】(902n －1)[解析] 当n ＝1时，∠A 1OB 1＝90°；当n ＝2时，∠A 2OB 2＝90°2＝45……所以∠A n OB n ＝(902n －1)°.16. 【答案】34 [解析] 如图，当CD ∥AB 时，PM 的长最大，连接OM ，OC .∵CD∥AB，CP⊥AB，∴CP⊥CD.∵M为CD的中点，OM过点O，∴OM⊥CD，∴∠OMC＝∠PCD＝∠CPO＝90°，∴四边形CPOM是矩形，∴PM＝OC.∵⊙O的直径AB＝8，∴半径OC＝4，∴PM＝4.三、解答题17. 【答案】证明：如图，连接AD，OC.∵OD⊥AC，∴AE＝EC.由翻折的性质，得AC是OD的垂直平分线，∴OE＝DE，∴四边形OADC是平行四边形，∴OA∥CD，OA＝CD.∵OA＝OB，∴OB＝CD，OB∥CD，∴四边形BCDO是平行四边形．又∵OB＝OD，∴四边形BCDO是菱形．18. 【答案】(1)如图所示：(2)OE AC ∥，12OE AC =．理由如下：∵AD 平分BAC ∠， ∴12BAD BAC ∠=∠， ∵12BAD BOD ∠=∠， ∴BOD BAC ∠=∠，∴OE AC ∥，∵OA OB =，∴OE 为ABC △的中位线，∴OE AC ∥，12OE AC =．19. 【答案】证明：如图，连接OC ，OD ，则OC ＝OD .∵M ，N 分别是半径OA ，OB 的中点，∴OM ＝ON .∵CM ⊥OA ，DN ⊥OB ，∴∠OMC ＝∠OND ＝90°.在Rt △OMC 和Rt △OND 中，⎩⎨⎧OC ＝OD ，OM ＝ON ，∴Rt △OMC ≌Rt △OND (HL)，∴∠MOC ＝∠NOD ，∴AC ︵＝BD ︵.20. 【答案】解：连接AC ，如图．∵BA平分∠DBE，∴∠1＝∠2.∵∠1＋∠ABC＝180°，∠ABC＋∠CDA＝180°，∴∠1＝∠CDA.又∵∠2＝∠3，∴∠3＝∠CDA，∴AC＝AD＝5.∵AE⊥CB，∴∠AEC＝90°，∴AE＝AC2－CE2＝52－（13）2＝2 3.21. 【答案】【思维教练】(1)观察表格可猜想β＝90°＋α，γ＝180°－α.连接BG，由直径所对的圆周角为90°和圆内接四边形的对角和为180°即可得出β＝90°＋α；由题干条件易知△EBD≌△EGD，∠EBC＝∠ECB，再由三角形的外角和定理和β＝90°＋α，利用角度之间的转化即可得出结论；(2)由(1)的结论可以得出α＝∠BAG＝45°，β＝∠ACB＝135°，∴∠ECB＝45°，∠CEB＝90°，△ECD、△BEC、△ABG 都是等腰直角三角形，由CD的长，可得出BE和CE的长，再由题干条件△ABE 的面积是△ABC的面积的4倍可得出AC的长，利用勾股定理在△ABE中求出AB的长，再利用勾股定理在△ABG求出AG的长，即可求出半径长．①(1)①β＝90°＋α，γ＝180°－α证明：如解图①，连接BG，∵AG是⊙O的直径，∴∠ABG＝90°，∴α＋∠BGA＝90°，(1分)又∵四边形ACBG内接于⊙O，∴β＋∠BGA＝180°，∴β－α＝90°，即β＝90°＋α；(3分)②∵D是BC的中点，且DE⊥BC，∴△EBD≌△ECD，∴∠EBC＝∠ECB，∵∠EAG＋∠EBA＝γ，∴∠EAB＋α＋∠EBC＋∠CBA＝γ，∵∠EAB＋∠CBA＝∠ECB，∴2∠ECB＋α＝γ，(4分)∴2(180°－β )＋α＝γ，由①β＝90°＋α代入后化简得，γ＝180°－α；(6分)(2)如解图②，连接BG，②∵γ＝135°，γ＝180°－α，∴α＝45°，β＝135°，∴∠AGB＝∠ECB＝45°，(8分)∴△ECD和△ABG都是等腰直角三角形，又∵△ABE的面积是△ABC的面积的4倍，∴AE＝4AC，∴EC＝3AC，(9分)∵CD＝3，∴CE＝32，AC＝2，∴AE＝42，(10分)∵∠BEA＝90°，∴由勾股定理得，AB＝BE2＋AE2＝（32）2＋（42）2＝50＝52，(11分)∴AG＝2AB＝2×52＝10，∴r＝5.(12分)。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第二十四章圆
24.1 圆（第一课时）
知识点
1、圆的定义：
⑴形成性定义：在一个平面内，线段OA绕它固定的一个端点O旋转一周，另一个端点A随之旋
转形成的图形叫做圆，固定的端点叫，线段OA叫做。
⑵描述性定义：圆是到定点的距离等于的点的集合
【特别注意】：1、在一个圆中，圆心决定圆的，半径决定圆的。
2、直径是圆中的弦，弦不一定是直径。
2、弦与弧：
弦：连接圆上任意两点的叫做弦。
弧：圆上任意两点间的叫做弧，弧可分为、、三类。
3、圆的对称性：
⑴轴对称性：圆是轴对称图形，有条对称轴，的直线都是它的
对称轴。
⑵中心对称性：圆是中心对称图形，对称中心是。

一、选择题
1．下列命题正确的有（）
①弦是圆上任意两点之间的部分 ②半径是弦 ③直径是最长的弦 ④弧是半圆，半圆是弧

A.1个B.2个 C.3个D.4个
2.如图所示，MN为⊙O的弦，∠N＝52°，则∠MON的度数为（）
A.38° B.52°C.76°D.104°

3.如图，已知CD为⊙O的直径，过点D的弦DE平行于半径OA，若∠D的度数是50°，则∠C
的度数是（）
A.25°B.40°C.30°D.50°

4．一个点到圆上的最小距离是4cm，最大距离是9cm，则圆的半径是（）.
A.2.5cm或6.5 cm B.2.5cm C.6.5cm D.5cm或13cm
5．如图，已知在⊙O中，AB、CD为直径，则AD与BC的关系是（）.
A.AD=BC B.AD∥BC C.AD∥BC 且AD=BC D.不能确定

A B
C

D
O
6．如图，已知AB为⊙O的直径，点C在⊙O上,∠C=15°,则∠BOC的度数为( )
A．15° B． 30° C． 45° D．60°

二、填空题
1.⊙O的半径为2cm，则它的弦长dcm的取值范围是 .
2．⊙O中若弦AB等于⊙O的半径，则△AOB的形状是 .
3．如图，已知AB是⊙O的直径，点C在⊙O上，点D是BC的
中点，若AC=10cm，则OD= cm.

4．如图4，AB是⊙O的直径，CD是⊙O的弦，AB，CD的延长线交于E，若AB=2DE，
∠E=18°，∠C=______,∠AOC=________；

5． P为⊙O内一点，OP=3cm，⊙O半径为5cm，则经过P点的最长弦长为_______，最短弦长为
________；

三、解答题
1.在Rt△ABC中，∠C=90°,BC=3cm,AC=4cm,D为AB的中点，E为AC的中点，以B为圆心，BC为半
径作⊙B，A、C、D、E与⊙B的位置关系如何？

E
D
C

A
2、如图， M,N为线段AB上的两个三等分点，点A、B在⊙O上，

B
D
O

C
A

A
B
C
O
求证：∠OMN=∠ONM。

N
M

B
A

O
24.1 圆（第一课时）
知识点

1.（1）圆心半径
（2）定长位置大小最长
2．线段部分优弧劣弧半圆
3.（1）无数经过圆心的直线（2）圆心
一、选择题
1．A ； 2. C ； 3. A ； 4．A ； 5．C ； 6．B 。

二、填空题
1. 0cm＜d≤4cm；2．等边三角形；3．5cm.；4．36°，108°；5．10 cm，8 cm ；

三、解答题
1. 解：连接BE,

2222

2222
C90,BC3cm,AC4cmABBCAC345cmDAB15ABcm22EAC1CEAC2cm2BEBCCE3213cmBABC,BEBCBDBC


oQQQeee是的中点BD=
是的中点

；
点A、E均在B外;点D在B内；点C在B上。

OANOBMOAOBOANOBMOMNONMQQ2、证明：连接OA、OBOA=OBA=BM、N是AB的三等分点AM=MN=NBAN=BM在和中
A=B
AN=BM