初一数学上期末基础知识复习-第四章:基本平面图形
北师大版七年级数学上册第四章:基本平面图形 复习课件

14.按下列线段长度,可以确定点A、B、C不在同 一条直线上的是( ) A.AB=8cm,BC=19cm,AC=27cm B.AB=10cm,BC=9cm,AC=18cm C.AB=11cm,BC=21cm,AC=10cm D.AB=30cm,BC=12cm,AC=18cm
27.已知一条射线OA,如果从点O再引两条射线OB和 OC,使∠AOB=60°, ∠BOC=20°,求∠AOC的度数。
28.已知P为线段AB的中点,Q为BP上的一点, 证明:2PQ=AQ-BQ
29.在桌面上放了一个正方体的盒子,一只蚂蚁在 顶点A处,它要爬到顶点B处,你能帮助蚂蚁设计 一条最短的爬行路线吗?
17.已知∠AOB=50°,∠BOC=30°,OD平分 ∠AOC,则∠AOD的度数为( ) A.20° B.80° C.10°或40° D.20°或80°
18.已知∠AOB=30°,∠BOC=45°,则∠AOC的 角度是( ) A.15° B.75° C.15°或75° D.不能确定
19.平面上有四点,经过其中的两点画直线最多可 画出( ) A.三条 B.四条 C.五条 D.六条
24.在时刻8∶30,时钟上时针和分针之间的夹角为( ) A、85° B、75° C、70° D、60°
25.下列说法中正确的是( ) A.8时45分,时针与分针的夹角是30° B.6时30分,时针与分针重合 C.3时30分,时针与分针的夹角是90° D.3时整,时针与分针的夹角是90°
26. 已知点A、B、C在同一条直线上,且AC=5cm, BC=3cm,M、N分别是AC、BC的中点。求线段MN 的长。(提示:未给出图形,注意C点位置有多种可 能)
2024-2025学年北师大版(2024)数学七年级上册 第四章 基本平面图形 课后作业
第四章基本平面图形一、比较线段的长短1.(2023·汕头金平区期末)如图,A,B是河l两侧的两个村庄,现要在河l上修建一个抽水站,使它到A,B两村庄的距离之和最小.数学老师说:连接AB,则线段AB与l的交点C即为抽水站的位置.其理由是:两点之间线段最短.2.如图,点B,C都在线段AD上,若AD=2BC,则()A.AB=CD B.AC-CD=BCC.AB+CD=BC D.AD+BC=2AC3.如图,A,B,C,D是一直线上的四点,则BC+CD=AD-AB,AB+CD=AD-BC.4.如图,已知线段a,b.求作:线段AB,使AB=2a+b.5.(2023·东莞期末)已知线段AB=10 cm,直线AB上有一点C,且BC=6 cm,AC的长为 4 cm或16 cm.6.已知线段AB=6 cm,点P到A,B两点的距离相等,则PA+PB的长()A.等于6 cm B.小于6 cmC.不小于6 cm D.大于6 cm7.(1)如图①,在四边形ABCD内找一点O,使它到四边形四个顶点的距离和OA+OB+OC+OD最小,并说出你的理由.由本题你得到什么数学结论?举例说明它在实际中的应用.(2)如图②,公路上有A1,A2,A3,A4,A5,A6,A7七个村庄,现要在这段公路上设一个车站,使这七个村庄到车站的路程总和最小,车站应建在何处?图②二、角的概念及表示方法1.(2023·湛江经开区期末)如图,下列说法:①∠1就是∠A;②∠2就是∠B;③∠3就是∠C;④∠4就是∠D.其中正确的是()A.①B.①②C.①②③D.①②③④2.下列图中的∠1也可以用∠O表示的是()3.如图,下列说法错误的是()A.∠AOB也可用∠O来表示B.∠β与∠BOC是同一个角C.图中共有三个角:∠AOB,∠AOC,∠BOC D.∠1与∠AOB是同一个角4.如图,将图中的角用不同方法表示出来,并对应填写在下表中:∠α∠β∠C∠θ∠ABC∠BAD5.如图,图中小于平角的角有()A.4个B.5个C.6个D.7个6.如图,请回答以下问题:(1)试用三个大写字母表示下列各角:∠2就是∠DBC,∠3就是∠BAD,∠4就是∠BDC;(2)图中共有9个角(除去平角),其中可以用一个大写字母表示的角有1个.7.如图,图中一共有几个角?它们应如何表示?8.(2023·河源紫金县期末)如图,在已知角的内部画射线,画1条射线,图中共有3个角;画2条射线,图中共有6个角;画3条射线,图中共有10个角;……若在角的内部画2 023条射线,图中共有 2 049 300个角.三、角的比较与运算1.如图,用“>”或“<”填空:(1)在图①中,∠AOB<∠AOC;(2)在图②中,∠POQ<∠ROQ.2.如图,OC平分∠AOB.(1)若∠1=22.5°,则∠2=22.5°,∠AOB=45°;(2)若∠AOB=60°,则∠1=30°.第2题图3.如图,点O是直线CD上的一点,以点O为端点在直线CD上方作射线OA和射线OB,若射线OA平分∠COB,∠DOB=110°,则∠AOB的度数是()第3题图A.32°B.35°C.40°D.42°4.(2024·揭阳惠来县期末)如图,用直尺和圆规作∠PCD=∠AOB,作图痕迹中,弧MN是()A.以点C为圆心,OE为半径的弧B.以点C为圆心,EF为半径的弧C.以点G为圆心,OE为半径的弧D.以点G为圆心,EF为半径的弧5.如图,∠AOC和∠BOD都是直角,且∠DOC=25°.则∠AOD=65°,∠AOB=155°.6.已知∠AOB=70°,以O为端点作射线OC,使∠AOC=42°,则∠BOC的度数为() A.28°B.112°C.28°或112°D.68°7.把一副三角尺按如图所示的方法拼在一起,其中B,C,D三点在同一直线上,CM平分∠ACB,CN平分∠DCE,则∠MCN=127.5°.8.如图,∠AOB是直角,∠AOC=50°,ON是∠AOC的平分线,OM是∠BOC的平分线,求∠MON的度数.四、第四章复习1.下列说法中正确的有()①过两点有且只有一条直线;②连接两点的线段叫两点的距离;③有公共端点的两条射线组成的图形叫作角;④若AB=BC,则点B是AC的中点.A.1个B.2个C.3个D.4个2.如图,已知∠AOB,以点O为圆心,以任意长为半径画弧MN,分别交OA,OB于点M,N,再以点N为圆心,以MN长为半径画弧PQ,交弧MN于点C,画射线OC.若∠AOB=31°,则∠AOC的度数为62°.第2题图3.一个圆被分为1∶5两部分,则较大的弧所对的圆心角是300°.4.如图,点C在线段AB上,点D是AC的中点.如果CD=3 cm,AB=10 cm,那么BC的长为()A.3 cm B.3.5 cmC.4 cm D.4.5 cm5.34.37°=34°22'12″.∠BOC,则∠BOD=54°.6.(2023·梅州期末)如图,O是直线AB上的点,OD是∠COB的平分线,若∠AOC=23第6题图7.(2023·佛山南海区期末)下列时刻,钟表的时针与分针所成的夹角是锐角的是()A.11:15 B.9:00C.6:00 D.3:30AC,D,E分别为AC,AB的中点,则DE的长为4.5 cm.8.如图,已知点C为线段AB上的一点,AC=15 cm,CB=359.如图,O为直线AB上的一点,∠BOE=80°,直线CD经过点O.(1)如图①,若OC平分∠AOE,求∠AOD的度数;(2)如图②,若∠BOC=2∠AOC,OE平分∠COF,求∠COF的度数.。
北师大版数学七年级上册期末复习 第四章 基本平面图形压轴题

北师大版数学七上期末复习专题第四章基本平面图形压轴题1.(2021七上·吉林月考)如图,数轴上点A表示的有理数为﹣4,点B表示的有理数为8,点P从点A出发以每秒2个单位长度的速度在数轴上向右运动,当点P到达点B后立即返回,再以每秒3个单位长度的速度向左运动.设点P运动时间为t(s).(1)当点P与点B重合时,t的值为;(2)当t=7时,点P表示的有理数为;(3)当点P与原点距离是2个单位长度时,t的值为;(4)当BP=3AP时,t的值为.2.(2021七下·长春期中)如图,已知点在数轴上对应的数为,点对应的数为,与之间的距离记作AB.(1)已知a=-2,b比a大12,(1)则B点表示的数是________;(2)设点在数轴上对应的数为,当PA-PB=4时,求的值;(3)若点M以每秒1个单位的速度从A点出发向右运动,同时点N以每秒2个单位的速度从B点向左运动.设运动时间是t秒,则运动t秒后,•用含t的代数式表示M点到达的位置表示的数为▲ , N点到达的位置表示的数为▲;‚当t为多少秒时,M与N之间的距离是9?3.(2021七上·长寿期末)如图,已知数轴上点A表示的数为8,点B表示的数为.动点P从点A出发,以每秒5个单位长度的速度沿数轴向左匀速运动,设运动时间为秒.(1)线段的长为________个单位长度,点P运动t秒后表示的数为________(用含t的代数式表示);(2)动点Q从点B出发,以每秒3个单位长度的速度沿数轴向左匀速运动,若点P、Q同时出发,问点P运动多少秒时与点Q相距4个单位长度?(3)若M为的中点,N为的中点.点P在运动的过程中,线段的长度是否发生变化?若变化,请说明理由;若不变,请求出线段的长.4.(2021七上·成都期末)已知点C在线段AB上,AC=2BC,点D,E在直线AB上,点D在点E的左侧.(1)若AB=15,DE=6,线段DE在线段AB上移动.①如图1,当E为BC中点时,求AD的长;②点F(异于A,B,C点)在线段AB上,AF=3AD,CF=3,求AD的长;(2)若AB=2DE,线段DE在直线AB上移动,且满足关系式=,求的值.5.(2021七上·西岗期末)如图,已知线段,动点P从A出发,以每秒2个单位的速度沿射线AB方向运动,运动时间为t秒,点M为AP的中点.(1)若点P在线段AB上运动,当t为多少时,?(2)若点P在射线AB上运动,N为线段PB上的一点.当N为PB的中点时,求线段MN的长度;当时,是否存在这样的t,使M、N、P三点中的一个点是以其余两点为端点的线段的中点.如果存在,请求出t的值;如不存在,请说明理由.6.(2020七上·电白期末)已知数轴上三点、、表示的数分别为4、0、,动点从点出发,以每秒3个单位的速度沿数轴向左匀速运动.(1)当点到点的距离与点到点的距离相等时,点在数轴上表示的数是 .(2)另一动点从点出发,以每秒2个单位的速度沿数轴向左匀速运动,若点、同时出发,问点运动多长时间追上点?(3)若点为的中点,点为的中点,点在运动过程中,线段的长度是否发生变化?若发生变化,请你说明理由;若不变,请你画出图形,并求出线段的长度.7.(2021七上·巴南期末)如图,数轴上三点、、对应的数是分别是、、,且,,若用表示、两点的距离,表示、两点的距离,则.(1)求的值.(2)若动点以每秒2个单位长度的速度从点向右出发运动,则动点运动多少秒时,动点到、两点的距离之和为12?(3)若动点从点、动点从点同时向右运动,当动点运动到点时,动点、同时停止运动.在运动过程中,点为线段的中点,点为线段的中点,已知动点运动的速度为每秒3个单位长度,动点运动的速度为每秒2个单位长度,请直接写出线段、、之间的数量关系.8.(2021七上·柳州期末)如图所示,线段,动点P从点A出发,以2个单位秒的速度沿射线AB运动,M 为AP的中点.(1)出发多少秒后,(2)当点P在线段AB上运动时,试说明为定值.(3)当点P在线段AB延长线上运动时,N为BP的中点,下列两个结论:长度不变;的值不变.选出一个正确的,并求其值.9.(2021七上·桐梓期末)如图,在数轴上点,点,点表示的数分别为(1)线段的长度为________个单位长度,线段的长度为________个单位长度.(2)点是数轴上的一个动点,从点出发,以每秒1个单位长度的速度,沿数轴的正方向运动,运动时间为秒. 用含的代数式表示:点在数轴上表示的数为________线段的长为________个单位长度;(3)点,点都是数轴上的动点,点从点出发以每秒2个单位长度的速度沿数轴正方向运动,点从点出发以每秒个单位长度的速度沿数轴负方向运动.设点同时出发,运动时间为秒当点两点间的距离为13个单位长度时,求的值,并直接写出此时点在数轴上表示的数.10.(2020七上·蚌埠期末)如图,点在数轴上分别表示有理数,且满足.(1)点表示的数是,点表示的数是.(2)若动点从点出发以每秒3个单位长度向右运动,动点从点出发以每秒1个单位长度向点运动,到达点即停止运动两点同时出发,且点停止运动时,也随之停止运动,求经过多少秒时,第一次相距3个单位长度?(3)在(2)的条件下整个运动过程中,设运动时间为秒,若的中点为的中点为,当为何值时,?11.(2019七上·港南期中)如图:在数轴上点表示数,点表示数,点表示数,是最大的负整数,且、满足与互为相反数.(1)________,________,________.(2)若将数轴折叠,使得点与点重合,则点与数________表示的点重合;(3)点、、开始在数轴上运动,若点以每秒2个单位长度的速度向左运动,同时,点和点分别以每秒1个单位长度和3个单位长度的速度向右运动,假设秒钟过后,若点与点之间的距离表示为,点与点之间的距离表示为.①请问:的值是否随着时间变化而改变?若变化,说明理由;若不变,请求其值.②探究:在(3)的情况下,若点、向右运动,点向左运动,速度保持不变,值是否随着时间的变化而改变,若变化,请说明理由;若不变,请求其值.12.(2021七上·章丘期末)乐乐对几何中角平分线部分的学习兴趣浓厚,请你和乐乐一起探究下面问题吧.已知∠AOB=100°,射线OE、OF分别是∠AOC和∠COB的平分线.(1)如图1,若射线OC在∠AOB的内部,且∠AOC=30°,求∠EOF的度数;(2)如图2,若射线OC在∠AOB的内部绕点O旋转,则∠EOF的度数;(3)若射线OC在∠AOB的外部绕点O旋转(旋转中∠AOC,∠BOC,均指小于180°的角),其余条件不变,请借助图3探究∠EOF的大小,请直接写出∠EOF的度数.(不写探究过程)13.(2021七下·青羊开学考)已知∠AOB=110°,∠COD=40°,OE平分∠AOC,OF平分∠BOD.(1)如图①,当OB、OC重合时,求∠AOE﹣∠BOF的值;(2)当∠COD从图①所示位置绕点O以每秒3°的速度顺时针旋转t秒(0<t<10);在旋转过程中∠AOE﹣∠BOF的值是否会因t的变化而变化,若不发生变化,请求出该定值;若发生变化,请说明理由.14.(2021七下·苏州开学考)如图1,已知点为直线上一点,将一个直角三角板的直角顶点放在点处,并使边、边始终在直线的上方,平分.(1)若,则________°;(2)若,求的度数(用含的代数式表示);(3)若在的内部有一条射线(如图2),满足,试确定与之间的数量关系,并说明理由.15.(2021七下·重庆开学考)如图1,射线OC,OD在的内部,且,,射线,分别平分,.(1)若,则________,________;(2)如图2,若将图1中在内部绕点О顺时针旋转.①旋转过程中的大小始终不变.求的值;②如图3,若旋转后OC恰好为的角平分线,请直接写出与的数量关系.16.(2021七上·成华期末)(1)如图1,∠AOC:∠COD:∠BOD=4:2:1,若∠AOB=140°,求∠BOC的度数;(2)如图2,∠AOC:∠COD:∠BOD=4:2:1,OP平分∠AOB,若∠AOB=β,求∠COP的度数(用含β的的代数式表示);(3)如图3,∠AOC=80°,∠BOD=20°,OE平分∠AOD,OF平分∠BOC,求∠EOF的度数.17.(2021七上·西岗期末)已知:,OB、OC、OM、ON是内的射线。
七年级数学上册第四章基本平面图形小结与复习教学

小结 与复习 (xiǎojié)
要点(yàodiǎn)梳理
考点讲练
课堂小结
第一页,共三十一页。
课后作业
要点(yàodiǎn)梳理
一、线段、射线(shèxiàn)、直线
1.线段、射线与直线(zhíxiàn)的特性
类别 线段
图形
端点 个数
是否 可以 延伸
两个
第二十八页,共三十一页。
课堂小结
直线(zhíxiàn)
性质
线段(xiànduàn)
线段(xiànduàn)的中点
射线 角的定义
角
基
角平分线
本
定义
平
面
多边形 对角线
图
形
正多边形
定义
弧 圆
扇形
圆心角
第二十九页,共三十一页。
第三十页,共三十一页。
内容(nèiróng)总结
小结与复习。一、线段(xiànduàn)、射线、直线。(1)角是由两条具有公共端点的射线组成的图形.。在靠近顶点 处画上弧线,并写上希腊字母(数字)。(1)角的度量单位是度、分、秒.。(1)多边形是由若干条不在同一直线上的 ________首尾顺次相连组成的封闭____________ .。各边相等,各角也相等的多边形叫做正多边形.。(3)由一条弧
端点 在前
以A为端 点
作射线
AB
直线
直线
无
向两 个
方向 延伸
不能 度量
AB 或直 线BA 或直
A,B
两点 无序
过A,B
两点 作直线
AB
线a
第三页,共三十一页。
2.两点确定(quèdìng)一条直线 经过两点有且只有一条(yī tiáo)直线.
北师版七年级数学上册 第四章 基本平面图形(易错题归纳)

第四章基本平面图形(易错题归纳)易错点一:直线、射线、线段的概念理解不透技巧点拨:代数式的书写要求:(1)在代数式中出现的乘号,通常简写成“⋅”或者省略不写;(2)数字与字母相乘时,数字要写在字母的前面;(3)在代数式中出现的除法运算,一般按照分数的写法来写.带分数要写成假分数的形式.根据代数式的书写要求判断各项即可1.直线a上有5个不同的点A、B、C、D、E,则该直线上共有()条线段.A.8B.9C.12D.102.下列叙述正确的是()A.线段AB可表示为线段BAB.射线AB可表示为射线BAC.直线可以比较长短D.射线可以比较长短3.下列说法正确的是()A.直线BA与直线AB是同一条直线B.延长直线ABC.射线BA与射线AB是同一条射线D.直线AB的长为2cm4.下列说法正确的是()A.延长直线ABB.延长射线ABC.反向延长射线ABD.延长线段AB到点C,使AC=BC易错点二:线段运用技巧点拨:正确掌握数线段方法5.A站与B站之间还有3个车站,那么往返于A站与B站之间的车辆,应安排多少种车票?()A.4B.20C.10D.96.由汕头开往广州东的D7511动车,运行途中须停靠的车站依次是:汕头→潮汕→普宁→汕尾→深圳坪山→东莞→广州东.那么要为D7511动车制作的车票一共有()A.6种B.7种C.21种D.42种7.往返于甲、乙两地的列车,中途需要停靠4个车站,如果每两站的路程都不相同,问:(1)这两地之间有种不同的票价;(2)要准备种不同的车票.易错点三:两点间的距离技巧点拨:题意不明确时注意分类讨论8.已知点A、B、C都是直线l上的点,且AB=5cm,BC=3cm,那么点A与点C之间的距离是()A.8cm B.2cm C.8cm或2cm D.4cm9.已知点A,B,C在同一条直线上,若线段AB=3,BC=2,AC=1,则下列判断正确的是()A.点A在线段BC上B.点B在线段AC上C.点C在线段AB上D.点A在线段CB的延长线上10.已知线段AB=6cm,点C在直线AB上,AC=AB,则BC=.11.如图,已知A、B、C是数轴上的三点,点B表示的数是﹣2,BC=6,AC=18,点P从A点出发沿数轴向右运动,速度为每秒2个单位.(1)数轴上点A表示的数为;点C表示的数为.(2)经过t秒P到B点的距离等于P点到C点距离的2倍,求此时t的值.(3)当点Q以每秒1个单位长度的速度从C点出发,沿数轴向终点A运动,N为BQ中点.P、Q同时出发,当一点停止运动时另一点也随之停止运动.用含t的代数式表示线段PN的长.12.P是线段AB上一点,AB=12cm,C,D两点分别从P,B同时向A点运动,且C点的运动速度为2cm/s,D点的运动速度为3cm/s,运动的时间为ts.(1)如图若AP=8cm,①运动1s后,求CD的长;②当D在线段PB上运动时,试说明线段AC和线段CD的数量关系;(2)如果t=2s时,CD=1.5cm,试探索AP的值.易错点四:比较线段的长短技巧点拨:注意点的位置进行分类讨论。
北师版七年级上数学第四章基本平面图形知识点及练习题
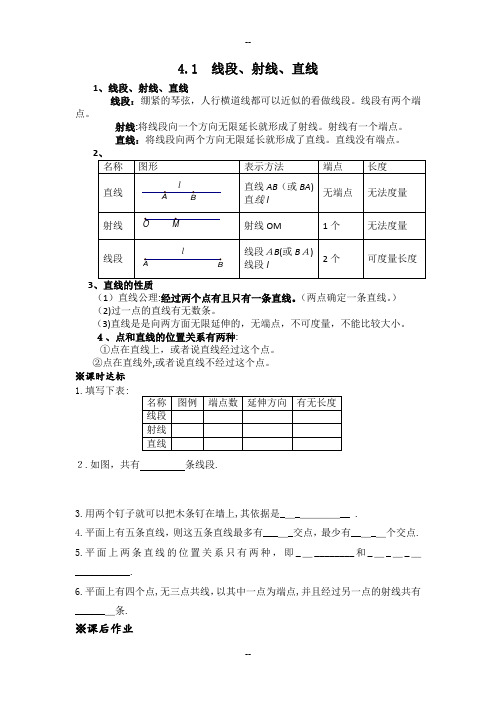
4.1 线段、射线、直线1、线段、射线、直线线段:绷紧的琴弦,人行横道线都可以近似的看做线段。
线段有两个端点。
射线:将线段向一个方向无限延长就形成了射线。
射线有一个端点。
直线:将线段向两个方向无限延长就形成了直线。
直线没有端点。
3(1)直线公理:经过两个点有且只有一条直线。
(两点确定一条直线。
) (2)过一点的直线有无数条。
(3)直线是是向两方面无限延伸的,无端点,不可度量,不能比较大小。
4、点和直线的位置关系有两种:①点在直线上,或者说直线经过这个点。
②点在直线外,或者说直线不经过这个点。
※课时达标 1.填写下表:2.如图,共有 条线段.3.用两个钉子就可以把木条钉在墙上,其依据是_________ .4.平面上有五条直线,则这五条直线最多有_____交点,最少有_____个交点.5.平面上两条直线的位置关系只有两种,即__________和_________________.6.平面上有四个点,无三点共线,以其中一点为端点,并且经过另一点的射线共有_______条.※课后作业★基础巩固1.下列各直线的表示法中,正确的是( ).A.直线AB.直线AB C直线abD.直线Ab 2.下列说法不正确的是( ) .A.直线AB与直线BA是同一条直线B.射线AB与射线BA是同一条射线C.线段AB与线段BA是同一条线段D.线段有两个端点,射线有一个端点,直线没有端点3.下列说法正确的是( ).A.射线比直线短B.两点确定一条直线C.经过三点只能作一条直线D.两条射线的长度的和等于直线的长度4.下列说法正确的是( ).A.过一点P只能作一条直线B.射线AB和射线BA表示同一条射线C.直线AB和直线BA表示同一条直线 D.射线a比直线b短5.下列说法正确的是( ).A.延长射线OAB.延长直线lC.延长线段CD D.反向延长直线l6.平面内的三点可确定直线的条数是( ).A.3B.1或3C.0或1D.07.已知C,D在直线AB上,那么直线AB上的射线共有( ).A.6条B.7条C.8条 D.9条8.下列说法中,错误的有( ).①射线是直线的一部分;②画一条射线,使它的长度为5厘米;③线段AB和线段BA是同一条线段;④射线AB和射线BA是同一条射线;⑤直线AB和直线BA 是同一条直线.A.1个B.2个C.3个D.4个9.在一条笔直的校园大道两旁种树时,先定下两棵树的位置,然后其它树的位置也就确定下来了,这说明了直线的基本性质:________________________.10.已知平面内的四个点A,B,C,D,过其中的两个点画直线:(1)若A,B,C,D四个点在同一条直线上,可以画出______条直线;(2)若A,B,C,D四个点有三个在同一条直线上,可以画出______条直线; (3)若A,B,C,D四个点中的任意三个都不在同一条直线上,可以画出_______条直线.11.读下列语句,并画出相应图形.(1)经过点M,N画一条直线;(2)直线ba,相交于点P,点A在直线a上,但不在直线b上;(3)三条直线c,两两相交于点A,B,C.ba,☆能力提高12.读句画图:如图所示,已知平面上四个点(1)画直线AB;(2)画线段AC;(3)画射线AD、DC、CB;(4)如图,指出图中有_____条线段,有___ 条射线并写出其中能用图中字母表示的线段和射线.13.已知直线l上有n个点,试问:(1)此图形上有多少条射线?(2)此图形上有多少条线段?14.如图,线段AB上的点数与线段的总数有如下关系:如果线段AB上有三个点时,线段总共有3条,如果线段AB上有4个点时,线段总数有6条,如果线段AB上有5个点时,线段总数共有10条,……A C B3=2+1ﻩA C D B6=3+2+1A C D E B10=4+3+2+1(1)当线段AB上有6个点时,线段总数共有__________条.(2)当线段AB上有100个点时,线段总数共有多少条?●中考在线15.平面上不重合的两点确定一条直线,不同三点最多可确定3条,若平面上不同的n个点最多可确定21条直线,则n的值为( ).A.5 B.6 C.7D.816.同一平面内互不重合的三条直线的公共点的个数是( ).A.可能是0个,1个,2个B.可能是0个,2个,3个C.可能是0个,1个,2个或3个D.可能是1个或3个4.2 比较线段的长短1、线段的性质(1)线段公理:两点之间的所有连线中,线段最短。
七年级数学上册 第四章 基本平面图形小结与复习教学课件上册数学课件
三、角
1.角的定义 (1)角是由两条具有公共端点的射线组成的图形. (2)角可以看做是一条射线绕着它的端点旋转而成.
2.角的表示方法
表示方法
用三个大写的 字母表示
用一个顶点的 字母来表示
用一个希腊字 母(数字)表示
12/7/2021
注意事项 表示顶点的字母要写在中间
一个字母只表示一个角 在靠近顶点处画上弧线, 并写上希腊字母(数字)
∠BOC)= 1 ∠AOB.
2
2
又因为∠AOB=90°,所以∠MON=45°.
12/7/2021
(2)如果(1)中∠AOB=α,其 他条件不变,求∠MON的度数;
解:由(1)可知∠MON= 1 ∠AOB. 2
因为∠AOB=α 所以∠MON= .
2
12/7/2021
(3)如果(1)中∠BOC=β(β为锐角), 其他条件不变,求∠MON的度数;
9.如图,∠AOB=∠COD=90°,
OC是∠AOB的平分线,OE是∠BOD的
三等分线,试求∠COE的度数.
解:因为∠AOB=90°,OC是∠AOB的平分线,
所以∠BOC=1 ∠AOB=45°. 因为∠BOD=2∠COD-∠BOC=45°,
又因为OE是∠BOD的三等分线,
所以∠DOE=
1 3
∠BOD=15°.
53
8
BC= 5
3
3
AB= 3 3 2 8
=12 (cm).
因为D是AC的中点,
1 2
所以AD= AC=10 cm,
所以DB=AB-AD=32-10=22(cm).
12/7/2021
因为O是AB的中点, 1 2
北师大版七年级数学上册第四章基本平面图形知识点总结【含答案】
北师大版七年级数学上册 第四章 基本平面图形 知识点总结知识点一:基本图形特点(1)线段 两个端点 可测量 线段CD 或线段DC ,或者线段m 。
(2)射线 一个端点 不可测量 射线DE ,其中D 点是端点(3)直线 没有端点 不可测量 直线EF 或直线FE ,或直线Ɩ 。
(4)角的表示方法:①用三个大写字母;如∠ABC (顶点字母在中间) ②用一个大写字母,如∠B (以这个点为顶点的角只有一个) ③用一个数字,如∠1;④用一个希腊字母,如∠ α 。
知识点二:(1)将一根细木条固定在墙上,至少需要钉 2个钉子,理由: 两点确定一条直线 。
(3)过平面内三个点中的任意两个点可作 1条或者3条 直线。
(2)若一条直线上有n 个点,则有 条线段、 2n 条射线和 1条直线。
(4)平面内n 条直线两两相交,有 个交点。
(5)平面内一个点O 发出n 条射线,那么角的个数为 个角。
知识点三:方位角方法:视角互换,度数不变,位相反。
如:操场上,小明对小亮说:“你在我的北偏东30°方向上”,那么小亮可以对小明说:“你在我的 A 方向上”( )A .南偏西30°B .北偏东30°C .北偏东60°D .南偏西60°2)1(-n n 2)1(-n n 2)1(-n nA B O 知识点四:时钟指针夹角 (1)一圈360° (2)一大格360÷12=30°(3)m 点整时,时针与分针夹角: 30m º 当度数大于180º时,再用(4)m 点n 分时,时针与分针夹角: |5.5n -30m |º 360º减去。
知识点五:度的换算(一)法则: 大单位化小单位乘以 进率60 。
小单位化大单位除以 进率60 。
(二)题型: ①45°= 87′ = 5220″②1800″= 30 分= 0.5 度 ③( )°= 15 ′④ 47.43°= 47 ° 25 ′ 48 ″。
2022年七年级数学上册 第四章 基本平面图形知识点归纳 (新版)北师大版
第四章 基本平面图形1.线段、射线、直线2.比较线段的长短3.角4.角的比较5.多边形和圆的初步认识一. 线段、射线、直线※1. 正确理解直线、射线、线段的概念以及它们的区别: 名称图形 表示方法 端点 长度 直线 lB A 直线AB (或BA ) 直线l无端点 无法度量 射线 M O 射线OM1个 无法度量 线段 l B A线段AB (或BA )线段l 2个 可度量长度※二.比较线段的长短※1. 线段公理:两点间线段最短;两之间线段的长度叫做这两点之间的距离.※2. 比较线段长短的两种方法:①圆规截取比较法;②刻度尺度量比较法.※3. 用刻度尺可以画出线段的中点,线段的和、差、倍、分;用圆规可以画出线段的和、差、倍.三.角※1. 角:有公共端点的两条射线组成的图形叫做角;这个公共端点叫做角的顶点;这两条射线叫做角的边.※2. 角的表示法:角的符号为“∠”①用三个字母表示,如图1所示∠AOB ②用一个字母表示,如图2所示∠b③用一个数字表示,如图3所示∠1④用希腊字母表示,如图4所示∠β ※经过两点有且只有一条直线。
※两点之间的所有连线中,线段最短。
※两点之间线段的长度,叫做这两点之间的距离........。
1º=60’ 1’=60”※角也可以看成是由一条射线绕着它的端点旋转而成的。
如图5所示:※一条射线绕它的端点旋转,当终边和始边成一条直线时,所成的角叫做平角..。
如图6所示:※终边继续旋转,当它又和始边重合时, A O B 图1 b 图2 终边图51 图3 β 图4所成的角叫做周角..。
如图7所示:※从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平...分线..。
※经过直线外一点,有且只有一条直线与这条直线平行。
※如果两条直线都与第三条直线平行,那么这两条直线互相平行。
※互相垂直的两条直线的交点叫做垂足..。
※平面内,过一点有且只有一条直线与已知直线垂直。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第四章:基本平面图形
★ 相关概念理解
●
角:①具有公共端点的两条射线组成的图形(静态);
②由一条射线绕着它的端点旋转而成的图形(动态).(默认小于平角的角)
平角不是直线;周角不是射线.(线与角是不同的概念)
●
方位角:南北在前,东西在后;如:北偏东30°;方向:东西在前,南北在后,如:东北方向.
●
多边形:由若干条不在同一直线上的线段首尾顺次相连组成的封闭平面图形(凸多边形).
●
正多边形:各边相等,各角也相等的多边形.
●
圆:到定点(圆心)的距离等于定长(半径)的点所组成的图形(一条封闭的曲线).
●
弧:圆上任意两点A,B间的部分,大于半圆的弧叫做优弧,小于半圆的弧叫做劣弧.
●
扇形:一条弧和经过这条弧的端点的两条半径所组成的图形(圆面的一部分:面).
●
圆心角:顶点在圆心上的角.
●
扇形面积公式:2360rnS扇(r是扇形(圆)半径,n是圆心角)扇形是圆面积的一部分.
●
弧长公式:rnl180弧(r是圆半径,n是弧所对的圆心角)弧长是圆周长的一部分.
★ 三线及角的表示
●
直线:①直线AB(点A,B是直线上任意两点,字母顺序可以交换,即直线BA);②直线a.
●
射线:①射线OA(点O是端点,字母顺序不可交换,即射线AO的端点是A点).
●
线段:①线段AB(点A,B是线段的两个端点,字母顺序可以交换,即线段BA);②直线a.
●
角:①三个大写字母(可以表示任意角):∠AOB(点O是角的顶点,必须是中间字母,点A,B是角
两边上各取一点,字母A,B顺序可以交换,即∠BOA);
②一个大写字母(顶点只有一个角时):∠O(点O是角的顶点);
③一个阿拉伯数字:∠1,∠2,∠3等,一个希腊字母:∠α,∠β,∠γ等.(表示单角时)
●
角的边:如∠AOB,边OA,边OB,(点O必须在前,因为角的边是以O为端点的射线)
●
角平分线:如OC平分∠AOB,OC是平分线,(点O必须在前,因为角平分线是以O为端点的射线)
★ 三线性质
●
直线的性质:
. ①直线公理:经过两点有且只有一条直线,即两点确定一条直线. 如:固定木板至少要2颗钉子.
②两直线相交:只有一个公共点.
③直线是向两方向无限延伸的,无端点,不可度量,不能比较大小,不能延长.
④直线上有无穷多个点.
⑤经过一点的直线有无穷多条.
⑥两条不同直线至多有一个公共点.
●
射线的性质:
①射线是直线的一部分.
②射线只向一方无限延伸,有一个端点,不可度量,不能比较大小,可以从端点处反向延长.
③射线上有无穷多个点.
④两条射线的公共点可能没有,可能只有一个,也可能有无穷多个.
●
线段的性质:
①线段公理:所有连接两点的线中,线段最短. 即两点之间,线段最短.如:把航道修成笔直.
②线段是直线的一部分.
③线段上有无穷多个点.
④线段有两个端点,可度量,可比较大小,可延长.
⑤两条线段的公共点可能没有,可能只有一个,也可能有无穷多个.
★ 几何语言理解
①连接AB:作线段AB.
②延长AB到C(反向延长BA到C);延长BA到C(反向延长AB到C);
C在线段AB的延长线上(两种情况);
③点与直线位置关系:点在直线上,点在直线外;
④点与线段:点在线段上,点在线段的延长线上(分类讨论时常用);
⑤两角的位置:边OC在∠AOB的内部或外部; 边OA,边OC在公共边OB的同侧或两侧(分类
讨论时常用)
★ 比较线段长短
①两点之间的距离:两点之间线段的长度.(长度是数值,而不是线段,线段是图形)
②线段中点:三种语言的转化,会用符号语言表示“等”“倍”“分”,并合理运用.
③注意分类讨论:点A,B,C三点在同一条直线上(两种情况);点C在线段AB上(一种情况).
★ 角的比较
①角平分线:三种语言的转化,会用符号语言表示“等”“倍”“分”,并合理运用.
②锐角(0°<α<90°)<直角(90°)<钝角(90°<α<180°)<平角(180°)<周角(360°)
③角的大小与角的两条边的张角的大小有关.
★ 度分秒换算及运算:
①度分秒换算关系及进制
1个周角的360分之一是1度的角,记作“1°”
1°的60分之一为1分,记作“1′”,即1°=60′
1′的60分之一为1秒,记作“1″”,即1′=60″
角的度量单位是度、分、秒,是六十进制。
②度分秒换算题型
●
度化分化秒:大化小,乘进制.
●
秒化分化度:小化大,除进制.
●
度化度分秒:不足1度的化成分,不足1分的化成秒.
●
度分秒化秒:先把度和分化成秒,再把秒相加.
●
度分秒化度:先把秒化成分,再把分化成度.
③度分秒的运算
●
加法运算:度分秒对齐,分别相加,满60进一.
● 减法运算:度分秒对齐,分别相减,不够,借一当60.
●
乘法运算:度分秒分别相乘,满60进一.
●
除法运算:先除以度,然后余下的度数要乘60(因为度要化成分要乘60),在加上给的分数一起
除,余下的分数要乘60(因为度要化成秒要乘60)再加上给的秒数一起除。最后把度
分秒依序排列即可.
★ 时钟问题:
①每一分钟:分针转6°,时针转0.5°;
②分针转过一个圆周(360°)的几分之几,时针就转过一个大格(30°)的几分之几.
★ 数几何图形个数的方法:
①数直线条数:过其中任意三点不在同一直线上的n个点中的两点可画2)1(nn条直线.
②数交点个数:n条直线最多有2)1(nn个交点.
③数直线分平面的份数:平面内n条直线最多将平面分成2)1(1nn个部分.
④数线段条数:直线上有n个点(包括线段两个端点)时,共有线段2)1(nn条.
⑤数角的个数:如图所示,以O点为端点引n条射线,∠AOB<180°,则小于平角的角的个数
为2)1(nn。
★ n边形及圆的探索:
①n边形有:n条边,n个顶点,n个内角.
②从n边形的一个顶点可以引(n-3)条对角线,将n边形分成(n-2)个三角形.
③n边形共有2)3(nn条对角线.
④n边形内角和为)(2-n180,正n边形每个内角的度数是n2-n180)(.
⑤1个扇形的弧上有n个点时,能得到2)1(nn个扇形,2)1(nn条弧.
⑥1个圆任意画n条半径,能得到)1(nn个扇形,)1(nn条弧.
E B A C D
O
