讲座1-3 离散频谱校正技术(DOC)
离散线性系统的分析与校正资料
ROC : z 0
常用单边序列的z变换
1) Z{[k]} 1, z 0
2)
Z{
k u[k ]}
1
1
z 1
za
3)
Z{e
j 0 k
u[k
]}
1
e
1
j 0
z
1
1 cos 0 z 1 j sin 0 z 1 1 2z 1 cos 0 z 2
cos( 0 k )u[k ] 1
1 cos 0 z 1 2z 1 cos 0
z max(Rx1, Rx2 )
21
3、单边z变换的主要性质
2. 位移特性
➢ 因果序列的位移
x[k n] u[k n] znX(z) |z|> Rx ➢ 非因果序列的位移
n 1
Z x[k n]u[k ] z n[ X ( z) x[k ]z k ] k 0 1
Z x[k n]u[k ] z n[ X (z) x[k ]z k ] k n
4、单边z反变换
➢ 部分分式法
X (z)
B( z) A( z )
b0 b1z 1 bm z m 1 a1z 1 an z n
1. m<n，分母多项式无重根
n
X (z) i 1
各部分分式的系数为
ri 1 pi z 1
ri (1 pi z 1 ) X ( z) z pi
4、单边z反变换
X
(z)
1
(1
2 2z 1 )21
4z 1
G(z)
G(z)
A (1 2z 1 )2
1
B 2z
1
1
C 4z
1
A (1 2z 1)2 G(z)
第二章 离散信号频谱的窗谱校正方法
A/2
t
X (f )
A/2
f
T0
-f 0
0
f0
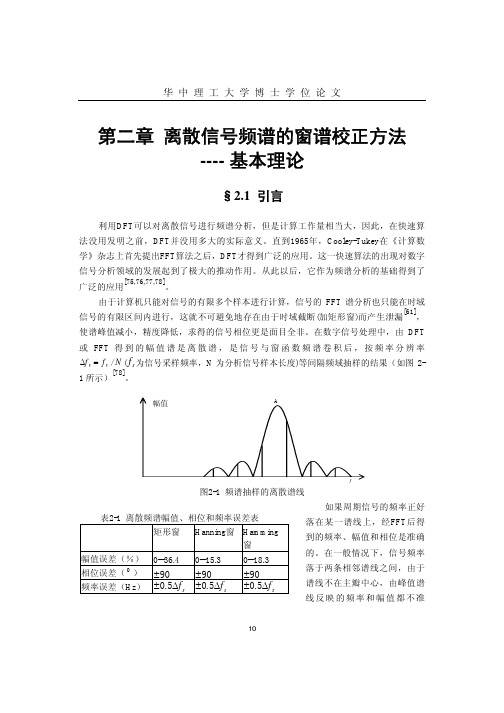
时域波形
傅里叶变换模函数
(c)单频率谐波的时域波形和频谱模函数
xT ( t ) A
Y yK
yK−1
0
T
t
n 0 k-2 k-1 f0 k k+1 k+2
时域波形
离散频谱模函数
(d)单频率谐波离散频谱模函数 图2-2 单频率谐波离散频谱的误差产生原因
12
华 中 理 工 大 学 博 士 学 位 论 文
根据傅氏变换的奇偶性质，当 w( t ) 是实偶函数时，W ( f ) 此时也为实偶函数。又由 傅氏变换的时移特性可知（如图2-2b），
F [ wT ( t )] = W ( f ) e − jπ⋅ f ⋅T ........................................................................................(2.4) 设有一周期信号 x ( t ) = ACos ( 2 π ⋅ f 0 ⋅ t + ϕ ) ,则其傅氏变换结果为（如图2-2c）：
∞
F [ x ( t ) ⋅ wT ( t )] =
−∞
∫ x( t ) ⋅ w
T
( t )e − j 2π ⋅ f ⋅t dt .............................................................(2.1)
其中， wT ( t ) 由对称窗 w( t ) 在时间上平移 T / 2 得到，即
函数，其 G ( v ) 是不同的。如果在同样的采样频率和同样的信号分析样本长度的情况下， 对加窗信号的频域抽样位置也就确定下来了，由于信号频率 f 0 的位置固定，即信号频域 峰值位置固定，则可得不管信号加了何种窗，所产生的频率误差都是一样的。 (2) 幅值校正 设窗函数的频谱模函数为W ( f ) ，则图2-4中主瓣函数为∶
离散系统的数字校正
1) 1)3
T
2 z 1 (1 z 1 2(1 z 1 )3
)
3
A(z) 1 Tz1
T 2z 1(1 z 1 ) 2
设计条件：G(z)中无单位圆上或外的
零 极
点,若有,需在
(z) e (z)
的零点中包含
设计原则：选择(z) ，使系统经最少拍后能在采样点上准确跟踪典型输
入， 由此确定满足条件的GD(z)
(3) 离散系统的稳定判据 z域中的朱利 (Jurry) 稳定判据
z域中的根轨迹法
一般方法
(4) 离散系统的稳态误差 静态误差系数法
5 离散系统的动态性能分析
例题
则调节时间 ts kT
依最少拍系统设计原则，应有 e(kiT) 0 (ki k, k 1,L ,)
E(z)
e(z)
R(z)
(1
A( z ) z1 )m
e(z)
e(T )
lim(1
z1
z1 )
A( z ) (1 z 1 )m
e(z)
0
为0的条件：应包含此因子
要求：
e
(z)
(1
z
1
)m
F
(z)
根据：U
(z)
Gd
(z)
E(z)
Gd
(z)
e
( z) R( z)
(z) G(z)
R(z)
应使：Gd (z) e (z) 为z-1的有限多项式。
条件为：(z) 的零点应抵消G(z)的全部零点，令 G(z) P(z)
Q(z)
即： (z) P(z)M(z)
M(z)为待定 z-1多项式。
综上： (1) (z)除满足最少拍要求外，附加条件是还必须包含G(z) 的全部零点，
离散系统的分析与校正
X(-k T 0 ) X[(1 - K)T0 ] X(-T 0) 0
-(k n ) Z[X[(t - KT0 )] X(0)Z-k X(T0 )Z-(k 1) X(n T )Z 0
Z -k [ X(0) X(T0 )Z 1 X(n T0 )Z n ] Z -k X( Z ) 证毕
而脉冲强度则由nT0时刻的连续函数e (nT0 )来确定
2、采样定理(Shannon)
如果采样角频率大于或等于2m ,即s 2m , 则经采样得到的 脉冲序列能无失真地再恢复到原连续信号.
m 连续信号频谱的上限频率 2 对s 2m ,有 2 T 2T
0 m
| e ( j ) |
证明:由Z变换定义
n Z[X(t - k T )] X ( n T k T ) Z 0 0 0 n0 -1 -k -(k 1) X(-k T ) X(T -k T )Z X(0)Z X(T )Z 0 0 0 0 -(k n ) X(n T 0 )Z
K -1
证明:Z[X(t kT0 )] X ( nT0 kT0 ) Z n X (kT0 ) X [(k 1)T0 ]Z 1 X [(k 2)T0 ]Z 2 ....... X ( nT0 kT0 ) Z n ...... Z k [ X (kT0 ) Z k X [(k 1)T0 ]Z ( k 1) ......] Z k { X (0) X (T0 ) Z 1 ...... X [(k 1)T0 ]Z ( k 1) X (kT0 ) Z k X [( K 1)T0 ]Z ( k 1) ...... X (0) X (T0 ) Z 1 ...... X [(k 1)T0 ]Z ( k 1) ]} Z [ X ( Z ) X (nT0 ) Z n ]
通用的离散频谱相位差校正方法
!
（!）
其中， 由对称窗 C（ 在时间上平移 B A " 得到， 即 CB（ ! &） ! &） ） （ ） （"） CB（ & Z C & R B A " ! ! 设 C（ 的傅立叶变换为： ! &） ［ C（ ］ D Z E（ ! &） ! *） （*）
%$ "
上式中， 必须保证 （&&） ,& , & ,! $ !"+ 上面所有推导没有具体利用哪一种窗函数， 所以通用的 相位差校正方法适用于所有的对称窗函数 % 时域平移相位差 法、 改变窗长的相位差法实际上分别是通用相位差当 ,& " ! 和 ,! " + 的特例 %
#
通用相位差法的离散频谱校正实现方法
摘 要： 现有三种离散频谱相位差校正法的基本原理是一致的， 通过时移和加不同的对称窗进行两次 ++, 分 析， 并利用离散频谱对应峰值谱线的相位差以求得频率和相位校正量 - 在此基础上提出了通用离散频谱相位差校正方 法： 时域平移 . 改变窗长 . 改变窗函数， 即第二段时域序列比第一段滞后 / 点， 采用不同窗函数对两段时域分别作 0 点和 1 点的 ++, 分析 - 文献 ［!%］ 、 文献 ［’］ 和文献 ［!!］ 提出的校正方法是此法改变不同参数的三个特例 - 仿真结果表 明， 该方法实现方便， 精度较高， 适合各种对称窗函数， 抗噪声能力强 关键词： 频谱分析；校正；信号处理；相位差 ,0’’!#) 文献标识码： 2 文章编号： %*$"3"!!"（"%%*）%!3%!&"3%& 中图分类号：
频谱校正方法
频谱校正方法
温馨提示：文档内容仅供参考
频谱校正是指对频谱信号进行校正以消除信号中的误差或非线性响应。
下面介绍几种常见的频谱校正方法：
线性插值法：该方法适用于频谱信号中的离散点不均匀分布的情况。
线性插值法通过在频率域上的两个离散点之间线性插值，获得一条直线，从而对频谱信号进行插值。
多项式拟合法：该方法适用于频谱信号中的误差具有一定的规律性。
多项式拟合法通过将原始信号拟合成一个多项式函数，从而对频谱信号进行校正。
傅里叶变换法：该方法适用于频谱信号中的非线性响应较为明显的情况。
傅里叶变换法通过将原始信号进行傅里叶变换，将频域中的非线性响应转换为时域中的线性响应，从而对频谱信号进行校正。
平滑法：该方法适用于频谱信号中存在噪声的情况。
平滑法通过对频谱信号进行平滑处理，从而减少噪声对频谱信号的影响。
需要根据实际情况选择适当的频谱校正方法进行使用。
线性离散系统的分析与校正 PPT课件
xiT t iT i0
2. 采样定理 采样定理给出了从离散信号不失真地恢复原来信号所需的 最低采样频率。
(1)采样信号的频谱
冲量为１的理想脉冲序列
Ts t t nTs
n
写成傅立叶级数的复数形式
Ts
1 Ts
e jnst
n
式中， s 2 / Ts ，称为采样角频率。
设： xt 0 t 0
Zx*t X z
注意： Z x*t记为 X z，借用了函数符号 X • ，但是，
X z X s |sz 。
还需指出， X z 是采样脉冲序列 x* t 的 Z 变换。
从定义可以看出，它只考虑了采样时刻的信号值 xnTs 。
对一个连续函数 xt ，由于在采样时刻 xt 的值就是 xnTs
例 试求正弦函数 sin t 的Z变换。
Lsint
s21/2 j
s j
Zsint
1 2j
z z e jTs
1 2j
z z e jTs
z2
z sin Ts
2 cosTs z
1
4 Z变换的基本定理
(1)线性定理
设连续时间函数 x1t及 x2 t的 Z 变换分别为 X1 z和
第七章 线性离散系统的分析与校正
7.1 离散时间控制系统
连续时间系统 离散时间系统
1. 采样控制系统
(1) 工业自动控制系统中，被控对象的惯性非常大， 且具有滞后特性，采用连续控制往往得不到高质 量的控制效果。而利用采样控制技术则可以解决 这类问题。适当选择控制周期，可以得到满意的 控制效果。
(2) 现代工业中，引入了质量测量仪表、成分分析仪 表等，这些质量仪表都含有定时采样器。因此， 含有质量仪表的控制系统就是一种采样控制系统。
离散频谱时移相位差校正法
!
收稿日期： &"""#"%#&%；修订日期： &""&#",#&) 基金项目： 国家自然科学基金资助项目 （)""%)",’） ； 国家教育部高等学校骨干教师资助计划项目 （教 技司 ［&"""］ *) 号） 作者简介： 丁康 （!’)%—） ， 男， 浙江天台人， 教授， 硕士 （ D#A35;： E=546F C?GH <=GH B4） H
表 . ? - 分别是当 & 取 ./ 点、 在没有噪声和加噪声情况下校正前后数据 .// 点和 ./*0 点， 对比・ 从图表中可以得出以下结论： 如本例中的 *+:9+12 和 ,:*9:12， 这种相位差法对频率、 幅值 .）对间隔较远的频率成分， 万方数据
图!
两段信号加窗作 谱后相位比较
# "&)’ "&’ # （ ’ ）$ # ! ! $ !（ "( " . " $ ! - ! $ " ’ ）% ! （ ’ - )’ ） # "& ， （!)） ! !%# "&’ + ! （!*） )’ $ ! # "& + ! ・ 令# $ ! （ ， 由于相位是在 （ %" ， ） 之间， 周期为 # ， 所以# 可能超过 （ %" ， ） ’ & + !） !%# " " " " 这一区间， 所以在实际计算中应取# 除以 # "后的余数： （ ） # # $ ( +,#， " ・ 再作如下调整 （ ） ， # / %" （ ） # 0 -" ・ 成立， 必须满足 此时要式 （!*） （!.）
离散频谱分析误差产生的原因及离散频谱校正技术【建筑工程类独家文档首发】
离散频谱分析误差产生的原因及离散频谱校正技术【建筑工程类独家文档首发】离散频谱校正理论和技术，不知道大家对这个名词熟不熟悉。
近来在声振论坛上看到一些帖子讨论为何经FFT得到的幅值、频率和相位不准的。
其实前面我也发过一篇介绍离散频谱校正的综述性的文章，可能大家都忙，没时间去看，呵呵，这里我就我的理解，把离散频谱分析的误差来源和校正方法做个简单的介绍。
离散频谱分析的误差产生的原因主要来自两方面，一方面是由于时域加窗截断产生的频域连续化，另一方面是由于计算机只能对有限的离散的频率进行计算，也即是频域离散化的结果。
其中，加窗截断的影响使一个无穷长单频率信号在频域对应的一根谱线，变成一个连续谱，以加矩形窗为例，则是变成一个sinc型函数的形状，其峰值对应的频率即为单频信号的频率。
但是由于频域的离散化，我们用FFT计算的频率一般都不会刚好会落在峰值处，这就是我们平时常说的泄露，这时我们就只能把计算得到的峰值谱线对应的频率做为估计的频率，如果以频率分辨率fs/N做归一 (即把频率分辨率看成1)的话，这个估计的频率的最大绝对值误差就是0.5，而幅值误差则依赖于加的窗的类型，由于矩形窗主瓣宽度为2，频谱开状较尖，幅值误差也就大。
至于相位的最大误差则会相应的达到正负90度，已经完全不能用了。
离散频谱校正就是针对这种误差提出的各种校正出实际的频率、幅值和相位的一门理论和技术。
国内现在比较常用的方法有比值(插值)法、能量重心法、FFT FT法和相位差法，都有其各自的特点和优缺点。
这里我给出一个比值校正法的程序供大家一起研究下。
当然，对于多频率成分的信号来说，离散频谱分析的另一个误差是来自于频率之间的相互干涉，这也是由于泄露所引起的，这个误差则主要靠加窗抑制旁瓣和减小频率分辨率、拉大频率间的距离(可通过ZFFT实现)来尽量减小。
%SpectrumCorrect_Test.mclose all;clear all;clc;fs=1024;N=1024;t=(0:N-1)/fs;x=4*cos(2*pi*80*t 30*pi/180) 3*cos(2*pi*150.232*t 80*pi/180)1*cos(2*pi*253.5453*t 240*pi/180);xf=fft(x);xf=xf(1:N/2)/N*2;XfCorrect=SpectrumCorrect(xf,3,1);XfCorrect(:,1)=XfCorrect(:,1)*fs/N;XfCorrectw=hann(N,’periodic’);xfw=fft(x.*w’);xfw=xfw(1:N/2)/N*4;XfCorrectW=SpectrumCorrect(xfw,3,2);XfCorrectW(:,1)=XfCorrectW(:,1)*fs/N;XfCorrectW%离散频谱比值校正法%by yangzj 2007.4.28%%xf为FFT后的复数谱%CorrectNum为校正的谱线条数%即校正最大的CorrectNum条%WindowType为加窗类型%1为矩形窗，2为Hanning窗%%SpectrumCorrect.mfunction XfCorrect=SpectrumCorrect(xf,CorrectNum,WindowType) XfCorrect=zeros(CorrectNum,3);for i=1:CorrectNumA=abs(xf);[Amax,index]=max(A);phmax=angle(xf(index));%比值法%加矩形窗if (WindowType==1)indsecL=A(index-1)>A(index 1);df=indsecL.*A(index-1)./(Amax A(index-1))-(1-indsecL).*A(index 1)./(Amax A(index 1));XfCorrect(i,1)=index-1-df;XfCorrect(i,2)=Amax/sinc(df);XfCorrect(i,3)=(phmax pi*df)*180/pi;xf(index-2:index 2)=zeros(1,5);end%比值法%加Hanning窗if (WindowType==2)indsecL=A(index-1)>A(index 1);df=indsecL.*(2*A(index-1)-Amax)./(AmaxA(index-1))-(1-indsecL).*(2*A(index 1)-Amax)./(Amax A(index 1)); XfCorrect(i,1)=index-1-df;XfCorrect(i,2)=(1-df )*Amax/sinc(df);XfCorrect(i,3)=(phmax pi*df)*180/pi;xf(index-4:index 4)=zeros(1,9);endXfCorrect(i,3)=mod(XfCorrect(i,3),360);XfCorrect(i,3)=XfCorrect(i,3)-(XfCorrect(i,3)>180)*360;end运行结果：XfCorrect =80.0014 4.0016 29.8261150.2333 2.9981 79.7127253.5397 0.9996 -118.7272XfCorrectW =80.0000 4.0000 30.0000150.2320 3.0000 80.0000253.5453 1.0000 -120.0002本文由声振论坛会员yangzj原创，结语：任何一个人，都要必须养成自学的习惯，即使是今天在学校的学生，也要养成自学的习惯，因为迟早总要离开学校的！自学，就是一种独立学习，独立思考的能力。
fft算法 离散频谱校正
fft算法离散频谱校正FFT（Fast Fourier Transform）算法是一种快速计算离散傅里叶变换（Discrete Fourier Transform）的算法。
它的主要思想是通过对称性将N点的DFT分解为两个N/2点的DFT，再通过重组得到最终结果。
该算法的时间复杂度为O(NlogN)，相较于传统的DFT算法，其计算速度更快，因此广泛应用在信号处理、图像处理、通信等领域中。
离散频谱校正是指在频域中对信号进行处理，以消除或校正频谱中的不良效应。
在进行频域处理时，可能会出现混叠效应（频谱重叠）或频率偏移等问题，这会导致信号的失真或干扰。
离散频谱校正的目的就是通过一系列算法和技术，对频谱进行调整和修正，以恢复信号的原始特性。
离散频谱校正的方法有很多种，下面将简要介绍几种常见的方法。
1. 频谱外插频谱外插是一种常见的频谱校正方法，它通过在频谱中插入一定数量的零值来改变信号的频谱特性。
这样可以使频谱变得更加平滑，并且减小混叠效应。
频谱外插在FFT算法中很容易实现，只需要将原始信号补零到2的幂次方长度即可。
2. 频谱滤波频谱滤波是指通过滤波器对频谱进行处理，以去除或衰减不需要的频率分量。
常见的滤波器包括低通滤波器、高通滤波器、带通滤波器等。
滤波器可以选择不同的截止频率、通带宽度和阻带宽度，以满足不同的要求。
3. 频谱修正频谱修正是一种校正频谱幅度和相位的方法。
通常在进行频域分析时，频率响应对于不同频率的信号可能有不同的增益和相位差，这就需要进行补偿和修正。
频谱修正的方法包括经验修正和数学模型修正等，可以根据信号的特性进行选择。
4. 非线性变换非线性变换是一种通过对频谱进行非线性操作，以改变频谱特性的方法。
常见的非线性变换包括幂律变换、对数变换、绝对值变换等。
非线性变换可以改变频谱的动态范围和分辨率，从而提取出信号的细节或增强信号的特征。
5. 频率域插值频率域插值是指通过对频谱进行插值，以增加频率的分辨率或减小频率的间隔。
讲座1-3离散频谱校正技术（DOC）
讲座1-3离散频谱校正技术（DOC）图3.1.1 窗函数的频谱函数讲座1-3三、离散频谱校正技术经FFT 得到的离散频谱其幅值、相位和频率都可能产生较大的误差。
从理论上分析，加矩形窗时单谐波频率的最大误差可达36.4％，即使加其它窗时，也不能完全消除此影响，如加Hanning 窗时，只进行幅值恢复时的最大误差仍高达15.3%，相位误差更大，高达90度。
目前国内外有四种对幅值谱或功率谱进行校正的方法：第一种方法是离散频谱能量重心校正法，第二种方法是对幅值谱进行校正的比值法，第三种方法是FFT+DFT 谱连续细化分析傅立叶变换法，第四种方法是相位差法，这些方法各有其特点。
在相位差校正法中，有时移法、缩短窗长法和综合法。
1．比值校正法这种方法利用频率归一化后差值为1的主瓣峰顶附近二条谱线的窗谱函数比值，建立一个以校正频率为变量的方程，解出校正频率，进而进行幅值和相位校正。
解方程求校正频率的方法是多样化的，直接导出公式的方法称比值公式法，利用迭代求解的方法称为比值迭代公式法，用搜索求解的方法称比值峰值搜索法。
研究表明，加Hanning 窗的比例校正法精度非常高，频率误差小于0.0001f ?，幅值误差小于万分之一，相位误差小于1度。
（1）频率校正频率校正即求出主瓣中心的横坐标。
设窗函数的频谱函数为()x f ，()x f 对称于y 轴，见图3.1.1。
对于任一x ，窗谱函数为()x f ，离散频谱为y x ；对于任一()1+x ，窗谱函数为()1+x f ，离散频谱为y x +1，构造v 为间隔为1的两点()x f 、()1+x f 的比值函数，由()x f 、()1+x f 、y x 和y x +1就能求出x 。
由于f(x)的函数表达式为已知，故可构造一函数v F x f x f x y y x x ==+=+()()()11(3.1.1)v 是间隔为1的两点的比值，是x 的函数，对上式解出其反函数：x g v =()(3.1.2)即求解谱线校正量x k x -=?=?，这种方法称为比值公式法。
离散频谱综合相位差校正法
离散频谱综合相位差校正法丁 康1 朱小勇2 谢 明2 钟舜聪1 罗江凯2(1汕头大学机械电子工程系 汕头,515063)(2重庆大学机械工程学院 重庆,400044)摘 要 提出一种利用相位差的离散频谱综合校正法——时域平移+改变窗长法,即第二段时域序列比第一段滞后L点,对这两段时域分别作N点和M点的FF T分析,利用对应峰值谱线的相位差进行频谱校正的方法。
这种方法是一种通用的离散频谱相位差校正法,文献[10～11]提出的校正方法只是此法的两个特例。
仿真结果表明,该方法实现方便,精度较高,适合于各种对称窗函数,抗噪声能力强。
关键词:频谱分析;校正;信号处理;相位差中图分类号:T N991.6 频谱分析是应用极为广泛的信号处理方法。
由于计算机只能对有限多个样本进行运算,FFT和谱分析也只能在有限区间内进行,这就不可避免地存在由于时域截断产生的能量泄漏,使谱峰值变小,精度降低。
从理论上分析,加矩形窗时单谐波频率成分的幅值最大误差达36.4%[1],即使加其它窗时,也不能完全消除此影响,如加Hanning窗时,只进行幅值恢复时的最大误差仍高达15.3%,相位误差更大,高达90°。
目前国内外有四种对幅值谱或功率谱进行校正的方法:第一种方法是能量校正法[1～3],第二种方法是对幅值谱进行校正的比值法[4～8],第三种方法是FFT+FT谱连续细化分析傅立叶变换法[9],第四种方法是相位差法[10～11],这些方法各有其特点,在工程实际中都得到了相应的应用。
在相位差校正法中,目前存在两种方法。
第一种作法是对连续时域信号分前后两段作FFT,利用其对应离散谱线的相位差校正出谱峰处的准确频率和相位[11];第二种作法是缩短窗长法:采样一段时域信号,对这一段序列分别进行N点和N/2点的FFT分析,利用其相位差进行频谱校正[10]。
如果作进一步的推广,第一种作法可以推广为时域平移法,第二种作法推广为改变窗长法。
五种离散频谱校正方法 python
一、介绍问题离散频谱校正是数字信号处理中的重要环节，通过对信号频谱进行校正可以提高信号质量，减少干扰和误差。
在Python中，有多种离散频谱校正的方法，本文将对其中五种常用的方法进行介绍和比较，以帮助读者理解和选择适合自己应用场景的方法。
二、基本概念在介绍具体的离散频谱校正方法之前，我们首先需要了解一些基本概念。
离散频谱是指在一定时间间隔内采样得到的信号频谱，校正即为对这些频谱进行修正和调整。
常见的离散频谱校正方法包括FFT变换、滤波器设计、频率域窗函数等。
三、离散频谱校正方法一：FFT变换1. FFT变换是离散频谱校正中应用最广泛的方法之一，其原理为将时域的离散信号通过快速傅里叶变换转换到频域，并对频域信号进行调整和校正。
在Python中，可以使用numpy库中的fft模块实现FFT变换。
2. 使用FFT变换对频谱进行校正需要注意的问题包括信号长度、采样率、窗函数选择等，合理的参数选择对校正效果具有重要影响。
四、离散频谱校正方法二：滤波器设计1. 滤波器设计是离散频谱校正的另一种常用方法，其原理为设计滤波器对频谱进行滤波，去除噪声和干扰成分。
在Python中，可以使用scipy库的signal模块实现滤波器设计。
2. 滤波器设计方法包括低通滤波、高通滤波、带通滤波等，选择合适的滤波器类型和参数是进行频谱校正的关键。
五、离散频谱校正方法三：频率域窗函数1. 频率域窗函数是一种常用的频谱校正方法，其原理为通过对频率域信号进行加窗处理，达到去除杂散信号、调整主要信号频谱的目的。
在Python中，可以使用scipy库的signal模块实现频率域窗函数。
2. 频率域窗函数的选择和参数设置对校正效果影响显著，读者在使用时需要根据具体信号特点进行调整。
六、离散频谱校正方法四：谱减法1. 谱减法是一种基于信噪比的离散频谱校正方法，其原理为利用信噪比信息对频谱进行减法处理，去除噪声成分。
在Python中，可以通过计算信号和噪声的功率谱密度来实现谱减法。
自动控制原理--离散系统的数字校正
最少拍统设计
• 设计要求：系统在稳定的基础上，必须满足： • ① 对典型输入函数，输出在采样时刻上无稳
态误差； • ② 过渡过程（函数）在最少个采样周期内结
束。
• 1. 稳定性
• 一个稳定系统的脉冲传递函数的特征方程 的根，必须全部位于单位圆内。如果G(z)中 包含有单位圆上或单位圆外的零点或极点时， 必须通过选择，使它们能抵消G(z)中的不稳 定零,极点。
1、间接设计法
先按连续系统进行设计，然后将所设计的模拟控制器 离散化得到数字控制器。 2、根轨迹法和频率法
根轨迹法和频率法在离散系统中的推广。将控制对象 离散化，并用离散系统理论在z平面或w平面上进行设计的 两种直接设计方法
3、直接数字设计法
直接根据离散系统理论在z域进行综合的解析方法。
最少拍离散控制系统的设计
8.7 离散控制系统的数字校正
控制系统在某些方面不能满足要求时， 必须对系统加以校正，并应设计使系统满 足要求的校正装置。在离散控制系统中， 大多用数字计算机来实现，只要改变计算 机程序就可以改变校正装置的形式和参数。 计算机还可以完成较复杂的运算，使系统 的性能得到极大的改善。
线性离散系统的设计方法：
• 方法：
• 在 1 (z) 中，以零点的形式把G(z)的不稳 定极点包含在内；
• 在 (z) 中，以零点的形式把G(z)的不稳定零 点包含在内；
• 2. 典型输入信号
• 最少拍系统的设计, 是针对典型输入作用进行的. 常见的典型输入, 有单位阶跃函数、单位速度函 数和单位加速度函数。误差传递函数与系统输入 类型的关系。典型的输入信号一般为：
三种输入的Z变换可以看出，它们都可用下式表示 :
R(z)
(1
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
矿产资源开发利用方案编写内容要求及审查大纲
矿产资源开发利用方案编写内容要求及《矿产资源开发利用方案》审查大纲一、概述
㈠矿区位置、隶属关系和企业性质。
如为改扩建矿山, 应说明矿山现状、
特点及存在的主要问题。
㈡编制依据
(1简述项目前期工作进展情况及与有关方面对项目的意向性协议情况。
(2 列出开发利用方案编制所依据的主要基础性资料的名称。
如经储量管理部门认定的矿区地质勘探报告、选矿试验报告、加工利用试验报告、工程地质初评资料、矿区水文资料和供水资料等。
对改、扩建矿山应有生产实际资料, 如矿山总平面现状图、矿床开拓系统图、采场现状图和主要采选设备清单等。
二、矿产品需求现状和预测
㈠该矿产在国内需求情况和市场供应情况
1、矿产品现状及加工利用趋向。
2、国内近、远期的需求量及主要销向预测。
㈡产品价格分析
1、国内矿产品价格现状。
2、矿产品价格稳定性及变化趋势。
三、矿产资源概况
㈠矿区总体概况
1、矿区总体规划情况。
2、矿区矿产资源概况。
3、该设计与矿区总体开发的关系。
㈡该设计项目的资源概况
1、矿床地质及构造特征。
2、矿床开采技术条件及水文地质条件。