全国版2019版高考数学一轮复习第1章集合与常用逻辑用语第1讲集合的概念与运算增分练
2019版高考数学(理)高分计划一轮高分讲义:第1章 集合与常用逻辑用语 命题及其关系、充分与必要条件
A.必要不充分条件
B.既不充分也不必要条件
C.充要条件
D.充分不必要条件
答案 A
用等价转化法.
解析 由题意得:
∵命题“若 a≠1 或 b≠2,则 a+b≠3”与命题“若 a+b=3,
则 a=1 且 b=2”互为逆否命题.
∴判断命题“若 a≠1 或 b≠2,则 a+b≠3”的真假只要判断命
题“若 a+b=3,则 a=1 且 b=2”的真假即可.
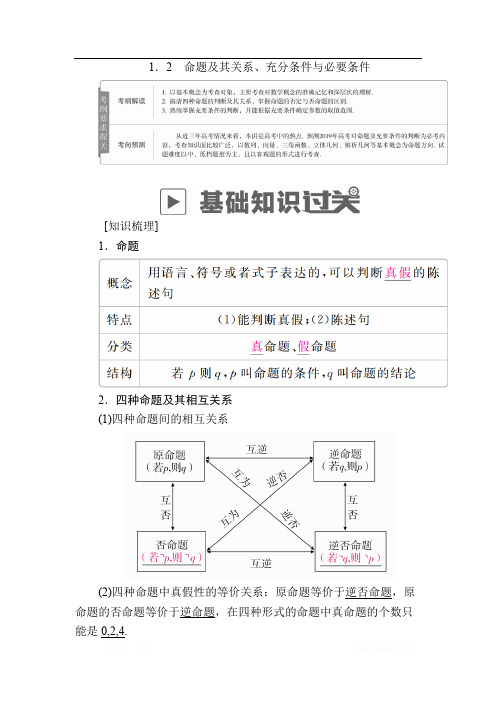
1.2 命题及其关系、充分条件与必要条件
[知识梳理] 1.命题
2.四种命题及其相互关系 (1)四种命题间的相互关系
(2)四种命题中真假性的等价关系:原命题等价于逆否命题,原 命题的否命题等价于逆命题,在四种形式的命题中真命题的个数只 能是 0,2,4.
(3)写一个命题的其他三种命题时,需注意: ①对于不是“若 p,则 q”形式的命题,需先改写; ②当命题有大前提时,写其他三种命题时需保留大前提; ③对于有多个并列条件的命题,应把其中一个作为大前提. 3.充要条件 (1)集合与充要条件
角度 4 探求结论成立的充分、必要条件
典例 (2018·延安质检)函数 f(x)=Error!有且只有一
个零点的充分不必要条件是( ) 1
A.a<0 1
B.0<a<2
C.2<a<1
D.a≤0 或 a>1
答案 A
用数形结合法.
解析 因为函数 f(x)过点(1,0),所以函数 f(x)有且只有一个零点
1.概念思辨
(1)“x2+2x-3<0”是命题.( ) (2)命题“若 p,则 q”的否定是“若綈 p,则綈 q”.( )
(3)若命题“若 p,则 q”为真命题,则这个命题的否命题、逆 命题、逆否命题中至少有一个为真. ( )
2019版高考数学(文)大一轮(全国通用版)课件:第1讲集合的概念与运算

栏目导 航
板 块 一
板 块 二
板 块 三
• 1.元素与集合 确定性 互异性 • (1)集合元素的特性:__________、 __________、无序性. a∈A b∉A • (2)集合与元素的关系:若 a属于集合A,记作 列举法 描述法 ________;若b不属于集合A,记作 ________. 数 自然数 整数 有理数 实数 • (3)集合的表示方法: ____________ 、 正整数集 集 集 集 集 集 ____________、图示法. 符 N Z Q R N*或N+ • (4)常见数集及其符号表示 号
1.思维辨析(在括号内打“√”或“×”). (1)集合{x2+x,0}中,实数 x 可取任意值.( (2)任何集合都至少有两个子集.(
× ×)
)
×
(3)集合{x|y= x-1}与集合{y|y= x-1}是同一个集合.( (4)若 A={0,1},B={(x,y)|y=x+1},则 A⊆B.(
×
)
)
第 一 章 集合与常用逻辑用语
第1讲 集合的概念与运算
考纲要求 1.了解集合的含义、元素与集 合的属于关系. 2.能用自然语言、图形语 言、集合语言(列举法或描述 法)描述不同的具体问题. 3.理解集合之间包含与相等 的含义,能识别给定集合的子 集. 4.在具体情境中了解全集与 空集的含义. 5.理解两个集合的并集与交 集的含义,会求两个简单集合 的并集与交集. 6.理解在给定集合中一个子 集的补集的含义,会求给定子 集的补集. 7.能使用韦恩(Venn)图表达集
{x|x∈A或x∈B}
{x|x∈A且x∈B}
• • • • •
(2)三种基本运算的常见性质 ①A∪B=A⇔B⊆A,A∩B=A⇔A⊆B; A ∅ ②A∩A=________,A∩∅=________; A A ③A∪A=________, A∪∅=________ ; U A ∅ ④A∩∁UA=________,A∪∁UA=________ ,∁U(∁UA)=________; • ⑤A⊆B⇔A∩B=A⇔A∪B= B⇔∁UA⊇∁UB⇔A∩(∁UB)=∅.
高中数学高考第1讲 集合的概念与运算

第一章 集合与常用逻辑用语
20
(1)已知集合 A={x|x2-3x+2=0,x∈R},B={x|0<x<5,x∈N},则满足条件
A⊆C⊆B 的集合 C 的个数为
()
A.1
B.2
C.3
D.4
(2)已知集合 A={x|-1<x<3},B={x|-m<x<m},若 B⊆A,则 m 的取值范围为______.
上一页
返回导航
下一页
第一章 集合与常用逻辑用语
24
2.已知集合 A={x|x2-2x-3≤0,x∈N*},则集合 A 的真子集的个数为
()
A.7
B.8
C.15
D.16
解析:选 A.法一:A={x|-1≤x≤3,x∈N*}={1,2,3},其真子集有:∅,{1},{2},
{3},{1,2},{1,3},{2,3}共 7 个.
下一页
第一章 集合与常用逻辑用语
8
2.设集合 A={x|-2≤x≤2},Z 为整数集,则集合 A∩Z 中元素的个数是 ( )
A.3
B.4
C.5
D.6
解析:选 C.A 中包含的整数元素有-2,-1,0,1,2,共 5 个,所以 A∩Z 中的元
素个数为 5.
上一页
返回导航
下一页
第一章 集合与常用逻辑用语
上一页
返回导航
下一页
第一章 集合与常用逻辑用语
11
2.已知集合 A={x|(x-1)(x-3)<0},B={x|2<x<4},则 A∩B=________,A∪B= ________,(∁RA)∪B=________. 解析:由已知得 A={x|1<x<3},B={x|2<x<4}, 所以 A∩B={x|2<x<3},A∪B={x|1<x<4},(∁RA)∪B={x|x≤1 或 x>2}. 答案:(2,3) (1,4) (-∞,1]∪(2,+∞)
2019版高考数学一轮复习 第一章 集合与逻辑用语 第1讲 集合的含义与基本关系配套课件 理

会求两个简单集合的并集与交集.
并集运算;
化为基础问题的
(2)理解在给定集合中一个子集的补集 2017年新课标Ⅱ第1题考查并集运算; 技巧与方法,就
的含义,会求给定子集的补集.
2017年新课标Ⅲ第1题考查交集运算及 会使看似复杂的
(3)能使用韦恩(Venn)图表达集合的关系 元素个数的判断
问题变得简单
{1,3,4,5,6,7},M∪N={2,3,5,6},∁U(M∪N)={1,4,7},(∁UM)∩N
={1,4,6,7}∩{2,6}={6}.故选C.
答案:C
26
(3)(2017年新课标Ⅰ)已知集合A={x|x<1},B={x|3x<1},
则( )
A.A∩B={x|x<0}
B.A∪B=R
C.A∪B={x|x>1}
答案:D
16
考向 3 集合与集合之间的关系 例 3:(1)已知集合 A={x|x2=1},B={x|ax=1},若 A∩B =B,则实数 a 的取值集合为( ) A.{-1,0,1} B.{-1,1} C.{-1,0} D.{0,1} 解析:若 A∩B=B,则有 B⊆A,A={1,-1}.当 a=0 时, B=∅,适合题意;当 a≠0 时,B=1a⊆A,则1a=1 或1a=-1, 解得 a=1 或 a=-1.所以实数 a 的取值集合为{-1,0,1}.
答案:{0,1,-1}
19
【规律方法】(1)含n个元素的集合有2n个子集;(2)注意∅的 特殊性.空集是任何集合的子集.当B⊆A时,需考虑B=∅的情形; 当A∩B=∅时,也需考虑B(或A)=∅的情形;当集合B不是空集 时,可以利用数轴,既直观又简洁.
20
考点 2 集合的基本运算
2019版高考数学微一轮复习 第一章 集合与常用逻辑用语 第1节 集合

考点二 集合的基本关系
【典例 2】 (1)(2018·青岛模拟)已知集合 A={x|y= 1-x2,x∈R},B={x|x=m2,
m∈A},则( )
A.A B
B.B A
C.A⊆B
D.B⊆A
(2)(2018·丹东市高三质检)已知集合 A={x|x≥2},B={x|x≤2m2},且 A⊆∁RB,那
么 m 的值可以是( )
=( )
A.3,-32 C.1,32
B.-3,32 D.32,3
解析:通过解不等式化简集合 A,B,再利用交集定义求解. ∵x2-4x+3<0,∴1<x<3, ∴A={x|1<x<3.} ∵2x-3>0,∴x>32,∴B=xx>32 . ∴A∩B={x|1<x<3}∩xx>32 =x32<x<3 . 故选 D. 答案:D
【反思归纳】 1求解集合概念问题关键要把握集合元素的特性,特别注意互异 性的验证.
2对于含有字母的集合求解要分类讨论并在求出字母的值后加以验证.
【即时训练】
(1)设集合 A={1,2,3},B={4,5},M={x|x=a+b,a∈A,b∈B},则 M 中的元素
个数为( )
A.3
B.4
C.5Leabharlann ()A.(-1,1)B.(0,1)
C.(-1,+∞)
D.(0,+∞)
(2)已知集合 A={x|x2-x-12≤0},B={x|2m-1<x<m+1},且 A∩B=B,则实数
m 的取值范围为( )
A.[-1,2)
B.[-1,3]
C.[2,+∞)
D.[-1,+∞)
解析:(1)∵A={y|y>0},B={x|-1<x<1},∴A∪B=(-1,+∞),故选 C. (2)由 x2-x-12≤0,得(x+3)(x-4)≤0,即-3≤x≤4,所以 A={x|-3≤x≤4}, 又 A∩B=B,所以 B⊆A. ①当 B=∅时,有 m+1≤2m-1, 解得 m≥2.
高三数学(文 新课标)一轮复习课件:第一章 集合与常用逻辑用语 ppt

2019年6月1日
缘分让我们相遇,缘分让我们在一起
1
2.常用逻辑用语 (1)理解命题的概念.
(2)了解“若 p,则 q”形式的命题及其逆命题、否命题
与逆否命题,会分析四种命题的相互关系. (3)理解必要条件、充分条件与充要条件的含义. (4)了.解逻辑联结词“或”“且”“非”的含义. (5)理解全称量词和存在量词的意义.
第一章 集合与常用逻辑用语
考纲链接
1.集合 (1)集合的含义与表示 ①了解集合的含义,体会元素与集合的属于关系. ②能用自然语言、图形语言、集合语言(列举法或描述法)描述不同的具体问题. (2)集合间的基本关系 ①理解集合之间包含与相等的含义,能识别给定集合的子集. ②在具体情境中,了解全集与空集的含义. (3)集合的基本运算 ①理解两.个集合的并集与交集的含义,会求两个简单集合的并集与交集. ②理解在给定集合中一个子集的补集的含义,会求给定子集的补集. ③能使用韦恩(Venn)图表达集合间的基本关系及集合的基本运算.
=∅,则实数 a 的取值范围为________.
2019年6月1日
缘分让我们相遇,缘分让我们在一起
19
解:(1)因为{1,a+b,a}=0,ba,b,a≠0, 所以 a+b=0,ba=-1,从而 b=1, 所以 a=-1,b=1,所以 b-a=2.故填 2. (2)由 A=∅知方程 ax2+3x-2=0 无实根, 当 a=0 时,x=23不合题意,舍去;
(6)能正确地对含一个量词的命题进行否定 .
2019年6月1日
缘分让我们相遇,缘分让我们在一起
2
• 1.1 集合及其运算
2019年6月1日
缘分让我们相遇,缘分让我们在一起
3
1.集合的基本概念
「精品」全国版高考数学一轮复习第1章集合与常用逻辑用语第1讲集合的概念与运算学案
第1讲集合的概念与运算板块一知识梳理·自主学习[必备知识]考点1 集合与元素1.集合中元素的三个特征:确定性、互异性、无序性.2.元素与集合的关系是属于或不属于两种,用符号∈或∉表示.3.集合的表示法:列举法、描述法、图示法.4.常见数集的记法A B或B A∅⊆A∅B(B≠∅)[必会结论]1.若有限集A 中有n 个元素,则集合A 的子集个数为2n ,真子集的个数为2n-1,非空真子集的个数为2n-2.2.A ⊆B ⇔A ∩B =A ⇔A ∪B =B .3.A ∩(∁U A )=∅;A ∪(∁U A )=U ;∁U (∁U A )=A .[考点自测]1.判断下列结论的正误.(正确的打“√”,错误的打“×”) (1)集合{x |y =x -1}与集合{y |y =x -1}是同一个集合.( )(2)已知集合A ={x |mx =1},B ={1,2},且A ⊆B ,则实数m =1 或m =12.( )(3)M ={x |x ≤1},N ={x |x >ρ},要使M ∩N =∅,则ρ所满足的条件是ρ≥1.( ) (4)若集合A ={-1,1},B ={0,2},则集合{z |z =x +y ,x ∈A ,y ∈B }中有4个元素.( ) (5)若5∈{1,m +2,m 2+4},则m 的取值集合为{1,-1,3}.( ) 答案 (1)× (2)× (3)√ (4)× (5)×2.[2017·北京高考]若集合A ={x |-2<x <1},B ={x |x <-1或x >3},则A ∩B =( ) A .{x |-2<x <-1} B .{x |-2<x <3} C .{x |-1<x <1} D .{x |1<x <3}答案 A解析 ∵A ={x |-2<x <1},B ={x |x <-1或x >3}, ∴A ∩B ={x |-2<x <-1}.故选A.3.[课本改编]已知集合A ={x |x 2-2x -3≤0},B ={x |0<x ≤4},则A ∪B =( ) A .[-1,4] B .(0,3]C .(-1,0]∪(1,4]D .[-1,0]∪(1,4]答案 A解析 A ={x |x 2-2x -3≤0}={x |-1≤x ≤3},故A ∪B =[-1,4].选A. 4.[2017·全国卷Ⅰ]已知集合A ={x |x <1},B ={x |3x<1},则( ) A .A ∩B ={x |x <0} B .A ∪B =R C .A ∪B ={x |x >1}D .A ∩B =∅解析∵B={x|3x<1},∴B={x|x<0}.又A={x|x<1},∴A∩B={x|x<0},A∪B={x|x<1}.故选A.5.[2018·重庆模拟]已知集合A={x∈N|πx<16},B={x|x2-5x+4<0},则A∩(∁R B)的真子集的个数为( )A.1 B.3C.4 D.7答案 B解析因为A={x∈N|πx<16}={0,1,2},B={x|x2-5x+4<0}={x|1<x<4},故∁R B={x|x≤1或x≥4},故A∩(∁R B)={0,1},故A∩(∁R B)的真子集的个数为3.故选B.板块二典例探究·考向突破考向集合的基本概念例1 (1)[2017·郑州模拟]已知集合A={x|y=1-x2,x∈Z},B={p-q|p∈A,q∈A},则集合B中元素的个数为( )A.1 B.3C.5 D.7答案 C解析由题意知A={-1,0,1},当p=-1,q=-1,0,1时,p-q=0,-1,-2;当p=0,q =-1,0,1时,p-q=1,0,-1;当p=1,q=-1,0,1时,p-q=2,1,0.根据集合中元素的互异性可知,集合B中的元素为-2,-1,0,1,2,共计5个,选C.(2)已知集合A={a2,a+1,-3},B={a-3,a-2,a2+1},若A∩B={-3},则a=________.答案-1解析由A∩B={-3}知,-3∈B.又a2+1≥1,故只有a-3,a-2可能等于-3.①当a-3=-3时,a=0,此时A={0,1,-3},B={-3,-2,1},A∩B={1,-3}.故a=0舍去.②当a-2=-3时,a=-1,此时A={1,0,-3},B={-4,-3,2},满足A∩B={-3},故a=-1.触类旁通解决集合概念问题的一般思路(1)研究一个集合,首先要看集合中的代表元素,然后再看元素的限制条件,当集合用描述法表示时,注意弄清其元素表示的意义是什么.本例(1)集合B中的代表元素为实数p-q.(2)要深刻理解元素的互异性,在解决集合中含有字母的问题时,一定要返回代入验证,防止与集合中元素的互异性相矛盾.【变式训练1】(1)[2018·昆明模拟]若集合A={x|x2-9x<0,x∈N*},B={|y 4y∈N*,y∈N*,则A∩B中元素的个数为________.解析 解不等式x 2-9x <0可得0<x <9,所以A ={x |0<x <9,x ∈N *}={1,2,3,4,5,6,7,8},又4y∈N *,y ∈N *,所以y 可以为1,2,4,所以B ={1,2,4},所以A ∩B =B ,A ∩B 中元素的个数为3.(2)已知集合A ={m +2,2m 2+m },若3∈A ,则m 的值为________. 答案 -32解析 因为3∈A ,所以m +2=3或2m 2+m =3. 当m +2=3,即m =1时,2m 2+m =3, 此时集合A 中有重复元素3, 所以m =1不符合题意,舍去;当2m 2+m =3时,解得m =-32或m =1(舍去),此时当m =-32时,m +2=12≠3符合题意.所以m =-32.考向集合间的基本关系例 2 已知集合A ={x |x <-3或x >7},B ={x |x <2m -1},若B ⊆A ,则实数m 的取值范围是________.答案 (-∞,-1]解析 由题意知2m -1≤-3,m ≤-1,∴m 的取值范围是(-∞,-1].本例中的B 改为B ={x |m +1≤x ≤2m -1},其余不变,该如何求解?解 当B =∅时,有m +1>2m -1,则m <2.当B ≠∅时,⎩⎪⎨⎪⎧m +1≤2m -1,2m -1<-3或⎩⎪⎨⎪⎧m +1≤2m -1,m +1>7,解得m >6.综上可知m 的取值范围是(-∞,2)∪(6,+∞).本例中的A 改为A ={x |-3≤x ≤7},B 改为B ={x |m +1≤x ≤2m -1},又该如何求解?解 当B =∅时,满足B ⊆A ,此时有m +1>2m -1,即m <2;当B ≠∅时,要使B ⊆A ,则有⎩⎪⎨⎪⎧m +1≥-3,2m -1≤7,m ≥2,解得2≤m ≤4.综上可知m 的取值范围是(-∞,4].根据两集合的关系求参数的方法(1)空集是任何集合的子集,在涉及集合关系时,必须优先考虑空集的情况,否则会造成漏解. (2)已知两个集合间的关系求参数时,关键是将条件转化为元素或区间端点间的关系,进而转化为参数所满足的关系,常用数轴、Venn 图等来直观解决这类问题.【变式训练2】 设A ={x |x 2-8x +15=0},B ={x |ax -1=0}. (1)若a =15,试判定集合A 与B 的关系;(2)若BA ,求实数a 组成的集合C .解 (1)由x 2-8x +15=0, 得x =3或x =5,∴A ={3,5}.若a =15,由ax -1=0,得15x -1=0,即x =5.∴B ={5}.∴B A . (2)∵A ={3,5},又BA ,故若B =∅,则方程ax -1=0无解,有a =0; 若B ≠∅,则a ≠0,由ax -1=0,得x =1a.∴1a =3或1a =5,即a =13或a =15. 故C =⎩⎨⎧⎭⎬⎫0,13,15.考向集合的基本运算命题角度1 集合的交集及运算例 3 [2017·山东高考]设集合M ={x ||x -1|<1},N ={x |x <2},则M ∩N =( ) A .(-1,1) B .(-1,2) C .(0,2) D .(1,2)答案 C解析 ∵M ={x |0<x <2},N ={x |x <2}, ∴M ∩N ={x |0<x <2}∩{x |x <2}={x |0<x <2}. 故选C.命题角度2 集合的并集及运算例 4 [2018·武汉模拟]设全集U =R ,集合A ={x |2x -x 2>0},B ={y |y =e x+1},则A ∪B 等于( )A .{x |x <2}B .{x |1<x <2}C .{x |x >1}D .{x |x >0}答案 D解析 由2x -x 2>0得0<x <2,故A ={x |0<x <2},由y =e x+1得y >1,故B ={y |y >1},所以A ∪B ={x |x >0}.故选D.命题角度3 集合的补集及运算例 5 [2016·浙江高考]已知集合P={x∈R|1≤x≤3},Q={x∈R|x2≥4},则P∪(∁R Q)=( )A.[2,3]B.(-2,3]C.[1,2)D.(-∞,-2]∪[1,+∞)答案 B解析∵Q=(-∞,-2]∪[2,+∞),∴∁R Q=(-2,2),∴P∪(∁R Q)=(-2,3].故选B.命题角度4 抽象集合的运算例 6 [2018·唐山统一测试]若全集U=R,集合A={|x x+1x-6≤0,B={x|2x<1},则下图中阴影部分表示的集合是( )A.{x|2<x<3} B.{x|-1≤x<0}C.{x|0≤x<6} D.{x|1≤x≤6}答案 C解析A={x|-1≤x<6},B={x|x<0},A∩(∁U B)={x|0≤x<6}.选C项.触类旁通集合的基本运算的关注点(1)看元素组成.集合是由元素组成的,从研究集合中元素的构成入手是解决集合运算问题的前提.(2)有些集合是可以化简的,先化简再研究其关系并进行运算,可使问题简单明了,易于解决.(3)注意数形结合思想的应用,常用的数形结合形式有数轴、坐标系和Venn图.核心规律解决集合问题,要正确理解有关集合的含义,认清集合元素的属性;再依据元素的不同属性,采用不同的方法对集合进行化简求解,一般的规律为:(1)若给定的集合是不等式的解集,用数轴来解;(2)若给定的集合是点集,用数形结合法求解;(3)若给定的集合是抽象集合,用Venn图求解.满分策略1.元素的属性:描述法表示集合问题时,认清集合中元素的属性(是点集、数集或其他情形)是正确求解集合问题的先决条件.2.元素的互异性:在解决含参数的集合问题时,要注意检验集合中元素的互异性,否则很可能会因为不满足“互异性”而导致解题错误.3.空集的特殊性:在解决有关A∩B=∅,A⊆B等集合问题时,要先考虑∅是否成立,以防漏解.板块三启智培优·破译高考创新交汇系列1——集合中的创新性问题[2018·吉林模拟]设全集U={1,2,3,4,5,6},且U的子集可表示由0,1组成的6位字符串,如:{2,4}表示的是自左向右的第2个字符为1,第4个字符为1,其余字符均为0的6位字符串010100,并规定空集表示的字符串为000000.(1)若M={2,3,6},则∁U M表示的6位字符串为________;(2)已知A={1,3},B⊆U,若集合A∪B表示的字符串为101001,则满足条件的集合B的个数是________.解题视点考查新定义问题,关键是正确理解题目中的新定义,利用集合间的关系及运算解决问题.解析(1)由已知得,∁U M={1,4,5},则∁U M表示的6位字符串为100110.(2)由题意可知A∪B={1,3,6},而A={1,3},B⊆U,则B可能为{6},{1,6},{3,6},{1,3,6},故满足条件的集合B的个数是4.答案(1)100110 (2)4答题启示解决以集合为背景的新定义问题,要抓住两点:(1)紧扣新定义.首先分析新定义的特点,把新定义所叙述的问题的本质弄清楚,并能够应用到具体的解题过程之中,这是破解新定义型集合问题难点的关键所在;(2)用好集合的性质.解题时要善于从试题中发现可以使用集合性质的一些因素,在关键之处用好集合的运算与性质.跟踪训练设A是整数集的一个非空子集,对于k∈A,如果k-1∉A且k+1∉A,那么k是A的一个“孤立元”,给定A={1,2,3,4,5},则A的所有子集中,只有一个“孤立元”的集合共有( ) A.10个B.11个C.12个D.13个答案 D解析“孤立元”是1的集合:{1},{1,3,4},{1,4,5},{1,3,4,5}.“孤立元”是2的集合:{2},{2,4,5}.“孤立元”是3的集合:{3}.“孤立元”是4的集合:{4},{1,2,4}.“孤立元”是5的集合:{5},{1,2,5},{2,3,5},{1,2,3,5}.共有13个.故选D.板块四模拟演练·提能增分[A级基础达标]1.[2017·全国卷Ⅱ]设集合A={1,2,4},B={x|x2-4x+m=0}.若A∩B={1},则B=( )A.{1,-3} B.{1,0}C.{1,3} D.{1,5}答案 C解析∵A∩B={1},∴1∈B.∴1-4+m=0,即m=3.∴B={x|x2-4x+3=0}={1,3}.故选C.2.若集合M={x||x|≤1},N={y|y=x2,|x|≤1},则( )A.M=N B.M⊆NC.N⊆M D.M∩N=∅答案 C解析M={x||x|≤1}=[-1,1],N={y|y=x2,|x|≤1}=[0,1],所以N⊆M.故选C.3.[2017·山东高考]设函数y=4-x2的定义域为A,函数y=ln (1-x)的定义域为B,则A∩B =( )A.(1,2) B.(1,2]C.(-2,1) D.[-2,1)答案 D解析∵4-x2≥0,∴-2≤x≤2,∴A=[-2,2].∵1-x>0,∴x<1,∴B=(-∞,1),∴A∩B=[-2,1).故选D.4.已知集合A={x|x2≥4},B={m}.若A∪B=A,则m的取值范围是( )A.(-∞,-2) B.[2,+∞)C.[-2,2] D.(-∞,-2]∪[2,+∞)答案 D解析因为A∪B=A,所以B⊆A,即m∈A,得m2≥4,解得m≥2或m≤-2.故选D.5.[2017·全国卷Ⅲ]已知集合A={(x,y)|x2+y2=1},B={(x,y)|y=x},则A∩B中元素的个数为( )A.3 B.2C.1 D.0答案 B解析集合A表示以原点O为圆心,半径为1的圆上的所有点的集合,集合B表示直线y=x上的所有点的集合.由图形可知,直线与圆有两个交点,所以A∩B中元素的个数为2.故选B.6.已知集合A={x|x2-3x+2=0,x∈R},B={x|0<x<5,x∈N},则满足条件A⊆C⊆B的集合C的个数为( )A.1 B.2C.3 D.4答案 D解析集合B={1,2,3,4},有4个元素,集合A={1,2},则集合C的个数问题可转化为{3,4}的子集个数问题,即22=4.7.[2018·陕西模拟]设全集U =R ,集合A ={|x ∈Z x3-x≥0},B ={x ∈Z |x 2≤9},则图中阴影部分表示的集合为( )A .{1,2}B .{0,1,2}C .{x |0≤x <3}D .{x |0≤x ≤3}答案 B解析 题图中阴影部分表示的是A ∩B ,因为A ={|x ∈Z xx -3≤0}={|x ∈Z ⎩⎪⎨⎪⎧x (x -3)≤0,x -3≠0}={x ∈Z |0≤x <3}={0,1,2},B ={x ∈Z |-3≤x ≤3}={-3,-2,-1,0,1,2,3},所以A ∩B ={0,1,2}.故选B.8.设集合A ={x |-1≤x <2},B ={x |x <a },若A ∩B ≠∅,则a 的取值范围是________. 答案 (-1,+∞)解析 因为A ∩B ≠∅,所以集合A ,B 有公共元素,作出数轴,如图所示,易知a >-1.9.[2018·郑州模拟]已知集合A ={x ∈R ||x +2|<3},集合B =⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ∈R ⎪⎪⎪x -mx -2<0,且A ∩B =(-1,n ),则m =________,n =________.答案 -1 1解析 A ={x ∈R ||x +2|<3}={x ∈R |-5<x <1}, 由A ∩B =(-1,n ),可知m <1,则B ={x |m <x <2},画出数轴,可得m =-1,n =1.10.设m ,n ∈R ,集合{1,m ,m +n }=⎩⎨⎧⎭⎬⎫0,n ,n m ,则m -n =________.答案 -2解析 ∵{1,m ,m +n }=⎩⎨⎧⎭⎬⎫0,n ,n m 且m ≠0,∴m +n =0, 即m =-n ,于是n m=-1.∴由两集合相等,得m =-1,n =1,∴m -n =-2.[B 级 知能提升]1.已知集合A ={|y y =⎝ ⎛⎭⎪⎫12x,x ∈R },B ={-2,-1,1,2},则下列结论正确的是( )A .A ∩B ={-2,-1} B .(∁R A )∪B =(-∞,0)C .A ∪B =(0,+∞)D .(∁R A )∩B ={-2,-1}答案 D解析 因为A =(0,+∞),所以A ∩B ={1,2},(∁R A )∪B ={y |y ≤0或y =1,2},A ∪B ={y |y >0或y =-1,-2},(∁R A )∩B ={-1,-2}.所以D 正确.2.[2018·湖南模拟]设常数a ∈R ,集合A ={x |(x -1)(x -a )≥0},B ={x |x ≥a -1},若A ∪B =R ,则a 的取值范围为( )A .(-∞,2)B .(-∞,2]C .(2,+∞)D .[2,+∞)答案 B解析 集合A 讨论后利用数轴可知⎩⎪⎨⎪⎧a ≥1,a -1≤1或⎩⎪⎨⎪⎧a ≤1,a -1≤a .解得1≤a ≤2或a ≤1,即a ≤2.故选B.3.已知数集A ={a 1,a 2,…,a n }(1≤a 1<a 2<…<a n ,n ≥2)具有性质P :对任意的i ,j (1≤i ≤j ≤n ),a i a j 与a ja i两数中至少有一个属于A ,则称集合A 为“权集”,则( )A .{1,3,4}为“权集”B .{1,2,3,6}为“权集”C .“权集”中元素可以有0D .“权集”中一定有元素1答案 B解析 由于3×4与43均不属于数集{1,3,4},故A 不正确;由于1×2,1×3,1×6,2×3,62,63,11,22,33,66都属于数集{1,2,3,6},故B 正确;由“权集”的定义可知a ja i 需有意义,故不能有0,同时不一定有1,故C ,D 错误.4.已知集合A ={x ∈R |x 2-ax +b =0},B ={x ∈R |x 2+cx +15=0},A ∩B ={3},A ∪B ={3,5}. (1)求实数a ,b ,c 的值;(2)设集合P ={x ∈R |ax 2+bx +c ≤7},求集合P ∩Z .解 (1)因为A ∩B ={3},所以3∈B ,所以32+3c +15=0,c =-8,所以B ={x ∈R |x 2-8x +15=0}={3,5}.又因为A ∩B ={3},A ∪B ={3,5},所以A ={3},所以方程x 2-ax +b =0有两个相等的实数根都是3,所以a =6,b =9,所以a =6,b =9,c =-8.(2)不等式ax 2+bx +c ≤7即6x 2+9x -8≤7, 所以2x 2+3x -5≤0,学习资料 值得拥有11 所以-52≤x ≤1, 所以P ={|x -52≤x ≤1}, 所以P ∩Z ={|x -52≤x ≤1}∩Z ={-2,-1,0,1}. 5.[2018·南宁段考]已知集合P ={x |a +1≤x ≤2a +1},Q ={x |x 2-3x ≤10}.(1)若a =3,求(∁R P )∩Q ;(2)若P ∪Q =Q ,求实数a 的取值范围.解 (1)因为a =3,所以P ={x |4≤x ≤7},∁R P ={x |x <4或x >7}.又Q ={x |x 2-3x -10≤0}={x |-2≤x ≤5},所以(∁R P )∩Q ={x |x <4或x >7}∩{x |-2≤x ≤5}={x |-2≤x <4}.(2)当P ≠∅时,由P ∪Q =Q 得P ⊆Q , 所以⎩⎪⎨⎪⎧ a +1≥-2,2a +1≤5,2a +1≥a +1,解得0≤a ≤2;当P =∅,即2a +1<a +1时,有P ⊆Q ,得a <0.综上,实数a 的取值范围是(-∞,2].。
(江苏专版)2019版高考数学一轮复习 第一章 集合与常用逻辑用语 第一节 集合的概念与运算课件 文
(2)元素与集合的两种关系:属于,记为_∈___;不属于,记为__∉_.
(3)集合的三种表示方法: 列举法 、 描述法 、 图示法 .
(4)五个特定的集合:
集合 自然数集 正整数集 整数集 有理数集 实数集
符号 _N__ __N_*_或 N+ _Z__
_Q__
_R__
2.集合间的基本关系
表示 关系
所以 0<m≤1.
综上所述 m 的取值范围为(-∞,1].
答案:(-∞,1]
3.(2018·海门中学测试)已知集合 A={1,3, x},B={2-x,1}. (1)记集合 M={1,4,y},若集合 A=M,求实数 x+y 的值; (2)是否存在实数 x,使得 B⊆A?若存在,求出 x 的值;若 不存在,请说明理由.
答案:4
课 堂 考点突破
自主研、合作探、多面观,全扫命题题点
考点一 集合的基本概念
[题组练透]
1.(易错题)已知集合 A={1,2,4},则集合 B={(x,y)|x ∈A,y∈A}中元素的个数为________. 解析:集合 B 中元素有(1,1),(1,2),(1,4),(2,1),(2,2), (2,4),(4,1),(4,2),(4,4),共 9 个. 答案:9
答案:{2,3}
必过易错关
1.认清集合元素的属性(是点集、数集或其他形式)和化简集合是 正确求解集合问题的两个先决条件.
2.解题时注意区分两大关系:一是元素与集合的从属关系;二是 集合与集合的包含关系.
3.注意空集的特殊性,在写集合的子集时不要忘了空集和它本身. 4.运用数轴图示法注意端点是实心还是空心. 5.在解决含参数的集合问题时,要注意检验集合中元素的互异性,
2.已知集合 A={x|-1<x<3},B={x|-m<x<m},若 B⊆A,则 m 的取值范围为________. 解析:当 m≤0 时,B=∅,显然 B⊆A. 当 m>0 时,因为 A={x|-1<x<3}. 当 B⊆A 时,在数轴上标出两集合,如图,
(福建专用)2019高考数学一轮复习-第一章 集合与常用逻辑用语 1.1 集合的概念与运算课件 理
求解;(3)若给定的集合是抽象集合,则用Venn图求解.
考点1
考点2
考点3
对点训练2已知集合A={x|x<-3或x>7},B={x|x<2m-1},若B⊆A,则
实数m的取值范围是
.
关闭
由题意知2m-1≤-3,m≤-1,所以m的取值范围是(-∞,-1].
A={2,4},B={y|y=log√3 (x-1),x∈A},则集合(∁UA)∩(∁UB)=(
)
A.{0,4,5,2} B.{0,4,5} C.{2,4,5}D.{1,3,5}
(3)(2017河北邯郸二模,理1)已知集合A={0,1,2,3,4},B={x|(x+5)(xm)<0,m∈Z},若A∩B中有三个元素,则m的值为(
x∈Z},B={p-q|p∈A,q∈A},则集合B中元素的个数为(
)
A.1 B.3
C.5 D.7
0, ,
(2)若 a,b∈R,集合{1,a+b,a}=
,则 b-a=
.
关闭
(1)由题意知 A={-1,0,1},当 p=-1,q=-1,0,1 时,p-q=0,-1,-2;当
p=0,q=-1,0,1 时,p-q=1,0,-1;当 p=1,q=-1,0,1 时,p-q=2,1,0.根据集
1<x<1},
B={x|lg(x+9)<1}={x|0<x+9<10}={x|-9<x<1},
则A∩B={x|-1<x<1}=(-1,1),故选A.
(2)由题意知B={0,2},所以∁UA={0,1,3,5},∁UB={1,3,4,5}.故
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第1讲 集合的概念与运算
板块四 模拟演练·提能增分
[A级 基础达标]
1.[2017·全国卷Ⅱ]设集合A={1,2,4},B={x|x2-4x+m=0}.若A∩B={1},则
B
=( )
A.{1,-3} B.{1,0}
C.{1,3} D.{1,5}
答案 C
解析 ∵A∩B={1},∴1∈B.
∴1-4+m=0,即m=3.
∴B={x|x2-4x+3=0}={1,3}.故选C.
2.若集合M={x||x|≤1},N={y|y=x2,|x|≤1},则( )
A.M=N B.M⊆N
C.N⊆M D.M∩N=∅
答案 C
解析 M={x||x|≤1}=[-1,1],N={y|y=x2,|x|≤1}=[0,1],所以N⊆M.故选C.
3.[2017·山东高考]设函数y=4-x2的定义域为A,函数y=ln (1-x)的定义域为B,
则A∩B=( )
A.(1,2) B.(1,2]
C.(-2,1) D.[-2,1)
答案 D
解析 ∵4-x2≥0,∴-2≤x≤2,∴A=[-2,2].
∵1-x>0,∴x<1,∴B=(-∞,1),∴A∩B=[-2,1).
故选D.
4.已知集合A={x|x2≥4},B={m}.若A∪B=A,则m的取值范围是( )
A.(-∞,-2) B.[2,+∞)
C.[-2,2] D.(-∞,-2]∪[2,+∞)
答案 D
解析 因为A∪B=A,所以B⊆A,即m∈A,得m2≥4,解得m≥2或m≤-2.故选D.
5.[2017·全国卷Ⅲ]已知集合A={(x,y)|x2+y2=1},B={(x,y)|y=x},则A∩B中
元素的个数为( )
A.3 B.2
C.1 D.0
答案 B
解析 集合A表示以原点O为圆心,半径为1的圆上的所有点的集合,集合B表示直线
y=x
上的所有点的集合.
由图形可知,直线与圆有两个交点,所以A∩B中元素的个数为2.故选B.
6.已知集合A={x|x2-3x+2=0,x∈R},B={x|0
的集合C的个数为( )
A.1 B.2
C.3 D.4
答案 D
解析 集合B={1,2,3,4},有4个元素,集合A={1,2},则集合C的个数问题可转化为
{3,4}的子集个数问题,即22=4.
7.[2018·陕西模拟]设全集U=R,集合A={|x∈Zx3-x≥0},B={x∈Z|x2≤9},则图
中阴影部分表示的集合为( )
A.{1,2} B.{0,1,2}
C.{x|0≤x<3} D.{x|0≤x≤3}
答案 B
解析 题图中阴影部分表示的是A∩B,因为A={|x∈Zxx-3≤0}=
{|
x
∈Z
xx
-,
x
-3≠0
}={x∈Z|0≤x<3}={0,1,2},B={x∈Z|-3≤x≤3}={-3,-2,-1,
0,1,2,3},所以A∩B={0,1,2}.故选B.
8.设集合A={x|-1≤x<2},B={x|x
解析 因为A∩B≠∅,所以集合A,B有公共元素,作出数轴,如图所示,易知a>-1.
9.[2018·郑州模拟]已知集合A={x∈R||x+2|<3},集合B=x∈R x-mx-2<0,且A∩
B
=(-1,n),则m=________,n=________.
答案 -1 1
解析 A={x∈R||x+2|<3}={x∈R|-5
则B={x|m
答案 -2
解析 ∵{1,m,m+n}=0,n,nm且m≠0,
∴m+n=0, 即m=-n,于是nm=-1.
∴由两集合相等,得m=-1,n=1,∴m-n=-2.
[B级 知能提升]
1.已知集合A={|yy=12x,x∈R},B={-2,-1,1,2},则下列结论正确的是( )
A.A∩B={-2,-1} B.(∁RA)∪B=(-∞,0)
C.A∪B=(0,+∞) D.(∁RA)∩B={-2,-1}
答案 D
解析 因为A=(0,+∞),所以A∩B={1,2},(∁RA)∪B={y|y≤0或y=1,2},A∪
B
={y|y>0或y=-1,-2},(∁RA)∩B={-1,-2}.所以D正确.
2.[2018·湖南模拟]设常数a∈R,集合A={x|(x-1)(x-a)≥0},B={x|x≥a-1},
若A∪B=R,则a的取值范围为( )
A.(-∞,2) B.(-∞,2]
C.(2,+∞) D.[2,+∞)
答案 B
解析 集合A讨论后利用数轴可知 a≥1,a-1≤1或 a≤1,a-1≤a. j(1≤i≤j≤n),aiaj与ajai两数中至少有一个属于A,则称集合A A.{1,3,4}为“权集” B.{1,2,3,6}为“权集” 解析 由于3×4与43均不属于数集{1,3,4},故A不正确;由于1×2,1×3,1×6,2×3, 不能有0,同时不一定有1,故C,D错误. 所以-52≤x≤1, 所以P={|x-52≤x≤1}, 所以 a+1≥-2,2a+1≤5,2a+1≥a+1,解得0≤a≤2;
解得1≤a≤2或a≤1,即a≤2.故选B.
3.已知数集A={a1,a2,…,an}(1≤a1
为“权集”,则( )
C.“权集”中元素可以有0 D.“权集”中一定有元素1
答案 B
62,63,11,22,33,6
6
都属于数集{1,2,3,6},故B正确;由“权集”的定义可知ajai需有意义,故
4.已知集合A={x∈R|x2-ax+b=0},B={x∈R|x2+cx+15=0},A∩B={3},A∪
B
={3,5}.
(1)求实数a,b,c的值;
(2)设集合P={x∈R|ax2+bx+c≤7},求集合P∩Z.
解 (1)因为A∩B={3},所以3∈B,所以32+3c+15=0,c=-8,所以B={x∈R|
x
2
-8x+15=0}={3,5}.
又因为A∩B={3},A∪B={3,5},所以A={3},所以方程x2-ax+b=0有两个相等的
实数根都是3,所以a=6,b=9,所以a=6,b=9,c=-8.
(2)不等式ax2+bx+c≤7即6x2+9x-8≤7,
所以2x2+3x-5≤0,
所以P∩Z={|x-52≤x≤1}∩Z={-2,-1,0,1}.
5.[2018·南宁段考]已知集合P={x|a+1≤x≤2a+1},Q={x|x2-3x≤10}.
(1)若a=3,求(∁RP)∩Q;
(2)若P∪Q=Q,求实数a的取值范围.
解 (1)因为a=3,所以P={x|4≤x≤7},
∁RP={x|x<4或x>7}.
又Q={x|x2-3x-10≤0}={x|-2≤x≤5},所以(∁RP)∩Q={x|x<4或x>7}∩{x|-
2≤x≤5}={x|-2≤x<4}.
(2)当P≠∅时,由P∪Q=Q得P⊆Q,
当P=∅,即2a+1
