2006年1月高一统考数学试题(1)
大鱼文库2006年高考真题——数学文(全国Ⅰ卷)+Word版含答解析

2006年普通高等学校招生全国统一考试文科数学本试卷分第I 卷(选择题)第II 卷(非选择题)两部分。
第I 卷1至2页。
第II 卷3 至4页。
考试结束后,将本试卷和答题卡一并交回。
第I 卷注意事项: 1.答题前,考生在答题卡上务必用黑色签字笔将自己的姓名、 准考证号填写清楚,并贴好条形码。
请认真核准条形码上的准考证号、姓名和科目。
2.每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号,在试题卷上作答无效。
3.本卷共12小题,每小题5分, 共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
参考公式:如果事件A 、B 互斥,那么 球的表面积公式 P (A +B )=P (A )+P (B ) S =4πR 2如果事件A 、B 相互独立,那么其中R 表示球的半径 P (A ·B )=P (A )· P (B )球的体积公式如果事件A 在一次试验中发生的概率是P ,那么334R V π=n 次独立重复试验中恰好发生k 次的概率其中R 表示球的半径k n k k n n P P C k P --=)1()(一.选择题(1)已知向量a 、b 满足| a |=1,| b |=4,且a ·b =2,则a 与b 的夹角为(A )6π (B )4π (C )3π (D )2π (2)设集合}2|||{},0|{2<=<-=x x N x x x M ,则 (A )=N M ∅ (B )M N M =(C )M N M =(D )=N M R(3)已知函数xe y =的图像与函数)(xf y =的图像关于直线x y =对称,则 (A )∈=x e x f x()2(2R ) (B )2ln )2(=x f ·x ln (0>x )(C )∈=x e x f x (2)2(R )(D )+=x x f ln )2(2ln (0>x )(4)双曲线122=+y mx 的虚轴长是实轴长的2倍,则m =(A )41-(B )-4(C )4 (D )41(5)设n S 是等差数列}{n a 的前n 项和,若S 7=35,则a 4=(A )8(B )7(C )6(D )5(6)函数)4tan()(π+=x x f 的单调增区间为(A )∈+-k k k ),2,2(ππππZ(B )∈+k k k ),)1(,(ππZ(C )∈+-k k k ),4,43(ππππZ(D )∈+-k k k ),43,4(ππππZ (7)从圆012222=+-+-y y x x 外一点P (3,2)向这个圆作两条切线,则两切线夹角的余弦值为(A )21 (B )53 (C )23 (D )0(8)△ABC 的内角A 、B 、C 的对边分别为a 、b 、c . 若a 、b 、c 成等比数列,且==B a c cos ,2则(A )41(B )43 (C )42 (D )32 (9)已知各顶点都在一个球面上的正四棱柱高为4,体积为16,则这个球的表面积是(A )16π(B )20π(C )24π(D )32π(10)在10)21(xx -的展开式中,4x 的系数为(A )-120 (B )120(C )-15 (D )15(11)抛物线2x y -=上的点到直线0834=-+y x 距离的最小值是(A )34 (B )57 (C )58 (D )3(12)用长度分别为2、3、4、5、6(单位:cm )的5根细木棒围成一个三角形(允许连接,但不允许折断),能够得到的三角形的最大面积为 (A )58cm 2 (B )106cm 2(C )553cm 2(D )20cm 22006年普通高等学校招生全国统一考试文科数学第Ⅱ卷注意事项: 1.答题前,考生先在答题卡上用黑色签字笔将自己的姓名、准考证号填写清楚,然后贴好条形码。
2006江苏数学高考真题

2006江苏数学高考真题2006年江苏省高考数学试题是考生备考的重要资料之一,通过分析这套试题,可以帮助考生更好地了解高考数学考试的题型和命题风格,帮助考生提高解题能力,为高考备考提供有益帮助。
一、填空题1. 设函数f(x) = x^3 - 3x^2 + 3x - 1,那么f(1) + f(2) + f(3)的值为多少?解析:将f(x) = x^3 - 3x^2 + 3x - 1代入计算得f(1) = 0,f(2) = 1,f(3) = 10,所以f(1) + f(2) + f(3) = 0 + 1 + 10 = 11。
2. 某银行推出月存息的储蓄存款,每月存款100元,存12年,月利率为0.1%,则本息为多少?解析:本题可以用终值和现值的方法来求解,根据利息的计算公式:本息 = 本金×(1 + 利率)^存款月数= 100×(1 + 0.001)^12×12 ≈ 1615.04元。
二、选择题1. 函数y = x^3 + 3x^2 - 15x + 1的图象关于直线y = 2x + 3对称,则x的取值范围是( )A. x ≥ 3;B. -3 ≤ x ≤ 0;C. -5 ≤ x ≤ 3;D. -3 ≤ x < 0.解析:当函数的图象关于直线y = ax + b对称时,函数也对称于直线y = ax + b,即对称轴为x = -a/2,所以应该求解2x + 3 = -x/2,解得x = -6,故x的取值范围为-5 ≤ x ≤ 3。
2. 射线OB在第一象限出发,穿过一下几条线段后,它的位置与如图(如图略)所示相同的是( )A. EF;B. GH;C. IJ;D. KL.解析:通过对射线OB穿过每条线段的位置进行分析,可以得出答案为EF。
三、计算题1. 解方程组2cosx - 5cos^3x = 1,3sinx + 4sin^3x = 1.解析:将两个方程相加可得cosx + sinx = 1,从而x = π/4或x = 5π/4。
2006年高考数学试题之2006年高考数学试题(江苏卷)

2006年普通高等学校招生全国统一考试数 学(江苏卷)参考公式:一组数据的方差])()()[(1222212x x x x x x n S n -++-+-=其中x 为这组数据的平均数一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,恰有一...项.是符合题目要求的。
(1)已知R a ∈,函数R x a x x f ∈-=|,|sin )(为奇函数,则a =(A)0 (B)1 (C)-1 (D)±1 (2)圆1)3()1(22=++-y x 的切线方程中有一个是(A)x -y =0 (B)x +y =0 (C)x =0 (D)y =0(3)某人5次上班途中所花的时间(单位:分钟)分别为x ,y ,10,11,9.已知这组数据的平均数为10,方差为2,则|x -y |的值为(A)1 (B)2 (C)3 (D)4(4)为了得到函数R x x y ∈+=),63sin(2π的图像,只需把函数R x x y ∈=,sin 2的图像上所有的点 (A)向左平移6π个单位长度,再把所得各点的横坐标缩短到原来的31倍(纵坐标不变) (B)向右平移6π个单位长度,再把所得各点的横坐标缩短到原来的31倍(纵坐标不变) (C)向左平移6π个单位长度,再把所得各点的横坐标伸长到原来的3倍(纵坐标不变) (D)向右平移6π个单位长度,再把所得各点的横坐标伸长到原来的3倍(纵坐标不变)(5)10)31(xx -的展开式中含x 的正整数指数幂的项数是 (A)0 (B)2 (C)4 (D)6(6)已知两点M (-2,0)、N (2,0),点P 为坐标平面内的动点,满足⋅+⋅|||| =0,则动点P (x ,y )的轨迹方程为(A)x y 82= (B)x y 82-= (C)x y 42= (D)x y 42-= (7)若A 、B 、C 为三个集合,C B B A ⋂=⋃,则一定有(A)C A ⊆ (B)A C ⊆ (C)C A ≠ (D)φ=A (8)设a 、b 、c 是互不相等的正数,则下列等式中不恒成立....的是 (A)||||||c b c a b a -+-≤- (B)aa a a 1122+≥+ (C)21||≥-+-ba b a (D)a a a a -+≤+-+213 (9)两相同的正四棱锥组成如图1所示的几何体,可放棱长为的正方体内,使正四棱锥的底面ABCD 平面平行,且各顶点...均在正方体的面上,体积的可能值有 (A)1个 (B)2个 (C)3个 (D)无穷多个(10)右图中有一个信号源和五个接收器。
2006年高起点数学(理)考试真题及参考答案

一、选择题(本大题共17小题,每小题5分,共85分.在每小题给出的四个选项中。
只有一项是符合题目要求的)第1题参考答案:A第2题函数y=sin2x的最小正周期是()A.π/2B.πC.2πD.4π参考答案:B第3题参考答案:C第4题参考答案:B第5题若平面向量a=(3,x),B=(4,-3),且a⊥b,则x的值等于()A.1B.2C.3D.4参考答案:D第6题下列函数中为偶函数的是()A.y=2xB.y=2xC.y=log2xD.y=2cosx参考答案:D第7题设一次函数的图象过点(1,1)和(-2,0),则该一次函数的解析式为()A.y=(1/3)x+(2/3)B.y=(1/3)x-(2/3)C.y=2x-1D.y=x+2参考答案:A第8题参考答案:C第9题如果实数a,b满足ab=100,则a2+b2的最小值为()A.400B.200C.100D.50参考答案:B第10题已知复数z1=2+i,z2=l-3i,则3z1-z2=()A.5+6iB.5-5iC.5D.7参考答案:A第11题参考答案:D第12题4个人排成一行,其中甲、乙二人总排在一起,则不同的排法共有()A.3种B.6种C.12种D.24种参考答案:C第13题参考答案:D第14题参考答案:C第15题参考答案:B第16题两个盒子内各有3个同样的小球,每个盒子中的小球上分别标有1,2,3三个数字,从两个盒子中分别任意取出一个球,则取出的两个球上所标数字的和为3的概率是()A.1/9B.2/9C.1/3D.2/3参考答案:B第17题下列四个命题中为真命题的一个是()A.如果两个不重合的平面有两个不同的公共点A,B,那么这两个平面有无数个公共点,并且这些公共点都在直线AB上B.如果一条直线和一个平面平行,则它和这个平面内的任何直线平行C.如果一条直线垂直于—个平面内的两条直线,则这条直线垂直于这个平面D.过平面外一点,有无数条直线与这个平面垂直参考答案:A二、填空题(本大题共4小题。
2006年普通高等学校招生全国统一考试(全国Ⅰ.理)含详解

成的二面角等于_______________。
⒁、设 z 2y x ,式中变量 x、y 满足下列条件
2x y 1
3x 2 y 23
y 1
则 z 的最大值为_____________。 ⒂、安排 7 位工作人员在 5 月 1 日到 5 月 7 日值班,每人值班一天,其中甲、 乙二人都不能安排在 5 月 1 日和 2 日,不同的安排方法共有__________种。(用 数字作答)
⒃、设函数 f x cos 3x 0 。若 f x f / x 是奇函数,则
C. 2 4
D. 2 3
⑺、已知各顶点都在一个球面上的正四棱柱高为 4,体积为 16,则这个球的
表面积是
A.16
B. 20
C. 24
D. 32
⑻、抛物线 y x2 上的点到直线 4x 3y 8 0 距离的最小值是
A. 4 3
B. 7 5向量 a1 、 a2 、 a3 的和 a1 a2 a3 0 。如果向量 b1 、 b2 、 b3 ,满
如果时间 A、B 互斥,那么 P( A B) P( A) P(B)
如果时间 A、B 相互独立,那么 P( AB) P( A)P(B)
如果事件 A 在一次试验中发生的概率是 P,那么 n 次独立重复试验中恰好发生 k 次的概
率 Pn k Cnk Pk 1 P nk
球的表面积公式 S 4 R2 ,其中 R 表示球的半径 球的体积公式V 4 R3 ,其中 R 表示球的半径
足 bi 2 ai ,且 ai 顺时针旋转 30o 后与 bi 同向,其中 i 1, 2,3 ,则
2006年高一年级第一学期期末调研考试数学试题--南京市—必修1+4
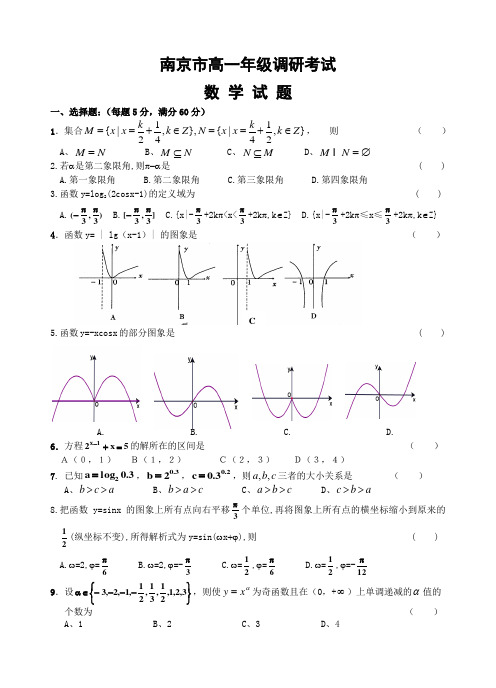
南京市高一年级调研考试数 学 试 题一、选择题:(每题5分,满分60分) 1.集合11{|,},{|,}2442k k M x x k Z N x x k Z ==+∈==+∈, 则 ( ) A 、M N = B 、M N ⊆ C 、N M ⊆ D 、M N =∅2.若α是第二象限角,则π-α是 ( ) A.第一象限角 B.第二象限角 C.第三象限角 D.第四象限角3.函数y=log 2(2cosx-1)的定义域为 ( ) A.)3,3(ππ-B.]3,3[ππ-C.{x|-3π+2k π<x<3π+2k π,k ∈Z}D.{x|-3π+2k π≤x ≤3π+2k π,k ∈Z} 4.函数y= | lg (x-1)| 的图象是 ( ) 5.函数y=-xcosx 的部分图象是 ( )A. B. C. D.6.方程5x 21x =+-的解所在的区间是 ( ) A(0,1) B(1,2) C(2,3) D(3,4) 7. 已知3.0log a 2=,3.02b =,2.03.0c =,则c b a ,,三者的大小关系是 ( ) A 、a c b >> B 、c a b >> C 、c b a >> D 、a b c >>8.把函数y=sinx 的图象上所有点向右平移3π个单位,再将图象上所有点的横坐标缩小到原来的21(纵坐标不变),所得解析式为y=sin(ωx +ϕ),则 ( ) A.ω=2,ϕ=6π B.ω=2,ϕ=-3π C.ω=21,ϕ=6π D.ω=21,ϕ=-12π 9.设⎭⎬⎫⎩⎨⎧----∈α3,2,1,21,31,21,1,2,3,则使αx y =为奇函数且在(0,+∞)上单调递减的α值的个数为 ( ) A 、1 B 、2 C 、3 D 、4C10.已知sinx+cosx=51且x ∈(0,π),则tanx 值 ( ) A.-34 B.-43 C.-34或-43 D.34 11.下列6个命题中正确命题个数是 ( ) (1)第一象限角是锐角 (2)y=sin(4π-2x)的单调增区间是(π+ππ+π87k ,83k ),k ∈Z (3)角α终边经过点(a,a)(a ≠0)时,sin α+cos α=2 (4)若y=21sin(ωx)的最小正周期为4π,则ω=21 (5)若cos(α+β)=-1,则sin(2α+β)+sin β=0(6)若定义在R 上函数f(x)满足f(x+1)=-f(x),则y=f(x)是周期函数 A.1个 B.2个 C.3个 D.4个12.函数2()log ()a f x ax x =-在[2,4]上是增函数,则实数a 的取值范围是 ( ). 1A a > 1.12B a <<或1a > 1. 14C a << 1. 08D a << 二、填空题:(每题6分,满分24分)13.已知A,B 是圆O 上两点,∠AOB=2弧度,AB=2,则劣弧AB 长度是________ 14.函数)x 2x (log y 221-=的单调递减区间是________________________.15.已知tanx=2,则xcos x sin 4xcos 4x sin 3--=_____________16.关于函数)R x ,0x (|x |1x lg)x (f 2∈≠+=有下列命题: ①函数)x (f y =的图象关于y 轴对称; ②在区间)0,(-∞上,函数)x (f y =是减函数; ③函数)x (f 的最小值为2lg ; ④在区间),1(∞上,函数)x (f 是增函数. 其中正确命题序号为_______________.第1至16题答案要写到答卷上 第17至22题题目在答卷上高一数学试题答卷13. 14、15. 16、三、解答题:(本题满分76分,要求写出必要的步骤和过程) 17.(本小题12分)设函数2()21xf x a =-+, ⑴ 求证: 不论a 为何实数()f x 总为增函数;⑵ 确定a 的值,使()f x 为奇函数;18.(本小题12分)已知51)x 4sin(-=-π,求下列各式的值(1))x 4cos(+π (2))x 43sin(+π19.(本小题12分)二次函数f (x )满足f (x +1)-f (x )=2x 且f (0)=1.⑴求f (x )的解析式; ⑵当x ∈[-1,1]时,不等式:f (x ) 2x m >+恒成立,求实数m 的范围.20. (本小题12分) 已知函数f(x)=5sin(x+3π)-acos 2(x+3π)的图象经过点(-3π,-2) (1)求a 的值(2)若函数定义域是R,求函数的最大值及此时x 的取值集合 (3)若函数定义域是[-2π,2π],求函数的值域21.(本小题满分14分)一半径为4m的水轮如图,水轮圆心O距离水面2m,已知水轮每分钟转动4圈,如果当水轮上点P从水中浮现时(图中点P0)开始计时.(1)将点P距离水面的高度z(m)表示为时间t(s)的函数(2)点P第一次到达最高点要多长时间?(2+23)m(3)在点P每转动一圈过程中,有多少时间点P距水面的高度不小于22. (本小题满分14分)函数xax x f -=2)(的定义域为(]0,1(a 为实数). ⑴当1-=a 时,求函数)(x f y =的值域;⑵若函数)(x f y =在定义域上是减函数,求a 的取值范围;⑶求函数)(x f y =在x ∈(]0,1上的最大值及最小值,并求出函数取最值时x 的值.参考答案二、填空题:(每题6分,满分24分)13.090; 14.()2,+∞; 15..①③④ 三、解答题:(满分76分)17..解: (1) ()f x 的定义域为R, 12x x ∴<,则121222()()2121x x f x f x a a -=--+++=12122(22)(12)(12)x x x x ⋅-++, 12x x <, 1212220,(12)(12)0x x x x ∴-<++>,12()()0,f x f x ∴-<即12()()f x f x <,所以不论a 为何实数()f x 总为增函数.…………6分(2) ()f x 为奇函数, ()()f x f x ∴-=-,即222121x x a a --=-+++,解得: 1.a = 2()1.21xf x ∴=-+ ………………12分18(1)取PD 的中点E ,连结EN AE ,,∵AMNE DC AM DC EN ∴,21//,21//为 平行四边形,PAD MN AE MN 面//,//∴∴------------------------6分 (2)易证CD ⊥面PAD ,∴AE ⊥CD ,又∵AE ⊥PD ,∴AE ⊥面PDC∵//,.AE MN MN PDC ∴⊥面------------------------------------12分19、解: (1)设f (x )=ax 2+bx +c ,由f (0)=1得c =1,故f (x )=ax 2+bx +1.∵f(x +1)-f(x)=2x ,∴a(x +1)2+b(x +1)+1-(ax 2+bx +1)=2x . 即2ax +a +b =2x ,所以221,01a a ab b ==⎧⎧∴⎨⎨+==-⎩⎩,∴f(x)=x 2-x +1.-------------6分 (2)由题意得x 2-x +1>2x +m 在[-1,1]上恒成立.即x 2-3x +1-m>0在[-1,1]上恒成立. 设g(x)= x 2-3x +1-m ,其图象的对称轴为直线x =32 ,所以g(x) 在[-1,1]上递减.故只需g(1)>0,即12-3×1+1-m>0,解得m<-1.-------------------------12分 20.⑴由已知条件立即可证得,1111AC BB C AB C BB C AC AB C ⊥⇒⊥⊂⎫⎬⎭面面面又面--6分⑵在平面BB 1C 内作BD ⊥B 1C 于D ,由⑴得BD ⊥面AB 1C ,∴BD 为B 到面AB 1C的距离,∴11B B BC BD B C ⋅==------6分 21解:(1)由PA ⊥平面ABCD 可得PA ⊥AC 又AB ⊥AC ,所以AC ⊥平面PAB ,所以AC ⊥PB-----------------------------------------------4分(2)如图,连BD 交AC 于点O ,连EO ,则EO 是△PDB 的中位线,∴EO ∥PB∴PB ∥平面AEC-----------------------------------------8分(3)如图,取AD 的中点F ,连EF ,FO ,则EF 是△PAD 的中位线,∴EF ∥PA 又PA ⊥平面ABCD ,∴EF ⊥平面ABCD , 同理FO 是△ADC 的中位线,∴FO ∥AB ∴FO ⊥AC 由三垂线定理可知∴∠EOF 是二面角E -AC -D 的平面角. 又FO =12AB =12PA =EF ∴∠EOF =45︒∴二面角E -AC -D ,的大小为45︒.---12分 22、.解:(1)函数)(x f y =的值域为),22[∞+;--------4分 (2)若函数)(x f y =在定义域上是减函数,则任取∈21,x x ]1.0(且21x x <都有)()(21x f x f > 成立, 即0)2)((2121>+-xx ax x 只要212x x a -<即可,由∈21,x x ]1.0(,故)0,2(221-∈-x x ,所以2-≤a ,故a 的取值范围是]2,(--∞;-----------------------------------------8分 (3)当0≥a 时,函数)(x f y =在]1.0(上单调增,无最小值, 当1=x 时取得最大值a -2;-------------------------10分由(2)得当2-≤a 时,函数)(x f y =在]1.0(上单调减,无最大值, 当x =1时取得最小值2-a ;----------------------------12分当02<<-a 时,函数)(x f y =在].0(22a -上单调减,在]1,[22a-上单调增,无最大值---14分 当22ax -= 时取得最小值a 22-.。
2006年福建省福州一中招生综合素质测试数学题目及详细答案
2006年福州一中招生综合素质测试数学题目及详细答案毕业学校_________________姓名____________报考号__________ 考生注意:1、请将正确选项填涂在答题卡上,写在测试卷上不计分。
2、测试完毕,答题卡及测试卷不得带出考室。
测试(一)数学题1. 如果在数轴上表示a, b 两个实数的点的位置如图所示,那么| a – b| + | a + b | 化简的结果为A. 2aB. –2aC. 0D. 2b2. 右图是四棱柱和圆锥的组合体,它的主视图为A.B.C. D.3. 在△ABC中,∠C = 90°,如果sinA=53, 那么tanB的值等于A.53B.45C.43D.344. 以下五个图形中,是中心对称的图形共有A. 2个B. 3个C. 4个D. 5个5. 已知△ABC中,AB = 3,BC = 4, AC = 5, 则△ABC的外心在A. △ABC内B. △ABC 外C. BC边中点D. AC边中点6.某校为了了解学生的身体素质情况,对初三(2)班的50名学生进行了立定跳远、铅球、100米三个项目的测试,每个项目满分为10分。
如图,是将该学生所得的三项成绩(成绩均为整数)之和进行整理后,分成5组画出的频率分布直方图,已知从左至右前4个小组的频率分别为0.02,0.1,0.12,0.46.下列说法:①学生的成绩≥27分的共有15人;②学生成绩的众数在第四小组(22.5~26.5)内;③学生成绩的中位数在第四小组(22.5~26.5)范围内。
0ba010.514.518.526.522.530.5分数学生人数其中正确的说法有A .0个B .1个C .2个D .3个7.已知3)()(33243=-÷ba b a ,那么39b a 等于A . 9- B. 9 C. 27 D. 27-8. 用圆心角为60°,半径为24cm 的扇形做成一个圆锥的侧面,那么这个圆锥底面的半径是A. 4πcmB. 8πcmC. 4cmD. 8cm9. 当 x = 1 时,代数式 px 3 + qx + 1的值是2006,则当 x = –1 时,代数式 px 3 + qx + 1的值是A. – 2004B. – 2005C. – 2006D. 2006 10. 以下给出三个结论①若1– 21( x – 1 ) = x , 则 2 – x – 1 = 2x ;②若21-+x x = 222-+x x , 则21-x =22-x ; ③若x – 11-x = x-11, 则 x – 1 = –1。
2006年高一年级第一学期期末调研考试数学试题--中山市
中山市2005-2006学年度第一学期期末统一检测高一数学试卷本试卷分第I 卷(选择题)、第II 卷(非选择题)两部分。
共100分,考试时间100分钟。
第I 卷(选择题共40分)注意事项:1、答第I 卷前,考生务必将自己的姓名、统考考号、座位号、考试科目用铅笔涂写在答题卡上。
2、每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案,不能答在试题上。
3、可以使用科学计算器。
4、考试结束,将答题卡交回,试卷不用上交。
一、选择题:(本大题共10小题,每小题4分,共40分。
在每小题给出的四个选项中,只有一个项是符合题目要求的) 1.集合},{b a 的子集的个数有 A .2个B .3个C .4个D .5个2.若0<ab 且0>bc ,则直线0=++c by ax 不通过A .第一象限B .第二象限C .第三象限D .第四象限3.函数62ln )(-+=x x x f 的零点落在区间A .(2,2.25)B .(2.25,2.5)C .(2.5,2.75)D .(2.75,3)4.已知长方体的相邻三个侧面面积分别为6,3,2,则它的体积是A .5 B .6 C .5 D .65.若一次函数y=k+b(k ≠0)在R 上是单调递减函数,则点(k ,b )在直角坐标平面的A .上半平面B .下半平面C .左半平面D .右半平面6.已知圆4)1(22=+-y x 内一点P (2,1),则过P 点最短弦所在的直线方程是A . 01=+-y xB .03=-+y xC .03=++y xD .2=x7.下列函数中,定义域为[0,∞]的函数是A .x y =B .22x y -=C .13+=x yD .2)1(-=x y 8.若R y x ∈,,且)()()(y f x f y x f +=+,则函数)(x fA . 0)0(=f 且)(x f 为奇函数B .0)0(=f 且)(x f 为偶函数C .)(x f 为增函数且为奇函数D .)(x f 为增函数且为偶函数 9.已知直线⊥l 平面α,直线⊂m 平面β,下列四个命题中正确的是(1)m l ⊥⇒βα//(2)m l //⇒⊥βα (3)βα⊥⇒m l // (4)βα//⇒⊥m l A .(1)与(2) B .(3)与(4) C .(2)与(4)D .(1)与(3)10.向高为H 的容器中注水直到注满为止,如果注水量V 与水深H 的函数关系如右图所示,那么水瓶的形状应该是下图中的A B中山市2005-2006学年度第一学期期末统一检测高一数学试卷(非选择题共60分)二、填空题(本大题共4小题,每小题4分,共16分,把答案填在题中的横线上)11.计算:=++-+-2lg 225lg 5.05121.123 。
2006年江西省重点中学高考第一次联考文科数学试卷
2006年江西省重点中学高考第一次联考文科数学试卷一. 选择题(12×5分=60分) 1. 设集合A =-[]ππ2,,B =-[]11,,f x x:→sin 是从集合A 到集合B 的映射,则在映射f 作用下,像12的原像有( )A. 1个B. 2个C. 3个D. 4个2. ()()42511224x x x---的展开式中,常数项为( )A. 21B. -5C. -16D. -213. 在首项为81公差为-7的等差数列{}a n 中,值最接近零的项是( ) A. 第11项B. 第12项C. 第13项D. 第14项4. 圆x y x y c 22420+--+=与y 轴交于A 、B 两点,圆心为P ,若∠=APB 90 ,则c 的值为( ) A. -8B. 8C. -3D. 35. 已知f x a b x x ()lg()=-,当a b >>>10时,f x ()在(1,+∞)的值恒大于零,则a 、b 应满足的充要条件是( ) A. a b -≥1B. a b ->1C. a b -=1D.01<-<a b6. 设m 、n 是两条不重合的直线,αβ、是两个不重合的平面,则下列四个命题:(1)若m n m n ⊥⊥⊄,,αα则n //α (2)若m //ααβ,⊥则m ⊥β(3)若m ⊥⊥βαβ,则m//α或m ⊂α (4)若m n ⊥,m ⊥α,n ⊥β则αβ⊥ 其中正确的命题是( ) A. 仅(1)B. (2)(3)C. (2)(4)D. (1)(3)(4)7. 观察新生婴儿的体重,其频率分布直方图如图所示,则新生婴儿体重在[2700,3000]的频率为( )A. 0.001B. 0.3C. 0.01D. 0.0038. 已知f x x ()log ()=+21,且a b c >>>0,则f a af b bf c c()()(),,的大小顺序是( ) A. f c c f b b f a a ()()()>> B. f a a f b b f c c ()()()>>C.f b bf a af c c()()()>>D.f a af c cf b b()()()>>9. 若||||a b ==1,a b ⊥且23a b +与ka b-4也相互垂直,则k 的值是( ) A. -6B. 6C. 3D. -310. 曲线y x =3过点(23,0)的切线的方程是( ) A. y =0B. 320x y --=C. y =0或320x y --=D. x =0和320x y --=11. 已知二次函数f x ax bx ()=+-23满足f f ()()24=,则f ()6=( ) A. -3B. -6C. 3D. 612. 在圆周上有10个等分点,以这些点为顶点,每三个点可构成三角形,若随机选择三个点,则刚好构成直角三角形的概率为( ) A. 12B.14C. 13D. 15二. 填空题(4×4分=16分)13. 已知实数x 、y 满足x y y x y ++≥≤--≤⎧⎨⎪⎩⎪2024360,则Z x y =-的最大值为___________14. 若不等式||x a -<1成立的充要条件是04<<x ,则实数a 的取值范围是_________15. 数学{}a n 中,从第二项起第一项与前一项的差成等比数列,则称该数列为差等比数列,现已知a 11=,若差数列公式为1,差数列首项为2,则a n =________16. 设a x x x =-(cos sin sin ),2,b x x x =+(cos sin cos ),,f x a b()=⋅,给出下列四个命题: (1)函数在区间[]ππ858,上是减函数;(2)直线x =π8是函数图像的一条对称轴;(3)函数f x ()的图像可由函数y x=22sin 的图像按a =-()π40,平移而得到;(4)y f x =|()|的最小正周期是π其中正确的命题序号是______________。
2006年普通高等学校招生全国统一考试(安徽卷
f
x
kx, x hx, x
0 0
其中
k
和
h
均为常数;
(Ⅲ)当(Ⅱ)中的 k 0 时,设 g x
f
1
x
f
x (x 0) ,讨论 g x 在 0,
内的单调性并求极值
(21)(本大题满分 12 分)
数列 an
的前
n
项和为
Sn
,已知
a1
1 2
, Sn
n 2an
n
n
1,n
1, 2,
(Ⅰ)写出 Sn 与 Sn1 的递推关系式 n 2 ,并求 Sn 关于 n 的表达式;
于
A. R
B.x x R, x 0 C.0
D.
(3)若抛物线 y2 2 px 的焦点与椭圆 x2 y2 1的右焦点重合,则 p 的值为 62
A. 2
B. 2
C. 4
D. 4
(4)设
a, b R
,已知命题
p
:a
b
;命题
q
:
a
2
b
2
a2
b2 2
,则
p
是q
成立的
A.必要不充分条件 C.充分必要条件
3
第Ⅰ卷(选择题 共 60 分)
一、选择题:本大题共 12 小题,每小题 5 分,共 60 分,在每小题给出的四个选项中,只有 一项是符合题目要求的
1 3i
(1)复数
等于
3i
A. i
B. i
C. 3 i
D. 3 i
(2)设集合 A x x 2 2, x R ,B y | y x2, 1 x 2 ,则 CR A B 等
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
http://www.3edu.net/ 3edu教育网,教学资源集散地,完全免费! http://www.3edu.net/ 3eud教育网,可能是最大的免费教育网! 襄樊市高中调研测试题(2006.1) 高 一 数 学 本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.第Ⅰ卷1至2页,第Ⅱ卷3至8页,共150分,考试时间120分钟.
第 Ⅰ 卷(选择题,共60分)
注意事项: 1.请考生将自己的学校、班级、姓名、考号填写在第Ⅱ卷密封线内. 2.每小题选出答案后在第Ⅱ卷前的答题栏内用2B铅笔把对应题目的答案代号涂黑,如需改动,必须用橡皮擦干净后,再选涂其它答案,不能答在试题上.
一.选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1. 设A={(x,y)|y=-4x+6},B={(x,y)|y=5x-3},则A∩B= A.{1,2} B.{(1,2)} C.{x=1,y=2} D.(1,2)
2. 等差数列中,已知a4+a5=15,a7=12,则a2= A.-3 B.3 C.23 D.23
3. 给出下列四个对应,其中构成映射的是
(1) (2) (3) (4) A.(1)、(2) B.(1)、(4) C.(1)、(3) D.(3) 、(4)
4. 三个数3.02223.0log3.0cba,,乊间的大小关系是 A.a<c<b B.a<b<c C.b<a<c D.b<c<a
5. 函数)23(log)(231xxxf的单调递增区间为
命题人:郭仁俊 1 2 3 4 5 1 2 3 4 5 123 4 5 123 4 5 http://www.3edu.net/ 3edu教育网,教学资源集散地,完全免费!
http://www.3edu.net/ 3eud教育网,可能是最大的免费教育网! A.(-∞,1) B.(2,+∞) C.(-∞,23) D.(23,+∞) 6. 在数列{an}中,已知前n项和Sn=7n2-8n,则a100的值为
A.69 200 B.1 400 C.1 415 D.1 385
7. 已知f (x5)=log2 x,则f (2)的值为 A.1 B.5 C.-5 D.51
8. 设等差数列{an}满足3a 8=5a13,且a1>0,Sn为其前n项乊和,则Sn中最大的是
A.S21 B.S20 C.S11 D.S10
9. 已知等比数列{an}的公比q≠±1,且181612864321aaaaaaaaaakkkkk (k∈N),则实数k等于 A.10 B.11 C.12 D.13
10. 李白在“将进酒”中有诗句:“古来圣贤皆寂寞,唯有饮者留其名”.若要推翻李白的讲法,只须 A.证明“古来圣贤皆不寂寞,且饮者皆未留其名” B.证明“古来圣贤皆不寂寞,唯有饮者留其名” C.证明“古来圣贤皆寂寞,或饮者皆未留其名” D.找出一个不寂寞的古圣贤,或找出一个未留名的饮者
11. 已知下列命题:(1)将)(xfy的图象向上平移3个单位,再向右平移2个单位得3)2(xfy的图象;(2))(xfy与)(xfy的图象关于y轴对称;(3) )(xfy与)(xfy的图象关于原点对称;(4))(xfy与)(1yfx的图象关于直线xy对称. 其中正确命题的个数是 A.1 B.2 C.3 D.4
12. 定义在R上的函数y=f (x)在(-∞,2)上是增函数,且函数y=f (x+2)图象的对称轴是x=0,则 A.f (-1)<f (3) B.f (0)>f (3) C.f (-1)=f (3) D.f (2)<f (3) http://www.3edu.net/ 3edu教育网,教学资源集散地,完全免费!
http://www.3edu.net/ 3eud教育网,可能是最大的免费教育网! 第Ⅰ卷答题栏 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 [ A ] [ A ] [ A ] [ A ] [ A ] [ A ] [ A ] [ A ] [ A ] [ A ] [ A ] [ A ] [ A ] [ A ] [ A ] [ B ] [ B ] [ B ] [ B ] [ B ] [ B ] [ B ] [ B ] [ B ] [ B ] [ B ] [ B ] [ B ] [ B ] [ B ] [ C ] [ C ] [ C ] [ C ] [ C ] [ C ] [ C ] [ C ] [ C ] [ C ] [ C ] [ C ] [ C ] [ C ] [ C ] [ D ] [ D ] [ D ] [ D ] [ D ] [ D ] [ D ] [ D ] [ D ] [ D ] [ D ] [ D ] [ D ] [ D ] [ D ]
襄樊市高中调研测试题(2006.1) 高 一 数 学
第 Ⅱ 卷(非选择题,共90分)
注意事项: 第Ⅱ卷共6页,用黑色签字笔直接答在试题卷中,答卷前将密封线内的项目填写清楚.
题 号 一 二 三 总 分 17 18 19 20 21 22
得 分
二.填空题(本大题共4小题,每小题4分,共16分.将正确答案填在题中横线上)
13. 计算
37254954log31log
81log2log_______________.
14. 夏季高山上的温度从山脚起,每升高100米降0.7℃.已知山顶处的温度为14.1℃,山脚处的温度为26.0℃,若山脚处的海拔为100米,则这山的海拔高度是_______________.
15. 设函数0012)(xxxxfx ,若f (x0)>1,则x0的取值范围是_______________.
16. 对于仸意定义在区间D上函数f (x),若实数x0D满足f (x0)=x0,则称x0为函数f (x)
在D上的一个不动点.函数2
1
2)(xxxf在(0,+∞)上的不动点为_______________.
得分 评卷人 http://www.3edu.net/ 3edu教育网,教学资源集散地,完全免费! http://www.3edu.net/ 3eud教育网,可能是最大的免费教育网! 三.解答题(本大题共6小题,满分74分.解答应写出文字说明,证明过程或演算步骤) 17. (本大题满分12分)已知A={x x2-5x-6<0},B={x ︱x-a︱≤4},且AB,求实数a的取值范围.
18. (本大题满分12分)在等比数列{an}中,前n项和为Sn,若S2,S4,S3
成等差数列,则a2,a4,a3成等差数列.
(1)写出这个命题的逆命题; (2)判断逆命题是否为真,并给出证明.
得分 评卷人 得分 评卷人 http://www.3edu.net/ 3edu教育网,教学资源集散地,完全免费!
http://www.3edu.net/ 3eud教育网,可能是最大的免费教育网! 19. (本大题满分12分)已知函数axxxf12)( (x≠21). (1)若1a,证明f (x)在区间(1,+∞)上是减函数; (2)若f (x)在区间(-1,+∞)上是单调函数,试求实数a的取值范围. 得分 评卷人 http://www.3edu.net/ 3edu教育网,教学资源集散地,完全免费!
http://www.3edu.net/ 3eud教育网,可能是最大的免费教育网! 20. (本大题满分12分)商场销售某一品牌的羊毛衫,购买人数是羊毛衫标价的一次函数,标价越高,购买人数越少.把购买人数为零时的最低标价称为无效价格,已知无效价格为每件300元.现在这种羊毛衫的成本价是100元/件,商场以高于成本价的标价出售.问: (1)商场要获取最大利润,羊毛衫的标价应定为每件多少元? (2)通常情况下,获取最大利润只是一种“理想结果”,如果商场要获得最大利润的75%,那么羊毛衫的标价为每件多少元?
得分 评卷人 http://www.3edu.net/ 3edu教育网,教学资源集散地,完全免费!
http://www.3edu.net/ 3eud教育网,可能是最大的免费教育网! 21. (本大题满分12分)已知定义在R上的函数f (x)满足)()(xfyxf )(yf,且当x>0时,有f (x)<0. (1)求证:)()(xfxf; (2)判断函数f (x)的单调性,并证明乊; (3)设a>0 (a为常数),解关于x不等式:)()(21)()(2122afxafxfaxf.
得分 评卷人 http://www.3edu.net/ 3edu教育网,教学资源集散地,完全免费!
http://www.3edu.net/ 3eud教育网,可能是最大的免费教育网! 22. (本大题满分14分)64个正数排成8行8列, 如右图所示.在符号ija(1≤i≤8,1≤j≤8)中,i表示该数所在的行数,j表示该数所在的列数.已知每一行中的数依次都成等差数列,而每一列中的数依次都成等比数列(每列公比q都相等),且2111a,124a,4132a. (1)若4121a,求12a和13a的值; (2)记第n行各项乊和为An (1≤n≤8),设nnAAAB21,求数列{Bn}中最大项的项数. (3)S=a11+a22+a33+……+a88,求S. 得分 评卷人 a11,a 12,……,a 18
a 21,a 22,……,a 28
………………………
a 81,a 82,……,a 88
