单元测试卷 个性化作业
乐学一百个性化作业提升学习效果
乐学一百个性化作业提升学习效果作者:李金霞来源:《学校教育研究》2020年第12期新冠肺炎疫情已经持续了很久的时间,教师学生们都宅在家,每天居家生活、学习、运动。
为了孩子们扎实数学基础,开学后进行新旧知识的衔接,上级要求开展“停课不停学”活动。
我一边利用教材巩固复习,预习新知。
还依托国家级课题“ 基于智能技术和大数据分析的个性化教学研究”,在网上进行乐学一百个性化作业系统教学辅助教学。
激发孩子们的学习热情,让孩子们自主进行个性化选择学习,提高孩子们的学习兴趣,起到宅在家不枯燥,还能有收获的实效。
每周或是隔周在群里给学生发通知布置一份乐学任务,让学生选择完成,学有所获。
一、重同步闯关,夯实基础系统里设置了五个项目的内容,我根据前期的调研,给孩子分组布置不同的作业。
重点布置同步作业,让孩子抓住基础的内容去理解。
系统设置的内容还有培优作业,还有易错题集锦,专题练习、练习试卷。
这部分内容我隔周去给孩子们布置。
并且随时去关注孩子们作业完成情况,并且微信进行个别沟通,表扬孩子自主能力强,能够做到积极自律学习的孩子。
二、抓强化技能助专项提高这是系统里的强化作业的错题本,我借助错题本,针对孩子的错题原因进行分析,通过微信,视频帮助孩子辅导,让孩子们掌握乘法简便运算规律的正确应用。
三、互动课堂智慧精讲目前绝大部分的学校的网络教学作业,都是老师在群里发送作业题目,学生有条件的下载打印完成,没有条件的标明题号对着屏幕把答案抄写在纸上完成,然后拍照、上传,作业批改有的是教师自己完成,有的是让学生自己批改,有的是让课代表批改,总而言之,流程繁琐耗时,效率很低,乐学一百互动作业线上完成,提交后即时反馈结果,作业完成情况、作业成绩、用时、错误题目系统也进行了统计分析,教学效率显著提升。
这是系统的互动课堂的智慧精讲模式,当发现孩子们的错题原因,可以借助钉钉软件进行3-5人小组直播,一起答疑分析此类题,并且让学生会举一反三。
课堂直播教学教师可以有的放矢,针对性强,吸引了同学们的注意,同时运用乐学一百作业系统的互动课堂进行随堂测试,即时检查学习效果,对学情精准定位,使得教师可以针对性的进行教学,提高了课堂教学效率。
试卷分析报告范文

试卷分析报告范文(经典版)编制人:__________________审核人:__________________审批人:__________________编制单位:__________________编制时间:____年____月____日序言下载提示:该文档是本店铺精心编制而成的,希望大家下载后,能够帮助大家解决实际问题。
文档下载后可定制修改,请根据实际需要进行调整和使用,谢谢!并且,本店铺为大家提供各种类型的经典范文,如公文写作、报告体会、演讲致辞、党团资料、合同协议、条据文书、诗词歌赋、教学资料、作文大全、其他范文等等,想了解不同范文格式和写法,敬请关注!Download tips: This document is carefully compiled by this editor. I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you!In addition, this shop provides you with various types of classic sample essays, such as official document writing, report experience, speeches, party and group materials, contracts and agreements, articles and documents, poems and songs, teaching materials, essay collections, other sample essays, etc. Learn about the different formats and writing styles of sample essays, so stay tuned!试卷分析报告范文试卷分析报告范文(精选7篇)试卷分析报告范文篇1一年级语文期末考试已经结束,仔细翻阅孩子们的试卷,有令我欣喜的地方,也有让我着急的不足之处。
八年级语文上册第一单元测试卷和答案

八年级语文上册第一单元测试卷和答案一、积累及运用(33分)1.在括号内填入拼音或汉字(2分)①祈dǎo( ) ②mù( )集③蹊( )跷④愠( )怒【答案】祷募 qī yùn【解析】试题分析:此题考查学生常用规范汉字的书写与拼音的掌握。
书写汉字时注意相近字形的区别,注意“祷”与“筹、寿”等字的区别。
“愠”不要写作“wēn”。
考点:识记并正确书写现代汉语普通话常用字的字音。
能力层级为识记A。
考点:识记并正确书写现代常用规范汉字。
能力层级为识记A。
2、解释下列文言加点字(4分)①齐人固善盗乎( ) ②叶徒相似( )③吏二缚一人诣王( ) ④缚者曷为者也( )【答案】本来只,只是往,到曷:同“何”,什么【解析】试题分析:本题重在考查课文中文言文实词用法与意义的理解。
“曷”的通假字现象,同“何”,什么。
考点:理解常见文言实词在文中的含义。
能力层级为理解B。
3、根据课文内容默写(10分)①五岭逶迤腾细浪,。
②,家书抵万金。
③,夜泊秦淮近酒家。
④,铁马冰河入梦来。
⑤人生自古谁无死,。
⑥梁园虽好,。
⑦感时花溅泪,。
⑧橘生淮南则为橘,。
⑨,寡人反取病焉。
⑩像山泉在呜咽,。
【答案】①乌蒙磅礴走泥丸②烽火连三月③烟笼寒水月笼沙④夜阑卧听风雨声⑤留取丹心照汗青⑥不是久恋之家⑦恨别鸟惊心⑧生于淮北则为枳⑨圣人非所与熙也⑩像波涛在澎湃考点:默写常见的名句名篇。
能力层级为识记A。
4.下列句子没有语病的一项是( )(3分)A.许多市民积极执行武汉市慈善会的倡议,将一天的所得送到灾区捐赠点,奉献爱心。
B.和煦的阳光驱散了夜幕的阴冷,草原展现出明媚、柔和、恬静之象。
C.游客一进入柳侯公园,看到的第一眼就是用花岗岩制作的古朴庄重的柳宗元雕像。
D.普及九年义务教育后,我市六县农村中小学的办学条件、教育质量有了很大提高。
【答案】B【解析】试题分析:本题考查学生修改病句的能力。
A、搭配不当,改为“许多市民积极响应武汉市慈善会的倡议”。
小数点加减法专项练习卷

1.34+0.7+0.3=6.4-0.7= 6-0.4-0.6=6.4+0.7-0.6= 6.4-(0.7-0.3)=0.38×101 (4.6 -3.2)×11.50.02×500= 3.6+0.4=0×4.32=2.8 ×10 =24.6-3.98+5.4-6.0264.3-18.75+15.7-11.25甲、乙、丙三条公路,甲公路的长度是乙公路的3倍,乙公路的长度是丙公路的2倍,甲公路的长度比丙公路长240千米,甲公路长多少千米?3 元5 角+2 元5 角-1 元8 角3 分(5)一个数减去9.09 得8.1,求这个数列式是6.09+8.1。
( ) (6)6 个十分之一和25 个0.01 的差是0.35 。
( ) 六、填一填(每空2 分,共22 分)①计算小数加减法,先把各数的_____对齐,也就是把_____上的数对齐,再按照______加减法的法则进行计算,最后在得数里对齐横线上的______点上小数点.②7.83 与2.37 的和与差分别是______和_______. ③整数的最小计数单位和小数的最大计数单位相差______. ④1 与0.09 多______,25 个0.01 比25 小_______ ⑤甲数是16.9,比乙数多7.26,甲、乙两数之和是_______ ⑥甲数增加1.2 后比乙数少0.75,已知数是2.95,甲数是_____. 七.竖式计算(前2 道验算)四、填空题。
(1) 0.8 里面有((2) 在()个0.1;0.025 里面有()个0.001。
)里填上合适的分数或小数。
) =( ) =( ) 0.09=( ) ),读作()个( )。
)。
0.18=((3) 一个数由3 个1,2 个0.1,7 个0.01 和5 个0.001 组成,这个数是( (4) 在2.649 中,6 在( )位上,表示( )个( );9 在()位上,表示((5) 按从大到小的顺序排列下面的数。
《小学数学个性化作业设计研究》课题实施方案

《小学数学个性化作业设计研究》课题实施方案一、问题的提出所谓“作业”是指儿童的一种活动方式,它是学生主动学习的一种方式,是学生以某一主题或某一领域的问题为主线进行的一种探究工作或活动,是学生对事物的不知,经过运用已有知识和经验,对材料的不断观察、筹划和思考,寻找合适的工具,像科学家那样自行探究达到认知的过程。
“作业”是为了巩固课堂教学效果而设计的供学生课外进行的练习。
它能够丰富学生的知识储备,扩大知识面,发展学生的智力和创造才能,是教学过程中一个不可缺少的重要环节。
当前,在新课程思想的指导下,课堂教学已经发生了可喜的变化,可是面临考试的压力,学生的作业依然沉重,呆板、重复、单一的现象依然存在。
作业随意性很大,教师很少从学生的实际与自身的研究出发,研制出适合学生兴趣的作业。
作业是课堂教学的补充与延伸,是学生学习生活的重要组成部分。
作业的改革也关系到课程改革的成败,关系到学生素养的提升和学习习惯的养成。
二、课题研究的目的、意义根据《国家中长期教育改革和发展规划纲要》的指示精神,结合我校的实际情况,我们对全处部分学校的学生(一二年级除外)做数学作业情况进行了调查,谈到作业内容,我们也惊奇地发现,70%以上的问卷上反应作业脱离生活实际,主要表现为:一是全由老师布置、批改、评价,学生处于被动地位;二是为了应付考试,教师不顾学生学习能力的差异,统一作业内容;三是简单重复、机械训练的书面抄写作业多。
这样,传统的作业,脱离了生活和学生实际,不利于学生个性和能力的发展,教师教得苦,学生学得累,作业效率可想而知。
从学校教学的现状分析来看,提到作业,我们就常常听到教师怨声载道,看到学生苦不堪言。
少做作业、不做作业、作业马虎、互抄作业的现象比比皆是。
随着课程改革的不断深入,课堂教学发生了较大的变化,学生的学习方式、教师的教学方法都有了一定的转变。
然而,在轰轰烈烈的课堂教学之后,却隐藏着许多缺憾,其中,作业问题尤为严重,普遍存在着师生对“作业”概念理解存在偏差、作业设计能力退化、作业时空安排不够合理、作业批阅与反馈效用不高等问题。
兰州市树人中学八年级数学下册第五单元《数据的分析》测试(包含答案解析)
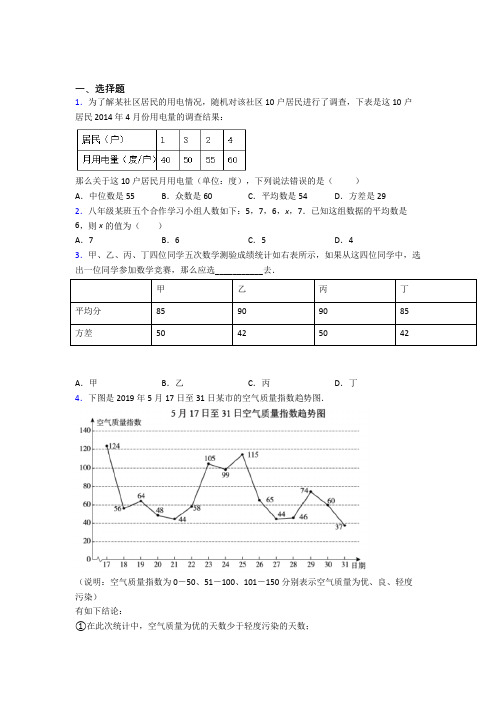
一、选择题1.为了解某社区居民的用电情况,随机对该社区10户居民进行了调查,下表是这10户居民2014年4月份用电量的调查结果:那么关于这10户居民月用电量(单位:度),下列说法错误的是()A.中位数是55 B.众数是60 C.平均数是54 D.方差是292.八年级某班五个合作学习小组人数如下:5,7,6,x,7.已知这组数据的平均数是6,则x的值为()A.7 B.6 C.5 D.43.甲、乙、丙、丁四位同学五次数学测验成绩统计如右表所示,如果从这四位同学中,选出一位同学参加数学竞赛,那么应选___________去.甲乙丙丁平均分85909085方差50425042A.甲B.乙C.丙D.丁4.下图是2019年5月17日至31日某市的空气质量指数趋势图.(说明:空气质量指数为0-50、51-100、101-150分别表示空气质量为优、良、轻度污染)有如下结论:①在此次统计中,空气质量为优的天数少于轻度污染的天数;②在此次统计中,空气质量为优良的天数占45;③20,21,22三日的空气质量指数的方差小于26,27,28三日的空气质量指数的方差.上述结论中,所有正确结论的序号是()A.①B.①③C.②③D.①②③5.为了让市民享受到更多的优惠,相关部门拟确定一个折扣线,计划使50%左右的人获得折扣优惠.某市针对乘坐地铁的人群进行了调查.调查小组在各地铁站随机调查了该市1000人上一年乘坐地铁的月均花费(单位:元),绘制了频数分布直方图,如图所示.下列说法正确的是()①每人乘坐地铁的月均花费最集中的区域在80~100元范围内;②每人乘坐地铁的月均花费的平均数范围是40~60元范围内;③每人乘坐地铁的月均花费的中位数在60~100元范围内;④乘坐地铁的月均花费达到80元以上的人可以享受折扣.A.①②④B.①③④C.③④D.①②6.若a、b、c这三个数的平均数为2,方差为S2,则a+2,b+2,c+2的平均数和方差分别是()A.2,S2B.4,S2C.2,S2+2 D.4,S2+47.在学校的体育训练中,小杰投掷实心球的7次成绩如统计图所示,则这7次成绩的中位数和平均数分别是()A.9.7m,9.9m B.9.7m,9.8m C.9.8m,9.7m D.9.8m,9.9m 8.某小组7名学生的中考体育分数如下:37,40,39,37,40,38,40,该组数据的众数、中位数分别为()A.40,37B.40,39C.39,40D.40,389.一组数据3,4,4,5,若添加一个数4,则发生变化的统计量是( ) A .平均数B .众数C .中位数D .方差10.实施新课改以来,某班学生经常采用“小组合作学习”的方式进行学习,值周班长小兵每周对各小组合作学习的情况进行综合评分,下表是其中一周的评分结果“分值”这组数据的中位数和众数分别是( ) A .89,90B .90,90C .88,95D .90,9511.某班体育委员记录了第一小组七位同学定点投篮(每人投10次)的情况,投进篮筐的个数为6,9,5,3,4,8,4,这组数据的众数是( ) A .3B .4C .5D .812.为了解某小区“全民健身”活动的开展情况,随机对居住在该小区的40名居民一周的体育锻炼时间进行了统计,结果如下表: 锻炼时间(时) 3 4 5 6 7 人数(人)6131452这40名居民一周体育锻炼时间的众数和中位数是( ) A .14,5B .14,6C .5,5D .5,6第II 卷(非选择题)请点击修改第II 卷的文字说明参考答案二、填空题13.已知一组数据a ,b ,c 的方差为2,那么数据3a +,3b +,3+c 的方差是________.14.已知一组数据a ,b ,c 的方差为2,那么数据a +3,b +3,c +3的方差是_____. 15.一组数据2,3,4,x ,6的平均数是4,则x 是_______.16.若一组数据4,a ,7,8,3的平均是5,则这组数据的方差是_______. 17.某次数学竞赛共有15道题,下表是对于做对n (n=0,1,2…15)道题的人数的一个统计,如果又知其中做对4道题和4道以上的学生每人平均做对6道题,做对10道题和10道题以下的学生每人平均做对4道题,问这个表至少统计了______人. n 0 1 23… 12 13 14 15做对 n 道题的人数7 8 10 21 … 15 63118.某同学记录了自己一周每天的零花钱(单位:元),分别如下:5,4.5,5,5.5,5.5,5,4.5这组数据的众数和平均数分别是_______和_______.19.已知一组数据5,10,15,x,9的平均数是8,那么这组数据的中位数是______.20.为调查某班学生每天使用零花钱的情况,张华随机调查了30名同学,结果如下表:每天使用零花钱(单位:元)12345人数25896则这30名同学每天使用的零花钱的中位数是_____元.三、解答题21.为选拔优秀选手参加瑶海区第八届德育文化艺术节“诵经典”比赛活动,九年级(1)、(2)班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩如图所示(1)根据图示填写下表班级平均数(分)中位数(分)众数(分)九(1)8585九(2)80(2)结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩较好;(3)计算两班复赛成绩的方差,并说明哪个班五名选手的成绩较稳定.22.“绿水青山就是金山银山”,北京市民积极参与义务植树活动.小武同学为了了解自己小区300户家庭在2018年4月份义务植树的数量,进行了抽样调查,随即抽取了其中30户家庭,收集的数据如下(单位:棵):1 123 2 3 2 3 34 3 3 4 3 35 3 4 3 4 4 5 4 5 3 4 3 4 5 6(1)对以上数据进行整理、描述和分析:①绘制如下的统计图,请补充完整;②求这30户家庭2018年4月份义务植树数量的平均数是和中位数分别是多少?(2)“互联网+全民义务植树”是新时代首都全民义务植树组织形式和尽责方式的一大创新,2018年首次推出义务植树网上预约服务,小武同学所调查的这30户家庭中有7户家庭采用了网上预约义务植树这种方式,由此可以估计该小区采用这种形式的家庭有多少户?23.受疫情影响,某地无法按原计划正常开学.在延迟开学期间该地区组织了在线教学活动.开学后,某校针对各班在线教学的个性化落实情况,通过初评决定从甲、乙、丙三个班中推荐一个作为在线教学先进班级,下表是这三个班的五项指标的考评得分表(单位:分):根据统计表中的信息解答下列问题:(1)请确定如下的“五项指标的考评得分分析表”中的a、b、c的值:(2)如果学校把“课程设置”、“课程质量”、“在线答疑”、“作业情况”、“学生满意度”这五项指标得分按照2∶2∶3∶1∶2的比例确定最终成绩,请你通过计算判断应推荐哪个班为在线教学先进班级?24.某初中要调查学校学生(总数 1000 人)双休日课外阅读情况,随机调查了一部分学生,调查得到的数据分别制成频数直方图(如图 1)和扇形统计图(如图 2).(1)请补全上述统计图(直接填在图中); (2) 试确定这个样本的中位数和众数;(3)请估计该学校 1000 名学生双休日课外阅读时间不少于 4 小时的人数.25.为宣传6月6日世界海洋日,某校九年级举行了主题为“珍惜海洋资源,保护海洋生物多样性”的知识竞赛活动.为了解全年级500名学生此次竞赛成绩(百分制)的情况,随机抽取了部分参赛学生的成绩,整理并绘制出如下不完整的统计表(表1)和统计图(如图).表1知识竞赛成绩分组统计表 组别分数/分 频数A6070x ≤< aB7080x ≤< 10 C8090x ≤< 14 D90100x ≤<18请根据图表信息解答以下问题:(1)本次调查一共随机抽取了________个参赛学生的成绩,表1中a =________; (2)所抽取的参赛学生的成绩的中位数落在的“组别”是________;(3)请你估计,该校九年级竞赛成绩达到80分以上(含80分)的学生约多少人? 26.某中学七、八年级各选10名同学参加“创全国文明城市”知识竞赛,计分10分制,选手得分均为整数,成绩达到6分或6分以上为合格,达到9分或9分以上为优秀,这次竞赛后,七、八年级两支代表队成绩分布的条形统计图和成绩分析表如下,其中七年级代表队得6分、10分选手人数分别为a ,b .队列 平均分 中位数 方差 合格率 优秀率七年级 6.7m3.41 90% n八年级7.1 7.5 1.6980%10%(1)根据图表中的数据,求a ,b 的值. (2)直接写出表中的m = ,n = .(3)你是八年级学生,请你给出两条支持八年级队成绩好的理由.【参考答案】***试卷处理标记,请不要删除一、选择题 1.D 解析:D 【分析】根据中位数、众数、平均数和方差的概念分别求得这组数据的中位数、众数、平均数和方差,即可判断四个选项的正确与否. 【详解】这组数据按照从小到大的顺序排列为:40,50,50,50,55,55,60,60,60,60, 则众数为:60,中位数为:55, 平均数为:405050505555606060606010++++++++++=54,方差为:22221(4054)3(5054)2(5554)4(6054)10⎡⎤-+⨯-+⨯-+⨯-⎣⎦=39. 故选D .2.C解析:C 【分析】根据平均数的计算公式列出算式,再进行计算即可得出x 的值.【详解】解:∵5,7,6,x,7的平均数是6,∴15(5+7+6+x+7)=6,解得:x=5;故选:C.【点睛】本题考查了算术平均数的知识,解题的关键是根据算术平均数求出数据总和.3.B解析:B【分析】本题首先可通过四位同学的平均分比较,择高选取;继而根据方差的比较,择低选取求解本题.【详解】通过四位同学平均分的比较,乙、丙同学平均数均为90,高于甲、丁同学,故排除甲、丁;乙、丙同学平均数相同,但乙同学方差更小,说明其发挥更为稳定,故选择乙同学.故选:B.【点睛】本题考查平均数以及方差,平均数表示其平均能力的高低;方差表示数据波动的大小,即稳定性高低,数值越小,稳定性越强,考查对应知识点时严格按照定义解题即可.4.C解析:C【分析】根据折线统计图的数据,逐一分析即可.【详解】解:①中:当空气质量指数为0-50时表示优,数出折线图中在这个范围内的天数有5天;当空气质量指数为101-150是表示轻度污染,数出折线图中在这个范围内的天数有3天,故空气质量优的天数大于轻度污染的天数,故①错误;②中:空气质量指数在0-100范围内为优良,其天数共有12天,故空气质量为优良的天数所占比例为:124=155,故②正确;③中:20,21,22三日的空气质量指数波动范围小于26,27,28三日的空气质量指数波动范围,故20,21,22三日的空气质量指数的方差小于26,27,28三日的空气质量指数的方差,故③正确.∴正确的有:②③.故答案为:C.【点睛】本题是复式折线统计图,要通过坐标轴以及图例等读懂本图,根据图中所示的数量解决问题.5.C解析:C 【分析】根据频数分布直方图中的数据,求得众数,平均数,中位数,即可得出结论. 【详解】解:①根据频数分布直方图,可得众数为60−80元范围,故每人乘坐地铁的月均花费最集中的区域在60−80元范围内,故①不正确;②每人乘坐地铁的月均花费的平均数=876001000=87.6=87.6元,所以每人乘坐地铁的月均花费的平均数范围是80~100元,故②错误;③每人乘坐地铁的月均花费的中位数约为80元,在60~100元范围内,故③正确;④为了让市民享受到更多的优惠,若使50%左右的人获得折扣优惠,则乘坐地铁的月均花费达到80元以上的人可以享受折扣,故④正确. 故选:C 【点睛】本题主要考查了频数分布直方图,平均数以及中位数的应用,将一组数据按照从小到大(或从大到小)的顺序排列,如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数.如果这组数据的个数是偶数,则中间两个数据的平均数就是这组数据的中位数.6.B解析:B 【分析】方差是用来衡量一组数据波动大小的量,每个数都加了2,所以波动不会变,方差不变,平均数增加2. 【详解】由题意知,原来的平均数为2,每个数据都加上2,则平均数变为4;原来的方差221=(2)(2)(2)3S a b c ⎡⎤---⎣⎦22++ 现在的方差:222222111=(24)(24)(24)=(2)(2)(2)33S a b c a b c S ⎡⎤⎡⎤+-+-+-=---=⎣⎦⎣⎦22++++ 方差不变. 故选:B. 【点睛】本题考查了方差和平均数,当数据都加上一个数(或减去一个数)时,方差不变,即数据的波动情况不变.7.B解析:B【分析】将这7个数据从小到大排序后处在第4位的数是中位数,利用算术平均数的计算公式进行计算即可.【详解】把这7个数据从小到大排列处于第4位的数是9.7m,因此中位数是9.7m,平均数为:(9.59.69.79.79.810.110.2)79.8++++++÷=m,故选B.【点睛】考查中位数、算术平均数的计算方法,将一组数据从小到大排列后处在中间位置的一个数或两个数的平均数就是这组数据的中位数,平均数则是反映一组数据的集中水平.8.B解析:B【分析】根据众数和中位数的概念求解可得.【详解】将数据重新排列为37,37,38,39,40,40,40所以这组数据的众数为40,中位数为39,故选B.【点睛】本题考查了中位数和众数的概念,一组数据中出现次数最多的数据叫做众数;将一组数据按照从小到大(或从大到小)的顺序排列,如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数;如果这组数据的个数是偶数,则中间两个数据的平均数就是这组数据的中位数.9.D解析:D【分析】依据平均数、中位数、众数、方差的定义和公式分别计算新旧两组数据的平均数、中位数、众数、方差求解即可.【详解】原数据的3,4,4,5的平均数为3+4+4+5=44,原数据的3,4,4,5的中位数为4+4=24,原数据的3,4,4,5的众数为4,原数据的3,4,4,5的方差为14×[(3-4)2+(4-4)2×2+(5-4)2]=0.5;新数据3,4,4,4,5的平均数为3+4+4+4+5=45,新数据3,4,4,4,5的中位数为4,新数据3,4,4,4,5的众数为4,新数据3,4,4,4,5的方差为15×[(3-4)2+(4-4)2×3+(5-4)2]=0.4;∴添加一个数据4,方差发生变化,故选D.【点睛】本题主要考查的是众数、中位数、方差、平均数,熟练掌握相关概念和公式是解题的关键.10.B解析:B【解析】【分析】根据中位数和众数的定义找出从小到大排列后最中间的数和出现次数最多的数即可.【详解】把这组数据从小到大排列:84,89,90,90,90,91,96,最中间的数是90,则中位数是90;90出现了3次,出现的次数最多,则众数是90;故选B.【点睛】此题考查了中位数和众数,中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数),叫做这组数据的中位数;众数是一组数据中出现次数最多的数.11.B解析:B【解析】【分析】众数是出现次数最多的数,据此求解即可.【详解】∵数据4出现了2次,最多,∴众数为4,故选:B.【点睛】本题考查了众数的知识,解题的关键是了解有关的定义,属于基础题,难度不大.12.C解析:C【解析】【分析】众数是一组数据中出现次数最多的数据,中位数是将一组数据按大小依次排列,把处在最中间位置的一个数据或者最中间两个数据的平均数叫这组数据的中位数.本组数据中,把数据按照从大到小的顺序排列,最中间的两个数的平均数即为中位数. 【详解】由统计表可知:体育锻炼时间最多的是5小时,故众数是5小时;统计表中是按从小到大的顺序排列的,最中间两个人的锻炼时间都是5小时,故中位数是5小时. 故选C . 【点睛】本题考查了确定一组数据的众数和中位数的能力.将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数),叫做这组数据的中位数.注意找中位数的时候一定要先排好顺序,然后再根据奇数和偶数个来确定中位数.如果数据有奇数个,则正中间的数字即为所求;如果是偶数,则找中间两位数的平均数.二、填空题13.2【分析】根据方差是用来衡量一组数据波动大小的量每个数都加3所以波动不会变方差不变【详解】解:设abc 的平均数是d 所以方差不变故答案为:2【点睛】本题主要考查了方差的公式解题的关键是当数据都加上一个解析:2 【分析】根据方差是用来衡量一组数据波动大小的量,每个数都加3,所以波动不会变,方差不变. 【详解】解:设a 、b 、c 的平均数是d,()222211S =()()23a d b d c d ⎡⎤-+-+-=⎢⎥⎣⎦ , ()222221S =33(33)(33)23a d b d c d ⎡⎤+-+++-+++-+=⎢⎥⎣⎦ , ()222221S =()()23a d b d c d ⎡⎤-+-+-=⎢⎥⎣⎦, 所以方差不变. 故答案为:2. 【点睛】本题主要考查了方差的公式,解题的关键是当数据都加上一个数时,方差不变.14.2【分析】根据数据abc 的方差为2由方差为2可得出数据a+3b+3c+3的方差【详解】解:∵数据abc 的方差为2设平均数为m 则则数据a+3b+3c+3的平均数是m+3∴方差为:故答案为:2【点睛】本解析:2 【分析】根据数据a ,b ,c 的方差为2,由方差为2可得出数据a+3,b+3,c+3的方差. 【详解】解:∵数据a ,b ,c 的方差为2,设平均数为m ,则2222()()()23a mb mc m S -+-+-==,则数据a +3,b +3,c +3的平均数是m+3,∴方差为:2222(33)(33)(33)3a mb mc m S +--++--++--=222()()()23a mb mc m -+-+-==,故答案为:2. 【点睛】本题考查的是方差,熟记方差的定义是解答此题的关键.15.5【分析】根据用平均数的定义列出算式再进行计算即可得出答案【详解】解:∵数据234x6的平均数是4∴(2+3+4+x+6)÷5=4解得:x=5;故答案为:5【点睛】本题考查了平均数的概念平均数是指在解析:5 【分析】根据用平均数的定义列出算式,再进行计算即可得出答案. 【详解】解:∵数据2,3,4,x ,6的平均数是4, ∴(2+3+4+x+6)÷5=4, 解得:x=5; 故答案为:5. 【点睛】本题考查了平均数的概念.平均数是指在一组数据中所有数据之和再除以数据的个数.16.【分析】根据平均数求出a 再根据方差的公式计算得到答案【详解】∵数据4783的平均是5∴∴这组数据的方差是=故答案为:【点睛】此题考查根据平均数求某一数据方差的计算公式熟记方差的计算公式是解题的关键 解析:225【分析】根据平均数求出a ,再根据方差的公式计算得到答案. 【详解】∵数据4,a ,7,8,3的平均是5, ∴5547833a =⨯----=, ∴这组数据的方差是22221(45)2(35)(75)(85)5⎡⎤-+⨯-+-+-⎣⎦=225, 故答案为:225.【点睛】此题考查根据平均数求某一数据,方差的计算公式,熟记方差的计算公式是解题的关键. 17.200【解析】【分析】设统计的总人数为x答对11道题的人数为a根据做对4个题和4个以上的人数乘以其平均分加上做对4个以下题的人答对的总题数等于所有被统计的人答对的总题数;做对10个题和10个以下的人解析:200【解析】【分析】设统计的总人数为x,答对11道题的人数为a,根据做对4个题和4个以上的人数乘以其平均分加上做对4个以下题的人答对的总题数等于所有被统计的人答对的总题数;做对10个题和10个以下的人数乘以其平均分加上做对10个以上题的人答对的总题数等于所有被统计的人答对的总题数.做对10个题和10个以下的人数乘以其平均分加上做对11,12,13,14道题的人答对的总题数等于所有被统计的人答对的总题数列方程求解即可.【详解】设统计的总人数为x,答对11道题的人数为a.∵做对4个题和4个以上的人数为(x-7-8-10-21)=(x-46)人,∴所有学生做的总题数为:(x-46)×6+0×7+1×8+2×10+3×21=6x-185;又∵做对10个题和10个以下的人数为(x-a-15-6-3-1)=(x-a-25)人,∴所有学生做的总题数为:(x-a-25)×4+15×1+14×3+13×6+12×15+11a=4x+215+7a,∴6x-185=4x+215+7a,2x=400+7a,x=200+ 72 a,∵a为自然数,∴当a=0时x取最小值200.所以至少统计了200人.故答案为200【点睛】本题考查了加权平均数及方程的应用,有一定的难度.解题关键是根据答对的总题数不变列方程.18.55【解析】【分析】根据众数和平均数的定义求解【详解】解:5出现了三次出现次数最多所以这组数据的众数是5这组数据的平均数=(5+45+5+55+55+5+45)=5故答案为:5;5【点睛】本题考查平解析:5 5【解析】【分析】根据众数和平均数的定义求解.【详解】解:5出现了三次,出现次数最多,所以这组数据的众数是5,这组数据的平均数=17(5+4.5+5+5.5+5.5+5+4.5)=5.故答案为:5;5.【点睛】本题考查平均数的求法以及众数的定义:一组数据中出现次数最多的数据叫做众数.19.9【解析】【分析】根据平均数的定义先求出x的值再根据中位数的定义即可得出答案【详解】根据平均数的定义可知(5+10+15+x+9)÷5=8解得:x=1把这组数据从小到大的顺序排列为1591015处于解析:9【解析】【分析】根据平均数的定义先求出x的值,再根据中位数的定义即可得出答案.【详解】根据平均数的定义可知,(5+10+15+x+9)÷5=8,解得:x=1,把这组数据从小到大的顺序排列为1,5,9,10,15,处于中间位置的那个数是9,那么由中位数的定义可知,这组数据的中位数是9;故答案为9.【点睛】考查了中位数,掌握中位数的定义是本题的关键;中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数),叫做这组数据的中位数.20.35【解析】分析:利用众数的定义可以确定众数在第三组由于张华随机调查了20名同学根据表格数据可以知道中位数是按从小到大排序第15个与第16个数的平均数详解:∵4出现了9次它的次数最多∴众数为4∵张华解析:3.5【解析】分析: 利用众数的定义可以确定众数在第三组,由于张华随机调查了20名同学,根据表格数据可以知道中位数是按从小到大排序,第15个与第16个数的平均数.详解: ∵4出现了9次,它的次数最多,∴众数为4.∵张华随机调查了30名同学,∴根据表格数据可以知道中位数=(3+4)÷2=3.5,即中位数为3.5.故答案为:3.5.点睛: 本题属于基础题,考查了确定一组数据的中位数和众数的能力.要明确定义,一些学生往往对这个概念掌握不清楚,计算方法不明确而误选其它选项,注意找中位数的时候一定要先排好顺序,然后再根据奇数和偶数个来确定中位数,如果数据有奇数个,则正中间的数字即为所求,如果是偶数个则找中间两位数的平均数.三、解答题21.(1)(3)九(1)班五名选手的成绩较稳定. 【分析】(1)观察图分别写出九(1)班和九(2)班5名选手的复赛成绩,然后根据中位数的定义和平均数的求法以及众数的定义求解即可; (2)在平均数相同的情况下,中位数高的成绩较好; (3)根据方差公式计算即可:()()()2222121x x x n n S x x x ⎡⎤=--++-⎢⎥⎣+⎦(可简单记忆为“等于差方的平均数”). 【详解】解:(1)由图可知九(1)班5名选手的复赛成绩为:75、80、85、85、100, ∴九(1)的中位数为85,把九(2)的成绩按从小到大的顺序排列为:70、75、80、100、100, ∴九(2)的平均数为(70+75+80+100+100)÷5=85, 九(2)班的众数是100;(3)215S =一班[(75﹣85)2+(80﹣85)2+(85﹣85)2+(85﹣85)2+(100﹣85)2]=70,21=5S 二班[(70﹣85)2+(100﹣85)2+(100﹣85)2+(75﹣85)2+(80﹣85)2]=160.∵22S S 一班二班,∴九(1)班五名选手的成绩较稳定.【点睛】本题考查了中位数、众数以及平均数的求法,同时也考查了方差公式,解题的关键是牢记定义并能熟练运用公式.22.(1)①补图见解析;②这30户家庭2018年4月份义务植树数量的平均数是3.4棵,中位数是3棵;(2)估计该小区采用这种形式的家庭有70户. 【分析】(1)①由已知数据知3棵的有12人、4棵的有8人,据此补全图形可得; ②根据平均数和众数的定义求解可得;(2)用总户数乘以样本中采用了网上预约义务植树这种方式的户数所占比例可得. 【详解】(1)①由已知数据知3棵的有12人、4棵的有8人, 补全图形如下:②这30户家庭2018年4月份义务植树数量的平均数是12233124854613.430⨯+⨯+⨯+⨯+⨯+⨯=(棵)中位数:从小到大排列,中位数应为第15位和第16位的数的平均值:3332+=(棵) 答:这30户家庭2018年4月份义务植树数量的平均数是3.4棵,中位数是3棵.(2)估计该小区采用这种形式的家庭有300×730=70户, 答:估计该小区采用这种形式的家庭有70户. 【点睛】本题主要考查了频数分布直方图,中位数、平均数的定义及样本估计总体思想的运用.读懂统计图,从统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据.23.(1)a =10,b =8,c =8.6;(2)推荐丙班级为网上教学先进班级. 【分析】(1)直接根据中位数、众数、平均分的概念即可求解;(2)先根据各项得分的权重求得各班的最终成绩,然后比较即可判断. 【详解】解:(1)∵甲班的五项指标得分由小到大重新排列为:6、7、10、10、10 ∴甲班的中位数为:10分;∵乙班的五项指标得分为:10、8、8、9、8 8分出现次数最多, ∴乙班的众数是:8分; ∵(9+10+8+7+9)÷5=8.6(分),∴丙班的平均分是:8.6分;∴a=10,b=8,c=8.6.(2)甲:10×20%+10×20%+6×30%+10×10%+7×20%=8.2(分)乙:10×20%+8×20%+8×30%+9×10%+8×20%=8.5(分)丙:9×20%+10×20%+8×30%+7×10%+9×20%=8.7(分),∴推荐丙班级为网上教学先进班级.【点睛】此题主要考查数据的统计和分析,正确理解每个概念是解题关键.24.(1)画图见解析;(2)中位数是3小时,众数是4小时;(3)400人.【分析】(1)根据阅读5小时以上频数为6,所占百分比为12%,求出数据的总数,再用数据总数减去其余各组频数得到阅读3小时以上频数,然后补全频数分布直方图,分别求得阅读0小时和4小时的人数所占百分比,补全扇形图;(2)利用各组频数和总数之间的关系确定中位数和众数;(3)用1000乘以每周课外阅读时间不小于4小时的学生所占百分比即可.【详解】解:(1)总人数:6÷12%= 50 (人),阅读3小时以上人数:50-4-6-8-14-6= 12 (人),阅读3小时以上人数的百分比为12÷50= 24% ,阅读0小时以上人数的百分比为4÷50= 8% .图如下:(2)中位数是3小时,众数是4小时;(3) 1000⨯(28% + 12%)= 1000⨯40%= 400(人)答:该学校1000名学生双休日课外阅读时间不少于4小时的人数为400人.【点睛】此题考查数据的收集,主要有中位数,众数,扇形图和直方图的画法及表达的意义.25.(1)50; 8;(2)C组;(3)320人。
双减课题《初中语文个性化作业设计与评价研究》结题报告
双减课题《初中语文个性化作业设计与评价研究》结题报告一、研究背景过重的课业负担严峻损害青少年的身心健康,危害民族将来。
只有通过减轻课业负担,才能保证学生生动活泼的个性、健康欢乐成长。
国家为了切实提升学校育人水平,持续规范校外培训,有效减轻义务教育阶段学生过重作业负担和校外培训负担,印发了《关于进一步减轻义务教育阶段学生作业负担和校外培训负担的意见》(简称“双减”)0从这开始,“双减”成了街头巷尾谈论的主要话题,更变成了教师的工作指针。
每位教师肩负起“双减提质"的研究任务。
语文作业是语文教学的重要组成部分。
它不仅是学生巩固学问、熟练技能的主要途径,还是教师检验课堂教学效果、改进课堂教学策略的主要手段。
语文作业的有效与否直接关乎语文教学质量,其地位之重显而易见。
但综观目前作业现状,传统作业的种种缺陷仍旧有目共睹。
作业设计的内容上机械单一,多从课后练习,配套习题中选择;形式上多是“一刀切”,缺乏自主性和合作性;注重基础学问、基本技能的训练,忽略了过程与方法、情感态度和价值观。
作业评价多以“""“X”和日期为主,片面单调,缺少激励性评语;作业答案确定化,扼杀学生的制造性。
鉴于此,我们旨在以作业为突破口,通过优化作业设计与评价,让学生在欢乐幸福的作业过程中把握学问与技能,并且使语文课程通过作业实现向学生经验和生活的回归。
彻底改革过去那种机械、枯燥、繁重的作业形式,还学生以自主、生动、布满智慧与情趣的作业,让每个学生都能“个性”成长。
二、课题研究的理论意义《语文课程标准》倡导学生做学习的主人,新课程改革由更多关注学习的结果转为更多地关注学习的过程,让学生乐于学习,主动参与学习活动,勤于动手动脑,乐观探究。
擅长收集和处理信息。
新课程标准出台后,对教材内容、课堂教学、课外活动、研究性学习都作了较为新颖的阐述和规定,但对于占据学生学习活动近三分之一时间量的作业活动却没有说明。
语文课程是“工具性与人文性的统一”,是“实践性很强的课程”,要想实现语文课程标准提出的众多目标,不仅依靠于课堂教学的改革,还要依靠于作业的改革,因为作业是为巩固课堂教学效果而设计的供学生完成的练习,对教师而言它就像一把尺子,既可以反映学生的问题和不足,又可以衡量某种教学方法使用的教学效果;对学生而言,适时适量适度的作业,能够巩固所学学问,扩大学问面,进展学生的智力和制造才能,所以新课程改革得更关注作业的优化设计,注重学生学习能力的培育。
双减课题初中语文个性化作业的实践研究结题报告
双减课题初中语文个性化作业的实践研究结题报告一、课题研究的背景及价值(一)课题研究的背景落实“双减”政策,提高教学质量,减轻义务教育阶段学生作业负担,“双减”背景下,如何困境突围?如何减“量”增“质”?如何从“固化的重复性作业”迈向“个性化作业”呢?作业既要让学生感兴趣,还能起到作业应有的作用。
作业除了是检验学和教的重要手段以外,还应起到指导学生学习的作用。
所以,老师们在设计作业时,要从本校的学情和教情出发,因地制宜地设计作业。
控制作业数量,注重思维质量,在减负的前提下力争实现增效。
“个性化作业设计”,是一种结合学生个人特色以及多种新型教学方法的新兴作业设计方法,教师利用这样的教学方法来来为学生布置作业,可以让学生在完成作业的过程中培养学生是特点,让学生做自己喜欢的事,因为教师为学生布置的作业是根据不同学生的特点来布置,完成满足学生的需求,以这样的教学方法为学生教学,可以引导学生是个性化发展,让学生在学习过程中提高自己的特点,同时提高学习效率。
在注重知识训练的同时,还要全面培养学生的能力,采用多样化的作业形式,吸引学生的学习兴趣,及时反馈学生的作业情况。
因此,语文教师可以根据不同的学生设计相应的作业。
更有利于在短时间内巩固知识,激发创新意识。
因此,我们的老师应该合理利用中学生愿意尝试新事物的特点,设计和实施个性化的语文作业,让个性化教育能够从头到尾地进行下去。
作业设计要针对不同学生的特点,体现作业设计的层次性、逻辑性,落实语文的学科核心能力。
(二)课题研究的价值本课题研究的重要意义在于:在“双减”政策背景下,特色个性化作业给学生们的学习增添兴趣,提供展示的舞台,锻炼学生的总结能力、实践能力、欣赏美、创造美的能力,提升学生的综合学科素养,也吸引更多的孩子投入到想学、会学、爱学、乐学的行动中来。
二、课题研究的构想个性化作业是根据学生的知识、学习能力、兴趣爱好而设计的。
也就是说,不同情境下的学生做不同的作业,每个学生都有自己的作业,这样才能根据自己的个性得到最大的发展。
小数点加减法专项练习卷
1.34+0.7+0.3=6.4-0.7= 6-0.4-0.6=6.4+0.7-0.6= 6.4-(0.7-0.3)=0.38×101 (4.6 -3.2)×11.50.02×500= 3.6+0.4=0×4.32=2.8 ×10 =24.6-3.98+5.4-6.0264.3-18.75+15.7-11.25甲、乙、丙三条公路,甲公路的长度是乙公路的3倍,乙公路的长度是丙公路的2倍,甲公路的长度比丙公路长240千米,甲公路长多少千米?3 元5 角+2 元5 角-1 元8 角3 分(5)一个数减去9.09 得8.1,求这个数列式是6.09+8.1。
( ) (6)6 个十分之一和25 个0.01 的差是0.35 。
( ) 六、填一填(每空2 分,共22 分)①计算小数加减法,先把各数的_____对齐,也就是把_____上的数对齐,再按照______加减法的法则进行计算,最后在得数里对齐横线上的______点上小数点.②7.83 与2.37 的和与差分别是______和_______. ③整数的最小计数单位和小数的最大计数单位相差______. ④1 与0.09 多______,25 个0.01 比25 小_______ ⑤甲数是16.9,比乙数多7.26,甲、乙两数之和是_______ ⑥甲数增加1.2 后比乙数少0.75,已知数是2.95,甲数是_____. 七.竖式计算(前2 道验算)四、填空题。
(1) 0.8 里面有((2) 在()个0.1;0.025 里面有()个0.001。
)里填上合适的分数或小数。
) =( ) =( ) 0.09=( ) ),读作()个( )。
)。
0.18=((3) 一个数由3 个1,2 个0.1,7 个0.01 和5 个0.001 组成,这个数是( (4) 在2.649 中,6 在( )位上,表示( )个( );9 在()位上,表示((5) 按从大到小的顺序排列下面的数。
最新人教版初中数学八年级数学下册第五单元《数据的分析》检测题(有答案解析)
一、选择题1.反映一组数据变化范围的是( ) A .极差B .方差C .众数D .平均数2.某市连续10天的最低气温统计如下(单位:℃):4,5,4,7,7,8,7,6,5,7,该市这10天的最低气温的中位数是( ) A .6℃B .6.5℃C .7℃D .7.5℃3.下表记录了甲、乙、丙、丁四名射击运动员最近几次选拔赛成绩的平均数和方差:甲 乙 丙 丁 平均数(环) 9.14 9.15 9.14 9.15 方差6.66.86.76.6根据表中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应选择( ) A .甲B .乙C .丙D .丁4.某校有21名同学们参加某比赛,预赛成绩各不同,要取前11名参加决赛,小颖已经知道了自己的成绩,她想知道自己能否进入决赛,只需要再知道这21名同学成绩的( ) A .最高分B .中位数C .极差D .平均数5.下列说法正确的是( )A .为了解我国中学生课外阅读的情况,应采取全面调查的方式B .一组数据1、2、5、5、5、3、3的中位数和众数都是5C .若甲组数据的方差是003,乙组数据的方差是0.1,则甲组数据比乙组数据稳定D .抛掷一枚硬币100次,一定有50次“正面朝上”6.已知一组数据a ,b ,c 的平均数为5,方差为4,那么数据22a -,22b -,22c -的平均数和方差分别是( ) A .8,16B .10,6C .3,2D .8,87.如图是根据我市某天七个整点时的气温绘制成的统计图,则下列说法正确的是( )A .这组数据的众数是14B .这组数据的中位数是31C .这组数据的标准差是4D .这组是数据的极差是98.有甲乙两个箱子,其中甲箱内有98颗球,分别标记号码1~98,且号码不重复的整数,乙箱内没有球。
已知某同学从甲箱内拿出49颗球放入乙箱后,乙箱内球的号码的中位数为40.若此时甲箱内有a颗球的号码小于40,有b颗球的号码大于40,则关于a,b的值,下列选项正确的是( )A.a=15 B.a=16 C.b=24 D.b=359.某校八年级有八个班,一次测试后,分别求得各个班级学生成绩的平均数,它们不完全相同,下列说法正确的是()A.将八个班级各自的平均成绩之和除以8,就得到全年级学生的平均成绩B.全年级学生的平均成绩一定在这八个班级各自的平均成绩的最小值与最大值之间C.这八个班级各自的平均成绩的中位数就是全年级学生的平均成绩D.这八个班级各自的平均成绩的众数不可能是全年级学生的平均成绩10.为了比较甲乙两足球队的身高谁更整齐,分别量出每人身高,发现两队的平均身高一样,甲、乙两队的方差分别是1.7、2.4,则下列说法正确的是()A.甲、乙两队身高一样整齐B.甲队身高更整齐C.乙队身高更整齐D.无法确定甲、乙两队身高谁更整齐11.某班体育委员记录了第一小组七位同学定点投篮(每人投10次)的情况,投进篮筐的个数为6,9,5,3,4,8,4,这组数据的众数是()A.3 B.4 C.5 D.812.下面的统计图表示某体校射击队甲、乙两名队员射击比赛的成绩,根据统计图中的信息,下列结论正确的是()A.甲队员成绩的平均数比乙队员的大B.乙队员成绩的平均数比甲队员的大C.甲队员成绩的中位数比乙队员的大D.甲队员成绩的方差比乙队员的大二、填空题13.某中学篮球队12名队员的年龄情况如下:年龄(单位:1415161718岁)人数14322则这个队队员年龄的众数和中位数分别是_____岁、_____岁.14.甲、乙两人参加某网站的招聘测试,测试由网页制作和语言两个项目组成,他们各自的成绩(百分制)如下表所示: 应聘者 网页制作 语言 甲 80 70 乙7080该网站根据成绩在两人之间录用了甲,则本次招聘测试中权重较大的是_____项目. 15.若一组数据1,2,a ,3,5的平均数是3,则这组数据的标准差是______. 16.小林同学对甲、乙、丙三个市场某月份每天的白菜价格进行调查,计算后发现这个月三个市场的价格平均值相同,方差分别为2S 7.5=甲,2S 1.5乙=,2S 3.1=丙,那么该月份白菜价格最稳定的是______市场.17.一组数2、a 、4、6、8的平均数是5,这组数的中位数是______.18.为迎接2018年的体育中考,甲、乙两位同学参加排球训练,体育老师根据训练成绩算出他们成绩的方差分别为S 甲2=1.6,S 乙2=2.8,则_____(填“甲”或“乙”)成绩较稳定. 19.已知一组数据的方差s 2=14[(x 1﹣6)2+(x 2﹣6)2+(x 3﹣6)2+(x 4﹣6)2],那么这组数据的总和为_____.20.一组数据1,3,2,7,x ,2,3的平均数是3,则该组数据的众数为________.三、解答题21.为了了解七年级学生零花钱的使用情况,校团委随机调查了本校七年级部分学生每人一周的零花钱数额,并绘制了如图甲、乙所示的两个统计图(部分未完成),请根据图中信息,回答下列问题:(1)校团委随机调查了多少学生?请你补全条形统计图; (2)表示“50元”的扇形的圆心角是多少度?(3)某地发生自燃灾害后,七年级800名学生每人自发地捐出一周零花钱的一半,以支援灾区恢复生产,请估算七年级学生捐款多少元?22.学校广播站要招聘一名播音员,考查形象、知识面、普通话三个项目(每个项目按百分制计分).若按形象占10%,知识面占40%,普通话占50%计算加权平均数,作为最后评定的总成绩.李颖和张明两位同学的各项成绩如表所示:项目形象知识面普通话选手李颖708088张明8075x(2)若张明同学要在总成绩上超过李颖同学,求x的范围.23.甲、乙两人在相同条件下各立定跳远5次,距离如下(单位:cm):甲:225,230,240,230,225;乙:220,235,225,240,230.(1)计算这两组数据的方差;(2)谁的跳远技术较稳定?为什么?24.在“全民读书月”活动中,小明调查了班级里40名同学本学期计划购买课外书的花费情况,并将结果绘制成如图所示的统计图,请根据相关信息,解答下列问题:(直接填写结果)(1)本次调查获取的样本数据的众数是;(2)这次调查获取的样本数据的中位数是;(3)若该校共有学生1000人,根据样本数据,估计本学期计划购买课外书花费50元的学生有人.25.受疫情影响,某地无法按原计划正常开学.在延迟开学期间该地区组织了在线教学活动.开学后,某校针对各班在线教学的个性化落实情况,通过初评决定从甲、乙、丙三个班中推荐一个作为在线教学先进班级,下表是这三个班的五项指标的考评得分表(单位:分):根据统计表中的信息解答下列问题:(1)请确定如下的“五项指标的考评得分分析表”中的a、b、c的值:(2)如果学校把“课程设置”、“课程质量”、“在线答疑”、“作业情况”、“学生满意度”这五项指标得分按照2∶2∶3∶1∶2的比例确定最终成绩,请你通过计算判断应推荐哪个班为在线教学先进班级?26.某工厂甲、乙两名工人参加操作技能培训.现分别从他们在培训期间参加的若干次测试成绩中随机抽取8次,数据如下(单位:分).甲9582888193798478乙8375808090859295(1)请你计算这两组数据的平均数、中位数.(2)现要从中选派一人参加操作技能比赛,从统计学的角度考虑,你认为选派哪名工人参加合适?请说明理由.【参考答案】***试卷处理标记,请不要删除一、选择题1.A解析:A【分析】根据极差是刻画数据离散程度的一个统计量.它能反映数据的波动范围大小解答.【详解】解:反映一组数据变化范围的是极差;故选:A.【点睛】本题考查了极差、方差、众数以及平均数的概念和意义,掌握极差是刻画数据离散程度的一个统计量.它能反映数据的波动范围是解题的关键.2.B解析:B【分析】由于10天天气,根据数据可以知道中位数是按从小到大排序,第5个与第6个数的平均数.【详解】解:10天的气温排序为:4,4,5,5,6,7,7,7,7,8, 中位数为:6+72=6.5, 故选B . 【点睛】本题属于基础题,要明确定义,一些学生往往对这个概念掌握不清楚,计算方法不明确而误选其它选项,注意找中位数的时候一定要先排好顺序,然后再根据奇数和偶数个来确定中位数,如果数据有奇数个,则正中间的数字即为所求,如果是偶数个则找中间两位数的平均数.3.D解析:D 【解析】【分析】首先比较平均数,平均数相同时选择方差较小的运动员参加. 【详解】∵==x x x x >乙丁甲丙, ∴从乙和丁中选择一人参加比赛,∵22S S >乙丁,∴选择丁参赛, 故选D .【点睛】本题考查了平均数和方差,正确理解方差与平均数的意义是解题关键.4.B解析:B 【解析】共有21名学生参加预赛,取前11名,小颖知道了自己的成绩,我们把所有同学的成绩按大小顺序排列,第11名的成绩是这组数据的中位数,所以小颖知道这组数据的中位数,才能知道自己是否进入决赛.故选B .5.C解析:C 【分析】可根据调查的选择、中位数和众数的求法、方差及随机事件的意义,逐个判断得结论. 【详解】解:因为我国中学生人数众多,其课外阅读的情况也不需要特别精确, 所以对我国中学生课外阅读情况的调查,宜采用抽样调查,故选项A 不正确; 因为B 中数据按从小到大排列为1、2、3、3、5、5、5,位于中间的数是3,故该组数据的中位数为3, 所以选项B 说法不正确;因为0.003<0.1,方差越小,波动越小,数据越稳定, 所以甲组数据比乙组数据稳定,故选项C 说法正确;因为抛掷硬币属于随机事件,抛掷一枚硬币100次,不一定有50次“正面朝上”故选项D 说法不正确. 故选:C . 【点睛】本题的关键在于掌握调查的选择、中位数和众数的求法、方差及随机事件的意义.6.A解析:A 【分析】如果一组的数据的每一个数都扩大或缩小相同的倍数,则平均数也扩大或缩小相同的倍数,方差则扩大或缩小平方倍;如果一组的数据的每一个数都增加或减少相同的数,则平均数也增加或减少相同的数,方差不变. 【详解】根据题意可知:这组数据的平均数为:2×5-2=8;方差为:24216⨯=. 故选:A 【点睛】本题主要考查的是数据的平均数和方差的变化规律,属于中等难度题型.解决这个问题的关键就是要明确变化规律,根据规律进行解答.7.D解析:D 【解析】 【分析】根据中位数,众数、极差、标准差的定义即可判断. 【详解】解:七个整点时数据为:22,22,23,26,28,30,31 所以中位数为26,众数为22,平均数为:22+22+23+26+28+3032167+= ;极差是31-22=9,标准差是:故D 正确, 故选:D 【点睛】此题考查中位数,众数、极差、标准差的定义,解题关键在于看懂图中数据8.A解析:A 【分析】先求出甲箱的球数,再根据乙箱中位数40,得出乙箱中小于、大于40的球数,从而得出甲箱中小于40的球数和大于40的球数,即可求出答案. 【详解】解:∵甲箱98−49=49(颗),∵乙箱中位数40,∴小于、大于40各有(49−1)÷2=24(颗),∴甲箱中小于40的球有39−24=15(颗),大于40的有49−15=34(颗),即a=15,b=34.故选:A【点睛】本题考查了中位数,正确进行分析,掌握中位数的概念是解题的关键.9.B解析:B【分析】A、由于这八个班的人数不一定相等,故全年级学生的平均成绩应等于所有学生成绩的和除以学生人数;B、由于全年级学生的平均成绩等于所有学生成绩的和除以学生人数,故全年级学生的平均成绩一定在这八个平均成绩的最小值与最大值之间;C、由于这八个班的人数不一定相等,故这10个平均成绩的中位数不一定是全年级学生的平均成绩;D、众数是一组数据中出现次数最多的数,能反映数据的集中程度,平均数也能反映数据的集中程度,是有可能相等的.【详解】A、全年级学生的平均成绩应等于所有学生成绩的和除以学生人数,而这八个班的人数不一定相等,故错误;B、由于全年级学生的平均成绩等于所有学生成绩的和除以学生人数,故全年级学生的平均成绩一定在这八个平均成绩的最小值与最大值之间,故正确;C、中位数不一定与平均数相等,故错误;D、众数与平均数有可能相等,故错误.故选B.【点睛】本题考查了平均数、中位数、众数的关系,它们有可能相等,也可能不相等.10.B解析:B【解析】【分析】根据方差的意义可作出判断,方差是用来衡量一组数据波动大小的量,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.【详解】∵S2甲=1.7,S2乙=2.4,∴S2甲<S2乙,∴甲队成员身高更整齐;故选B.【点睛】此题考查方差,掌握波动越小,数据越稳定是解题关键11.B解析:B【解析】【分析】众数是出现次数最多的数,据此求解即可.【详解】∵数据4出现了2次,最多,∴众数为4,故选:B.【点睛】本题考查了众数的知识,解题的关键是了解有关的定义,属于基础题,难度不大.12.D解析:D【解析】【分析】根据平均数、中位数和方差的计算公式分别对每一项进行分析,即可得出答案.【详解】甲队员10次射击的成绩分别为6,7,7,7,8,8,9,9,9,10,则中位数882=8,甲10次射击成绩的平均数=(6+3×7+2×8+3×9+10)÷10=8(环),乙队员10次射击的成绩分别为6,7,7,8,8,8,8,9,9,10,则中位数是8,乙10次射击成绩的平均数=(6+2×7+4×8+2×9+10)÷9=8(环),甲队员成绩的方差=110×[(6-8)2+3×(7-8)2+2×(8-8)3+3×(9-8)2+(10-8)2]=1.4;乙队员成绩的方差=110×[(6-8)2+2×(7-8)2+4×(8-8)3+2×(9-8)2+(10-8)2]=1.2,综上可知甲、乙的中位数相同,平均数相同,甲的方差大于乙的方差,故选D.【点睛】本题考查了平均数、中位数和方差的定义和公式,熟练掌握平均数、中位数、方差的计算是解题的关键.二、填空题13.1615【分析】根据中位数和众数的定义求解【详解】解:从小到大排列此数据数据15出现了四次最多为众数16和16处在第5位和第六位它两个数的平均数为16为中位数故答案为:1615【点睛】本题属于基础题解析:16 15【分析】根据中位数和众数的定义求解.【详解】解:从小到大排列此数据,数据15出现了四次最多为众数,16和16处在第5位和第六位,它两个数的平均数为16为中位数.故答案为:16,15.【点睛】本题属于基础题,考查了确定一组数据的中位数和众数的能力.注意找中位数的时候一定要先排好顺序,然后再根据奇数和偶数个来确定中位数,如果数据有奇数个,则正中间的数字即为所求,如果是偶数个则找中间两位数的平均数.14.网页制作【分析】根据加权平均数的定义解答即可【详解】解:设网页制作的权重为a语言的权重为b则甲的分数为80a+70b乙的分数为70a+80b而甲的分数高所以80a+70b>70a+80b解得a>b则解析:网页制作【分析】根据加权平均数的定义解答即可.【详解】解:设网页制作的权重为a,语言的权重为b,则甲的分数为80a+70b,乙的分数为70a+80b,而甲的分数高,所以80a+70b>70a+80b,解得a>b,则本次招聘测试中权重较大的是网页制作项目.故答案为:网页制作.【点睛】本题考查了加权平均数的和解一元一次不等式的知识,属于基础题型,熟练掌握加权平均数的定义是关键.15.【分析】根据题意可得×(1+3+2+5+a)=3解这个方程就可以求出a的值;根据标准差的计算公式即可求出样本标准差【详解】根据题意由平均数的定义得×(1+3+2+5+a)=3解得a=4所以方差为:S【分析】根据题意可得15×(1+3+2+5+a)=3,解这个方程就可以求出a的值;根据标准差的计算公式即可求出样本标准差.【详解】根据题意由平均数的定义得15×(1+3+2+5+a)=3,解得,a=4.所以方差为:S 2=()()()()()2222213-1+3-3+3-2+3-5+3-4=5⎡⎤⨯⎣⎦2,.【点睛】此题考查平均数的概念,解题关键在于掌握计算公式.16.乙【分析】根据方差的定义方差越小数据越稳定即可得出答案【详解】该月份白菜价格最稳定的是乙市场;故答案为乙【点睛】本题考查了方差的意义方差是用来衡量一组数据波动大小的量方差越大表明这组数据偏离平均数越 解析:乙【分析】根据方差的定义,方差越小数据越稳定,即可得出答案.【详解】2S 7.5=甲,2S 1.5乙=,2S 3.1=丙,222S S S ∴>>甲乙丙,∴该月份白菜价格最稳定的是乙市场;故答案为乙.【点睛】本题考查了方差的意义.方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.17.5【解析】【分析】由平均数可求解a 的值再根据中位数的定义即可求解【详解】解:由平均数可得a=5×5-2-4-6-8=5则该组数由小至大排序为:24568则中位数为5故答案为:5【点睛】本题考查了平均解析:5【解析】【分析】由平均数可求解a 的值,再根据中位数的定义即可求解.【详解】解:由平均数可得,a=5×5-2-4-6-8=5,则该组数由小至大排序为:2、4、5、6、8,则中位数为5,故答案为:5.【点睛】本题考查了平均数和中位数的概念.18.甲【分析】根据方差的意义即方差越小波动越小方差越大波动越大解答【详解】∵<∴甲稳定【点睛】本题考查的知识点是方差解题的关键是熟练的掌握方差解析:甲【分析】根据方差的意义,即方差越小波动越小,方差越大波动越大解答.【详解】∵2S甲<2S乙,∴甲稳定.【点睛】本题考查的知识点是方差,解题的关键是熟练的掌握方差.19.24【分析】根据方差公式S2=(x1﹣)2+(x2﹣)2+…+(xn﹣)2中各个字母表示的意义得出这组数据的平均数是6数据个数是4从而得出这组数据的总和【详解】∵s2=(x1﹣6)2+(x2﹣6)2解析:24【分析】根据方差公式S2=1n[(x1﹣x)2+(x2﹣x)2+…+(x n﹣x)2]中各个字母表示的意义,得出这组数据的平均数是6,数据个数是4,从而得出这组数据的总和.【详解】∵s2=14[(x1﹣6)2+(x2﹣6)2+(x3﹣6)2+(x4﹣6)2],∴这组数据的平均数是6,数据个数是4,∴这组数据的总和为4×6=24.故答案为24.【点睛】本题考查了方差的定义:一般地设n个数据,x1,x2,…x n的平均数为x,则方差S2=1n[(x1﹣x)2+(x2﹣x)2+…+(x n﹣x)2].20.3【分析】首先根据这组数据的总和等于各个数据之和或等于这组数据的平均数乘以这组数据的个数列出方程得出x的值再根据众数的概念这组数据中出现次数最多的是3从而得出答案【详解】解:1+3+2+7+x+2+解析:3【分析】首先根据这组数据的总和等于各个数据之和,或等于这组数据的平均数乘以这组数据的个数,列出方程,得出x的值,再根据众数的概念,这组数据中出现次数最多的是3,从而得出答案.【详解】解: 1+3+2+7+x+2+3=3×7解得:x=3,这组数据中出现次数最多的是3,故该组数据的众数为3.故答案为3.点睛: 本题考查的是平均数和众数的概念.注意一组数据的众数可能不只一个.三、解答题21.(1)40;补图见详解;(2)36°;(3)13200元.【分析】(1)用捐款40元的人数除以所占百分比即可求出调查的学生数,用调查的学生数乘以15%求出捐款20元的学生数,不去统计图即可;(2)用捐款50元的学生人数除以调查总人次再乘以360°即可求解;(3)计算出本次调查的平均数,再根据题意列式计算即可求解.【详解】解:(1)10÷25%=40(人),40×15%=6(人),∴校团委随机调查了40名学生,补全条形统计图如图:(2)表示“50元”的扇形的圆心角为4360=36 40⨯︒︒;(3)206302040105041800=13200402⨯+⨯+⨯+⨯⨯⨯(元),答:七年级学生捐款约为13200元.【点睛】本题考查了条形统计图与扇形统计图,用样本估计总体,加权平均数等知识,根据条形统计图和扇形统计图的关联量求出各组数据是解题关键.22.(1)83;(2)90<x≤100【分析】(1)按照各项目所占比求得总成绩;(2)各项目所占比求得总成绩大于83分即可,列出不等式求解.【详解】(1)70×10%+80×40%+88×50%=83(分);(2)80×10%+75×40%+50%•x>83,∴x >90.∵每个项目按百分制计分∴90<x≤100∴李颖同学的总成绩是83分,张明同学要在总成绩上超过李颖同学,则他的普通话成绩应90<x≤100.【点睛】本题综合考查平均数的运用.解题的关键是正确理解题目的含义.23.(1)30;50(2)甲稳定;见解析.【分析】(1)根据平均数的计算公式先求出甲和乙的平均数,再代入方差公式()()()2221221=.....n S x x x x x x n ⎡⎤-+-++-⎢⎥⎣⎦,进行计算即可得出答案; (2)根据方差的意义,方差越小数据越稳定,即可得出答案.【详解】 解:(1)甲的平均数是:()1225+230+240+230+225=2305cm ⨯, 乙的平均数是:()1220+235+240+230+225=2305cm ⨯, 甲的方差是:()()()()()22222221=225230230230240230230230225230305S cm ⎡⎤⨯-+-+-+-+-=⎣⎦, 乙的方差是:()()()()()22222221=220230235230240230230230225230505S cm ⎡⎤⨯-+-+-+-+-=⎣⎦;(2)由(1)知,S 甲2<S 乙2,∴甲的跳远技术较稳定.【点睛】本题主要考查平均数与方差,熟练掌握方差及平均数的运算公式是解题的关键.24.(1)30元;(2)50元;(3)250.【分析】(1)根据众数的定义即可判判断;(2)根据中位数的定义即可判断;(3)先计算出样本中计划购买课外书花费50元的学生所占的比例,然后在乘以总人数即可;【详解】(1)花费30元的有12人,最多,故众数是30元;(2)一共有40个数据,排序后第20、21个数据的平均数即是中位数,6+12=18<20,6+12+10=28>20,故第20、21个数据都是50元,故中位数是50元;(3)10÷40×2400=600(人),故估计本学期计划购买课外书花费50元的学生有50人. 25.(1)a =10,b =8,c =8.6;(2)推荐丙班级为网上教学先进班级.【分析】(1)直接根据中位数、众数、平均分的概念即可求解;(2)先根据各项得分的权重求得各班的最终成绩,然后比较即可判断.【详解】解:(1)∵甲班的五项指标得分由小到大重新排列为:6、7、10、10、10∴甲班的中位数为:10分;∵乙班的五项指标得分为:10、8、8、9、88分出现次数最多,∴乙班的众数是:8分;∵(9+10+8+7+9)÷5=8.6(分),∴丙班的平均分是:8.6分;∴a =10,b =8,c =8.6.(2) 甲:10×20%+10×20%+6×30%+10×10%+7×20%=8.2(分)乙:10×20%+8×20%+8×30%+9×10%+8×20%=8.5(分)丙:9×20%+10×20%+8×30%+7×10%+9×20%=8.7(分),∴推荐丙班级为网上教学先进班级.【点睛】此题主要考查数据的统计和分析,正确理解每个概念是解题关键.26.(1)甲、乙两组数据的平均数都是85分,中位数分别为83分、84分;(2)派乙参赛更合适.理由见解析.【分析】(1)根据平均数、中位数的计算方法分别计算即可;(2)从平均数、中位数、方差以及数据的变化趋势分析.【详解】()1()19582888193798478858x =+++++++=甲(分),()18375808090859295858x =+++++++=乙 将甲工人的测试成绩从小到大排序,处在第45、位的平均数为()8284283+÷=(分), 因此甲工人测试成绩的中位数是83分,将乙工人的测试成绩从小到大排序,处在第45、位的平均数为()8385284+÷=(分), 因此乙工人测试成绩的中位数是84分,答:甲、乙两组数据的平均数都是85分,中位数分别为83分、84分.()2(答案不唯一,合理即可) ()()()2222195858285...788535.58S =-+-+⎤⎣⎦=⎡+-甲(分2)()()()2222183857585...9585418S =-+-+-⎡⎤⎣⎦+=乙(分2) ①从平均数看,甲、乙均为85分,平均水平相同;②从中位数看,乙的中位数大于甲,乙的成绩好于甲;③从方差来看,因为22S S <甲乙,所以甲的成绩较稳定;④从数据特点看,获得85分以上(含85分)的次数,甲有3次,而乙有4次, 故乙的成绩好些;⑤从数据的变化趋势看,乙后几次的成绩均高于甲,且呈上升趋势,因此乙更具潜力. 综上分析可知,甲的成绩虽然比乙稳定,但从中位数、获得好成绩的次数及发展势头等方面分析,乙具有明显优势,所以派乙参赛更合适.【点睛】考查平均数、中位数、方差的意义及计算方法,从多角度分析数据的发展趋势是一项基本的能力.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
个性化教案 (内部资料,存档保存,不得外泄)
海豚教育个性化作业 编号:
苏教版小学数学三年级下册第十单元
(考试时间90分钟)
一、填空(8、9、10每空1分,其余每题3分,共29分)
1、小林三次口算分别算对了14题、10题、18题。平均每次算对了( )题。
2、学校气象小组一天中测得气温如下:14度、16度、20度、21度、14度,这一天的平均气
温是( )度。
3、三个笔筒平均每个笔筒是6枝笔,第1个笔筒里有6枝笔,第2个笔筒里有7枝笔,第3
个笔筒里有( )枝笔。
4、在读书比赛中,小朱读了6本,小明读了4本,小华读了3本,小军读了7本,平均每人
读( )本课外书。
5、小华一星期共练了84个大字,平均每天练( )个大字。
6、三(5)班有69人,平均每人向学校捐2本书,一共捐了( )本。
7、
平均每堆有( )个小方块
8、今年2月27日的后三天是( )月( )日,3月1日的前两天是( )月( )
日。
9、小红生日是第三季度的第一天,她的生日是( )月( )日。
10、小明生日是一年的倒数第三天,他的生日是( )月( )日。
二、选择正确答案的序号填在括号里。(每题3分,共24分)
1、下面( )平均数是不合理的。
①小力走8步,共走了520厘米。他每步都是走65厘米。
②学校买来120盒粉笔,平均分给6个年级,每个年级分得20盒。
③电梯里有8人,他们体重的和是430千克。平均每人的体重大约是54千克。
2、池溏的平均水深140厘米,小华身高是145厘米。他下河玩水( )。①不会有危险 ②
可能有危险
3、四(1)班平均身高135厘米,五(2)班平均身高147厘米。王民在四(1)班,张建在
五(2)班,王民比张建( )。
①高 ②矮 ③有可能高,有可能矮,也可能一样高。
4、四位同学进行100米跑的成绩分别是:小明15.3秒,小军16.8秒,小华16秒,小山15.1
秒。跑第一的是( )
①小明 ②小军 ③小华 ④小山
5、在“书香校园”活动中,我校同学平均每人捐书5本。
①全校每个同学一定都捐了5本书。②可能有捐4本书的。
6、学校篮球队队员的平均身高是160cm。( )
①李强是学校篮球队队员,他的身高不可能是155㎝。
②学校篮球队中可能有身高超过160cm的队员。
7、下面图形中,( )是轴对称图形。
① ② ③
8、将一张长方形纸对折3次,其中的1份是这张纸的( )。
①13 ②.16 ③.18
四、解决问题(共47分)
1、小明从家到学校的路程是540米,小明上学要走9分钟,回家时比上学少用两分钟,那么
小明往返一趟平均每分钟走多少米?(5分)
2、四年级5个班参加植树活动,第一天植树33棵,第二天植树38棵,第三天植树39棵。(3+3)
分
(1)四年级平均每天植树多少棵?
(2)三天中平均每班植树多少棵?
3、修路队一周修路的情况如下表。(2+2+4+4)分
时间 周一 周二 周三 周四 周五 周六 周日
米数 250 300 280 320 360 300 381
(1)( )修得最多,( )修得最少。
(2)平均每天修的米数大概在( )到( )之间。
(3)实际算算,平均每天修多少米?
(4)照这样计算,再修6天,还能修多少米?
4、算一算再填表。算出小芳期中考试的英语成绩是多少。(4分)
语文 数学 英语 平均成绩
88分 98分 90分
5、李强的书法作品参加比赛,7个评委的打分分别为89分、91分、62分、90分、92分、88
分、97分。(4+4+1)
① 这7个评委打的平均分是多少?
② 如果先去掉一个最高分和一个最低分后再计算平均分,这时的平均分是多少?
③ 我认为( )个平均分更公平合理。
6、下面是周爷爷某星期每天锻炼的统计图。(单位:千米)(2+3+4+2)
(1)根据统计图提供的信息,制成统计表。
星期 一 二 三 四 五 六 日
路程(KM)
(2)跑得路程最远的是星期( ),最少的路程是星期( )。
平均每天大约跑( )千米。
(3)实际算一算,周爷爷平均每天跑多少千米?
(4)( )跑的比平均数多,( )跑的比平均数少。
