利用FLUENT 软件模拟圆柱绕流
圆柱绕流的数值模拟研究

圆柱绕流的数值模拟研究摘要:选取直径为D=10mm的圆柱及6D×3D的计算区域,利用GAMBIT进行模型的创建模型,对计算区域采用分块网格划分与结构化网格划分相结合的技术进行网格划分。
对0.03m/s~1.0m/s的低流速情况下的圆柱绕流进行模拟研究,结果发现在速度达到0.1m/s前圆柱后侧没有出现明显的漩涡,在速度大于0.1m/s后漩涡开始出现,当速度达到0.5m/s时漩涡的范围最大。
最后利用FLUENT的网格自适应技术对入口速度为0.5m/s的情况进行了网格加密,发现网格自动加密可以改进网格分布情况,但对计算结果的影响程度有限。
关键词:网格划分;圆柱绕流;涡量;网格自适应钝体绕流中尤其以圆柱体的绕流问题最为经典和引起人们的注意。
圆柱绕流属于非定常分离流动问题,在工业工程中的应用非常广泛。
圆柱绕流同时也是一个经典的流体力学问题,流体绕圆柱体流动时,过流断面收缩,流速沿程增加,压强沿程减小,由于黏性力的存在,就会在柱体周围形成附面层的分离,形成圆柱绕流。
而由于圆柱的存在,会在圆柱迎水面产生壅水现象,同时也增加了圆柱的受力,使得圆柱绕流问题变得十分复杂。
研究圆柱绕流问题在工程实际中也具有很重要的意义。
如在水流对桥梁、海洋钻井平台支柱、海底输运管线、桩基码头等的作用中,风对塔建筑、化工塔设备、高空电缆等的作用中,都有重要的工程应用背景。
因此,对圆柱绕流进行深入研究,了解其流动机理和水动力学规律,不仅具有理论意义,还具有明显的社会经济效益。
1数学模型与计算方法1.1几何模型结合本文研究目标,取圆柱直径D=10mm,计算区域为6D×3D的矩形区域,如图1所示。
上游尺寸1.5D,下游尺寸4.5D。
使用GAMBIT建模软件按照图1所示的计算域建立了二维的计算模型。
图1 计算区域1.2网格划分及边界条件设置为提高模拟精度,计算区域采用分块网格划分与结构化网格划分相结合的技术。
计算区域共分两块,尺寸见图1所示。
正交双圆柱绕流建模及模拟

三维风洞动态数字试验的模拟——正交双圆柱绕流根据实际需要,采用与模拟软件匹配的的建模软件构建模型,以便能够绘制网格及进行模拟计算,本试验将采用Gambit软件建模及绘制网格,再倒入Fluent 中进行计算。
实验要求:本次试验与实际风洞测试结合,风洞尺寸为1000*300*300mm,风洞中均为直径d=1mm的两圆柱,两圆柱正交放置,间距为6mm。
进口风速取1m/s。
一、构建模型1、打开Gambit软件,选择求解器Solver-FLUENT5/62、建立风洞模型,点击Operation—Geometry—V olume—Create Real Brick,选择坐标系,输入尺寸1000*300*300,将Direction改为,点击apply。
3、点击Active下面的、按钮,调整风洞模型在可视窗口中自适应的尺寸,如下图所示。
(注:鼠标左键点击图形,可对图形进行旋转,点击,即可恢复)4、建立双圆柱模型,输入尺寸height 300mm,r=0.5mm,选择,点击apply创建第一个圆柱,同理,改为,创建第二个圆柱,尺寸不变。
5、移动圆柱。
按下图输入移动坐标,按住shift键,点击鼠标左键选择圆柱体,分别移动Z向和Y向圆柱,圆柱间距保持6d=6mm。
6、将两圆柱从风洞中挖去。
通过布尔算符,选择subtract,第一个volumes中选择风洞,第二个volumes中选中两圆柱(注意:两个都要选中),点击apply。
7、复制移动进口面。
本试验主要关注圆柱附近的监控点模拟情况,故而需要使得前后网格疏密不同(关注部分局部加密)。
选择——,选中进口面,选择输入X方向300。
8、将原风洞分为两个风洞。
针对体的情况下,选择分别选中整体(此时只有一个体)和中间分界面。
注意:spilt with应调整为Faces(real),且将系统默认的connected点击不进行,这样才能产生两个面,后面会提到这样设置的作用。
二、网格绘制1、绘制线网格由于圆柱部分是重点关注的,可从线网格开始。
FLUENT动网格-圆柱体在管道内运动模拟
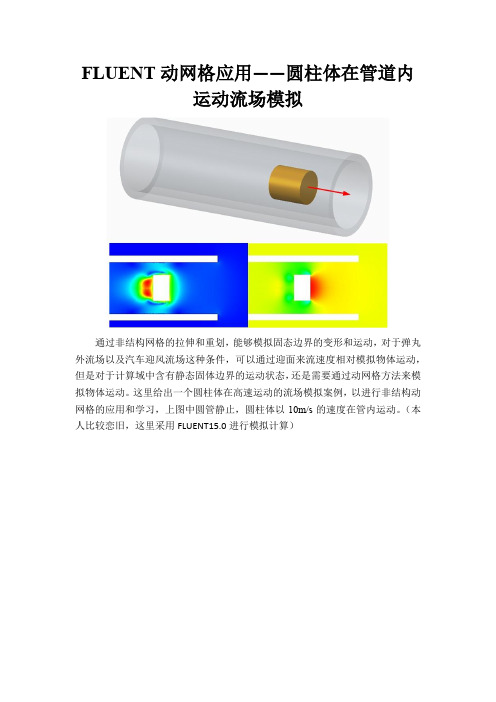
FLUENT动网格应用——圆柱体在管道内
运动流场模拟
通过非结构网格的拉伸和重划,能够模拟固态边界的变形和运动,对于弹丸外流场以及汽车迎风流场这种条件,可以通过迎面来流速度相对模拟物体运动,但是对于计算域中含有静态固体边界的运动状态,还是需要通过动网格方法来模拟物体运动。
这里给出一个圆柱体在高速运动的流场模拟案例,以进行非结构动网格的应用和学习,上图中圆管静止,圆柱体以10m/s的速度在管内运动。
(本人比较恋旧,这里采用FLUENT15.0进行模拟计算)。
基于H-O型网格的圆柱绕流的数值模拟

基于H-O型网格的圆柱绕流的数值模拟摘要:本文用GAMBIT针对相同的模型划分了不同结构的网格,用FLUENT进行了圆柱绕流的数值模拟,并将模拟结果跟文献的实验数值做了对比,数值计算的结果与相关实验结果具有合理的一致性。
同时也证明了基于H-O型网格的圆柱绕流的模拟精度要高于普通的四边形网格。
关键词:H-O型网格圆柱绕流数值模拟Numerical Simulation of Fluid Flow around Circular-cylinder Based on theH-O GridAbstract: This paper supplies different grids for the same model based on the GAMBIT. Numerical simulation of the fluid flow around circular-cylinder is executed by the software of FLUENT. Compared the result with the tested data, the result of the numerical simulation is coincidental with that of experimental. The numerical simulation results also approve that the result based on the H-O grid is more exacted than the traditionally quadrangular grid.Key words: H-O Grid;Fluid Flow around Circular-cylinder;Numerical Simulation1 引言静止地圆柱绕流早期的研究由于受到理论和实验条件的限制,圆柱绕流主要侧重于对圆柱体受力的实验测定,随着计算流体力学和现代实验技术的迅速发展,数值模拟及实验测定方法被广泛地应用于这些方面。
fortran 理想流体的平面圆柱绕流程序

题目:用Fortran 语言编写程序解决理想流体的平面圆柱绕流问题,如下图所示。
由于流动的对称性,可以只研究其中的四分之一区域,如图中abcde 所示。
u x =1在理想流体的平面运动中,流函数ψ和势函数Φ均满足拉氏方程:02222=∂∂+∂∂y x ψψ,02222=∂∂+∂∂yx φφ 其边界条件如下表所示。
说明:n∂是切向流速, n ∂是法向流速。
下面就流函数进行讨论,为便于分析,把边界条件写成:ψψ~= 在1Γ上 其中:1Γ为具有本质B 、C 的边界 0=∂∂nψ在2Γ上 2Γ为具有自然B 、C 的边界解题步骤:(1)写出Галёркин积分表达式02222=⎪⎪⎭⎫⎝⎛∂∂+∂∂⎰⎰Ωdxdy y x δψψψ 通过分部积分,可得:⎰⎰⎰ΓΩ=⎪⎪⎭⎫ ⎝⎛∂∂∂∂+∂∂∂∂2ds g dxdy y y x x δψδψψδψψ (2)区域剖分横向剖分数为9,纵向剖分数为10,其中圆弧段剖分数为5。
利用作业三中的程序实现(由于网格内要画流速矢量图,故单元编号未写出),另外,还需要建立本质B.C 表。
(3)确定单元基函数()e i ϕ设网格划分后任意三角形单元的三个结点的坐标值别为()())3,2,1)(,(=i y x e i e i ,函数值分别为()(1,2,3)e i i ψ=,根据基函数的构造思想,单元内近似函数可表示为式:()())3,2,1()(==i e i e i e ϕψψ。
在单元内作线性插值函数如下:()()()111122223333e e e a b x c y a b x c y a b x c y φφφ=++=++=++;;根据基函数的插值条件,得到系数:,,(1,2,3)i i i a b c i =。
则基函数为:()y c x b a i i i e i ++=ϕ,()3,2,1=i 。
(4)单元分析 将()()()e i e i e ϕψψ=代入Галёркин积分表达式:()()()()()()⎰⎰⎰ΩΓ=⎪⎪⎭⎫ ⎝⎛∂∂∂∂+∂∂∂∂2ds g dxdy y y x xe e e e e e δψδψψδψψ 得单元有限元方程组为:()()()e e eij j i A F ψ=(i=1,2,3)由()e i i i i a b x c y φ=++(i=1,2,3),可得:()()()(),,,e e e e j j i i j i j i b b c c x x y yφφφφ∂∂∂∂====∂∂∂∂ 于是:()111112121313212122222323313132323333e ij b b c c b b c c b b c c A A b b c c b b c c b b c c b b c c b b c c b b c c +++⎡⎤⎢⎥=+++⎢⎥⎢⎥+++⎣⎦,()()()⎰=2e ds g F e i e i τϕ自然B.C 处理: 由于自然边界条件02=∂∂Γnψ,则()0e i F =。
两个Fluent实验

一、实验目的1、计算圆柱绕流问题,比较不同雷诺数下的异同,并截图查看相关涡街。
2、模拟不同雷诺数下的方腔环流,并比较不同的网格设置对方腔环流的影响。
二、实验原理1、Re=20的圆柱绕流问题。
Setup and solution of a classical problems of fluid mechanics such as a steady flow past circular cylinder. (Re =20) We know D = 2 m. To obtain Re = 20, we can arbitrarily set ρ, V and μ. For our case, let's set ρ = 1 kg/m 3 , V = 1 m/s and μ = 0.1 k g/ms.我们取大圆半径为10,小圆半径为2,矩形区域为10*40。
在Gambit软件中建模,并导出为msh文件。
将msh 导入fluent软件中进行求解,相应的参数如上所述,作出相应结果的图。
2、Re=150的圆柱绕流问题。
setup and solution of a classical problems of fluid mechanics such as a steady flow past circular cylinder. (Re =150) We know D = 2 m. To obtain Re = 150, we can arbitrarily set ρ, V and μ. For our case, let's set ρ = 75 kg/m 3 , V = 1 m/s and μ = 1 kg/ms.与上一个问题的建模相同,在fluent软件中需要调整部分参数。
3、方腔环流问题。
使用fluent计算之前的方腔环流问题,并与Fortran程序计算结果进行对比。
(1)均匀网格计算Re=100,1000,5000的情况(2)加密网格(边界加密)计算Re=100,1000,5000的情况4、注:本实验部分采用Fluent 6.3,部分采用Fluent 15 完成。
双圆柱在不同排列方式下绕流流态模拟

双圆柱在不同排列方式下绕流流态模拟
滕丽娟
【期刊名称】《水科学与工程技术》
【年(卷),期】2016(000)004
【摘要】双圆柱绕流伴随着流动分离、旋涡生成与脱落、旋涡间相互干扰等复杂
问题,其流动形态和流动特征受圆柱相对位置影响。
使用FLUENT流体软件,选
取间距比1.75,2.5和4,在二维层流模型下,模拟了双圆柱串列、30°夹角错置、60°夹角错置和双圆柱并列绕流,分析了双柱绕流流态、旋涡脱落形态、升力、阻力系数随圆柱相对位置改变而变化的规律,并对比已有的试验成果和模拟成果,为桥梁建设和圆柱绕流理论研究提供了基础数据。
【总页数】3页(P39-41)
【作者】滕丽娟
【作者单位】河北省张家口水文水资源勘测局,河北张家口 075000
【正文语种】中文
【中图分类】TV143
【相关文献】
1.高雷诺数下阵列四圆柱绕流流动形态数值模拟 [J], 贺然
2.用FLUENT模拟不同排列下的双柱绕流流场 [J], 杨纪伟;滕丽娟;郑薇薇;李书芳
3.采气井筒不同流动阶段两相管流流态模拟实验 [J], 韩倩;徐骞;陆俊华
4.不同排列方式和间隙比下双圆柱流致振动特性研究 [J], 刘巨保;杨明;岳欠杯;丁
宇奇;姚利明
5.较小Kc数下振荡流绕圆柱流动的数值模拟 [J], 凌国平;凌国灿
因版权原因,仅展示原文概要,查看原文内容请购买。
流体经典教学案例之圆柱绕流仿真分析

流体经典教学案例之圆柱绕流仿真分析1. 摘要圆柱低速定常绕流的流型只与Re数有关。
在Re≤1时,流场中的惯性力与粘性力相比居次要地位,圆柱上下游的流线前后对称,阻力系数近似与Re成反比(阻力系数为10~60),此Re数范围的绕流称为斯托克斯区;随着Re的增大,圆柱上下游的流线逐渐失去对称性。
当Re>4时,沿圆柱表面流动的流体在到达圆柱顶点(90度)附近就离开了壁面,分离后的流体在圆柱下游形成一对固定不动的对称漩涡(附着涡),涡内流体自成封闭回路而成为“死水区”(阻力系数2~4);随着Re的增大,死水区逐渐拉长圆柱前后流场的非对称性逐渐明显,此Re数范围称为对称尾流区。
Re>40以后,附着涡瓦解,圆柱下游流场不再是定常的,圆柱后缘上下两侧有涡周期性地轮流脱落,形成规则排列的涡阵,这种涡阵称为卡门涡街;此Re数范围称为卡门涡街区(阻力系数1~2)。
Re>300以后,圆柱后的“涡街”逐渐失去规则性和周期性,但分离点(约82度)前圆柱壁面附近仍为层流边界层,分离点后为层流尾流。
当Re*>200000~400000时,层流边界层随时有可能转涙为湍流,分离点后移至100度以后,湍流时绕流尾迹宽度减小,阻力系数骤减(从1减到0.2)。
2. 物理模型介绍在一定条件下的来流绕过一些物体是,物体两侧会周期性地脱落处旋转方向相反,并排列成有规则的双列涡旋。
为研究这一具有明显流动特征的流动,现以ANSYS18.0作为计算平台,并将圆柱作为绕流流动结构研究的物理模型进行研究。
本案例所模拟的是低雷诺数圆柱绕流。
图1是模型示意图,模型中圆柱直径10mm,计算域X*Y*Z为100mm*200mm*1mm。
图1 模型示意图3. 前处理采用ICEM对圆柱绕流计算域进行结构化网格划分,距离圆柱面第一层网格尺寸为0.1D(为充分捕捉近壁区流动结构,近壁区网格尺寸为特征长度的0.1倍),如图2所示。
图2 计算域网格将模型边界分别命名为进口inlet、出口outlet、圆柱面Cylinder、上下壁面wall以及对称面Sym,如图2所示。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
利用FLUENT软件模拟圆柱绕流 摘 要:使用计算流体力学软件FLUENT,模拟均匀来流绕固定圆柱的流动,模拟雷诺数为20 ,40 ,100 时的绕流流动,得到流场的流函数等值线图和速度矢量图。计算结果表明:当雷诺数增加时,流动表现出一系列不同的构造。在雷诺数约为40 前后流场有明显变化。小于这个数时,存在一对位置固定的旋涡。大于40 时,流场开始变得不稳定,旋涡扩大、脱落、又生成,逐渐发展成两排周期性摆动和交错的旋涡。并与实验及数值模拟结果比较,确认FLUENT能够很好地预测流动结构。 关键词: 圆柱绕流 FLUENT软件 雷诺数
1 圆柱绕流理论分析研究的状况 一个世纪以来,圆柱绕流一直是众多理论分析、实验研究及数值模拟对象。但迄今对该流动现象物理本质的理解仍是不完整的。圆柱绕流中,起决定作用的是雷诺数,但还受到许多因素,如阻塞比,来流湍流度,下游边界条件等的影响。 随着雷诺数的增加,粘性不可压缩流体绕圆柱的流动会呈现各种不同的流动状态,在小雷诺数时,流动是定常的,随着雷诺数的增加,圆柱后会出现一对尾涡。当雷诺数较大时,尾流首先失稳,出现周期性的振荡。而后附着涡交替脱落, 泻入尾流形成Karman 涡街,随着雷诺数的增加,流动变得越来越复杂,最后发展为湍流。White[1]认为“圆柱涡流具有经典性的重要意义”。 一般认为圆柱绕流有2 种定常的流动图案:雷诺数为较小时,圆柱后无尾涡;当雷诺数为较大时,圆柱后有一对对称的尾涡。关于定常流失稳以及出现湍流的临界雷诺数主要是通过应用流场显示技术观察流动形态得到的,所以不是准确值。对于分界点雷诺数就有不同的见解,Kovasznay 、Roshko 等认为定常流动失稳的临界雷诺数大约为40。而从周期性尾流到湍流的详细的转变过程的实验研究似乎还是空白。 对均匀来流绕固定圆柱的二维平面流动,国内外许多学者进行过大量的研究。决定圆柱绕流流态的是雷诺数(Re)的值, Re5时,流动不发生分离,5Re40,在圆柱体后面出现一对位置固定的旋涡; 40Re150 ,旋涡扩大,然后有一个旋涡开始脱落,接着另一个也脱落,在圆柱体后面又生成新的旋涡,这样逐渐发展成两排周期性摆动和交错的旋涡,即Karman 涡街。Re150,涡街是层流,150Re300,
旋涡由层流向湍流转变。
5300Re310
,称为亚临界区。此时,
柱体表面上的边界层为层流,而柱体后面的涡街已完全转变为湍流,并按一定的频率发
放旋涡。56310Re310,称为过渡区。此时,柱体表面上的边界层也转变为湍流,分离点后移,阻力显著下降,旋涡的发放不规则,发放频率是宽频率随机的。
6Re310
称为超临界区。此时,重新建
立起比较规则的准周期性发放的涡街。目前,
对圆柱绕流的三维数值研究则不多,然而试验表明,即使均匀来流垂直流过等截面的圆柱体,当Re足够大时,也会呈现三维的流动状态。 圆柱绕流属于非定常分离流动问题,在工业工程中的应用非常广泛,数值模拟是研究这类问题的有力工具。但是,控制方程的高度非线性以及边界条件的多样性严重阻碍了这类问题的解决。到目前为止,有限差分、有限元、大涡模拟(LES) 、直接数值模拟(DNS) 等方法都先后被应用。但是,这些方法都需要增加网格生成的附加工作,尤其是在遇到复杂几何区域时更需要巨大的网格数量,大大影响计算效率。 本文利用N-S 方程,对固定圆柱绕流进行了三维数值模拟,利用计算流体力学软件FLUENT ,选取Re = 20 ,40 ,100 ,模拟了圆柱周围的流场,得到流场的涡量等值线和速度矢量图,并与实验结果进行了比较。 2 数学模型与数值方法 对不可压缩粘性流体,在直角坐标系下,其运动规律可用N-S 方程来描述,连续性方程和动量方程分别为 0jjux 1 1jijijjjjuuPuuvtxxxx 2 圆柱周围的流场利用FLUENT 求得,采用有限体积法和SMPLEC算法。 3 数值计算与结果讨论 一个无穷长直径为2.0m 的圆面积柱体,放置在无穷远来流速度为1.0 m/ s 不受干扰的均匀横流中,其他参数如图1、图2 所示。 图1 计算域 雷诺数由圆柱体直径和自由来流速度确定。通过改变粘度,得到不同的雷诺值(20 ,40 ,100) , ReUD ,当雷诺数为100 时,试验的Strouhal 数是0.165 , DSU。 边界条件:进口和侧面边界始终为自由来流条件1.0/Ums ,流动出口为零法向梯度出口边界。 流体特性假定为常数,结果见表1。 表1 流体特性 Re 20 40 100 密度ρ/(kg/ m3) 1 1 1 动力粘度μ/ (Pa2s)
0.1 0.05 0.02
网格示意图如图2 所示。
图2 网格剖分 Re = 20 和Re = 40
时的流函数和速度
矢量如图3、图4、图5、图6 所示,流动是对称的。
图3 流函数等值线图( Re = 20)
图4 速度向量图( Re = 20) 图5 流函数等值线图( Re = 40) 图6 速度向量图( Re = 40) 图7 流函数等值线图( Re = 100) 图8 速度向量图( Re = 100) 4 结论 (1) 计算结果表明:当雷诺数增加时,流
动表现出一系列不同的构造。在Re < 40 时,
存在一对位置固定的旋涡。Re > 40 时,流场开始变得不稳定,旋涡扩大、脱落、又生成,
逐渐发展成两排周期性摆动和交错的旋涡。与实验及数值模拟结果比较,确认FLUENT
能够很好地预测流动结构。 (2) 利用计算流体力学软件FLUENT 可以成功地模拟圆柱绕流问题,反映出流动特性。 (3) 可以对大于100 的雷诺数做进一步的研究,探讨其机理。
FLUENT应用发展现状 FLUENT 软件于1998 年进人中国市场。FLUENT软件在我国应用的也很广泛。FLUENT 软件在空气流场中的应用已比较成熟。田铖等[2]模拟了地铁专用轴流风机的内部流场;李磊等[3]模拟了两种风向条件下街区风速分布和CO 质量浓度的分布情况;杨伟等[4]计算了大气边界层中单栋高层建筑的定常风流场; 赵琴[5]对空调室内的温度场进行了计算机模拟。 FLUENT 软件在水流流场中的应用不同于单纯的空气流场。水利工程问题边界复杂,水气混掺,存在多个自由水面,需要采用二相流模型,计算机模拟的成果还不多。Salaheldin 等[9]对垂直圆墩周围的三维流场进行了计算机模拟;刘加海等[6]在水槽中对二维规则波进行了计算机模拟;韩龙喜等[6]在环形水槽中对三维流场进行了计算机模拟。Chen 等[8]采用双方程紊流模型,对阶梯溢流坝流场进行了三维紊流计算机模拟,得出溢流坝沿程的自由水面位置、速度大小和分以及阶梯面上的压力等重要流场特性。刁明军等[9]采用VOF法对挑流消能从库区到下游水垫塘进行了水气二相流计算机模拟,得到射流的空中轨迹线、水垫塘的自由水面和计算域的压力、流速、紊动能及紊动能耗散率分布。杨忠超等[10]结合向家坝水电工程,采用VOF 法和RNG 紊流模型对多股多层水平淹没射流进行三维计算机模拟, 得出中孔和表孔联合泄洪时消力池的流速和紊动能分布。陈云良等[11]根据某电站进水口1:50 模型试验结果,对进水口流场进行了计算,研究来流、复杂地形边界等对进水口流态的影响。张挺等[12-13]对索风营电站X 形宽尾墩和阶梯溢流坝联合消能的三维流场进行数值计算,给出压力特性、流速分布、阶梯及墩后水气两相流的部分特性。周勤等[14]对小南海水库双弯曲型溢洪道原型流场进行三维计算机模拟, 得出溢洪道沿程水面线和速度等重要水力参数。叶茂等[15] 结合典型工程算例,就复杂水气交界面的处理、模型建体和网格划分等问题作详细介绍。罗挺等[16]以windows2000 操作系统和通用CFD 软件工具FLUENT 为基础,研究构建了不同的并行计算硬件平台的力法,计算了典型的山谷污染物扩散过程的湍流流场。 可见,FLUENT 软件在水力学中的应用已逐步展开,计算机模拟同试验研究相比,具有成本低、方案变化快、无测量仪器干扰、无比尺效应和数据信息完整等优势,可作为模型试验的有力补充,如进水口模型试验在高水位时,无法用常规仪器测量进口周围的流速,而数值计算则可得到全域流场特性。另外,由于其减少了研究者在计算方法、编程、前后处理等方而投入的重复、低效的劳动,将更多的精力和时间投入到考虑问题的物理本质,优化算法选用,参数的设定,因而提高了工作效率,其必然会获得越来越多的应用,应用效果也必将越来越好。
参考文献: [1] Frank M. White. Viscous Fluid Flow[M] . McGraw2Hill Inc ,1974. [2] 田铖,张欢,由世俊,等. 利用FLUENT 软件模拟地铁专用轴流风机的内部流场(一):对称翼叶片轴流风机[J].流体机械,2003,31(11):13-15. [3] 李磊,胡非,程雪玲,等. FLUENT 在城市街区大气环境中的一个应用[J].中国科学院研究生院学报,2004,21(4):476-480. [4] 杨伟, 顾明. 高层建筑三维定常风场数值模拟[J].同济大学学报,2003,31(6):647-651. [5] 赵琴. FLUENT 软件的技术特点及其在暖通空调领域的应[J].计算机应用,2003,23(12):424-425. [5] SALAHELDIN T M, IMRAN J. CHAUDHRY M H. Numericalmodeling of three -dimensional flow field aroundcircular piers [J].Journal of Hydraulic Engineering,2003,130(2):91-100. [6] 刘加海, 杨永全, 张洪雨,等. 二维数值水槽波浪生成过程及波浪形态分析[J]. 四川大学学报: 工程科学版,2004, 36(6):28-31. [7] 韩龙喜, WAJ Wing-hong. 加长型环形水槽水流特性的数值模拟[J].河海大学学报:自然科学版,2003,31(6):639 -643. [8] CHEN Qun, DAI Guang-qing, LIU Hao-wu.Volume offluid model for turbulence numerical simulation of steppedspillway overflow [J]. Journal of Hydraulic Engineering,2002, 128 (7):683-688. [9] 刁明军,杨水全,王玉蓉,等.挑流消能水气二相流数值模拟[J].水利学报,2003,9:77-82. [10] 杨忠超,邓军, 杨永全,等.多股多层水平淹没射流数值模拟研究[J].水利学2004,5:31-38. [11] 陈云良,伍超,叶茂.水电站进水口水流[12] 陈云良,伍超,叶茂.水电站进水口水流流态的研究[J].水动力学研展,2005,20(3):340-345. [13] 张挺,伍超,卢红,等. X 型宽尾墩+阶梯滋流坝流场三维数值模拟[J].水利学报,2004,8:15-20. [14] ZHANG Ting, WU Chao, LIAO Hue-sheng, et al. 3Dnumerical simulation on water and air two-phase flows ofthe steps end flaring gate pier [J].Journal of Hydrodynamics:Ser.B,2005, 17(3):338-343. [15] 周勤,伍超, 赵元弘,等."S"型溢洪道水流特性试验与数值模拟研究[J].水力发电学报,2005,24(3):88-92. [16] 叶茂,伍超,陈云良,张挺,周勤.FLUENT 软件在水利工程中的应用[J].水利水电科技进展,2006,26(3):78-81.
