第11章力法
船舶结构力学课后题答案(上海交大版)之欧阳道创编

s目录第1章绪论1第2章单跨梁的弯曲理论2第3章杆件的扭转理论8第4章力法10第5章位移法13第6章能量法24第7章矩阵法40第9章矩形板的弯曲理论53第10章杆和板的稳定性59第1章绪论1.1题1)承受总纵弯曲构件:连续上甲板,船底板,甲板及船底纵骨,连续纵桁,龙骨等远离中和轴的纵向连续构件(舷侧列板等)2)承受横弯曲构件:甲板强横梁,船底肋板,肋骨3)承受局部弯曲构件:甲板板,平台甲板,船底板,纵骨等4)承受局部弯曲和总纵弯曲构件:甲板,船底板,纵骨,递纵桁,龙骨等1.2 题甲板板:纵横力(总纵弯曲应力沿纵向,横向货物或上浪水压力,横向作用)舷侧外板:横向水压力等骨架限制力沿中面 内底板:主要承受横向力货物重量,骨架限制力沿中面为纵向力舱壁板:主要为横向力如水,货压力也有中面力第2章 单跨梁的弯曲理论2.1题设坐标原点在左跨时与在跨中时的挠曲线分别为v(x)与v(1x )1)图2.133323034243()()()424()26666llll l l p x p x p x M x N xv x EI EIEIEIEI---=++++原点在跨中:3230111104()4()266ll p x M x N x v x v EI EIEI-=+++,'11'11()0()022(0)0(0)2l l v v p v N ⎧==⎪⎨⎪==⎩2)33203()32.2()266ll p x N x Mx v x x EI EIEIθ-=+++图 3)333002()22.3()666xx x ll p x N x qx dxv x x EI EIEIθ-=++-⎰图 2.2题 a)33111311131(3)(2)616444641624pp p pl pl v v v EI EI ⎡⎤⎡⎤=+=⨯⨯-+⨯-⨯⎢⎥⎢⎥⎣⎦⎣⎦ =3512pl EIb)2'292(0)(1)3366Ml Ml Pl v EI EI EI-=+++=2220.157316206327Pl Pl Pl EI EI EI-+=⨯=2220.1410716206327Pl Pl Pl EI EI EI---=⨯=2372430pl EIc)()44475321927682304ql ql qll v EI EI EI=-=d)2.1图、2.2图和2.3图的弯矩图与剪力图如图2.1、图2.2和图2.3图2.1 图2.2图2.32.3题 1)2)32101732418026q l Ml l l Ml lq EI EI EI EI θ⎡⎤=-++-⎢⎥⎣⎦ =3311117131824360612080q l q l EI EI⎛⎫-++-=-⎪⨯⎝⎭ 2.4 题2.5图3000()6N x v x v x EIθ=++,()00v A p N =-如图2.4, ()()0v l v l '==由得3333()1922pl x x v x EI l l ⎛⎫∴=-+ ⎪⎝⎭图2.4 2.5题2.5图:(剪力弯矩图如2.5)()132023330222002332396522161848144069186pl Mp pR p ll p pl v AR EI EI v l Mlpl pl pl v EI EI EI EI v Ml pl pl pl v l EI EI EI EIθ-∴==-===⋅=⎛⎫=-=-=⎪⎝⎭-'==--=-=-()16A pa b b M A l K l ⎡⎤=++⎢⎥⎣⎦,图2.5111,0,6632A l a l b A K ====+=将代入得:()16312pl pl M ==2.7图:(剪力弯矩图如2.6)图2.62.8图(剪力弯矩图如2.7)图2.72.6题.[]1max 2max 2113212132142.()()62()()62()()242(0)sN EIv s sss s N dv dx dx dx G GA N EI v dx v C GA GA EI ax bx v v v f x cx d f x ax b C GA EI EIax bx f x f x c a x d GA GA qx qx f x f x EI EIv v τγ'''====-''=−−−→-+⎡⎤''∴=+=++++-+++⎢⎥⎣⎦⎛⎫''=-+++-+ ⎪⎝⎭''==''=⎰式中由于11142323432342(0)00()()00242602,224()241222425()23848s s s s sd b v l v l ql EI ql al EI c a l EI GA EIGA qlal EIql ql c EI EI qx qlx qx qx qlv x x EI EI GA EI GA l ql ql v EI GA ===''==⎧⎛⎫-++-=⎪⎪⎪⎝⎭⎨⎪+=⎪⎩=⎛⎫∴=--++⎪⎝⎭∴=+可得出由得方程组:解出:a=2.7.题先推广到两端有位移,,,i i j jθθ∆∆情形:212,i j s EI GA l β⎛⎫∆=∆-∆= ⎪⎝⎭令 2.8题已知:20375225,1.8,751050kgl cm t cm s cm cm σ=⨯====面积2cm 距参考轴cm面积距3cm惯性矩 4cm自惯性矩4cm外板1.845⨯ 81 0 0 0 (21.87)略 球扁钢O N 24a38.75 9430.2 2232 ∑119.8 15.6 604.5 9430.22253.9ABC=11662224604.55.04116628610119.8BBe cm I C cm AA===-=-=275 1.838.75174min ,4555A cm l lI be s cm=⨯+=⎧⎫===⎨⎬⎩⎭计算外力时面积计算时,带板1).计算组合剖面要素:形心至球心表面1240.9 5.0419.862t y h e cm =+-=+-=形心至最外板纤维若不计轴向力影响,则令u=0重复上述计算: 2.9.题解得:2.10题 2.11题 图2.120 2.12题1)先计算剖面参数:图2.8a2422u u P P l δδδ⎛⎫⋅⎛⎫ ⎪⋅+= ⎪⎝⎭ ⎪⎝⎭p M 图2.8b 2.13补充题剪切对弯曲影响补充题,求图示结构剪切影响下的v(x)解:可直接利用 2.14. 补充题试用静力法及破坏机构法求右图示机构的极限载荷 p ,已知梁的极限弯矩为p M (20分) (1983年华中研究生入学试题)解: 1)用静力法:(如图2.9)由对称性知首先固端和中间支座达到塑性铰,再加力u p p →,当p作用点处也形成塑性铰时结构达到极限状态。
力法ppt课件PPT文档86页

q
4 .建立力法基本方程 A
将 ∆11=11x1代入(b)得
EI
l
1X 111P0 (7—1) L
B
↑ M 1图
此方程便为一次超静定结
构的力法方程。
qL 2 2
5. 计算系数和常数项
11
2
M1ds EI
=
E1IL2223L
L3 3 EI
qL 2 8
q
qL 2 8
X1 1
MP图
M图
1P
M1MPds= _ EI
X 1←↓↑→X 2
X 1←↓↑→X 2
n=6
→X←3 X←4 ↓↑→X 5
X6
→X←3
X4
←X 5
X6
n=3×7=21
对于具有较多框格的结构,可 按 框格的数目确定,因为一个封 闭框格,其 超 静定次数等于三。 当结构的框格数目为 f ,则 n=3f 。
8
§7—3 力法的基本概念
首先以一个简单的例子,说明力法的思路和基本概
21
22
..........
2
n
.................................
n1
n2
..........
nn
主系数: ii 0
>0
副系数:δij =0
<
0
3)δij 表示柔度,只与结构本身和基本未知力的选择有关,与外荷载无关;
4) 位移互等定理: δij = δji
各项系数和自由项,均是基本结构在已知力作用下 的位移,可以用第七章的方法计算。对于平面结构, 这些位移的计算公式为
据叠加原理,上述位移条件可写成
△1=11X1+12X2+13X3+△1P=0 △2=21X1+22X2+23X3+△2P=0 △3=31X1+32X2+33X3+△3P=0
第十一章-位移法

X
3
0
即:
M
AB
4i A
2i B
6i
l
M BA
2i A
4i B
6i
l
为杆件AB的刚度方 程(转角位移方程)
§11-2 等截面杆件的刚度方程
讨论:当分别作用有单位位移情况
当 A 1,B 0, 0 时:
则有:
M M
AB BA
4i 2i
当 1, A 0,B 0 时:
则有:
M
AB
M BA
第 十 章 位移法
本章主要内容
➢位移法的基本概念 ➢等截面杆件的刚度方程 ➢无侧移刚架的计算 ➢有侧移刚架的计算 ➢位移法的基第本八章 位体移法 系 ➢位移法应用举例 ➢对称结构的计算
§11-1 位移法的基本概念
一.基本思路
如下图为一个对称结构承受对称荷
载 P。结点B只发生竖向位移 ,
水平位移为零。在位移法中,我们
在上例中,如只有二根杆,则结构是静定的,当杆数 3 时,结构
是超静定的。可见用位移法计算时,计算方法并不因结构的静定或 超静定而有所不同。
§11-1 位移法的基本概念
三.总结位移法计算的要点
要点:
(1) 位移法的基本未知量是位移。 (2) 位移法的基本方程是平衡方程。 (3) 建立基本方程的过程分为两步:
pq
11X1 12 X 2 13 X 3 1P 0 21X1 22 X 2 23 X 3 2P 0 31X1 32 X 2 33 X 3 3P 0
解力法方程,得:
X1 X2
? ?
X 3 0
A
B
运用力法解,取基本体系如下:
pq
X1
X2
第九讲-卡氏定理

基本公式
一般物体 载荷 f : 0 → F 相应位移 δ : 0 → ∆ 线性弹性体
dW= fdδ =
W = ∫ fdδ
0
∆
f ∝δ f =kδ
k - 线弹体在载荷作
用点、 用点、沿其作用方向 产生单位位移所需之 力,称为刚度系数 称为刚度系数
W = ∫ kδdδ
0
∆
k∆2 = 2
F∆ W= = 2
施加矩为 Me的力偶 -附加力偶
θB(q) = [θB(q, Me )]M =0
e
θB (q) =
∫
e
2. 位移计算
ql Me FAy = − 2 l x ∂M qlx Me x qx2 =− M( x) = − − l ∂Me 2 l 2 M( x) ∂M( x) θB (q) = dx l EI ∂Me M =0
∆A
A1 A′
B
B
合力的相应位移
∆A =
2 ∆A = (∆A + fA ) 2
2 ∂U 2 ∂U ∂U = = = (∆A + fA ) 2 ∂F 2 ∂F ∂ 2 F
(
)
FN2 = −F
2F ⋅ 2l (-F)l ⋅ 2+ ⋅ (-1) EA EA (2 2 + 1)Fl EA
∆By =
∆By =
(↓ )
例 3-2 利用卡氏定理计算θB
EI EI
-附加力法
解:1. 分析方法
转角θ 所对应的载荷? 转角θB所对应的载荷?
M( x) ∂M( x) dx l EI ∂Me M =0
∂Vc ∵ ∆k = ∂Fk
My ( x) ∂My Mz ( x) ∂Mz FN ( x) ∂FN ( x) T( x) ∂T( x) ∆k = ∫ dx+∫ dx+∫ dx+∫ dx l EA l GI l EI l EI ∂Fk ∂Fk t y ∂F k z ∂F k
结构力学课后习题答案
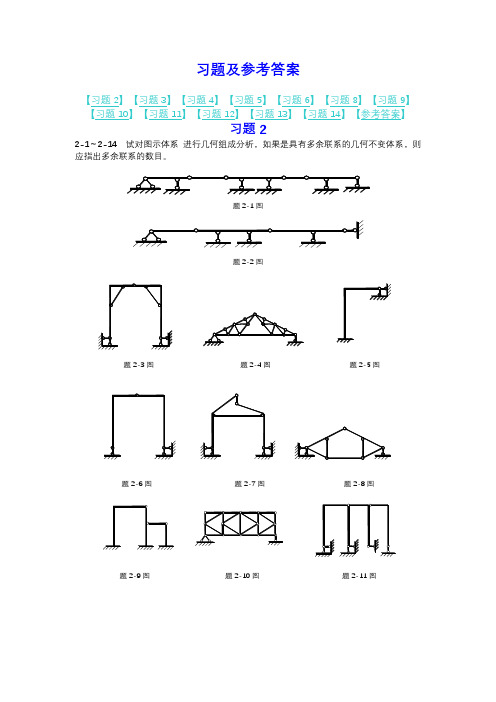
习题及参考答案【习题2】【习题3】【习题4】【习题5】【习题6】【习题8】【习题9】【习题10】【习题11】【习题12】【习题13】【习题14】【参考答案】习题22-1~2-14试对图示体系进行几何组成分析,如果是具有多余联系的几何不变体系,则应指出多余联系的数目。
题2-1图题2-2图题2-3图题2-4图题2-5图题2-6图题2-7图题2-8图题2-9图题2-10图题2-11图题2-12图 题2-13图 题2-14图习题33-1 试作图示多跨静定梁的M 及Q 图。
题3-1图3-2 试不计算反力而绘出梁的M 图。
题3-2图习题44-1 作图示刚架的M 、Q 、N 图。
题4-1图4-2 作图示刚架的M 图。
(b)(a)20kN40kN20kN/m40kN(b)5kN/m40kN(a)(c)(b)(a)题4-2图4-3 作图示三铰刚架的M 图。
题4-3图4-4 作图示刚架的M 图。
题4-4图4-5 已知结构的M 图,试绘出荷载。
P(e)(d)(a)(b)(c)/4kN(b)(a)(a)(b)(a)题4-5图4-6 检查下列刚架的M 图,并予以改正。
题4-6图习题55-1 图示抛物线三铰拱轴线方程,试求D 截面的内力。
题5-1图5-2 带拉杆拱,拱轴线方程,求截面K 的弯矩。
题5-2图 题5-3图5-3 试求图示带拉杆的半圆三铰拱截面K 的内力。
习题66-1 判定图示桁架中的零杆。
(e)(g)(h)P(d)(c)(a)(b)(f)x x l l fy )(42-=x x l lfy )(42-=C题6-1图6-2 用结点法计算图示桁架中各杆内力。
题6-2 图6-3 用截面法计算图示桁架中指定各杆的内力。
题6-3图6-4 试求图示组合结构中各链杆的轴力并作受弯杆件的M 、Q 图。
题6-4图6-5 用适宜方法求桁架中指定杆内力。
(c)(b)(b)(b)(a)题6-6图习题88-1 试作图示悬臂梁的反力V B 、M B 及内力Q C 、M C 的影响线。
2结构计算简图物体受力分析

建筑结构的支座通常分为固定铰支座,可 动铰支座,和固定(端)支座三类。
第二章
1 绪论 2 简图受力分析 3 力系简化 4 平面力系简化 5 几何组成分析 6 静定结构内力 7 轴向拉压 8 剪切和扭转 9 梁的应力 10 组合变形 11 梁和结构位移 12 力法 13 位移法 14 力矩分配法 15 压杆稳定
第二章
1 绪论 2 简图受力分析 3 力系简化 4 平面力系简化 5 几何组成分析 6 静定结构内力 7 轴向拉压 8 剪切和扭转 9 梁的应力 10 组合变形 11 梁和结构位移 12 力法 13 位移法 14 力矩分配法 15 压杆稳定
结构计算简图 物体受力分析 3、光滑铰链约束(简称铰约束)
结构计算简图 物体受力分析
2、力的三要素: 力的大小 、力的方向 、力的作用点 。 3、 力的图示法
力具有大小和方向, 所以说力是矢量(vector )。 可以用一带箭头的直 线段将力的三要素 表示出来,
如图所示。
第二章
1 绪论 2 简图受力分析 3 力系简化 4 平面力系简化 5 几何组成分析 6 静定结构内力 7 轴向拉压 8 剪切和扭转 9 梁的应力 10 组合变形 11 梁和结构位移 12 力法 13 位移法 14 力矩分配法 15 压杆稳定
结构计算简图 物体受力分析
4.链杆约束
链杆就是两端铰接而中间不受力的刚性直杆,由此所 形成的约束称为链杆约束。这种约束只能限制物体沿链 杆轴线方向上的移动。链杆可以受拉或者是受压,但不
能限制物体沿其他方向的运动和转动,所以,链杆约束
的约束反力沿着链杆的轴线,其指向假设。
第二章
1 绪论 2 简图受力分析 3 力系简化 4 平面力系简化 5 几何组成分析 6 静定结构内力 7 轴向拉压 8 剪切和扭转 9 梁的应力 10 组合变形 11 梁和结构位移 12 力法 13 位移法 14 力矩分配法 15 压杆稳定
结构力学I课程标准

“结构力学I”课程标准课程名称:结构力学I英文名称:Structural Mechanics I课程代码:课程类别:专业教育必修课程(专业核心课程)课程学时:56课程学分:3.5适用专业:土木工程先修课程:高等数学、理论力学、材料力学等授课学院:建筑工程学院教研室:土木工程教研室制定人:赵腾飞、袁立群、孟昭博审定人:张绪涛、孟昭博、崔诗才一、课程性质《结构力学I》是土木工程专业必修的专业核心课程之一,将为后续专业课程学习打下良好的基础。
通过本课程的学习,学生在理论力学和材料力学的基础上可以进一步掌握分析计算杆件体系的基本原理和方法,了解各类结构的受力性能,培养学生结构分析与计算的能力,为学习有关专业课程及进行结构设计和科学研究打下基础,并能够应用结构力学基本理论和方法解决工程实际问题。
二、目标要求(一)总体目标掌握结构在荷载、支座移动等因素作用下结构强度、刚度等的分析、计算方法;掌握结构的合理组成形式及分析方法;熟悉结构力学相关的基本概念,了解近似计算方法、了解计算结构力学的相关分析方法。
在头脑中初步建立结构的力学思维方式,能正确应用力学知识对结构的强度、刚度以及结构合理组成进行分析。
(二)具体目标1.知识目标(1)能理解结构力学的一般概念及结构受力、变形等特点;(2)能正确建立力学相关计算模型并对其进行结构几何组成分析;(3)能正确利用多种方法对结构进行受力分析、绘制相应的内力图;(4)能正确通过虚功法求解结构的位移,并能大致绘制结构的变形图。
2.能力目标(1)能熟练计算、绘制静定结构、超静定结构的内力;(2)能熟练求出指定截面的广义位移;(3)能判别平面杆系结构的几何组成合理性。
3.素质目标(1)能将力学知识应用于实际工程中,着力培养工程实践能力;(2)引入前延、后续课程,做好课程衔接,形成课程体系,为后学专业课学习打好基础;(3)培养学生的受力概念、直观受力感觉和力学意识,勇于担当结构安全和经济两大重任。
第十一章动荷载优秀课件

Q Fd
st d
Fd
Q
st
d
得Q(hd)12Q stdd
Q
h Fd
d
Q st
Q(hd)12Fdd
Q Fd
st d
Fd
Q
st
d
得Q(hd)12Q stdd
整理 d 2 得 2std : 2 hst0 d可解
dst s2t2hst (实际 d st, “”不取
一、冲击问题的假定
1.不计冲击物的变形(刚体); 2.冲击物与构件(被冲击物)接触后无回弹,
二者合为一个运动系统; 3.被冲击物的质量(惯性)与冲击物相比很小,
可略去不计,冲击应力瞬时传遍整个被冲击物; 4.整个冲击过程中,构件在线弹性范围内; 5.冲击过程中,声、热等能量损耗很小,可略去
不计。(能量守恒)
q d (5)求动应力
d
FNd 2A
A
FNd
d
R2 2
g
qd
2R
qd
A
qd
A R2
g
FNdqd2R2AgR22
FNd (5)求动应力
d
R2 2
g
vR圆环轴线上的点的 度线速
d
v2 g
说明:圆环内的动应力只与γ和v有关,而与横截面面积无关, 要保证旋转圆环的强度,只能限制圆环的转速,增加面积是不起 作用的。
二、自由落体冲击
Q
h
Fd
d
Q
冲击物Q由高h的地方自由落下 h 被冲击物在线弹性范围
d
Fd 冲 击 荷 载
d 动变形
冲击前
重物Q 被冲击杆
动能
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
11.4 力法应用举例
一、力法计算超静定结构的步骤 (1)选取基本结构。 确定原结构的超静定次数,去掉多余约束代之以相 (2)根据变形协调条件建立力法方程。 (3)计算系数和自由项。 首先作基本结构在荷载和各单位未知力分别单独作 用在基本结构上的弯矩图或写出内力表达式,然后计算 (4)求多余未知力。将计算的系数和自由项代入力 (5)绘制内力图。
第八章 力
本章提要
法
本章主要介绍超静定结构计算的基本方法——力法。 介绍了超静定次数的确定、如何选择力法的基本结构、 建立力法典型方程,并求出超静定结构的内力图。 通过本章的学习应重点掌握: 1、超静定次数的确定;
2、力法的基本原理;
3、基本结构的选择方法; 4、力法解低次超静定结构的方法。
本章内容
由图乘法计算各系数和自由项分别为: δ11= 4a3/3EI δ22=a3/3EI δ12=δ21=a3/2EI Δ1P=-5qa4/8EI Δ2P=-qa4/4EI (4)求多余未知力 将以上各系数和自由项代入力法方程得:
(5) ① 根据叠加原理作弯矩图,如图(f)所示。 ② 根据弯矩图和荷载作剪力图,如图(g)所示。 ③ 根据剪力图和荷载利用结点平衡作轴力图,如 图(h)所示。
一、力法的基本思路 力法是计算超静定结构最基本的方法。基本思路是 把超静定结构的计算问题转化为静定结构的计算问题, 利用以熟知的静定结构的计算方法达到计算超静定结构 的目的。 二、力法的基本结构
如图11(a)所示为一次超静定梁,虚线表示梁在受 力后的弹性变形情况。拆去B端的多余约束链杆并用多余 未知力X1代替B端的约束对原结构的作用,得到如图7(b) 所示静定梁。这种去掉多余约束后所得到的静定结构, 称为原结构的基本结构,待求的多余未知力X1称为力法 的基本未知量。
凡在几何组成上为几何不变且有多余约束的结构, 其全部的反力和内力不能完全由静力平衡方程唯一地确 定。如图1(b)、(d)所示。
图 1
3、多余未知力 多余约束中产生的约束力称为多余未知力。 二、超静定次数的确定 超静定结构中多余约束的数目称为超静定次数。 判断超静定次数可以用去掉多余约束使原结构变成 静定结构的方法进行。 去掉多余约束的方式一般 (1) 去掉一根支座链杆或切断一根链杆等于去掉一 个约束,如图3 (2) 去掉一个铰支座或拆去联结两刚片的单铰等于 去掉两个约束,如图4
例 试求图(a)所示超静定刚架横梁BC中点D的竖向位移 ΔDV。 解:1、力法解超静定刚架,绘出弯矩图如图(b)所示。 2、采用悬臂刚架作为基本结构,并绘出单位荷载作 用于D点的弯矩图M如图(d)所示。 3、图乘法计算ΔDV 将MP图改成易于图乘的简单的图形组合,如图(c)所 示。
再 见
图 7
三、力法的基本方程 基本结构在B端不受约束限制,在外力P作用下B点竖 向位移Δ1P向下(图7(c)),在X1作用下B点竖向位移 Δ11向上(图7(d))。由于X1是取代了被拆去约束对原结 构的作用,因此基本结构的变形位移状态应与原结构完 全一致,即B点的竖向位移Δ1必须为零,也就是说基本 结构在已知荷载与多余未知力X1共同作用下,在拆除约 束处沿多余未知力X1作用方向产生的位移应与原结构在 X1方向的位移相等。即:
11.3 力法的典型方程
如图10(a)所示的为一个三次超静定刚架。现去掉 固定端支座B,加上相应的多余未知力X1、X2和X3,便得 到图10(b)所示的基本结构。由位移条件可知,基本结构 在外荷载和多余未知力X1、X2及X3共同作用下,B处的水 平位移Δ1、竖向位移Δ2和角位移Δ3即分别沿X1、X2及 X3方向的位移都应等于零,即: Δ1=0 Δ2=0 Δ3=0
11.1 11.2 11.3 11.4 11.5 超静定结构概述 力法基本原理 力法的典型方程 力法应用举例 超静定结构位移计算
11.1 超静定结构概述
一、超静定结构的概念
1、静定结构
凡在几何组成上为几何不变且无多余约束的结构, 其全部的反力和内力都可由静力平衡方程唯一地确定。 如图1(a)、(c)所示。 2、超静定结构
图 3
图 4
(3) 将固定端支座改成铰支座,或将刚性联结改成 单铰联结,等于去掉一个约束,如图5。 (4) 去掉一个固定端支座或切开刚性联结等于去掉 三个约束,如图6
图 5
图 6
所去掉的多余约束的总数即为结构的超静定次ቤተ መጻሕፍቲ ባይዱ。 如从原结构中去掉n个约束结构就成为静定结构,则原结 构称为n
11.2 力法原理
例3 计算图 (a)所示铰结排架的内力,并作出弯矩图。 解:(1)选取基本结构 此排架是一次超静定结构, 切断横梁代之以多余未知力X1得 到基本结构如图(b) (2)建立力法方程 δ11X1+Δ1P=0 (3)计算系数和自由项 分别作基本结构的荷载弯矩 图MP图和单位弯矩图M1图如图 (c)、(d) 利用图乘法计算系数和自由 项分别如下:
根据叠加原理得: Δ1=δ11X1+δ12X2+δ13X3+Δ1P=0 Δ2=δ21X1+δ22X2+δ23X3+Δ2P=0 Δ3=δ31X1+δ32X2+δ33X3+Δ3P=0 对于n次超静定结构有: δ11X1+δ12X2+…+δ1nXn+Δ1P=0 …… δi1X1+δi2X2+…+δinXn+ΔiP=0 …… δn1X1+δn2X2+…+δnnXn+ΔnP=0 上式为力法方程的一般形式,通常称为力法典型 方程。
Δ1=0 由叠加原理根据位移条件可得下列方程 Δ1=Δ11+Δ1P=0
若X1=1时在X1方向产生的位移为δ11,则有: Δ11=δ11X1 δ11X1+Δ1P=0 此求解多余未知力的补充方程,称为力法基本方程。
为了计算δ11和Δ1P,分别作基本结构在荷载q作用 下的弯矩图MP(图8(a))和在单位力X1=1作用下的单位弯 矩图M1(图8(b)),应用图乘法可得:
式中:δ11、δ22、δ33 ……δnn----主系数 δ12、δ21、δ13 ……δij----副系数 Δ1P、Δ2P、Δ3P ……ΔnP-----自由项
由力法方程解出多余未知力X1,X2,…,Xn后,即可 按照静定结构的分析方法求得原结构的反力和内力,或 按叠加原理求出弯矩:
M=M1X1+M2X2+…+MnXn+MP
(4)计算多余未知力 将系数和自由项代入力法方程得:
解得:
X1=-5kN
(5) 作弯矩图 M=M1X1+MP 作出排架最后弯矩图如图(e)所示。
11.5
超静定结构的位移计算
计算超静定结构的位移时可以用原超静定结构已经 求出的弯矩图与静定的基本结构的单位荷载弯矩图用图 乘法求位移。 (1) 力法解超静定结构,并绘出弯矩图(即MP图); (2) 选择一个最简单的基本结构作为虚拟状态,并 绘出相应的弯矩图(即M图) (3) 图乘法求位移。
例1 图示两跨连续梁,作其内力图。 解:1.选取基本结构,确定基本未知量X1: 2.建立力法典型方程:
Δ11=δ11X1+Δ1P=0
3.计算系数和自由项:
4、求基本末知量:
5、作内力图 M=M1X1+MP
例2 作图(a)所示超静定刚架的内力图。已知刚架各杆EI 均为常数。 解:(1) 选取基本结构 此为二次超静定刚架,去掉C支座约束得如图(b)所 示悬臂刚架作为基本结构。 (2) 建立力法方程 δ11X1+δ12X2+Δ1P=0 δ21X1+δ22X2+Δ2P=0 (3) 计算系数和自由项 分别作基本结构的荷载弯矩图MP图和单位弯矩图M1 图、M2图,如图(c)、(d)、(e)所示。
图 8
代入力法方程得:
多余未知力X1求得后,即可由静力平衡条件求得其 余的约束反力和内力。最后弯矩图也可以利用已经绘出 的基本结构的M1图和MP图,由叠加原理按下式求得
M=M1X1+MP
最后内力图如图9所示。
图 9
综上所述,我们把这种取多余未知力作为基本未 知量,通过基本结构,利用计算静定结构的位移,达到 求解超静定结构的方法,称为力法。
