小学五年级数学思维能力测试
小学五年级数学思维拓展训练题

小学五年级数学思维拓展训练题1.已知四箱水果,其中苹果、梨、橘子平均每箱42个,梨、橘子、桃平均每箱36个,苹果和桃平均每箱37个。
求一箱苹果和一箱桃各有多少个?2.甲乙丙三人平均得分为91分,乙丙丁三人平均得分为89分,甲丁两人平均得分为95分。
求甲和丁各得多少分?3.五个数的平均数为18,将其中一个数改为6后,这五个数的平均数为16.原来的这个数是多少?4.将五个数从小到大排列,它们的平均数为38,前三个数的平均数为27,后三个数的平均数为48.求中间一个数是多少?5.求等差数列3、7、11、……、643的平均数。
6.XXX上山时每小时行3千米,原路返回时每小时行5千米。
XXX往返的平均速度是多少?7.有一个正方形的草坪,沿草坪四周向外修建一米宽的小路,路面面积是80平方米。
求草坪的面积。
8.五年级有六个班,每班人数相等。
从每班选16人参加少先队活动,剩下的同学相当于原来4个班的人数。
原来每班有多少人?9.一个两位数,两个数字的和为10.如果把这个两位数的两个数字对调位置,组成一个新的两位数,就比原数大72.求原来的两位数。
10.一个两位数,十位上的数字是个位上的数字的3倍。
如果把这两个数字对调位置,组成一个新的两位数,与原数的差是54.求原数。
11.一个两位数,十位上的数字是个位上的数字的2倍。
如果把这两个数字对调位置,组成一个新的两位数,与原数的和是132.求原数。
12.一个两位数,十位上的数字比个位上的数字少2.如果把这两个数字对调位置,组成一个新的两位数,与原数的和是154.求原数。
6.将橙和柑分别装入袋中,每袋分别有6个橙和5个柑。
当橙分完时,还剩下3个柑。
另一种情况下,每袋有8个柑和6个橙。
当柑分完时,还剩下18个橙。
现在需要求出橙和柑的总数。
7.XXX骑自行车从甲地到乙地,下午1时到达,行程中包括上午和下午两部分。
他想在中午12时到达,因此需要计算他在上午应该以多少的速度骑行。
(完整word版)人教版小学五年级上册数学拓展思维测试题

雅阳镇小五年级上册数学思维拓展测试题班级姓名得分温馨提示:1、本卷共三部分, 第一部分:填空题, 共计50分;第二部分:计算题, 共计26分;第三部分:解答题, 共计74分。
2.比赛时不能使用计算工具。
3.本卷中所有附图不一定依比例绘成。
(本试卷满分150分 , 考试时间90分钟)一、填空题(每题5分, 共计50分)。
1、小丽在计算3.6除以一个数时, 由于把商的小数点向右多点了一位, 结果得24.这道题的除数是()。
2.有自然数A.B.C, A和B的和是86, B加C的和是120, A加C的和是110。
那么A.B.C 分别是()、()、()。
3.1÷7=0.142857142857……小数点后面第100个数字是()。
4.如果A*B=4A+3B, 例如2*4=4×2+3×4=20,那么求(2*3)*(4*5)的值是()。
5.一个自然数与它本身相加、相减、相除的和、差、商的和是101, 这个数是()。
6.有一个长80米, 宽20米的长方形游泳池, 现在要在离池边4米的外围圈上的每条边上每隔2米种一棵树, 顶点上均要种上树。
一共要种()棵树。
7、在一道有余数的除法算式中, 被除数、除数、商和余数的和是599, 已知商是15, 余数是12。
题目中的除数是()。
8、右面图形中, 大正方形的边长是4厘米, 小正方形的边长是3厘米, 阴影部分的面积是()平方厘米。
9、有一个三位数, 数位上三个数之和是12, 十位上的数字和百位数上的数字一样大小, 个位上的数字是十位上的数字的2倍, 这个三位数是()。
10、一个学生做25道数学题, 对一题得4分, 不答不给分也不扣分, 答错一题倒扣1分, 他有3题未做, 得了73分, 他共答对了()题。
二、计算题(第11.12题每题5分, 第13.14题每题8分, 共计26分)。
11. 0.9999×1.3-0.1111×2.7 12、1998×19991999-1999×1998199813.(1+0.23+0.45)× (0.45+0.67+0.89)—(1+0.45+0.67+0.89) ×(0.23+0.45)14.已知: a=2.5×2.5×…×2.5, b=0.4×0.4×…×0.4 , 求: a×b100个2.5。
五年级下册小学数学思维训练题及答案

五年级下册小学数学思维训练题1. 新民小学 133 个少先队员担任卫生宣传,把他们分成几个人数相等的小组,有()种分法。
2.三根钢筋的长分别是18 米、 24 米、 36 米。
现在要把它们截成同样长的小段而没有剩余,每段最长可截成()米。
3.把110 个桔子分装在10 全篮子里,每个篮子里所装的桔子数正好是10 个连续偶数,是怎样分装的?4、99个连续的自然数相加,它们的和是奇数还是偶数?()99个连续的奇数相加,它们的和是奇数还是偶数?()99个连续的偶数相加的和是奇数还是偶数?()5.四个连续自然数的乘积是3024,这四个数分别是()。
6.一个长方体沿着高的方向截去2cm,表面积就减少48cm2,剩下的部分成为一个正方体,求原长方体的体积是()。
7.已知 60 = 2 ×2×3×5,,知道 60 除了有因数 1 以外,还有因数()。
8.从 2、3、5、7、11 这五个数中,任取两个不同的数分别当作一个分数的分子和分母,这样的分数有()个。
9.把一些橙和柑分装入袋,如果每袋 6 个橙、 5 个柑,橙分完了还剩 3 个柑;如果每袋8 个柑、 6 个橙,柑分完了还剩18 个橙。
橙和柑一共有()个。
10.有一筐苹果每次按 2 个、 3 个、 4 个、 5 个地数,数到最后都是多一个,如果按每次数6 个,最后篮子里还剩 1 个。
这个篮子里至少有()个苹果。
11.一个两位数十位上的数字是个位上数字的 3 倍,这个两位数减 9,则个位上的数字与十位上的数字相等。
这个两位数是()。
12. 计算 22+42+62+⋯⋯ +402=()13.五年级数学竞赛,小明获得的名次与他的年龄和竞赛的成绩相乘之积是2134,小明获得的名次()名,成绩是()分。
14、把三个长 5dm、宽 4dm、高 3dm的长方体礼品盒包装在一起,怎样包装用的包装纸最少?(请画出图)要用()平方分米的包装纸。
15、把 210 个零件分装在几个盒子里,要使每个盒子的零件数相等,有()种装法。
小学五年级数学思维专题训练—等积变形(含答案解析)
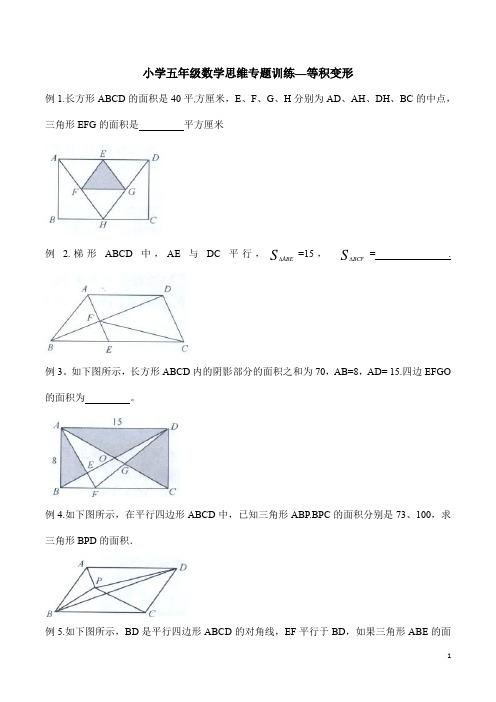
小学五年级数学思维专题训练—等积变形例1.长方形ABCD的面积是40平方厘米,E、F、G、H分别为AD、AH、DH、BC的中点,三角形EFG的面积是平方厘米例 2.梯形ABCD中,AE与DC平行,S ABE∆=15,S BCF∆= .例3。
如下图所示,长方形ABCD内的阴影部分的面积之和为70,AB=8,AD= 15.四边EFGO 的面积为。
例4.如下图所示,在平行四边形ABCD中,已知三角形ABP.BPC的面积分别是73、100,求三角形BPD的面积.例5.如下图所示,BD是平行四边形ABCD的对角线,EF平行于BD,如果三角形ABE的面积是12平方厘米,那么三角形AFD的面积是平方厘米。
例6.如下图所示,已知AE=EC,CD=DB,S ABC =60,求四边形FDCE的面积.例7.如右图所示,正方形ABC D和正方形ECGF并排放置,BF与CD相交于点H,已知AB=6厘米,则阴影部分的面积是平方厘米.例8.如下图所示,E、F、G、H分别是四边形ABCD各边的中点,EG与FH交于点O,S1、S2、S3及S4分别表示4个小四边形的面积.试比较S1+S3与S2+S4的大小.例9.将长15厘米、宽9厘米的长方形的长和宽都分成三等份,长方形内任意一点与分点及顶点连结,如右图所示,则阴影部分的面积是 平方厘米.例10.右图所示ABCD 是个直角梯形(∠DAB=∠ABC= 900),以 , AD 为一边向外作长方形ADEF ,其面积为6.36平方厘米,连接BE 交AD 于P ,再连接PC .则图中阴影部分的面积是 平方厘米。
A.6.36B.3.18C.2.12D.1.59例11.如下图所示,平行四边形内有两个大小一样的正六边形,那么阴影部分的面积占平行四边形面积的 。
A .21B .32C .52D .125例12.如下图所示,矩形ABCD 的面积是24平方厘米,三角形ADM 与三角形BCN 的面积之和是7.8平方厘米,则四边形PMON 的面积是 平方厘米.例13.一个矩形分成4个不同的三角形(如下图),绿色三角形面积占矩形面积的15%,黄色三角形的面积是21平方厘米.问:矩形的面积是多少平方厘米?例14.如下图所示,正方形每条边上的三个点(端点除外)都是这条边的四等分点,则阴影部分的面积是正方形面积的。
小学数学五年级上册思维训练题(附解析和答案)

五年级数学上册思维训练题1班级考号姓名总分1.已知一张桌子的价钱是一把椅子的10倍,又知一张桌子比一把椅子多288元,一张桌子和一把椅子各多少元?2. 3箱苹果重45千克。
一箱梨比一箱苹果多5千克,3箱梨重多少千克?3. 甲乙二人从两地同时相对而行,经过4小时,在距离中点4千米处相遇。
甲比乙速度快,甲每小时比乙快多少千米?4. 李军和张强付同样多的钱买了同一种铅笔,李军要了13支,张强要了7支,李军又给张强0.6元钱。
每支铅笔多少钱?5. 甲乙两辆客车上午8时同时从两个车站出发,相向而行,经过一段时间,两车同时到达一条河的两岸。
由于河上的桥正在维修,车辆禁止通行,两车需交换乘客,然后按原路返回各自出发的车站,到站时已是下午2点。
甲车每小时行40千米,乙车每小时行 45千米,两地相距多少千米?(交换乘客的时间略去不计)6. 学校组织两个课外兴趣小组去郊外活动。
第一小组每小时走4.5千米,第二小组每小时行3.5千米。
两组同时出发1小时后,第一小组停下来参观一个果园,用了1小时,再去追第二小组。
多长时间能追上第二小组?7. 有甲乙两个仓库,每个仓库平均储存粮食32.5吨。
甲仓的存粮吨数比乙仓的4倍少5吨,甲、乙两仓各储存粮食多少吨?8. 甲、乙两队共同修一条长400米的公路,甲队从东往西修4天,乙队从西往东修5天,正好修完,甲队比乙队每天多修10米。
甲、乙两队每天共修多少米?9. 学校买来6张桌子和5把椅子共付455元,已知每张桌子比每把椅子贵30元,桌子和椅子的单价各是多少元?10. 一列火车和一列慢车,同时分别从甲乙两地相对开出。
快车每小时行75千米,慢车每小时行65千米,相遇时快车比慢车多行了40千米,甲乙两地相距多少千米?11. 某玻璃厂托运玻璃250箱,合同规定每箱运费20元,如果损坏一箱,不但不付运费还要赔偿100元。
运后结算时,共付运费4400元。
托运中损坏了多少箱玻璃?12. 五年级一中队和二中队要到距学校20千米的地方去春游。
【免费】小学五年级数学上册经典思维训练题(全)

小学五年级数学上册经典思维训练题(全)1、一个直角梯形的一个底是5厘米,如果把它的另一个底减少2厘米,这个梯形就变成了一个正方形,这个梯形的面积是( )平方厘米。
2、1.348的小数部分第30位数字是( )。
① 1 ② 3 ③ 4 ④ 83、有五个数,按从小到大的顺序从左至右依次排开着。
这五个数的总和是113,其中前三个数的平均数是18.2.后三个数的平均数是26.8,你能求出这五个数的中位数吗?4、把一张长方形的纸对折3次,其中一份是这张纸的( )。
A 、31B 、81C 、91D 、1815、求下列图中阴影部分的面积。
6、在平行四边形的地旁边有一块三角形的地(如下图阴影部分,单位:米)准备出售,售价是每平方米4200元,买这块地需要多少钱?7、一个用小正方体拼摆的立体图形,从上面、左面看到的图形分别如下:拼摆这个立体图形至少要用( )个小正方体。
8、求出下面两个图形的面积。
9、同时掷两个骰子,得到两个数,这两个数的和最大是(),最小是()。
10、图中每个小方格表示1平方厘米,比较阴影部分的面积,()图与其他三个图形不相等。
11、食品店要将2千克薯片分装成每袋0.1千克和每袋0.25千克的两种包装出售,两种包装必须都有,可以怎么装,各是几袋?请你设计3种不同的包装方案。
方案一: 0.1千克/袋,装()袋,0.25千克/袋,装()袋。
方案二: 0.1千克/袋,装()袋,0.25千克/袋,装()袋。
方案三: 0.1千克/袋,装()袋,0.25千克/袋,装()袋。
12、如右图,平行四边形的面积是18平方分米,阴影部分两个三角形的面积之和是()平方分米。
13、一个直角三角形的三条边分别是6厘米,8厘米和10厘米,这个三角形的面积是()平方厘米,它斜边上的高是()厘米。
14、“水是生命之源”。
某市自来水公司为鼓励居民节约用水,对用水量采取按月分段计费的方法收取水费,用水量在规定吨数以内的按基本标准收费,超过规定吨数的部分提高收费标准。
五年级数学思维训练:应用题拓展(五年级)竞赛测试.doc
五年级数学思维训练:应用题拓展(五年级)竞赛测试姓名:_____________ 年级:____________ 学号:______________一、xx 题(每空xx 分,共xx 分)【题文】(4分)水果店运来了西瓜和哈密瓜共234个,如果西瓜和哈密瓜的个数比为5:4,那么水果店运来西瓜和哈密瓜各多少个?【答案】西瓜和哈密瓜各是130个及104个. 【解析】试题分析:把234平均分成5+4=9(份),求出一份有多少个,用一份的个数乘以5就是西瓜的个数,总个数减去西瓜的个数就是哈密瓜的个数. 解:234÷(5+4)×5 =26×5 =130(个) 234﹣130=104(个)答:水果店运来西瓜和哈密瓜各是130个及104个.点评:本题关键求出一份有多少个,进一步求出西瓜的个数,用总个数减去西瓜的个数即可得到哈密瓜的个数.【题文】(4分)有429名小学生参加数学冬令营,其中男生和女生的人数比为7:6.后来又有一些女生报名参赛,这时男生和女生的人数比变为11:10.请问:后来报名的女生有多少人? 【答案】有12人. 【解析】试题分析:运用和比问题的解答方法,先求出男生的人数,因为男生的人数没有发生变化,由男生的人数求出总共的人数,然后运用总共的人数减去429人,即可得到后来报名的女生的人数. 解:429÷(7+6)×7÷11×(11+10)﹣429 =33×7÷11×21﹣429 =21×21﹣429 =12(人)答:后来报名的女生有12人.点评:本题运用和比问题的解答方法进行解答,先求出男生人数,进一步取消最后的总人数,最后求出问题.【题文】(4分)松鼠一家三口出门采摘松果,松鼠爸爸采得最快,他每采摘7颗松果,松鼠妈妈只能采摘6颗;松鼠宝宝采得最慢,他每采摘2颗,松鼠妈妈已经采摘了3颗.一天下来,他们一共采摘了340颗松果.试问:其中有多少颗是松鼠宝宝采的?【答案】80颗【解析】试题分析:由于松鼠爸爸每采摘7颗松果,松鼠妈妈采摘6颗;松鼠宝宝采每采摘2颗,松鼠妈妈采摘3颗.依此可知松鼠爸爸采摘松果颗数:松鼠妈妈采摘松果颗数:松鼠宝宝采摘松果颗数=7:6:4,再根据按比例分配即可求得松鼠宝宝采摘松果颗数.解:3:2=6:4鼠爸爸采摘松果颗数:松鼠妈妈采摘松果颗数:松鼠宝宝采摘松果颗数=7:6:4340×=340×=80(颗).答:其中有80颗是松鼠宝宝采的.点评:本题关键是得到松鼠爸爸采摘松果颗数:松鼠妈妈采摘松果颗数:松鼠宝宝采摘松果颗数=7:6:4.【题文】(4分)育才小学五年级学生分成三批去参观博物馆,第一批与第二批的人数比是5:4,第二批与第三批的人数比是3:2.已知第一批的人数比第二、三批的总和少55人.请问:育才小学五年级一共有多少人?【答案】385人.【解析】试题分析:第一批与第二批的人数比是5:4,第二批与第三批的人数比是3:2,据此设第二批有x人,则第一批有x人,第三批有x人.根据第一批的人数比第二、三批的总和少55人,列出方程x+x﹣55=x,解答即可.解:设第二批有x人,则第一批有x人,第三批有x人.x+x﹣55=xx﹣x=55x=55x=132x=×132=165x=×132=88132+165+88=385(人)答:育才小学五年级一共有385人.点评:本题含有3个未知数,设出其中一个,然后用含x的代数式,表示出另外两个,根据题意列出方程解答即可.【题文】(4分)小明将100枚棋子分成三堆,已知第一堆比第二堆的2倍还多,第二堆比第三堆的2倍也要多.请问:第三堆最多有多少枚棋子?【答案】13枚【解析】试题分析:设第三堆最多有x枚棋子,则第二堆至少有2x+1枚棋子,第一堆至少有2(2x+1)+1枚棋子,然后根据三堆的数量总和是100,求出x的值,进而判断出出第三堆最多有多少枚棋子即可.解:设第三堆最多有x枚棋子,则第二堆至少有2x+1枚棋子,第一堆至少有2(2x+1)+1枚棋子,则x+(2x+1)+2(2x+1)+1=1007x+4=1007x=967x÷7=96÷7x=13所以第三堆最多有13枚棋子.答:第三堆最多有13枚棋子.点评:此题主要考查了最大与最小问题的应用,解答此题的关键是弄清楚三堆棋子数量的关系.【题文】(4分)博雅小学五年级有200人,在一次数学竞赛中,参赛人数的获得优胜奖,获得鼓励奖,其余的人没有得奖.试问:该校五年级学生中有多少人没有参加这次数学竞赛?【答案】96人.【解析】试题分析:由于参赛人数的获得优胜奖,获得鼓励奖,可以通过求8和13的最小公倍数确定参赛人数,再用五年级的人数﹣参赛人数,列式计算即可求解.解:因为8和13的最小公倍数是8×13=104,五年级有200人所以参赛人数为104人,200﹣104=96(人)答:该校五年级学生中有96人没有参加这次数学竞赛.点评:此题属于公约数和公倍数问题,解答此题的关键是通过分析,确定范围,进而根据公倍数知识进行解答.【题文】(4分)甲、乙、丙三堆棋子总共有100多枚.先从甲堆分一些棋子给另外两堆,使得乙、丙两堆的棋子数增加1倍;接着,从乙堆分一些棋子给另外两堆,使得甲、丙两堆各增加2倍;最后,从丙堆分一些棋子给另外两堆,使得甲、乙两堆各增加3倍,此时甲、乙、丙三堆棋子数的比是1:2:3.请问:原来三堆棋子各有多少枚?【答案】甲、乙、丙原来各有73、50和21枚.【解析】试题分析:首先由丙分之后甲、乙、丙三堆棋子数的比是1:2:3,根据比的基本性质变形,进一步得到丙分之前,乙分之前,甲分之前甲、乙、丙三堆棋子数的比,再根据甲、乙、丙三堆棋子总共有100多枚即可求解.解:丙分之后甲、乙、丙三堆棋子数的比是1:2:3=4:8:124÷(3+1)=18÷(3+1)=212+(4﹣1)+(8﹣2)=21丙分之前是1:2:21=3:6:633÷(2+1)=163÷(2+1)=216+(3﹣1)+(63﹣21)=50乙分之前是1:50:21=2:100:42100÷(1+1)=5042÷(1+1)=212+(100﹣50)+(42﹣21)=73甲分之前是73:50:21又因为甲、乙、丙三堆棋子总共有100多枚,73+50+21=144(枚),所以甲、乙、丙原来各有73、50和21枚.点评:考查了按比例分配应用题和逆推问题,解题的关键是得到甲分之前甲、乙、丙三堆棋子数的比是73:50:21.【题文】(4分)今年,爷爷的年龄是小明年龄的6倍.若干年后,爷爷的年龄将是小明年龄的5倍.再过若干年,爷爷的年龄将是小明年龄的4倍.求爷爷今年的年龄.【答案】72岁.【解析】试题分析:由题意,可设爷爷今年x岁,则小明今年y岁,第一过了a年,第二次又过了b年,根据“爷爷的年龄是小明年龄的6倍.若干年后,爷爷的年龄将是小明年龄的5倍,再过若干年,爷爷的年龄将是小明年龄的4倍”列方程解答即可.解:设爷爷今年x岁,则小明今年y岁,第一过了a年,第二次又过了b年,x=6yx+a=5(y+a) x=5y+4ax+a+b=4(y+a+b) x=4y+3a+3b解x=24ay=4ab=根据实际a=3 b=5y=12x=72答:爷爷今年72岁.点评:此题等量关系较复杂,要求学生要审清题意找准等量关系,列出方程解答.【题文】(4分)甲、乙、丙三人各有一些书,甲、乙共有54本,乙、丙共有79本,已知三人中书最多的那个人书的数量是书最少的人的2倍.请问:乙有多少本书?【答案】乙有32本或乙有32本.【解析】试题分析:三人有书由少到多的情况有以下6种:(1)甲乙丙,(2)甲丙乙,(3)乙甲丙,(4)乙丙甲,(5)丙甲乙,(6)丙乙甲;又由于甲和乙的本数和小于乙和丙的本数和,故此可得:甲的本数一定小余丙的本数,故此(4)(5)(6)三种情况不可能会有,在其余的三种情况里,设最少的有x本,那么最多的就有2x本,中间数量的有y本,根据甲有的本数+乙有的本数=54本,以及乙有的本数+丙有的本数=79本,分别列出方程,依据等式的性质即可求解.解:设最少的有x本,那么最多的就有2x本,中间数量的有y本情况(1):x+y=54y+2x=79故此可得:x=2254﹣22=32(本)答:乙有32本.情况(2):x+2x=543x=543x÷3=54÷3x=1818×2=36(本)答:乙有乙有32本情况(3):x+2x=793x=793x÷3=79÷3x=26由于书的本数只能是整数,所以情况(3)不存在.点评:解答本题要明确三人有数多少的情况,再判断出不可能情况,根据可能情况列方程解答即可.【题文】(4分)某乡水电站按户收取电费,具体规定是:如果每月用电不超过24度,就按每度9分钱收费;如果超过24度,超出的部分按每度2角钱收费.已知在某月中,甲家比乙家多交了电费9角6分钱(用电按整度计算),问甲、乙两家各交了、电费.【答案】2元7角6分,1元8角.【解析】试题分析:如果甲、乙两家用电均超过24度,那么他们两家的电费差应是2角钱的整数倍;如果甲、乙两家用电均不超过24度,那么他们两家的电费差应是9分钱的整数倍.现在9角6分既不是2角钱的整数倍,又不是9分钱的整数倍,所以甲家的用电超过了24度,乙家的用电不超过24度.设甲家用了24+x度电,乙家用了24﹣y度电,有20x+9y=96,得x=3,y=4.即甲家用了27度电,乙家用了20度电,那么乙家应交电费20×9=180分=1元8角,则甲家交了180+96=276分=2元7角6分.即甲、乙两家各交电费2元7角6分,1元8角.解:设甲家用了24+x度电,乙家用了24﹣y度电,有20x+9y=96,得x=3,y=4.即甲家用了27度电,乙家用了20度电,那么乙家应交电费20×9=180分=1元8角,则甲家交了180+96=276分=2元7角6分.答:甲家交电费2元7角6分,乙家交电费1元8角.故答案为:2元7角6分,1元8角.点评:完成此题,关键是根据整数倍来确定两家的用电范围,进一步解决问题.【题文】(4分)红旗小学共有师生1081人,其中老师与学生的人数之比为2:45,男生与女生的人数之比为5:4.请问:红旗小学的老师、男生和女生各有多少人?【答案】老师46人,男生575人,女生460人.【解析】试题分析:设男生的人数人数为x人,则女生为0.8x人.男女生总人数是x+0.8x=1.8x人.又老师与学生的人数之比为2:45,所以老师人数是×1.8x人.然后根据师生总数1081,列出方程为x+0.8x+×(x+0.8x )=1081,解答即可.解:设男生的人数人数为x人,则女生为0.8x人,由题意得:x+0.8x+×(x+0.8x)=10811.8x+0.08x=10811.88x=1081x=5750.8x=0.8×575=460(人).×(x+0.8x)=×(575+460)=×1035=46(人).答:老师46人,男生575人,女生460人.点评:本题设男生的人数为x人,用含x的代数式表示出女生人数和老师人数是解答此题的关键.【题文】(4分)小悦去商店买了4斤水果糖、2斤奶糖和3斤巧克力糖,如果每块糖果的重量都相同,奶糖和巧克力糖一共有160块,那么水果糖有多少块?【答案】128块.【解析】试题分析:由题意,先求1进糖有多少块,即160÷(2+3),再求4斤水果糖有多少块;据此解答.解:160÷(2+3)×4=32×4=128(块)答:水果糖有128块.点评:此题考查了简单的归一问题,先求单一量是关键.【题文】(4分)万泉小学的师生在植树节栽种柳树、杨树和槐树共860棵,其中柳树和杨树棵数的比为3:4,杨树与槐树棵数的比为5:2.请问:这三种树各栽种了多少棵?【答案】杨树400棵,柳树300棵,槐树160棵.【解析】试题分析:设杨树有x棵.根据柳树和杨树棵数的比为3:4,杨树与槐树棵数的比为5:2,表示出柳树的棵数为x,槐树的棵数为x.根据柳树、杨树和槐树共860棵,列出方程为x+x+x=860,解出x,进而求出柳树和槐树的棵数即可.解:设杨树有x棵,由题意得:x+x+x=8602.15x=860x=400x=×400=300(棵)860﹣400﹣300=160(棵)答:杨树400棵,柳树300棵,槐树160棵.点评:本题须设其中一个未知数为x,用含x的代数式表示出另外两个.然后根据等量关系列出方程即可.【题文】(4分)某厂一月份与二月份生产零件的个数比为4:5.后来改进生产技术,三月份生产的零件个数与前丽个月的总产量之比为4:3,且三月份比二月份多生产了1610个零件.请问:这家工厂第一季度共生产多少个零件?【答案】4830个.【解析】试题分析:设二月份生产零件x个,则一月份生产零件x个.三月份生产的零件个数与前丽个月的总产量之比为4:3,所以三月份生产零件(x+x)个.根据三月份比二月份多生产了1610个零件,列出方程为(x+x)﹣x=1610,解答即可.解:设二月份生产零件x个,则一月份生产零件x个.由题意得:(x+x)﹣x=1610x+x﹣x=16101.4x=1610x=11501150+1150×+(1150+1150×)=1150+920+2760=4830(个)答:这家工厂第一季度共生产4830个零件.点评:对应这种较为复杂的数量关系的题目,设未知数列方程解答较好.【题文】(4分)有48本书分给两组小朋友,已知第二组比第一组多5人.如果把书全都分给第一组,一部分小朋友每人能拿到5本,其他小朋友每人能拿到4本;如果把书全都分给第二组,一部分小朋友每人能拿到4本,其他小朋友每人能拿到3本,问:两组一共有多少人?【答案】25人.【解析】试题分析:如果把书全部分给第一组,那么每人有4本的,每人有5本的.说明第一组人数少于48÷4=12人,多于48÷5=9…3,即9人;如果把书全分给第二组,那么每人有3本的,每人有4本的.说明第二组人数少于48÷3=16人,多于48÷4=12人;因为已知第二组比第一组多5人,所以,第一组只能是10人,第二组15人.由此解决问题.解:由于48÷4=12人,48÷5=9人…3本,所以,第一组少于12人,多于9人;由于48÷3=16,48÷4=12,所以第二组多于12人,少于16人;又已知第二组比第一组多5人,所以,第一组只能是10人,第二组只能是10+5=15人.两组一共有:10+15=25(人)答:两组一共有25人.点评:根据题意得出两组人数的取值范围是完成本题的关键.【题文】(4分)22名家长(爸爸或妈妈,他们都不是老师)和老师陪同一些小学生参加某次数学竞赛,已知家长比老师多,妈妈比爸爸多,女老师比妈妈多2人,至少有一名男老师,那么在这22人中,共有爸爸多少人?【答案】5人.【解析】试题分析:本题根据已知条件进行推敲,得出各类人数的范围,进而求出爸爸的人数.具体解题步骤如下:解:家长比老师多,所以老师少于22÷2=11人,也就是不超过10人,家长就不少于12人.在至少12个家长中,妈妈比爸爸多,所以妈妈要多于12÷2=6人,也就是不少于7人.因为女老师比妈妈多2人,所以女老师不少于9人,但老师最多就10个,并且还至少有1个男老师,所以老师必须是10个(9个女老师,1个男老师),家长12个人中,有7个妈妈,那么爸爸就有12﹣7=5人.答:在这22人中,爸爸有5人.点评:本题多次运用最值问题思考方法,且巧借半差关系,得出不等式的范围.【题文】(4分)志远中学有三个年级,共900多名学生,其中初一的学生数恰好占学生总数的,初三的学生恰好占学生总数的,请问:志远中学初二有多少名学生?【答案】376名.【解析】试题分析:因为8和15的最小公倍数是120,因此三个年级总人数应为120的公倍数,因为共900多名学生,所以总人数应是120×8=960人.因此志远中学初二有学生:960×(1﹣﹣),解决问题.解:三个年级总人数应为8和15的最小公倍数120的倍数,因此总人数应为:120×8=960(人).初二有学生:960×(1﹣﹣)=960×=376(人)答:志远中学初二有376名学生.点评:此题解答的关键在于根据分母的最小公倍数确定出总人数,进而解决问题.【题文】(4分)把100个人分成四队,第一队人数是第二队人数的1倍,是第三队人数的1倍,求第四队的人数.【答案】49人.【解析】试题分析:根据题意,可得前三队的人数比是:1::=20:15:16,因为20+15+16=51,四个队的总人数为100人,所以前三队的人数只能是20人,15人,16人,第四队人数为:100﹣20﹣15﹣16=49人,据此解答即可.解:根据题意,可得前三队的人数比是:1:(1÷1):(1÷1)=1::=20:15:16,因为20+15+16=51,四个队的总人数为100人,所以前三队的人数只能是20人,15人,16人,故第四队人数为:100﹣20﹣15﹣16=49(人).答:第四队的人数是49人.点评:解答此题的关键是首先求出前三队的人数比是多少,进而判断出前三队的人数.【题文】(4分)甲、乙、丙三人各有一些棋子,其中棋子数最多的人比最少的人多出60多枚棋子,甲先拿出自己的一半平分给乙、丙,然后乙拿出自己的平分给甲、丙,最后丙拿出自己的平分给甲、乙.这时三人的棋子数正好相同.请问:三个人一共有多少枚棋子?【答案】432枚.【解析】试题分析:反过来想:最后三人都是X枚,之前丙应该是X,乙和甲都是X;再之前乙为X,丙为X,甲为X;开始为甲X,乙为X,丙为X;从这看出X一定是48的倍数,又甲X减去丙等于60多,即X=60多,所以应该等于63(7的倍数),所以X=144,三人一共为432枚棋子.解:设最后三人都是X枚,之前丙应该是X,乙和甲都是X;再之前乙为X,丙为X,甲为X;开始为甲X,乙为X,丙为X;X﹣X=63X=63X=144144×3=432(枚)答:三个人一共有432枚棋子.点评:解决此类问题的关键是抓住最后得到的数量,从后向前进行推理,根据逆运算思维进行解答.【题文】(4分)有两堆石头,如果从第一堆中取出20块石头放进第二堆,那么第二堆的石头是第一堆的2倍;如果从第二堆中取出一些石头放进第一堆,那么第一堆的石头是第二堆的6倍.问:第一堆中最少可能有多少块石头?【答案】34块.【解析】试题分析:设第一堆有x块石头,第二堆有y块石头,从第二堆取出z块放进第一堆,然后根据“从第一堆中取出20块石头放进第二堆,那么第二堆的石头是第一堆的2倍”以及“从第二堆中取出一些石头放进第一堆,那么第一堆的石头是第二堆的6倍”这两个等量关系,列出三元一次方程组,求解即可.解:设第一堆有x块石头,第二堆有y块石头,从第二堆取出z块放进第一堆,则,由①,可得y=2x﹣60…③,把③代入②,整理得11x﹣7z=360,所以x=32;又因为x,z都是自然数,所以7z+8是11的倍数,当z=2时,x有最小值为:x=32=34,即第一堆中最少可能有34块石头.答:第一堆中最少可能有34块石头.点评:此题主要考查了多元一次方程的应用,弄清题意,找出合适的等量关系,进而列出方程组是解答此类问题的关键.【题文】(4分)北京市出租车的起步价是33公里以内10元,公里后按每公里2元计费,当里程超过15公里后,超出部分按每公里3元计费.小悦、冬冬两人都从游乐园分别坐出租车回家,小悦比冬冬多花了23元,请问:小悦家距离游乐园最远是多少公里?(不足1公里按1公里计,假定两人回家一路上没有红绿灯,也没有堵车)【答案】22公里.【解析】试题分析:3公里以内10元,而公里后按每公里2元计费,所以在15公里之内车费都是偶数,小悦比比冬冬多花23元,23不是2的倍数,也不是3的倍数,说明小悦里程超过15公里,冬冬不超过15公里,然后把23进行分解,得到一部分2的倍数和一部分3的倍数组成,从而解决问题.解:在3~15公里内花的车费都是偶数,小悦比比冬冬多花23元,23不是2的倍数,也不是3的倍数,说明小悦里程超过15公里,冬冬不超过15公里,23是由一部分2的倍数和一部分3的倍数组成,23=2×10+323=2×7+3×323=2×4+3×523=2×1+3×7当小悦里程超过15公里越多,里程越远,因此小悦里程最远是15+7=22(公里)答:小悦家距离游乐园最远是22公里.点评:本题需要根据每公里车费的情况,得出小悦里程超过15公里,冬冬不超过15公里,再把23进行拆分即可求解.【题文】(4分)(2012•仙游县)某公园对团体游园购买门票的规定如下表:购票人数 50人以下 51~100人 100人以上每人门票价 12元 10元 8元今有甲、乙两个旅游团,若分别购票,两团总计应付门票费1142元.如合在一起作为一个团体购票,总计只应付门票费864元.问:这两个旅游团各有多少人?【答案】甲旅游团有31 人,乙旅游团有77人.【解析】试题分析:根据两个团合在一起作为一个团体购票,总计只应付门票费864元.这样就可以求此两个团一共有多少人,用864÷8=108人,设甲团有x人,则乙团有(108﹣x)人,已知分别购票,两团总计应付门票费1142元,由此列方程解答.解:两个团的总人数;864÷8=108(人),设甲团有x人,则乙团有(108﹣x)人,12x+(108﹣x)×10=1142,12x+1080﹣10x=1142,2x+1080=1142,2x+1080﹣1080=1142﹣1080,2x=62,2x÷2=62÷2,x=31;108﹣31=77(人);答:甲旅游团有31 人,乙旅游团有77人.点评:此题属于含有两个未知数的应用题,这类题用方程解答比较容易,关键是找准数量间的相等关系,设一个未知数为x,另一个未知数用含x的式子来表示,进而列并解方程即可【题文】(4分)植物园里菊花与月季花的盆数之比是3:4,兰花与郁金香的盆数之比是5:6,菊花与郁金香的盆数之比是4:5.如果月季比兰花多50多盆,那么菊花比郁金香少多少盆?【答案】48盆.【解析】试题分析:兰花与郁金香的盆数之比是5:6,菊花与郁金香的盆数之比是4:5.我们设郁金香有x盆,则兰花有x盆,菊花有x盆.又菊花与月季花的盆数之比是3:4,所以月季有×(x)盆.根据月季比兰花多50多盆,列出方程50<×(x)﹣x<60,解出x,然后再求出菊花的盆数,用郁金香的盆数减去菊花的盆数即可.解:设郁金香有x盆,月季比兰花多m盆.且50<m<60根据题意得:×(x)﹣x=mx﹣x=mx=mx=因为x代表花的盆数,不能是分数,30不能被7整除.所以m应是7的倍数,有50<m<60,所以m=56.x===240(盆)x﹣x=240﹣×240=240﹣192=48(盆)答:菊花比郁金香少48盆.点评:本题含有多个未知数,要设其中的一个,然后用含x的代数式,表示出另外几个,根据题目中的等量关系列出方程解答.【题文】(4分)甲、乙、丙、丁包揽了班里期中考试的前四名.甲、乙的得分之和是108分,乙、丙的得分之和是149分,丙、丁的得分之和是121分,并且知道其中第一名的得分是第三名的2倍,那么第二名的得分是多少?【答案】67分.【解析】试题分析:由题意,甲、乙的得分之和是108分,乙、丙的得分之和是149分,丙、丁的得分之和是121分,相比得到:丙﹣甲=41,乙﹣丁=28,所以第一名是乙或者丙;分乙是第一或丙是第一两种情况来推理得出第二名的得分即可.解:相比得到:丙﹣甲=41,乙﹣丁=28,所以第一名是乙或者丙:(1)若乙是第一,则因为149不能被3整除,所以丙不为第三,只能是第二,丁第三,因为乙﹣丁=28,所以乙=56,但丙=149﹣56=93>乙,矛盾;(2)若丙第一,则因为149不能被3整除,乙只能是第二,又因为121不能被3整除,所以丁只能是第四,所以甲第三,丙﹣甲=41,即丙=82,甲=41,最后得:第二名乙=108﹣41=67;答:第二名的得分是67分.点评:此题考查利用整除性解决问题.【题文】(4分)有四位好朋友的体重都是整千克数.他们两两合称体重,共称了五次.称得的千克数分别是99、113、125、130、144.其中两人没有一起合称过,那么这两人中较重一人的体重是千克.【答案】66.【解析】试题分析:设四人体重分别是A、B、C、D,其中A、B没同时称重,而(A+C)+(B+D)=(A+D)+(B+C)(每个括号表示两人合称重量),注意到五个重量中只有99+144=113+130,因此得到C+D=125,这样就可以求出A+B=118.由此知A、B同奇偶,C、D必一奇一偶,故四人重量中必有三人同奇偶,由此即可求出A 、B、C,也就求出了这两人体重较大的体重.解:设四人是A、B、C、D,其中A、B没同时称重,于是必有(A+C)+(B+D)=(A+D)+(B+C)(每个括号表示两人合称重量),注意到五个重量中只有:99+144=113+130,故剩下的125必是C、D的重量和,即有C+D=125,所以A+B=99+144﹣125=118.由此知A、B同奇偶,C、D必一奇一偶,故四人重量中必有三人同奇偶,不妨令A、B、C同奇偶,于是A+C与B+C的值也是偶数,即有:A+C=144,B+C=130,或A+C=130,B+C=144,由前者求得:A=66,B=52,C=78,由后者求得:A=52,B=66,C=78,故合称的两人体重较大的是66kg.故答案为:66.点评:此题主要考查了多元一次方程组的应用,解题的关键是正确理解题意,把握题目中的数量关系,然后列出方程组解决问题.【题文】(4分)有若干盒卡片,每盒中卡片数一样多.把这些卡片分给一些小朋友,如果只分一盒,每人至少可以得到7张;如果每人分8张卡片,则还缺少5张.现在把所有卡片都分完,每人分到60张,而且还多出4张.问:共有多少个小朋友?【答案】11个.【解析】试题分析:由题意,60÷7=8…4,60÷8=7…4,说明卡片的盒数是8盒,“若都分8张则还缺少5张”,即如果我们在每盒中加5张(8盒共加40张),每人就可以得到8×8=64张,现在实际每人得到60张,即每人需要退出4张,其中要有4张是每人60张后多下来的,还有40张是我们一开始借来的要还出去,即要退出44张,44÷4═11,说明有11人.解:60÷7=8…4,60÷8=7…4,说明卡片的盒数是8盒,(4+5×8)÷4=44÷4=11(人),答:共有11个小朋友.点评:根据“只分一盒,每人至少可以得到7张;如果每人分8张卡片,则还缺少5张”推出共有8盒卡片是解题的关键.【题文】(4分)某次考试共有100道题,每题一分,做错不扣分,甲、乙、丙三位同学分别得90分、70分、50分,其中3个人都做出来的题叫作“容易题”,只有1个人做出来的题目叫作“较难题”,没人做出来的题目叫作“特难题”,且“较难题”是“特难题”的3倍,又已知丙同学做出的题中超过80%的是“容易题”,但又不全是“容易题”,请问:“特难题”共有多少道?【答案】7道.【解析】试题分析:通过分析,可设特难题a道,较难题有3a道,容易题有b道,则有2人做出的题有(100﹣4a ﹣b)道,易知3a+2(100﹣4a﹣b)+3b=210,可知b=5a+10>40,则有a≥7,又a<100﹣90=10,则有a ≤9,所以a=7,8,9,解得a=7,b=45;a=8,b=50;a=9,b=55,由于b<50,所以只有a=7,b=45满足条件,据此解答即可.解:设特难题a道,较难题有3a道,容易题有b道,则有2人做出的题有(100﹣4a﹣b)道:可得方程:3a+2(100﹣4a﹣b)+3b=210。
小学五年级数学思维训练(奥数)《最大公因数》专题训练(含答案)
最大公因数专题简析:几个数公有的因数叫做这几个数的公因数,其中最大的一个就是这几个数的最大公因数。
课本向我们介绍了用列举法来求几个数的最大公因数。
本讲我们一起来探讨用短除法、辗转相除法等几个方法求几个数的最大公因数。
自然数a、b的最大公因数可以记作(a,b)。
例1用短除法求36和54的最大公因数。
分析与解答:人们常常用短除法求两个数的最大公因数,短除法的形式如下:2 36 54 ……先同时除以公因数2;3 18 27 ……再同时除以公因数3;3 6 9 ……再同时除以公因数3;2 3 ……除到两个商为互质数为止。
把上式中所有的除数相乘所得的积即为36和54的最大公因数,即(36,54)=2×3×3=18.随堂练习:用短除法求40和32的最大公因数。
例2求45、60、90这三个数的最大公因数。
分析与解答:与前面的例1不同的是这道题要求三个数的最大公因数。
方法1:可以用列举法。
45的因数有:1,3,4,5,9,15,45;60的因数有:1,2,3,4,5,6,10,12,15,20,30,60;90的因数有:1,2,3,4,5,6,10,15,18,30,45,90.45,60和90的公因数有:1,3,5,15;所以(45,60,90)=15.方法2:也可以用短除法。
345 60 90 ……先同时除以公因数3;5 15 20 30 ……再同时除以公因数5;3 4 6 ……除到三个商只有公因数1为止。
把上式的除数3和5相乘所得的积即为45,60,和90的最大公因数,即(45,60,90)=3×5=15.随堂练习:用短除法求36、48和60的最大公因数。
例3求319和377的最大公因数。
分析与解答:求这两个数的最大公因数如果用短除法很难找出它们的公因数,我们可以用下面这种新的方法:用较大的数377除以较小的数319;377÷319=1 (58)上面的算式中有余数58,用上式中的除数319除以余数58:319÷58=5 (29)上面的算式中仍有余数,再用上式中的除数58除以余数29:58÷29=2上式中没有余数了,这时算式中的除数29就是想319和377的最大公因数,即(319,377)=29上面这张求最大公因数的方法被古希腊的大数学家欧几里德命名为“辗转相除法”。
五年级下册小学数学思维训练题及答案
五年级下册小学数学思维训练题1。
新民小学133个少先队员担任卫生宣传,把他们分成几个人数相等的小组,有()种分法。
2.三根钢筋的长分别是18米、24米、36米。
现在要把它们截成同样长的小段而没有剩余,每段最长可截成()米。
3.把110个桔子分装在10全篮子里,每个篮子里所装的桔子数正好是10个连续偶数,是怎样分装的?4、99个连续的自然数相加,它们的和是奇数还是偶数?()99个连续的奇数相加,它们的和是奇数还是偶数?()99个连续的偶数相加的和是奇数还是偶数? ( )5.四个连续自然数的乘积是3024,这四个数分别是( ).6.一个长方体沿着高的方向截去2cm,表面积就减少48cm²,剩下的部分成为一个正方体,求原长方体的体积是()。
7.已知60 = 2×2×3×5,,知道60除了有因数1以外,还有因数( ). 8。
从2、3、5、7、11这五个数中,任取两个不同的数分别当作一个分数的分子和分母,这样的分数有()个.9.把一些橙和柑分装入袋,如果每袋6个橙、5个柑,橙分完了还剩3个柑;如果每袋8个柑、6个橙,柑分完了还剩18个橙。
橙和柑一共有()个.10.有一筐苹果每次按2个、3个、4个、5个地数,数到最后都是多一个,如果按每次数6个,最后篮子里还剩1个。
这个篮子里至少有()个苹果。
11。
一个两位数十位上的数字是个位上数字的3倍,这个两位数减9,则个位上的数字与十位上的数字相等。
这个两位数是( )。
12。
计算22+42+62+……+402=( )13.五年级数学竞赛,小明获得的名次与他的年龄和竞赛的成绩相乘之积是2134,小明获得的名次()名,成绩是()分。
14、把三个长5dm、宽4dm、高3dm的长方体礼品盒包装在一起,怎样包装用的包装纸最少?(请画出图)要用()平方分米的包装纸。
15、把210个零件分装在几个盒子里,要使每个盒子的零件数相等,有()种装法。
小学五年级数学思维训练(奥数)《巧用公倍数》讲解及练习题(含答案)
巧用公倍数专题简析:最小公倍数的知识在解决实际问题中有一定的作用。
解题时关键要根据题目中的已知条件,对问题作全面的分析,要避免与求最大公因数的类型混淆。
学习这类问题的规律与解题方法,可以使同学们的视野更开阔、思考问题更机敏。
例1有一种规格的地砖,长45厘米,宽30厘米,至少要用多少块这样的地砖才能铺成正方形地?分析与解答:要用这样的地砖铺成正方形地,可知正方形地的边长是地砖长和宽的公倍数;又因为要用尽可能少的地砖铺地,可知铺成的正方形地要尽可能小,所以正方形的边长是地砖长和宽的最小公倍数。
[45,30]=90(90÷45)×(90÷30)=2×3=6(块)答:至少要6块才能铺成正方形地。
随堂练习:柴油机上有两个互相咬合的齿轮,甲齿轮有56个齿,乙齿轮有84个齿,其中某一对齿从第一次相遇到第二次相遇,两个齿轮各转了多少圈?例2甲、乙、丙三人是好朋友,他们每隔不同的天数同一时间到图书馆去借书。
甲3天去一次,乙2天去一次,丙4天去一次。
8月4日他们恰好在图书馆相遇,几月几日他们又再次在图书馆相遇?分析与解答:从8月4日三人恰好在图书馆相遇到下一次三人再次相遇,相隔的天数应该是3、2、4的最小公倍数,因为3、2、4的最小公倍数是12,所以从8月4日起再过12天即8月16日他们又再次在图书馆相遇。
[3,2,4]=124+12=16答:8月16日他们又再次在图书馆相遇。
随堂练习:汽车总站是1路车、4路车和6路车的起点站,1路车每隔5分钟发一辆,4路车每隔8分钟发一辆,6路车每隔10分钟发一辆。
这三路车早上6:00同时从汽车总站发车,第二次同时发车是什么时间?例3一种长方体积木,长8厘米,宽6厘米,高4厘米。
用这些积木堆成一个正方体,至少需要用多少块?分析与解答:把若干个长方体堆成一个正方体,这个正方体的棱长必须是所用长方体长、宽、高的公倍数。
现在要求最少需要多少块,那么这个正方体的棱长就是长方体长、宽、高的最小公倍数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
小学五年级数学思维能力测试
(时间为80分钟、本卷共为120分 ) 姓名
一、填空题(每空格2分、共46分)
1、 9.7×4.58积是 位小数,保留两位小数是 ;精确到十分位是 。
2、 小林买了a支钢笔,每支1.8元,又买了b本练习本,每本2.9元,共需 元。
3、 一个两位小数的小数点向右移一位后,与原数的和是6.16,这个数是 。
4、 5÷7商的小数部分第2008位上的数是 ;前43位上数字之和是 。
5、 一根木头长4.8米,锯5次,每次用时8秒,每段长 米,共用时 秒。
6、 按规律计算: a*b=(a+b)×b÷2;求6*4= ;(3*2)*8= 。
7、 一个长方形的周长为60米,长比宽多4米,这个长方形的面积是 。
8、 一个两位数小数四舍五入得到的近似数是5.8, 这个数最大可能是 ;最小可能是 。
9、 一桶油连桶重5.6千克,用了一半油后,连桶还剩3.1千克,则油重 千克;桶重 千克。
10、 当a=0.5,b=0.8时,4a+2b的值是 ;7a-4b的值是 。
11、 1×2×3×4……×98×99×100的积末尾有 0。
12、 某人要到十层大楼的八层去办事,当他从一层到四层时正好用60秒,如果每层楼都一样高,
按这样的速度要上到八层还需 秒。
13、 一个三角形的面积为48cm2,则它的等底等高的平行四边形的面积是 cm2。
14、 一个梯形草坪的面积是120m2, 且上底与下底的和是12米,高是 m2。
15、 △+△=a, △-△=b,△×△=c, ,△÷△=d,且a+b+c+d=100,则△= 。
二、 计算题(能简便的用简便方法计算)(每题6分、共30分)
①3.85×42+385×0.63-38.5×0.5 ②0.8×2.7×12.5 ③4.7×2.34-34×0.047
④6.8×0.56+4.4×0.68 ⑤0.96-0.92+0.88-0.84+0.80-0.76+0.72-0.68+0.64-0.60
三、应用题(每题是6分 共24分。)
1、 学校买8张课桌和一些椅子,共付了442.8元,每张桌子35.6元,比每把椅子贵19.8元,买了多少把椅子? 2、如买了3kg苹果和5kg梨,需48元钱,如果买2kg苹果和6kg梨需48.8元,如果小王同学要买1kg苹果和5kg梨,那么需要多少元? 3、 甲乙两车同时从A地出发到B地,甲车的
速度为每小时45km, 乙车的速度为每小时50km,
乙车到达B地后立即返回.在距B地5km与甲
车相遇,那么A,B两地相距多少千米?
4、A市出租车车费的起步价是1.5千米以内都
是5元,往后都每增加0.5千米,计价器就增加0.
9元。现在某人从甲地到乙地乘出租车共支付车
费18.5元,这个人乘了多少千米?如果这个人
从甲地到乙地行了4.5千米共需付多少车费?
