基于Matlab的离散卷积
matlab离散化处理

matlab离散化处理Matlab是一种常用的数学计算软件,可以进行各种数学运算和数据处理。
离散化处理是一种常见的数据处理方法,可以将连续的数据转化为离散的数据,方便进行进一步的分析和处理。
本文将介绍如何使用Matlab进行离散化处理,并给出具体的实例演示。
我们来了解一下离散化处理的概念。
离散化处理是指将连续的数据划分成离散的几个区间,每个区间代表一种状态或取值。
通过离散化处理,可以将复杂的连续数据转化为离散的数据集,方便进行分析和处理。
离散化处理在数据挖掘、模式识别、机器学习等领域都有广泛的应用。
在Matlab中,可以使用一些函数来进行离散化处理。
其中一个常用的函数是`discretize`函数,该函数可以将输入向量或矩阵中的数据进行离散化处理。
`discretize`函数可以指定离散化的方法和参数,如区间宽度、分段方式等。
下面我们通过一个具体的例子来演示如何使用Matlab进行离散化处理。
假设我们有一组身高数据,我们想要将这些身高数据进行离散化处理,分成几个区间,每个区间代表一种身高范围。
首先,我们需要定义离散化的区间范围。
假设我们将身高分为"矮"、"中等"和"高"三个区间,分别对应身高范围为[0, 160]、(160, 180]和(180, ∞)。
接下来,我们可以使用`discretize`函数对身高数据进行离散化```matlabheight = [150, 165, 170, 185, 190, 195]; % 身高数据edges = [0, 160, 180, inf]; % 离散化的区间范围labels = {'矮', '中等', '高'}; % 离散化的区间标签result = discretize(height, edges, 'categorical', 'categoricallabels', labels); % 离散化处理```在上面的代码中,我们首先定义了身高数据`height`和离散化的区间范围`edges`,然后通过`discretize`函数对身高数据进行离散化处理,并指定了离散化的方式为分类变量,同时使用`categoricallabels`参数指定了离散化的区间标签。
实验报告信号卷积实验

一、实验目的1. 理解卷积的概念及其物理意义。
2. 掌握卷积运算的原理和方法。
3. 通过实验加深对卷积运算在实际应用中的理解。
二、实验原理1. 卷积的定义:卷积是一种线性运算,它描述了两个信号在时域上的相互作用。
对于两个连续时间信号f(t)和g(t),它们的卷积定义为:F(t) = ∫f(τ)g(t-τ)dτ其中,F(t)是卷积结果,f(τ)是信号f(t)的任意时刻的值,g(t-τ)是信号g(t)在时刻t-τ的值。
2. 卷积的性质:卷积具有交换律、结合律和分配律等性质。
其中,交换律是指f(t)和g(t)的卷积与g(t)和f(t)的卷积相等;结合律是指三个信号f(t)、g(t)和h(t)的卷积可以分别进行两两卷积后再进行一次卷积;分配律是指一个信号与两个信号的卷积等于该信号分别与两个信号卷积后的和。
三、实验内容1. 实验一:连续时间信号卷积实验(1)选用信号:选取两个连续时间信号f(t)和g(t),其中f(t)为矩形脉冲信号,g(t)为指数衰减信号。
(2)卷积计算:根据卷积的定义,计算f(t)和g(t)的卷积F(t)。
(3)结果分析:观察F(t)的波形,分析卷积结果的物理意义。
2. 实验二:离散时间信号卷积实验(1)选用信号:选取两个离散时间信号f[n]和g[n],其中f[n]为单位阶跃信号,g[n]为矩形脉冲信号。
(2)卷积计算:根据离散时间信号卷积的定义,计算f[n]和g[n]的卷积F[n]。
(3)结果分析:观察F[n]的波形,分析卷积结果的物理意义。
3. 实验三:MATLAB仿真实验(1)选用信号:选取两个连续时间信号f(t)和g(t),其中f(t)为正弦信号,g(t)为余弦信号。
(2)MATLAB编程:利用MATLAB的信号处理工具箱,编写程序实现f(t)和g(t)的卷积运算。
(3)结果分析:观察MATLAB仿真得到的卷积结果,分析其物理意义。
四、实验结果与分析1. 实验一:连续时间信号卷积实验(1)实验结果:通过计算得到f(t)和g(t)的卷积F(t)的波形。
matlabdirac函数和函数的卷积

matlabdirac函数和函数的卷积Dirac 函数,即 Delta 函数,是一种在函数分析与信号处理中常用的理想化函数。
它在实数轴上除了原点位置,其他地方取值都为零。
在原点位置,它的值为无穷大,但是满足归一化条件,即积分结果等于1、在MATLAB 中,可以通过调用 dirac( 函数来生成 Dirac 函数。
卷积是一种基本的数学操作,用于将两个函数合并到一起,并给出它们之间的关系。
在信号处理中,卷积通常用于分析信号与系统之间的相互作用。
在 MATLAB 中可以使用 conv( 函数来计算函数的卷积。
下面我们将详细介绍如何在 MATLAB 中使用 Dirac 函数和计算函数的卷积。
1. Dirac 函数:在 MATLAB 中,可以通过调用 dirac( 函数来生成 Dirac 函数。
dirac( 函数的输入参数是一个时间向量 t,输出参数是一个与输入向量相同大小的向量,其中 Dirac 函数在原点位置上的值为无穷大,其他位置上的值都为零。
例如,以下代码生成了一个 Dirac 函数,并将其绘制为图像:```t=-10:0.01:10;%定义时间范围x = dirac(t); % 生成 Dirac 函数plot(t, x); % 绘制图像xlabel('时间');ylabel('振幅');title('Dirac 函数');```运行该代码,您将看到 Dirac 函数的图像,其中只有原点位置的值非零。
2.函数的卷积:可以使用 conv( 函数在 MATLAB 中计算两个函数的卷积。
conv( 函数的输入参数是两个函数,输出参数是它们的卷积结果。
例如,以下代码计算了两个函数的卷积,并将其绘制为图像:```t=-10:0.01:10;%定义时间范围x1 = exp(-t.^2); % 定义函数1x2 = heaviside(t); % 定义函数2plot(t, y); % 绘制图像xlabel('时间');ylabel('振幅');title('函数的卷积');```在上述示例中,我们定义了两个函数 x1 = exp(-t.^2) 和 x2 = heaviside(t)。
[整理]matlab离散信号的DFT及其快速算法fft以及ifft
![[整理]matlab离散信号的DFT及其快速算法fft以及ifft](https://img.taocdn.com/s3/m/3ea2fe253868011ca300a6c30c2259010202f3fa.png)
实验四离散信号的DFT及其快速算法一、实验目的1.在学习DFT理论的基础上,通过本实验,加深对FFT的理解,体会二者之间的关系。
2.熟悉应用FFT实现两个序列的线性卷积的方法。
二、实验原理N点序列x[n] 的DFT和IDFT定义:可以用函数U=fft(u,N)和u=ifft(U,N)计算N点序列的DFT正、反变换。
三、实验内容(n),求N分别取8,32时的X(k),最后绘出图形。
1. x(n)=R5离散傅立叶变换函数的MATLAB实现如下:N=8;x=[ones(1,5),zeros(1,N-5)];n=0:N-1;X=dft(x,N);magX=abs(X);phaX=angle(X)*180/pi;k=(0:length(magX)'-1)*N/length(magX);subplot(2,2,1);stem(n,x);title('x(n)—8点');subplot(2,2,2);stem(k,magX);axis([0,8,0,6]);title('|X(k)|--8点');N=32;x=[ones(1,5),zeros(1,N-5)];n=0:N-1;X=dft(x,N);magX=abs(X);phaX=angle(X)*180/pi;k=(0:length(magX)'-1)*N/length(magX);subplot(2,2,3);stem(n,x);title('x(n)—32点');subplot(2,2,4);stem(k,magX);axis([0,32,0,5]);title('|x(k)|--32点');% dft函数function[Xk]=dft(xn,N)n=[0:1:N-1];k=[0:1:N-1];WN=exp(-j*2*pi/N);nk=n'*k;WNnk=WN.^nk;Xk=xn*WNnk;2. 已知一个8点的时域非周期离散阶跃信号,n1=0,n2=7,在n0=4前为0,n0以后为1。
matlab数据离散化处理

matlab数据离散化处理离散化,也叫等频,是数据挖掘中一个重要的预处理步骤,它将连续值的数据转化为离散数据,使得数据集更加易于处理和分析。
Matlab提供了多种方法来进行数据离散化处理,下面我们将介绍其中两种方法:等频分箱和等宽分箱。
一、等频分箱等频分箱方法将取值分为等频的若干个区间,每个区间内的数据个数相同,它的优点是:易于实现,可以处理不均匀的分布和异常值。
具体实现方法如下:1. 确定分箱数n和数据样本总数m,将数据按大小顺序排列。
2. 确定步长k=m/n。
3. 将数据分为n组,每组包含k个数据,如果有剩余的数据,则将其分为多余的一组。
4. 计算每组的上下限值,上限为第k*i个数据,下限为第k*(i-1)+1个数据。
5. 将数据按组的编号进行编码(从1到n)。
下面是等频分箱方法的Matlab代码实现:```matlab%数据离散化-等频分箱function [data_bin] = freq_bin(data,n)% n为分箱数[m,~] = size(data); %获取样本总数data = sort(data); %按大小排序step = floor(m/n); %计算步长last = mod(m,n); %判断是否有多余数据idx = zeros(1,m); %用于编码的数组for i = 1 : nif i == n && last > 0 %处理多余的数据idx(step*(i-1)+1 : step*(i-1)+last) = i;elseidx(step*(i-1)+1 : step*i) = i;endend%计算每组的上下限值group = unique(idx);limits = zeros(n,2);for i = 1 : nlimits(i,1) = data(min(find(idx == i))); %下限值limits(i,2) = data(max(find(idx == i))); %上限值end%根据上下限值进行分类data_bin = zeros(m,1);for i = 1 : mfor j = 1 : nif data(i) >= limits(j,1) && data(i) <= limits(j,2) %判断分组 data_bin(i) = j;endendend```2. 计算最大值max和最小值min,确定每个区间的宽度w=(max-min)/n。
连续信号卷积
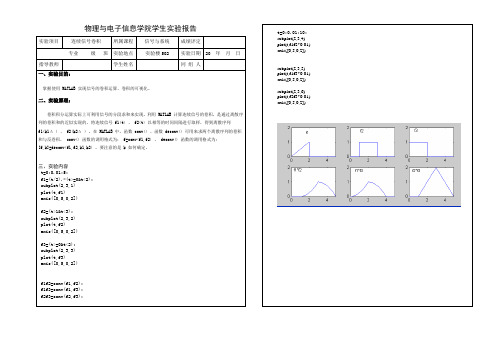
物理与电子信息学院学生实验报告t=0:0.01:10; subplot(2,3,4) plot(t,f1f2*0.01) axis([0,5,0,2])subplot(2,3,5) plot(t,f1f3*0.01) axis([0,5,0,2])subplot(2,3,6) plot(t,f2f3*0.01) axis([0,5,0,2])实验项目连续信号卷积所属课程信号与系统 成绩评定专业 级 班 实验地点 实验楼502实验日期 20 年 月 日 指导教师 学生姓名同 组 人一、实验目的:掌握使用 MATLAB 实现信号的卷积运算、卷积的可视化。
二、实验原理:卷积积分运算实际上可利用信号的分段求和来实现。
利用 MATLAB 计算连续信号的卷积,是通过离散序列的卷积和的近似实现的,将连续信号 f1(t) 、 f2(t) 以相等的时间间隔进行取样,得到离散序列 f1(k1Δ ) 、 f2(k2Δ ) 。
在 MATLAB 中,函数 conv() 、函数 deconv() 可用来求两个离散序列的卷积和与反卷积, conv() 函数的调用格式为: f=conv(f1,f2) 、 deconv() 函数的调用格式为: [f,k]=deconv(f1,f2,k1,k2) 。
要注意的是 k 如何确定。
三、实验内容 t=0:0.01:5;f1=(t/2).*(t>=0&t<2); subplot(2,3,1) plot(t,f1)axis([0,5,0,2])f2=(t>1&t<3); subplot(2,3,2) plot(t,f2)axis([0,5,0,2])f3=(t>=0&t<2); subplot(2,3,3) plot(t,f3)axis([0,5,0,2])f1f2=conv(f1,f2); f1f3=conv(f1,f3); f2f3=conv(f2,f3);四、实验总结(实验中所遇问题的原因分析及解决措施;本实验未解决的问题;对实验的改进;个人的收获等)。
毕业设计(论文)-信号与系统中的典型问题的matlab分析[管理资料]
2011届学士学位论文信号与系统中典型问题的MATLAB分析系别: 电子信息系专业: 电子信息科学与技术学号:姓名:指导教师:指导教师职称: 教授2011年4月30日信号与系统中典型问题的MATLAB分析摘要从信号与系统课程的特点出发,结合MATLAB软件优势,针对实例进行分析。
主要从连续信号、离散信号两方面应用MATLAB软件进行仿真和分析。
分别对连续信号和离散信号中线性时不变(LTI)系统信号分析,应用MATLAB软件进行仿真和分析。
对连续时间信号和离散时间信号的线性时间不变(LTI)系统的变换域,卷积和采样定理进行了模拟。
实例中运用了连续模块库、离散模块库等。
通过实例表明了MATLAB软件的便捷性,可以提高工作效率。
实践证明,采用MATLAB软件进行辅助分析可以我们对知识点的理解更深入更透彻。
关键词MATLAB仿真;时域分析;频域分析;卷积;序列卷和;冲激响应;阶跃响应;The Applied Research of Signal ProcessingBased on MATLABAbstract we give an overview of the examples from the characteristics of signal and system course, combining with MATLAB software advantages. The main idea is that MATLAB simulation and analysis software were applied in the continuous-time signals and discrete-time signals. In continuous-time signals and discrete-time signals the response signal of linear time invariant(LTI) system and its analysis of the transform domain and convolution and Sampling theorem were simulated. The examples used the continuous and discrete blocks library and communication toolbox, etc. Some examples show that processing signals can bring us great convenience and high efficiency. Practice has proved, using MATLAB software were aided analysis on knowledge points we can understand deeper and more thoroughly.Key-words MATLAB; the Time-domain Analysis;Frequency domain analysis;convolution ;Sequence convolution ;Impulse response ;Order step-response目录1引言 (1)2 MATLAB软件介绍 (2)3 MATLAB对连续时间信号的分析 (3)MATLAB仿真线性时不变(LTI)系统响应的信号表示 (3)MATLAB对连续信号变换域的分析 (4)连续时间信号的卷积计算及MATLAB的实现 (5)连续时间系统抽样定理的验证 (6)84 MATLAB对离散时间信号的分析 (10)离散系统的单位样值响应 (11)离散系统的变换域分析 (12)离散时间信号的卷积计算 (13)结论 (15)参考文献 (16)致谢 (17)附录一 (18)附录二 (19)附录三 (21)1 引言随着软件的发展,为仿真实验提供了另一思路,MATLAB软件具有强大的数值计算和矩阵处理功能。
基于MATLAB的信号与系统实验教程
基于MATLAB的信号与系统实验教程第一部分 MATLAB基础第1章 MATLAB环境1.1 MATLAB界面图1.1 MATLAB主界面图1.2 Workspace图1.3 MATLAB.m文件编辑窗口界面1.2 文件类型图1.4 设置路径图1.5 例1-1运行结果1.3 系统和程序控制指令1.4 练习第2章 数据类型与数学运算2.1 数值、变量和表达式2.1.1 数值的记述2.1.2 变量命名规则2.1.3 运算符和表达式2.2 数组、矩阵及其运算2.2.1 复数和复数矩阵2.2.2 数组和矩阵的运算2.2.3 特殊矩阵(Specialized matrices)2.3 关系和逻辑运算2.4 练习第3章 数值计算与符号计算3.1 线性代数与矩阵分析3.1.1 线性代数3.1.2 特征值分解3.1.3 奇异值分解3.1.4 矩阵函数3.2 线性方程组求解3.2.1 确定性线性方程组求解3.2.2 线性最小二乘问题的方程求解3.3 数据分析函数图3.1 例3-4运行结果3.4 符号计算图3.2 数值型与符号型数据转换关系3.5 练习第4章 绘图4.1 基本绘图指令4.1.1 plot的基本调用格式图4.1 例4-1运行结果4.1.2 stem: 离散数据绘制(火柴杆图)图4.2 例4-2运行结果4.1.3 polar: 极坐标图图4.3 例4-3运行结果4.2 各种图形标记、控制指令图4.4 例4-4运行结果4.2.1 图的创建与控制4.2.2 轴的产生与控制4.2.3 分格线(grid)、坐标框(box)、图保持(hold)4.2.4 图形标志4.3 其他常用绘图指令4.3.1 其他类型图的绘制图4.5 例4-5运行结果图4.6 例4-6运行结果简易绘图指令图4.7 例4-7运行结果4.4 练习第5章 SIMULINK5.1 SIMULINK的基本使用方法图5.1 Simulink Library Browser窗口图5.2 Pulse Generator模块的参数设置5.2 SIMULINK模型概念及基本模块介绍图5.4 SIMULINK模型的一般结构5.2.1 常用的sources——信号源模块5.2.2 常用的sinks——信号显示与输出模块图5.5 示波器纵坐标设置对话框图5.6 示波器属性对话框5.2.3 math operations——数学运算单元模块5.2.4 continuous——连续系统模块5.2.5 discrete——离散系统模块5.3 SIMULINK模型的仿真5.3.1 仿真参数设置图5.7 仿真设置对话框5.3.2 建立子系统图5.8 例5-2的SIMULINK模型图5.9 例5-2的子系统模型图5.10 例5-2仿真输出波形5.4 练习第6章 M函数和工具箱6.1 M函数6.2 工具箱图6.1 演示程序中的工具箱(Toolbox)使用帮助6.3 练习第7章 MATLAB实用技术遴选7.1 图形用户界面设计7.1.1 设计原则与设计步骤7.1.2 界面与控件介绍图7.1 标准菜单样式7.1.3 GUI实例分析。
卷积 频域乘法 证明matlab
卷积频域乘法证明matlab一、概述卷积是信号处理和图像处理中常用的一种运算,它在时域和频域都有不同的表示方式。
频域乘法是利用信号的频域表示进行运算的一种方法。
本文将对卷积、频域乘法进行解释,并通过使用MATLAB进行具体的证明。
二、卷积的定义1. 时域卷积时域卷积是指两个信号经过卷积运算得到一个新的信号。
设有两个信号$f(t)$和$g(t)$,它们的卷积表示为:\[h(t) = f(t) * g(t) = \int_{-\infty}^{\infty}f(\tau)g(t-\tau)d\tau\] 其中,$h(t)$表示卷积结果。
2. 频域卷积频域卷积是指对信号进行傅里叶变换,然后在频域进行乘法运算,最后再进行傅里叶逆变换得到卷积结果。
设有两个信号$f(t)$和$g(t)$,它们的傅里叶变换分别为$F(\omega)$和$G(\omega)$,则频域卷积可以表示为:\[H(\omega) = F(\omega)G(\omega)\]三、频域乘法的原理频域乘法是一种利用信号在频域的表示进行运算的方法。
它可以在计算复杂度较高的时域乘法运算中起到简化计算的作用,特别是对于大规模数据的处理。
四、MATLAB实现卷积和频域乘法MATLAB是一种强大的数学计算软件,它提供了丰富的信号处理函数和工具箱,可以方便地进行卷积和频域乘法的计算。
五、卷积和频域乘法的比较1. 计算复杂度在时域上,卷积的计算复杂度为$O(n^2)$,而在频域上,频域乘法的计算复杂度为$O(n\log n)$,因此对于大规模数据的处理,频域乘法具有明显的优势。
2. 计算精度尽管频域乘法在计算上具有优势,但在一些情况下,由于离散傅里叶变换的精度问题,可能会出现计算误差。
六、MATLAB中的代码实现以下是一个简单的MATLAB代码示例,演示如何利用MATLAB进行卷积和频域乘法的计算:```matlab生成信号x = [1, 2, 3, 4];y = [5, 6, 7, 8];时域卷积conv_result = conv(x, y);频域乘法fft_result = ifft(fft(x) .* fft(y));打印结果disp('时域卷积结果:');disp(conv_result);disp('频域乘法结果:');disp(fft_result);```七、结论卷积和频域乘法是信号处理和图像处理中常用的一种运算方法,它们分别在时域和频域上进行运算。
基于Mathematica的卷积计算
基于Mathematica的卷积计算作者:李春然来源:《现代电子技术》2010年第19期摘要:介绍了用Mathematica计算连续信号卷积和离散信号卷积和的方法。
所提出的方法可得到连续信号卷积的精确解析解,而非用Matlab得到的近似解。
对于离散信号,无论是有限长序列还是无限长序列的卷积和均可求解。
与传统计算方法相比,该方法避开了繁琐的做图或积分求和过程,使计算更简便、快速。
关键词:Mathematica; Matlab; 延续信号卷积; 离散信号卷积和中图分类号-34文献标识码:A文章编号:1004-373X(2010)19-0081-02Mathematica-based Computation of ConvolutionLI Chun-ran(Department of Physics, Bohai University, Jinzhou 121000, China)Abstract: The method to compute the convolution of continuous signals and the convolution sumapproximate solutions gained by Matlab are obtained by the method mentioned above. As for the discrete signals, the convolution sum of both finite and infinite sequences can be solved. In comparison with the traditional computation, this method avoids the complicated procedures such as drawing or integral summations, and makes the computation more convenient and swift.Keywords: Mathematica; Matlab; continuous signal convolution; convolution sum of discrete signal0 引言卷积在分析系统的零状态响应过程中有着重要作用,是线性时不变系统时域分析的基本数学工具,广泛应用于通信系统、信号处理、电子工程和微分方程等领域[1]。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
基于Matlab的离散卷积刘国良(洛阳理工学院 河南洛阳 471000)
摘 要:卷积运算广泛用于通讯、电子、自动化等领域的线性系统的仿真、分析及数字信号处理等方面。在Matlab中可以使用线性卷积、圆周卷积和快速傅里叶运算实现离散卷积。线性卷积是工程应用的基础,但圆周卷积和快速傅里叶运算实现线性离散卷积具有速度快等优势,圆周卷积采用循环移位,在Matlab中没有专用函数,需要根据圆周卷积的运算过程编制程序代码;快速傅里叶运算(FFT)是DSP的核心算法,在序列比较长时FFT是一种最合适的方法,运算速度快、程序简单,序列越长其优势越明显。以同一个例子介绍了进行离散卷积仿真运算的两种方法与特点。关键词:Matlab;数字信号处理;离散卷积运算;快速傅里叶运算中图分类号:TP311 文献标识码:B 文章编号:10042373X(2009)052125202
DiscretedConvolutionBasedonMatlabLIUGuoliang(LuoyangInstituteofScienceandTechnology,Luoyang,471000,China)
Abstract:Theconvolutionoperationiswidelyappliedinthefieldoflinearsystemsimulations,analysisandDSPdesignofcommunication,electronics,automaticsystemandsoon,linearconvolution,circularconvolutionandFFTfordiscretedconvolu2tionemulationoperationcanbeadoptedinMatlab.Linearconvolutionisthefoundationofprojectapplication,butcircularcon2volutionandFFTinlinearconvolutionhaveadvantagesoffastspeed.Circularconvolutionadoptscirculatingshift,thereisnotprivatelyfunctioninMatlab,itneedstodrawupprogramcodeaccordingtotheoperationalcourseofcircularconvolution.FFTisthemajoroperationofDSP,whensequencegrowsfairly,FFTisakindofmostsuitablemethod,itismorerapidlyinopera2tionalspeedandprogramsimple,thelongerofthesequencethemoreofitsadvantage.Withasameexample,tocarryoutcharacteristicandtwokindsofmethodofemulationoperationfordiscretedconvolutionareintroduced.Keywords:Matlab;DSP;discretedconvolutionoperation;FFT
收稿日期:2008207202
0 引 言在数字信号处理(DSP)系统中,无论在时域或频域都离不开卷积运算和快速傅里叶(FFT)运算。Matlab
具有强大的矩阵运算能力,方便实用的绘图功能和语言的高度集成性,在DSP开发中,使用Matlab可以快速对系统进行仿真运算。设输入信号为x(t),其频谱函数为X(jΩ),该信号通过滤波器h(t)后,其输出信号y(t)的频谱函数Y(jΩ)是频谱函数X(jΩ)与滤波器的频谱函数H(jΩ)的乘积,即:
Y(jΩ)=X(jΩ)H(jΩ)(1) 该信号通过低通滤波器的示意图如图1所示。而在时域,输出信号y(t)实际是输入信号x(t)与滤波器h(t)的卷积。就是说频谱函数的乘积相当于时
间函数的卷积,反之亦然。即:
y(t)=x(t)3h(t)=∫∞-∞x(τ)h(t-τ)dτ(2)
图1 信号通过低通滤波器的示意图 由于DSP主要依靠计算机完成,而计算机无论在时域或频域只能处理有限长的离散信号,因此上述关系
521
《现代电子技术》2009年第5期总第292期 测试・试量・自动化可表示为:Y(ω)=X(ω)H(ω)(3)y(n)=∑∞m=-∞x(m)h(n-m)=x(n)3h(n)(4)式中:n表示离散时间;数字频率ω=ΩTs=2πf/fs;f为输入信号频率;fs,Ts为抽样频率和周期。1 实现离散卷积的方法可以使用线性卷积、圆周卷积实现离散卷积,也可以根据时域信号函数与频谱函数的关系,使用快速傅里叶变换(FFT,IFFT)实现离散卷积。1.1 圆周卷积线性卷积是求离散系统响应的主要方法之一,许多重要应用都建立在这一理论基础上,如卷积滤波等,专用函数conv(x,h)可完成线性卷积过程。圆周卷积的计算速度要远远快于线性卷积,如果选择圆周卷积的长度L≥N1+N2-1,则可以用圆周卷积取代线性卷积。方法如下:(1)定义圆周卷积的长度:选择L=N1+N2-1。(2)将两个序列的长度都补足为L:将长为N1的序列x(n)延长到L,补L-N1个零,将长为N2的序列h(n)延长到L,补L-N2个零。(3)反转x(n),周期延拓为序列x(n),取主周期。(4)循环移位:与线性卷积不同,圆周卷积运算中采用的是循环移位,有限长序列x(n)的循环移位定义为:f(n)=x((n+m))NRN(n)其含义如下:①x((n+m))N表示x(n)的周期延拓序列x(n)的移位:x((n+m))N=x(n+m) ②x((n+m))NRN(n)表示对移位的周期序列x((n+m))N取主值序列,所以f(n)仍然是一个长度为N的有限长序列。为此定义一个位移函数cirshiftd.m如下:%保存函数为cirshiftd.mfunctionfm=cirshiftd(x,m,N);n=[0:1:N-1];fm=x(mod(n-m,N)+1);这里的x[mod(n-m,N)+1]即表示对向右移位N位的周期序列x((n+m))N取主值序列的运算。(5)将序列x与h进行循环移位生成的矩阵H的转置矩阵相乘,即完成将x(m)和h(n-m)所有对应项相乘之后相加,完成圆周卷积。例:已知x=[1 2 3 2]和h=[1 1 1],求两序列的卷积。用圆周卷积的计算程序如下:
%′圆周卷积′主程序x=[1 2 3 2];h=[1 1 1];N=length(x)+length(h)-1;x=[x,zeros(1,N-length(x))];h=[h,zeros(1,N-length(h))];n=[0:1:N-1];h=h(mod(-n,N)+1);H=zeros(N,N);forn=1:1:NH(n,:)=cirshiftd(h,n-1,N); %调用位移函数endy=x3H′;n0=[0:1:N-1];stem(n0,y);title(′圆周卷积′);xlabel(′(n)′);ylabel(′y(n)′);
运行结果:y=[1 3 6 7 5 2]
1.2 线性卷积的FFT算法FFT运算具有速度快、计算量小等优越性,是DSP的核心算法。根据信号在时域与频域的关系,可以用FFT计算线性卷积。方法如下:(1)定义长度:选择N=N1+N2-1。
(2)求两个要卷积序列的N点频谱函数:
求X(k)=FFT[x(n)]
求H(k)=FFT[h(n)]
(3)将两个频谱函数相乘
:
求Y(k)=H(k)X(k)
(4)对乘积进行N点快速傅里叶反变换(IFFT):
求y(n)=IFFT[Y(k)]
可见,只要进行二次FFT,一次IFFT就可完成线性卷积计算。在x(n),h(n)两序列长度比较接近或相等的情况,当运算的序列长度N>32时,上述计算线性卷积的方法比直接计算线性卷积有明显的优越性,长度值越大优势越明显。上例用FFT运算的程序如下:
x=[1 2 3 2];h=[1 1 1];N=length(x)+length(h)-1;X=fft(x,N);H=fft(h,N);Y=X.3H;
y=ifft(Y,N);n=0:1:N-1;stem(n,y);title(′FFT线性卷积′);xlabel(′(n)′);ylabel(′y(n)′);
(下转第138页)
621
自动化技术刘国良:基于Matlab的离散卷积图6 串行口中断服务子程序流程图5 结 语与传统智能家居系统相比,该系统控制中心硬件采用ARM微处理器作为控制核心,软件采用Linux216
内核作为系统的嵌入式操作系统,采用Boa为嵌入式Web服务器,采用SQLite为系统嵌入式数据库,使控制中心具有丰富的软硬件资源和可扩展接口,便于系统的开发、调试、维护、升级及扩展,同时也提高了系统的稳定性、可靠性。该系统控制中心与智能终端之间采用
蓝牙无线传输方式,避免了有线连接方式布线复杂、线路易腐蚀、维护不方便、影响室内美观等缺点。因此,该系统设计在实际应用中具有一定的借鉴意义。
参 考 文 献[1]薛晓明,陈震.蓝牙芯片BlueCore03b在远程控制智能家居系统的应用[J].泰州职业技术学院学报,2004,4(4):
26228.
[2]于明,范书瑞,曾祥烨.ARM9嵌入式系统设计与开发教程[M].北京:电子工业出版社,2006.[3]刘淼.嵌入式系统接口设计与Linux驱动程序开发[M].北京:北京航空航天大学出版社,2006.
[4]付保川,王中杰.基于ARM的嵌入式Web服务器研究[J].电子器件,2006,29(2):42245.
[5]陆永健,王萍,吴佳,等.嵌入式Web服务器Boa的移植及其应用[J].河海大学常州分校学报,2005,19(4):44247.
[6]赖于树,李迅波,杜平安.基于嵌入式Web服务器的多通道温湿度监测仪[J].仪表技术与传感器,2006(5):16218.
[7]雷小俊,李伟.SQLite在嵌入式Web服务器中的应用[J].信息技术,2006(6):1282130.
作者简介 李红刚 男,工学硕士。主要研究方向为计算机测控、嵌入式系统及农业信息化。张素萍 女,硕士研究生。主要研究方向为电路设计自动化及集成电路IC设计。方 佳 男,研究员,硕士生导师。主要研究方向为农业信息化。董玲娇 女,硕士,讲师。主研方向为计算机智能控制。
(上接第126页)2 结 语用圆周卷积和FFT运算离散卷积具有很大优势,
在Matlab中圆周卷积没有专用函数,需要自己编制,在序列比较长时FFT是一种最合适的方法,可以快速得出仿真运算的结果。选择圆周卷积或FFT运算线性离散卷积可提高DSP设计的效率。
