函数的定义域和值域知识点总结
函数的概念及定义域、值域基本知识点总结.doc
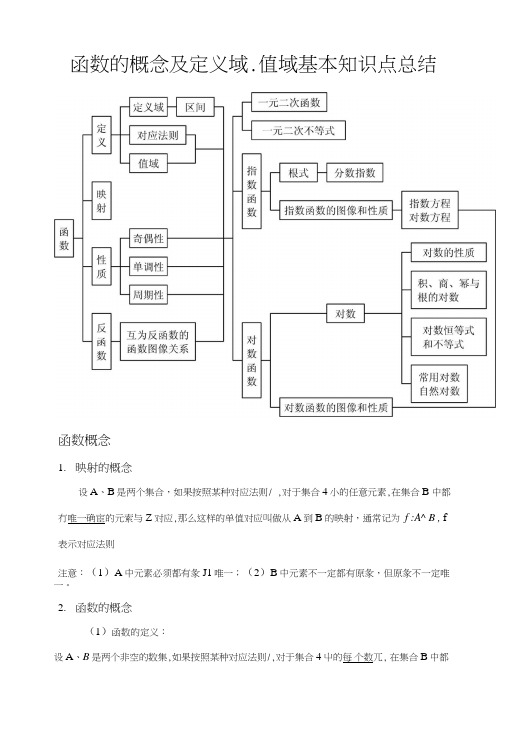
函数的概念及定义域.值域基本知识点总结函数概念1.映射的概念设A、B是两个集合,如果按照某种对应法则/ ,对于集合4小的任意元素,在集合B 中都冇唯一确宦的元索与Z对应,那么这样的单值对应叫做从A到B的映射,通常记为f :A^ B , f 表示对应法则注意:(1)A中元素必须都有彖J1唯一;(2)B中元素不一定都有原彖,但原彖不一定唯一。
2.函数的概念(1)函数的定义:设A、B是两个非空的数集,如果按照某种对应法则/,对于集合4屮的每个数兀, 在集合B中都冇唯一确怎的数和它对应,那么这样的对应叫做从A到B的一个函数,通常⑵函数的定义域、值域在函数y = f(x\xeA中,x叫做自变量,x的取值范围A叫做y = f(x)的定义域;与x的值相对应的y值叫做两数值,函数值的集合{/⑴卜e △}称为函数y = /(%)的值域。
(3)函数的三要素:定义域、值域和对丿应法则3.函数的三种表示法:图象法、列表法、解析法(1).图象法:就是用函数图象表示两个变量之间的关系;(2).列表法:就是列出表格来表示两个变量的函数关系;(3).解析法:就是把两个变量的函数关系,用等式來表示。
4.分段函数在H变量的不同变化范围屮,对应法则用不同式子來表示的函数称为分段函数。
(-)考点分析考点1:映射的概念例1. (1) A = R , B = {yly〉O}, f :x —> y =1 xI ;(2) A = {x\ x>2,x e N^}, B = {y\ y>O,y e N], / : x y = x2 - 2x + 2 ;(3) A = {xI x > 0}, = {>' I y e R}, / : x —> y = ±\[x .上述三个对应是A到B的映射.例2.若A = {1,2,3,4}, B = {aM,a,b,cwR,则A到B的映射有个,B到A的映射有个,A到B 的函数有个例3.设集合M ={-1,0,1}, 7V = {-2,-1,0,1,2},如果从M到N的映射/满足条件:对(4)8 个(3)12 个(C)16 个(0)18 个M中的每个元素兀与它在N中的象/(兀)的和都为奇数,则映射/的个数是()考点2:判断两函数是否为同一个函数例1.试判断以下各组函数是否表示同一函数?(1) /(X )= , g(x) = V?":⑶ /(x) = 2n ^X^ , g(X )= (2“V7)2"T (/7GN 4);(4) /(x) = Vx Jx + 1 , g(x) = Jx ,十 x ;(5) /(x) = x 2 -2x -1, g(t) = t 2 -2r -1 考点3:求函数解析式方法总结:(1)若已知函数的类型(如一次函数、二次函数),则用待定系数法;(2) 若已知复合函数f[g(x)]的解析式,则可用换元法或配凑法;(3) 若已知抽象函数的表达式,则常用解方程组消参的方法求出/(%)题型1:由复合函数的解析式求原来函数的解析式例1.已知二次函数/(X )满足/(2X + 1) = 4X 2-6X + 5,求/U)(三种方法)| + V* | _ Y 2例2. (09湖北改编)已知/(-—)=—v ,则/(X )的解析式可取为 l-x 1 + JC题型2:求抽象函数解析式例1.已知函数/⑴满足/U) + 2/(-) = 3x,求/⑴函数的定义域题型1:求有解析式的函数的定义域(1) 方法总结:如没有标明定义域,则认为定义域为使得函数解析式有意义的X 的取值范 围,实际操作时要注意:酚母不能为0;②对数的真数必须为正;酬次根式中被开方数应 为非负数;歿指数幕中,底数不等于0;矽分数指数幕中,底数应人于0;魁解析式由 儿个部分组成,则定义域为各个部分相应集合的交集;⑦n 果涉及实际问题,还应使得实际 问题有意义,而11注意:研究函数的有关问题一定要注意定义域优先原则,实际问题的定义 域不耍漏写。
小学数学函数知识点总结

小学数学函数知识点总结函数是数学中非常重要的一个概念,它在小学阶段的数学学习中占据着重要地位。
了解函数的定义、性质及其应用,对于解决数学问题和提高数学思维能力都具有重要作用。
本文将对小学数学函数的知识点进行总结。
一、函数的定义函数是一个集合之间的关系,它将某个集合中的元素映射到另一个集合中的元素。
在小学数学中,我们通常用代数式表示函数关系,如y = f(x)。
其中,x是自变量,y是因变量,f(x)表示函数关系。
函数关系可以用表格、图像以及公式等形式来表示。
二、函数的性质1. 定义域:函数的定义域是指自变量的取值范围。
对于小学数学来说,通常要求函数的定义域是实数集或某个给定的数集。
2. 值域:函数的值域是指因变量的取值范围,也就是函数在定义域内实际能够取到的值。
3. 单调性:函数的单调性是指函数在定义域内是否单调递增或单调递减。
可以通过求导数或观察函数图像来确定函数的单调性。
4. 奇偶性:函数的奇偶性是指函数关系是否满足f(-x) = f(x)。
如果满足,则函数为偶函数;如果不满足,则函数为奇函数。
5. 对称轴:对于偶函数来说,它存在对称轴,对称轴是y轴;对于奇函数来说,它不存在对称轴。
三、常见的函数类型1. 线性函数:线性函数是函数关系y = kx + b,其中k和b分别是常数。
线性函数的图像是一条直线,斜率k决定了直线的倾斜方向和斜率大小,截距b决定了直线和y轴的交点位置。
2. 平方函数:平方函数是函数关系y = x²,其中x为任意实数。
平方函数的图像是一个开口朝上或朝下的抛物线。
平方函数的顶点为坐标原点(0, 0),函数图像关于y轴对称。
3. 开方函数:开方函数是函数关系y = √x,其中x为非负实数。
开方函数的图像是一个开口朝右上方的抛物线。
4. 绝对值函数:绝对值函数是函数关系y = |x|,其中x为任意实数。
绝对值函数的图像是一条折线,以原点为转折点。
5. 倒数函数:倒数函数是函数关系y = 1/x,其中x不等于0。
高中函数知识点总结log

高中函数知识点总结log一、函数的基本概念1. 函数的定义:函数是一个映射关系,用来描述自变量和因变量之间的对应关系。
一般地,函数f是一个从集合A到集合B的映射,记作f:A→B,其中A称为定义域,B称为值域。
2. 自变量和因变量:自变量是函数中的输入变量,通常用x表示;而因变量是函数中的输出变量,通常用y表示。
3. 函数的图象:函数的图象是指在平面直角坐标系中由函数的所有定义域内的自变量和相应的因变量所构成的点的集合。
通常用一条曲线或者一条直线来表示函数的图象。
4. 函数的性质:函数有定义域、值域、奇偶性、单调性、最值、周期性等不同的性质。
5. 特殊函数:包括常函数、一次函数、二次函数、多项式函数、分式函数、幂函数、指数函数、对数函数、三角函数等特殊类型的函数。
二、函数的运算1. 函数的加法和减法:如果f和g是两个函数,则它们的和函数和差函数分别定义为(f+g)(x) = f(x) + g(x)和(f-g)(x) = f(x) - g(x)。
2. 函数的乘法和除法:如果f和g是两个函数,且g(x)≠0,则它们的乘积函数和商函数分别定义为(fg)(x) = f(x)g(x)和(f/g)(x) = f(x)/g(x)。
3. 复合函数:如果f和g是两个函数,则它们的复合函数定义为(f∘g)(x) = f(g(x))。
4. 反函数:如果函数f的定义域和值域分别为A和B,并且f是双射的,则可以定义其反函数f^-1。
三、函数的基本性质1. 定义域与值域:函数f的定义域是所有自变量可能取值的集合,值域是所有因变量可能取值的集合。
2. 奇偶性:如果对于函数f的定义域内的任意x都有f(-x) = f(x),则称函数f是偶函数;如果对于函数f的定义域内的任意x都有f(-x) = -f(x),则称函数f是奇函数。
3. 单调性:如果对于函数f的定义域内的任意x1和x2,有x1<x2时,f(x1)≤f(x2),则称函数f是单调增加的。
高二数学函数知识点总结

高二数学函数知识点总结一、基本概念函数是一种特殊的关系,它将每一个自变量值与唯一一个因变量值相对应。
函数可以用符号关系表示为y = f(x),其中x为自变量,y为因变量。
二、函数的表示与图像1. 函数的表示形式(1) 方程式:常见的函数形式有代数函数、三角函数、指数函数、对数函数等。
(2) 函数图像:图像可以直观地展示函数的性质,包括增减性、奇偶性、周期性等。
2. 常见函数的图像特征(1) 线性函数:图像呈直线,斜率代表函数的增减趋势。
(2) 幂函数:图像可以是开口向上或开口向下的曲线,指数越大,曲线变化越快。
(3) 二次函数:图像是开口向上或开口向下的抛物线,顶点坐标表示对称轴。
(4) 正弦函数和余弦函数:图像是周期性波动的曲线,振幅表示波动的幅度,周期表示波动的重复时间。
(5) 指数函数:图像是递增的曲线,以(0,1)为底的指数函数在x轴右侧逐渐增长。
(6) 对数函数:图像是递增的曲线,以(0,1)为底的对数函数在y轴右侧逐渐增长。
三、函数的性质1. 定义域和值域(1) 定义域:函数能够接受的自变量值的范围。
(2) 值域:函数所有可能的因变量值的范围。
2. 奇偶性和周期性(1) 奇偶性:关注函数图像关于y轴或者原点的对称性。
(2) 周期性:函数在一定区间内是否有重复的规律性。
3. 单调性和极值点(1) 单调性:函数在定义域上的变化趋势,包括增加、减少、不增不减和不减不增。
(2) 极值点:函数在单调区间内的最大值和最小值,可以通过导数判断。
4. 零点和交点(1) 零点:函数在定义域上使得函数值为0的点。
(2) 交点:函数与坐标轴或者其他函数图像相交的点。
四、函数的运算1. 函数的四则运算(1) 加法:两个函数相加后得到的函数的值等于两个函数对应点的值之和。
(2) 减法:两个函数相减后得到的函数的值等于两个函数对应点的值之差。
(3) 乘法:两个函数相乘后得到的函数的值等于两个函数对应点的值之积。
值域、定义域、求解析式总结

第7课时函数的定义域的求法知识点1函数的定义域的求法1、函数的定义域分为自然定义域和实际定义域两种,如果给定的函数解析式(不注明定义域),其定义域值得是使该解析式有意义的自变量x 的取值范围(称为自然定义域),如果函数是由实际问题确定的,这时应根据自变量的实际意义来确定。
2、定义域是函数y=f(x)中的自变量x 的范围。
求函数的定义域需要从这几个方面入手: (1)分母不为零(2)偶次根式的被开方数非负。
(3)对数中的真数部分大于0。
(4)指数、对数的底数大于0,且不等于1(5)y=tanx 中x ≠k π+π/2;y=cotx 中x ≠k π等等。
( 6 )0x 中x 0≠例:求下列函数的定义域:①21)(-=x x f ;② 23)(+=x x f ;③ xx x f -++=211)( 解:①∵x-2=0,即x=2时,分式21-x 无意义,而2≠x 时,分式21-x 有意义,∴这个函数的定义域是{}2|≠x x .②∵3x+2<0,即x<-32时,根式23+x 无意义,而023≥+x ,即32-≥x 时,根式23+x 才有意义,∴这个函数的定义域是{x |32-≥x }.③∵当0201≠-≥+x x 且,即1-≥x 且2≠x 时,根式1+x 和分式x-21同时有意义, ∴这个函数的定义域是{x |1-≥x且2≠x }另解:要使函数有意义,必须: ⎩⎨⎧≠-≥+0201x x ⇒ ⎩⎨⎧≠-≥21x x函数的定义域练习题1、求下列函数的定义域: ①14)(2--=x x f解:①要使函数有意义,必须:142≥-x即: 33≤≤-x∴函数14)(2--=x x f 的定义域为: [3,3-]②2143)(2-+--=x x x x f解:要使函数有意义,必须:⎩⎨⎧≠-≠-≤≥⇒⎩⎨⎧≠-+≥--13140210432x x x x x x x 且或 4133≥-≤<--<⇒x x x 或或∴定义域为:{ x|4133≥-≤<--<x x x 或或}③=)(x f x11111++解:要使函数有意义,必须: 011110110≠++≠+≠⎪⎪⎪⎩⎪⎪⎪⎨⎧xx x ⇒ 2110-≠-≠≠⎪⎩⎪⎨⎧x x x∴函数的定义域为:}21,1,0|{--≠∈x R x x 且④xx x x f -+=0)1()(解:要使函数有意义,必须: ⎩⎨⎧≠-≠+001x x x ⎩⎨⎧<-≠⇒01x x∴定义域为:{}011|<<--<x x x 或⑤373132+++-=x x y解:要使函数有意义,必须: ⎩⎨⎧≠+≥+-073032x x ⎪⎩⎪⎨⎧-≠∈⇒37x R x 即 x<37- 或 x>37- ∴定义域为:}37|{-≠x x⑥y=x 11x 1x 2—)(-++解:要是函数有意义,自变量x 的取值必须满足:x+1≠0 1-x ≥0 解得:x ≤1且x ≠1,即函数的定义域为{x |x ≤1且x ≠-1}2、 若函数a ax ax y 12+-=的定义域是R ,求实数a 的取值范围 解:∵定义域是R,∴恒成立,012≥+-a ax ax∴⎪⎩⎪⎨⎧≤<⇒≤⋅-=∆>2001402a a a a a 等价于3、若函数)(x f y =的定义域为[-1,1],求函数)41(+=x f y )41(-⋅x f 的定义域解:要使函数有意义,必须:43434543434514111411≤≤-⇒⎪⎩⎪⎨⎧≤≤-≤≤-⇒⎪⎩⎪⎨⎧≤-≤-≤+≤-x x x x x ∴函数)41(+=x f y )41(-⋅x f 的定义域为:⎭⎬⎫⎩⎨⎧≤≤-4343|x x 4、已知f(x)的定义域为[-1,1],求f(2x -1)的定义域。
九年级函数的知识点总结

九年级函数的知识点总结函数是数学中的重要概念,九年级学生在学习数学时将会涉及到一系列与函数相关的知识点。
下面将对九年级函数的知识点进行总结,以帮助学生们更好地理解和掌握这一内容。
1. 函数的定义和表示方法函数是一种特殊的关系,它将一个集合中的每个元素都对应到另一个集合中的唯一元素上。
函数用来描述变量之间的依赖关系,常用符号表示为:y = f(x),其中y表示函数的输出,x表示函数的输入,f表示函数本身。
2. 定义域和值域对于一个函数,定义域是指所有可能的输入值的集合,而值域则是函数所有可能的输出值的集合。
在确定函数的定义域和值域时,需要考虑约束条件和函数的性质。
3. 函数的图像和性质函数的图像是通过将定义域中的各个元素对应到值域中的元素所得到的一组点的集合。
通过观察函数的图像,可以了解函数的增减性、奇偶性、周期性等性质。
4. 函数的分类根据输入和输出的类型,函数可以分为数字函数、几何函数和符号函数等类型。
数字函数是指输入输出都是数字的函数,几何函数是指通过几何性质来表达的函数,而符号函数则是以符号表示的函数。
5. 常见函数类型线性函数、二次函数、指数函数和对数函数是九年级常见的函数类型。
线性函数的图像为一条直线,表达式为y = kx+b;二次函数的图像为开口向上或向下的抛物线,表达式为y = ax²+bx+c;指数函数的图像为递增或递减的曲线,表达式为y = aˣ;对数函数的图像为递增或递减的曲线,表达式为y = logₐx。
6. 函数的运算和复合函数函数之间可以进行加减乘除的运算,通过运算可以得到新的函数。
此外,函数还可以相互复合,形成复合函数。
复合函数是指一个函数的输出作为另一个函数的输入,通过符号表示为(f∘g)(x) = f(g(x))。
7. 函数的零点与极值函数的零点是指满足函数值等于零的输入值,常用解方程的方法求得。
函数的极值是指在定义域内,函数的值达到最大或最小的点。
求解函数的极值可以使用导数或者图像上的最高点和最低点。
高中数学必修一函数知识点总结

高中数学必修一函数知识点总结高中数学必修一的函数部分主要包括函数的定义、函数的性质、函数的图像与变化规律、函数的应用等方面的知识点。
下面是一份关于该部分知识点的详细总结。
一、函数的定义1. 定义域和值域:函数的定义域是指使函数有意义的自变量的取值范围,值域是函数的所有可能的因变量的取值范围。
2. 函数的表示方法:函数可以用公式、关系式、图像、表格等形式表示。
3. 函数的图像:函数的图像是由函数的各个值构成的点的集合,可以用直角坐标系来表示。
二、函数的性质1. 奇函数和偶函数:若对于定义域内的任何实数x,有f(-x) = -f(x),则函数f为奇函数;若对于定义域内的任何实数x,有f(-x) = f(x),则函数f为偶函数。
2. 单调性:函数在定义域上的增减关系称为函数的单调性。
若对于定义域内的任意两个实数x1和x2,有f(x1) ≤ f(x2),则函数f在该区间上递增;若对于定义域内的任意两个实数x1和x2,有f(x1) ≥ f(x2),则函数f在该区间上递减。
3. 周期性:若存在常数T>0,对于定义域内的任意实数x,有f(x+T) = f(x),则称函数f具有周期性,T为函数f的周期。
4. 奇偶性:若函数f(x)满足f(-x) = f(x),则称函数f为偶函数;若函数f(x)满足f(-x) = -f(x),则称函数f为奇函数。
三、函数的图像与变化规律1. 零点:函数f(x)在定义域内的一个实数x,使得f(x) = 0,称为函数f(x)的零点。
即f(x) = 0的解即为函数的零点。
2. 极值点:函数在定义域内取得最大值或最小值的点称为函数的极值点。
极大值点是局部最大值点,极小值点是局部最小值点。
3. 拐点:函数图像上的一点,使得该点两侧的曲线分别凸向上和凸向下,并且在该点的左右连续性方向上函数的变化趋势相反,称为函数的拐点。
4. 渐近线:若函数的图像在某个方向上无限地靠近一条直线,且与该直线的距离无限缩小,那么称该直线为函数图像的渐近线。
高一整数函数知识点总结

高一整数函数知识点总结整数函数是高中数学中的重要内容之一,它是函数的一种特殊形式。
在高一数学学习中,掌握整数函数的知识点对于深入理解函数的性质和解题技巧至关重要。
下面将对高一整数函数的知识点进行总结。
知识点一:整数函数的定义整数函数是指定义域为整数集合、值域也是整数集合的函数。
用符号表示,通常写为f(x)。
整数函数一般可以表达成f(x)=ax+b 的形式,其中a和b为整数。
知识点二:整数函数的图像特点整数函数的图像一般是由一系列相互独立的点组成。
因为定义域和值域都是整数集合,所以图像上的点的横坐标和纵坐标均为整数。
整数函数的图像通常以折线的形式出现,呈现出不连续的特点。
知识点三:整数函数的线性关系整数函数可以表示成y=ax+b的形式,其中a和b为整数。
整数函数的线性关系让我们更容易理解和分析函数的性质。
当a为正数时,整数函数呈现递增的趋势;当a为负数时,整数函数呈现递减的趋势;当a为零时,整数函数的值保持不变。
知识点四:整数函数的奇偶性奇函数和偶函数是整数函数中常见的两种特殊情况。
奇函数满足f(-x)=-f(x),即关于原点对称;偶函数满足f(-x)=f(x),即关于y 轴对称。
判断一个整数函数的奇偶性,可以观察函数图像或进行简单的运算。
知识点五:整数函数的应用整数函数在实际问题中有着广泛的应用。
通过整数函数,我们可以描述一些离散的情况,如人口增长、货物销售等。
在解决实际问题时,可以根据已知条件建立整数函数模型,并利用函数的性质进行问题的分析和求解。
以上就是高一整数函数的主要知识点总结。
通过对整数函数的学习,我们可以更好地理解函数的基本概念和特点,为后续的函数研究打下坚实的基础。
在学习整数函数时,需要注意理论与实际问题的结合,多进行练习和实际应用,提高对整数函数的认识和运用能力。
希望同学们能够在高中数学学习中,深入理解整数函数的知识,拓宽数学思维,提升解题能力。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
函数定义域的几种求法:
一、已知复杂函数,求f(x)
例1. 若函数f(x+1)的定义域是[-2,3],求f(x)的定义域
例2. 若f( √x+1 )的定义域为[0,3],求f(x)的定义域
总结:
二、已知简单函数f(x),求复杂函数
例1.若函数f(x)的定义域为[1,4],求函数f(x+2)的定义域
总结:
三、综合一和二,求函数的定义域
例1.若函数f(x+1) 的定义域是[-2,3],求函数f(2x-1)的定义域
四、当定义域为R时,求未知数的取值范围
例1.已知函数y=√mx2−6mx+m+8的定义域为R,求m 的取值范围
例3. 已知函数y=ax−1√ax2+4ax+33的定义域为R,求实数a的取值范围
总结:
函数值域
基本初等函数的定义域和值域
1. 一次函数f(x)=kx+b(k≠0)的定义域是R,值域是R
2. 反比例函数f(x)=kx(k≠0)的定义域是(-∞,0)∪(0,+ ∞),值域是(-∞,0)∪(0,+ ∞)
3. 二次函数f(x)=ax2+bx+c(a≠0)的定义域是R。
当a>0时,值域是[f(-b2a),+ ∞); 当a<0,时,值域是(-∞,f(-b2a)]
函数值域的常用方法:
一、利用简单函数值域求复杂函数值域
例1.求函数y=√x-1的值域
解:已知√x≧0,所以√x-1≧-1,所以函数y=√x-1的值域为[-1, + ∞]
例2.求函数y=- x2的值域 例3.求函数y=√4−x2的值域
例4.求函数y=1x+1的值域 例5.求函数y=6x+1的值域
二、配方法
例6.求函数y= x2-4x+5的值域 例7.求函数y= x2-6x+10的值域
解:y= x2-4x+5=(x-2)2+1≧1
所以,函数y= x2-4x+5的值域为[1,+∞)
例8.求函数y=8x2−4x+5的值域
三、将函数形式变成x=( )y的形式,利用已知函数值或者Δ的取值范围来判定
例9.求函数y=2x2+4x−7x2+2x+3的值域
解:函数变形:y x2+2yx+3y=2 x2+4x-7即:(y-2) x2+2(y-2)x+3y+7=0
当y=0时,显然不成立;
当y≠0时,上式可以看作是关于x的一元二次方程,由于定义域x∈R,则有Δ≧0,
即:Δ=4(y-2)2-4(y-2)(3y+7) ≧0
所以2y2+5y-18≦0,解得:-92≦y﹤2(x=2舍去)
所以函数y=2x2+4x−7x2+2x+3的值域为[-92,2)
