2007年中考数学试题分类汇编(圆含答案) - 英才苑

合集下载

07年中考数学答案

2007年上海市初中毕业生统一学业考试数学试卷答案要点与评分标准说明：1．解答只列出试题的一种或几种解法．如果考生的解法与所列解法不同，可参照解答中评分标准相应评分．2．第一大题只要求直接写出结果，每个空格填对得3分，否则得零分；第二大题每题选对得4分，不选、错选或者多选得零分；17题至25题中右端所注的分数，表示考生正确做对这一步应得分数，评分时，给分或扣分均以1分为单位．答案要点与评分标准一、填空题（本大题共12题，满分36分） 1．3 2．2()a a b - 3．1(1)x x + 4．1 5．2x ≥ 6．2 7．3x =-8．3y x = 9．AFD EFC △∽△（或EFC EAB △∽△，或EAB AFD △∽△） 10．1 11．2- 12．答案见图1二、选择题（本大题共4题，满分16分） 13． C 14．B 15．D 16．B 三、（本大题共5题，满分48分） 17．解：由30x ->，解得3x <． ····················································································· 3分由43326x x+>-，解得1x >-． ·························································································· 3分 ∴不等式组的解集是13x -<<．························································································· 1分解集在数轴上表示正确． ······································································································· 2分 18．解：去分母，得23(21)(1)0x x x x -+-+=， ···························································· 3分整理，得23210x x --=， ··································································································· 2分解方程，得12113x x ==-，． ······························································································ 2分经检验，11x =是增根，213x =-是原方程的根，∴原方程的根是13x =-． ·················· 2分 19．解：（1）如图2，作BH OA ⊥，垂足为H ， ······························································ 1分在Rt OHB △中，5BO = ，3sin 5BOA ∠=，3BH ∴=． ··························································································································· 2分图14OH ∴=．……………………………… 1分∴点B 的坐标为(43)，．……………………2分（2） 10OA =，4OH =，6AH ∴=．………………1分在Rt AHB △中，3BH =，AB ∴= 1分cos AH BAO AB ∴∠==2分 20．（1）小杰；1.2． ··································································································· 2分，2分（2）直方图正确． ················································································································· 3分（3）0~1． ······························································································································ 3分 21．解：[解法一]设2003年和2007年的药品降价金额分别为x 亿元、y 亿元． ············· 1分根据题意，得226543540269y x x y =⎧⎨++++=⎩………………………………………………………………分………………………………………………分解方程组，得2220120x y =⎧⎨=⎩………………………………………………………………………分………………………………………………………………………分答：2003年和2007年的药品降价金额分别为20亿元和120亿元． ·································· 1分 [解法二]设2003年的药品降价金额为x 亿元， ···································································· 1分则2007年的药品降价金额为6x 亿元． ················································································ 2分根据题意，得5435406269x x ++++=． ······································································· 2分解方程，得20x =，6120x ∴=． ······················································································ 4分答：2003年和2007年的药品降价金额分别为20亿元和120亿元． ·································· 1分四、（本大题共4题，满分50分） 22．解：（1）设二次函数解析式为2(1)4y a x =--， ······················································· 2分二次函数图象过点(30)B ，，044a ∴=-，得1a =． ···················································· 3分 ∴二次函数解析式为2(1)4y x =--，即223y x x =--． ·············································· 1分（2）令0y =，得2230x x --=，解方程，得13x =，21x =-． ································· 2分∴二次函数图象与x 轴的两个交点坐标分别为(30)，和(10)-，． ∴二次函数图象向右平移1个单位后经过坐标原点． ························································· 2分平移后所得图象与x 轴的另一个交点坐标为(40)，． ··························································· 2分23．（1）证明：DE AC ∥， BCA E ∴∠=∠． ·················································································································· 1分 CA 平分BCD ∠， 2BCD BCA ∴∠=∠， ·········································································································· 1分 2BCD E ∴∠=∠， ··············································································································· 1分x又2B E ∠=∠ ， B BCD ∴∠=∠． ·················································································································· 1分∴梯形ABCD 是等腰梯形，即AB DC =． ········································································ 2分（2）解：如图3，作AF BC ⊥，DG BC ⊥，垂足分别为F G ，，则AF DG ∥．在Rt AFB △中，tg 2B =，2AF BF ∴=．…………1分又AB 222AB AF BF =+，2254BF BF ∴=+，得1BF =．……………………1分同理可知，在Rt DGC △中，1CG =．……………1分 AD BC ∥，DAC ACB ∴∠=∠．又ACB ACD ∠=∠ ，DAC ACD ∴∠=∠，AD DC ∴=．DC AB ==AD ∴······················································································ 1分 AD BC ∥，AF DG ∥，∴四边形AFGD是平行四边形，FG AD ∴= ······ 1分2BC BF FG GC ∴=++=． ···················································································· 1分 24．（1）解：函数(0my x x=>，m 是常数）图象经过(14)A ，，4m ∴=． ··············· 1分设BD AC ，交于点E ，据题意，可得B 点的坐标为4a a ⎛⎫ ⎪⎝⎭，，D 点的坐标为40a ⎛⎫ ⎪⎝⎭，，E 点的坐标为41a ⎛⎫⎪⎝⎭，， ·········································································································· 1分1a > ，DB a ∴=，44AE a=-．由ABD △的面积为4，即14442a a ⎛⎫-= ⎪⎝⎭， ······································································ 1分得3a =，∴点B 的坐标为433⎛⎫ ⎪⎝⎭，． ···················································································· 1分（2）证明：据题意，点C 的坐标为(10)，，1DE =， 1a > ，易得4EC a=，1BE a =-， 111BE a a DE -∴==-，4414AE a a CEa-==-． ···································································· 2分图3BE AEDE CE ∴=． ······················································································································· 1分 DC AB ∴∥． ······················································································································· 1分（3）解：DC AB ∥，∴当AD BC =时，有两种情况： ①当AD BC ∥时，四边形ADCB 是平行四边形，由（2）得，1BE AEa DE CE==-，11a ∴-=，得2a =． ∴点B 的坐标是（2，2）． ···································································································· 1分设直线AB 的函数解析式为y kx b =+，把点A B ，的坐标代入，得422k b k b =+⎧⎨=+⎩，解得26.k b =-⎧⎨=⎩，∴直线AB 的函数解析式是26y x =-+． ··········································································· 1分 ②当AD 与BC 所在直线不平行时，四边形ADCB 是等腰梯形，则BD AC =，4a ∴=，∴点B 的坐标是（4，1）． ························································· 1分设直线AB 的函数解析式为y kx b =+，把点A B ，的坐标代入，得414.k b k b =+⎧⎨=+⎩，解得15k b =-⎧⎨=⎩，∴直线AB 的函数解析式是5y x =-+． ············································································· 1分综上所述，所求直线AB 的函数解析式是26y x =-+或5y x =-+． 25．（1）证明：如图4，连结OB OP ，，O 是等边三角形BPQ 的外心，OB OP ∴=， ································································ 1分圆心角3601203BOP ∠==．当OB 不垂直于AM 时，作OH AM ⊥，OT AN ⊥，垂足分别为H T ，．由360HOT A AHO ATO ∠+∠+∠+∠=，且60A ∠=，90AHO ATO ∠=∠= ，120HOT ∴∠= ．BOH POT ∴∠=∠． ··········································································································· 1分 Rt Rt BOH POT ∴△≌△． ······························································································· 1分 OH OT ∴=．∴点O 在MAN ∠的平分线上． ·································································· 1分当OB AM ⊥时，36090APO A BOP OBA ∠=-∠-∠-∠=．即OP AN ⊥，∴点O 在MAN ∠的平分线上．综上所述，当点P 在射线AN 上运动时，点O 在MAN ∠的平分线上．（2）解：如图5，AO 平分MAN ∠，且60MAN ∠= ，30BAO PAO ∴∠=∠= ． ··································································································· 1分由（1）知，OB OP =，120BOP ∠=，30CBO ∴∠= ，CBO PAC ∴∠=∠．BCO PCA ∠=∠ ，AOB APC ∴∠=∠． ········································································ 1分 ABO ACP ∴△∽△． AB AO AC AP∴=．AC AO AB AP ∴= ．4y x ∴=． ·························································· 1分定义域为：0x >． ················································································································ 1分（3）解：①如图6，当BP 与圆I相切时，AO = ·················································· 2分 ②如图7，当BP 与圆I相切时，AO =； ································································· 1分 ③如图8，当BQ 与圆I 相切时，0AO =． ······································································· 2分图6()P A图7M图8图4图5。

2007中考真题分类汇编_用样本的平均数、中位数、众数、方差估计总体的平均数和方差

8.用样本的平均数、中位数、众数、方差估计总体的平均数和方差第1题. (2007福建宁德课改,8分)育才中学现有学生2870人，学校为了进一步丰富学生课余生活，拟调整兴趣活动小组，为此进行一次抽样调查．根据采集到的数据绘制的统计图（不完整）如下：请你根据图中提供的信息，完成下列问题：（1）图1中“电脑”部分所对应的圆心角为度；（2）在图2中，将“体育”部分的图形补充完整；（3）爱好“书画”的人数占被调查人数的百分数是；（4）估计育才中学现有的学生中，有人爱好“书画”．答案：（1）126；（2）画图，如图所示；（3）10%；（4）287．第2题. （2007甘肃陇南非课改，3分）一养鱼专业户从鱼塘捕得同时放养的草鱼100条，他从中任选5条，称得它们的质量如下（单位：kg ）：1.3， 1.6， 1.3， 1.5， 1.3．则这100条鱼的总质量约为 kg ．答案：140第3题. （2007甘肃兰州课改，7分）兰州市某校对九年级学生进行“综合素质”评价，评价的结果为A （优）、B （良好）、C （合格）、D （不合格）四个等级．现从中抽测了若干名学生的“综合素质”等级作为样本进行数据处理，并作出如图所示的统计图，已知图中从左到右的四个长方形的高的比为： 14:9:6:1，评价结果为D 等级的有2人，请你回答以下问题：（1）共抽测了多少人？（2）样本中B 等级的频率是多少？C 等级的频率是多少？（3）如果要绘制扇形统计图，A D ，两个等级在扇形统计图中所占的圆心角分别是多少度？（4）该校九年级的毕业生共300人，假如“综合素质”等级为A 或B 的学生才能报考示范性高中，请你计算该校大约有多少名学生可以报考示范性高中？书画电脑 35%音乐体育图1 图2答案：解：（1）122306030÷=⨯=（人），所以抽测了60人．（2）9300.3÷= ∴样本中B 等级的频率是0.3 9300.2÷= ∴样本中C 等级的频率是0.2（3）A 等级在扇形统计图中所占的圆心角为：1436016830⨯= D 等级在扇形统计图中所占的圆心角为：13601230⨯=（4）2330023030⨯=名答：估计该校大约有230名学生可以报考示范性高中．第4题. （2007山西临汾课改，8分）某中学学生会为考察该校学生参加课外体育活动的情况，采取抽样调查的方法从篮球、排球、乒乓球、足球及其他等五个方面调查了若干名学生的兴趣爱好（每人只能选其中一项），并将调查结果绘制成如下两幅不完整的统计图，请根据图中提供的信息解答下列问题：（1）在这次考察中一共调查了多少名学生？（2）在扇形统计图中，“乒乓球”部分所对应的圆心角是多少度？（3）补全条形统计图；（4）若全校有1800名学生，试估计该校喜欢篮球的学生约有多少人？答案：解：（1）66010%=∵， ∴这次考察中一共调查了60名学生． 2分（2）125%10%20%20%25%----=∵， 36025%90⨯=∴°°， ∴在扇形统计图中，“乒乓球”部分所对应的圆心角为90°．4分（3）6020%12⨯=，∴补全统计图如图： 6分（4）180025%450⨯=∵，蓝球排球乒乓球足球其他项目蓝球排球乒乓球足球其他项目∴可以估计该校学生喜欢篮球活动的约有450人．第5题. （2007山东临沂课改，6分）某校为了解全校2000名学生的课外阅读情况，在全校范围内随机调查了50名学生，得到他们在某一天各自课外阅读所用时间的数据，将结果绘制成频数分布直方图（如图所示）．（1）这50名学生在这一天课外阅读所用时间的众数是多少？（2）这50名学生在这一天平均每人的课外阅读所用时间是多少？（3）请你根据以上调查，估计全校学生中在这一天课外阅读所用时间在1.0小时以上（含1.0小时）的有多少人？答案：解：（1）众数是1.0小时；（2）1(0.515 1.020 1.510 2.05)50x =⨯+⨯+⨯+⨯ 1.05=（小时），这50名学生这一天平均每人的课外阅读时间是1.05小时；（3）352000140050⨯=．全校学生中这一天课外阅读时间在1.0小时以上（含1.0小时）的约为1400人．第6题. （2007广东佛山课改，6分）一个瓶中装有一些幸运星，小王为了估计这个瓶中幸运星的颗数，他是这样做的：先从瓶中取出20颗幸运星做上记号，然后把这些幸运星放回瓶中，充分摇匀；再从瓶中取出30颗幸运星，发现有6颗幸运星带有记号. 请你帮小王估算出原来瓶中幸运星的颗数.答案：【方法一】解：设原来瓶子中幸运星大约有x 颗．则有30620=x . 解得100=x .答：原来瓶子中幸运星大约有100颗【方法二】解：∵30颗幸运星中带记号的幸运星的频率为51306=. ∴1005120=÷. 答：原来瓶子中幸运星大约有100颗．人数（人）时间（小时）第7题. （2007江苏连云港课改，8分）国家规定“中小学生每天在校体育活动时间不低于1小时”．为此，某市就“你每天在校体育活动时间是多少”的问题随机调查了辖区内300名初中学生．根据调查结果绘制成的统计图（部分）如图所示，其中分组情况是：Ａ组：0.5h t <；Ｂ组：0.5h 1h t <≤ Ｃ组：1h 1.5h t <≤ Ｄ组： 1.5h t ≥ 请根据上述信息解答下列问题：（1）Ｃ组的人数是；（2）本次调查数据的中位数落在组内；（3）若该辖区约有24 000名初中学生，请你估计其中达国家规定体育活动时间的人约有多少？答案：解：（1）120；（2）Ｃ；（3）达国家规定体育活动时间的人数约占12060100%60%300+⨯=．所以，达国家规定体育活动时间的人约有2400060%14400⨯=（人）．第8题. （2007江苏南京课改，6分）某养鸡场分3次用鸡蛋孵化出小鸡，每次孵化所用的鸡蛋数、每次的孵化率（孵化率=100%⨯孵化出的小鸡数孵化所用的鸡蛋数）分别如图1，图2所示：（1）求该养鸡场这3次孵化出的小鸡总数和平均孵化率；（2）如果要孵化出2000只小鸡，根据上面的计算结果，估计该养鸡场要用多少个鸡蛋？答案：解：（1）该养鸡场这3次孵化出的小鸡总数为4082.550786080120⨯+⨯+⨯=％％％（只）．这3次的平均孵化率为12010080405060⨯=++％％．图1 孵化出用的鸡蛋数统计图图2 孵化率统计图（2）2000802500÷= ％（个）． ∴估计该养鸡场要用2 500个鸡蛋．第9题. （2007江苏南通课改，8分）某市图书馆的自然科学、文学艺术、生活百科和金融经济四类图书比较受读者的欢迎．为了更好地为读者服务，该市图书馆决定近期添置这四方面的图书，为此图书管理员对2007年5月份四类图书的借阅情况进行了统计，得到了四类图书借阅情况的频数表．请你根据表中提供的信息，解答以下问题：（1）填空：表中数据的极差是；（2）请在右边的圆中用扇形统计图表示四类图书的借阅情况；（3）如果该市图书馆要添置这四类图书10000册，请你估计“文学艺术”类图书应添置多少册较合适？答案：解：（1）800；（2）借阅自然科学类图书的频率是0.25，在扇形统计图中对应的圆心角是90；借阅文学艺术类图书的频率是0. 30，在扇形统计图中对应的圆心角是108；借阅生活百科类图书的频率是0.20，在扇形统计图中对应的圆心角是72；借阅金融经济类图书的频率是0.25，在扇形统计图中对应的圆心角是90．（扇形图正确）（3）因为100000.303000⨯=，所以如果该市图书馆添置这四类图书10000册，则“文学艺术”类图书应添置3000册较合适．第10题. （2007辽宁大连课改，10分）某学校为丰富大课间自由活动的内，随机选取本校100名学生进行调查，调查内容是“你最喜欢的自由活动项目是什么？”，整理收集到的数据，绘制成下图．（1）学校采用的调查方式是；（2）求喜欢“踢毽子”的学生人数，并在图8中将“踢毽子”部分的图形补完整；（3）该校共有800名学生，请估计喜欢“跳绳”的学生人数躲避球跳绳踢毽子其他自由活动项目答案：解：（1）抽样调查；（2）10040201525---=（人）．答：喜欢“踢毽子”的学生人数为25人．如图；（3）20800160100⨯=（人）．答：估计学校喜欢“跳绳”的学生有160人．第11题. （2007辽宁12市课改，3分）为了估计某市空气质量情况，某同学在30天里做了如下记录：100<w ≤150时空气质量为轻度污染，若1年按365天计算，请你估计该城市在一年中空气质量达到良以上（含良）的天数为天．答案：292第12题. （2007辽宁12市课改，10分）为了丰富校园文化生活，某校计划在午间校园广播台播放“百家讲坛”的部分内容．为了了解学生的喜好，抽取若干名学生进行问卷调查（每人只选一项内容），整理调查结果，绘制统计图如下：请根据统计图提供的信息回答以下问题：（1）抽取的学生数为_______名；（2）该校有3000名学生，估计喜欢收听易中天《品三国》的学生有_______名；自由活动项目18题《红楼梦》《品三国》《论语》博物院《庄子》内容（3）估计该校女学生喜欢收听刘心武评《红楼梦》的约占全校学生的_ ___%；（4）你认为上述估计合理吗？理由是什么？答案：（1）300；（2）1060；（3）15；（4）合理．理由中体现用样本估计总体即可．（只答“合理”得1分）第13题. (2007内蒙鄂尔多斯课改，6分)某市教育行政部门为了解初中学生参加综合实践活动的情况，随机抽取了本市初一、初二、初三年级各500名学生进行了调查．调查结果如图所示，请你根据图中的信息回答问题．（1）在被调查的学生中，参加综合实践活动的有多少人？参加科技活动的有多少人？（2）如果本市有3万名初中学生，请你估计参加科技活动的学生约有多少名？答案：解：（1）450350150950++=（人）950(1601614)95⨯---=％％％（人）答：参加综合实践活动的有950人，参加科技活动的有95人．（2）95030000105003⨯⨯⨯％95201900=⨯=（人）答：参加科技活动的学生估计有1900人．第14题. （2007内蒙呼和浩特课改，8分）某中学初二年级开设了排球、篮球、足球三项体育兴趣课，要求每位学生必须参加，且只能参加其中一种球类运动；下图是该年级四班学生参加排球、篮球、足球三项运动的人数频数分布直方图和扇形分布图．（1）求四班有多少名学生；（2）请你在下图中补上频数分布直方图的空缺部分；（3）在扇形统计图中，求表示篮球人数的扇形的圆心角度数；年级参加综合实践活动人数统计图文体活动社会调查社区服务科技活动参加综合实践活动人数分布统计图（4）若初二年级有500人，按照四班参加三种球类的规律性，请你估计初二年级参加排球的人数？答案：解：（1）40名学生（2）见下图（3）圆心角度数30360108100=⨯=°° （4）估计初二年级参加排球的人数50020100=⨯=%（人）请你用学过的统计知识解决下面的问题：（1）小辰家的轿车每月（按30天计算）要行驶多少千米？（2）若每行驶100千米需汽油8升，汽油每升4.74元，请你算出小辰家一年（按12个月计算）的汽油费用大约是多少元（精确到百元）．答案：解：（1）36292740437233407++++++=∵，40301200⨯=∴．即小辰家的轿车每月要行驶1200千米．（2）4.7481200121005460.485500⨯⨯⨯÷=≈．即小辰家一年的汽油费用大约是5500元．第16题. （2007山东泰安非课改，6分）某中学为了解毕业年级800名学生每学期参加社会实践活动的时间，足球 20 12 球类排球篮球足球 20128 球类排球篮球（1）补全右面的频率分布表；（2）请你估算这所学校该年级的学生中，每学期参加社会实践活动的时间大于7天的约有多少人？答案：解：（1）21，0，35；15，0，25（2）4280056060⨯=第17题. （2007山东潍坊课改，8分）2006年潍坊市学业水平考试数学学科的考试成绩以等级公布．以县（市）为单位将所有考生成绩按由高到低分为A B C D E ，，，，五个等级，五个等级所占比例依次为15％，20％，30％，20％，15％．小明所在学习小组随机抽查本学校2006年毕业学生，了解参加学业水平考试的考生数学成绩（等级）情况，统计如下表：（1）根据小明所在学习小组抽查到的学生数学成绩五个等级人数的分布情况，绘制扇形统计图；（2）根据小明所在学习小组的调查，估计2006年全校1320名参加数学考试的学生中，数学成绩（等级）为A B ，等的考生各有多少人？（3）根据抽查结果，请你对小明所在学校参加2006年学业水平考试的数学成绩在全县（市）内的情况发表自己的看法．答案：（1）如右图（2）A 等人数为20%1320264⨯=（人）B 等人数为25%1320330⨯=（人）（3）A 等、B 等人数都比全市A 等、B 等平均人数多，C 等人数与全市C 等平均人数持平，D 等、E 等人数都比全市D 等、E 等平均人数少．第18题. （2007山西课改，10分）母亲节过后，某校在本校学生中做了一次抽样调查，并把调查结果分为三种类型：Ａ．不知道哪一天是母亲节的；Ｂ．知道但没有任何行动的；Ｃ．知道并问候母亲的．下图是根据调查结果绘制的统计图（部分）．根据下图提供的信息回答问题：（1）已知Ａ类学生占被调查学生人数的30%，则被调查学生有多少人？（2）计算Ｂ类学生的人数并根据计算结果补全统计图；（3答案：解：（1）6030%200÷=（人）．（2）2006030110--=（人）．统计图如右图．（3）302000300200⨯=（人）． 10分第19题. （2007山西太原课改，8分）某地区教育部门要了解初中学生阅读课外书籍的情况，随机调查了本地区500名初中学生一学期阅读课外书的本数，并绘制了如图的统计图．请根据统计图反映的信息回答问题．（1）这些课外书籍中，哪类书的阅读量最大？（2）这500名学生一学期平均每人阅读课外书多少本？（精确到1本）（3）若该地区共有2万名初中学生，请估计他们一学期阅读课外书的总本数．类型30 60 90120 类型术类种类阅读数量（百本）技类记类说类他类漫类答案：解：（1）这些类型的课外书籍中，小说类课外书阅读数量最大．（2）(2.0 3.5 6.48.4 2.4 5.5)100500 5.646+++++⨯÷=≈（本）．答：这500名学生一学期平均每人阅读课外书6本．（3）200006120000⨯=（本）或2612⨯=（万本）答：他们一学期阅读课外书的总数是12万本．第20题. （2007江苏盐城课改，9分）为了解中学生的视力情况，某市有关部门采用抽样调查的方法，从全市10万名中学生中抽查了部分学生的视力，分成以下四类进行统计：Ａ．视力在4.2及以下Ｂ．视力在4.3～4.5之间Ｃ．视力在4.6～4.9之间Ｄ．视力在5.0及以上图一、二是根据调查结果绘制的两幅不完整的统计图，请根据统计图提供的信息，解答下列问题：（1）这次抽查中，一共抽查了名学生；（2）“类型Ｄ”在扇形图中所占的圆心角是度；（3）在统计图一中将“类型Ｂ”的部分补充完整；（4）视力在5.0以下（不含5.0）均为不良，试估计全市视力不良的中学生人数．答案：（1）200 （2）162（3）补全图一（图略，D 数字不标不扣分）（4）解：10(51040) 5.5⨯++=%%%∴估计全市视力不良的中学生有5.5万人．第21题. (2007湖北潜江课改，6分)今年4月，国民体质监测中心等机构开展了青少年形体测评.专家组随机抽查了某市若干名初中学生坐姿、站姿、走姿的好坏情况.我们对专家的测评数据作了适当处理(如果一个学生有一种以上不良姿势，我们以他最突出的一种作记载)，并将统计结果绘制了如下两幅不完整的统计图，请你根据图中所给信息解答下列问题：（1）请将两幅统计图补充完整；（2）在这次形体测评中，一共抽查了名学生，如果全市有10万名初中生，那么全市初中生中，三姿良好的学生约有人；（3）根据统计结果，请你简单谈谈自己的看法.视力类型图二答案：解：（1条形统计图，如图所示（2）500，12000（3要点：进身心健康发育.第22题. （2007湖北孝感课改，10分）某中学为了培养学生的社会实践能力，今年“五一”长假期间要求学生参加一项社会调查活动.为此,小明在他所居住小区的600个家庭中，随机调查了50个家庭在新工资制度实施后的收入情况，并绘制了如下的频数分布表和频数分布直方图（收入取整数，单位：元）.请你根据以上提供的信息，解答下列问题: （1）补全频数分布表和频数分布直方图；（2）这50个家庭收入的中位数落在小组；（3）请你估算该小区600个家庭中收入较低（不足1400元）的家庭个数大约有多少？答案：解：（1）10 , 0.100 ;评分说明：补全直方图2分（频数为10）.（2）第三小组 1400～1600 （3）(0.060＋0.240)×600=180 .第23题. (2007广东课改，4分)池塘中放养了鲤鱼8000条，鲢鱼若干．在几次随机捕捞中，共抓到鲤鱼320条，鲢鱼400条．估计池塘中原来放养了鲢鱼______条．答案：10 00025 50 75 100125150175200坐姿不良站姿不良走姿不良三姿良好类别第24题. (2007黑龙江非课改，6分)为了解“宏亮”中学初四男生身高情况，抽测了该校初四20名男生身高，结果如下（单位：厘米）：165 172 183 179 174 175 181 170 175 171176 175 169 188 179 172 177 176 182 173（1）在这个问题中，样本的容量是；（2）填写表中未完成的部分；（3）如果该校初四男生共有400人，那么该校初四男生身高不低于175厘米的约有多少人？答案：解：（1）20；（2）在表中所填数据由左至右，由上至下依次为6，0.30，1，0.05；⨯++=（人），（3）400(0.40.150.05)240于是可以估计，该校初四男生身高不低于175厘米的约有240人．第25题. (2007青海课改，2分)为了发展农业经济，致富奔小康，李伯伯家2006年养了4000条鲤鱼，现在那么，估计鱼塘中鲤鱼的总质量为千克．答案：6800。

备战2007中考《圆》的试题集锦与单元测试-19.doc

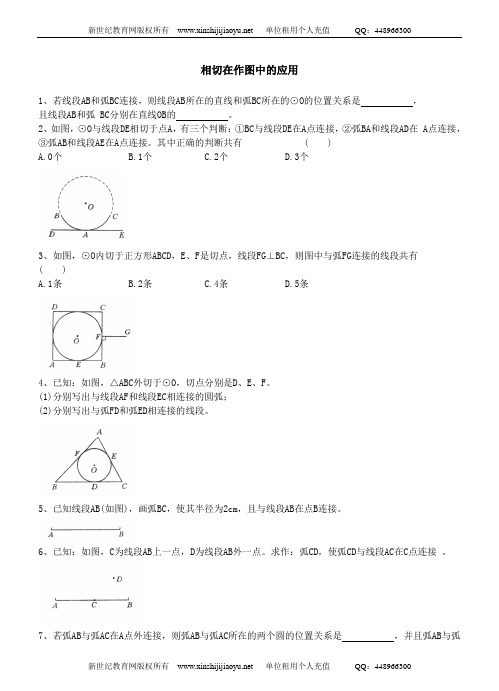
相切在作图中的应用1、若线段AB和弧BC连接，则线段AB所在的直线和弧BC所在的⊙O的位置关系是，且线段AB和弧 BC分别在直线OB的。

2、如图，⊙O与线段DE相切于点A，有三个判断：①BC与线段DE在A点连接，②弧BA和线段AD在 A点连接，③弧AB和线段AE在A点连接。

其中正确的判断共有 ( )A.0个B.1个C.2个D.3个3、如图，⊙O内切于正方形ABCD，E、F是切点，线段FG⊥BC，则图中与弧FG连接的线段共有( )A.1条B.2条C.4条D.5条4、已知：如图，△ABC外切于⊙O，切点分别是D、E、F。

(1)分别写出与线段AF和线段EC相连接的圆弧；(2)分别写出与弧FD和弧ED相连接的线段。

5、已知线段AB(如图)，画弧BC，使其半径为2cm，且与线段AB在点B连接。

6、已知：如图，C为线段AB上一点，D为线段AB外一点。

求作：弧CD，使弧CD与线段AC在C点连接。

7、若弧AB与弧AC在A点外连接，则弧AB与弧AC所在的两个圆的位置关系是，并且弧AB与弧AC分别在连心线的。

8、若弧AB与弧AC在A点内连接，则弧AB与弧AC所在的两个圆的位置关系是，并且弧AB与弧AC分别在连心线的。

9、如图，⊙O1与⊙O2外切，⊙O1与⊙O3内切，切点均为P，有四个判断：①弧AP与弧PB在P点外连接，②弧PE与弧FP在点P内连接，③弧PE与弧PB在点P内连接，④弧PC与弧PD在点P外连接。

其中正确的判断共有 ( )A.1个B.2个C.3个D.4个10、如图，已知P是线段AB上一点，分别以A、B为圆心作弧PC和弧PD，使弧PC和弧PD在点P外连接。

11、已知：如图，A、B是⊙O上两点，C为⊙O内一点。

求作：弧AC，使弧AC与弧AB在点A内连接。

参考答案1、相切，两侧2、B3、B4、(1)与线段AF相连接的弧有FD，与线段EC相连接的圆弧有EF；(2)与FD连接的线段有FA、DC，与ED连接的线段有DB、EA。

备战2007中考《圆》的试题集锦与单元测试-13.doc

圆的基本性质1、点P 在圆内，经过P 的任何一条弦都把这个圆分成两个全等形，那么这个点是。

2、Rt △AOC 中，∠C=90°，AC=4，OC=3，E 为AO 中点，以O 为圆心，OC 为半径作圆，试判断：点E 和⊙O 的位置关系是。

3、在Rt △ABC 中，∠C=90°，BC=1，AC=3，(1)以B 为圆心，3为半径作圆时，A 与圆的位置关系怎样?(2)以AB 为直径作⊙O ，它与A 、B 、C 点的位置关系怎样?4、圆是到的距离等于的点的集合，定点就是，定长是。

5、⊙O 的半径r=5cm ，圆心O 到直线l 的距离OD=3cm ，点P 、M 、N 在直线l 上，若32 PD ，MD=4cm ，ND=5cm ，则点P 在⊙O ，点M 在⊙O ，点N 在⊙O 。

6、⊙O 的半径为4cm ，若线段OA 的长为12cm ，则OA 的中点P 在⊙O________；若OA=8cm ，则OA 的中点P 在⊙O________；若OA=5cm ，则OA 的中点P 在⊙O________。

7、先画图，再证明：(1)画△ABC ，使∠C=90°，∠A=60°，AB=5cm 。

(2)以C 为圆心，2.5cm 为半径画⊙C 。

(3)取AB 的中点为D ，证明：点B 在⊙C 外，点D 、A 都在⊙C 上，(写出已知、求证、证明)。

8、正方形ABCD 的边长为4cm ，对角线AC 、BD 相交于点O ，以O 为圆心，分别以2cm 、4cm 、22cm 为半径作三个圆。

问：正方形的顶点与这三个圆的位置关系怎样?9、(1)直径是圆的最大弦，圆的最大弦是直径。

( ) (2)由弦及弧组成的图形叫弓形。

( )(3)半圆是弧。

( ) (4)圆心相同的圆叫同心圆。

( )(5)半径相等的圆是等圆。

( ) (6)长度相等的弧是等弧。

( )10、以已知点O 为圆心作圆，半径不相等，可画________个圆，它们是________圆。

2007年中考“圆”试题选编(选择题)

2007年中考“圆”试题选编(选择题)（2007年无锡市）圆锥的底面半径为2，母线长为4，则它的侧面积为（）Ａ．8π Ｂ．16πＣ．Ｄ．4π（2007年泸州）已知⊙1O 的半径为2cm ，⊙2O 的半径为4cm ，圆心距21O O 为3cm ，则⊙1O 与⊙2O 0的位置关系是（）A ．外离B ．外切 c ．相交 D ．内切（2007年泸州）已知圆锥的母线长为5cm ，底面半径为3 cm ，则它的全面积为（）A ．301rcm 。

B ．24'from 。

C ．15,rrcm 。

D ．9'rrem2（2007年陕西课改）如图，圆与圆之间不同的位置关系有（）A ．2种B ．3种C ．4种D ．5种（2007年盐城市）如图，A B C ，，为O 上三点，60ABC ∠=°，则AO C ∠的度数为（）Ａ．30° Ｂ．60° Ｃ．100° Ｄ．120°（2007年浙江宁波市）已知两圆的半径分别为3和5，圆心距为4，则这两圆的位置关系是( )(A)内切 (B)外切 (C)相交 (D)相离（2007年苏州）如图，MN 为⊙O 的弦，∠M=50°，则∠MON 等于（）A ．50°B ．55°C ．65°D ．80°（2007年济宁）已知圆锥的底面半径为1cm ，母线长为3cm ，则其全面积为（）。

A 、πB 、3πC 、4πD 、7π（2007年温州市）已知两圆半径分别为3和5，圆心距为8，则这两圆的位置关系是（）A.内切B.外切C.相交D.相离（2007年温州市）如图，已知ACB ∠是O 的圆周角，50ACB ∠=︒，则圆心角AOB ∠是（）A ．40︒ B. 50︒ C. 80︒ D. 100︒A( 2007年诸暨)已知圆锥的底面半径为9㎝，母线长为30㎝，则圆锥的侧面积为（）A 、270π2cmB 、360π2cmC 、450π2cmD 、540π2cm（2007年威海）已知圆锥的底面半径为6，高为8，则它的侧面积是（）A ．30πB ．48πC ．60πD ．96π（2007年金华市）如图，点A 、B 、C 都在⊙O 上，若∠C=34°，则∠AOB 的度数为（）DA 、34°B 、56°C 、60°D 、68°（2007年怀化市）圆的半径为13cm ，两弦AB CD ∥，24cm AB =，10cm CD =，则两弦AB CD ，的距离是（）Ａ．7cm Ｂ．17cm Ｃ．12cm Ｄ．7cm 或17cm（2007年武汉）如图，把自行车的两个车轮看成同一平面内的两个圆，则它们的位置关系是（）。

2007年全国100多个地区中考数学试题分类汇编格点

2007年中考数学试题分类-格点问题（2007年滨州）如图3所示，每个小方格都是边长为1的正方形，点A B ，是方格纸的两个格点（即正方形的顶点），在这个66 的方格纸中，找出格点C ，使ABC △的面积为1个平方单位的直角三角形的个数是．（2007年某某某某）如图所示，在4×4的菱形斜网格图中（每一个小菱形的边长为1，有一个角是60°），菱形ABCD 的边长为2，E 是AD 的中点，按CE 将菱形ABCD 剪成①、②两部分，用这两部分可以分别拼成直角三角形，要求所拼成图形的顶点均落在格点上．（1）在下面的菱形斜网格中画出示意图；（2）判断所拼成的三种图形的面积（s ）、周长（l ）的大小关系（用“=”、“＞”或“＜”（直角三角形）（等腰梯形）（矩形）图3AB连接）：面积关系是；周长关系是．（2007年眉山市）在如图所示的56⨯方格中（每个方格的边长为1）画一圆，要求所画的圆经过四个格点，并求出你画的圆的半径．（2007年某某课改）如图，横、纵相邻格点间的距离均为1个单位．（1）在格点中画出图形ABCD 先向右平移6个单位，再向上平移2个单位后的图形；（2）请写出平移前后两图形应对点之间的距离．（2007年某某市）如图，在22⨯的正方形格纸中，有一个以格点为顶点的ABC △，请你找出格纸中所有与ABC △成轴对称且也以格点为顶点的三角形，这样的三角形共有个．（2007年某某市）正方形网格中，AOB ∠如图放置，则cos AOB ∠的值为（）（第20题图） ABC AＡ．55Ｂ．55Ｃ．12Ｄ．2（2007年清流县）如图，在4×4的正方形方格中，△ABC 和△DEF 的顶点都在边长为1的正方形的顶点上．(1)填空：∠ABC ＝_______°；BC ＝________； (2)判断△ABC 与△DEF 是否相似，并说明理由．FEDCBA( 2007年某某)如图是5×5的正方形网络，以点D 、E 为两个顶点作位置不同的格点三角形，使所作的格点三角形与△ABC 全等，这样的格点三角形最多可以画出（） A 、2个 B 、4个 C 、6个 D 、8个EDCBABO( 2007年某某)如图，在5×5的正方形网格中，每个小正方形的边长都为1，请在所给网格中按下列要求画出图形。

2007年中考数学分类讨论题型整编华东师大版

2007年中考数学分类讨论题型整编【知识整合创新】整体感悟：分类讨论问题是创新性问题之一，此类题综合性强，难题较大，在各地中考试题中多以压轴题出现，对考生的能力要求较高，具有选拔性。

目前，中考试卷中，觉见的需分类讨论的知识点有三大类：1．代数类：代数有绝对值、方程及根的定义，函数的定义以及点（坐标未给定）所在象限等.2．几何类：几何有各种图形的位置关系，未明确对应关系的全等或相似的可能对应情况等.3．综合类：代数与几何类分类情况的综合运用.特例探究：以性质、公式、定理的使用条件为标准分类的题型.中考高分解密：题型1.考查数学概念及定义的分类规律提示:熟练掌握数学中的概念及定义，其中以绝对值、方程及根的定义，函数的定义尤为重要，必须明确讨论对象及原因，进而确定其存在的条件和标准。

考题1．求函数251()(3)22y k x k x =-+-+的图象与x 轴的交点？名师点拔：二次项系数中含有参数k ，此函数可能是二次函数，也可能是一次函数，故应对52k -分类讨论.解：（1）当502k -=时，即52k =时，此函数为1122y x =-+，故其与x 轴只有一个交点（1，0）（2）当55022k k -≠≠，即时，此函数为二次函数，2251(3)4()(2)22k k k ∆=--⨯-⨯=-.①当2k =时，Δ＝0.抛物线与x 轴的交点只有一个.212110,122x x x x -+===，交点坐标为（1，0）②当2k ≠时，Δ＞0，函数与x 轴有两个不同的交点.1(1,0)(,0)52k-和. 综合所述：当52k =或2k =时，函数图像与x 轴只有一个交点（1，0）；当52k ≠且2k ≠时，函数图像与x 轴有两个不同交点1(1,0),(,0)52k -. 变式思考1已知关于x 的方程22(4)(4)0kx k x k +++-=（1）若方程有实数根，求k 的取值X 围（2）若等腰三角形ABC 的边长a=3，另两边b 和c 恰好是这个方程的两个根，求ΔABC 的周长. 易误点睛：根据方程定义确定方程到底是一次方程还是二次方程，同时应注意的是第（2）问中并无说明哪两边是ΔABC 的腰，故应考虑其所有可能情况.题型2：考查字母的取值情况或X 围的分类.规律提示：此类问题通常在函数中体现颇多，考查自变量的取值X 围的分类，解题中应十分注意性质、定理的使用条件及X 围.考题2．（2004，某某）如图（1）边长为2的正方形ABCD 中，顶点A 的坐标是（0，2）一次函数y x t =+的图像l 随t 的不同取值变化时，位于l 的右下方由l 和正方形的边围成的图形面积为S （阴影部分）.（1）当t 取何值时，S ＝3？（2）在平面直角坐标系下（图2），画出S 与t 的函数图像.名师点拔：设l 与正方形ABCD 的交点为M ，N ，易知ΔDMN 是等腰Rt Δ，只有当MD ＝2时，1MDN S ∆=，那么3ABCD MDN S S S =-=，此时求得42t =-，第（2）问中，随着t 的变化，S 的表达式发生变化，因而须分类讨论t 在不同取值时S 的表达式，进而作出图像.解：（1）设l 与正方形ABCD 的交点为M ，N ，∵l 的解析式y x t =+，在x 轴，y 轴上所截线段相等.∴ΔDMN 为等腰Rt ΔDMN∵S ＝3，∴2231DMN ABCD S S S ∆=-=⨯-=又∵21122DMN S MD ND ND ∆=⋅= ∴MD ＝ND ＝2，∴ON ＝OD －DM ＝4－2，即D 点的坐标为（0，4－2）∴42t =-，即当42t =-时，S ＝3.（2）∵直线l 与y 轴的交点M 的坐标为(0,)t∴当0≤t ＜2时，21122S B B t =M ⋅N = 当2≤t ＜4时，21(4)42ABCD DMN S S S t ∆=-=--+ 当t ≥4时，S ＝4根据以上解析式，作图如下图（图2）变式思考2 （2004 资阳）如图所示，在平行四边形ABCD 中，4AD cm =，∠A ＝60°，BD ⊥AD ，一动点P 从A 出发，以每秒1cm 的速度沿A B C →→的路线匀速运动，过点P 作直线PM ，使PM ⊥AD.（1）当点P 运动2秒时，设直线PM 与AD 相交于点E ，求△APE的面积；（2）当点P 运动2秒时，另一动点Q 也从A 出发沿A B C→→的路线运动，且在AB 上以每秒1cm 的速度匀速运动，在BC 上以每秒2cm 的速度匀速运动.过Q 作直线QN ，使QN//PM.设点Q 运动的时间为t 秒（0≤t ≤10），直线PM 与QN 截平行四边形ABCD 所得图形的面积为Scm 2.①求S 关于t 的函数关系式；②（附加题）求S 的最大值.易误点睛：讨论变量t 的取值X 围，是解本题的关键，解此类题应十分注意变量的取值须符合题意，逐层分析.题型3．考查图形的位置关系或形状的分类.规律提示：熟知直角三角形的直角，等腰三角形的腰与角以及圆的对称性，根据图形的特殊性质，找准讨论对象，逐一解决.考题3．（2004 某某）在ΔABC 中，∠BAC ＝90°，AB ＝AC ＝22，圆A 的半径为1，如图所示，若点O 在BC 边上运动，（与点B 和C 不重合），设BO ＝x ，ΔAOC 的面积为y .（1）求y 关于x 的函数解析式，并写出函数的定义域.（2）以点O 为圆心，BO 长为半径作圆O ，求当圆O与圆A 相切时ΔAOC 的面积.图（2）名师点拔：（1）过点A 作AD ⊥BC 于D 点 ∵AB ＝AC ＝22∴AD ＝AB sin 45⋅︒=2445AB BC Sin ==︒∴OC=BC －BO=4－x ，故ΔAOC 的面积y 与x 的函数解析式为12y OC AD =⋅即1(4)242y x x =-⨯=- （2）由于圆与圆相切有两种情况：外切和内切，故解题中须分类讨论.解：（1）过点A 作AD ⊥BC 于点D.∵∠BAC=90° AB=AC=22∴BC=4 AD ＝12BC ＝2 ∴112(4)422AOC S OC AD x x ∆=⋅=⨯⨯-=- 即4(04)y x x =-+<<（2）当点O 与点D 重合时，圆O 与圆A 相交，不合题意；当点O 与点D 不重合时，在Rt ΔAOD 中，222224248AO AD OD x x x =+=+-=-+∵⊙A 的半径为1，⊙O 的半径为x∴①当⊙A 与⊙O 外切时 22(1)48x x x +=-+ 解得76x =此时，ΔAOC 的面积717466y =-= ②当⊙A 与⊙O 内切时，22(1)48x x x +=-+ 解得72x =此时ΔAOC 的面积71422y =-= ∴当⊙A 与⊙O 相切时，ΔAOC 的面积为17162或. 变式思考3（2003 某某）如图，直线443y x =-+与x 轴，y 轴分别交于点M ，N （1）求M ，N 两点的坐标；（2）如果点P 在坐标轴上，以点P 为圆心，125为半径的圆与直线443y x =-+相切，求点P 的坐标. 易误点睛：本题是一道函数与圆的综合题，注意第（2）小问涉及到分类讨论，与直线相切时的情况，本题可分为两大类，四小类，切勿漏掉，解决此类问题关键是把握标准，正确的分类.题型4.考查图形的对应关系可能情况的分类规律提示：图形的对应关系多涉及到三角形的全等或相似问题，对其中可能出现的有关角、边的可能对应情况加以分类讨论. 考题4（2004 某某）如图所示，抛物线2()y x m =--的顶点为A ，直线:33l y x m =-与y 轴的交点为B ，其中m ＞0.（1）写出抛物线对称轴及顶点A 的坐标（用含有m 的代数式表示）（2）证明点A 在直线l 上，并求∠OAB 的度数.（3）动点Q 在抛物线的对称轴上，则抛物线上是否存在点P ，使以P 、Q 、A 为顶点的三角形与△OAB 全等？若存在，求出m 的值，并写出所有符合上述条件的P 点坐标；若不存在，说明理由.名师点拨：（1）对称轴x m =，顶点A （m,0）（2）把x ＝m 代入33y x m =-得330y m m =-=∴点A （m,0）在直线l 上，直线l 与y 轴相交，则B 点的横坐标为：3y m =-；B 点坐标为(0,3)m -，由三角函数知识可得：3tan 3OB m OAB OA m∠=== 即∠OAB ＝60° （3）因为全等的对应关系，因而需进行分类论，找准对应关系，从而解决问题。

2007中考真题分类汇编_弧、圆心角、圆周角、圆内接四边形的性质[1]

、圆心角、圆周角、第1题. ()如图，AB 是O 的直径，20C ∠=，则BOC ∠的度数是（）A ．40B ．30C ．20D ．10第2题. （2007福建龙岩课改，3分）如图，已知点A B C ，，在O 上，若40ACB ∠=°，则AOB ∠= 度．第3题. （2007福建泉州课改，4分）如图，A B C ，，三点都在O 上，若80BOC ∠=，则A ∠的度数等于（） A ．20B ．40C ．60D ．80第6题. （2007甘肃白银3市非课改，3分）如图，四边形ABCD 内接于⊙O ，若∠BOD ＝140°，则∠BCD ＝ ( ) A ．140° B ．110° C ．70° D ．20°第7题. (2007广东韶关课改，3分)如图，AD 是⊙O 的直径，AB ∥CD ，60AOC ︒∠=，则BAD ∠= 度.第8题. （2007广东河池非课改，2分）如图，BD 是⊙O 的直径，∠A = 30°，则∠CBD = ．第9题. （2007广西玉林课改，3分）如图，在锐角ABC △中，AB AC >，AD BC ⊥于D ，以AD 为直径的O 分别交AB ，AC 于E F ，，连结DE DF ，．（1）求证：180EAF EDF ∠+∠=；B AA图2O CDBA第10题. （2007贵州贵阳课改，3分）如图，A B C ，，是O 上三点，40ACB =∠，则ABO ∠等于度．第11题. （2007山西太原课改，3分）如图，CD 是O 的直径，A B ，是O 上的两点，若20ABD ∠=，则ADC ∠的度数为（） A ．40B ．50C ．60D ．70第12题. (2007浙江嘉兴课改,5分)如图，AB 是O 的直径，C D ，是圆上的两点（不与A B ，重合），已知52tan 4BC ADC =∠=，，则AB = ．第13题. （2007山东滨州课改，3分）如图，AB 是O 的直径，C 是O 上的一点，若8AC =，10AB =，OD BC ⊥于点D ，则BD 的长为（）A ．3cm 2B ．3cmC ．5cmD ．6cm第14题. （2007江西南昌课改，3分）如图，AB 是O 的直径，点C D ，是圆上两点，100AOC ∠=，则D ∠= 度．第15题. （2007内蒙赤峰课改，4分）如图，点A B C ，，是O 上的三点，若50BOC ∠= ，则A ∠的度数为．第16题. (2007内蒙鄂尔多斯课改，9分)如图，在ABC △中，90ACB =∠，D 是AB 的中点，以DC 为直径的O 交ABC △的边于G F E ，，点．求证：（1）F 是BC 的中点；（2）A GEF =∠∠．三角形，AC BC =，D 为O 中 AB 上一点，延长DA 至点E ，使CE CD =．CDDACA BCDEFG O（1）求证：AE BD =；（2）若AC BC ⊥，求证：AD BD +=．第20题. （2007山东聊城课改，4分）如图，ABC △内接于O ，30C ∠= ，2AB =，则O 的半径为（） AB ．2C．D ．4第21题. (2007山东威海课改，3分)如图，AB 是O 的直径，点C D E ，，都在O 上，若C D E ==∠∠∠，则A B +=∠∠º．第25题. （2007天津非课改，3分）已知，如图 BC 与 AD的度数之差为20，弦AB 与CD 交于点E ，60CEB ∠= ，则CAB ∠等于（）A ．50B ．45C ．40D ．35第27题. （2007浙江金华课改，4分）如图，点A B C ，，都在O 上，若34C =∠，则AOB ∠的度数为（）A ．34B ．56C ．60D ．68第31题. （2007江苏盐城课改，3分）如图，A B C ，，为O 上三点，60ABC ∠=°，则AOC ∠的度数为（）Ａ．30° Ｂ．60° Ｃ．100°Ｄ．120°A BA B DEC。

2007年中考“圆”试题选编(填空题)

2007年中考“圆”试题选编(填空题)（2007年十堰）已知Rt △ABC 的两直角边的长分别为6cm 和8cm ，则它的外接圆的半径为_____________cm 。

（2007年南昌市）相交两圆的半径分别为5和3，请你写出一个符合条件的圆心距为．（2007年旅顺口区）如图，AB C ，，是⊙O 上的三点，2AB =，30ACB ∠=，那么⊙O 的半径等于．CA O（2007年常州市）已知扇形的半径为2cm ，面积是24cm 3π，则扇形的弧长是 cm ，扇形的圆心角为 °．（2007年遵义市）如图所示，C 是O 上一点，O 是圆心，若80AOB =∠，则A B +=∠∠ ．（2007年深圳市）直角三角形斜边长是6，以斜边的中点为圆心，斜边上的中线为半径的圆的面积是．（2007年株洲市）已知△ABC 的三条边长分别为6cm ，8cm ，10cm ，则这个三角形的外接圆的面积为__________cm 2．（结果用含π的代数式表示）（2007年贵阳市）如图2，A B C ，，是O 上三点，40ACB =∠，则ABO ∠等于______度．（2007年无锡市）如图，AB 是O 的弦，OC AB ⊥于C ，若AB =，1cm OC =，则O 的半径长为cm ．（2007年淮安市）如图，在⊙O 中，弦AB 、CD 相交于点E ，∠BDC ＝45°，∠BED ＝95°，则∠C 的度数为______。

（2007年苏州）如图，已知扇形的半径为3cm ，圆心角为120°，则扇形的面积为__________cm 2（结果保留π）（2007年株洲市）已知△ABC 的三边长分别为6cm 、8cm 、10cm ，则这个三角形的外接圆的面积为__________cm 2.（结果用含π的代数式表示）（2007年安顺市）如图3，O 的直径为26cm ，弦AB 长为24cm ，则点O 到AB 的距离OPC第10题(第16题图)为．（2007年福州）已知一个圆锥体的底面半径为2，母线长为4，则它的侧面展开图面积是____________。

甘肃省天水市2007-2012年中考数学试题分类汇编专题9 圆

第 19 题Ⅰ图
16、【2010,19，Ⅰ】如图，要把残缺的圆片修复完整，请你 3/6
甘肃省天水市 2007-2012 年中考数学试题分类汇编
专题 9 圆
刘永智
在图上用尺规作图法来完成．（只保留作图痕迹，不写作法） 17、【2011,03】如果两圆的半径分别为 2 和 1，圆心距为 3，那么能反映这两圆位置关系的图是（）
甘肃省天水市 2007-2012 年中考数学试题分类汇编
专题 9 圆
刘永智Biblioteka BE=CE．在直角△OBD 中利用勾股定理即可求得 BD 的长，再在直角△BED 中，利用勾股定理求得 BE 的长；在直角△ABE 中求得 AB 的长，据此即可求得四边形的周长．解答：解：（1）连接 OB． ∵BQ 与⊙O 相切， ∴∠OBQ=90° ∴OB= 故半径是：；（2）∵AB=AC，O 是△ABC 的内心． ∴ = ， = ∴AB=AC，BE=CE ∴BC⊥AE ∵OE=OB= ， ∴OD=OE﹣DE= ﹣ = ∴在直角△ODB 中，BD2=OB2﹣OD2=（）2﹣（）2= 在直角△BDE 中，BE= ∴CE=BE= ∵AE 是直径． ∴∠ABE=90° ∴在直角△ABE 中，AE=2OB=2× =3， AB= ∴AC=AB= ． + + + = ． = = ． = = = = = ．
4、【2007,28】（9 分）如图，在 Rt△ABC 中， C 90o ． BE 平分 ABC 交 AC 于点 E ，点 D 在 AB 上， DE EB 于点 E ．（1）求证： AC 是 △DBE 外接圆的切线；（2）若 AD 6 ， AE 6 2 ，求 BC 的长． 5、【2007,31】（12 分）以边长为 a 的正方形 ABCD 的对角线 AC 长为半径，以点 A 为圆心作弧交 AB 边的延长线于点 E ，交 AD 边的延长线于点 F ，得扇形

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2007年中考数学试题分类汇编（圆含答案）一、选择题 1、（2007山东淄博）一个圆锥的高为33，侧面展开图是半圆，则圆锥的侧面积是（）B （A）9 （B）18 （C）27 （D）39 2、（2007四川内江）如图（5），这是中央电视台“曲苑杂谈”中的一副图案，它是一扇形图形，其中AOB为120，OC长为8cm，CA长为12cm，则阴影部分的面积为（） A．264πcm B．2112πcm C．2144πcm D．2152πcm

解：S＝212020360－21208360＝2112πcm 选（B）。 3、（2007山东临沂）如图，在△ABC中，AB＝2，AC＝1，以AB为直径的圆与AC相切，与边BC交于点D，则AD的长为（）。A

A、552 B、554 C、352 D、354 4、（2007浙江温州）如图，已知ACB是O的圆周角，50ACB，则圆心角AOB是（）D A．40 B. 50 C. 80 D. 100 5、（2007重庆市）已知⊙O1的半径r为3cm，⊙O2的半径R为4cm，两圆的圆心距O1O2为1cm，则这两圆的位置关系是（）C （A）相交（B）内含（C）内切（D）外切 6、（2007山东青岛）⊙O的半径是6，点O到直线a的距离为5，则直线a与⊙O的位置关系为（）．C A．相离 B．相切 C．相交 D．内含

7、（2007浙江金华）如图，点ABC，，都在O上，若34C∠，则AOB∠的度数为（）D A．34 B．56 C．60 D．68 8、（2007山东济宁）已知圆锥的底面半径为1cm，母线长为3cm，则其全面积为（）。C A、π B、3π C、4π D、7π 9、（2007山东济宁）如图所示，小华从一个圆形场地的A点出发，沿着与半径OA夹角为α的方向行走，走到场地边缘B后，再沿着与半径OB夹角为α的方向折向行走。按照这种方式，小华第五次走到场地边缘时处于弧AB上，此时∠AOE＝56°，则α的度数是（）。A A、52° B、60° C、72° D、76°

A C O

图（5）

O C B A 10、（2007福建福州）如图2，O中，弦AB的长为6cm，圆心O到AB的距离为4cm，则O的半径长为（） A．3cm B．4cm C．5cm D．6cm C

11、（2007双柏县）如图，已知PA是⊙O的切线，A为切点，PC与⊙O相交于B、C两点，PB＝2 cm，BC＝8 cm，则PA的长等于（） A．4 cm B．16 cm C．20 cm D．25cm D 12、（2007浙江义乌）如图，已知圆心角∠BOC=100°、则圆周角∠BAC的大小是（） A．50° B．100° C．130° D．200° A

13、（2007四川成都）如图，O内切于ABC△，切点分别为DEF，，．已知50B°，60C°，连结OEOFDEDF，，，，那么EDF等于（）Ａ．40° Ｂ．55° Ｃ．65° Ｄ．70° B 二、填空题 1、（2007山东淄博）如图1，已知：△ABC是⊙O的内接三角形，

AD⊥BC于D点，且AC=5，DC=3，AB=24，则⊙O的直径等于。 52 2、（2007重庆市）已知，如图：AB为⊙O的直径，AB＝AC，BC交⊙O于点D，AC交⊙O于点E，∠BAC＝450。给出以下五个结论：①∠EBC＝22.50，；②BD＝DC；③AE

＝2EC；④劣弧AE是劣弧DE的2倍；⑤AE＝BC。其中正确结论的序号是。①②④；

3、（2007浙江金华）如图所示为一弯形管道，其中心线是一段圆弧AB．已知半径60cmOA，108AOB∠，则管道的长度（即AB的长）为 cm．（结

果保留） 36π 4、（2007山东济宁）如图，从P点引⊙O的两切线PA、PA、PB，A、B为切点，已知⊙O的半径为2，∠P＝60°，则图中阴影部分的面积为。

A B 60cm 108

O B A 图2 A ·O P C B

B A C D

图1

D O A F

C B

E CPAO

43－43 5、（2007山东枣庄）如图，△ABC内接于⊙O，∠BAC=120°， AB=AC，BD为 ⊙O的直径，AD=6，则BC＝。

6、（2007双柏县）如图6，⊙O是等边三角形ABC的外接圆，

点D是⊙O上一点，则∠BDC = ． 60° 7、（2007福建晋江）如图，点P是半径为5的⊙O内的一点，且OP＝3，设AB是过点P的⊙O内的弦，且AB⊥OP，则弦AB长是________。 8 8、（2007四川成都）如图，已知AB是O的直径，弦CDAB，

22AC，1BC，那么sinABD的值是

． 223 三、解答题 1、（2007浙江温州）如图，点P在O的直径BA的延长线上，AB＝2PA，PC切O于点C，连结BC。（1）求P的正弦值；

（2）若O的半径r＝2cm，求BC的长度。

解：（1）连结OC，因为PC切O于点C，PCOC 1AB2PA,30,21sin.2OCAOAPPOPP又直径＝

（或：在1,sin22OCOCRtPOCPPOPO） (2)连结AC，由AB是直90,903060,ACBCOA

42,2,4223OCOACAOCArCB又是正三角形。

2、（2007浙江金华）如图，AB是O的切线，A为切点，AC是O的弦，过O作OHAC于点H．若2OH，12AB，13BO．

B A C D

图6

CPAO

A H C

A C B D O 求：（1）O的半径；（2）sinOAC∠的值；（3）弦AC的长（结果保留两个有效数字）．

解：（1）AB是O的切线，90OAB，

222AOOBAB，5OA．

（2）OHAC⊥，90OHA，2sin5OHOACOA．（3）OHAC，222AHAOOH，AHCH，225421AH， 21AH，22219.2ACAH≈．

3、（2007山东济宁)如图，AB为⊙O的直径，弦CD⊥AB于点M，过点B作BE∥CD，交AC的延长线于点E，连结BC。 (1)求证：BE为⊙O的切线；

(2)如果CD＝6，tan∠BCD＝21，求⊙O的直径。

4、（2007山东枣庄）如图，AB是⊙O的直径，BC是弦，OD⊥BC于E，交BC于D． (1)请写出五个不同类型的正确结论； (2)若BC=8，ED＝2，求⊙O的半径．解：(1)不同类型的正确结论有：

①BC=CE ;②BDCD= ③∠BED=90°④∠BOD=∠A;⑤AC∥OD，⑥AC⊥BC; ⑦OE2+BE2=OB2;⑧S△ABC＝BC·OE;⑨△BOD是等腰三角形，⑩△BOE∽△BAC;等

(2)∵OD⊥BC， ∴BE＝CE=12BC=4．设⊙O的半径为R，则OE=OD-DE=R-2．在Rt△OEB中，由勾股定理得 OE2＋BE2=OB2，即(R-2)2＋42=R2．解得R＝5．∴⊙O的半径为5．

5、（2007福建福州）如图8，已知：ABC△内接于O，点D

在OC的延长线上，1sin2B，30D．（1）求证：AD是O的切线；（2）若6AC，求AD的长．（1）证明：如图9，连结OA．

1sin2B∵，30B∴°．

2AOCB∵，60AOC∴°．

30D∵°，18090OADDAOD∴°°．

AD∴是O的切线．

（2）解：OAOC∵，60AOC°． AOC∴△是等边三角形，6OAAC∴．

90OAD∵°，30D°，363ADAO∴．

6、（2007山东临沂）如图，已知点A、B、C、D均在已知圆上，AD∥BC，AC平分∠BCD，∠ADC＝120°，四边形ABCD的周长为10。 (1)求此圆的半径； (2)求图中阴影部分的面积。

7、（2007山东德州）如图12，ABC△是O的内接三角形，ACBC，D为O中AB上一点，延长DA至点E，使CECD．

A C D B O

图8 A C

B O

图9

ＣＥ

ＡＯ

ＤＢ

图12