【同步练习】2017-2018学年人教A版必修2《2.3.1直线与平面垂直的判定》课后导练含解析
用2.3.1.2直线与平面垂直的判定习题课03

练 如图在正方体ABCD-A1B1C1D1中,O是底面ABCD的中心,B1H⊥D1O,H 习 为垂足,则B1H与平面AD1C的位置关系是( A )
A.垂直 B.平行 C.斜交 D.以上都不对
解:连结B1D1,BD, ∵几何体是正方体,底面ABCD是正方形, ∴AC⊥BD, 又∵B1B⊥AC, ∴AC⊥平面BDD1B1,B1H⊂平面BDD1B1, ∴AC⊥B1H, ∵B1H⊥D1O,AC∩D1O=O, ∴B1H⊥平面AD1C. 故选A.
三、正三棱锥(正四面体)中的垂直关系
1.正三棱锥P-ABC:PA=PB=PC,AB=AC=BC。 取BC的中点D,连接PD、AD, 则PD⊥BC,AD⊥BC, ∴BC⊥面PAD, ∴BC⊥PA。
P
A
C
结论:正三棱锥(正四面体)中, B (1)对边垂直; (2)底边中点与对边确定的平面垂直于这条底边。
空间问题
平面问题
三棱锥的顶点在底面的射影是底面的什么心问题 1.已知在三棱锥P-ABC中,PA=PB=PC,则P点在平面α内的射影一定是△ABC 的( ) A.内心 B.外心 C.垂心 D.重心
2.三棱锥P-ABC的高为PH,若P到△ABC的三边的距离相等,若H在△ABC内, 则H为△ABC的( ) A.内心 B.外心 C.旁心 D.旁心或内心 3.已知在三棱锥P-ABC中,PA⊥BC,PB⊥AC,则点P在平面ABC上的射影为 △ABC的( ) A.重心 B.外心 C.内心 D.垂心 4.三棱锥的三条侧棱两两垂直,则顶点在底面的射影是底面三角形的( A.内心 B.外心 C.重心 D.垂心 )
五、正棱锥中的垂直关系 正棱锥的定义:底面为正多边形,顶点在底面上的射影是底面的中心的棱锥。
1.正三棱锥P-ABC
2018-2019学年高中数学必修二人教A版练习:2.3.1 直线与平面垂直的判定 Word版含解析

2.3 直线、平面垂直的判定及其性质2.3.1 直线与平面垂直的判定【选题明细表】知识点、方法题号线面垂直的定义及判定定理的理解1,2,3,5线面垂直的判定及证明4,6,8,9直线与平面所成的角7综合问题10,11,121.(2018·甘肃兰州二十七中高二上期末 )设l,m是两条不同的直线,α是一个平面,则下列命题正确的是( A )(A)若l⊥α,l∥m,则m⊥α(B)若l∥α,m⊂α,则l∥m(C)若l⊥m,m⊂α,则l⊥α(D)若l∥α,m∥α,则l∥m解析:易知A正确.B.l与m可能异面,也可能平行.C.当l与α内两条相交直线垂直时,才能判定l⊥α,D.l与m可能平行、异面或相交.2.(2018·广西桂林期末)已知m,n表示两条不同直线,α表示平面,下列说法正确的是( C )(A)若m∥α,n∥α,则m∥n(B)若m⊥α,m⊥n,则n∥α(C)若m⊥α,n⊂α,则m⊥n(D)若m∥α,m⊥n,则n⊥α解析:对于选项A,若m∥α,n∥α,则m与n可能相交、平行或者异面;故A错误;对于B,若m⊥α,m⊥n,则n与α可能平行或者n在α内;故B错误;对于C,若m⊥α,n⊂α,则m⊥n;故C正确;对于D,若m∥α,m⊥n,则n⊂α,或n与α相交;故D错误.故选C.3.在△ABC中,AB=AC=5,BC=6,PA⊥平面ABC,PA=8,则P到BC的距离是( D )(A)(B)2(C)3(D)4解析:如图所示,作PD⊥BC于D,连接AD.因为PA⊥平面ABC,所以PA⊥CD.所以CB⊥平面PAD,所以AD⊥BC.在△ACD中,AC=5,CD=3,所以AD=4.在Rt△PAD中,PA=8,AD=4,所以PD==4.故选D.4.已知P为△ABC所在平面外一点,PA⊥PB,PB⊥PC,PC⊥PA,PH⊥平面ABC,垂足H,则H为△ABC的( B )(A)重心(B)垂心(C)外心(D)内心解析:连接AH并延长,交BC于D,连接BH并延长,交AC于E;因为PA⊥PB,PA⊥PC,故PA⊥平面PBC,故PA⊥BC;因为PH⊥平面ABC,故PH⊥BC,故BC⊥平面PAH,故AH⊥BC;同理BH⊥AC;故H是△ABC的垂心.5.(2018·唐山高二期末)△ABC所在平面α外一点P到三角形三顶点的距离相等,那么点P在α内的射影一定是△ABC的( A )(A)外心(B)内心(C)重心(D)以上都不对解析:由题意PA=PB=PC,PO⊥平面ABC,所以PO⊥OA,PO⊥OB,PO⊥OC,所以由HL定理知Rt△POA≌Rt△POB≌Rt△POC.于是OA=OB=OC,所以O 为三边中垂线的交点,O是三角形的外心,故选A.6.如图所示,PA⊥平面ABC,△ABC中BC⊥AC,则图中直角三角形的个数是( D )(A)1(B)2(C)3(D)4解析:⇒⇒BC⊥平面PAC⇒BC⊥PC,所以直角三角形有△PAB,△PAC,△ABC,△PBC.故选D.7.(2018·浙江杭州月考)如图所示,∠ACB=90°,平面ABC外有一点P,PC=4 cm,PF,PE垂直于BC,AC于点F,E,且PF=PE=2 cm,那么PC与平面ABC所成角的大小为 .解析:过P作PO垂直于平面ABC于O,连接CO,则CO为∠ACB的平分线.连接OF,可证明△CFO为直角三角形,CO=2,Rt△PCO中,cos∠PCO=,∠PCO=45°.答案:45°8.(2018·陕西西安高一期末)在四棱锥P ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,过E点作EF⊥PB交PB于点F.求证:(1)PA∥平面DEB;(2)PB⊥平面DEF.证明:(1)连接AC,BD,交于O,连接EO.因为底面ABCD是正方形,所以点O是AC的中点.所以在△PAC中,EO是中位线,所以PA∥EO,因为EO⊂平面DEB,且PA⊄平面DEB,所以PA∥平面DEB.(2)因为PD⊥底面ABCD,且BC⊂底面ABCD,所以PD⊥BC.因为底面ABCD 是正方形,所以DC⊥BC,可得BC⊥平面PDC.因为DE⊂平面PDC,所以BC⊥DE.又因为PD=DC,E是PC的中点,所以DE⊥PC.所以DE⊥平面PBC.因为PB ⊂平面PBC,所以DE⊥PB.又因为EF⊥PB,且DE∩EF=E,所以PB⊥平面DEF.9.如图甲所示,在正方形ABCD中,E,F分别是BC,CD的中点,G是EF的中点,现在沿AE,AF及EF把这个正方形折成一个四面体,使B,C,D三点重合,重合后的点记为H,如图乙所示,那么,在四面体A EFH中必有( A )(A)AH⊥△EFH所在平面(B)AG⊥△EFH所在平面(C)HF⊥△AEF所在平面(D)HG⊥△AEF所在平面解析:根据折叠前、后AH⊥HE,AH⊥HF不变,所以AH⊥平面EFH,故选A.10.如图,四棱锥S ABCD的底面为正方形,SD⊥底面ABCD,给出下列结论:①AC⊥SB;②AB∥平面SCD;③SA与平面ABD所成的角等于SC与平面ABD所成的角;④AC⊥SO.正确结论的序号是 .解析:连接SO,如图所示,因为四棱锥S ABCD的底面为正方形,所以AC⊥BD.因为SD⊥底面ABCD,所以SD⊥AC,因为SD∩BD=D,所以AC⊥平面SBD,因为SB⊂平面SBD,所以AC⊥SB,则①正确;因为AB∥CD,AB⊄平面SCD,CD⊂平面SCD,所以AB∥平面SCD,则②正确;因为SD⊥底面ABCD,所以∠SAD和∠SCD分别是SA与平面ABD所成的角、SC与平面ABD 所成的角,因为AD=CD,SD=SD,所以∠SAD=∠SCD,则③正确;因为AC⊥平面SBD,SO⊂平面SBD,所以AC⊥SO,则④正确.答案:①②③④11.(2018·宁夏石嘴山第三中学高二上期末)侧棱垂直于底面的三棱柱ABC A′B′C′满足∠BAC=90°,AB=AC=AA′=2,点M,N分别为A′B,B′C′的中点.(1) 求证:MN∥平面A′ACC′;(2) 求证:A′N⊥平面BCN;(3) 求三棱锥C MNB的体积.(1)证明:如图,连接AB′,AC′,因为四边形ABB′A′为矩形,M为A′B的中点,所以AB′与A′B交于点M,且M为AB′的中点,又点N为B′C′的中点,所以MN∥AC′,又MN⊄平面A′ACC′,且AC′⊂平面A′ACC′,所以MN∥平面A′ACC′.(2)证明:因为A′B′=A′C′=2,点N为B′C′的中点,所以A′N⊥B′C′.又BB′⊥平面A′B′C′,所以A′N⊥BB′,所以A′N⊥平面BCN.(3)解:由图可知=,因为∠BAC=90°,所以BC==2,S△BCN=×2×4=4.由(2)及∠B′A′C′=90°可得A′N=,因为M为A′B的中点,所以M到平面BCN的距离为,所以==×4×=.12.如图(1),在Rt△ABC中,∠C=90°,D,E分别为AC,AB的中点,点F为线段CD上的一点.将△ADE沿DE折起到△A1DE的位置,使A1F⊥CD,如图(2).(1)求证:DE∥平面A1CB;(2)求证:A1F⊥BE;(3)线段A1B上是否存在点Q,使A1C⊥平面DEQ?说明理由.(1)证明:因为D,E分别为AC,AB的中点,所以DE∥BC.又因为DE⊄平面A1CB,BC⊂平面A1CB,所以DE∥平面A1CB.(2)证明:由已知得AC⊥BC且DE∥BC,所以DE⊥AC.所以DE⊥A1D,DE⊥CD.所以DE⊥平面A1DC.而A1F⊂平面A1DC,所以DE⊥A1F.又因为A1F⊥CD,所以A1F⊥平面BCDE.所以A1F⊥BE.(3)解:线段A1B上存在点Q,使A1C⊥平面DEQ.理由如下:如图,分别取A1C,A1B的中点P,Q,则PQ∥BC.又因为DE∥BC,所以DE∥PQ.所以平面DEQ即为平面DEP.由(2)知,DE⊥平面A1DC,所以DE⊥A1C.又因为P是等腰三角形DA1C底边A1C的中点,所以A1C⊥DP.所以A1C⊥平面DEP.从而A1C⊥平面DEQ.故线段A1B上存在点Q,使得A1C⊥平面DEQ.。
2018-2019学年人教A版必修二2.3.1直线与平面垂直的判定作业

2.3直线、平面垂直的判定及其性质2.3.1直线与平面垂直的判定课后篇巩固探究1.已知m,n是两条不同直线,α,β,γ是三个不同平面,下面命题正确的是()A.若α⊥γ,β⊥γ,则α∥βB.若m⊥α,n⊥α,则m∥nC.若m∥α,n∥α,则m∥nD.若m∥α,m∥β,则α∥β解析选项A中,α⊥γ,β⊥γ?α与β平行或相交,故A不正确;选项C中,m∥α,n∥α?m与n平行、相交或异面,故C不正确;选项D中,m∥α,m∥β?α与β平行或相交,故D不正确.故选B.答案 B2.若空间四边形ABCD的四边相等,则它的两对角线AC,BD的关系是()A.垂直且相交B.相交但不一定垂直C.垂直但不相交D.不垂直也不相交解析取BD的中点O,连接AO,CO,则BD⊥AO,BD⊥CO,故BD⊥平面AOC,BD⊥AC.又BD,AC异面,故选C.答案 C3.如图,在正方形ABCD中,E,F分别是BC,CD的中点,G是EF的中点,现在沿AE,AF及EF把这个正方形折成一个空间图形,使B,C,D三点重合,重合后的点记为H,那么,在这个空间图形中必有()A.AH⊥△EFH所在平面B.AG⊥△EFH所在平面C.HF⊥△AEF所在平面D.HG⊥△AEF所在平面解析原题图中AD ⊥DF ,AB ⊥BE,所以折起后AH ⊥FH ,AH ⊥EH,FH ∩EH=H ,所以AH ⊥△EFH 所在平面.答案 A4.如果PA,PB,PC 两两垂直,那么点P 在平面ABC 内的投影一定是△ABC 的()A.重心B.内心C.外心D.垂心解析如图,由PA,PB,PC 两两互相垂直,可得AP ⊥平面PBC,BP ⊥平面PAC,CP ⊥平面PAB,所以BC ⊥OA,AB ⊥OC,AC ⊥OB,所以点O 是△ABC 三条高的交点,即点O 是△ABC 的垂心,故选D.答案 D5.在四棱锥P-ABCD 中,底面ABCD 是边长为1的正方形,PA ⊥平面ABCD ,且PA=6,则PC 与平面ABCD 所成角的大小为() A.30° B.45° C.60° D.90°解析如图,连接AC.∵PA ⊥平面ABCD ,∴∠PCA 就是PC 与平面ABCD 所成的角.∵AC=2,PA=6,∴tan ∠PCA=????????=62= 3.∴∠PCA=60°.答案 C6.如图,在正方体ABCD-A 1B 1C 1D 1中,E,F 分别是棱AB,BC 的中点,O 是底面ABCD 的中心,则EF 与平面BB 1O 的位置关系是.(填“平行”或“垂直”)解析∵ABCD 为正方形,∴AC ⊥BO.∵BB 1⊥平面ABCD ,AC?平面ABCD ,。
2017-2018学年人教A版必修2 2.3.1 直线与平面垂直的判定 课件(28张)

题型一
题型二
题型三
题型四
题型二
求直线与平面所成的角
【例2】 如图,在四棱锥P-ABCD中,底面ABCD是矩形,且PA⊥平面 ABCD,PA=5,AB=4,AD=3.求直线PC与平面ABCD所成的角的大小.
题型一
题型二
题型三
题型四
解:
如图,连接 AC,因为 PA⊥平面 ABCD,则 AC 是 PC 在平面 ABCD 上的射影,所以∠PCA 是 PC 与平面 ABCD 所成的角. 在△PAC 中,PA⊥AC,PA=5, AC= ������������2 + ������������ 2 = 42 + 32 = 5. 则∠PCA=45°, 即直线 PC 与平面 ABCD 所成的角的大小为 45°.
解析:因为B1B⊥平面ABCD, 所以∠B1AB是AB1与平面ABCD所成的角.在正方体ABCDA1B1C1D1中,四边形ABB1A1是正方形, 所以∠B1AB=45°. 答案:45°
1
2
1.理解直线与平面垂直的判定定理 剖析:(1)在判定定理的条件中,“平面内两条相交直线”是关键性 词语,此处强调相交. (2)要判断一条已知直线和一个平面是否垂直,只需要在该平面内 找出两条相交直线与已知直线垂直即可.至于这两条直线是否与已 知直线有交点,这是无关紧要的. (3)判定定理是由线线垂直推导出线面垂直,其最终仍归结为证明 线线垂直,即证明线与平面内的两条相交直线垂直. (4)判定线面垂直的方法有: ①利用线面垂直的定义:一条直线垂直于平面内的任意一条直线, 则该直线垂直于这个平面; ②利用线面垂直的判定定理.
1
2
3
【做一做1】 已知直线l⊥平面α,直线m⊂α,则l与m不可能( ) A.平行 B.相交 C.异面D.垂直 解析:因为直线l⊥平面α, 所以l与α相交, 又因为m⊂α,所以l与m相交或异面.由直线与平面垂直的定义,可 知l⊥m.故l与m不可能平行. 答案:A
高中数学必修2单元配套练习试题2.3.1直线与平面垂直的判定及参考答案解析
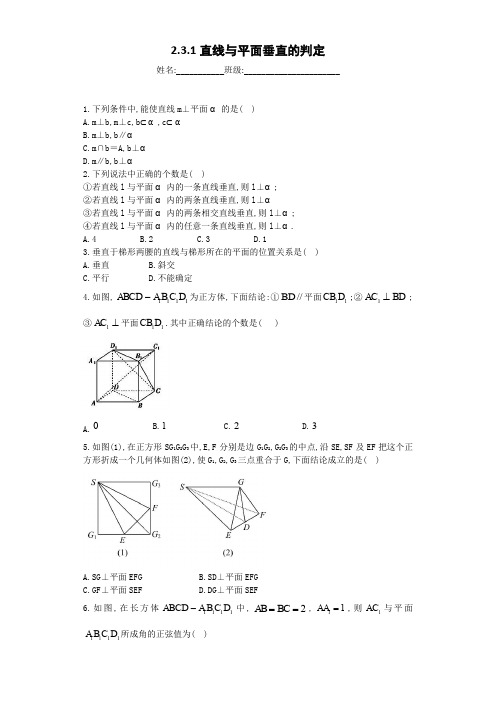
2.3.1直线与平面垂直的判定姓名:___________班级:______________________1.下列条件中,能使直线m⊥平面α的是( )A.m⊥b ,m⊥c ,b ⊂α,c ⊂αB.m⊥b ,b∥αC.m∩b=A,b⊥αD.m∥b ,b⊥α2.下列说法中正确的个数是( )①若直线l 与平面α内的一条直线垂直,则l⊥α;②若直线l 与平面α内的两条直线垂直,则l⊥α③若直线l 与平面α内的两条相交直线垂直,则l⊥α;④若直线l 与平面α内的任意一条直线垂直,则l⊥α.A.4B.2C.3D.13.垂直于梯形两腰的直线与梯形所在的平面的位置关系是( )A.垂直B.斜交C.平行D.不能确定4.如图,1111D C B A ABCD -为正方体,下面结论:①//BD 平面11D CB ;②BD AC ⊥1;③⊥1AC 平面11D CB .其中正确结论的个数是( )A.0B.1C.2D.35.如图(1),在正方形SG 1G 2G 3中,E,F 分别是边G 1G 2,G 2G 3的中点,沿SE,SF 及EF 把这个正方形折成一个几何体如图(2),使G 1,G 2,G 3三点重合于G,下面结论成立的是( )A.SG⊥平面EFGB.SD⊥平面EFGC.GF⊥平面SEFD.DG⊥平面SEF6.如图,在长方体1111ABCD A B C D -中,2AB BC ==,11AA =,则1AC 与平面1111A B C D 所成角的正弦值为( )B.2313 7.已知P 为△ABC 所在平面外一点,且PA ,PB ,PC 两两垂直,则下列结论:①PA BC ⊥;②PB AC ⊥;③PC AB ⊥;④AB BC ⊥.其中正确的是( )A.①②③B.①②④C.②③④D.①②③④8.正方体ABCD -A 1B 1C 1D 1中,BB 1与平面ACD 1所成的角的余弦值为( )C.239.已知△ABC 所在平面外一点P 到△ABC 三顶点的距离都相等,则点P 在平面ABC 内的射影是△ABC 的________.10.在Rt△ABC 中,D 是斜边AB 的中点,AC =6,BC =8,EC⊥平面ABC,且EC =12,则ED =_______.11.正方体ABCD -A 1B 1C 1D 1中,点P 在侧面BCC 1B 1及其边界上运动,并且总是保持AP⊥BD 1,则动点P 的轨迹是________.12.如图所示,在三棱柱ABC -A 1B 1C 1中,侧棱AA 1⊥底面ABC,AB =AC =1,AA 1=2,∠B 1A 1C 1=90°,D 为BB 1的中点.求证:AD⊥平面A 1DC 1.13.如图,ABCD 为正方形,过A 作线段SA⊥平面ABCD,过A 作与SC 垂直的平面交SB,SC,SD 于E,K,H,求证:E 是点A 在直线SB 上的射影.14.如图,已知PA⊥平面ABCD,且四边形ABCD 为矩形,M 、N 分别是AB 、PC 的中点.(2)若∠PDA=45°,求证:MN⊥平面PCD.参考答案1.D【解析】对于选项A:如果直线b,c 不相交,则m 不一定垂直于平面α;对于选项B:显然不正确;对于选项C:显然不正确,故选D.考点:线面垂直的判定.2.B【解析】对于①②,不能断定该直线与平面垂直,该直线与平面可能平行,也可能斜交,也可能在平面内,所以是错误的,③④是正确的,故选B.考点:线面垂直的判定.3.A【解析】梯形的两腰所在的直线相交,根据线面垂直的判定定理可知A 正确.考点:线面垂直的判定.4.D【解析】由正方体的性质得,BD ∥B 1D 1,结合线面平行的判定定理可得BD ∥平面CB 1D 1,所以①正确;由正方体的性质得 AC ⊥BD,因为AC 是AC 1在底面ABCD 内的射影,所以由三垂线定理可得AC 1⊥BD,所以②正确;由正方体的性质得 BD ∥B 1D 1,由②可得AC 1⊥BD,所以AC 1⊥B 1D 1,同理可得AC 1⊥CB 1,进而结合线面垂直的判定定理得到AC 1⊥平面CB 1D 1,所以③正确.考点:直线与平面平行的判定,空间中直线与直线之间的位置关系,直线与平面垂直的判定.5.A【解析】由折叠前后不变的元素关系,知SG⊥GE ,SG⊥GF ,又GE∩GF=G,所以SG⊥平面GEF,故选A.考点:线面垂直的判定.6.D【解析】连接11A C ,因为1111ABCD A B C D -是长方体,所以1AA ⊥平面1111A B C D ,所以11A C 是1AC 在平面1111A B C D 内的射影,所以11A C A ∠为1AC 与平面1111A B C D 所成的角.在11Rt AAC 中,11AA =,13AC ==,1190AAC ∠=︒,所以11111sin 3AA A C A AC ∠==. 考点:线面角的求法.7.A【解析】由PA ,PB ,PC 两两垂直可得PA ⊥平面PBC ,PB ⊥平面PAC ,PC ⊥平面PAB ,所以PA BC ⊥,PB AC ⊥,PC AB ⊥,①②③正确.④错误,假设AB BC ⊥,由PA ⊥平面PBC 得PA BC ⊥,又PA AB A =,所以BC ⊥平面PAB ,又PC ⊥平面PAB ,这与过一点有且只有一条直线与已知平面垂直矛盾.考点:线面垂直.8.D【解析】解法一:如图,设正方体的棱长为1,上,下底面的中心分别为1O ,O ,则11OO BB ,1O O 与平面ACD 1所成的角就是BB 1与平面ACD 1所成的角,即∠O 1OD 1,cos∠O 1OD 1=11O OOD =.解法二:画出图形,如图,BB 1与平面ACD 1所成的角等于DD 1与平面ACD 1所成的角,在三棱锥D -ACD 1中,由三条侧棱两两垂直且相等得点D 在底面ACD 1内的射影为等边三角形ACD 1的重心,即中心H,连接D 1H,DH,则∠DD 1H 为DD 1与平面ACD 1所成的角,设正方体的棱长为a,则cos∠DD 1H=3a =考点:求线面角的余弦值9.外心【解析】P 到△ABC 三顶点的距离都相等,则点P 在平面ABC 内的射影到△ABC 三顶点的距离都相等,所以是外心.考点:线面垂直的应用.10.13【解析】如图,∵AC=6,BC =8,∴AB=10,∴CD=5.在Rt△ECD 中,EC =12,13.考点:线面垂直的应用.11.B1C【解析】BD1⊥平面B1AC,平面B1AC∩平面BCC1B1=B1C,所以P为B1C上任何一点时,均有AP⊥BD1.考点:线面垂直的应用.12.见解析【解析】证明:∵AA1⊥底面ABC,平面A1B1C1∥平面ABC, ∴AA1⊥平面A1B1C1,∴A1C1⊥AA1.又∠B1A1C1=90°,∴A1C1⊥A1B1,又A1B1∩AA1=A1,∴A1C1⊥平面AA1B1B,又AD⊂平面AA1B1B,∴A1C1⊥AD.由已知计算得AD=2,A1D=2,又AA1=2,∴AD2+A1D2=AA21,∴A1D⊥AD,∵A1C1∩A1D=A1,∴AD⊥平面A1DC1.考点:线面垂直的判定.13.见解析【解析】证明:SA ABCDBC ABCD⊥⎫⎬⊂⎭平面平面⇒SA⊥BC,又∵AB⊥BC,SA∩AB=A,∴BC⊥平面SAB.又AE⊂平面SAB,∴BC⊥AE,∵SC⊥平面AHKE,AE⊂平面AHKE,∴SC⊥AE.又BC∩SC=C,∴AE⊥平面SBC,∵SB⊂平面SBC,∴AE⊥SB,即E为A在SB上的射影.考点:线面垂直的应用.14.见解析【解析】证明:(1)如图所示,取PD的中点E,连接AE、NE,∵N为PC的中点,E为PD的中点,∴NE∥CD且NE=12CD,而AM∥CD且AM=12AB=12CD,∴NE∥AM且NE=AM,∴四边形AMNE为平行四边形,∴MN∥AE.又PA⊥平面ABCD,∴PA⊥CD,又∵ABCD为矩形,∴AD⊥CD,又AD∩PA=A,∴CD⊥平面PAD,∴CD⊥AE,又AE∥MN,∴MN⊥CD.(2)由(1)可知CD⊥AE,MN∥AE.又∠PDA=45°,∴△PAD为等腰直角三角形,又E为PD的中点,∴AE⊥PD,∴AE⊥平面PCD. 又AE∥MN,∴MN⊥平面PCD.【考点】线面垂直的证明.。
人教A版高中数学必修二2.3.1直线与平面垂直的判定同步练习B卷

人教A版高中数学必修二 2.3.1直线与平面垂直的判定同步练习B卷姓名:________ 班级:________ 成绩:________一、单选题 (共8题;共16分)1. (2分) (2016高二上·温州期末) 给定下列四个命题:①若一个平面内的两条直线与另一个平面都平行,那么这两个平面相互平行;②若一个平面经过另一个平面的垂线,那么这两个平面相互垂直;③垂直于同一直线的两条直线相互平行;④若两个平面垂直,那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直.其中,为真命题的是()A . ①和②B . ②和③C . ③和④D . ②和④2. (2分)设是平面内两条不同的直线,是平面外的一条直线,则是的()A . 充要条件B . 充分不必要条件C . 必要不充分条件D . 既不充分也不必要条件3. (2分)(2018·银川模拟) 是两个平面,是两条直线,则下列命题中错误的是()A . 如果,那么B . 如果,那么C . 如果,那么D . 如果,那么4. (2分) PA垂直于以AB为直径的圆所在平面,C为圆周上除A、B外的任意一点,下列不成立的是()A . PC⊥CBB . BC⊥平面PACC . AC⊥PBD . PB与平面PAC的夹角是∠BPC5. (2分) (2015高二上·天水期末) 如图,在空间直角坐标系中有直三棱柱ABC﹣A1B1C1 , CA=2CB,CC1=3CB,则直线BC1与直线AB1夹角的余弦值为()A .B .C .D .6. (2分)如图所示,面积为S的平面凸四边形的第i条边的边长记为,此四边形内任一点P到第i条边的距离为,若,则.类比以上性质,体积为V 的三棱锥的第i个面的面积记为,此三棱锥内任一点Q到第i个面的距离记为,若,则()A .B .C .D .7. (2分)如图,正方体ABCD-A'B'C'D'中,E是棱BC的中点,G是棱DD'的中点,则异面直线GB与B'E所成的角为()A .B .C .D .8. (2分) (2016高二上·秀山期中) 如图所示,在正方体ABCD﹣A1B1C1D1中,点M是平面A1B1C1D1内一点,且BM∥平面ACD1 ,则tan∠DMD1的最大值为()A .B . 1C . 2D .二、解答题 (共4题;共40分)9. (10分) (2017高三上·安庆期末) 如图:四棱锥P﹣ABCD中,底面ABCD是矩形,PA⊥底面ABCD,PA=AB=1,AD= ,点F是PB的中点,点E在边BC上移动.(1)证明:无论点E在BC边的何处,都有PE⊥AF;(2)当BE等于何值时,PA与平面PDE所成角的大小为45°.10. (10分)(2013·湖南理) 如图,在直棱柱ABCD﹣A1B1C1D1中,AD∥BC,∠BAD=90°,AC⊥BD,BC=1,AD=AA1=3.(1)证明:AC⊥B1D;(2)求直线B1C1与平面ACD1所成的角的正弦值.11. (10分)(2017·泸州模拟) 如图,在四棱锥P﹣ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,Q为AD的中点,M是棱PC的中点,PA=PD=PC,BC= AD=2,CD=4(1)求证:直线PA∥平面QMB;(2)若二面角P﹣AD﹣C为60°,求直线PB与平面QMB所成角的余弦值.12. (10分) (2015高二上·孟津期末) 如图,已知正方形ABCD的边长为6,点E,F分别在边AB,AD上,AE=AF=4,现将△AEF沿线段EF折起到△A′EF位置,使得A′C=2 .(1)求五棱锥A′﹣BCDFE的体积;(2)求平面A′EF与平面A′BC的夹角.三、填空题 (共2题;共2分)13. (1分) EC垂直Rt△ABC的两条直角边,D是斜边AB的中点,AC=6,BC=8,EC=12,则DE的长为________.14. (1分)如图,在三棱柱ABC﹣A1B1C1中,AA1⊥平面ABC,∠ACB=90°,CA=CB=CC1=1,则直线A1B与平面BB1C1C所成角的正弦值为________参考答案一、单选题 (共8题;共16分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、二、解答题 (共4题;共40分)9-1、9-2、10-1、10-2、11-1、11-2、12-1、12-2、三、填空题 (共2题;共2分) 13-1、14-1、。
人教A版高中数学必修二 2.3.1直线与平面垂直的判定 同步练习(II)卷
人教A版高中数学必修二 2.3.1直线与平面垂直的判定同步练习(II)卷姓名:________ 班级:________ 成绩:________一、单选题 (共8题;共16分)1. (2分) (2019高三上·浙江月考) 已知是不同的直线,是不同的平面,若,,,则下列命题中正确的是()A .B .C .D .2. (2分)如图所示,三棱锥P-ABC的底面在平面α内,且AC⊥PC,平面PAC⊥平面PBC,点P,A,B是定点,则动点C的轨迹是()A . 一条线段B . 一条直线C . 一个圆D . 一个圆,但要去掉两个点3. (2分) (2018高三上·西安模拟) 在平行四边形中,,且,若将其沿折起使平面平面,则三棱锥的外接球的表面积为()A .B .C .D .4. (2分)设a、b是不同的直线,、是不同的平面,则下列命题:①若,则;②若,则;③若,则;④若,则.其中正确命题的个数是()A . 0B . 1C . 2D . 35. (2分)把正方形ABCD沿对角线AC折起,当以A,B,C,D四点为顶点的三棱锥体积最大时,直线BD和平面ABC所成的角的大小为()A .B .C .D .6. (2分) (2017高二上·佳木斯期末) 如图所示,面积为的平面凸四边形的第条边的边长为,此四边形内在一点到第条边的距离记为,若,则 .类比以上性质,体积为的三棱锥的第个面的面积记为,此三棱锥内任一点到第个面的距离记为 ,若 ,().A .B .C .D .7. (2分)如图所示,在正方体ABCDA1B1C1D1中,E , F分别是AB , AD的中点,则异面直线B1C与EF 所成的角的大小为()A . 30°B . 45°C . 60°D . 90°8. (2分)已知平面α⊥平面β,α∩β=l,点A∈α,A∉l,直线AB∥l,直线AC⊥l,直线m∥α,m∥β,则下列四种位置关系中,不一定成立的是()A . AB∥mB . AC⊥mC . AB∥βD . AC⊥β二、解答题 (共4题;共35分)9. (10分) (2017高二下·辽宁期末) 已知△BCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E、F分别是AC、AD上的动点,且(1)求证:不论为何值,总有平面BEF⊥平面ABC;(2)当λ为何值时,平面BEF⊥平面ACD ?10. (5分)如图,四棱锥P﹣ABCD中,底面ABCD为正方形,PD⊥平面ABCD,PD=AB,E,F,G,H分别为PC、PD、BC、PA的中点.求证:(1)PA∥平面EFG;(2)DH⊥平面EFG.11. (10分) (2015高二下·赣州期中) 如图,四边形PDCE为矩形,四边形ABCD为梯形,平面PDCE⊥平面ABCD,∠BAD=∠ADC=90°,AB=AD= CD=a,PD= a.(1)若M为PA中点,求证:AC∥平面MDE;(2)求平面PAD与PBC所成锐二面角的大小.12. (10分)如图,四棱锥P﹣ABCD中,底面ABCD是直角梯形,∠ABC=90°,AB∥CD,AB=AD=2,CD=1,侧面PAD⊥底面ABCD,且△PAD是以AD为底的等腰三角形(1)证明:AD⊥PB;(2)若三棱锥C﹣PBD的体积等于,问:是否存在过点C的平面CMN,分别交PB、AB于点M,N,使得平面CMN∥平面PAD?若存在,求出△CMN的面积;若不存在,请说明理由.三、填空题 (共2题;共2分)13. (1分) (2018高二下·佛山期中) ,为两个不同的平面,,为两条不同的直线,下列命题中正确的是________(填上所有正确命题的序号).①若,,则;②若,,则;③若,,,则;④若,,,则.14. (1分) (2018高二上·嘉兴月考) 是两个平面,是两条直线,有下列四个命题:①如果 ,那么;②如果 ,那么;③如果 ,那么;④如果 ,那么与所成的角和与所成的角相等,其中正确的命题为________.参考答案一、单选题 (共8题;共16分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、二、解答题 (共4题;共35分)9-1、9-2、10-1、11-1、11-2、12-1、12-2、三、填空题 (共2题;共2分) 13-1、14-1、。
2017-2018学年高中新课标 数学A版 必修②课时作业:2-
C.0 D.2
解析:因为直线l的倾斜角为135°,直线l1经过点A(3,2),B(a,-1),且l1与l垂直,
所以 =1,所以a=0,
又直线l2:2x+by+1=0与直线l1平行,所以- =1,所以b=-2,因此a+b=-2.
答案:B
12.已知A(2,3),B(1,-1),C(-1,-2),点D在x轴上,则当点D坐标为________时,AB⊥CD.
解析:直线2x-3y+4=0的斜率为 ,又直线l与该直线垂直,所以直线l的斜率为- .又直线l过点(-2,-3),因此直线l的方程为y-(-3)=- ×,即3x+2y+12=0.
答案:3x+2y+12=0
8.已知△ABC的三个顶点的坐标分别为A(-1,0),B(0,2),C(a,0),若AB⊥BC,则a=__,解得 或 .
当a=0,b=0时不合题意,舍去.
∴a=2,b=-2.
(2)∵l1∥l2,∴a-b(a-1)=0,③
由题意知a>0,b>0,直线l2与两坐标轴的交点坐标分别为 ,
则 × × =2,
得ab=4,④
由③④,得a=2,b=2.
答案:B
5.下列直线中,与已知直线y=- x+1平行,且不过第一象限的直线的方程是()
A.3x+4y+7=0 B.4x+3y+7=0
C.4x+3y-42=0 D.3x+4y-42=0
解析:先看斜率,A、D选项中斜率为- ,排除掉;再看纵截距,要使纵截距小于0,才能使直线不过第一象限,只有B选项符合.
课时作业
|
一、选择题(每小题5分,共25分)
1.下列命题中,正确的是()
A.斜率相等的两条直线一定平行
B.若两条不重合的直线l1,l2平行,则它们的斜率一定相等
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
课后导练
基础达标
1空间四边形的四边相等,那么它的对角线……( )
A.相交且垂直
B.不相交也不垂直
C.相交不垂直
D.不相交但垂直
解析:如图空间四边形ABCD,假设AC与BD相交,则它们共面α,从而四点A,B,C,
D都在α内,这与ABCD为空间四边形矛盾,所以AC与BD不相交;取BD中点O,连结
OA与OC,因为AB=AD=DC=BC,所以AO⊥BD,OC⊥BD,从而可知BD⊥面AOC,故
AC⊥BD.
答案:D
2如果一条直线垂直于一个平面内的下列各种情况,能保证该直线与平面垂直的是( )
①三角形的两边 ②梯形的两边 ③圆的两条直径
④正六边形的两条边
A.①③ B.② C.②④ D.①②④
解析:由线面垂直的判定定理知,直线垂直于①③平面;对于②④图形中的两边不一定是相
交直线,所以该直线与它们不一定垂直.
答案:A
3如图,PA⊥⊙O所在的平面,AB是⊙O的直径,C是⊙O上的一点,E、F分别是A在
PB、PC上的射影.给出下面结论,其中正确命题的个数是( )
①AF⊥PB ②EF⊥PB ③AF⊥BC ④AE⊥平面PBC
A.2 B.3 C.4 D.5
解析:∵PA⊥⊙O所在平面,
∴PA⊥BC,又BC⊥AC,PA∩AC=A,
∴BC⊥面PAC,
∴BC⊥AF,又AF⊥PC,PC∩BC=C,
∴AF⊥面PBC,
∴AF⊥PB,又AE⊥PB,AE∩AF=A,
∴PB⊥面AEF,
∴EF⊥PB.
从而可知①②③正确.
答案:B
4直线a不垂直于平面α,则α内与a垂直的直线有( )
A.0条 B.1条
C.无数条 D.α内所有直线
解析:①当aα时,显然C正确,②当a∥α时,过a作平面β,使α∩β=a′,则a∥a′,显然在
α内与a′垂直的直线也与a垂直,从而也选C.③当a与α斜交时,在α与a的射影垂直的直
线也与a垂直,也选C.
答案:C
5如图所示,PO⊥平面ABC,BO⊥AC,在图中与AC垂直的线段有( )
A.1条 B.2条 C.3条 D.4条
解析:∵PO⊥面ABC,
∴PO⊥AC.
又∵BO⊥AC,PO∩BO=O,
∴AC⊥面PBD,
∴AC⊥BP,AC⊥PD,AC⊥BD,AC⊥PO.
答案:D
6如图所示,直四棱柱A1B1C1D1-ABCD中,当底面四边形ABCD满足________时,有
A1C⊥B1D1(注:填上你认为正确的一种条件即可,不必考虑所有可能的情况).
解析:四边形ABCD的两条对角线互相垂直时,A′C⊥B′D′.
∵若AC⊥BD,又AA′⊥平面ABCD,
∴BD⊥AA′.
又∵AC∩AA′=A,
∴BD⊥平面A′AC,
∴BD⊥A′C.
又∵BD∥B′D′,∴A′C⊥B′D′.
答案:AC⊥BD或ABCD为正方形,菱形等.
7如图,已知矩形ABCD中,AB=3,BC=a(a>0),PA⊥平面ABCD,在BC上取点Q,使PQ⊥QD,
当满足条件的点Q有两个时,a的取值范围是__________.
解析:连结AQ,∵PA⊥平面ABCD,
∴PA⊥QD,若PQ⊥QD,则必有AQ⊥QD,
设BQ=x,则QC=a-x,从而有:
AQ2=AB2+BQ2=9+x2,DQ2=9+(a-x)2,
由AD2=AQ2+QD2,即a2=18+x2+(a-x)2,
∴x2-ax+9=0,由Δ=a2-36>0得a>6.
答案:a>6
8如图,平面α∩平面β=CD,EA⊥α于点A,EB⊥β于点B.
求证:AB⊥CD.
证明:∵EA⊥α,CDα,
根据直线和平面垂直的定义,则有CD⊥EA.
同样∵EB⊥β,CDβ,则有EB⊥CD.
又EA∩EB=E,
根据直线和平面垂直判定定理,则有
CD⊥平面AEB.
又∵AB平面AEB,
∴CD⊥AB.
综合应用
9在空间四边形ABCD中,若AB⊥CD,BC⊥AD,则对角线AC与BD的位置关系为( )
A.相交但不垂直 B.垂直但不相交
C.不相交也不垂直 D.无法判断
解析:如图,作AO⊥面BCD,由AB⊥CD,知CD⊥面ABO,
∴BO⊥CO,同理DO⊥BC,∴O为△BCD的垂心,
∴OC⊥BD,故BD⊥AC.
答案:B
10在正方体A1B1C1D1-ABCD中,E、F分别是棱AB,BC的中点,O是底面ABCD的中点,
(如图),则EF与面BB1O的关系是___________
解析:∵BB1⊥面ABCD,
∴BB1⊥AC,又∵AC⊥BD,∴AC⊥面BB1O,又知E,F分别为AB,CB中点,
∴EF∥AC,∴EF⊥面BB1O.
答案:垂直
11设三棱锥P-ABC的顶点P在平面ABC上的射影是H,给出下列命题:
①若PA⊥BC,PB⊥AC,则H是△ABC的垂心;
②若PA、PB、PC两两互相垂直,则H是△ABC的垂心;③若∠ABC=90°,H是AC的中
点,则PA=PB=PC;④若PA=PB=PC,则H是△ABC的外心.
请把正确命题的序号填在横线上_____________
解析:①若PA⊥BC,PB⊥AC,则H为垂心(前面已证).
②∵PA⊥PB,PA⊥PC.
∴PA⊥面PBC,
∴PA⊥BC,又PH⊥面ABC,
∴PH⊥BC,∴BC⊥面PAH,∴AH⊥BC.
同理BH⊥AC,∴H为垂心.
③∵H为AC中点,∠ABC=90°,
∴AH=BH=CH,
又PH⊥面ABC,
由勾股定理知PA=PB=PC,
④PA=PB=PC,又PH⊥面ABC,同③可知AH=BH=CH,
∴H为外心.
答案:①②③④
拓展探究
12已知:矩形ABCD,过A作SA⊥平面AC,再过A作AE⊥SB交于E,过E作EF⊥SC
交SC于F.
(1)求证:AF⊥SC;
(2)若平面AEF交SD于G,求证:AG⊥SD.
思路分析:本题是证线线垂直问题,可通过证线面垂直来实现.结合图形,欲证AF⊥SC,只
需证SC垂直于AF所在平面,即SC⊥平面AEF,由已知,欲证SC⊥平面AEF,只需证
AE垂直于SC所在平面,即AE⊥平面SBC,再由已知只需证AE⊥BC,而要证AE⊥BC,
只需证BC⊥平面SAB,而这可由已知得证.
证明:(1)∵SA⊥平面AC,BC平面AC,
∴SA⊥BC.
∵矩形ABCD,∴AB⊥BC,
∴BC⊥平面SAB,
∴BC⊥AE.又SB⊥AE,
∴AE⊥平面SBC,∴AE⊥SC.又EF⊥SC,
∴SC⊥平面AEF,
∴AF⊥SC.
(2)∵SA⊥平面AC,∴SA⊥DC.
又AD⊥DC,
∴DC⊥平面SAD.
∴DC⊥AG.
又由(1)有SC⊥平面AEF,AGAEF.
∴SC⊥AG,∴AG⊥平面SDC.∴AG⊥SD.
