高三数学第一轮复习《直线与圆 圆与圆 》讲义
2023高考数学一轮总复习第九章平面解析几何第四节直线与圆圆与圆的位置关系pptx课件北师大版

第四节
直线与圆、圆与圆的位置关系
内
容
索
引
01
强基础 增分策略
02
增素能 精准突破
课标解读
衍生考点
核心素养
1.能根据给定直线、圆的方程,
判断直线与圆、圆与圆的位置 1.直线与圆的位置关系 直观想象
关系.
2.圆的切线与弦长问题 数学运算
2.能用直线和圆的方程解决一
3.圆与圆的位置关系
些简单的数学问题与实际问题.
设圆C1:x2+y2+D1x+E1y+F1=0,①
圆C2:x2+y2+D2x+E2y+F2=0,②
若两圆相交,则有一条公共弦,其公共弦所在直线的方程可由①-②得到,即
(D1-D2)x+(E1-E2)y+(F1-F2)=0.
(2)两个圆系方程
①过直线Ax+By+C=0与圆x2+y2+Dx+Ey+F=0交点的圆系方
典例突破
例1.(1)已知直线l:ax+by-r2=0与圆C:x2+y2=r2,点A(a,b),则下列说法错误的
是(
)
A.若点A在圆C上,则直线l与圆C相切
B.若点A在圆C内,则直线l与圆C相离
C.若点A在圆C外,则直线l与圆C相离
D.若点A在直线l上,则直线l与圆C相切
(2)(2021北京人大附中模拟)已知圆C过点(-1,0)和(1,0),且与直线y=x-1只有
对点演练
1.判断下列结论是否正确,正确的画“√”,错误的画“×”.
(1)若两圆的圆心距小于两圆的半径之和,则两圆相交.( × )
2024届新高考一轮复习人教B版 主题三 第八章 第4节 直线与圆、圆与圆的位置关系 课件(36张)

4
3
2
.
.
1
0
1.圆的切线方程常用结论
(1)过圆x2+y2=r2(r>0)上一点P(x0,y0)的圆的切线方程为x0x+y0y=r2.
(2)过圆x2+y2=r2外一点M(x0,y0)作圆的两条切线,则两切点所在直线方程为
x0x+y0y=r2.
2.当两圆外切时,两圆有一条内公切线,该公切线垂直于两圆圆心的连线;当两
(-) + ( + ) = ,r1+r2=3,r2-r1=1,所以 r2-r1<|O1O2|<r1+r2,即两圆的
位置关系为相交.
5.圆(x-2)2+y2=4与圆x2+(y-2)2=4的公共弦所在直线的方程为
解析:根据题意(x-2)2+y2=4,
即x2+y2-4x=0,①
x2+(y-2)2=4,即x2+y2-4y=0.②
|-+-| |+|
+
=
+
=
++
+
=
判断直线与圆的位置关系的常见方法
(1)几何法:利用d与r的关系.
(2)代数法:联立方程之后利用Δ判断.
(3)点与圆的位置关系法:若直线恒过定点且定点在圆内,可判断直线与圆相交.
弦长问题
[例2] 过点(-4,0)作直线l与圆(x+1)2+(y-2)2=25交于A,B两点,如果|AB|=8,求
直线l的方程.
解:圆(x+1)2+(y-2)2=25 的圆心坐标是(-1,2),半径 r=5.
2015届高三数学(文)第一轮总复习课件 第55讲 直线与圆、圆与圆的位置关系

学海导航
文数
(3)已知圆C:x2+y2-4x=0,l是过点P(3,0)的直线, 则( ) A.l与C相交 C.l与C相离 B.l与C相切 D.以上三个选项均有可能
18
学海导航
文数
解析:(3)圆的方程可化为(x-2)2+y2=4,易知圆心 为(2,0),半径为2,圆心到点P的距离为1,所以点P在圆 内,所以直线与圆相交,故选A.
21
学海导航
文数
(2)“a=3”是“直线y=x+4与圆(x-a)2+(x-3)2=8相 切”的( ) B.必要不充分条件 D.既不充分也不必要条件
A.充分不必要条件 C.充要条件
22
学海导航
文数
|a-3+4| 解析:(2)若直线与圆相切,则 =2 2 ,a=3或 2 a=-5,所以“a=3”是“直线y=x+4与圆(x-a)2+(x- 3)2=8相切”的充分不必要条件,故选A.
学海导航
文数
第55讲
直线与圆、圆与圆的位置关系
1
学海导航
文数
2
学海导航
文数
1.直线4x+3y=40和圆x2+y2=100的位置关系是( A ) A.相交 C.相切 B.相离 D.无法确定
3
学海导航
文数
40 解析:因为 d= =8<10=r,所以直线与圆相交. 5
4
学海导航
文数
2.以点(2,-1)为圆心,且与直线 3x-4y+5=0 相切 的圆的方程为( C ) A.(x-2)2+(y+1)2=3 B.(x+2)2+(y-1)2=3 C.(x-2)2+(y+1)2=9 D.(x+2)2+(y-1)2=9
15
学海导航
文数
(2)已知过点P(2,2)的直线与圆(x-1)2+y2=5相切,且 与直线ax-y+1=0垂直, 则a=( 1 A.-2 C.2 ) B.1 1 D. 2
高中数学高考高三理科一轮复习资料第8章 8.4 直线与圆、圆与圆的位置关系

题型探究 题型一 直线和圆相交 例 1 已知圆 C:(x-1)2+(y-2)2=25,直线 l:(2m+1)x +(m+1)y-7m-4=0(m∈R). (1)证明:无论 m 取何实数,直线 l 与圆恒交于两点; (2)求直线 l 被圆 C 截得的线段的最短长度以及此时直线 l 的方程.
高中数学
8.4 直线与圆、圆与圆的位置关系
考纲点击 1.能根据给定直线、圆的方程判断直线与圆的位置关系; 能根据给定两个圆的方程判断两圆的位置关系. 2.能用直线和圆的方程解决一些简单的问题. 3.初步了解用代数方法处理几何问题的思想.
说基础
课前预习读教材
考点梳理 一、直线与圆的位置关系 1.直线与圆的位置关系有三种:相离、相切、相交. 判断直线与圆的位置关系常见的有两种方法: (1)代数法:利用判别式 Δ>0⇔① 判别式 Δ=0⇔② ――→ 2 Δ=b -4ac Δ<0⇔③ (2)几何法: 利用圆心到直线的距离 d 和圆半径 r 的大小关 系 d<r⇔④______;d=r⇔⑤______;d>r⇔⑥______.
说考点
拓展延伸串知识
疑点清源 一、圆的切线方程的求法 1.求过圆上的一点(x0,y0)的切线方程 先求切点与圆心连线的斜率 k,由垂直关系知切线斜率为 1 - k ,由点斜式方程可求切线方程.若切线斜率不存在,则由 图形写出切线方程 x=x0.
2.求过圆外一点(x0,y0)的圆的切线方程 (1)几何方法 当斜率存在时,设为 k,切线方程为 y-y0=k(x-x0),即 kx-y+y0-kx0=0.由圆心到直线的距离等于半径, 即可得出切 线方程. (2)代数方法 设切线方程为 y-y0=k(x-x0),即 y=kx-kx0+y0,代入 圆方程,得一个关于 x 的一元二次方程,由 Δ=0,求得 k,切 线方程即可求出. 【说明】 过圆外一点作圆的切线有两条, 若在解题过程中, 只解出一个答案,说明另一条直线的斜率不存在.
高考数学一轮总复习课件:圆的方程及直线与

(2)(2021·辽宁大连模拟)在直线l:y=x-1上有两个点A, B,且A,B的中点坐标为(4,3),线段AB的长度|AB|=8,则过 A,B两点且与y轴相切的圆的方程为____(_x_-_4_)_2+__(y_-__3)_2=__1_6___
解析 (x+2m)2+(y-1)2=4m2-5m+1表示圆,则 4m2-5m+1>0,解得m<14或m>1.
3.(2021·成都七中月考)圆心在y轴上,且过点(3,1)的圆与
x轴相切,则该圆的方程是( B )
A.x2+y2+10y=0
B.x2+y2-10y=0
C.x2+y2+10x=0
D.x2+y2-10x=0
第3课时 圆的方程及直线与 圆的位置关系
[复习要求] 1.掌握确定圆的几何要素.2.掌握圆的标准方 程和一般方程.3.掌握直线与圆的位置关系.
课前自助餐
圆的定义 平面内到定点的距离__等_于__定_长___的点的集合(轨迹)是圆,定点 是圆心,定长是半径. 注:平面内动点 P 到两定点 A,B 距离的比值为 λ,即||PPAB||= λ, ①当 λ=1 时,P 点轨迹是线段 AB 的垂直平分线; ②当 λ≠1 时,P 点轨迹是圆.
A=B≠0,
__D_2+__E_2_-_4_A_F_>_0.
圆的参数方程 圆心为(a,b),半径为 r 的圆的参数方程为xy==ab++rrcsoinsθθ,(θ 为参数).
确定圆的方程的方法和步骤 确定圆的方程的主要方法是待定系数法,大致步骤为: (1)根据题意,选择标准方程或一般方程; (2)根据条件列出关于 a,b,r 或 D,E,F 的方程组; (3)解出 a,b,r 或 D,E,F 代入标准方程或一般方程.
高三数学(文)一轮复习课件8-4 直线与圆、圆与圆的位置关系ppt版本

微知识❸ 两圆公切线的条数
位置关系 内含 内切 相交
公切线条数 0
12
外切 3
外离 4
二、小题查验 1.思维辨析(在括号内打“√”或“×”) (1)如果直线与圆组成的方程组有解,则直线与圆相交或相切。(√) 解析:正确。直线与圆组成的方程组有一组解时,直线与圆相切, 有两组解时,直线与圆相交。
解析:(1)如图,若|MN|=2 3 ,则由圆与直线的位置关系可知圆心到直线 的距离满足d2=22-( 3)2=1。
∵直线方程为y=kx+3, ∴d=|k·2-1+3+k2 3|=1,
解得k=±
3 3
若|MN|≥2 3,则- 33≤k≤ 33。
(2)把圆的方程化为标准方程是x+12k2+(y+1)2=16-34k2,
【微练3】(1)两个圆:C1:x2+y2+2x+2y-2=0与C2:x2+y2-4x-2y+1
=0的公切线有且仅有( B )
A.1条 B.2条 C.3条 D.4条 (2)在平面直角坐标系xOy中,圆C的方程为x2+y2-8x+15=0,若直线y= kx-2上至少存在一点,使得以该点为圆心,1为半径的圆与圆C有公共点,则k
方法
位置关系
几何法:圆心距d与r1,r2的关系
代数法:两圆方程联立 组成方程组的解的情况
外离 外切 相交 内切 内含
d>r1+r2
d=r1+r2 |r1-r2|<d<r1+r2 d=_|r_1_-__r2_| (r1≠r2) 0_≤____ d__<__ |r1-r2|(r1≠r2)
_无__解 _一__组___实数解 __两__组__不__同__的__实数解
(2)如果两个圆的方程组成的方程组只有一组实数解,则两圆外切。 (×)
高考数学一轮复习---直线与圆、圆与圆的位置关系知识点与题型复习
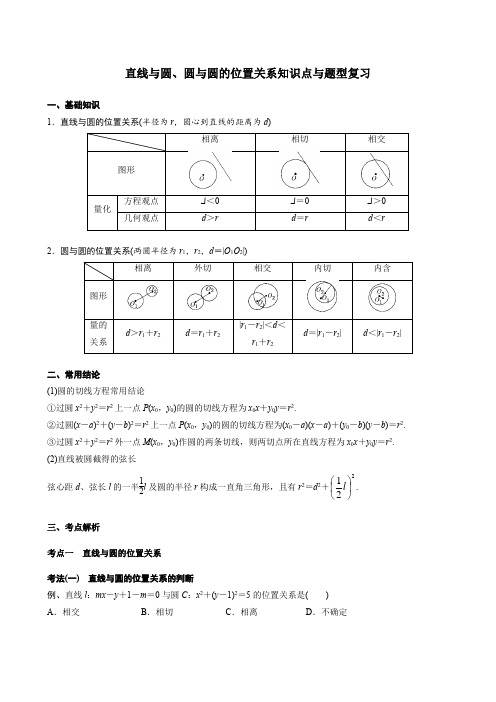
直线与圆、圆与圆的位置关系知识点与题型复习一、基础知识1.直线与圆的位置关系(半径为r ,圆心到直线的距离为d )Δ<0 Δ=0 Δ>02.圆与圆的位置关系(两圆半径为r 1,r 2,d =|O 1O 2|)|r -r |<d <二、常用结论(1)圆的切线方程常用结论①过圆x 2+y 2=r 2上一点P (x 0,y 0)的圆的切线方程为x 0x +y 0y =r 2.②过圆(x -a )2+(y -b )2=r 2上一点P (x 0,y 0)的圆的切线方程为(x 0-a )(x -a )+(y 0-b )(y -b )=r 2. ③过圆x 2+y 2=r 2外一点M (x 0,y 0)作圆的两条切线,则两切点所在直线方程为x 0x +y 0y =r 2. (2)直线被圆截得的弦长弦心距d 、弦长l 的一半12l 及圆的半径r 构成一直角三角形,且有r 2=d 2+221⎪⎭⎫⎝⎛l .三、考点解析考点一 直线与圆的位置关系 考法(一) 直线与圆的位置关系的判断例、直线l :mx -y +1-m =0与圆C :x 2+(y -1)2=5的位置关系是( ) A .相交 B .相切 C .相离 D .不确定[解题技法]判断直线与圆的位置关系的常见方法: (1)几何法:利用d 与r 的关系.(2)代数法:联立方程组,消元得一元二次方程之后利用Δ判断.(3)点与圆的位置关系法:若直线恒过定点且定点在圆内,可判断直线与圆相交.考法(二) 直线与圆相切的问题例、(1)过点P (2,4)作圆(x -1)2+(y -1)2=1的切线,则切线方程为( )A .3x +4y -4=0B .4x -3y +4=0C .x =2或4x -3y +4=0D .y =4或3x +4y -4=0 (2)已知圆C :x 2+y 2-2x -4y +1=0上存在两点关于直线l :x +my +1=0对称,经过点M (m ,m )作圆C 的切线,切点为P ,则|MP |=________.考法(三) 弦长问题例、(1)若a 2+b 2=2c 2(c ≠0),则直线ax +by +c =0被圆x 2+y 2=1所截得的弦长为( ) A.12 B .1 C.22D.2 (2)设直线y =x +2a 与圆C :x 2+y 2-2ay -2=0相交于A ,B 两点,若|AB |=23,则圆C 的面积为( ) A .4π B .2π C .9π D .22π跟踪练习:1.已知圆的方程是x 2+y 2=1,则经过圆上一点M ⎪⎪⎭⎫⎝⎛2222,的切线方程是________. 2.若直线kx -y +2=0与圆x 2+y 2-2x -3=0没有公共点,则实数k 的取值范围是________.3.设直线y =kx +1与圆x 2+y 2+2x -my =0相交于A ,B 两点,若点A ,B 关于直线l :x +y =0对称,则|AB |=________.考点二 圆与圆的位置关系例、已知圆M :x 2+y 2-2ay =0(a >0)截直线x +y =0所得线段的长度是22,则圆M 与圆N :(x -1)2+(y -1)2=1的位置关系是( )A .内切B .相交C .外切D .相离变式练习:1.若圆C 1:x 2+y 2=1与圆C 2:x 2+y 2-6x -8y +m =0外切,则m =( )A .21B .19C .9D .-112.(变结论)若本例两圆的方程不变,则两圆的公共弦长为________.[解题技法]几何法判断圆与圆的位置关系的3步骤: (1)确定两圆的圆心坐标和半径长;(2)利用平面内两点间的距离公式求出圆心距d ,求r 1+r 2,|r 1-r 2|; (3)比较d ,r 1+r 2,|r 1-r 2|的大小,写出结论.课后作业1.若直线2x +y +a =0与圆x 2+y 2+2x -4y =0相切,则a 的值为( ) A .±5 B .±5 C .3 D .±32.与圆C 1:x 2+y 2-6x +4y +12=0,C 2:x 2+y 2-14x -2y +14=0都相切的直线有( ) A .1条 B .2条 C .3条 D .4条3.直线y =kx +3被圆(x -2)2+(y -3)2=4截得的弦长为23,则直线的倾斜角为( ) A.π6或5π6 B .-π3或π3 C .-π6或π6 D.π64.过点(3,1)作圆(x -1)2+y 2=r 2的切线有且只有一条,则该切线的方程为( ) A .2x +y -5=0 B .2x +y -7=0 C .x -2y -5=0 D .x -2y -7=05.若圆x 2+y 2+2x -6y +6=0上有且仅有三个点到直线x +ay +1=0的距离为1,则实数a 的值为( ) A .±1 B .±24 C .± 2 D .±326.过点P (1,-2)作圆C :(x -1)2+y 2=1的两条切线,切点分别为A ,B ,则AB 所在直线的方程为( ) A .y =-34 B .y =-12 C .y =-32 D .y =-147.在平面直角坐标系xOy 中,直线x +2y -3=0被圆(x -2)2+(y +1)2=4截得的弦长为________. 8.若P (2,1)为圆(x -1)2+y 2=25的弦AB 的中点,则直线AB 的方程为________. 9.过点P (-3,1),Q (a,0)的光线经x 轴反射后与圆x 2+y 2=1相切,则a 的值为________.10.点P 在圆C 1:x 2+y 2-8x -4y +11=0上,点Q 在圆C 2:x 2+y 2+4x +2y +1=0上,则|P Q |的最小值是________.11.已知圆C 1:x 2+y 2-2x -6y -1=0和圆C 2:x 2+y 2-10x -12y +45=0. (1)求证:圆C 1和圆C 2相交;(2)求圆C 1和圆C 2的公共弦所在直线的方程和公共弦长.12.已知圆C 经过点A (2,-1),和直线x +y =1相切,且圆心在直线y =-2x 上. (1)求圆C 的方程;(2)已知直线l 经过原点,并且被圆C 截得的弦长为2,求直线l 的方程.提高练习1.过圆x 2+y 2=1上一点作圆的切线,与x 轴、y 轴的正半轴相交于A ,B 两点,则|AB |的最小值为( ) A. 2 B.3 C .2 D .32.在平面直角坐标系xOy 中,A 为直线l :y =2x 上在第一象限内的点,B (5,0),以AB 为直径的圆C 与直线l 交于另一点D .若AB ―→·CD ―→=0,则点A 的横坐标为________. 3.已知圆C :x 2+(y -a )2=4,点A (1,0).(1)当过点A 的圆C 的切线存在时,求实数a 的取值范围; (2)设AM ,AN 为圆C 的两条切线,M ,N 为切点,当|MN |=455时,求MN 所在直线的方程.。
高考数学(理)总复习讲义:直线与圆、圆与圆的位置关系

)
A. [- 3 ,- 1]
B.[- 1,3]
C. [- 3,1]
D. (-∞,- 3]∪ [1,+∞ )
解析: 选 C 由题意可得,圆的圆心为 (a,0),半径为 2,
|a- 0+ 1| 所以 12+ - 1 2≤ 2,
即 |a+ 1|≤2,解得- 3≤ a≤ 1,故选 C. 4.已知直线 l:y= k(x+ 3)和圆 C:x2+ (y- 1) 2=1,若直线 l 与圆 C 相切,则 k= ________.
A .相切
B.相交
C .相离
D .不确定
解析: 选 B 因为 M (a, b)在圆 O: x2+ y2= 1 外,所以 a2+b2> 1,而圆心 O 到直线
ax+ by= 1 的距离 d=
1 a2+
b2<
1.所以直线与圆相交.
2.(2019 杭·州模拟 )若无论实数 a 取何值时, 直线 ax+ y+a+ 1= 0 与圆 x2+ y2- 2x- 2y
所以该圆的圆心坐标为 (1,2),半径 r= 5,
又圆心 (1,2)到直线
3x- y- 6= 0 的距离为
d=
|3- 2-6| 32+ - 1 2=
210,由
|AB| 2
2= r2- d2,
得|AB|2= 4
5 5- 2
=10,即 |AB|=
10.
答案: 10
考点一 直线与圆的位置关系的判断
[ 师生共研过关 ]
= 0 与圆相交, l1, l2 与 l 平行,且与直线 l 的距离为 1,故可以看出,圆的
半径应该大于圆心到直线 l2 的距离 2+ 1.
[ 答案 ] (1)A (2)D (3)A
[ 解题技法 ]
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
直线与圆、圆与圆的位置关系 要点梳理 1.直线与圆的位置关系
位置关系有三种:___相离_____、___相切_____、___相交_____. 判断直线与圆的位置关系常见的有两种方法:
(1)代数法:――→判别式Δ=b2-4ac >0⇔相交=0⇔相切<0⇔相离 (2)几何法:利用圆心到直线的距离d和圆半径r的大小关系: dr⇔___相离_____..
2.计算直线被圆截得的弦长的常用方法 (1)几何方法 运用弦心距(即圆心到直线的距离)、弦长的一半及半径构成直角三角形计算. 弦长|AB|=2r2-d2 (2)代数方法 运用韦达定理及弦长公式 |AB|=1+k2|xA-xB|=(1+k2)[(xA+xB)2-4xAxB]. 说明:圆的弦长、弦心距的计算常用几何方法. 3.求过点P(x0,y0)的圆x2+y2=r2的切线方程与切线长 (1)过点P作圆的切线有三种类型: 若圆的方程为x2+y2=r2,点P(x0,y0)在圆上,则过P点且与圆x2+y2=r2相切的切线方程为____ x0x+y0y=r2________________________. 注:点P必须在圆x2+y2=r2上. 经过圆(x-a)2+(y-b)2=r2上点P(x0,y0)的切线方程为___ _(x0-a)(x-a)+(y0-b)(y-b)=r2__________.
若P(x0,y0)在圆外时,则过P的切线方程可设为y-y0=k(x-x0),利用待定系数法求解.一般运用圆心到直线的距离等于半径,但注意有两条切线说明:k为切线斜率,同时应考虑斜率不存在的情况. 当P在圆内时,不存在. (2)切线长的求法: 过圆C外一点P作圆C的切线,切点为M,半径为R,则|PM|=|PC|2-R2. 4.判断圆与圆的位置关系常用方法:从圆心距和两圆半径的关系入手 (几何法)设⊙C1:(x-a1)2+(y-b1)2=r21(r1>0),⊙C2:(x-a2)2+(y-b2)2=r22(r2>0),则有: |C1C2|>r1+r2⇔⊙C1与⊙C2____相离____; |C1C2|=r1+r2⇔⊙C1与⊙C2____外切 ____; |r1-r2|<|C1C2||C1C2|=|r1-r2|(r1≠r2)⇔⊙C1与⊙C2___内切_____; 0≤|C1C2|<|r1-r2|⇔⊙C1与⊙C2___内含_____. 设两圆圆心分别为O1、O2,半径为r1、r2 (r1≠r2),则|O1O2|>r1+r2__相离______; (2)已知两圆x2+y2+D1x+E1y+F1=0和x2+y2+D2x+E2y+F2=0相交,则与两圆共交点的圆系方程为___(x2+y2+D1x+E1y+F1)+λ(x2+y2+D2x+E2y+F2)=0____,其中λ为λ≠-1的任意常数,因此圆系不包括第二个圆. 当λ=-1时,为两圆公共弦所在的直线,方程为(D1-D2)x+(E1-E2)y+(F1-F2)=0. 5.求圆外一点P到圆O上任意一点距离的最小值为|PO|-r,最大值为|PO|+r(其中r为圆O的半径).
基础自测 1. 已知圆C经过M(2,-1)和直线x+y=1相切,且圆心在直线y=-2x上,则圆C的方程为_____(x-1)2+(y+2)2=2_________________ 2.直线y=ax+1与圆x2+y2-2x-3=0的位置关系是__相交______. 3.若直线3x+4y+m=0与圆x2+y2-2x+4y+4=0没有公共点,则实数m的取值范围是___(-∞,0)∪(10,+∞)_____________. 4.圆C1:x2+y2+2x+2y-2=0与圆C2:x2+y2-4x-2y+1=0的公切线有且仅有( ) A.1条 B.2条 C.3条 D.4条 5.直线y=kx+3与圆(x-3)2+(y-2)2=4相交于M,N两点,若|MN|≥23,则k的取值范围是( )
A.-34,0 B.-∞,-34∪[)0,+∞ C.-33,33 D.-23,0 6.圆x2+y2-4x=0在点P(1,3)处的切线方程为( ) A.x+3y-2=0 B.x+3y-4=0 C.x-3y+4=0 D.x-3y+2=0
题型一 直线与圆的位置关系 例1已知直线l:y=kx+1,圆C:(x-1)2+(y+1)2=12. 试证明:不论k为何实数,直线l和圆C总有两个交点; (1)方法一 证明
由 y=kx+1,(x-1)2+(y+1)2=12, 消去y得(k2+1)x2-(2-4k)x-7=0, 因为Δ=(2-4k)2+28(k2+1)>0, 所以不论k为何实数,直线l和圆C总有两个交点. 方法二证明 圆心C(1,-1)到直线l的距离d=|k+2|1+k2,圆C的半径R=23,R2-d2=12
-k2+4k+41+k2=11k2-4k+81+k2,而在S=11k2-4k+8中,Δ=(-4)2-4×11×8<0,故11k2-4k+8>0对k∈R恒成立, 所以R2-d2>0,即d方法三 (1)证明 因为不论k为何实数,直线l总过点A(0,1),而|AC|=5<23=R,所以点A(0,1)在圆C的内部,即不论k为何实数,直线l总经过圆C内部的定点A. 所以不论k为何实数,直线l和圆C总有两个交点.
题型二 圆的弦长、中点弦问题 例2 已知点P(0,5)及圆C:x2+y2+4x-12y+24=0. (1)若直线l过点P且被圆C截得的线段长为43,求l的方程; (2)求过P点的圆C的弦的中点的轨迹方程. 解 (1)方法一
如图所示,|AB|=43,取AB的中点D,连接CD,则CD⊥AB,连接AC、BC, 则|AD|=23,|AC|=4, 在Rt△ACD中,可得|CD|=2. 当直线l的斜率存在时,设所求直线的斜率为k,则直线的方程为y-5=kx, 即kx-y+5=0.
由点C到直线AB的距离公式,得|-2k-6+5|k2+-12=2,解得k=34.
当k=34时,直线l的方程为3x-4y+20=0. 又直线l的斜率不存在时,也满足题意,此时方程为x=0. ∴所求直线的方程为3x-4y+20=0或x=0. 方法二 当直线l的斜率存在时,设所求直线的斜率为k, 则直线的方程为y-5=kx,即y=kx+5.
联立直线与圆的方程 y=kx+5,x2+y2+4x-12y+24=0, 消去y,得(1+k2)x2+(4-2k)x-11=0.① 设方程①的两根为x1,x2,
由根与系数的关系,得 x1+x2=2k-41+k2,x1x2=-111+k2.② 由弦长公式,得1+k2|x1-x2| =1+k2[x1+x22-4x1x2]=43.
将②式代入,解得k=34, 此时直线方程为3x-4y+20=0. 又k不存在时也满足题意,此时直线方程为x=0. ∴所求直线的方程为x=0或3x-4y+20=0.
(2)设过P点的圆C的弦的中点为D(x,y),则CD⊥PD,即CD→·PD→=0, (x+2,y-6)·(x,y-5)=0, 化简得所求轨迹方程为x2+y2+2x-11y+30=0.
变式训练2已知直线l:y=kx+1,圆C:(x-1)2+(y+1)2=12.求直线l被圆C截得的最短弦长.
方法一 设直线与圆交于A(x1,y1)、B(x2,y2)两点,则直线l被 圆C截得的弦长 |AB|=1+k2|x1-x2|=28-4k+11k21+k2=2 11-4k+31+k2, 令t=4k+31+k2,则tk2-4k+(t-3)=0, 当t=0时,k=-34,当t≠0时,因为k∈R, 所以Δ=16-4t(t-3)≥0,解得-1≤t≤4,且t≠0,故t=4k+31+k2的最大值为4,此时|AB|最小为27. 方法二解 由平面几何知识,
知|AB|=2R2-d2=2 8-4k+11k21+k2,下同方法一. 方法三 由平面几何知识知过圆内定点A(0,1)的弦,只有和AC (C为圆心)垂直时才最短,而此时点A(0,1)为弦AB的中点,由勾股定理,知|AB|=212-5=27, 即直线l被圆C截得的最短弦长为27.
题型三 圆的切线问题 例3 已知点M(3,1),直线ax-y+4=0及圆(x-1)2+(y-2)2=4. (1)求过M点的圆的切线方程; (2)若直线ax-y+4=0与圆相切,求a的值; 解 (1)圆心C(1,2),半径为r=2, ①当直线的斜率不存在时,方程为x=3. 由圆心C(1,2)到直线x=3的距离d=3-1=2=r知,此时,直线与圆相切. ②当直线的斜率存在时, 设方程为y-1=k(x-3), 即kx-y+1-3k=0. 由题意知|k-2+1-3k|k2+1=2,解得k=34.
∴方程为y-1=34(x-3),即3x-4y-5=0. 故过M点的圆的切线方程为x=3或3x-4y-5=0. (2)由题意有|a-2+4|a2+1=2,
解得a=0或a=43. 探究提高 求过一点的圆的切线方程,首先要判断此点是否在圆上.若在圆上,该点为切点;若不在圆上,切线应该有两条,设切线的点斜式方程,用待定系数法求解.注意,需考虑无斜率的情况.求弦长问题,要充分运用圆的几何性质.
变式训练3已知圆C:x2+y2+2x-4y+3=0.若圆C的切线在x轴和y轴上的截距相等,求此切线的方程; 解 将圆C配方得(x+1)2+(y-2)2=2. ①当直线在两坐标轴上的截距为零时,设直线方程为y=kx,
