人教版初中八年级数学上册专题三角形全等之动点问题讲义及答案
八年级 数学 人教版全等三角形 动点问题【精编版】

动点问题辅导教案第7讲动点问题所谓“动点型问题”是指题设图形中存在一个或多个动点,它们在线段、射线或弧线上运动的一类开放性题目.解决这类问题的关键是动中求静,灵活运用有关数学知识解决问题.课前回顾:1、(2014•齐齐哈尔)在等腰直角三角形ABC中,∠BAC=90°,AB=AC,直线MN过点A且MN∥BC,过点B为一锐角顶点作Rt△BDE,∠BDE=90°,且点D在直线MN上(不与点A重合),如图1,DE与AC交于点P,易证:BD=DP.(无需写证明过程)(1)在图2中,DE与CA延长线交于点P,BD=DP是否成立?如果成立,请给予证明;如果不成立,请说明理由;(2)在图3中,DE与AC延长线交于点P,BD与DP是否相等?请直接写出你的结论,无需证明.2、(2014•牡丹江)如图,在等边△ABC中,点D在直线BC上,连接AD,作∠ADN=60°,直线DN交射线AB 于点E,过点C作CF∥AB交直线DN于点F.(1)当点D在线段BC上,∠NDB为锐角时,如图①,求证:CF+BE=CD;(提示:过点F作FM∥BC交射线AB于点M.)(2)当点D在线段BC的延长线上,∠NDB为锐角时,如图②;当点D在线段CB的延长线上,∠NDB为钝角时,如图③,请分别写出线段CF,BE,CD之间的数量关系,不需要证明;(3)在(2)的条件下,若∠ADC=30°,S△ABC=4,则BE=,CD=.考点一:点动型:匀速运动1. 如图,在直角梯形ABCD 中,AD ∥BC ,∠B=90°,AD=24cm ,AB=8cm ,BC=26cm ,动点P 从A 开始沿AD 边向D 以1cm/s 的速度运动;动点Q 从点C 开始沿CB 边向B 以3cm/s 的速度运动.P 、Q 分别从点A 、C 同时出发,当其中一点到达端点时,另外一点也随之停止运动,设运动时间为ts . (1)当t 为何值时,四边形PQCD 为平行四边形? (2)当t 为何值时,四边形PQCD 为等腰梯形? (3)当t 为何值时,四边形PQCD 为直角梯形?2. 如图,在梯形ABCD 中,AD ∥BC ,∠B=90°,AB=14cm ,AD=15cm ,BC=21cm ,点M从点A 开始,沿边AD 向点D 运动,速度为1cm/s ;点N 从点C 开始,沿边CB 向点B 运动,速度为2cm/s 、点M 、N 分别从点A 、C 出发,当其中一点到达端点时,另一点也随之停止运动,设运动时间为t 秒.(1)当t 为何值时,四边形MNCD 是平行四边形? (2)当t 为何值时,四边形MNCD 是等腰梯形?3. 如图,已知ABC △中,10AB AC ==厘米,8BC =厘米,点D 为AB 的中点.(1) 如果点P 在线段BC 上以3厘米/秒的速度由B 点向C 点运动,同时,点Q 在线段CA 上由C 点向A 点运动.a) 若点Q 的运动速度与点P 的运动速度相等,经过1秒后,BPD △与CQP △是否全等,请说明理由; b) 若点Q 的运动速度与点P 的运动速度不相等,当点Q 的运动速度为多少时,能够使BPD △与CQP △全等?(2) 若点Q 以②中的运动速度从点C 出发,点P 以原来的运动速度从点B 同时出发,都逆时针沿ABC △三边运动,求经过多长时间点P 与点Q 第一次在ABC △的哪条边上相遇?4. 如图,在梯形ABCD中,3545AD BC AD DC AB B ====︒∥,,,.动点M 从B 点出发沿线段BC 以每秒2个单位长度的速度向终点C 运动;动点N 同时从C 点出发沿线段CD 以每秒1个单位长度的速度向终点D 运动.设运动的时间为t 秒. (1) 求BC 的长.(2) 当MN AB ∥时,求t 的值.(3) 试探究:t 为何值时,MNC △为等腰三角形.【练习】1. 如图,在等边ABC ∆的顶点A 、C 处各有一只蜗牛,它们同时出发,分别以每分钟1个单位的速度由A 向B和由C 向A 爬行,其中一只蜗牛爬到终点时,另一只也停止运动,经过t 分钟后,它们分别爬行到D,E 处,请问(1)在爬行过程中,CD 和BE 始终相等吗?(2)若蜗牛沿着AB 和CA 的延长线爬行,EB 与CD 交于点Q ,其他条件不变,蜗牛爬行过程中CQE ∠ 的大小不变,求证:︒=∠60CQE(3)如果将原题中“由C 向A 爬行”改为“沿着BC 的延长线爬行,连接DE 交AC 于F ”,其他条件不变,则爬行过程中,DF 始终等于EF 是否正确C2. 已知:如图,△ABC 是边长3cm 的等边三角形,动点P 、Q 同时从A 、B 两点出发,分别沿AB 、BC 方向匀速移动,它们的速度都是1cm/s ,当点P 到达点B 时,P 、Q 两点停止运动.设点P 的运动时间为t (s ),解答下列问题:(1)当t 为何值时,△PBQ 是直角三角形? (2)设四边形APQC 的面积为y (cm 2),①求y 与t 的关系式及自变量t 的取值范围;②是否存在某一时刻t ,使四边形APQC 的面积是△ABC 面积的三分之二?如果存在,求出相应的t 值;不存在,说明理由;(②问给学过一元二次方程基本知识的同学做)3.在Rt △ABC 中,∠ABC=90°,AB=6cm ,BC=8cm ,P 从A 开始出发向点B 以2cm/s 的速度移动,同时点Q 从点B 开始出发向C 以沿1cm/s 的速度移动,一个点到达终点后,另一个点也随之停止移动,设运动的时间为x 秒. (1)求AC 的长度;(2)当x 为何值时,△PBQ 为等腰三角形,并求PQ 的长.4.如图,在平面直角坐标系中,O 为坐标原点,函数y=﹣x +2的图象与x 轴交与点A ,与y 轴交与点B ,点P 为直线AB 上一动点,若△POA 是等腰三角形,求所有符合条件的点P 的坐标.5.(2014秋•江都市校级月考)如图:直线y=﹣x+3与x轴、y轴分别交于A、B两点,点C(x,y)是直线y=﹣x+3与A、B不重合的动点.(1)当点C运动到什么位置时△AOC的面积是6;(2)过点C的另一直线CD与y轴相交于D点,是否存在点C使△BCD与△AOB全等?若存在,请求出点C的坐标;若不存在,请说明理由.6.(2015•枣庄)如图,直线y=x+2与抛物线y=ax2+bx+6(a≠0)相交于A(,)和B(4,m),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.(1)求抛物线的解析式;(2)是否存在这样的P点,使线段PC的长有最大值?若存在,求出这个最大值;若不存在,请说明理由;(3)求△PAC为直角三角形时点P的坐标.7.(2014秋•历城区期末如图,抛物线y=ax2﹣2ax+c(a≠0)交x轴于A、B两点,A点的坐标为(3,0),与y轴交于点C(0,4),以OC、OA为边作矩形OADC交抛物线于点G.(1)求抛物线的解析式;(2)点E在边OA(不包括O、A两点)上移动,过点E作平行于抛物线的对称轴l的直线分别交CD于点F,交AC于点M,交抛物线于点P,若点E的横坐标为m,请用含m的代数式表示PM的长;8.(2014•琼海模拟)如图,直线与y轴交于A点,过点A的抛物线与直线交于另一点B,过点B作BC⊥x轴,垂足为点C(3,0).(1)求B点坐标以及抛物线的函数解析式.(2)动点P在线段OC上,从原点O出发以每秒一个单位的速度向C运动,过点P作x轴的垂线交直线AB于点M,交抛物线于点N.设点P运动的时间为t秒,求线段MN的长与t的函数关系式,当t为何值时,MN的长最大,最大值是多少?(3)在(2)的条件下(不考虑点P与点O、点C重合的情况),连接CM、BN,当t为何值时,四边形BCMN为平行四边形?问对于所求的t的值,平行四边形BCMN是否为菱形?说明理由.9.(2015秋•淮安校级期中)如图,在平面直角坐标系中,直线l:y=﹣2x﹣8分别与x轴,y轴相交于A,B两点.(1)若点P(0,k)是y轴的负半轴上的一个动点,以P为圆心,3为半径作⊙P.当k=时,以⊙P 与x轴的两个交点和圆心P为顶点的三角形是正三角形?(2)若点P在原点,试探讨在以P为圆心,r为半径的圆上,到直线l:y=﹣2x﹣8的距离为的点的个数与r的关系.10.(2015•徐州)如图,平面直角坐标系中,将含30°的三角尺的直角顶点C落在第二象限.其斜边两端点A、B 分别落在x轴、y轴上,且AB=12cm(1)若OB=6cm.①求点C的坐标;②若点A向右滑动的距离与点B向上滑动的距离相等,求滑动的距离;(2)点C与点O的距离的最大值=cm.11.(2010秋•厦门校级期中)如图,直线l的解析式为y=﹣x+4,它与x轴、y轴分别相交于A、B两点.平行于直线l的直线m从原点O出发,沿x轴的正方向以每秒1个单位长度的速度运动,它与x轴、y轴分别相交于M、N两点,设运动时间为t秒(0<t≤4).(1)求A、B两点的坐标;(2)以MN为对角线作矩形OMPN,记△MPN和△OAB重合部分的面积为S1,在直线m的运动过程中,当t为何值时,S1为△OAB面积的?12.(2011•崇左)已知抛物线y=x2+4x+m(m为常数)经过点(0,4)(1)求m的值;(2)将该抛物线先向右、再向下平移得到另一条抛物线.已知这条平移后的抛物线满足下述两个条件:它的对称轴(设为直线l2)与平移前的抛物线的对称轴(设为l1)关于y轴对称;它所对应的函数的最小值为﹣8.①试求平移后的抛物线所对应的函数关系式;②试问在平移后的抛物线上是否存在着点P,使得以3为半径的⊙P既与x轴相切,又与直线l2相交?若存在,请求出点P的坐标,并求出直线l2被⊙P所截得的弦AB的长度;若不存在,请说明理由.【课后练习】1. 已知:等边三角形ABC 的边长为4厘米,长为1厘米的线段MN 在ABC △的边AB 上沿AB 方向以1厘米/秒的速度向B 点运动(运动开始时,点M 与点A 重合,点N 到达点B 时运动终止),过点M N 、分别作AB边的垂线,与ABC △的其它边交于P Q 、两点,线段MN 运动的时间为t 秒.(1)线段MN 在运动的过程中,t 为何值时,四边形MNQP 恰为矩形?并求出该矩形的面积;(2)线段MN 在运动的过程中,四边形MNQP 的面积为S ,运动的时间为t .求四边形MNQP 的面积S 随运动时间t 变化的函数关系式,并写出自变量t 的取值范围.2. 如图,已知ABC △中,10AB AC ==厘米,8BC =厘米,点D 为AB 的中点.(1)如果点P 在线段BC 上以3厘米/秒的速度由B 点向C 点运动,同时,点Q 在线段CA 上由C 点向A 点运动. ①若点Q 的运动速度与点P 的运动速度相等,经过1秒后,BPD △与CQP △是否全等,请说明理由; ②若点Q 的运动速度与点P 的运动速度不相等,当点Q 的运动速度为多少时,能够使BPD △与CQP △全等? (2)若点Q 以②中的运动速度从点C 出发,点P 以原来的运动速度从点B 同时出发,都逆时针沿ABC △三边运动,求经过多长时间点P 与点Q 第一次在ABC △的哪条边上相遇?CPQA MN CPQB A MNCPQA M N3.(2009•黄冈校级模拟)正方形ABCD的边长与等腰直角三角形PMN的腰长均为4cm,且AB与MN都在直线l 上,开始时点B与点M重合.让正方形沿直线向右平移,直到A点与N点重合为止,设正方形与三角形重叠部分的面积为y(cm2),MB的长度为x(cm),则y与x之间的函数关系的图象大致是()A.B.C.D.。
数学人教版八年级上册全等三角形之动态问题

全等三角形之动态问题教学目标1、知识与技能了解全等三角形动态问题的常见类型,掌握旋转中的全等三角形的证明;2、过程与方法在观察、操作、推理、归纳等探索过程中,发展学生的合情推理能力,逐步培养数学推理的习惯;3、情感、态度与价值观体会数学与现实生活的联系,增强克服困难的勇气和信心。
教学重、难点重点:利用所学的定理证明、性质进行相关的证明与计算;难点:在动态问题中找寻全等的条件。
教学用具三角板、ppt、几何画板教学过程一、复习引入师:通过全等三角形这一章知识的学习,你掌握了哪些方法证明三角形全等?学会了哪些常见的辅助线构造全等三角形?生:......师:数学中还有一类问题是大家比较害怕和缺少信心的题。
生:动点问题。
师:那么这节课我们就一起来探讨一下全等三角形中的动态问题。
(板书课题)数学中所谓的动态问题常见的有以下几种:1、动点问题;2、图形变换:平移、旋转、翻折(即轴对称)。
下面我们先来看第一类型。
二、新课讲解例题1 如图,在等边△ABC的顶点A、C处各有一只蜗牛,它们同时出发,分别以相同的速度由A向B和由C向A 爬行,经过t分钟后,它们分别爬行到D、E处,请问(1)在爬行过程中,CD和BE始终相等吗?(2)如果将原题中的“由A向B和由C向A爬行”,改为“沿着AB和CA的延长线爬行”,EB与CD交于点Q,其他条件不变,如图所示,蜗牛爬行过程中CD、BE相等吗?思路点拨:由动点的运动速度和时间相等得到其中一组对应边相等,从而为证明三角形全等提供条件。
此类题目通常抓住动点的运动速度和时间推到相应线段长度关系。
同步练习.如图,已知△ABC中,AB=AC=12厘米,BC=9厘米,点D为AB的中点.如果点P在线段BC上以3厘米/秒得速度由B点向C点运动,同时点Q在线段CA上由C点向A点运动.①若点Q的运动速度与点P的运动速度相等,1秒钟时,△BPD与△CPQ是否全等,请说明理由;②若点Q的运动速度与点P的运动速度不相等,且△BPD≌△CPQ,求点Q的运动速度为多少时?变式:当点Q的运动速度为多少时,能够使△BPD与△CQP全等?师:接下来我们来看看图形变换与全等三角形的相关题型。
(完整)八年级数学全等三角形之动点问题(精品)

八年级数学全等三角形之动点问题(全等三角形)拔高练习解答题(本大题共8小题,共120分)1.(本小题15分)如图,在等边△ABC的顶点A、C处各有一只蜗牛,它们同时出发,分别以相同的速度由A向B和由C向A爬行,经过t分钟后,它们分别爬行到D、E处,请问(1)在爬行过程中,CD和BE始终相等吗?(2)如果将原题中的“由A向B和由C向A爬行”,改为“沿着AB和CA的延长线爬行”,EB与CD交于点Q,其他条件不变,如图(2)所示,蜗牛爬行过程中∠CQE的大小保持不变.请利用图(2)情形,求证:∠ CQE =60°;(3)如果将原题中“由C向A爬行”改为“沿着BC的延长线爬行,连接DE交AC于F”,其他条件不变,如图(3),则爬行过程中,DF始终等于EF是否正确.2.(本小题15分)如图,已知△ABC中,AB=AC=12厘米,BC=9厘米,点D为AB的中点.(1)如果点P在线段BC上以3厘米/秒得速度由B点向C点运动,同时点Q在线段CA上由C点向A点运动.①若点Q的运动速度与点P的运动速度相等,1秒钟时,△BPD与△CQP是否全等,请说明理由;②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD≌△CQP?(2)若点Q以(1)②中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿△ABC三边运动,求经过多长时间点P与点Q第一次在△ABC的哪条边上相遇?3.(本小题15分)如图,△ABC的边BC在直线l上,AC⊥BC,且AC=BC;△EFP的边FP也在直线l上,边EF与边AC重合,且EF=FP.(1)请你通过观察,测量,猜想并写出AB与AP所满足的数量关系和位置关系;(2)将△EFP沿直线l向左平移到图2的位置时,EP交AC于点Q,连接AP,BQ,猜想并写出BQ与AP所满足的数量关系和位置关系,请证明你的猜想;(3)将△EFP沿直线l向左平移到图3的位置时,EP的延长线交AC的延长线于点Q,连接A P,BQ.你认为(2)中所猜想的BQ与AP的数量关系和位置关系还成立吗?若成立,给出证明;若不成立,请说明理由.3.4.(本小题15分)如图,在△ABC中,∠CAB=70°. 在同一平面内, 将△ABC绕点A旋转到△AB′C′ 的位置, 使得 CC′∥AB, 则∠B′AB = _________5.(本小题15分)已知如图(1),△ABC中,∠BAC=90°,AB=AC,AE是过A的一条直线,且B、C在AE的异侧,BD⊥AE于D,CE⊥AE于E,求证:(1)BD=DE+CE;(2)若直线AE绕A点旋转到(2)位置时(BD<CE),其余条件不变,问BD与DE、CE的关系如何?请予证明.(3)若直线AE绕A点旋转到图(3)位置时,(BD>CE),其余条件不变,问BD与DE、CE的关系如何?请直接写出结果,不须证明.(4)归纳(1)、(2)、(3),请用简捷语言表述BD、DE、CE的关系.6.(本小题15分)在图中,直线MN与线段AB相交于点O,∠1 = ∠2 = 45°.(1)如图,若AO = OB,请写出AO与BD 的数量关系和位置关系;(2)将图中的MN绕点O顺时针旋转得到下图,其中AO = OB.求证:AC = BD,AC ⊥ BD;7.(本小题15分)如图,A、B、C、D在同一直线上,AB=CD,DE∥AF,且DE=AF,求证:△AFC≌△DEB.如果将BD沿着AD边的方向平行移动,如图,B点与C点重合时,如图,B 点在C点右侧时,其余条件不变,结论是否仍成立,如果成立,请予证明;如果不成立,请说明理由.8.(本小题15分)已知,如图,E、F分别为线段AC上的两个动点,且DE⊥AC于E点,BF⊥AC 于F点,若AB=CD,AF=CE,BD交AC于M点,(1)求证:MB=MD,ME=MF(2)当E、F两点移到至如图所示的位置时,其它条件不变,上述结论能否成立?若成立,请说明你的理由。
全等三角形之动点问题

全等三角形之动点问题(一)1、已知:如图,在△ABC中,AB=AC=18,BC=12,点D为AB的中点.点P在线段BC上以每秒3个单位的速度由B点向C点运动,同时点Q在线段CA上由C点向A点以每秒a个单位的速度匀速运动.设运动时间为t秒,若某一时刻△BPD与△CQP全等,求t的值与相应的点Q的运动速度a2、如图,在等边ABC∆的顶点A、C处各有一只蜗牛,它们同时出发,分别以每分钟1各单位的速度油A向B和由C向A爬行,其中一只蜗牛爬到终点时,另一只也停止运动,经过t分钟后,它们分别爬行到D,E处,请问(1)在爬行过程中,CD和BE始终相等吗?(2)若蜗牛沿着AB和CA的延长线爬行,EB与CD交于点Q,其他条件不变,如图(2)所示,,求证:︒CQE=∠60(3)如果将原题中“由C向A爬行”改为“沿着BC的延长线爬行,连接DE交AC于F”,其他条件不变,则爬行过程中,DF始终等于EF是否正确3、在△ABC中,,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E(1)当直线MN绕点C旋转到图①的位置时,求证:DE=AD+BE(2)当直线MN绕点C旋转到图②的位置时,求证:DE=AD-BE(3)当直线MN绕点C旋转到图③的位置时,试问:DE、AD、BE有怎样的等量关系?请写出这个等量关系,并加以证BA O DC E图84. 如下图,已知正方形ABCD 中,边长为10厘米,点E 在AB 边上,BE=6厘米.(1)如果点P 在线段BC 上以4厘米/秒的速度由B 点向C 点运动,同时,点Q 在线段CD 上由C 点向D 点运动. ①若点Q 的运动速度与点P 的运动速度相等,经过1秒后,△BPE 与△CQP 是否全等,请说明理由; ②若点Q 的运动速度与点P 的运动速度不相等,当点Q 的运动速度为多少时,能够使△BPE 与△CQP 全等? (2)若点Q 以②中的运动速度从点C 出发,点P 以原来的运动速度从点B 同时出发,都逆时针沿正方形ABCD 四边运动,求经过多长时间点P 与点Q 第一次在正方形ABCD 边上的何处相遇?5、如图7,点O 是线段AD 的中点,分别以AO 和DO 为边在线段AD 的同侧作等边三角形OAB 和等边三角形OCD ,连结AC 和BD ,相交于点E ,连结BC .求∠AEB 的大小;6、ΔOAB 固定不动,保持ΔOCD 的形状和大小不变,将ΔOCD 绕着点O 旋转(ΔOAB 和ΔOCD 不能重叠),求∠AEB 的大小.C B OD图7AE全等构造角平分线类1如图,在ABC ∆中,2B C ∠=∠,BAC ∠的平分线AD 交BC 与D .求证:AB BD AC +=.DC B A2如图,在ABC ∆中,AB BD AC +=,BAC ∠的平分线AD 交BC 与D .求证:2B C ∠=∠.DC B A3如图,ABC ∆中,AB=2AC ,AD 平分BAC ∠,且AD=BD ,求证:CD ⊥AC4如图,在四边形ABCD 中,BC >BA,AD =CD ,BD 平分ABC ∠,求证: 0180=∠+∠C A5已知ABC ∆中,60A ∠=,BD 、CE 分别平分ABC ∠和ACB ∠,BD 、 CE 交于点O ,试判断BE 、CD 、BC 的数量关系,并加以证明.OED CBA6如图,在ABC ∆中,60B ∠=︒,AD 、CE 分别平分BAC ∠、BCA ∠,且AD 与CE 的交点为F .求证:FE FD =.CDBACBAFBEDCA7如图,已知在ABC 内,060BAC ∠=,040C ∠=,P ,Q 分别在BC ,CA 上,并且AP ,BQ 分别是BAC ∠,ABC ∠的角平分线。
八年级数学等边三角形中的动点问题[1].doc1
![八年级数学等边三角形中的动点问题[1].doc1](https://img.taocdn.com/s3/m/530de62fb52acfc789ebc9ff.png)
等边三角形中的动点问题1、已知,如图△ABC 是边长3cm 的等边三角形.动点P 以1cm/s 的速度从点A 出发,沿线段AB 向点B 运动.设点P 的运动时间为(s ),那么t 为何值时,△PBC 是直角三角形?2、已知,如图△ABC 是边长3cm 的等边三角形. 动点P 从点A 出发,沿AB 向点B 运动,动点Q 从点B 出发,沿BC 向点C 运动,如果动点P 、Q 都以1cm/s 的速度同时出发. 设运动时间为t (s ),那么t 为何值时,△PBQ 是直角三角形?3、已知,如图△ABC 是边长3cm 的等边三角形. 动点P 从点A 出发,沿AB 向点B 运动,动点Q 从点C 出发,沿射线BC 方向运动. 连接PQ 交AC 于D. 如果动点P 、Q 都以1cm/s 的速度同时出发.设运动时间为t (s ),那么 当t 为何值时,△DCQ 是等腰三角形?4、已知,如图△ABC 是边长3cm 的等边三角形.动点P 从点A 出发,沿AB 向点B 运动,动点Q 从点C 出发,沿射线BC 方向运动. 连接PQ 交AC 于D. 如果动点P 、Q 都以1cm/s 的速度同时出发. 设运动时间为t (s ),连接PC. 请探究:在点P 、Q 的运动过程中△PCD 和△QCD 的面积是否相等? CQBP AQDBCPA DPA BCP A5、已知等边三角形△ABC ,(1)动点P 从点A 出发,沿线段AB 向点B 运动,动点Q 从点B 出发,沿线段BC 向点C 运动,连接CP 、AQ 交于M ,如果动点P 、Q 都以相同的速度同时出发, 则∠AMP=___度。
(2)若动点P 、Q 继续运动,分别沿射线AB 、BC 方向运动,(1)题中的结论还成立吗?6.在等边ABC ∆的顶点A 、C 处各有一只蜗牛,它们同时出发,分别以每分钟1各单位的速度由A 向B 和由C 向A 爬行,其中一只蜗牛爬到终点时,另一只也停止运动,经过t 分钟后,它们分别爬行到D,E 处,请问:(1)在爬行过程中,CD 和BE 始终相等吗?(2)若蜗牛沿着AB 和CA 的延长线爬行,EB 与CD 交于点Q ,其他条件不变,所示,蜗牛爬行过程中CQE ∠ 的大小条件不变,求证:︒=∠60CQE(3)如图。
全等三角形动点问题(人教版)(含答案)

全等三角形动点问题(人教版)一、单选题(共8道,每道12分)1.已知:如图,在长方形ABCD中,AB=6厘米,BC=9厘米,点P从点A出发,沿AB边向终点B以1厘米/秒的速度移动,同时点Q从点B出发沿BC边向终点C以2厘米/秒的速度移动,如果P,Q两点同时出发,当其中一点到达终点后停止运动,另一点也随之停止运动,设点P的运动时间为t秒,连接PQ,DQ.若△DCQ≌△QBP,则t的值为( )A.1B.2C. D.3答案:D解题思路:试题难度:三颗星知识点:动点问题2.已知:如图,在梯形ABCD中,AD∥BC,∠ABC=90°,AD=12,BC=24,动点P从点A出发沿AD向点D以每秒1个单位的速度运动,动点Q从点C出发沿CB向点B以每秒2个单位的速度运动,P,Q同时出发,当点P停止运动时,点Q也随之停止,连接PQ,DQ.设点P的运动时间为t秒,当t为( )时,△PDQ≌△CQD.A.12B.8C.6D.4答案:D解题思路:试题难度:三颗星知识点:动点问题3.已知:如图,在长方形ABCD中,AB=4,AD=6.延长BC到点E,使CE=2,连接DE.动点P从点B出发,以每秒2个单位的速度沿BC-CD-DA向终点A运动,设点P的运动时间为t 秒.当t的值为( )时,△ABP和△DEC全等.A.1B.1或3C.1或7D.3或7答案:C解题思路:试题难度:三颗星知识点:动点问题4.已知:如图,在△ABC中,AB=AC=10cm,BC=8cm,点D为AB的中点.点P在线段BC上以每秒2cm的速度由点B向点C运动,同时点Q在线段CA上由点C向点A运动.设点P 运动时间为t秒,当t的值为( )时,△BPD与△CQP全等.A. B.3C.或2D.或3答案:C解题思路:试题难度:三颗星知识点:动点问题5.已知:如图,在矩形ABCD中,AB=4cm,BC=6cm,点E为AB中点,如果点P在线段BC 上以每秒2cm的速度由点B向点C运动,同时,点Q在线段CD上由点C向点D运动.设点P的运动时间为t秒,若某一时刻△BPE与△CQP全等,则点Q的运动速度是( )A.cm/sB.2cm/sC.2cm/s或4cm/sD.cm/s或2cm/s答案:D解题思路:1.思路分析首先判断这是一道动点问题,对于动点问题,我们的解决套路是:①研究基本图形,动点的运动状态;②分析状态转折点,分段;③画出符合题意的图形,表达线段长,建等式.2.解题过程试题难度:三颗星知识点:动点问题6.如图,在矩形ABCD中,AB=6m,BC=8m,AC=10m,动点P以2m/s的速度从点A出发,沿AC方向向点C移动,同时动点Q以1m/s的速度从点C出发,沿CB方向向点B移动,当P,Q两点中其中一点到达终点时则停止运动.设运动时间为t秒,则当t为( )时,△PQC 是以PQ为底的等腰三角形.A.5B.C.4D.答案:D解题思路:试题难度:三颗星知识点:动点问题7.如图,在矩形ABCD中,AB=20cm,BC=4cm,动点P以3cm/s的速度从B点出发,沿BA 方向向点A移动,同时动点Q以1cm/s的速度,沿CD方向向点D移动,当其中一点到达终点时,另一点也随之停止运动,设运动时间为t(s),则当t为( )时,线段PQ恰好平分矩形ABCD的面积.A.3B.4C.5D.6答案:C解题思路:试题难度:三颗星知识点:动点问题8.已知:如图,等边△ABC的边长为6,动点P从点A出发沿AB-BC-CA方向以每秒2个单位的速度运动,再次回到点A时停止运动.连接BP,CP,设点P运动的时间为t秒.若△BCP的面积是△ABC面积的,则t的值为( )A.2或7B.4或14C.2或14D.4或7答案:A解题思路:1.思路分析首先判断这是一道动点问题,对于动点问题,我们的解决套路是:①研究基本图形,动点的运动状态;②分析状态转折点,分段;③画出符合题意的图形,表达线段长,建等式.2.解题过程试题难度:三颗星知识点:动点问题。
八年级数学全等三角形(含知识点练习题答案)

三角形综合讲义全等综合随堂练习1.1如图,将两个全等的直角三角形ABD ∆、ACE ∆拼在一起(图1),ABD ∆不动,(1)若将ACE ∆绕点A 逆时针旋转,连接DE ,M 是DE 的中点,连接MB 、MC (图2),证明:MB=MC .(2)若将图1的CE 向上平移,CAE ∠不变,连接DE ,M 是DE 的中点,连接MB 、MC (图3),判断并直接写出MB 、MC 的数量关系.(3)在(2)中,若CAE ∠的大小改变(图4),其他条件不变,则(2)中的MB 、MC 的数量关系还成立吗?说明理由. 【答案】见解析.【解析】证明:(1)如图2,连接AM ,由已知得ABD ACE ∆∆≌,AD AE ∴=,AB AC =,BAD CAE ∠=∠ MD ME =,M AD M AE ∴∠=∠ MAD BAD MAE CAE ∴∠-∠=∠-∠ 即BAM CAM ∠=∠,在ABM ∆和ACM ∆中,AB ACBAM CAM AM AM =⎧⎪∠=∠⎨⎪=⎩()ABM ACM SAS ∴∆∆≌MB MC ∴=.(2)MB =MC .理由如下:如图3,延长DB 、AE 相交于E ',延长EC 交AD 于F ,BD BE '∴=,CE CF = M 是ED 的中点,B 是DE '的中点,//MB AE '∴ MBC CAE ∴∠=∠,同理//MC AD ,BCM BAD ∴∠=∠ BAD CAE ∠=∠ MBC BCM ∴∠=∠ MB MC ∴=. (3)MB =MC 还成立.如图4,延长BM 交CE 于F ,//CE BD ,M DB M EF ∴∠=∠,M BD M FE ∠=∠ M 是ED 的中点 M D M E ∴=在M DB ∆和M EF ∆中,MDB MEF MBD MFE MD ME ∠=∠⎧⎪∠=∠⎨⎪=⎩()MDB MEF AAS ∴∆∆≌ M B M F ∴=90ACE ∠=︒ 90BCF ∴∠=︒ MB MC ∴=.1.2如图,在ABC ∆中,90ACB ∠=︒,AC BC =,E 为AC 边的一点,F 为AB 边上一点,连接CF ,交BE 于点D 且ACF CBE ∠=∠,CG 平分ACB ∠交BD 于点G , (1)求证:CF=BG ;(2)延长CG 交AB 于H ,连接AG ,过点C 作//CP AG 交BE 的延长线于点P ,求证:PB CP CF =+; (3)在(2)问的条件下,当2GAC FCH ∠=∠时,若AEG S ∆=BG=6,求AC 的长.【答案】见解析;【解析】解:(1)如图1,90ACB ∠=︒,AC BC = 45A ∴∠=︒CG 平分ACB ∠45ACG BCG ∴∠=∠=︒,A BCG ∠=∠ 在BCG ∆和CAF∆中,A BC G A C B C A C F C B E ∠=∠⎧⎪=⎨⎪∠=∠⎩()BCG CAF ASA ∴∆∆≌ CF BG ∴=.(2)如图2,//PC AG PCA CAG ∴∠=∠AC BC =,ACG BCG ∠=∠,CG CG =ACG BCG ∴∆∆≌ CAG CBE ∴∠=∠4545PCG PCA ACG CAG CBE ∠=∠+∠=∠+︒=∠+︒ PCG PGC ∴∠=∠ PC PG ∴=PB BG PG =+,BG CF = PB CF CP ∴=+.(3)如图3,过E 作EM AG ⊥,交AG 于M ,1332AEG S AG EM ∆== 由(2)得:ACG BCG ∆∆≌ 6BGAG ∴== 162EM ∴⨯⨯= EM设FCH x ∠=︒,则2GAC x ∠=︒,2ACF EBC GAC x ∴∠=∠=∠=︒ 45ACH ∠=︒ 245x x ∴+=︒,15x =︒ 30ACF GAC ∴∠=∠=︒在Rt AEM ∆中,2AE EM ==3AMM ∴是AG 的中点AE EG ∴==6BE BG EG ∴=+=+ 在Rt ECB∆中,30ECB ∠=︒132CE BE∴==33AC AE EC ∴=+=+=+1.3如图1,在ABC ∆中,36A ∠=︒,AB=AC ,ABC ∠的平分线BE 交AC 于E .(1)求证:AE=BC ;(2)如图(2),过点E 作EF//BC 交AB 于F ,将AEF ∆绕点A 逆时针旋转角α(0144α︒<<︒)得到AE F ''∆,连结CE ',BF ',求证:CE BF ''=;(3)在(2)的旋转过程中是否存在CE '//AB ?若存在,求出相应的旋转角α;若不存在,请说明理由.【答案】见解析.【解析】(1)证明:∵AB =BC ,36A ∠=︒,72ABC C ∴∠=∠=︒ 又∵BE 平分ABC ∠ 36ABE CBE ∴∠=∠=︒ 18072BEC C CBE ∴∠=︒-∠-∠=︒,ABE A ∴∠=∠,BEC C ∠=∠ AE BE ∴=,BE BC =,AE BC ∴=.(2)证明:∵AC=AB 且EF//BC ,AE AF ∴=;由旋转的性质可知:E AC F AB ''∠=∠,AE AF ''=,在CAE '∆和BAF '∆,AC AB E AC F AB AE AF =⎧⎪''∠=∠⎨⎪''=⎩CAE BAF ''∴∆∆≌;CE BF ''∴=.(3)存在//CE AB ',理由:由(1)可知AE=BC ,所以,在AEF ∆绕点A 逆时针旋转过程中,E 点经过的路径(圆弧)与过点C 且与AB 平行的直线l 交于M 、N 两点,如图:①当点E 的像E '与点M 重合时,则四边形ABCM 为等腰梯形,72BAM ABC ∴∠=∠=︒ 又36BAC ∠=︒,36CAM α∴=∠=︒②当点E 的像E '与点N 重合时,由//AB l 得,72AMN BAM ∠=∠=︒ AM AN = 72ANM AMN ∴∠=∠=︒ 18027236MAN ∴∠=︒-⨯︒=︒72CAN CAM MAN α∴=∠=∠+∠=︒ 所以当旋转角为36︒或72︒时,//CE AB '.()EAM EPN ASA ∴∆∆≌ EM EN ∴=.1.4(1)问题发现如图1,△ACB 和△DCE 均为等边三角形,点A ,D ,E 在同一直线上,连接BE .填空:①∠AEB 的度数为________;②线段AD ,BE 之间的数量关系为____________. (2)拓展探究如图2,△ACB 和△DCE 均为等腰直角三角形,∠ACB=∠DCE=90°,点A ,D ,E 在同一直线上,CM 为△DCE 中DE 边上的高,连接BE ,请判断∠AEB 的度数及线段CM ,AE ,BE 之间的数量关系,并说明理由.【答案】(1)AD=BE;∠AEB=∠CEB ﹣∠CED=60° (2)AE=AD+DE=BE+2CM .【解析】(1)∵∠ACB=∠DCE ,∠DCB=∠DCB , ∴∠ACD=∠BCE , 在△ACD 和△BCE 中, AC BC ACD BCE CD CE =⎧⎪∠=∠⎨⎪=⎩, ∴△ACD ≌△BCE (SAS ),∴AD=BE ,∠CEB=∠ADC=180°﹣∠CDE=120°, ∴∠AEB=∠CEB ﹣∠CED=60°; (2)∠AEB=90°,AE=BE+2CM , 理由:如图2,∵△ACB 和△DCE 均为等腰直角三角形, ∴CA=CB ,CD=CE ,∠ACB=∠DCE=90°,∴∠ACD=∠BCE . 在△ACD 和△BCE 中, CA CB ACD BCE CD CE =⎧⎪∠=∠⎨⎪=⎩, ∴△ACD ≌△BCE (SAS ), ∴AD=BE ,∠ADC=∠BEC . ∵△DCE 为等腰直角三角形, ∴∠CDE=∠CED=45°,∵点A 、D 、E 在同一直线上, ∴∠ADC=135°. ∴∠BEC=135°,∴∠AEB=∠BEC ﹣∠CED=90°. ∵CD=CE ,CM ⊥DE , ∴DM=ME . ∵∠DCE=90°, ∴DM=ME=CM ,∴AE=AD+DE=BE+2CM .自我总结课后作业1已知ABC ∆,90BAC ∠=︒,等腰直角BDE ∆,90BDE ∠=︒,BD=DE ,点D 在线段AC 上. (1)如图1,当30ACB ∠=︒,点E 在BC 上时,试判断AD 与CE 的数量关系,并加以证明;(2)如图2,当45ACB ∠=︒,点E 在BC 外时,连接EC\、BD 并延长交于点F ,设ED 与BC 交于点N ,图中是否存在与BN 相等的线段?若存在,请加以证明.若不存在,请说明理由.【答案】见解析.【解析】解:(1)2ED AD =.理由是:BDE ∆是等腰直角三角形 ∴45DBE DEB ∠=∠=︒又Rt ABC ∆中,30ACB ∠=︒,60ABC ∴∠=︒ 604515ABD ABC DBE ∴∠=∠-∠=︒-︒=︒ 同理60CEP ∠=︒,180180604515PED CEP DEB ∴∠=︒-∠-∠=︒-︒-︒=︒PDE ABD ∴∠=∠ ∴在ABD ∆和PDE ∆中,90DPE A PDE ABD DE BD ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩()ABD PDE AAS ∴∆∆≌AD PE ∴= 又∵Rt PCE ∆中,30C ∠=︒,2CE PE ∴= 2CE AD ∴=.(2)BN EF =,理由是:如图2,过E 作EG AC ⊥,交AC 的延长线于G 90BDE ∠=︒ 90BDE EDF ∴∠=∠=︒ 90GDE ADB ∠+∠=︒90A ∠=︒,90ADB ABD ∴∠+∠=︒ GDE ABD ∴∠=∠在ABD ∆和GDE ∆中,90GDE ABD G A DE BD ∠=∠⎧⎪∠=∠=︒⎨⎪=⎩,()ABD GDB AAS ∴∆∆≌ AD GE ∴=,DG AB =AB AC =,AC DG ∴= AD DG GE ∴== CGE ∴∆是等腰直角三角形 45GCE ∴∠=︒ 45DCF GCE ∴∠=∠=︒ 90FCB ∴∠=︒ 90F FBC ∴∠+∠=︒ 90FBC DNB ∠+∠=︒F DNB ∴∠=∠ 在FDE ∆和NDB ∆中,F DNB FDE NDB DE BD ∠=∠⎧⎪∠=∠⎨⎪=⎩()FDE NDB AAS ∴∆∆≌ BN EF ∴=.2如图1,在ABC ∆中,ACB ∠是锐角,点D 为射线BC 上的一点,连接AD ,以AD 为一边且在AD 的右侧作正方形ADEF .(1)如果AB=AC ,90BAC ∠=︒,①当点D 在线段BC 上时(与点B 不重合),如图2,线段CF 、BD 所在直线的位置关系为 ,线段CF 、BD 的数量关系为 ;②当点D 在线段BC 的延长线上时,如图3,①中的结论是否依然成立,并说明理由;(2)如果AB=AC ,BAC ∠是锐角,点D 在线段BC 上,当ACB ∠满足什么条件时,CF BC ⊥(点C 、F 不重合),并说明理由.【答案】见解析.【解析】证明:(1)①正方形ADEF 中,AD=AF ,90BAC DAF ∠=∠=︒ BAD CAF ∴∠=∠ 又AB AC = DAB FAC ∴∆∆≌ CF BD ∴=,B ACF ∠=∠ 90ACB ACF ∴∠+∠=︒ 即CF BD ⊥.②当点D 在BC 的延长线上时①的结论仍成立.由正方形ADEF 得AD=AF ,90DAF ∠=︒ 90BAC ∠=︒ DAF BAC ∴∠=∠ DAB FAC ∴∠=∠ 又AB AC = DAB FAC ∴∆∆≌ CF BD ∴=,ACF ABD ∠=∠ 90BAC ∠=︒ ,AB AC = 45ABC ∴∠=︒ 45ACF ∴∠=︒ 90BCF ACB ACF ∴∠=∠+∠=︒ 即CF BD ⊥.(2)当45ACB ∠=︒时,CF BD ⊥(如图).理由:过点A 作AG AC ⊥交CB 的延长线于点G ,则90GAC ∠=︒,45ACB ∠=︒,90AGC ACB ∠=︒-∠,904545AGC ∴∠=︒-︒=︒ 45ACB AGC ∴∠=∠=︒,AC AG ∴= DAG FAC ∠=∠(同角的余角相等),AD=AF GAD CAF ∴∆∆≌ 45ACF AGC ∴∠=∠=︒,454590BCF ACB ACF ∠=∠+∠=︒+︒=︒ 即CF BC ⊥.3如图1,将两个完全相同的三角形纸片ABC 和DEC 重合放置,其中90C ∠=︒,30B E ∠=∠=︒. (1)操作发现如图2,固定ABC ∆,使DEC ∆绕点C 旋转,当点D 恰好落在AB 边上时,填空: ①线段DE 与AC 的位置关系是 ;②设BDC ∆的面积为1S ,AEC ∆的面积为2S ,则1S 与2S 的数量关系是 .(2)猜想论证当DEC ∆绕点C 旋转到如图3所示的位置时,小明猜想(1)中1S 与2S 的数量关系仍然成立,并尝试分别作出了BDC ∆和AEC ∆中BC 、CE 边上的高,请你证明小明的猜想. (3)拓展探究已知60ABC ∠=︒,点D 是角平分线上一点,BD=CD=4,DE//ABA 交BC 于点E (如图4).若在射线BA 上存在点F ,使DCF BDE S S ∆∆=,请直接写出相应的BF 的长.【答案】见解析.【解析】解:(1)①∵DEC ∆绕点C 旋转点D 恰好落在AB 边上,AC CD ∴= 90903060BAC B ∠=︒-∠=︒-︒=︒,ACD ∴∆是等边三角形,60ACD ∴∠=︒ 又60CDE BAC ∠=∠=︒ ACD CDE ∴∠=∠ //DE AC ∴. ②30B ∠=︒,90C ∠=︒ 12CD AC AB ∴==BD AD AC ∴== 根据等边三角形的性质,ACD ∆的边AC 、AD 上的高相等∴BCD ∆的面积和AEC ∆的面积相等(等底等高的三角形的面积相等),即12S S =(2)如图,DEC ∆是由ABC ∆绕点C 旋转得到,BC CE ∴=,AC CD = 90ACN BCN ∠+∠=︒,1809090DCM BCN ∠+∠=︒-︒=︒,ACN DCM ∴∠=∠ 在ACN ∆和DCM ∆中,90ACN DCM CMD N AC CD ∠=∠⎧⎪∠=∠=︒⎨⎪=⎩()ACN DCM AAS ∴∆∆≌ AN DM ∴=BDC ∴∆的面积和AEC ∆的面积相等(等底等高的三角形的面积相等)即12S S =;(3)如图,过点D 作DF 1//BE ,易求四边形BE DF 1是菱形,所以BE= DF 1,且BE 、DF 1上的高相等,此时1DCF BDE S S ∆∆=;过点D 作2DF BD ⊥,60ABC ∠=︒,DF 1//BE , 2160F F D ABC ∴∠=∠=︒,∵B F 1=D F 1,11302F BD ABC ∠=∠=︒,290F DB ∠=︒,1260F DF ABC ∴∠=∠=︒ 12DF F ∴∆是等边三角形,12DF DF ∴=BD CD =,60ABC ∠=︒,点D 是角平分线上一点,160302DBC DCB ∴∠=∠=⨯︒=︒ 118018030150CDF BCD ∴∠=︒-∠=︒-︒=︒ 236015060150CDF ∠=︒-︒-︒=︒12CDF CDF ∴∠=∠ 在1CDF ∆和2CDF ∆中,1212DF DF CDF CDF CD CD =⎧⎪∠=∠⎨⎪=⎩()12CDF CDF SAS ∴∆∆≌∴点F 2也是所求的点,60ABC ∠=︒,点D 是角平分线上的一点,DE //AB160302DBC BDE ABD ∴∠=∠=∠=⨯︒=︒ 又4BD =14cos3022BE ∴=⨯÷︒==,1BF ∴=,2112BF BF F F =+==故BF. 4某数学兴趣小组开展了一次活动,过程如下:如图1,在等腰直角ABC ∆中,AB=AC ,90BAC ∠=︒,小敏将一块三角板中含45︒角的顶点放在A 上,从AB 边开始绕点A 逆时针旋转一个角α,其中三角板斜边所在的直线交直线BC 于点D ,直角边所在的直线交直线BC 于点E .(1)小敏在线段BC 上取一点M ,连接AM ,旋转中发现:若AD 平分BAM ∠,则AE 也平分MAC ∠.请你证明小敏发现的结论;(2)当045α︒<≤︒时,小敏在旋转中还发现线段BD 、CE 、DE 之间存在如下等量关系: 222BD CE DE +=.同组的小颖和小亮随后想出了两种不同的方法进行解决;小颖的想法:将ABD ∆沿AD 所在的直线对折得到ADF ∆,连接EF (如图2) 小亮的想法:将ABD ∆绕点A 逆时针旋转90︒得到ACG ∆,连接EG (如图3);请你从中任选一种方法进行证明;(3)小敏继续旋转三角板,在探究中得出当45135α︒<<︒且90α≠︒时,等量关系222BD CE DE +=仍然成立,先请你继续研究:当135180α︒<<︒时(如图4)等量关系222B DC EDE +=是否仍然成立?若成立,给出证明;若不成立,说明理由.【答案】见解析.【解析】(1)证明:如图1,90BAC ∠=︒,90BAD DAM MAE EAC ∴∠+∠+∠+∠=︒ 45DAE ∠=︒ 45BAD EAC ∴∠+∠=︒ BAD DAM ∠=∠45BAD EAC DAM EAC ∴∠+∠=∠+∠=︒ DAM MAE DAM EAC ∴∠+∠=∠+∠DAM MAE DAM EAC ∴∠+∠=∠+∠ MAE EAC ∴∠=∠,即AE 平分MAC ∠(2)选择小颖的方法.证明:如图2,连接EF .由折叠可知,BAD FAD ∠=∠,AB=AF ,BD=DF ∵BAD FAD ∠=∠,∴由(1)可知,CAE FAE ∠=∠在AEF ∆和AEC ∆中,AF AC FAE CAE AE AE =⎧⎪∠=∠⎨⎪=⎩()AEF AEC SAS ∴∆∆≌ CE EF ∴=,45AFE C ∠=∠=︒ 90DFE AFD AFE ∴∠=∠+∠=︒.在Rt Rt DFE ∆中,222DF EF DE += 222BD CE DE ∴+=(3)当135180α︒<<︒时,等量关系222BD CE DE +=仍然成立.证明如下: 如图4,按小颖的方法作图,设AB 与EF 相交于点G∵将ABD ∆沿AD 所在的直线对折得到ADF ∆,AF AB ∴=,135AFD ABD ∠=∠=︒,BAD FAD ∠=∠.又AC AB =,AF AC ∴=.又()9090454545CAE BAE BAD BAD FAD FAE ∠=︒-∠=︒-︒-∠=︒+∠=︒+∠=∠CAE FAE ∴∠=∠.在AEF ∆和AEC ∆中,AF AC FAE CAE AE AE =⎧⎪∠=∠⎨⎪=⎩()AEF AEC SAS ∴∆∆≌CE FE ∴=,45AFE C ∠=∠=︒.1351354590DFE AFD AFE C ∴∠=∠-∠=︒-∠=︒-︒=︒ 90DFE ∴∠=︒在Rt DFE ∆中,222DF FE DE += 222BD CE DE ∴+=5如图1,已知ABC ∆中,AB=BC=1,90ABC ∠=︒,把一块含30°角的三角板DEF 的直角顶点D 放在AC 的中点上(直角三角板的短直角边为DE ,长直角边为DF ),将直角三角板DEF 绕D 点按逆时针方向旋转.(1)在图1中,DE 交AB 于M ,DF 交BC 于N .①证明DM DN =;②在这一过程中,直角三角板DEF 与ABC ∆的重叠部分为四边形DMBN ,请说明四边形DMBN 的面积是否发生变化?若发生变化,请说明是如何变化的;若不发生变化,求出其面积;(2)继续旋转至如图2的位置,延长AB 交DE 于M ,延长BC 交DF 于N ,DM=DN 是否仍然成立?若成立,请给出证明;若不成立,请说明理由;【答案】见解析.【解析】(1)①如图1,连接DB ,在R t A B C ∆中,AB =BC ,AD =DC ,DB DC AD ∴==,90BDC ∠=︒45ABD C ∴∠=∠=︒,90MDB BDN CDN BDN ∠+∠=∠+∠=︒ MDB NDC ∴∠=∠()BMD CND ASA ∴∆∆≌ DM DN ∴=②四边形DMBN 的面积不发生变化;由①知BMD CND ∆∆≌ B M D C N S S ∆∆∴=1124DMBN DBN DMB DBN DNC DBC ABC S S S S S S S ∆∆∆∆∆∆∴=+=+===(2)DM DN=依然成立;证明:如图2,连接DB,在Rt ABC∆中,AB=BC,AD=DC,DB DC∴=,90BDC∠=︒45DCB DBC∴∠=∠=︒,135DBM DCN∴∠=∠=︒90NDC CDM BDM CDM∠+∠=∠+∠=︒CDN BDM∴∠=∠则在BM D∆和CND∆中,BDM CDNDB DCDBM DCN∠=∠⎧⎪=⎨⎪∠=∠⎩()BMD CND ASA∴∆∆≌DM DN∴=.。
八年级数学上册 三角形全等之类比探究(习题及答案)(人教版)
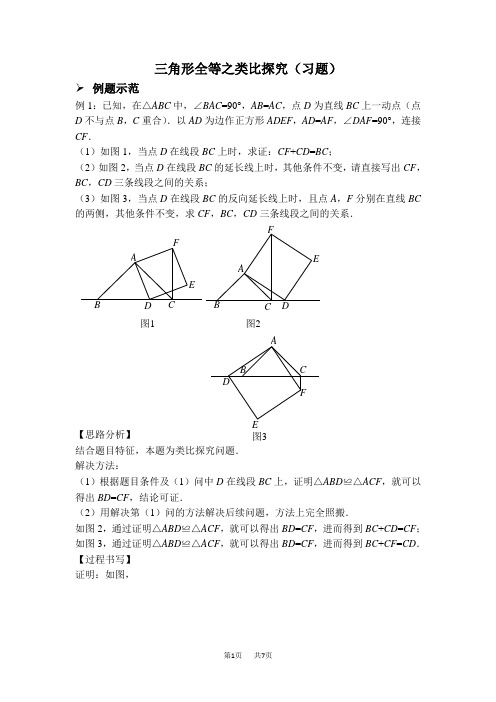
三角形全等之类比探究(习题)➢ 例题示范例1:已知,在△ABC 中,∠BAC =90°,AB =AC ,点D 为直线BC 上一动点(点D 不与点B ,C 重合).以AD 为边作正方形ADEF ,AD =AF ,∠DAF =90°,连接CF .(1)如图1,当点D 在线段BC 上时,求证:CF +CD =BC ;(2)如图2,当点D 在线段BC 的延长线上时,其他条件不变,请直接写出CF ,BC ,CD 三条线段之间的关系;(3)如图3,当点D 在线段BC 的反向延长线上时,且点A ,F 分别在直线BC 的两侧,其他条件不变,求CF ,BC ,CD 三条线段之间的关系.图2图1ABCDEFFED CBA【思路分析】结合题目特征,本题为类比探究问题. 解决方法:(1)根据题目条件及(1)问中D 在线段BC 上,证明△ABD ≌△ACF ,就可以得出BD =CF ,结论可证.(2)用解决第(1)问的方法解决后续问题,方法上完全照搬.如图2,通过证明△ABD ≌△ACF ,就可以得出BD =CF ,进而得到BC +CD =CF ; 如图3,通过证明△ABD ≌△ACF ,就可以得出BD =CF ,进而得到BC +CF =CD . 【过程书写】 证明:如图,图3ABC DEF图1FEDCBA∵∠DAF =90°,∠BAC =90° ∴∠BAD =∠CAF 在△BAD 和△CAF 中,AB AC BAD CAF AD AF =⎧⎪∠=∠⎨⎪=⎩∴△BAD ≌△CAF (SAS ) ∴BD =CF ∵BD +CD =BC ∴CF +CD =BC (2)BC +CD =CF(3)BC +CF =CD ,理由如下: ∵∠DAF =90°,∠BAC =90° ∴∠BAD =∠CAF 在△BAD 和△CAF 中,AB AC BAD CAF AD AF =⎧⎪∠=∠⎨⎪=⎩∴△BAD ≌△CAF (SAS ) ∴BD =CF ∵BC +BD =CD ∴BC +CF =CD➢ 巩固练习1. 已知AB ⊥BD ,ED ⊥BD ,AC ⊥CE ,BC =DE ,如图1.图3AB CDF(1)求证:AC =CE .(2)若将△ECD 沿CB 方向平移至如图2的位置(C 1,C 2不重合),其余条件不变,结论AC 1=C 2E 还成立吗?请说明理由. (3)若将△ECD 沿CB 方向平移至如图3的位置(B ,C 2重合),其余条件不变,结论AC 1=C 2E 还成立吗?请说明理由.2. (1)【问题发现】小明学习中遇到这样一个问题:如图1,△ABC 是等边三角形,点D 为BC 的中点,且满足∠ADE =60°,DE 交等边三角形外角平分线CE 所在直线于点E ,试探究AD 与DE 的数量关系.小明发现,过点D 作DF ∥AC ,交AB 于点F ,通过构造全等三角形,经过推理论证,能够使问题得到解决,请直接写出AD 与DE 的数量关系:图3图2图1ABC DEEDB AEDB 2)A2C 1C 1_______________;(2)【类比探究】如图2,当点D 是线段BC 上(除B ,C 外)任意一点时(其他条件不变),试猜想AD 与DE 之间的数量关系,并证明你的结论; (3)【拓展应用】如图3,当点D 在线段BC 的延长线上(其他条件不变),试猜想AD 与DE 之间的数量关系,并证明你的结论.图1FED CB A图2EDCBA图3EDC B A3. 如图1所示,在△A B C 和△A D E 中,A B =A C ,A D =A E ,∠BAC =∠DAE ,且点B ,A ,D 在一条直线上,连接BE ,CD ,M ,N 分别为BE ,CD 的中点,连接AM ,AN ,MN . (1)求证:①BE =CD ;②△AMN 是等腰三角形.(2)在图1的基础上,将△ADE 绕点A 按顺时针方向旋转180°,其他条件不变,得到如图2所示的图形.(1)中的两个结论是否仍然成立?若成立,请给予证明;若不成立,请说明理由.图1A BCDE M N【参考答案】1. 证明略路线图: (AAS) A DCEABC CDE AC CE∠=∠↓↓=△≌△ 提示:(1)AC=CE ,由垂直转互余可以得到∠A =∠DCE , 结合BC=DE 证明△ABC ≌△CDE ,得到对应边相等, 可以得到AC=CE .(2)成立,照搬第一问的字母、思路和过程可以得到AC 1=C 2E . (3)成立,照搬第一问的字母、思路和过程可以得到AC 1=C 2E .2. 证明略D DF AC AB F 过点作∥,交于点路线图(AAS)BDF BF BD AF CDADF DEC AD DE ↓==↓↓=△为等边三角形,△≌△ 提示:(1)AD =DE(2)AD =DE 成立,根据△ABC 以及△BDF 是等边三角形,得到AF =DC ,再结合∠ADE =60°,倒角,得到∠DAF =∠EDC ,结合外角平分线,知∠DCE =∠AFD =120°,得到△ADF ≌△DEC ,得到对应边相等,可得AD =DE .(3)成立,照搬第二问的字母、思路和过程可以得到AD =DE .3. 证明略路线图(SAS) (SAS) BAE CAD BE CD ABE ACD ABM ACN AM AN AMN ↓=∠=∠↓↓=↓△≌△,△≌△△是等腰三角形提示:(1)由已知条件先证明△BAE ≌△CAD (SAS),得到BE=CD ,结合第一次全等提供的条件证明△ABM ≌△ACN (SAS)得到AM=AN ,因而△AMN 是等腰三角形.(2)成立,照搬第一问的字母、思路和过程可以得到BE=CD ,△AMN 是等腰三角形.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三角形全等之动点问题(讲义)
➢课前预习
已知:如图,AB=18 cm,动点P从点A出发,沿AB以2 cm/s的速度向点B
运动,动点Q从点B出发,沿BA以1 cm/s的速度向点A运动.P,Q两点
同时出发,当点P到达点B时,点P,Q同时停止运动.设点P运动的时间
为t秒,请解答下列问题:
(1)AP=_______,QB=_______(含t的式子表达);
(2)在P,Q相遇之前,若P,Q两点相距6 cm,则此时t的值为_______.
➢知识点睛
由点(___________)的运动产生的几何问题称为动点问题.
动点问题的解决方法:
1.研究_____________;
2.分析_____________,分段;
3.表达_____________,建等式.
➢精讲精练
1.已知:如图,在矩形ABCD中,AB=4,AD=10,点E为边AD上一点,且
AE=7.动点P从点B出发,以每秒2个单位的速度沿BC
向点C运动,连接AP,DP.设点P运动时间为t秒.A E D
A E D
(1)当t =1.5时,△ABP 与△CDE 是否全等?请说明理由;(2)当t 为何值时,△DCP ≌△CDE .
2. 已知:如图,在梯形ABCD 中,AD ∥BC ,∠ABC =90°,AD =12,BC =24,动
点P 从点A 出发以每秒1个单位的速度沿AD 向点D 运动,动点Q 从点C 出发以每秒2个单位的速度沿CB 向点B 运动,P ,Q 同时出发,当点P 停止运动时,点Q 也随之停止,连接PQ ,DQ .设点P 运动时间为x 秒,请求出当x 为何值时,△PDQ ≌△CQD .
Q
P D
C
B A
3. 已知:如图,在△ABC 中,AB =AC =10 cm ,BC =8 cm ,点D 为AB 的中点.点
P 在线段BC 上以每秒3 cm 的速度由点B 向点C 运动,同时点Q 在线段CA 上由点C 向点A 运动.设点P 运动时间为t 秒,若某一时刻△BPD 与△CQP 全等,求此时t 的值及点Q 的运动速度.
D C
B
A
4. 已知:如图,正方形ABCD 的边长为10 cm ,点E 在边AB 上,且AE =4 cm ,
点P 在线段BC 上以每秒2 cm 的速度由点B 向点C 运动,同时点Q 在线段CD 上由点C 向点D 运动.设点P 运动时间为t 秒,若某一时刻△BPE 与△CQP 全等,求此时t 的值及点Q 的运动速度.
A
5. 已知:如图,在长方形ABCD 中,AB =DC =4,AD =BC =5.延长BC 到E ,使
CE =2,连接DE .动点P 从点B 出发,以每秒2个单位的速度沿BC -CD -DA 向终点A 运动,设点P 运动时间为t 秒. (1)请用含t 的式子表达△ABP 的面积S .
(2)是否存在某个t 值,使得△DCP 和△DCE 全等?若存在,请求出所有满足条件的t 值;若不存在,请说明理由.
D
A
6.
A
D
C
B
【参考答案】
➢课前预习
(1)2t,t
(2)4s
➢知识点睛
速度已知
1.研究背景图形,标注;
2.分析运动过程,分段;
3.表达线段长,建等式.
➢精讲精练
1.解:(1)当t=1.5时,△ABP≌△CDE.
理由如下:
如图,由题意得BP=2t
∴当t=1.5时,BP=3
∵AE=7,AD=10
∴DE=3
∴BP=DE
在矩形ABCD中
AB=CD,∠B=∠CDE
在△ABP 和△CDE 中
AB CD B CDE BP DE =⎧⎪
∠=∠⎨⎪=⎩
∴△ABP ≌△CDE (SAS ) (2)如图,由题意得BP =2t ∵BC =10 ∴CP =10-2t
若使△DCP ≌△CDE ,则需CP =DE
即10-2t =3,t =7
2
∴当t =7
2
时,△DCP ≌△CDE .
2. 解:如图,由题意得AP =x ,CQ =2x
∵AD =12 ∴DP =12-x
要使△PDQ ≌△CQD ,则需DP =QC 即12-x =2x ,x =4
∴当x =4时,△PDQ ≌△CQD .
3. 解:如图,由题意得BP =3t
∵BC =8 ∴PC =8-3t
∵AB =10,D 为AB 中点 ∴BD =12
AB =5
①要使△BDP ≌△CPQ , 则需BD =CP ,BP =CQ 即5=8-3t ,t =1 ∴CQ =3t =3
则Q 的速度为Q v =s t =3
1
=3(cm/s )
即当t =1,Q 的速度为每秒3cm 时,△BDP ≌△CPQ . ②要使△BDP ≌△CQP ,则需BP =CP ,BD =CQ 即3t =8-3t ,CQ =5 ∴t =43
则Q 的速度为Q v =s t
=5×34=
15
4
(cm/s ) 即当t =43,Q 的速度为每秒15
4
cm 时,△BDP ≌△CQP .
综上所述,当t =1,Q 的速度为每秒3cm 或t =4
3
,Q 的速度
为每秒15
4cm 时,△BPD 与△CQP 全等.
4. 解:如图,由题意得BP =2t
∵正方形ABCD 的边长为10cm ∴AB =BC =10 ∴PC =10-2t ∵AE =4 ∴BE =10-4 =6
①要使△BEP ≌△CPQ , 则需EB =PC ,BP =CQ 即6=10-2t ,CQ =2t ∴t =2,CQ =4
则点Q 的速度为Q v =s t =4
2
=2(cm/s )
即当t =2,Q 的速度为每秒2cm 时,△BEP ≌△CPQ . ②要使△BEP ≌△CQP , 则需BP =CP ,BE =CQ 即2t =10-2t ,CQ =6
∴t =52
则点Q 的速度为Q v =s t
=6×25=12
5(cm/s )
即当t =52
,Q 的速度为每秒12
5cm 时,△BEP ≌△CQP .
综上所述,当t =2,Q 的速度为每秒2cm 或t =5
2
,Q 的速度
为每秒12
5
cm 时,△BEP 与△CQP 全等.
5. 解:(1)①当P 在BC 上时,
如图,由题意得BP =2t (0<t ≤2.5)
1
21
4224ABP S AB BP t t
∆=
⋅=⨯⨯=∴
②当P 在CD 上时,(2.5<t ≤4.5)
1
21
45210
ABP S AB BC
∆=⋅=⨯⨯=∴ ③当P 在AD 上时,由题意得AP =14-2t (4.5<t <7)
1
21
41422
284ABP S AB AP
t t ∆=⋅=⨯⨯=∴--() (2)①当P 在BC 上时, 如图,由题意得BP =2t
要使△DCP ≌△DCE ,则需CP =CE ∵CE =2 ∴5-2t =2,t =1.5
即当t =1.5时,△DCP ≌△DCE
②当P 在CD 上时,不存在t 使△DCP 和△DCE 全等 ③当P 在AD 上时,由题意得BC +CD +DP =2t ∵BC =5,CD =4, ∴DP =2t -9
要使△DCP ≌△CDE ,则需DP =CE 即2t -9=2,t =5.5
即当t =5.5时,△DCP ≌△CDE .
综上所述,当t =1.5或t =5.5时,△DCP 和△DCE 全等.
6. 解:(1)①当Q 在CD 上时,
如图,由题意得CQ =2t ,BP=t ∴CP=5-t (0<t ≤1.5)
2
1
21
(5)22 5CPQ S CP CQ
t t t t ∆=⋅=-⋅=-∴
11 ②当Q 在DA 上时,(1.5<t ≤4)
1
21
(5)327.5 1.5CPQ S CP CD
t t
∆=⋅=⨯=∴--
③当Q 在AB 上时,由题意得BQ =11-2t (4<t <5) 21
21
(5)(112)22155
22
CPQ S CP BQ
t t t t ∆=⋅=-⨯-=-+∴
(2)①当Q 在CD 上时,不存在t 使△ABP 和△CDQ 全等 ②当Q 在AD 上时,
如图,由题意得DQ =2t -3
要使△ABP ≌△CDQ ,则需BP =DQ
∵DQ =2t -3,BP =t
∴t =2t -3,t =3
即当t =3时,△ABP ≌△CDQ .
③当Q 在AB 上时,不存在t 使△ABP 和△CDQ 全等 综上所述,当t =3时,△ABP 和△CDQ 全等.。
