单向应力条件下松弛时间率相关的非线性粘弹性本构模型
混凝土本构模型

混凝土本构关系模型 一、线弹性本构模型1、 线弹性均质的本构模型当混凝土无裂缝时,可以将混凝土看成线弹性均质材料,用广义胡克定律来表达本构关 系:kl ijkl ij C εσ=式中,ijklC 为材料常数,为一四阶张量,一般有81个常数,如果材料为正交异性时,常数可减少至9个,如材料为各向均质时,可用两个常数λ、μ来表达,λ、μ称为Lame 常数。
ijkk ij ij δλεμεσ+=2当j i =,μλσε23+=kkkk ,代入上式()kk ijij ij σμμλλσσε2232/+-=E 、ν、λ、μ之间的关系如下:()ν213-=E K ,()ν+=12EG GK KGE +=39,()G K G K +-=3223ν 在工程计算中采用下列形式⎪⎭⎫ ⎝⎛+-=E EE 33221111σσνσε 同样可写出22ε、33ε的表达式。
()12121112τντγEG+==同样可写出22γ、33γ的表达式。
如上述各式用张量表示可写成:ij kk ij ij EE δσνσνε-+=1,()()ij kk ij ij E E δενννενσ2111-+-+=用矩阵形式表达时,可写成张量描述用矩阵形式表达,可写成:3、正交异性本构模型 矩阵描述分块矩阵描述1.3横观各向同性弹性体本构模型其中[]D 表达式为kl ijkl ij C εσ=1、Cauchy 模型Cauchy 模型建立的各向同性一一对应的应力应变关系为()kl ij ij F εσ=可展开为:+++=jk ik ij ij ij εεαεαδασ210根据Caley-Hamilton 定理有:jkik ij ij ij εεϕεϕδϕσ210++=但Cauchy 模型在)2,1,0(=i i ϕ时,一般不能满足ij kk ij ij δλεμεσ+=2。
因而,Cauchy 模型在不同加载途径下得到的应变能和余能表达式不是唯一的或者不存在,不能满足弹性体能量守恒定律,但在单调比例加载途径下还是适用的。
《流变学》 第四章 第二部分

• White-Metzner推广经典的Maxwell模型,其方法就是采 用对应力张量求Oldroyd随流微商代替一般偏微商。 • 为检验White-Metzner模型的说明能力,将该模型用于 描述稳态简单剪切流场: 1 r x2 2 3 0
• 首先考察偏应力张量σ的 Oldroyd随流微商的具体表达式。 由于流动是稳定的,所以式中等号右边第一项 i j 0 t 注意:这儿将偏应力张量分量σij代替了原公式中Tij。又 因为v2=v3=0,偏应力分量σ12沿x1方向无变化,故有
11 12 21 22 31 32
0 r/ 2 0 13 2 0 r/ 2 0 0 23 0 33 0 0
将方程中等号两边张量的各个对应分量分别联立起来,就得 到一个由九个方程组成的方程组。由此解得:
.
例1 Maxwell模型用于描述稳态简单剪切流场
简单剪切流场形式如图
速度场方程为: 0
L
0 x 0
0 0
0 0 0
0
简单剪切流场中由于流场是稳定的, 因此该点的应力状态不随时间变化, 故有:
0 t d 对于稳态简单剪切流场,其形变率张量为
( X , t)
dt dt
dui ( X R , t ) dxi ( X R , t ) (i 1, 2,3) dt dt
展开来写,可写成分量式:
( X R , t)
这种导数因为是针对具体流体元而求的,所以称为对时间的 物质导数。
若将这种物质导数用空间描述法表示 ,则应把上式中的X替 换成式中的x,表达成x的函数。有: du ( x, t ) Du ( x, t )
workbench建立橡胶的超弹性和粘弹性本构模型
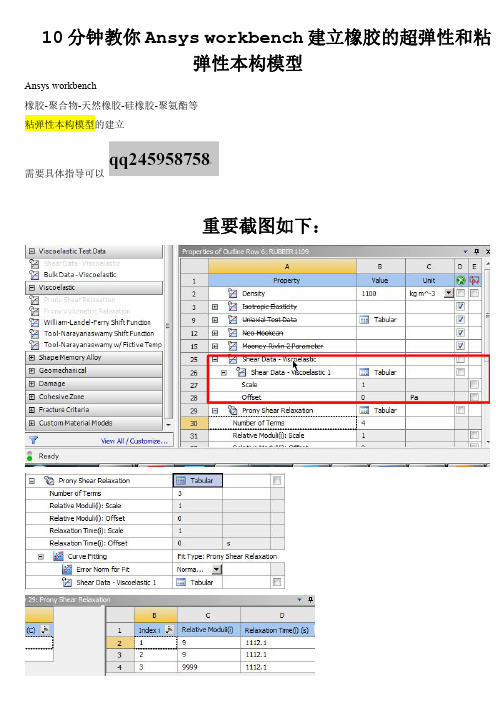
10分钟教你Ansys workbench建立橡胶的超弹性和粘弹性本构模型Ansys workbench橡胶-聚合物-天然橡胶-硅橡胶-聚氨酯等粘弹性本构模型的建立需要具体指导可以重要截图如下:补充:ANSYS 粘弹性材料1.1ANSYS 中表征粘弹性属性问题粘弹性材料的应力响应包括弹性部分和粘性部分,在载荷作用下弹性部分是即时响应的,而粘性部分需要经过一段时间才能表现出来。
一般的,应力函数是由积分形式给出的,在小应变理论下,各向同性的粘弹性本构方程可以写成如下形式:()()002t t de d G t d I K t d d d σττττττ∆=-+-⎰⎰(1)其中σ=Cauchy 应力()G t =为剪切松弛核函数()K t =为体积松弛核函数e =为应变偏量部分(剪切变形)∆=为应变体积部分(体积变形)t =当前时间τ=过去时间I =为单位张量。
该式是根据松弛条件本构方程(1),通过将一点的应变分解为应变球张量(体积变形)和应变斜张量(剪切变形)两部分,推导而得的。
这里不再敖述,可参考相关文献等。
ANSYS 中描述粘弹性积分核函数()G t 和()K t 参数表示方式主要有两种,一种是广义Maxwell 单元(VISCO88和VISCO89)所采用的Maxwell 形式,一种是结构单元所采用的Prony 级数形式。
实际上,这两种表示方式是一致的,只是具体数学表达式有一点点不同。
1.2Prony 级数形式用Prony 级数表示粘弹性属性的基本形式为:()1exp G n i G i i t G t G G τ∞=⎛⎫=+- ⎪⎝⎭∑(2)()1exp K n i K i i t K t K K τ∞=⎛⎫=+- ⎪⎝⎭∑(3)其中,G ∞和i G 是剪切模量,K ∞和i K 是体积模量,G i τ和K i τ是各Prony 级数分量的松弛时间(Relative time)。
再定义下面相对模量(Relative modulus)0G i i G G α=(4)0K i i K K α=(5)其中,0G ,0K 分别为粘弹性材质的瞬态模量,并定义式如下:()010G n i i G G t G G ∞====+∑(6)()010Kn i i K K t K K ∞====+∑(7)在ANSYS 中,Prony 级数的阶数G n 和K n 可以不必相同,当然其中的松弛时间G i τ和K i τ也不必相同。
材料本构模型

材料本构模型材料本构模型是指用来描述材料行为的数学模型,它是材料力学研究的基础。
材料本构模型的选择对于材料力学分析和工程设计具有重要意义。
在工程实践中,我们常常需要根据材料的本构特性来选择合适的材料,预测材料的性能,以及进行结构的强度和稳定性分析。
因此,了解材料本构模型的基本原理和应用是非常重要的。
材料本构模型的基本原理是通过建立材料应力与应变之间的关系来描述材料的力学行为。
在材料力学中,通常将材料的本构行为分为线弹性、非线弹性和塑性等不同阶段。
不同的材料在不同的应力和应变条件下会呈现出不同的本构行为,因此需要针对不同的材料和工程问题选择合适的本构模型。
常见的材料本构模型包括弹性模型、塑性模型、粘弹性模型等。
弹性模型是最基本的材料本构模型,它描述了材料在弹性阶段的应力-应变关系。
在弹性阶段,材料的应力与应变呈线性关系,可以通过弹性模量来描述。
当材料受到超过一定限度的应力时,就会进入非线性阶段,这时就需要采用塑性模型或者其他非线性模型来描述材料的本构行为。
除了弹性模型和塑性模型,粘弹性模型也是材料力学中常用的本构模型之一。
粘弹性模型描述了材料在受到应力作用时会出现的时间依赖性和历史依赖性。
这种模型常用于描述高分子材料、土壤和生物材料等具有粘弹性特性的材料。
在工程实践中,我们需要根据具体的材料特性和工程问题选择合适的本构模型。
有时候,为了简化分析,我们会采用简化的本构模型来描述材料的力学行为。
但是需要注意的是,简化的本构模型可能会忽略一些重要的材料特性,导致分析结果的不准确性。
因此,在工程设计中,选择合适的本构模型是非常重要的。
总之,材料本构模型是材料力学研究的基础,它对于材料的力学行为和工程设计具有重要意义。
了解不同的材料本构模型的基本原理和应用是非常重要的,可以帮助我们更好地选择材料、预测材料性能,以及进行结构的强度和稳定性分析。
希望本文能够对材料本构模型有所帮助,谢谢阅读!。
粘弹性材料的应力松弛行为研究

粘弹性材料的应力松弛行为研究粘弹性材料是一种特殊的材料,它具有固体和流体的特性。
在应力作用下,粘弹性材料会发生应力松弛现象,即在一段时间后,应力会逐渐减小,直至达到稳定状态。
本文将研究粘弹性材料的应力松弛行为,并探讨其机制。
1. 引言粘弹性材料广泛应用于工程、生物医学和地球科学等领域。
在这些应用中,了解粘弹性材料的应力松弛行为对于设计和有效利用这些材料至关重要。
2. 粘弹性材料的特性粘弹性材料具有两个主要特性:粘性和弹性。
粘性是指粘弹性材料在应力作用下会发生变形,并且在停止应力作用后,会继续保持形变的能力。
弹性是指粘弹性材料在应力作用下会发生变形,但一旦停止应力作用,会迅速恢复原来的形状。
3. 应力松弛行为应力松弛是指粘弹性材料在受到一定应力后,应力会逐渐减小的现象。
这是由于材料内部结构的重排和分子间的滑动引起的。
应力松弛的速率取决于材料的粘性和弹性特性。
4. 应力松弛的实验研究为了研究粘弹性材料的应力松弛行为,科学家们进行了一系列的实验。
其中一种常用的方法是应用恒定的应力,在一定时间内观察应力的变化。
实验结果表明,粘弹性材料的应力松弛行为可以用指数函数来描述。
5. 应力松弛的机制应力松弛的机制涉及到材料内部的分子结构和形变。
当材料受到应力时,分子会发生滑动和重排,导致应力的逐渐减小。
这种分子间的相对位移和重排是应力松弛的主要原因。
6. 应力松弛的影响因素粘弹性材料的应力松弛行为受到多种因素的影响。
其中包括材料的粘性、温度、应力水平和时间等因素。
不同材料和条件下的应力松弛行为也可能存在差异。
7. 应力松弛的应用了解和控制粘弹性材料的应力松弛行为对于在工程和科学领域的应用具有重要意义。
例如,在生物医学领域,研究粘弹性材料的应力松弛行为有助于设计更好的人工关节和组织工程材料。
结论粘弹性材料的应力松弛行为是一个复杂的现象,涉及到材料内部的分子结构和形变。
通过实验和研究,我们可以更好地理解和应用这种特性。
开尔文模型

速度矢量:流体元的位移矢量的时间变化率。因为要针对 一个具体的流体元求速度,所以应当采用物质描述, 一个具 体流体元的物质坐标XR是常数,所以速度矢量等于:
第二节、空间描述法和物质描述法
物质描述法
观察者的视点集中于一个具体的 流体元及其邻域所发生的事件, 研究它在不同时刻所处的位置, 以及它的速度,加速度等,与通 常力学中集中于一个质点的方法 相同。 拉格朗日描述法
空间描述法
观察者的。
0
0 d 2 0
2 0 0
0 0 0
将方程中等号两边张量的各个对应分量分别联立起来,就得 到一个由九个方程组成的方程组。由此解得:
12 21 0 r 23 32 13 31 0 11 22 0 22 33 0
简单剪切流场中由于流场是稳定的, 因此该点的应力状态不随时间变化, 故有:
0 t 对于稳态简单剪切流场,其形变率张量为
0 d 2 0
2 0 0
0 0 0
代入式中得到:
11 12 21 22 31 32 0 r / 2 0 13 23 2 0 r/ 2 0 0 0 33 0 0
t=τ 时, σ (t) = σ0 /e
d 0 dt 1 d 0 E dt
d
3_弹性模型

A-3 实体模型概述 直接输入几何实体来建模很方便,但有些情况下需 要在ANSYS中来建立实体模型。例如:
需要建立参数模型时,— 在优化设计及参数敏感性分 析时建立的包含变量的模型。 没有ANSYS能够读入的几何实体模型时。 计算机上没有相关的绘图软件时(与ANSYS程序兼容 的)。 在对输入的几何实体需要修改或增加时,或者对几何 实体进行组合时。
4
3.2 线性弹性模型
5
线性弹性模型
线性弹性模型是最简单的力学本构方程,其一般表达式为
材料刚度张量 或模量张量
ij Dijkl kl
各向同性 弹性体
ij 2 ij kk ij
四阶张量Dijkl 一般有 81 个元素; 均质连续各向异性弹性体,Dijkl 有 21个元素是独立的; 对三向正交各向异性弹性体, Dijkl中 9 个元素就可确定 ; 横观各向同性体是三向正交各向 异性体的特殊情况,Dijkl需要 5 个 独立参数即可确定; 对各向同性弹性体,Dijkl只有两 个独立的参数。
15
K
G
超弹性模型
超弹性模型( HyPerelastic models)又称 Green超弹性模型。它通过材料的应变能函 数或余能函数来建立材料的本构方程。
考虑-体积为V,表面积为 A 的物体。物体上作用有体力 Fi和表面上作用有外力Ti,物体中产生的应力为 ij,相应的 位移和应变分别为uij 和 ij 。对弹性材料,应力可由应变唯 一确定,即
应力张量增量可分解为应力球张量增量和应力偏张量增量两部分
ij Sij 8ij
八面体正应变增量可表示为
ij Sij 3Kt8ij
8 kk kl kl
橡胶材料非线性高弹-粘弹性本构模型的研究

其 中对 橡 胶 材料 性 能影 响较 大 的 因素 ( 如 频 率 和 温度 等) 也 是 构 建橡 胶 材 料本 构 模 型 时应 考 虑 的
重要 因素 。文献 [ 9 — 1 0 ] 报 道 的基 于温 度 、 时间和应 变 的本构模 型 能够模 拟一 定 条件下 的加 载或 卸载
响 应无 关 ; B 部 分 为粘 弹性 , 由非线 性 弹簧 与非 线 性 粘 壶 串联 而成 , 与 时 间响应 密 切相 关 。Y e o h 高 弹 性模 型I 具 有 形 式 简单 、 适 用 于单 轴 条件 的特 点n 卜 H 】 , 因此本 工作采用 Y e o h 高弹性模 型计算A部
修正Z e n e r 模型 ( 见图1 ) 可 以描述 橡胶 材料 的 力 学 性 能 。从 图 1 可 以看 出 , 修 正Z e n e r 模 型 为 非
线 性 弹簧 ( A部 分) 并 联 非线 性 Ma x we l l 模型 ( B部
分) 。其 中 , A部 分 为不 可压 缩 的高 弹性 , 与 时 间
性应 力 与粘性 应力 之和 。弹性 应力 由经典 的高 弹 性模 型得 到 , 粘 性应 力 由加载 与 卸载 过程 的瞬 时 应力 积分变换得 到 。
1 . 1 修 正Z e n e r 模 型
研 究通 常采 用遗 传 积分法 或乘 法分 解 法。遗 传积
分法用 记忆 函数 反 映应变 历史 对 当前应 变状 态 的 影 响H J , 是 描 述粘 弹 行为 的一种 有 效方 法 。乘法 分 解法 将变形梯 度分解 为 弹性和 非弹性 部 ,
关键词 : 橡胶材料 ; 非线 性 ; 高弹一 粘 弹性 ; 本 构 模型 ; 应 力 松 弛 中 图分 类 号 : T Q3 3 0 . 1 ; O 2 4 1 . 8 2 文 献 标 志码 : A 文章 编 号 : 1 0 0 0 — 8 9 0 X( 2 0 1 7 ) l 2 — 0 7 1 9 — 0 5
