金属橡胶粘弹性本构模型研究
金属橡胶模型原理及应用

金属橡胶模型原理及应用金属橡胶模型是一种将金属和橡胶复合材料加工成具有金属外观和橡胶弹性的模型材料。
其原理是通过将金属粉末与橡胶胶料混合,在一定的工艺条件下,经过热压和硫化等工艺处理,使金属粉末与橡胶形成牢固的结合。
这样,即可制得具有金属外观和橡胶弹性的模型材料。
金属橡胶模型具有许多优点,因此得到广泛应用。
首先,金属橡胶模型可以实现金属外观和橡胶弹性的双重优势。
金属外观可以使模型具有更好的美观性和装饰性,而橡胶弹性则能使模型具有更好的柔软性和耐用性。
其次,金属橡胶模型具有良好的可塑性,可以制成各种复杂的形状和结构。
再次,金属橡胶模型具有较高的韧性和强度,能够承受一定的拉伸、压缩和弯曲作用。
此外,金属橡胶模型还具有良好的耐磨性和耐腐蚀性,能够适应各种复杂的使用环境。
因此,金属橡胶模型广泛应用于各个领域,如机械、汽车、电子、航空航天等工业制造和产品开发领域。
金属橡胶模型的应用范围非常广泛。
在机械制造领域,金属橡胶模型可以用于制作机械密封件、垫片、减震垫等零部件,以提高机械设备的稳定性和性能。
在汽车制造领域,金属橡胶模型可以用于制作悬挂系统、制动系统、传动系统等关键零部件,以提高汽车的安全性和舒适性。
在电子制造领域,金属橡胶模型可以用于制作电子包装、电子连接器、导电垫片等电子组件,以提高电子设备的可靠性和性能。
在航空航天领域,金属橡胶模型可以用于制作飞机结构、导向系统、防护设备等关键部件,以提高航空航天器的安全性和可靠性。
此外,金属橡胶模型还可以应用于建筑、医疗、体育器材等领域,如制作门窗密封条、医疗器械配件、体育器械垫片等。
总之,金属橡胶模型是一种具有金属外观和橡胶弹性的复合材料,通过金属粉末与橡胶胶料的混合,经过热压和硫化等处理步骤,制成具有双重优势的模型材料。
金属橡胶模型具有良好的可塑性、韧性和强度,以及耐磨性和耐腐蚀性,广泛应用于机械、汽车、电子、航空航天等领域,为各个行业的产品开发和制造提供了可靠的解决方案。
epdm薄膜橡胶包覆材料的粘-超弹本构模型研究

epdm薄膜橡胶包覆材料的粘-超弹本构模型研究摘要:本研究旨在分析epdm薄膜橡胶包覆材料的粘-超弹性本构模型。
为此,实验研究中采用了拉伸、压缩、剪切和滚动测试。
研究结果表明,在拉伸过程中,epdm薄膜橡胶的弹性模量在10kPa-1000kPa之间变化较大,而在压缩拉伸过程中,模量基本保持不变。
此外,剪切和滚动测试表明,由于EPDM薄膜橡胶具有优异的粘合弹性特性,因此可以应用于各种行业中。
例如,它可以用于制造高质量的密封件,可以帮助降低系统泄漏和损坏的风险。
同样,EPDM薄膜橡胶可以用于阻尼装置,可以减少由于强度变化而引起的冲击和振动。
除此之外,EPDM薄膜橡胶还可以用于家具和家用电器,以减少使用者受到的损伤。
而且,它还可以用来制作高性能的导热垫,可以有效地减少工厂的热损失。
此外,EPDM薄膜橡胶还用于制作软管和电缆线,可以增强其耐久性和抗拉强度,可以有效保护电气系统免受破坏。
因此,EPDM薄膜橡胶是一种多功能材料,可以满足各种应用要求。
此外,EPDM薄膜橡胶还可以用于建筑行业,主要是用于制作隔热材料,防止室内温度的变化对建筑物结构产生不利影响。
EPDM薄膜橡胶也可以用于过滤器或制作过滤器外壳,有效减少污染物的污染。
此外,它还可以用于船舶、汽车和其他交通工具,使之具有更强的抗老化性和耐腐蚀性。
最后,还可以将EPDM薄膜橡胶用于制造建筑材料,如PVC管道和橡胶地板,增强其耐磨性和抗氧化性。
因此,EPDM薄膜橡胶在各种行业中都有广泛的应用,为消费者提供了很多实用的解决方案。
此外,由于EPDM膜橡胶对温度有一定的要求,因此在使用过程中需要注意。
例如,当它暴露在115°C以上的高温环境中时,其性能会大大降低,而在低温下,其抗紫外线性能也会受到影响。
此外,它也不适合长期暴露于酸碱性材料中,因为它们会破坏EPDM薄膜橡胶的结构,减弱其性能。
因此,在使用EPDM薄膜橡胶时,应避免将其暴露于高温或酸碱性材料中,否则它的性能会受到不利影响。
workbench建立橡胶的超弹性和粘弹性本构模型
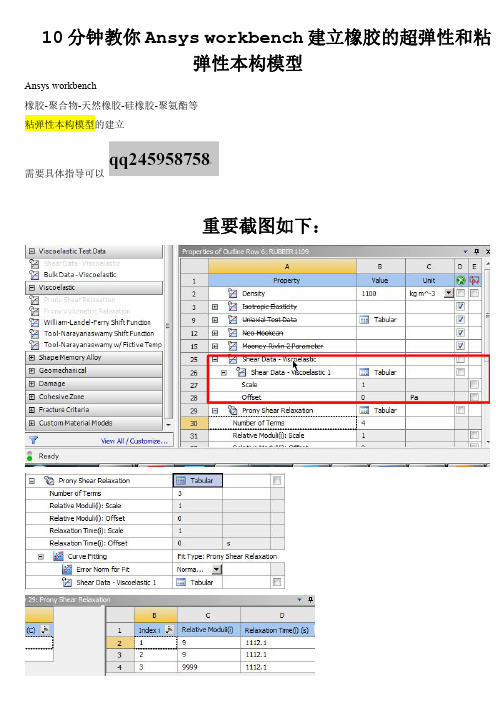
10分钟教你Ansys workbench建立橡胶的超弹性和粘弹性本构模型Ansys workbench橡胶-聚合物-天然橡胶-硅橡胶-聚氨酯等粘弹性本构模型的建立需要具体指导可以重要截图如下:补充:ANSYS 粘弹性材料1.1ANSYS 中表征粘弹性属性问题粘弹性材料的应力响应包括弹性部分和粘性部分,在载荷作用下弹性部分是即时响应的,而粘性部分需要经过一段时间才能表现出来。
一般的,应力函数是由积分形式给出的,在小应变理论下,各向同性的粘弹性本构方程可以写成如下形式:()()002t t de d G t d I K t d d d σττττττ∆=-+-⎰⎰(1)其中σ=Cauchy 应力()G t =为剪切松弛核函数()K t =为体积松弛核函数e =为应变偏量部分(剪切变形)∆=为应变体积部分(体积变形)t =当前时间τ=过去时间I =为单位张量。
该式是根据松弛条件本构方程(1),通过将一点的应变分解为应变球张量(体积变形)和应变斜张量(剪切变形)两部分,推导而得的。
这里不再敖述,可参考相关文献等。
ANSYS 中描述粘弹性积分核函数()G t 和()K t 参数表示方式主要有两种,一种是广义Maxwell 单元(VISCO88和VISCO89)所采用的Maxwell 形式,一种是结构单元所采用的Prony 级数形式。
实际上,这两种表示方式是一致的,只是具体数学表达式有一点点不同。
1.2Prony 级数形式用Prony 级数表示粘弹性属性的基本形式为:()1exp G n i G i i t G t G G τ∞=⎛⎫=+- ⎪⎝⎭∑(2)()1exp K n i K i i t K t K K τ∞=⎛⎫=+- ⎪⎝⎭∑(3)其中,G ∞和i G 是剪切模量,K ∞和i K 是体积模量,G i τ和K i τ是各Prony 级数分量的松弛时间(Relative time)。
再定义下面相对模量(Relative modulus)0G i i G G α=(4)0K i i K K α=(5)其中,0G ,0K 分别为粘弹性材质的瞬态模量,并定义式如下:()010G n i i G G t G G ∞====+∑(6)()010Kn i i K K t K K ∞====+∑(7)在ANSYS 中,Prony 级数的阶数G n 和K n 可以不必相同,当然其中的松弛时间G i τ和K i τ也不必相同。
胶黏剂超弹性理论与试验力学及ABAQUS仿真案例总结

胶黏剂超弹性理论及ABAQUS仿真案例总结摘要:一部胶黏剂固化后呈现的是橡胶这种超弹性状态,对齐固化后的性能研究与计算基本等于橡胶超弹性研究。
框架:一、超弹性材料本构模型理论二、橡胶材料力学行为的实验研究三、基于ABAQUS橡胶材料的工程实例仿真与实验验证方法四、基于COMSOL胶黏剂超弹性仿真案例一、超弹性材料本构模型理论对于固化后呈现软而韧的胶黏剂,基本可等同于橡胶超弹性材料。
二、橡胶材料力学行为的实验研究2.1引言试验设计与研究是材料设计的关键,主要研究各类配合剂与材料性能,诸如力学性能、功能性能、耐久性及加工性能等之间的相关性,进而从中解析材料组分的品种、类型和用量对橡胶材料性能的影响规律。
本章主要是通过对密封件橡胶试样EP7001和EP7118F进行单向拉伸的准静态力学实验,研究分析橡胶的各种力学行为,主要包括橡胶的Mullins效应及其能量损耗、橡胶材料的应力应变行为和起始模量、橡胶材料力学行为的调制应变相关性、橡胶材料变形行为的率相关性以及橡胶材料应力行为的应变历史相关性等。
另外,还特别针对9种不同体积含量的N330炭黑填充天然橡胶材料进行了单向拉伸的准静态力学实验,研究分析炭黑的填充对硫化橡胶相关力学行为的影响规律。
2.2橡胶材料试样的制备及实验准备在试验方法中,拉伸试验是评价力学、机械特性最基本的方法,所以在各国标准中都放在首要位置。
拉伸试验时,采用某橡胶制品公司生产的EP7001橡胶、EP7118F橡胶以及天然(NR)橡胶为原材料,所制备试样的形状与尺寸满足国家标准《硫化橡胶或热塑性橡胶拉伸应力应变性能的测定》(GB/T528-2009)中“1型”哑铃状试样的要求,试样狭窄部分的标准厚度为2mm。
试验在美特斯工业系统(中国)有限公司生产的CMT4104微机控制电子万能试验机上进行,如图2-1所示,其力值和位移精度均为0.5级,大变形传感器选用25mm标距,夹具选用偏心轮夹具PA103A,此夹具特别适用于橡胶材料的拉伸试验,随着拉伸力的增大,夹具钳口对试样的夹持也越来越紧,避免了试样夹持部分的打滑。
橡胶Mooney-Rivlin超弹性本构模型的参数特性研究

橡胶Mooney-Rivlin超弹性本构模型的参数特性研究V ol 38No.Z1Apr.2018噪声与振动控制NOISE AND VIBRATION CONTROL 第38卷第Z1期2018年4月文章编号:1006-1355(2018)Z1-0427-04橡胶Mooney-Rivlin 超弹性本构模型的参数特性研究张良,李忠华,马新强(美的中央研究院,广东佛山528311)摘要:橡胶元件在工业界得到广泛的应用,橡胶材料在不同动态激励下,其力学特征会发生较大变化。
橡胶材料是一种典型的非线性材料,其弹性性能与硬度、载荷等多种因素有关,不能使用简单的弹性模量来表征。
通过对橡胶材料的力学特性进行实验和分析,研究硬度对橡胶弹性模量的影响。
通过对实验数据的整理分析,得到硬度对Mooney-Rivlin 模型参数的影响规律,为深入分析橡胶超弹性特性提供可靠支持。
关键词:振动与波;超弹性;橡胶特性;数据拟合;非线性回归中图分类号:TB535;TM925;V231.92文献标志码:ADOI 编码:10.3969/j.issn.1006-1355.2018.Z1.091Study on Parameter Characteristics ofRubber Mooney-rivlin modelZHANG Liang ,LI Zhonghua ,MA Xinqiang(Midea Corporate Research Center,Foshan 528311,Guangdong China )Abstract :Rubber components are widely used inindustry.The mechanical characteristics of rubber materials will change greatly under different dynamic excitations.Rubber material is a typical nonlinear material.Since its elastic properties are related to many factors,such as hardness,load,and so on,rubber material cannot be characterized by a simple elastic modulus.Based on the experiment and analysis of the mechanical properties of rubber materials,the influence of the hardness on the elastic modulus of rubber is studied.By analysis of the experimental data,the influence of the hardness on the parameters of the Mooney-Rivlin model is obtained.This research will provide reliable support for the thoroughly analysis of the super-elastic properties of rubber.Keywords :vibration and wave;hyper-elasticity;rubber characteristics;data fitting;nonlinear regression静音技术成为家电行业重要的研究方向,很多家电企业推出了静音空调、静音电磁炉、静音冰箱等。
几种典型的橡胶材料超弹性本构模型及其适用性

⼏种典型的橡胶材料超弹性本构模型及其适⽤性橡胶材料具有良好的粘弹性,被⼴泛⽤作密封、减振部件。
橡胶作为⼀种超弹性材料,其物理化学性能与⾦属材料有很⼤差别。
橡胶材料的主要特点不可压缩性:橡胶材料的泊松⽐µ⼀般在0.45~0.4999范围内变化,接近于液体的泊松⽐(1) 不可压缩性:0.5,因此橡胶可以看作是⼀种体积近似不可压缩的材料。
⼤变形特性:橡胶⾼分⼦材料变形很⼤,⽽其弹性模量与⾦属材料相⽐却⼩很多。
橡胶材料(2) ⼤变形特性:的变形范围⼀般在200%~500%,甚⾄能够达到1000%,很多⾦属材料的变形则不⾜0.5%。
(3) ⾮线性:⾮线性:橡胶材料具有三重⾮线性,即⼏何⾮线性、材料⾮线性和边界⾮线性。
橡胶材料的应⼒-应变关系具有明显的⾮线性,其⼒学性能与环境条件、应变历程、加载速率等因素有很⼤关联,且随时间延长⽽不断变化。
本构模型及其适⽤性从20世纪40年代⾄今,国内外许多学者提出了许多橡胶材料的本构模型,⼤致可分为两⼤类:基于应变能函数的唯象模型和基于分⼦链⽹络的统计模型。
基于应变能函数的唯象模型⼜可分为两类。
⼀类是以应变不变量表⽰的应变能密度函数模型,这类模型在处理橡胶弹性时,可以把橡胶材料的变形看成是各向同性的均匀变形,从⽽将应变能密度函数表⽰成变形张量不变量的函数,⽐如:Mooney-Rivlin模型、Yeoh模型等。
另⼀类是以主伸长表⽰的应变能函数模型,⽐如:Valanis-Landel模型、Ogden模型等。
基于分⼦链⽹络的统计模型按照分⼦链的统计特性可分为两类:⾼斯链⽹络模型和⾮⾼斯链⽹络模型。
其中最具代表性的分⼦统计学模型包括Treloar模型以及Arruda-Boyce的8链模型。
下⾯对⼏种常见的本构模型进⾏简要介绍:Mooney-Rivlin模型Mooney-Rivlin模型是⼀个⽐较常⽤的模型,⼏乎可以模拟所有橡胶材料的⼒学⾏为。
其应变能密度函数模型为:对于不可压缩材料,典型的⼆项三阶展开式为:式中:N、Cij和dk为材料常数,由实验确定。
橡胶材料的本构模型

橡胶材料的本构模型橡胶材料的本构模型是描述橡胶材料力学行为的数学模型。
本构模型是材料力学研究中的重要理论工具,通过数学方程形式对材料的应力-应变关系进行描述。
橡胶是一类具有高可拉伸性和高回弹性的材料,其力学行为与其他材料有很大的不同,因此需要特别的本构模型进行描述。
在橡胶材料力学行为的研究中,最广泛应用的两个本构模型是针对小变形的线性弹性模型和针对大变形的高度非线性模型。
线性弹性模型是最简单的橡胶本构模型,假设橡胶材料的应力和应变之间是线性关系。
这个模型适用于小变形范围内的橡胶材料力学行为分析,可以方便地通过材料的弹性常数进行描述。
线性弹性模型的基本形式为:σ=Cε其中,σ表示应力,ε表示应变,C为弹性常数。
线性弹性模型可以通过杨氏模量和泊松比来描述橡胶材料的力学性质。
然而,橡胶材料的应力-应变关系在大变形情况下会呈现高度非线性行为。
在这种情况下,采用线性弹性模型进行描述就不合适了。
因此,需要使用高度非线性的本构模型。
高度非线性的本构模型主要有聚合物链模型、统计力学模型、应变能密度函数模型和粘弹性模型等。
这些模型的共同特点是考虑了橡胶材料的非线性变形,并可以用来描述大变形下橡胶材料的应力-应变关系。
聚合物链模型是最简单的非线性本构模型之一、它通过一维线性弹簧链表示聚合物链,考虑了链的拉伸、弯曲和扭转等非线性效应。
通过调整弹簧的弹性系数和链的长度可以得到不同力学行为的橡胶材料的本构关系。
统计力学模型基于聚合物链模型进一步发展,考虑了链的各向异性和随机性。
该模型通过统计力学方法,描述橡胶材料中具有不同平衡态的链的分布情况,并计算出平衡态下的应力-应变关系。
应变能密度函数模型是一种常用的非线性本构模型。
它将应变能密度函数表示为材料的位移梯度和位移梯度的统计平均,通过这个函数可以计算得到材料的应力-应变关系。
粘弹性模型是描述橡胶材料在弹性行为和粘性行为之间转变的一种本构模型。
在这个模型中,应力和应变同时取决于弹性效应和粘性效应,并通过两个弹性模量和一个粘性模量来描述材料的力学行为。
橡胶超弹-黏弹模型建立及结构动态响应

摘摇 要: 为了研究橡胶结构的动态响应,需要准确建立本构模型. 通过动态热机械分析仪( dynamic thermomechani鄄 cal analysis,DMA) 测试圆盘形橡胶试样,获得橡胶黏弹因子、储能模量、损耗模量等力学数据,建立超弹- 黏弹本构 模型,超弹模型表征橡胶的大变形特性,黏弹模型表征橡胶的滞后效应,其中黏弹模型参数是通过利用 ANSYS 拟 合 DMA 实验所得松弛曲线数据获得,超弹模型参数是通过利用经验公式辨识得到. 建立与实验条件一致的动力 学仿真模型,实验数据与仿真数据的误差较小,在合理范围内,验证了通过上述方法辨识模型参数所建立超弹- 黏 弹本构模型的正确性. 仿真获得了圆盘形橡胶试样、立方块橡胶试样分别在周期性扭转载荷和垂直载荷作用下的 应力、应变、损耗等响应特性,并验证了所建立本构模型的适用性. 通过研究立方块橡胶试样在超弹- 黏弹本构模 型、线弹- 黏弹本构模型、单一的超弹本构模型下的动态响应特性,表明了本构模 型 的 选 择 对 橡 胶 结 构 动 态 响 应 分 析的重要性,为工程实际问题中橡胶本构模型的选择提供参考.
CHU Hongyan, SUN Dongming, CHEN Qi, CAI Ligang
( Beijing Key Laboratory of Advanced Manufacturing Technology, Institute of Advanced Manufacturing and Intelligent Technology of Beijing University of Technology, Beijing 100124, China)
关键词: 橡胶; 黏弹性; 超弹性; 参数辨识; 本构模型; 滞后特性
中图分类号: TQ 333郾 7
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
由于水膜厚度的调节十分方便 ,因而此种复合 结构可能成为一种可变吸声结构 。又因为其调节 机制在于改变水膜厚度和复合材料的面密度 M ,进 而可研究其吸声特性 ,因而也就具有用于降低噪声 和调节厅堂音质的潜力 。水具有极大的汽化潜热 和比热容 ,可以大大改变室内热湿环境 。本文所研 究的结构 ,可以同时改善室内声环境和热湿环境 , 一举多得 ,具有很大的发展前景 。该方法和结构证 明有可能把室内声环境和热湿环境综合考虑的可 能性 ,本文对平面静态水的研究是初步的 ,也未涉 及垂直面动态水 ,有必要进一步深入研究 。
图 5 solid186单元几何形状 Fig. 5 Geometrical figures of solid186 units
(下转第 155页 )
基于混响法测试架空水膜的吸声特性
155
有了很大的提高 (见图 10) 。架空薄膜加入水膜比未 加水膜吸声能力强 ,特别是在低频部分 (见图 11) 。
Kelvin模型认为 ,粘弹性材料可以等效为一个 弹簧和一个粘壶元件相互并联而成 ,如图 2 所示 。 其本构关系为
图 2 Kelvin模型 Fig. 2 Kelvin model
简谐应变的激励下 ,由本构关系式 5可得 G1 = ( q0 + p1 q1ω2 ) / ( 1 + p21ω2 ) G2 = ( q1 - p1 q0 )ω / ( 1 + p21ω2 ) η = G2 /G1 = ( q1 - p1 q0 )ω / ( q0 + p1 q1ω2 )
Industry M anagement, Zhengzhou 450015, China; 2. School of M echanical Engineering, Zhengzhou University, Zhengzhou 450001, China)
Abstract: App lying the tension2comp ression viscoelastic model of m etallic rubber (MR ) , the constitutive law of MR is obtained by m eans of ANSYS code w ith equilibrium iteration. The computation result is in good accordance w ith the experim ental data. This work p rovides a reference for further study of MR.
G1 = p1 q1ω2 / ( 1 + p21ω2 )
G2 = q1ω / ( 1 + p21ω2 )
(2)
η = G2 /G1 = 1 / p1ω 式中 : G1 、G2 ———储能模量 (剪切模量 ) 和损耗 模量 ;η———损耗因子 ,用于描述粘弹性材料的阻尼
性能 ,η越大 ,材料阻尼性能越好 ,η越小 , 材料阻尼
求解收敛后 ,进入 ANSYS的 post26 后处理模 块 ,选择顶面中心节点 ,导出该节点的力 - 位移值 。 由于 ANSYS的计算结果是压力和沿 - Z方向位移 数据 ,为了便于同压缩实验所得到的力 2位移曲线相 比较 ,将试验数据换算为压力并将有限元计算的位 移转变为正值 ,图 8 为换算后的计算曲线与试验 曲线 。
τ( t) + p1τ( t) = q0γ( t) + q1γ( t)
(5)
式中 :τ( t) 、γ( t) 、p1、q0 及 q1 ———意义同上 。在
图 4 金属橡胶本构模型 Fig. 4 Constitutive model of MR
图 4本构模型在一维应力作用下的应力 2应变 关系用应变能函数形式可表述为
表 1 试样 X3结构参数
Table 1 Structura l param eters of X3
试样号
高 /mm
直径 /mm 密度 / g/ cm3
X3
17. 27
20. 39
1. 74
设定好边界条件后即可进入 ANSYS的 solution 模块 ,设置求解参数进行求解 。由于该模型属于大 应变非线性分析 。应在求解选项里面选择大变形 静态求解 ,并选择自动时间步长 ,为了便于收敛使 用力收敛准则 ,并设定收敛值为 0. 005 N。设定求 解载荷步为 1 200 Pa,最大步长为 400 Pa,最小步长 为 25 Pa。
1 模型分析
1. 1 现有 M axwell模型
M axwell模型认为 ,粘弹性材料可以等效为一个
弹簧和一个粘壶元件相串联而成 ,如图 1所示 ,其本
构关系为
τ( t) + p1τ( t) = q1γ( t)
(1)
式中 :τ( t)和 γ( t) ———粘弹性材料的剪应力和剪应
变 ; p1 和 q1 ———由粘弹性材料性能确定的系数 。在 简谐应变的激励下 ,由本构关系式 1可得
N
∑ U =
Cij ( I1 - 3) i ( I2 - 3) j
(8)
i+j =1
许多有限元分析软件 ,如 ANSYS和 ABAQUS向用户
推荐的应变能函数形式 ,都是基于上式级数一次、二
次和三次的完整幂级数 。这里 ,选取一次完整幂级数
金属橡胶粘弹性本构模型研究
89
形式 ,即取 N = 1,可 λ2
-
1 λ
9U 9I1
+λI99UI2
(7)
I1 、I2 为应变不变量 ;λ为伸长率 ; U 为应变能
函数 。
λ = 1 +ε; I1 =λ2 + λ2 ; I2 = 2λ +λ12
这里应变为工程应变 , 应力为真实应力 , 取压 缩为负 。
各向同性不可压缩材料的应变能函数可以表 示为以下各项的和
(6) 式中 : G1 、G2 及 η———意义同上 。研究表明 , 标 准线性固体模型能够描述粘弹性材料的蠕变及松 弛特性 ,但不能确切地描述频率对其力学性能的影 响规律 。
2 金属橡胶的粘弹性本构模型
为了表现橡胶的大变形和粘弹性特征 , R ivilin 将应变能函数和松弛函数联系起来 ,建立如图 4 所 示模型 ,并使用该模型推导了橡胶的应变能密度函 数 。该模型由两个非线性弹簧和 M axwell体并联而 成 。其中两个非线性弹簧用来表征金属橡胶的非 线性大变形行为 ,M axwell体用来表征金属橡胶的粘 弹性行为 。此模型可作为金属橡胶材料单轴冲击 压缩和拉伸时的本构模型 [ 2 ] 。
关键词 : 振动与波 ;金属橡胶 ;粘弹性 ;本构模型 中图分类号 : O241. 82 文献标识码 : A
Study on V iscoela stic Con stitutive M odel of M R
ZHAO Cheng1, 2 , ZHAN G J un2 (1. School of M echatronics Engineering, Zhengzhou Institute of Aeronautical
收稿日期 : 2009 - 01 - 12 基金项目 : 河南省科技厅科技攻关项目 (项目编号 072102240024 ) 、
河南省青年骨干教师资助计划项目 。 作者简介 : 赵程 (1967 - ) ,男 ,河南人 ,博士 ,副教授 ,主要从事金属
材料及其改性研究 。 E2mail: zc19671117@ yahoo. com. cn
切地描述粘弹性材料的松弛特性及损耗因子 η、储
能模量 G1 随频率 ω的变化趋势 , 并且没有体现出 温度对粘弹性材料力学性能的影响 。
1. 3 标准线性固体模型 标准线性固体模型是将粘弹性材料等效为一
个弹簧和一个 Kelvin元件相串联 ,如图 3 所示 。其 本构关系为
图 3 标准线性固体模型 Fig. 3 Standard linear solid model
Key words: vibration and wave; metallic rubber (MR ) ; viscoelasticity; constitutive model
金属橡胶是由螺旋卷经过铺放和模压而成型 的 。金属橡胶受力时由于金属丝之间的摩擦而表 现出粘弹性行为 ,故可将其应用于隔振 、减振等场 合 [ 1 ] 。要使其在工程应用中发挥良好的阻尼耗能 性能 ,关键是构建能够精确描述材料本构关系的粘 弹性本构模型 。然而粘弹性材料的力学性能受环 境温度 、振动频率 、应变幅值等影响很大 ,因此 ,其 本构关系的建立非常复杂 。本文利用现有的粘弹 性材料本构模型 [ 2 ]并参考橡胶本构模型的建立方 法 [ 3 ] ,并应用通用有限元软件 ANSYS进行求解 。
性能越差 。
2009年 10月
噪 声 与 振 动 控 制
第 5期
图 1 M axwell模型 Fig. 1 M axwell model
研究表明 , M axw ell模型能够描述粘弹性材料的 松弛特性及储能模量 G1 随频率 ω的变化趋势 , 而 不能确切地描述粘弹性材料的儒变特性及损耗因 子 η随频率 ω的变化趋势 , 并且没有体现出温度对 粘弹性材料力学性能的影响 。 1. 2 现有 Kelv in模型
U = C10 ( I1 - 3) + C01 ( I2 - 3)
(9)
将式 9代入式 7中 ,可以得到一个基于应变能函数
的超弹性本构模型
σ
=2
1
-
1 λ3
[ C10λ + C01 ]
( 10 )
式中 C10 、C01为模型参数 。
3 金 属 橡 胶 准 静 态 拉 压 模 型 有 限 元 分析
根据以上金属橡胶拉压本构模型 ,在通用有限 元结构分析软件 ANSYS中可根据材料应力 - 应变 关系建立非线性材料的有限元模型 ,通过平衡迭代 求解可得到模型的力 - 位移曲线 ,该曲线可与实际 曲线进行对比 。
