橡胶本构模型
橡胶材料本构模型及其在工程设计中的应用

橡胶材料本构模型及其在工程设计中的应用橡胶材料是一种具有特殊性能的高分子材料,在工程设计中具有广泛的应用。
橡胶材料的本构模型是工程设计中不可忽视的重要部分,它描述了材料的力学行为和性能,对于优化设计、预测材料寿命和性能至关重要。
1. 橡胶材料的力学特性橡胶材料具有高度的弹性和可塑性,能够在较大的应变范围内发生可逆变形。
这种特性使得橡胶材料在工程设计中广泛应用于缓冲、密封、减振等领域。
橡胶材料的力学特性与其分子结构密切相关。
橡胶分子链上的交联点使得材料具有高度的可拉伸性和回弹性,同时也决定了材料的耐磨性和耐化学性。
此外,橡胶材料中的填料还会影响其力学性能,如增强材料可以增加材料的强度和刚度。
2. 橡胶材料的本构模型橡胶材料的力学行为通常可以由本构模型来描述。
本构模型是基于一些假设和实验数据,通过数学公式来表达材料的应力与应变的关系。
常见的橡胶材料本构模型有胶粘弹性本构模型和超弹性本构模型。
胶粘弹性本构模型主要用来描述橡胶材料在低频振动或大变形条件下的力学行为。
它通过组合弹性、粘性和黏弹性部分,可以较好地描述橡胶材料的非线性、时变行为。
常见的胶粘弹性本构模型有Maxwell模型和Burgers模型等。
超弹性本构模型主要用来描述橡胶材料在小应变范围内的力学行为。
它假设材料满足能量守恒和等效应力功率关系,通过超弹性函数来描述应力与应变之间的关系。
常见的超弹性本构模型有Mooney-Rivlin模型和Ogden模型等。
3. 橡胶材料本构模型在工程设计中的应用橡胶材料的本构模型在工程设计中有着重要的应用价值。
首先,本构模型可以用来预测橡胶材料的性能和行为。
通过对材料进行拉伸、压缩、剪切等实验,得到的实验数据可以用来拟合本构模型参数,从而预测材料在特定载荷下的应力和应变分布。
其次,橡胶材料的本构模型可以用于优化设计。
在工程设计中,橡胶材料通常需要满足一定的性能要求,如承载能力、耐磨性等。
通过建立合适的本构模型,并结合优化算法,可以得到最优的材料形状和结构,以满足设计要求。
workbench建立橡胶的超弹性和粘弹性本构模型
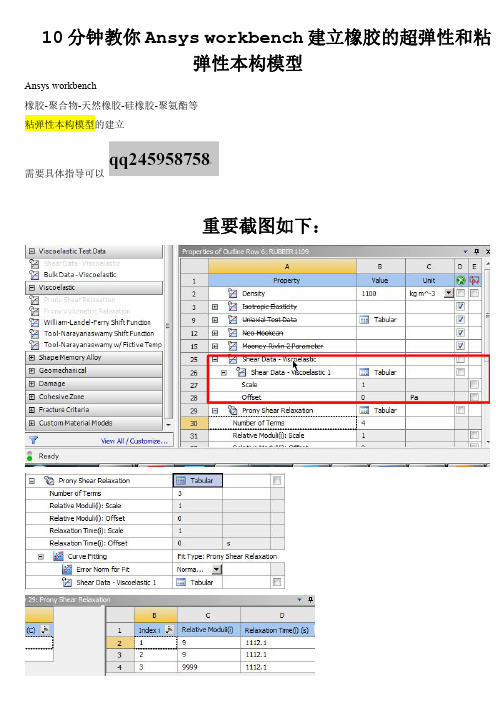
10分钟教你Ansys workbench建立橡胶的超弹性和粘弹性本构模型Ansys workbench橡胶-聚合物-天然橡胶-硅橡胶-聚氨酯等粘弹性本构模型的建立需要具体指导可以重要截图如下:补充:ANSYS 粘弹性材料1.1ANSYS 中表征粘弹性属性问题粘弹性材料的应力响应包括弹性部分和粘性部分,在载荷作用下弹性部分是即时响应的,而粘性部分需要经过一段时间才能表现出来。
一般的,应力函数是由积分形式给出的,在小应变理论下,各向同性的粘弹性本构方程可以写成如下形式:()()002t t de d G t d I K t d d d σττττττ∆=-+-⎰⎰(1)其中σ=Cauchy 应力()G t =为剪切松弛核函数()K t =为体积松弛核函数e =为应变偏量部分(剪切变形)∆=为应变体积部分(体积变形)t =当前时间τ=过去时间I =为单位张量。
该式是根据松弛条件本构方程(1),通过将一点的应变分解为应变球张量(体积变形)和应变斜张量(剪切变形)两部分,推导而得的。
这里不再敖述,可参考相关文献等。
ANSYS 中描述粘弹性积分核函数()G t 和()K t 参数表示方式主要有两种,一种是广义Maxwell 单元(VISCO88和VISCO89)所采用的Maxwell 形式,一种是结构单元所采用的Prony 级数形式。
实际上,这两种表示方式是一致的,只是具体数学表达式有一点点不同。
1.2Prony 级数形式用Prony 级数表示粘弹性属性的基本形式为:()1exp G n i G i i t G t G G τ∞=⎛⎫=+- ⎪⎝⎭∑(2)()1exp K n i K i i t K t K K τ∞=⎛⎫=+- ⎪⎝⎭∑(3)其中,G ∞和i G 是剪切模量,K ∞和i K 是体积模量,G i τ和K i τ是各Prony 级数分量的松弛时间(Relative time)。
再定义下面相对模量(Relative modulus)0G i i G G α=(4)0K i i K K α=(5)其中,0G ,0K 分别为粘弹性材质的瞬态模量,并定义式如下:()010G n i i G G t G G ∞====+∑(6)()010Kn i i K K t K K ∞====+∑(7)在ANSYS 中,Prony 级数的阶数G n 和K n 可以不必相同,当然其中的松弛时间G i τ和K i τ也不必相同。
橡胶材料的本构模型

上的分量 。
E=
1 ( C - I) 2
( 18 )
© 1994-2010 China Academic Journal Electronic Publishing House. All rights reserved.
第2期
朱艳峰等 1 橡胶材料的本构模型
121
( 16 ) ( 17 )
1 1 2 2 θ θ+ θ θ + c3 E θ θ Ezz c1 E c2 E 2 2
式中 , c1 , c2 和 c3 为材料的无量纲常数 ,材料各向 2 同性时 , c1 = c2 = c3 = ( J m / 8) - 1 , E θ θ 和 Ezz 分别为
Lagrangian 或 Green 变形张量 E 在环向和轴向
19 世纪以来 ,橡胶材料本构关系的研究不断
C = F F C = 5 x / 5 X J = det F
T
( 5) ( 6) ( 7)
式中 , I 为二阶张量不变量 , F 为变形梯度 , x 和 X 分别为同一点在变形前后的坐标 , J 为变形后与 变形前的体积比 。
2 分子统计学本构模型
3. 2 改进 Mooney2 Rivl in 模型 Tschoegl N W[ 11 ] 认为含高阶项的 Moo ney2 Rivlin 模型能更好地适应填充与非填充橡胶材
发展 ,建立了众多基于不理论的本构模型 现将这些本构模型简介如下 。
1 基本概念
[1 ]
。
对于各向同性材料 , 假设 I1 , I2 和 I3 分别为 右 Cauchy2 Green 变形张量 C 的第一 、 第二 、 第三 基本不变量 ,对于初始无应力构形的超弹性材料 , 应变能函数 W 可表示为 : W = W ( I1 , I2 , I3 )
不同温度下橡胶的动态力学性能及本构模型研究

第22卷 第1期2007年2月实 验 力 学J OU RNAL OF EXPERIM EN TAL M ECHANICSVol.22 No.1Feb.2007文章编号:100124888(2007)0120001206不同温度下橡胶的动态力学性能及本构模型研究3王宝珍1,胡时胜1,周相荣2(1.中国科学技术大学中国科学院材料力学行为和设计重点实验室,安徽合肥230026;2.中国船舶重工集团上海船舶设备研究所,上海200031)摘要:利用带有温度调控装置的SHPB(Split Hop kinson Pressure Bar)试验装置和岛津材料试验机,测定了CR橡胶在不同温度(-20℃~50℃),不同应变率(5×10-3/s~3×103/s)条件下的应力应变曲线。
结果表明:CR橡胶的力学性能具有温度敏感性和应变率敏感性,两者有一定的等效性,且在动态条件下,-20℃时的应力应变曲线表现出向“玻璃态”转变的特性。
本文在以前研究者提出的率相关本构模型的基础上进行了改进,同时考虑了温度效应的影响,提出了一个能描述CR橡胶在不同温度和应变率下的一维压缩力学行为的本构模型,该模型和试验数据有很好的一致性,为数值模拟提供了重要的依据。
关键词:橡胶;SH PB;温度效应;应变率效应;玻璃化转变温度中图分类号:O347;TQ33.7+3 文献标识码:A0 引言 橡胶属于一种高聚物材料,具有高弹性、低阻抗、粘弹性等力学性能,在汽车、船舶、电子、建筑及机械工业等行业中常用作冲击吸能和抗震材料,具有重要的社会价值和经济价值。
但橡胶材料的力学性能会受到环境温度和应变率的影响,且两者还存在一定的等效关系。
不仅如此,随着温度和应变率的变化,橡胶材料还可呈现出三种不同的力学形态,即:粘流态、橡胶态和玻璃态。
一旦力学状态发生改变,其良好的力学性能也无法体现,使用价值就会受到很大的影响。
因此研究橡胶在不同温度、不同应变率下的力学性能具有十分重要的意义。
几种典型的橡胶材料超弹性本构模型及其适用性

⼏种典型的橡胶材料超弹性本构模型及其适⽤性橡胶材料具有良好的粘弹性,被⼴泛⽤作密封、减振部件。
橡胶作为⼀种超弹性材料,其物理化学性能与⾦属材料有很⼤差别。
橡胶材料的主要特点不可压缩性:橡胶材料的泊松⽐µ⼀般在0.45~0.4999范围内变化,接近于液体的泊松⽐(1) 不可压缩性:0.5,因此橡胶可以看作是⼀种体积近似不可压缩的材料。
⼤变形特性:橡胶⾼分⼦材料变形很⼤,⽽其弹性模量与⾦属材料相⽐却⼩很多。
橡胶材料(2) ⼤变形特性:的变形范围⼀般在200%~500%,甚⾄能够达到1000%,很多⾦属材料的变形则不⾜0.5%。
(3) ⾮线性:⾮线性:橡胶材料具有三重⾮线性,即⼏何⾮线性、材料⾮线性和边界⾮线性。
橡胶材料的应⼒-应变关系具有明显的⾮线性,其⼒学性能与环境条件、应变历程、加载速率等因素有很⼤关联,且随时间延长⽽不断变化。
本构模型及其适⽤性从20世纪40年代⾄今,国内外许多学者提出了许多橡胶材料的本构模型,⼤致可分为两⼤类:基于应变能函数的唯象模型和基于分⼦链⽹络的统计模型。
基于应变能函数的唯象模型⼜可分为两类。
⼀类是以应变不变量表⽰的应变能密度函数模型,这类模型在处理橡胶弹性时,可以把橡胶材料的变形看成是各向同性的均匀变形,从⽽将应变能密度函数表⽰成变形张量不变量的函数,⽐如:Mooney-Rivlin模型、Yeoh模型等。
另⼀类是以主伸长表⽰的应变能函数模型,⽐如:Valanis-Landel模型、Ogden模型等。
基于分⼦链⽹络的统计模型按照分⼦链的统计特性可分为两类:⾼斯链⽹络模型和⾮⾼斯链⽹络模型。
其中最具代表性的分⼦统计学模型包括Treloar模型以及Arruda-Boyce的8链模型。
下⾯对⼏种常见的本构模型进⾏简要介绍:Mooney-Rivlin模型Mooney-Rivlin模型是⼀个⽐较常⽤的模型,⼏乎可以模拟所有橡胶材料的⼒学⾏为。
其应变能密度函数模型为:对于不可压缩材料,典型的⼆项三阶展开式为:式中:N、Cij和dk为材料常数,由实验确定。
橡胶材料的本构模型

橡胶材料的本构模型橡胶材料的本构模型是描述橡胶材料力学行为的数学模型。
本构模型是材料力学研究中的重要理论工具,通过数学方程形式对材料的应力-应变关系进行描述。
橡胶是一类具有高可拉伸性和高回弹性的材料,其力学行为与其他材料有很大的不同,因此需要特别的本构模型进行描述。
在橡胶材料力学行为的研究中,最广泛应用的两个本构模型是针对小变形的线性弹性模型和针对大变形的高度非线性模型。
线性弹性模型是最简单的橡胶本构模型,假设橡胶材料的应力和应变之间是线性关系。
这个模型适用于小变形范围内的橡胶材料力学行为分析,可以方便地通过材料的弹性常数进行描述。
线性弹性模型的基本形式为:σ=Cε其中,σ表示应力,ε表示应变,C为弹性常数。
线性弹性模型可以通过杨氏模量和泊松比来描述橡胶材料的力学性质。
然而,橡胶材料的应力-应变关系在大变形情况下会呈现高度非线性行为。
在这种情况下,采用线性弹性模型进行描述就不合适了。
因此,需要使用高度非线性的本构模型。
高度非线性的本构模型主要有聚合物链模型、统计力学模型、应变能密度函数模型和粘弹性模型等。
这些模型的共同特点是考虑了橡胶材料的非线性变形,并可以用来描述大变形下橡胶材料的应力-应变关系。
聚合物链模型是最简单的非线性本构模型之一、它通过一维线性弹簧链表示聚合物链,考虑了链的拉伸、弯曲和扭转等非线性效应。
通过调整弹簧的弹性系数和链的长度可以得到不同力学行为的橡胶材料的本构关系。
统计力学模型基于聚合物链模型进一步发展,考虑了链的各向异性和随机性。
该模型通过统计力学方法,描述橡胶材料中具有不同平衡态的链的分布情况,并计算出平衡态下的应力-应变关系。
应变能密度函数模型是一种常用的非线性本构模型。
它将应变能密度函数表示为材料的位移梯度和位移梯度的统计平均,通过这个函数可以计算得到材料的应力-应变关系。
粘弹性模型是描述橡胶材料在弹性行为和粘性行为之间转变的一种本构模型。
在这个模型中,应力和应变同时取决于弹性效应和粘性效应,并通过两个弹性模量和一个粘性模量来描述材料的力学行为。
橡胶材料的基本实验及本构关系模型

第3章:橡胶材料的基础实验及本构模型作为一种具有良好弹性性能的工程材料,硫化橡胶早在19世纪就被广泛应用于密封、承载、减振降噪等工业领域。
而橡胶轨道减振器的使用则是最近20年来的事情,然而,不同于金属材料仅需要几个参数描述其材料特性,橡胶的行为复杂,材料本构关系是非线性的。
它的力学行为对温度,环境,应变历史,加载的速率都非常敏感,这样使得描述橡胶的行为变得更为复杂。
而橡胶的制造工艺和成分也对橡胶力学性能有显著的影响。
简单依赖单向拉伸性能实验并不能完全描述材料包括压缩及剪切在内的所有力学行为,这也意味着对橡胶轨道减振器进行有限元分析和结构模拟,必须对橡胶材料进行包括拉伸、压缩,剪切及体积实验等在内的全部基础实验。
3.1 橡胶基础实验简介描述橡胶材料的基础实验有8种(如图3-1):单轴拉伸和压缩实验,双轴拉伸和压缩实验,平面拉伸和压缩(纯剪)实验以及测定体积变化的实验(拉或压)。
在长期的研究和实验,发现从单轴拉伸,双轴拉伸,平面拉伸及体积压缩实验中能够获得足够精确的实验数据。
因此,目前国际上定义橡胶材料力学行为的实验为:单向拉伸、双向拉伸、平面剪切及体积压缩。
图3-1 橡胶材料的8种基础实验对有限元分析所用的实验数据,一个重要的要求是,实验时实验试样应能达到“纯”的应变状态,这样得到的应力应变曲线是我们期望的能代表橡胶的行为特性的状态。
有限元程序通常需要输入的应力应变实验数据范围应大于要分析结构的预期的最大应力应变范围。
通常,理想状态应该是测得在几种准静态荷载模式下的应力应变曲线,这样可以选择出最合适的材料的本构模型以及反映这种模型的参数。
图3-2是本课题研究工作中所用到的一组橡胶材料数据,该实验在美国AXEL实验室完成,材料是公司生产轨道减振器产品所用配方。
图3-2 橡胶基础实验数据3.2 橡胶材料的基础实验3.2.1单轴拉伸实验单轴拉伸实验是最常用到的一种实验,有很多种橡胶拉伸的实验标准。
但是为有限元分析的实验要求比标准的实验方法还要高些,最为明显的是实验要达到一个纯的拉伸状态,也就是实验应该尽量减小对试样侧面的约束。
橡胶材料的基本实验及本构关系模型

橡胶材料的基本实验及本构关系模型第3章:橡胶材料的基础实验及本构模型作为一种具有良好弹性性能的工程材料,硫化橡胶早在19世纪就被广泛应用于密封、承载、减振降噪等工业领域。
而橡胶轨道减振器的使用则是最近20年来的事情,然而,不同于金属材料仅需要几个参数描述其材料特性,橡胶的行为复杂,材料本构关系是非线性的。
它的力学行为对温度,环境,应变历史,加载的速率都非常敏感,这样使得描述橡胶的行为变得更为复杂。
而橡胶的制造工艺和成分也对橡胶力学性能有显著的影响。
简单依赖单向拉伸性能实验并不能完全描述材料包括压缩及剪切在内的所有力学行为,这也意味着对橡胶轨道减振器进行有限元分析和结构模拟,必须对橡胶材料进行包括拉伸、压缩,剪切及体积实验等在内的全部基础实验。
3.1 橡胶基础实验简介描述橡胶材料的基础实验有8种(如图3-1):单轴拉伸和压缩实验,双轴拉伸和压缩实验,平面拉伸和压缩(纯剪)实验以及测定体积变化的实验(拉或压)。
在长期的研究和实验,发现从单轴拉伸,双轴拉伸,平面拉伸及体积压缩实验中能够获得足够精确的实验数据。
因此,目前国际上定义橡胶材料力学行为的实验为:单向拉伸、双向拉伸、平面剪切及体积压缩。
图3-1 橡胶材料的8种基础实验对有限元分析所用的实验数据,一个重要的要求是,实验时实验试样应能达到“纯”的应变状态,这样得到的应力应变曲线是我们期望的能代表橡胶的行为特性的状态。
有限元程序通常需要输入的应力应变实验数据范围应大于要分析结构的预期的最大应力应变范围。
通常,理想状态应该是测得在几种准静态荷载模式下的应力应变曲线,这样可以选择出最合适的材料的本构模型以及反映这种模型的参数。
图3-2是本课题研究工作中所用到的一组橡胶材料数据,该实验在美国AXEL实验室完成,材料是公司生产轨道减振器产品所用配方。
图3-2 橡胶基础实验数据3.2 橡胶材料的基础实验3.2.1单轴拉伸实验单轴拉伸实验是最常用到的一种实验,有很多种橡胶拉伸的实验标准。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
橡胶本构模型
橡胶是一种高弹性材料,它在外力作用下能够发生大变形而不破断,广泛应用于工业
制品、生活用品和医疗器械等领域。
为了预测和控制橡胶材料的力学性能,我们需要建立
橡胶的本构模型,描述其应力-应变关系,以及有关的力学参数。
橡胶的本构模型,通常分为三类:经典连续介质力学模型,统计力学模型和分子力学
模型。
下面将分别介绍这三类模型,并重点介绍其中最常用的两个模型:高斯模型和Mullins效应模型。
1. 经典连续介质力学模型
连续介质力学是传统力学的一部分,它认为物质是由连续的、无限小的区域所组成的。
对于固体材料,连续介质力学模型从宏观上分析材料的应力-应变关系,假定材料是均匀、各向同性的,所以它们的应力可以表示为应变的函数。
在橡胶材料中,经典连续介质力学
模型主要有线性弹性模型(Hooke定律)和非线性弹性模型。
线性弹性模型适用于小应力下的弹性变形情况,它规定应力与应变之比为常数,即Hooke定律:$\sigma = E\epsilon$,其中$\sigma$是应力,$\epsilon$是应变,$E$是弹性模量。
非线性弹性模型适用于大应力下弹性变形情况,也适用于橡胶材料的变形特性,如泊
松比、流变特性、时间效应等。
其中,高斯模型是最常用的非线性弹性模型之一。
2. 统计力学模型
统计力学模型假设橡胶材料是由链状聚合物组成的,这些聚合物可以发生旋转、弯曲、拉伸等变形,从而引起橡胶材料的变形。
这些变形可以用热力学平衡来描述,因此,统计
力学模型包括自由能分析、弹性分布分析等方法。
统计力学模型对于深入理解橡胶材料的
力学性质具有重要的作用,但也存在着复杂的计算和预测问题。
分子力学模型是指通过数学模拟和计算机模拟,从微观的原子、分子层面来分析材料
的力学性质。
对于橡胶材料的模拟,最常用的方法是分子动力学模拟和蒙特卡罗模拟。
分
子动力学模拟利用牛顿定律和势能函数来模拟分子之间的相互作用,蒙特卡罗模拟则利用
可能的状态的随机性来进行模拟。
分子力学模型可以为橡胶材料的理解和预测提供微观层
面的支撑,但也存在着计算量大、时间长、结果不稳定等不足之处。
高斯模型
高斯模型是通过经典连续介质力学理论,对橡胶材料进行建模的一种方法,它假设橡
胶材料是由一个大量的、任意长的链状分子所组成的。
这些链状分子在无应力下是随机卷
曲状态,而在受到拉伸应力作用下,链状分子变成延伸的线状分子。
橡胶材料的力学性质,主要和这些线状分子的延伸程度有关。
线状分子的延伸程度可以用延伸比($b$)来描述,即变形后的长度与初始长度之比。
当延伸比较大(大于0.5)时,橡胶材料就会进入马尔科夫区域,此时,线状分子的拉伸强度逐渐增加。
高斯模型认为,橡胶材料的静态弹性模量非常小,而本构方程则使用三个参数来描述材料的应力-应变关系。
这三个参数分别是:延伸比下拉伸强度($S$)、拉伸比下应变劣化($C$)以及抗剪强度($\lambda$)。
本构方程可以表示为:
$$\sigma = S
\left\{1+\left(\frac{C^2}{b^2}-\frac{C}{b}\right)\left[\exp(-b)+\left(1-\frac{ 1}{b}\right)\left(\frac{b}{\exp(b)-1}\right)\right]\right\}-\lambda\gamma$$
其中,$\sigma$是应力,$\gamma$是剪应变,$S$、$C$和$\lambda$分别是高斯模型
中的三个参数。
此外,$b$为拉伸比,$b=\frac{l}{l_0}$,其中$l$是被测橡胶的长度,$l_0$是橡胶原始长度。
Mullins效应模型
Mullins效应模型是描述橡胶材料非线性行为的模型之一,它假设橡胶材料是由应变畸变的分子网所组成的。
这种畸变在内部形成了非均匀分布的各向异性和非线性效应。
在前面的延伸中,这种畸变留下了一个"记忆"。
换句话说,橡胶材料的特性随着密度的变化而变化,因此,无论是拉伸还是压缩,材料都会展现出不同的性能,从而使延伸和回缩之间的行为发生了改变。
Mullins效应模型使用了一个附属量来描述这个记忆/历史依赖性:$\beta$。
这个附属量类似于韧性,在应变循环的每一个周期里都被保存和更新。
当材料从高应变状态回到初始状态时,Mullins效应模型允许附属量$\beta$进行不断的更新。
它考虑到了拉伸-回弹循环中能量的滞后和一部分能量的损失,也可以用于描述橡胶材料的持久形状变化,
Mullins效应模型则通过应力张量($\sigma_{ij}$)和应变张量($\epsilon_{ij}$)之间的关系来描述橡胶材料的变形特性。
模型可以表示为:
其中,$\Psi$是材料的应变能量密度。
Mullins效应模型可以很好地描述橡胶材料的非线性特性,尤其在应变循环实验中更能体现其实用价值。
