平面向量四心问题[最全]
平面向量与三角形四心问题老师

平面向量基本定理与三角形四心引理:已知O 是ABC ∆内的一点,AOB AOC BOC ∆∆∆,,的面积分别为A S ,B S ,C S ,求证:0=++•••OC S OB S OA S C B A如图2延长OA 与BC 边相交于点D 则BCCOD ACD BOD ABD COD BOD ACD BD S S DC BD S S S S S S S S A =--===∆∆∆∆∆∆∆ =OD BC DC OB +BCBDOC =C B BS SS +OB +CB C S S S +OCCB ACOA BOA COD BOD COA COD BOABOD S S S S S S S S S SSOA OD +=++===∴ CB A S S S OD +-=OA ∴CB A S S S +-OA =C B BS S S +OB +CB C S S S +OC∴ 0=++•••OC S OB S OA S C B A推论O 是ABC ∆内的一点,且0=++•••OC OB OA z y x ,则z y x S S S AOB COA BOC ::::=∆∆∆引理1.设O 为ABC ∆内一点,321,,λλλ均为正实数,321=++λλλ,则有3213λλλλ++=∆∆ABC AOB S S ,3211λλλλ++=∆∆ABC BOC S S ,3212λλλλ++=∆∆ABC AOC S S引理 2.设O 为ABC ∆内一点,S S S C B ,,分别表示ABC AOB AOC S S S ∆∆∆,,的面积,则AC SS AB S SAO C B +=一.知识梳理:基础知识定义 向量的数量积,若非零向量a , b 的夹角为θ,则a ,b 的数量积记作cos a b a b ,也称内积,其中|b |cos θ叫做b 在a 上的投影(注:投影可能为负值).OA BCDOABC定义 若点P 是直线P 1P 2上异于p 1,p 2的一点,则存在唯一实数λ,使21PP P P λ=,λ叫P 分21P P 所成的比,若O 为平面内任意一点,则λλ++=121OP OP OP .由此可得若P 1,P ,P 2的坐标分别为(x 1, y 1), (x, y), (x 2, y 2),则..1121212121y y y y x x x x y y y x x x --=--=⎪⎪⎩⎪⎪⎨⎧++=++=λλλλλ定义 设F 是坐标平面内的一个图形,将F 上所有的点按照向量a =(h, k)的方向,平移|a |=22k h +个单位得到图形'F ,这一过程叫做平移。
平面向量 三角形四心应用

平面向量 三角形“四心”应用一、三角形四心:重心:ABC ∆三边中线交点小结论:M 是三角形ABC ∆的重心(中线交点),则=++。
外心:ABC ∆外接圆的圆心(ABC ∆三边垂直平分线的交点)。
内心:ABC ∆的内角平分线交点。
垂心:ABC ∆三条高现的交点。
1、已知A ,B ,C 是圆O 上的三点,若1()2AO AB AC =+,则AB 与AC 的夹角为 . 90° 1()2AO AB AC =+,所以O 为线段BC 的中点,故BC 为圆O 的直径,090=∠∴BAC , 2、△ABC 外接圆的半径等于1,其圆心O 满足AO →=12(AB →+AC →),|AO →|=|AC →|,则向量BA →在BC →方向上的投影= 解析 由AO →=12(AB →+AC →)可知O 是BC 的中点,即BC 为外接圆的直径,所以|OA →|=|OB →|=|OC →|, 又因为|AO →|=|AC →|=1,故△OAC 为等边三角形,即∠AOC =60°,由圆周角定理可知∠ABC =30°,且|AB →|=3,所以BA →在BC →方向上的投影为|BA →|·cos ∠ABC =3×cos 30°=32,故选C.答案 C3、4、18、O 是平面上的一5、定点,A ,B ,C 是平面上不共线的三个动点,若动点P 满足OP →=OA →+λ(AB →+AC →),λ∈(0,+∞),则点P的轨迹一定通过△ABC 的( )由原等式,得OP →-OA →=λ(AB →+AC →),即AP →=λ(AB →+AC →),根据平行四边形法则,知AB →+AC →是△ABC 的中线AD(D为BC 的中点)所对应向量AD →的2倍,所以点P 的轨迹必过△ABC 的重心.6、(第五章第解课时作业16)解析 作∠BAC 的平分线AD .∵OP →=OA →+λ⎝ ⎛⎭⎪⎪⎫AB →|AB →|+AC →|AC →|,∴AP →=λ⎝ ⎛⎭⎪⎪⎫AB →|AB →|+AC →|AC →|=λ′·AD →|AD →|(λ′∈[0,+∞)), ∴AP →=λ′|AD →|·AD →,∴AP →∥AD →.∴P 的轨迹一定通过△ABC 的内心. 答案 B7、O 为ABC ∆外接圆的圆心,且=++,则A ∠= 0608、设O 是△ABC 的外心(三角形外接圆的圆心).若AO →=13AB →+13AC →,则∠BAC 的度数等于= 解析 取BC 的中点D ,连接AD ,则AB →+AC →=2 AD →.由题意得3AO →=2AD →,∴AD 为BC 的中线且O 为重心.又O 为外心,∴△ABC 为正三角形,∴∠BAC =60°9、在△ABC 中,若OA →·OB →=OB →·OC →=OC →·OA →,则点O 是△ABC 的( )解析 ∵OA →·OB →=OB →·OC →,∴OB →·(OA →-OC →)=0,∴OB →·CA →=0,∴OB ⊥CA ,即OB 为△ABC 底边CA 上的高所在直线.同理OA →·BC →=0,OC →·AB →=0,故O 为△ABC 的垂心.10、已知A ,B ,C 是圆O 上的三点,若)(31AC AB AO +=,则AB 与的夹角为二、三点共线向量:设向量,不共线 1、作业题(创新设计)2、平面直角坐标系中,O 为坐标原点,已知两点A (3,1),B (-1,3)平面直角坐标系中,O 为坐标原点,已知两点A(3,1),B(-1,3),若点C 满足=α+β,其中α,β∈R 且α+β=1,则点C 的轨迹方程为( ) A .(x-1)2+(y-2)2=5 B .3x+2y-11=0 C .2x-y=0 D .x+2y-5=0解:设C(x,y),则=(x,y),=(3,1),=(-1,3).由=α+β,得(x,y)=(3α,α)+(-β,3β)=(3α-β,α+3β).于是由③得β=1-α代入①②,消去β得,再消去α得x+2y=5,即x+2y-5=0. 1OP mOA nOB m n =++=,且三点P 、A 、B共线【一题多解】由平面向量共线定理,得当=α+β,α+β=1时,A,B,C 三点共线.因此,点C 的轨迹为直线AB,由两点式求直线方程得=,即x+2y-5=0.3、(第五章第解课时作业16)如图,在平行四边形ABCD 中,O 是对角线AC ,BD 的交点,N 是线段OD 的中点,AN 的延长线与CD 交于点E ,若AE →=mAB →+AD →,则实数m 的值为________.解析 由N 是OD 的中点得AN →=12AD →+12AO →=12AD →+14(AD →+AB →)=34AD →+14AB →,又因为A ,N ,E 三点共线,故AE →=λAN →,即mAB →+AD →=λ⎝ ⎛⎭⎪⎫34AD →+14AB →,又AB →与AD →不共线,所以⎩⎪⎨⎪⎧m =14λ,1=34λ,解得⎩⎪⎨⎪⎧m =13,λ=43,故实数m =13.答案 13。
平面向量七种解法及四心问题及常见题型汇总
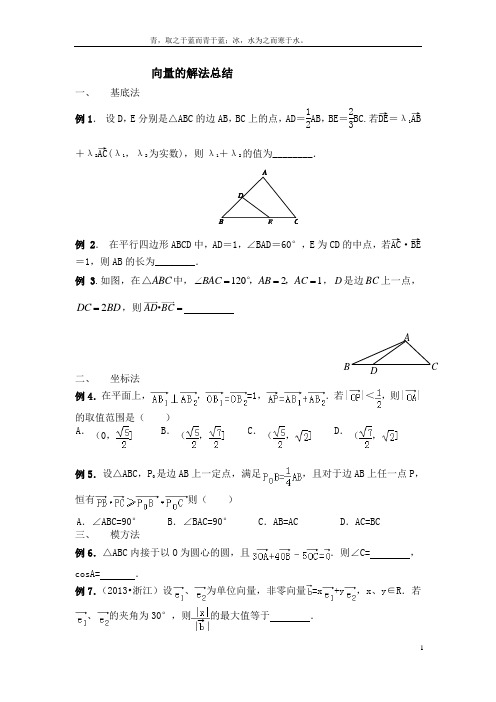
向量的解法总结一、基底法例1. 设D ,E 分别是△ABC 的边AB ,BC 上的点,AD =12AB ,BE =23BC.若DE →=λ1AB→+λ2AC →(λ1,λ2为实数),则λ1+λ2的值为________.例 2. 在平行四边形ABCD 中,AD =1,∠BAD=60°,E 为CD 的中点,若AC →·BE →=1,则AB 的长为________.例3.如图,在ABC △中,12021BAC AB AC ∠===,,°,D 是边BC 上一点,2DC BD =,则AD BC =·二、坐标法例4.在平面上,,=1,.若||<,则||的取值范围是( ) A . (0,] B .(,] C .(,] D .(,]例5.设△ABC,P 0是边AB 上一定点,满足,且对于边AB 上任一点P ,恒有则( ) A . ∠ABC=90° B . ∠BAC=90°C . A B=ACD . A C=BC 三、 模方法例6.△ABC 内接于以O 为圆心的圆,且.则∠C= ,cosA= . 例7.(2013•浙江)设、为单位向量,非零向量=x +y ,x 、y ∈R .若、的夹角为30°,则的最大值等于 .ABD C四、数量积法例8.给定两个长度为1的平面向量OA和OB,它们的夹角为120o. 如图所示,点C在以O为圆心的圆弧AB上变动.若,OC xOA yOB=+其中,x y R∈,则x y+的最大值是________.例9.在△ABC中,AB=2AC=2,∠BAC=120°,,若(O是△ABC的外心),则x1+x2的值为.五、几何法例10.在△ABC中,若对任意k∈R,有|﹣k|≥||,则△ABC的形状是()A.直角三角形B.等腰三角形C.等腰三角形或直角三角形D.等腰直角三角形例11.已知,是单位向量,,若向量满足,则的取值范围为()A.B.C.D.例12.ABC∆的外接圆的圆心为O,两条边上的高的交点为H,()OH m OA OB OC=++,则实数m=________六、面积法例13.已知O是△ABC内一点,,则△AOB与△AOC的面积的比值为.七、射影法例14.已知P为△ABC的外心,且||=4,||=2,则•BC等于.例15.已知O为△ABC的外心,的最大值为()A.B.C.D.“四心”问题1、重心——三角形的三条中线的交点;2、垂心——三角形的三条垂线的交点;3、内心——三角形的三个内角角平分线的交点(三角形内切圆的圆心);4、外心——三角形的三条垂直平分线的交点(三角形外接圆的圆心)根据概念,可知各心的特征条件.比如:重心将中线长度分成2:1;垂线与对应边的向量积为0;角平分线上的任意点到角两边的距离相等;外心到三角形各顶点的距离相等.与三角形的“四心”有关的一些常见的重要的向量关系式有: ① 设()+∞∈,0λ,则向量)(AC AC AB AB +λ必平分∠BAC ,该向量必过△ABC 的内心;② 设()+∞∈,0λ,则向量)(ACAC ABAB -λ必平分∠BAC 的邻补角③ 设()+∞∈,0λ,则向量)cos cos (CAC AC BAB AB +λ必垂直于边BC ,该向量必通过△ABC 的垂心④ △ABC 中AC AB +一定过BC 的中点,通过△ABC 的重心 ⑤ 点O 是△ABC 的外心 222OC OB OA ==⇔ ⑥ 点O 是△ABC 的重心 0=++⇔OC OB OA⑦ 点O 是△ABC 的垂心 ⇔ OA OC OC OB OB OA ⋅=⋅=⋅⇔222222AB OC CA OB BC OA +=+=+⑧ 点O 是△ABC 的内心 0=⋅+⋅+⋅⇔OC c OB b OA a (其中a 、b 、c 为△ABC 三边)-⋅=-⋅=-⋅⇔||()||||()||||(CA CA OC BC BC BA BA OB AC AC AB AB OA )||CB CB 0=⑨ 设O 为△ABC 所在平面内任意一点,G 为△ABC 的重心,则有)(31OC OB OA OG ++= 并且重心G (X A +X B +X C 3 ,Y A +Y B +Y C 3 )例1 已知O 是平面上一 定点,A ,B ,C 是平面上不共线的三个点,动点P 满足:,则P 的轨迹一定通过△ABC 的 ( )A 外心 B 内心 C 重心 D 垂心例2 P 是△ABC 所在平面上一点,若,则P 是△ABC的( ).A .外心B .内心C .重心D .垂心 例3 已知P 是△ABC 所在平面内的一动点,且点P 满足,则动点P 一定过△ABC 的〔 〕.A 、重心B 、垂心C 、外心D 、内心 四、 外心问题例4 已知O 是△ABC 内的一点,若,则O 是△ABC 的〔 〕.A .重心 B.垂心 C.外心 D.内心练习1:已知O 为三角形ABC 所在平面内一点,且满足AB OC CA OB BC OA =+=,则点O 是三角形ABC 的( )(A )外心 (B )内心 (C )重心 (D )垂心2:设O 是平面上一定点,A 、B 、C 是平面上不共线的三点, 动点P 满足)cos cos (CAC AC BAB AB OA OP ++=λ,()+∞∈,0λ,则动点P 的轨迹一定通过△ABC 的( )(A )外心 (B )内心 (C )重心 (D )垂心3、已知向量123,,OP OP OP 满足条件1230OP OP OP ++=,123||||||1OP OP OP ===,求证:123PP P △是正三角形.4、ABC ∆的外接圆的圆心为O ,两条边上的高的交点为H ,()OH m OA OB OC =++,则实数m = .平面向量常见习题汇总:1.(2020•北京卷)已知正方形ABCD 的边长为2,点P 满足1()2AP AB AC =+,则||PD =_________;PB PD ⋅=_________.(建系)2.(2020•全国1卷)设,a b 为单位向量,且||1a b +=,则||a b -=______________.(模方)3.(2020•全国2卷)已知单位向量a →,b →的夹角为45°,k a b →→-与a →垂直,则k =________(垂直)4.(2020•全国3卷)已知向量a ,b 满足||5a =,||6b =,6a b ⋅=-,则cos ,=+a a b _____(夹角)5.(2020•江苏卷)在△ABC 中,43=90AB AC BAC ==︒,,∠,D 在边BC 上,延长AD到P ,使得AP =9,若3()2PA mPB m PC =+-(m 为常数),则CD 的长度是______.(相交问题运用向量共线定理)6.(2020•新全国1山东)已知P 是边长为2的正六边形ABCDEF 内的一点,则AP AB ⋅的取值范用是( )(射影) A. ()2,6- B. (6,2)- C. (2,4)-D. (4,6)-7.(2020•天津卷)如图,在四边形ABCD 中,60,3B AB ︒∠==,6BC =,且3,2AD BC AD AB λ=⋅=-,则实数λ的值为_________,若,M N 是线段BC 上的动点,且||1MN =,则DM DN ⋅的最小值为_________.(建系转化为函数最值问题)8.(2020•浙江卷)设1e ,2e 为单位向量,满足21|22|-≤e e ,12a e e =+,123b e e =+,设a ,b 的夹角为θ,则2cos θ的最小值为_______.【点睛】本题考查利用模求向量数量积、利用向量数量积求向量夹角、利用函数单调性求最值,考查综合分析求解能力,属中档题.9.10.11.(难题)。
平面向量与三角形四心问题(最新整理)

O 是 ABC 的垂心
SBOC S: COA S: AOB tan A : tan B : tan C
tan A OA tan B OB tan C OC 0
C
O
A
D
B
证明:如图 O 为三角形的垂心, tan A CD , tan B CD tan A: tan B DB : AD
O 是 ABC 的重心
SBOC S: COA S: AOB 1:1:1 OA OB OC 0
O 是 ABC 的内心
SBOC S: COA S: AOB a : b : c a OA b OB c OC 0
O 是 ABC 的外心
SBOC S: COA S: AOB sin 2A : sin 2B : sin 2C
OG
1
(OA
OB
OC )
3
3.三角形的外心、重心、垂心的向量关系及应用 设 △ABC 的外心、重心、垂心分别为 O 、 G 、 H ,则 O 、 G 、 H 三点共线( O 、 G 、 H 三点连线称为欧拉线),且 OG 1 GH 。
2 相关题目
10.设△ABC 外心为 O,重心为 G.取点 H,使
AB AB
AC AC
,
∴ AI
bc
AB
AC
.∵
AB
与
AC
分别为 AB 和 AC 方向
AB
AC
AB AC
AI 与∠BAC 平分线共线,即 AI 平分 BAC .
同理可证: BI 平分 ABC , CI 平分 ACB .从而 I 是 △ABC 的内心,如图⑸.
的轨迹一定通过 △ABC 的外心,如图⑻
平面向量三角形四心(有详解)

平面向量三角形四心(有详解)平面向量三角形四心(有详解)平面向量是数学中的重要概念,可以用来表示空间中的点、线、面等几何对象。
在平面向量的运算和应用中,三角形是常见的几何形状之一。
本文将介绍平面向量与三角形四心的关系,并详细解析其性质和应用。
1. 三角形的四心概述三角形的四心是指三角形内部的四个特殊点,包括重心、外心、内心和垂心。
这四个点有着各自的特点和性质,对于研究三角形的形状和性质非常重要。
1.1 重心三角形的重心是三条中线的交点,即三角形三个顶点与对应中点的连线交于一点。
重心在三角形中心位置,对称性较强,具有重要的几何意义。
1.2 外心三角形的外心是外接圆的圆心,即三角形三个顶点的垂直平分线的交点。
外心离三角形各顶点的距离相等,是三角形的外接圆的圆心。
1.3 内心三角形的内心是内切圆的圆心,即三角形三条边的角平分线的交点。
内心到三角形三边的距离相等,是三角形的内切圆的圆心。
1.4 垂心三角形的垂心是三条高线的交点,即三角形三个顶点与对边垂线的交点。
垂心所在的直线被称为垂心线,与三角形的三条边垂直。
2. 平面向量与四心关系的性质平面向量与三角形的四心之间具有一些重要的几何性质和关系,下面将分别介绍。
2.1 重心与向量以三角形的重心为原点建立直角坐标系,三角形三个顶点的位置向量相对于重心的位置向量之和为零。
即,三角形三个顶点的位置向量和为零向量。
2.2 外心与向量三角形的三个顶点为A、B、C,以外心O为原点建立直角坐标系。
则三角形顶点A、B、C的位置向量之和等于三倍的外心O的位置向量。
即,OA + OB + OC = 3OO。
2.3 内心与向量设三角形的内心为I,以内心I为原点建立直角坐标系。
则三角形三个顶点的位置向量与对边的位置向量之和分别为倍数的内心I的位置向量。
即,AI + BI = CI = 2II。
2.4 垂心与向量以三角形的垂心为原点建立直角坐标系,三角形三个顶点的位置向量与对边垂线的位置向量之和为零。
平面向量中的三角形四心问题教师版

平面向量中的三角形四心问题向量是高中数学中引入的重要概念,是解决几何问题的重要工具。
本文就平面向量与三角形四心的联系做一个归纳总结。
在给出结论及证明结论的过程屮,可以体现数学的对称性与推论的相互关系。
—、重心(barycenter)三角形重心是三角形三边屮线的交点。
重心到顶点的距离与重心到对边屮点的距离之比为2: lo结论1:若G为AAB俩在平面内一点,贝^A + GB + GC = Z结论2:・・•I ・■•I •若P为AABEf在平面内一点,贝^G = -(PA+PB+PQoG是AABC^]重心• I ・・'・—•・•....... ••「■ 1 • I •I •・,•—♦证明:PG = -(PA + PB+ PC) « (PG-PA) + (PG-PB) + (PG-PC) = 0«GA + GB + GC = 0oG是AABC^J重心三角形的三条高线的交点叫做三角形的垂心。
结论3:若H为AA3CW在平面内一点,贝麻•丽=而•就=万乙•页OH 是△朋血垂心证明:阪•屈二= 0 A0 HB・ AC = Oo//B 丄AC 同理,有HA丄CB,HC丄故H为三角形垂心结论4:____ 7________ ? ____ _ 9 ____ 9 ____ 7 ____ ?若H为AAB俩在平面内一点,贝^A~ +BC~ =HB~ + AC =HC~ +AB~ oH是AA3制垂心___ ? ___ 9 ____ 9 ___ 7 ___ 7 ___ _ _______ ________ 7 ____ _ ______证明:^HA -vBC = HB「+ CA「得,HA「+ (HB - HC『=HB~ + (HC- HAf<^HBHC = HCHA同理可证得页•而=而就1 =说页由结论3可知命题成立三、夕卜心(c i rcumcenter)三角形三条边的垂直平分线(屮垂线)的相交点。
微专题8 平面向量与三角形的“四心”
+
| |
或=+
若△ABC及内一点O满足关系式:S△OBC·+S△OAC·+S△OAB·=0,即为经
典的“奔驰定理”.若△ABC的三边为a,b,c,有a·+b·+c·=0,则O
为△ABC的 (
)
A.外心
B.内心
C.重心
D.垂心
解析:B
∵=+,=+,∴a·+b·+c·=a·
=·,则点G可能通过△ABC的
(填:重心、内心、垂心或外
心).
解析:由·=·⇔·-·=0⇔·(-)=0,
【例4】 在△ABC中,设 2 - 2 =2·,那么动点M形成的图形必经过
△ABC的
A.垂心
(
)
B.内心
C.外心
D.重心
解析 如图所示,设线段BC的中点为D,则+=2,
∵ 2 - 2 =2·
,∴(+)·
(-)=
2·
,∴·
(+-2)=0,∴·
【例1】 已知点O为△ABC所在平面内一点,若动点P满足=+λ(+
)(λ≥0),则动点P的轨迹一定经过△ABC的 (
A.外心
B.内心
C.垂心
D.重心
)
解析 因为动点P满足=+λ(+)(λ≥0),所以=λ(+
),取BC中点D(图略),则=2λ,则动点P的轨迹一定过△ABC的重
+b(+)+c(+)=(a+b+c)·+b·+c·=0,
∴=
++
+
,∵ , 分别是,方向上的单位向量,∴向
量 + 平分∠BAC,即AO平分∠BAC,同理BO平分∠ABC,∴O为
(完整版)平面向量、三角形“四心”与三角形面积的关系及其证明
一、知识要点1、若O 为ABC ∆内一点,则m n r S S S OC r OB n OA m OBC OAC OAB ::::0=⇔=++∆∆∆→→→2、若O 为ABC ∆的重心,则ABC OBC OAC OAB S S S S ∆∆∆∆===313、若O 为ABC ∆的垂心,则A B C S S S OBC OAC OAB tan :tan :tan ::=∆∆∆,故0tan tan tan=⋅+⋅+⋅→→→OA A OB B OC C4、若O 为ABC ∆的内心,则a b c S S S OBC OAC OAB ::::=∆∆∆,故0=⋅+⋅+⋅→→→OA a OB b OC c5、若O 为ABC ∆的外心,AB C BOC AOC AOB S S S OBC OAC OAB 2sin :2sin :2sin sin :sin :sin ::==∆∆∆故02sin 2sin 2sin=⋅+⋅+⋅→→→OA A OB B OC C二、要点证明1、若O 为ABC ∆内一点,则m n r S S S OC r OB n OA m OBC OAC OAB ::::0=⇔=++∆∆∆→→→证明:先证充分性,即已知0=++→→→OC r OB n OA m ,求证m n r S S S OBC OAC OAB ::::=∆∆∆ 如图所示,分别在射线OA ,OB 上去点1A ,1B ,使得→→=OA m OA 1,→→=OB n OB 1,并以→→11,OB OA 为邻边作平行四边形11DB OA ,连接OD ,11B A故→→→→→→-=+=+=OC r nOB OA m OB OA OD 11,因此OC r OD =。
设S S DB OA 211=,则S S S S S DB A B OA ODB D OA ====111111,mn S OB A n OB m OA AOB OB OA S OAB =⋅=⋅⋅=1111sin 21sin 21,同理mrSS nr S S OAC OBC ==,。
平面向量四心问题
三角形“四心”向量形式的充要条件及其应用1.三角形的“四心”定理的平面几何证明①三角形三边的中垂线交于一点, 这一点为三角形外接圆的圆心, 称外心。
证明: 设AB BC 的中垂线交于点 0,则有0A=0B=QC 故Q 也在AC 的中垂线上,因为 Q 到三顶点的距离相等, 故点Q 是厶ABC 外接圆的圆心.因而称为外心. ②三角形三边上的高交于一点,这一点叫三角形的垂心。
证明:AD 、BE 、CF 为厶ABC 三条高,过点 A 、B C 分别作对边的平行线, 相交成△ A B ' C',AD 为B' C'的中垂线;同理BE 、CF 也分别为 A ' C'、 A B '的中垂线, 由外心定理,它们交于一点, 命题得证. C J B f③三角形三边中线交于一点,这一点叫三角形的重心。
证明:(同一法)设中线BE,CF 交于点G 连结EF, 贝V EF//BC,且EF:BC=FG:GC=EG:GB=1:2. 同理中线AD,B 咬于G,连结DE,则:B °CDE//AB,且 EG:G B 二DGG A 二DE:AB=1:2,故 G,G 重合. ④三角形三内角平分线交于一点,这一点为三角形内切圆的圆心,称内心。
证明:设/ A 、/ C 的平分线相交于I, 过 I 作 ID 丄 BC, IE 丄 AC, IF 丄 AB,则有 IE=IF=ID . 因此I 也在/ C 的平分线上,即三角形三内角平分线交于一点. 2.三角形的“四心” 定理的平面向量表达式及其证明T —f T T① 0是 A ^P 2F > 的重心二 0R +0F 2 +0F 3 =0(其中 a,b,c 是 A ^P 2P 3三边) 证明:充分性 OR +0F 2 +0R = 0= 0是也PP 2P 3的重心若 0R +0巳 +0及=0 ,贝U 0R +0F 2 = -0F >,以 0R , 0F 2 为邻边作PP 2P 3方向上的单位向量,所以向量吧+电 平分N P 2RP 3,即RO 平分N P 2PP 3,同理P 2O 平分N PP 2P 3, c b得到点0是也RP 2F 3的内心。
第7讲 平面向量的奔驰定理与四心问题(解析版)
第7讲 平面向量的奔驰定理与四心问题【考点分析】考点一:三角形四心的概念:①重心:各边中线的交点,重心将中线长度分成2:1.①内心:各角平分线的交点(内切圆的圆心),角平分线上的任意点到角两边的距离相等. ①外心:各边中垂线的交点(外接圆的圆心),外心到三角形各顶点的距离相等. ④垂心:各边上高线的交点,高线与对应边垂直. 考点二:三角形四心的向量表示: ①内心:三角形的内心在向量AB AC ABAC+所在的直线上.0AB PC BC PC CA PB ⋅+⋅+⋅=⇔P 为ABC △的内心. ①外心:PA PB PC ==⇔P 为ABC △的外心.①垂心:PA PB PB PC PC PA ⋅=⋅=⋅⇔P 为ABC △的垂心. ④重心:0PA PB PC ++=⇔P 为ABC △的重心. 考点三:重心坐标公式已知ABC △的顶点11()A x y ,,22()B x y ,,33()C x y ,,则①ABC 的重心坐标为123123()33x x x y y y G ++++,. 考点四:奔驰定理奔驰定理:0321=++OC OB OA λλλ,则AOB △、AOC △、BOC △的面积之比等于321::λλλ 证明:如图,令112131OA OA OB OB OC OC λλλ===,,,即满足1110OA OB OC ++=11121AOB A OB S S λλ=△△,11131AOC A OC S S λλ=△△,11231BOC B OC S S λλ=△△,故321::::AOB AOC BOC S S S λλλ=△△△.考点五:三角形四心与奔驰定理的关系①O 是ABC △的重心:::1:1:10BOC COA A0B S S S OAOB OC =⇔++=△△△.①O 是ABC △的内心:::::0B0C COA AOB S S S a b c OA OB OC =⇔++=△△△.①O 是ABC △的外心:0::sin 2:sin 2:sin 2sin 2sin 2sin 20B C COA AOB S S S A B C AOA BOB COC =⇔++=△△△. ④O 是ABC △的垂心:0::tan :tan :tan tan tan tan 0B C COA AOB S S S A B C AOA BOB COC =⇔++=△△△. 【题型目录】题型一:四心的向量表示 题型二:奔驰定理的应用 【典型例题】题型一: 四心的向量表示【例1】已知O ,N ,P 在所在ABC ∆的平面内,且||||||,0OA OB OC NA NB NC ==++=,且PA PB PB PC PA PC ==,则O ,N ,P 分别是ABC ∆的( )A .重心 外心 垂心B .重心 外心 内心C .外心 重心 垂心D .外心 重心 内心【解析】解:因为且||||||OA OB OC ==,所以0到顶点A ,B ,C 的距离相等,所以O 为ABC ∆的外心. 由PA PB PB PC PA PC ==得()0PA PC PB -=,即AC PB ,所以AC PB ⊥. 同理可证AB PC ⊥,所以P 为ABC ∆的垂心.若0NA NB NC ++=,则NA NB NC +=-,取AB 的中点E ,则2NA NB NE CN +==,所以2||||NE CN =, 所以N 是ABC ∆的重心. 故选:C .【例2】已知M 点在ABC 所在的平面内,满足()(|si |||n sin AB ACOM OA AB B AC Cλλ=++∈R),则动点M 的轨迹一定通过ABC 的( ) A .内心 B .垂心 C .外心 D .重心||sin ||sin AB B AC C =,由,AB AC 表示出AM 即可判断作答令ABC 边BC 上的高为h ,则有||sin ||sin AB B AC C h ==,令边BC 的中点为则2AB AC AD +=, 因此,2()()AB AC AB AC AD h h h AM OM OA hλλλ+=-=+==,即//AM AD , 所以动点M 的轨迹一定通过ABC 的重心. D【例3】设O 为ABC ∆的外心,若OA OB OC OM ++=,则M 是ABC ∆的( ) A .重心(三条中线交点) B .内心(三条角平分线交点) C .垂心(三条高线交点) D .外心(三边中垂线交点)【答案】C【解析】设AB 的中点为D ,根据题意可得OD AB ⊥,由题中向量的等式化简得CM AB ⊥,即CM 在AB 边的高线上.同理可证出AM 在BC 边的高线上,故可得M 是三角形ABC 的垂心. 【详解】在ABC ∆中,O 为外心,可得OA OB OC ==, ①OA OB OC OM ++=, ①OA OB OM OC +=-,设AB 的中点为D ,则OD AB ⊥,2CM OD =, ①CM AB ⊥,可得CM 在AB 边的高线上. 同理可证,AM 在BC 边的高线上,故M 是三角形ABC 两高线的交点,可得M 是三角形ABC 的垂心, 故选:C【点睛】本题给出三角形中的向量等式,判断点M 是三角形的哪一个心.着重考查了向量加法法则、三角形的外接圆性质和三角形“五心”的判断等知识点,属于中档题.【例4】已知点O 是ABC ∆所在平面内的一定点,P 是平面ABC 内一动点,若1,(0,)2OP OA AB BC λλ⎛⎫=++∈+∞ ⎪⎝⎭,则点P 的轨迹一定经过ABC ∆的( )A .重心B .垂心C .内心D .外心由12AB BC AD +=,12OP OA AB BC λλ⎛⎫=++∈ ⎪⎝⎭,知OP OA AD λ=+,,故点P 的轨迹一定经过①ABC 的重心. 的中点, ①12AB BC AD +=,12OP OA AB BC λλ⎛⎫=++∈ ⎪⎝⎭,①OP OA AD λ=+, 即AP AD λ=①点P 的轨迹是射线AD , ①AD 是①ABC 中BC 边上的中线,点P 的轨迹一定经过故选:A .【点睛】本题考查三角形五心的应用,是基础题.解题时要认真审题,仔细解答.【例5】点O 为ABC 所在的平面内,给出下列关系式: ①0OA OB OC ++=;①0AB A OA AB C AC ⎛⎫ ⎪⋅= ⎪⎝-⎭且0BC BA OB BC BA ⎛⎫⎪⋅-= ⎪⎝⎭; ①()()0OA OB AB OB OC BC +⋅=+⋅=.则点O 依次为ABC 的( )A .内心、重心、垂心B .重心、内心、垂心C .重心、内心、外心D .外心、垂心、重心 AB AB和AC AC,从而得出点的平分线上,这就涉及三角形的内心;第三条可以推导出OA OB +和AB 垂直,从而和三角形的外心由于()2OA OB OC OD =-+=-,其中的中点,可知O 为BC 边上中线的三等分点(靠近O 为ABC 的重心; AC AC,AB AB,分别表示在边AC 和AB 上取单位向量AC '和AB ',它们的差是向量B C '',当0AB A OA AB C AC ⎛⎫ ⎪⋅= ⎪⎝-⎭,即OA 的平分线上,同理由0BC BA OB BC BA ⎛⎫⎪⋅-= ⎪⎝⎭,在ABC ∠的平分线上,故O 为ABC 的内心;①OA OB +是以OA ,OB 为边的平行四边形的一条对角线的长,而AB 是该平行四边形的另一条对角线的长,()0OA OB AB +⋅=表示这个平行四边形是菱形,即OA OB =,同理有OB OC =,故O 为ABC 的外. 故选:C【点睛】本题考查利用向量的方法去研究三角形的内心,外心,重心的性质,属于有一定难度的综合题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
学习参考 近年来,对于三角形的"四心”问题的考察时有发生,尤其是和平面向量相结合来考 察很普遍,难度上偏向中等,只要对于这方面的知识准备充分,就能应付自如 •下面就平面 向量和三角形的“四心”问题的类型题做一阐述:
一、 重心问题 三角形“重心”是三角形三条中线的交点, 所以“重 心”就在中线上•
例1 已知0是平面上一 定点,A, B, C是平面上 不共线的三个点,动点 P满足: -■- -■ -f|,贝U P 的轨迹一定通过厶 ABC
的 (
) 解析:如图1,以AB AC为邻边构造平行四边形 ABCD E为对角线的交点,根据向量
所以,上式可化为一二一 一一上,E在直线AP上,因为AE为 UBC 的中线,所以选C. 点评:本题在解题的过程中将平面向量的有关运算与平行四边形的对角线互相平分及 三角形重心性质等相关知识巧妙结合 •
垂心冋题 三角形“垂心”是三角形三条高的交点,所以“垂心”就在高线上 屮 * $ [ 申 斗
例2 P是厶ABC所在平面上一点,若 FT —丄工1 ,贝U P是厶ABC
的( )•
A 外心 B 内心 C 重心
D 垂心
. 片 片 平行四边形法则山匚■ ,因为
AD = 2AE 学习参考
D .垂心 PE (PA-PW即丹创=0
则门.爲邛汗工m汀
所以 P为—二 的垂心.故选D. 点评:本题考查平面向量有关运算,及“数量积为零,则两向量所在直线垂直”、三 角形垂心定义等相关知识.将三角形垂心的定义与平面向量有关运算及“数量积为零,则两 向量所在直线垂直”等相关知识巧妙结合 .
三、 内心问题 三角形“内心”是三角形三条内角平分线的交点, 所以“内心”就在内角平分线线上 例3 已知P是厶ABC所在平面内的一动点,且点 P满足
知AP平分——:-,那么在 —-1'-" 中,AP平分——:-,则知选 B.
A.外心 B .内心 C .重
解析:由 PAPB^PBPC^PAPB-PBPC^Ot
P 一定过△ ABC的〔 A重心 垂心 C、外
,由菱形的基本性质
则动点
解析:如图 分别为 向量AS的单位向量设
则原式可化为 方向上的单位向量 学习参考
点评:这道题给人的印象当然是“新颖、陌生”,首先 AB是什么?想想一个非零向 量除以它的模不就是单位向量? 此题所用的都必须是简单的基本知识,如向量的加减法、
向量的基本定理、菱形的基本性质、 角平分线的性质等,若十分熟悉,又能迅速地将它们迁 移到一起,这道题就迎刃而解了 •
四、 外心问题 三角形“外心”是三角形三条边的垂直平分线的交点,所以“外心”就在垂直平分线 线上• 例4已知0是厶ABC内的一点,若 农二苛二疋 ,贝U 0是厶ABC的〔 〕. A.重心 B.垂心 C.外心 D. 内心
解析:虽二画冃亦冃阳,由向量模的 定义知 _•到—二 的三顶点距离相等•故 -是—二 的外心,选C.
点评:本题将平面向量模的定义与三角形外心的定义及性质等相关知识巧妙结合 三角形的“四心”与平面向量 向量本身是一个几何概念, 具有代数形式和几何形式两种表示方法, 易于数形结合,而 且向量问题在进行数形结合时具有新形式、 新特点,因此可称为高中数学的一个交汇点。 三 角形的“四心”(外心、内心、重心、垂心)是与三角形有关的一些特殊点,各自有一些特 殊的性质。在高考中,往往将“向量作为载体”对三角形的“四心”进行考查。这就需要我 们在熟悉向量的代数运算的基础上读懂向量的几何意义。 与三角形的“四心”有关的一些常见的重要的向量关系式有:
①设;.三|0,:: AB AC
则向量 九(| |十| J必平分/ BAC该向量必通过△ lACl ABC的内心;
AB
则向量 AC ^)必平分/ BAC的邻补角 AC 学习参考
的垂心 a OA b OB c OC = 0 (其中 a、b、c 为AABC三边)
⑨ △ ABC的外心0、重心G、垂心H共线,即0G // OH
例1 : (2003年全国高考题) O是平面上一定点,A、B、C是平面上不共线的三点,动 —— — AB AC 点P满足OP =OA::;*( ' ),:二[0,亠「],则动点P的轨迹一定通过厶ABC的()
易知四边形AETF是菱形 故选答案B 例2 : ( 2005年北京市东城区高三模拟题) O ABC所在平面内一点,如果 OA OB =OB OC =OC OA,贝U O必为△ ABC的( )
(A)外心 (B)内心 (C)重心 (D)垂心
事实上 OA OB =OB OC 二(OA — OC) OB =0= CA OB = 0= OB 丄 CA 故选答案D
设八三10,则向量■( AB AC —— ------ +
AB cosB )必垂直于边BC,该向量必通过△ ABC
AC cosC
△ ABC中AB - AC 一定过BC的中点, 通过△ ABC的重心
点0是△ ABC的外心 一 2 — 2 OA -OB __ 2
=0C
点0是厶ABC的重心 OA OB 0C = 0 点0是厶ABC的垂心 OA OB =0B OC =0C OA 点O是厶ABC的内心
⑩ 设0 ABC所在平面内任意一点, GABC的重心,,I ABC的内心, 则有 OG =1(0A OB OC) 3 OI
aOA bOB cOC
a + b + c
并且重心 XA+X+XC G( —T- YA+YB+YC ) 内心I a—A+ bX B+ CX C
a+b+c
ayA+ by B+ cy
C
AB AC
(A)外心 (C)重心 (B)内心 (D)垂心
事实上如图设 忑3,昴=— AB AC
AC
AC都是单位向量
C 学习参考
例3 :已知0为三角形ABC所在平面内一点,且满足 4 例 5、 已知向量0P,0F2,0R满足条件0 P Q P 炉P
|OP|=|OPP|OP3“1,求证:△ PP2P3 是正三角形. T ~I ―― J 分析 对于本题中的条件|OP |=|OR冃OPJ=1,容易想到,点O是△ PP2P3的
T -1 -H 外心,而另一个条件 0P+0F2+0R=0表明,点0是厶RP2P3的重心.
故本题可描述为,若存在一个点既是三角形的重心也是外心,则该三角形一 定是正三角形•在1951年高考中有一道考题,原题是:若一三角形的重心与外 接圆圆心重合,则此三角形为何种三角形?与本题实质是相同的.
显然,本题中的条件 QP |=|OP2|=|OF3|=1 可改为 |Op|=|OF2|=|OF3| .
高考原题 例6、0是平面上一 定点,A、B、C是平面上不共线的三个点,动点 P满足 _. . T T OP =0A • '(-AB AC) • [0,=).则 P 的轨迹一定通过厶 ABC£( ). |AB| |AC|
A. 外心 B. 内心 C. 重心 D. 垂心
0A 2 _______ + BC =OB 2 + CA =0卸+阴2,
(A)外心 (B)内心 (0重心
则点0是三角形ABCW( (D)垂心 事实上由条件可推出 OA OB =0B 0C =0C 0A 故选答案D
例4 :设O是平面上一定点,A、B、C是平面上不共线的三点, 动点P满足OP =0A…( AB AC —— ------ +
AB cosB ),扎w (0,垃),则动点P的轨迹一定通
AC cosC
过厶ABCW() (A)外心 (B) 内心 (C)重心 (D)垂心
事实上■( AB +
AB cos B
AC
AC cosC 厂 BC (一阴 BC) =0
故选答案D 学习参考 图1
「(绸•竺),设忑=竺澤=竺,显然 | AB| | AC | |AB| |AC |
AE, AF 都是单位向量, 以二者为邻边构造平行四边
形, 则结果为菱形,故AP为
.ABC的平分线,选B . 例7、 ABC的外接圆的圆心为0,两条边上的高的交点为H, > T T T 0H 二 m(0A OB 0C),则实数 m = __________ .
分析:本题除了利用特殊三角形求解外,纯粹利用向量知识推导则比较复杂, 更加重要的一点是缺乏几何直观.解法如下,由已知,有向量等式
, 将其中的向量分解,向已知等式形式靠拢,有(0H—0AL(0C-OB)= O,将已知 代 入, 有 [m(0A OB OC)_OA]|_(OC—OB)= O , 即 2 2 m(OC -OB ) (m-1)OABC=O,由 O是外心,得(m-1)OALBC =0,由于 ABC
是任意三角形,则OABC不恒为0,故只有m=1恒成立.
1 - 或者,过点0作0M _ BC与M,则M是BC的中点,有OM (OB 0C);
H 是垂心,则 AH _ BC, 故 AH 与 oM 共线,设"AH = kOM ,则 k OH =OA AH =OA (OB OC), 又 OH =m(OA OB OC), 故可得 k T k m OB ) m (
> T T T T T T 根据已知式子OH二m(OA OB OC)中的OA • OB • OC部分,很容易想到三 (m— OA
k
心),有 m01"厂 0,得 心.
角形的重心坐标公式,设三角形的重心为G,O是平面内 任 OA OB OC 3 由题意,题目显然叙
述的是一个一般的结论,先作图使问题直观化,如图1, 由图上观察,很容易猜想到 HG-2GO,至少有两个产生 猜想的诱因,其一是,BF,OT均与三角形的边AC垂直, 则BF//OT ;其二,点G是三角形的中线 BT的三等分 点.此时,会先猜想 △ BHG TOG,但现在缺少一个
分析 已知等式即AP
