2010年1月MBA数学真题及答案
2010年1月管综逻辑真题及答案解析

基于以上陈述能得出以下哪项结论?
A.小张输入的密码是错误的
B.小张的计算机不属于这个域
C.如果小张的计算机属于这个域,那么他输入的密码是错误的
D.只有小张输入的密码是正确的,它的计算机才属于这个域
E.如果小张输入的密码是正确的,那么它的计算机属于这个域
【答案】C
【解析】试题类型:逻辑推断:命题推理
(域归属正确账号正确密码正确)允许登陆
36.太阳风中的一部分带电粒子可以到达M星表面,将足够的能量传递给M星表面粒子,使后者脱离M星表面,逃逸到M星大气中。为了判定这些逃逸的粒子,科学家们通过三个实验获得了如下信息:
试验一:或者是X粒子,或者是Y粒子
试验二:或者不是Y粒子,或者不是Z粒子
试验三:如果不是Z粒子,就不是Y粒子
根据上述三个实验,以下哪项一定为真?
账号正确允许登陆Biblioteka ――――――――――――――――――――――――――――
?
①(域归属正确账号正确密码正确)允许登陆
允许登陆
――――――――――――――――――――――――――
域归属正确账号正确密码正确
②域归属正确账号正确密码正确
账号正确
――――――――――――――――――――――――――
域归属正确密码正确
B.该国成品油价格根据市场供需确定,随着国际原油市场价格的上涨,该国政府为成品油生产商提供相应的补助。
MBA历年数学真题及答案精装打印版

2009年联考MBA 联考真题—综合试卷一、问题求解(本大题共15题,每小题3分,共45分。
在下列每题给出的五个选项中,只有一项是符合试题要求的。
请在答题卡...上将所选的字母涂黑。
) 1.一家商店为回收资金把甲乙两件商品均以480元一件卖出。
已知甲商品赚了20%,乙商品亏了20%,则商店盈亏结果为(A )不亏不赚 (B )亏了50元 (C )赚了50元 (D )赚了40元 (E )亏了40元2.某国参加北京奥运会的勇女运动员比例原为19:12,由于先增加若干名女运动员.使男女运动员比例变为20:13.后又增加了若干名男运动员,于是男女运动员比例.最终变为30:19.如果后增加的男运动员比先增加的女运动员多3人,则最后运员的总人数为( )。
(A )686 (B )637 (C )700 (D )661 (E )6003.某工厂定期购买一种原料,已知该厂每天需用该原料6吨,每吨价格1800元.原料的保管等费用平均每吨3元,每次购买原料支付运费900元,若该厂要使平均每天支付的总费用最省,则应该每()天购买一次原料。
(A )11 (B )10 (C )9 (D )8 (E )74.在某实验中,三个试管各盛水若千克。
现将浓度为12%的盐水10克倒入A 管中,混合后,取10克倒入口管中,混合后再取10克倒入C 管中,结果 A ,B ,C 三个试管中盐水的浓度分别为6%、2%、0.5%,那么三个试管中原来盛水最多的试管及其盛水量各是(A )A 试管,10克 (B )B 试管,20克 (C )C 试管,30克(D )B 试管,40克 (E )C 试管,50克5.一艘轮船往返航行于甲、乙两码头之间,着船在静水中的速度不变,则当这条河的水流速度增加50%时,往返一次所需的时间比原来将( ).(A )增加 (B )减少半个小时 (C )不变 (D )减少1个小时 (E )无法判断6.方程214x x -+=的根是( )。
2010年MBA联考综合能力模拟试卷及解析

2010年MBA联考综合能力模拟试卷及解析一、问题求解(本大题共15小题,每小题3分,共45分)。
下列每题给出的五个选项中,只有一项是符合试题要求的,请在答题卡上将所选项的字母涂黑。
1.已知a=2005/2006, b=2006/2007, c=2007/2008, 则( )。
A. a>b>c B.b>c>a C.c>a>b D.c>b>a E.以上结论均不正确2.由整数的唯—分解定理:任一大于1的整数都能表成质数(素数)的乘积,即对于任一整数n>1,有n=P1P2…Ps,P1≤P2≤…≤Ps这里P1P2,…,Pn 是质数,且这种表示法是唯一的。
现定义n的长度为S,则小于1000的正整数的长度最大可能是( )。
A. 10B. 9 C.8 D.7 E.63.一个四面体的所有棱长都为,四个顶点在同一球面上,则此球的表面积为( )。
A. 3πB.4πC.πD.6πE.6 π4.某单位有同规格的办公室若干间。
若2人一间,则还有10人没有办公室,若4人一间,则仅有一间办公室不到4人,该单位的员工人数是( )。
A.18 B. 20 C.22 D.26 E.285.两个相同规格的容器,分别装上A,B两种液体后的总重量是1800克和1250克,已知A液体的重量是B液体的两倍,那么这个空容器的重量是( )克。
A. 550 B.600 C.700 D.1100 E.12006.A,B两地相距96公里,甲,乙两辆车同时从A地出发匀速驶往B地。
开车1小时后,甲车在乙车前方12公里处,甲车比乙车早40分钟到达B地,甲车的行车速度是( )。
A. 12 B.24 C.36 D.48 E.607.某车间开展劳动竞赛后,每人1天多做10个零件,这样8个工人一天所做的零件就超过了200个。
后来改进技术,每人1天又多做27个零件。
这样他们4个人l天所做的零件就超过劳动竞赛中8个人所做的零件个数,则该车间改进技术后的生产效率是劳动竞赛前的( )。
2010年考研数学一真题及解析(公式及答案修正版)

2010年全国硕士研究生入学统一考试数学试题详解及评分参考数 学(一)一.选择题:1 - 8小题,每小题4分,共32分.下列每题给出的四个选项中,只有一个 是符合题目要求的,请将所选项前的字母填在答题纸指定的位置上.(1)极限2lim ()()()x x x x a x b ®¥=-+(A)1(B)e(C)a be -(D)b ae -【答】 应选 (C) .【解】 因22ln ln()ln()lim ln()lim()()1/x x x x x x a x b x a x b x®¥®¥---+=-+()()()3222112=lim lim 1x x a b x abx x x a x b a b x x a x b x ®¥®¥---+-+==--+-,所以2lim (()()x a x b x x a x b e ®¥-=-+,故选 (C) .(2)设函数(,)z z x y =由方程(,0y zF x x=确定,其中F 为可微函数,且20F ¢¹,则z z x y x y ¶¶+=¶¶(A)x (B)z (C)x -(D)z-【答】 应选 (B) .【解】 在方程两边分别对x 和对y 求偏导,得122211()0y z F z F x x x x ¶¢¢-+-=¶,12110z F F x x y¶¢¢+=¶于是有 22()z z x y F zF x y ¶¶¢¢+=¶¶, 即z zx y z x y ¶¶+=¶¶,故选 (B) .(3)设,m n均是正整数,则反常积分ò的收敛性(A)仅与m 的取值有关(B)仅与n 的取值有关(C)与,m n 的取值都有关(D)与,m n 的取值都无关【答】 应选 (D) .【解】 显然该反常积分有且仅有两个瑕点0,1x x ==,于是需分成两个积分加以考察:dx =+ò(1)对于,易见被积函数非负,且只在0x +®时无界,于是当1n >时,由+0lim 0x®=及120ò收敛,知收敛;当1n=时12/1mx-:及212101mdx x-ò收敛,知收敛;(2)对于,易见被积函数非负,且只在1x -®时无界,于是当1m >时,由11lim lim 0x x --®®==及1收敛,知 收敛;当1m =时,由21/211ln (1)lim lim 0(1)x x x x ---®®-==-及212101m dx x -ò收敛,知收敛;由此可见,无论正整数,m n如何取值,0ò都是收敛的,故选 (D) .(4) 2211lim()()n nn i j nn i n j ®¥===++åå (A) 12001(1)(1)x dx dy x y ++òò(B)1001(1)(1)xdx dy x y ++òò(C) 11001(1)(1)dx dyx y ++òò(D) 112001(1)(1)dx dyx y ++òò【答】 应选 (D) .【解】 记21(,)(1)(1)f x y x y =++,(){},y 01,01D x x y =££££,知(,)f x y 在D 上可积. 用直线()0,1,2,,i i x x i n n ===L 与()0,1,2,,j j y y j n n===L 将D 分成2n等份,可见22221111211()()(1)(1)n n n ni j i j n i j n i n j n n n=====×++++åååå是(,)f x y 在D 上的二重积分的一个和式,于是112222001111lim ()()(1)(1)(1)(1)nnn i j Dn dxdy dx dy n i n j x y x y ®¥====++++++ååòòòò.故选 (D) . (5)设A 为m n ´矩阵,B 为n m ´矩阵,E 为m 阶单位矩阵. 若AB E =,则(A)秩()r A m =,秩()r B m =(B)秩()r A m =,秩()r B n =(C)秩()r A n =,秩()r B m =(D)秩()r A n =,秩()r B n=【答】 应选 (A) .【解】 因A 是m n ´矩阵,故()r A m £,又()()()r A r AB r E m ³==,故()r A m =. 同理,可得()r B m =,故选 (A) .(6)设A 为4阶实对称矩阵,且2A A O +=. 若A 的秩为3,则A 相似于(A) 1110æöç÷ç÷ç÷ç÷èø(B) 1110æöç÷ç÷ç÷-ç÷èø(C) 1110æöç÷-ç÷ç÷-ç÷èø(D) 1110-æöç÷-ç÷ç÷-ç÷èø【答】 应选 (D) .【解】 设l 为A 的特征值,则由2A A O +=知2+=0l l ,即=0l 或1-. 又因A 是实对 称矩阵,故A 必相似于对角矩阵L ,其中L 的对角线上的元素为特征值1-或0. 再由()3r A =可知()3r L =,故选 (D) .(7)设随机变量X 的分布函数0,0,1(),01,21,1xx F x x e x -<ìïï=£<íï-³ïî则{1}P X ==(A)0 (B)12(C)112e --(D)11e--【答】 应选 (C) .【解】 由分布函数的用途,知{1}(1)(1)P X F F -==-1111122e e --=--=-. (8)设1()f x 为标准正态分布的概率密度,2()f x 为[1,3]-上均匀分布的概率密度,若12(),0()(0,0)(),0af x x f x a b bf x x £ì=>>í>î为概率密度,则,a b 应满足(A)234a b +=(B)324a b +=(C)1a b +=(D)2a b +=【答】 应选 (C) .【解】 由题意,有221()x f x -=,21/4,(1,3)()0x f x Î-ì=íî,其他,()1f x dx +¥-¥=ò而0120()()()f x dx af x dx bf x dx +¥+¥-¥-¥=+òòò()3201=2a b f x dx +ò13=24a b +,于是有13124a b +=,即234a b +=. 故选 (C) .二、填空题:9:14小题,每小题4分,共24分. 请将答案写在答题纸...指定位置上. (9)设20,ln(1),t tx e y u du -ì=ïí=+ïîò则220t d y dx == .【答】 应填 0.【解】 因2/ln(1)=/t dy dy dt t dx dx dt e -+=-, 22222ln(1+)12=[][ln(1)]/1t td y d t te t dx dt e dx dt t -=++-+, 故2020t d ydx==.(10)2p =ò.【答】 应填 4p -.【解】t =,则2dx tdt =,于是有2220002cos 2sin 4sin 4cos 4cos 4.t tdt t tt tdt t tdt p pppp p p ==-=-=-òòòò(11)已知曲线L 的方程为1||([1,1])y x x =-Î-,起点是(1,0)-,终点为(1,0),则曲线积分2Lxydx x dy +=ò.【答】 应填 0.【解法一】 补有向线段:0([1,1])L y x =Î-,起点为(1,0),终点为(1,0)-,设由L 与L 围成的平面区域为D ,则利用格林公式及区域D 关于y 轴的对称性,得222(2)00LDL LLxydx x dy xydx x dy xydx x dy x x dxdy ++=+-+=---=òòòòò【解法二】 记1:1([1,0])L y x x =+Î-,起点是(1,0)-,终点是(0,1);2:1([0,1])L y x x =-Î, 起点为(0,1),终点为(1,0)有12222+LL L xydx x dy xydx x dy xydx x dy+=++òòò 012210=[(1)][(1)]x x x dx x x x dx -+++--òò1212=()(02323-++-=.(12)设22{(,,)|1}x y z x y z W =+££,则W 的形心的竖坐标z = .【答】 应填23.【解】 记(){}22,y 1D x x y =+£,有221x y Ddxdydz dxdy dz +W=òòòòòò22=(1)Dx y dxdy --òò212=(1)d r rdr p q -òò=2p,2212122240011[1()]=(1)223x yDD zdxdydz dxdy zdz x y dxdy d r rdr p p q +W==-+-=òòòòòòòòòò, 从而W 的形心的竖坐标为23DDzdxdydzz dxdydz==òòòòòò. (13)设1(1,2,1,0)Ta =-,2(1,1,0,2)Ta =,3(2,1,1,)Ta a =. 若由123,,a a a 生成的向量空间的维数为2,则a = .【答】 应填 6.【解】 因由123,,a a a 生成的向量空间的维数为2,故矩阵()123,,a a a 的秩为2,而()123112112211013,,=101006020000a a a a æöæöç÷ç÷ç÷ç÷®ç÷ç÷--ç÷ç÷èøèø,故6a =.(14)设随机变量X 的概率分布为{},0,1,2,!CP X k k k ===L ,则2EX =.【答】 应填 2.【解】 由概率分布的性质,有{}01k k P X x ¥===å,即01!k Ck ¥==å,亦即1Ce =,1C e -=.由此可见,X 服从参数为1的泊松分布,于是22()112EX DX EX =+=+=.三、解答题( 15 ~ 23小题,共94分.)(15)(本题满分10分)求微分方程322xy y y xe ¢¢¢-+=的通解.解:对应齐次方程320y y y ¢¢¢-+=的两个特征根为121,2r r ==,其通解为212x x Y C e C e =+.……4分设原方程的特解形式为*()x y x ax b e =+,则*2((2))xy ax a b x b e ¢=+++,*2((4)22)x y ax a b x a b e ¢¢=++++,代入原方程解得1,2a b =-=-,……8分 故所求通解为212(2)x x xy C e C e x x e=+-+ ……10分(16)(本题满分10分)求函数2221()()x t f x x t e dt -=-ò的单调区间与极值.解: ()f x 的定义域为(,)-¥+¥,由于2222211()x x t t f x xe dt te dt --=-òò,2224423311()2222xxt x x t f x x e dt x ex ex e dt ----¢=+-=òò,所以()f x 的驻点为0,1x =± ……3分列表讨论如下:x (,1)-¥-1-(1,0)-0 (0,1) 1 (1,)+¥()f x ¢-0 +0 -0 +()f x ↘极小↗极大↘极小↗……6分因此,()f x 的单调增加区间为(1,0)-及(1,)+¥,单调减少区间为(,1)-¥-及(0,1);极小值为(1)0f ±=,极大值为21101(0)(1)2t f te dt e --==-ò……10分(17)(本题满分10分) (I)比较1|ln |[ln(1)]nt t dt +ò与1|ln |(1,2,)ntt dt n =òL 的大小,说明理由;(II)记1|ln |[ln(1)](1,2,)n n u t t dt n =+=òL ,求极限lim n n u ®¥.解:(I )当01t ££时,因为ln(1)t t +£,所以|ln |[ln(1)]|ln |n n t t t t +£,因此11|ln |[ln(1)]|ln |n n t t dt t t dt+£òò ……4分(II )由 (I) 知,110|ln |[ln(1)]|ln |n n n u t t dt t t dt £=+£òò.因为1112011|ln |ln 1(1)n n n t t dt t tdt t dt n n =-==++òòò,所以1lim|ln |0nn tt dt ®¥=ò ……8分 从而 lim 0n n u ®¥=……10分(18)(本题满分10分) 求幂级数121(1)21n nn x n -¥=--å的收敛域及和函数. 解:记12(1)()21n nn u x x n --=-, 由于221()21lim lim ()21n n n nu x n x x u x n +®¥®¥-==+,所以当21x <,即||1x <时,1()n u x ¥=å绝对收敛,当||1x >时,1()n u x ¥=å发散,因此幂级数的收敛半径1R =……3分当1x =±时,原级数为11(1)21n n n -¥=--å,由莱布尼茨判别法知此级数收敛,因此幂级数的收敛域为[1,1]-……5分设1211(1)()(11)21n n n S x x x n -¥-=-=-££-å,则122211()(1)1n n n S x x x ¥--=¢=-=+å,又(0)0S =,故201()arctan 1xS x dt x t==+óôõ, ……8分 于是121(1)()arctan ,[1,1]21n nn x xS x x x x n -¥=-==Î--å ……10分(19)(本题满分10分)设P 为椭球面222:1S x y z yz ++-=的动点,若S 在点P 处的切平面与xOy 面垂直,求点P 的轨迹C ,并计算曲面积分I S=,其中S 是椭球面S 位于曲线C 上方的部分.解: 椭球面S 上点(,,)P x y z 处的法向量是{2,2,2}n x y z z y =--r, ……2分点P 处的切平面与xOy 面垂直的充要条件是0({0,0,1})n k k ×==r r r,即20z y -=所以点P 的轨迹C 的方程为222201z y x y z yz -=ìí++-=î,即2220314z y x y -=ìïí+=ïî ……5分取223{(,)|1}4D x y x y =+£,记S 的方程为(,),(,)z z x y x y D =Î,==,所以DI =óóôôôôõõ(D x dxdy =+òò ……8分2Ddxdy p== ……10分(20)(本题满分11分) 设1101011A l l l æöç÷=-ç÷ç÷èø,11a b æöç÷=ç÷ç÷èø. 已知线性方程组Ax b =存在2个不同的解,(I )求,a l ; (II )求方程组Ax b =的通解.解:(I )设12,h h 为Ax b =的2个不同的解,则12h h -是0Ax =的一个非零解, 故2||(1)(1)0l l =-+=A ,于是1l =或1l =- ……4分当1l =时,因为()()r A r A b ¹M ,所以Ax b =无解,舍去. 当1l =-时,对Ax b =的增广矩阵施以初等行变换,有1111013/2()02010101/211110002a A b B a æ-öæ-öç÷ç÷=-=-=ç÷ç÷ç÷ç÷-+èøèøM .因为Ax b =有解,所以2a =- ……8分(II )当1l =-,2a =-时,1013/20101/20000B æ-öç÷=-ç÷ç÷èø,所以x =A b 的通解为31110201x k æöæöç÷ç÷=-+ç÷ç÷ç÷ç÷èøèø,其中k 为任意常数. ……11分(21)(本题满分11分) 已知二次型123(,,)Tf x x x x Ax =在正交变换x Qy =下的标准形为2212y y +,且Q 的第3列为,0,22T. (I )求矩阵A ;(II )证明A E +为正定矩阵,其中E 为3阶单位矩阵.解:(I )由题设,A 的特征值为1,1,0,且(1,0,1)T为A 的属于特征值0的一个特征向量.……3分 设123(,,)Tx x x 为A 的属于特征值1的一个特征向量,因为A 的属于不同特征值的特征向量正交,所以1231(,,)001x x x æöç÷=ç÷ç÷èø,即130x x +=.取,0,22T æö-ç÷ç÷èø,(0,1,0)T 为A 的属于特征值1的两个正交的单位特征向量 ……6分令022010022Q æöç÷ç÷=ç÷ç÷ç÷-ç÷èø,则有110T Q AQ æöç÷=ç÷ç÷èø,故1101112020101T -æöæöç÷ç÷==ç÷ç÷ç÷ç÷-èøèøA Q Q . ……9分评分说明:求出满足条件的一个矩阵A ,即可给9分.(II )由(I )知A 的特征值为1,1,0,于是A E +的特征值为2,2,1,又A E +为实对称矩阵,故A E +为正定矩阵.……11分(22)(本题满分11分)设二维随机变量(,)X Y 的概率密度为2222(,),,x xy y f x y Ae x y -+-=-¥<<+¥-¥<<+¥,求常数A 及条件概率密度|(|)Y X f y x .解:因2222()(,)x xy y X f x f x y dy A edy +¥+¥-+--¥-¥==òò22()y x x A e dy+¥----¥=ò222(),x y x x Aeedy x +¥-----¥==-¥<<+¥ò,……4分所以21()x X f x dx e dx A p +¥+¥--¥-¥===ò,从而 1A p=……7分当(,)x Î-¥+¥时,22222|1(,)(|)1()x xy y Y X x X ef x y f y x f x p-+--==222x xy y -+-=2(),x y y --=-¥<<+¥ ……11分(23)(本题满分11分)设总体X 的概率分布为X 1 2 3p1q-2q q -2q其中参数(0,1)q Î未知.以i N 表示来自总体X 的简单随机样本(样本容量为n )中等于i 的个数(1,2,3i =).试求常数123,,a a a ,使31i ii T a N==å为q 的无偏估计量,并求T 的方差.解: 记11p q =-,22p q q =-,23p q =. 由于(,),1,2,3i i N B n p i =:,故i iEN np = ……4分 于是22112233123[(1)()]ET a EN a EN a EN n a a a q q q q =++=-+-+ ……6分为使T 是q 的无偏估计量,必有22123[(1)()]n a a a q q q q q -+-+=,因此12132010a a a n a a =ìïï-=íï-=ïî,……8分由此得 12310,a a a n===……9分由于123N N N n ++=,故123111()()1N T N N n N n n n =+=-=-.注意到1~(,1)N B n q -,故1221(1)(1)n DT DN n n nq q q q --=== ……11分。
2010年1月MBA联考逻辑真题及解析

2010年1月MBA联考逻辑真题及解析26.针对威胁人类健康的甲型H1N1流感,研究人员研制出了相应的疫苗,尽管这些疫苗是有效的,但某大学研究人员发现,阿司匹林、痉苯基乙酰胺等抑制某些酶的药物会影响疫苗的效果,这位研究人员指出:“如果你使用了阿司匹林或者对乙酰氢基酚,那么你注射疫苗后就必然不会产生良好的抗体反映。
”如果小张注射疫苗后产生了良好的抗体反映,那么根据上述研究结果可以得出以下哪项结论?A.小张服用了阿司匹林,但没有服用对乙酰氢基酚。
B.小张没有服用阿司匹林,但感染了H1N1流感病毒。
C.小张服用了阿司匹林,但没有感染H1N1流感病毒。
D.小张没有服用阿司匹林,也没有服用对乙酰氨基酚。
E.小张服用了对乙酰氨基酚,但没有服用痉苯基乙酰胺。
【答案】:D【解析】:研究结果的逻辑形式:使用了阿司匹林或者对乙酰氢基酚→不会产生良好的抗体反映。
A或B→C 根据逆否命题非C→非A且非B,即如果小张注射疫苗后产生了良好的抗体反映,那么他一定既没有服用阿司匹林,也没有服用对乙酰氨基酚。
【考点】:假言命题的推理规则27. 为了调查当前人们的识字水平,实验者列举了20个词语,请30位文化人士识读,这些人的文化程度都在大专以上。
识读结果显示,多数人只读对3到5个词语,极少数人读对15个以上,甚至有人全部读错。
其中,“蹒跚”的辨识率最高,30人中有19人读对;“呱呱坠地”所有人偶读错。
20个词语的整体误读率接近80%。
该实验者由此得出,当前人们的识字水平并没有提高,甚至有所下降。
以下哪项如果为真,最能对该实验者的结论构成质疑?A.实验者选取的20个词语不具有代表性。
B.实验者选取的30位识读者均没有博士学位。
C.实验者选取的20个词语在网络流行语言中不常用。
D.“呱呱坠地”这个词的读音有些大学老师也经常读错。
E.实验者选取的30位识读者中约有50%大学成绩不佳。
【答案】:A【解析】:实验者选取的20个词语不具有代表性,样本不当,能对实验者的结论构成质疑。
2010、2011年1月MBA逻辑真题类型一览
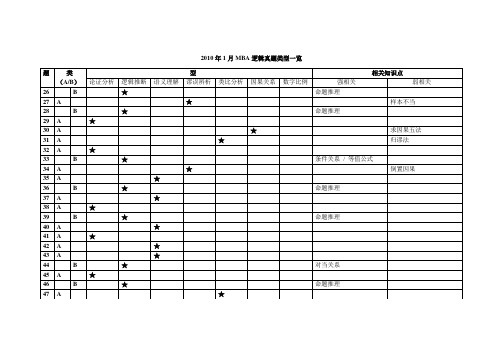
2010年1月MBA逻辑真题类型一览
说明:第53题分别作逻辑推断和数字比例型分析。
合计:
类:A类题:21题,占70%
B类题:9题,占30%
型:论证分析:5题,占16%
逻辑推断:10题,占33%
语义理解:8题,占26%
谬误辨析:3题,占10%
类比分析:2题,占6%
因果关系:1题,占3%
数字比例;2题占6%
2011年1月MBA逻辑真题类型一览
说明:上述试题中,有6题宜作跨题型分析,例如,第37题宜分别作论证分析和语义理解型分析。
合计:
类:A类题:24题,占80%
B类题:6题,占20%
型:论证分析:11题,占36%
逻辑推断:10题,占33%
语义理解:8题,占26%
谬误辨析:1题,占3%
类比分析:1题,占3%
因果关系:5题,占16%
数字比例;0题。
数学mba联考试题及答案
数学mba联考试题及答案数学MBA联考试题及答案一、选择题(每题2分,共20分)1. 某公司年销售额为500万元,预计明年增长10%,那么明年的预计销售额为:A. 550万元B. 510万元C. 540万元D. 600万元答案:A2. 一项投资的年回报率为5%,如果投资100万元,一年后的收益是多少?A. 5万元B. 10万元C. 15万元D. 20万元答案:A3. 一个圆的半径是5厘米,那么它的面积是多少平方厘米?A. 25πB. 50πC. 75πD. 100π答案:B4. 如果一个数列的前四项是2, 4, 6, 8,那么这个数列的第五项是多A. 10B. 12C. 14D. 16答案:A5. 一个直角三角形的两条直角边分别为3和4,那么斜边的长度是多少?A. 5B. 6C. 7D. 8答案:A6. 一个公司有10个员工,如果每个员工的工作效率提高了20%,那么整体工作效率提高了百分之多少?A. 10%B. 20%C. 22%D. 25%答案:C7. 如果一个数的平方根是4,那么这个数是多少?A. 16B. 8C. 12D. 20答案:A8. 一个班级有30名学生,其中15名学生是男生,那么女生的比例是A. 1/2B. 2/3C. 3/4D. 4/5答案:A9. 一个数的立方是125,那么这个数是多少?A. 5B. 10C. 15D. 20答案:A10. 如果一个产品的成本是50元,售价是100元,那么利润率是多少?A. 50%B. 100%C. 150%D. 200%答案:B二、填空题(每题2分,共10分)11. 如果一个数的平方是36,那么这个数是________。
答案:±612. 一个直角三角形的斜边长度是13,一个直角边是5,那么另一个直角边的长度是________。
答案:1213. 一个圆的直径是14厘米,那么它的半径是________。
答案:7厘米14. 如果一个数的对数(以10为底)是2,那么这个数是________。
MBA联考综合能力数学平均值函数历年真题试卷汇编1_真题(含答案与解析)-交互
MBA联考综合能力数学(平均值、函数)历年真题试卷汇编1(总分58, 做题时间90分钟)1. 问题求解问题求解本大题共15小题。
下列每题给出的五个选项中,只有一项是符合试题要求的。
1.[2013年1月]甲班共有30名学生,在一次满分为100分的考试中,全班平均成绩为90分,则成绩低于60分的学生至多有( )。
SSS_SINGLE_SELA 8个B 7个C 6个D 5个E 4个该问题分值: 2答案:B解析:设60分以下的学生有x人,则他们的总分至多为59x,剩下人的分数和至多为100(30—x),因此总分至多为59x+100(30—x)=3 000—41x,由题意知3 000—41x≥30×90,解得x≤7,即至多7人,因此选B。
2.[2010年10月]某学生在军训时进行打靶测试,共射击10次。
他的第6、7、8、9次射击分别射中9.0环、8.4环、8.1环、9.3环,他的前9次射击的平均环数高于前5次的平均环数。
若要使10次射击的平均环数超过8.8环,则他第10次射击至少应该射中( )(打靶成绩精确到0.1环)。
SSS_SINGLE_SELA 9.0环B 9.2环C 9.4环D 9.5环E 9.9环该问题分值: 2答案:E解析:第6、7、8、9次射击的平均环数为=8.7,而10次射击的平均环数超过8.8环,则总环数至少为8.8×10+0.1,则前9次射击的总环数至多为8.7×9—0.1.则第10次射击至少为(8.8×10+0.1)一(8.7×9—0.1)=9.9环。
因此选E。
3.[2009年10月]已知某车间的男工人数比女工人数多80%,若在该车间一次技术考核中全体工人的平均成绩为75分.而女工平均成绩比男工平均成绩高20%,则女工的平均成绩为( )。
SSS_SINGLE_SELA 88分B 86分C 84分D 82分E 80分该问题分值: 2答案:C解析:设女工人数为x,男工平均成绩为y,利用十字交叉法,有即,解得y=70,所以女工平均成绩为70×1.2=84。
MBA联考综合能力数学(平均值、函数)历年真题试卷汇编1(题后含答
MBA联考综合能力数学(平均值、函数)历年真题试卷汇编1(题后含答案及解析)题型有:1. 问题求解 2. 条件充分性判断问题求解本大题共15小题,每小题3分,共45分。
下列每题给出的五个选项中,只有一项是符合试题要求的。
1.[2013年1月]甲班共有30名学生,在一次满分为100分的考试中,全班平均成绩为90分,则成绩低于60分的学生至多有( )。
A.8个B.7个C.6个D.5个E.4个正确答案:B解析:设60分以下的学生有x人,则他们的总分至多为59x,剩下人的分数和至多为100(30—x),因此总分至多为59x+100(30—x)=3 000—41x,由题意知3 000—41x≥30×90,解得x≤7,即至多7人,因此选B。
知识模块:平均值2.[2010年10月]某学生在军训时进行打靶测试,共射击10次。
他的第6、7、8、9次射击分别射中9.0环、8.4环、8.1环、9.3环,他的前9次射击的平均环数高于前5次的平均环数。
若要使10次射击的平均环数超过8.8环,则他第10次射击至少应该射中( )(打靶成绩精确到0.1环)。
A.9.0环B.9.2环C.9.4环D.9.5环E.9.9环正确答案:E解析:第6、7、8、9次射击的平均环数为=8.7,而10次射击的平均环数超过8.8环,则总环数至少为8.8×10+0.1,则前9次射击的总环数至多为8.7×9—0.1.则第10次射击至少为(8.8×10+0.1)一(8.7×9—0.1)=9.9环。
因此选E。
知识模块:平均值3.[2009年10月]已知某车间的男工人数比女工人数多80%,若在该车间一次技术考核中全体工人的平均成绩为75分.而女工平均成绩比男工平均成绩高20%,则女工的平均成绩为( )。
A.88分B.86分C.84分D.82分E.80分正确答案:C解析:设女工人数为x,男工平均成绩为y,利用十字交叉法,有即,解得y=70,所以女工平均成绩为70×1.2=84。
2011年1月MBA数学真题及解析汇报
2011年一月联考真题一、问题求解:第1-15小题,每小题3分,共45分。
下列每题给出的A 、B 、C 、D 、E 五个选项中,只有一项是符合试题要求的,请在答题卡上将所选项的字母涂黑。
1. 已知船在静水中的速度为28km/h ,河水的流速为2km/h ,则此船在相距78km 的两地间往返一次所需的时间是 (A)5.9h(B)5.6h(C)5.4h(D)4.4h(E)4h2. 若实数,,a b c 满足()2335540a b c -+++-=,则abc =(A)-4 (B)-35 (C) -34 (D) 54(E)33. 某年级60名学生中,有30人参加合唱团、45人参加运动队,其中参加合唱团而未参加运动队的有8人,则参加运动队而未参加合唱团的有 (A)15人(B)22人(C)23人(D)30人(E)37人4. 现有一个半径为R 的球体,拟用刨床将其加工成正方体,则能加工成的最大正方体的体积是(A)338R (B)3938R (C) 334R (D) 331R (E) 393R5. 2007年,某市的全年研究与试验发展(R&D )经费支出300亿元,比2006年增长20%,该市的GDP 为10000亿元,比2006年增长10%。
2006年,该市的R&D 经费支出占当年GDP 的 (A)1.75%(B) 2%(C) 2.5%(D) 2.75% (E)3%6.现从5名管理专业、4名经济专业和1名财会专业的学生中随机派出一个3人小组,则该小组中3个专业各有1名学生的概率为(A)12 (B)13 (C)14 (D)15 (E)167.一所四年制大学每年的毕业生七月份离校,新生九月份入学,该校2001年招生2000名,之后每年比上一年多招200名,则该校2007年九月的在校学生有(A)14000名 (B)11600名 (C)9000名 (D)6200名 (E)3200名8.将2个红球与1个白球随机地放入甲、乙、丙三个盒子中,则乙盒子中至少有1个红球的概率为(A)19(B)827 (C)49(D)59(E)17279.如图1,四边形ABCD 是边长为1的正方形,弧AOB 、BOC 、COD 、DOA 均为半圆,则阴影部分的面积为(A)12 (B)2π (C)14π- (D)12π- (E)22π-10.3个3口之家在一起观看演出,他们购买了同一排的9张连座票,则每一家的人都在一起的不同坐法有(A)()23!种 (B)()33!种 (C)()333!种 (D)()43!种(E)9! 种11. 设P 是圆222x y +=上的一点,该圆在点P 的切线平行于直线20x y ++=,则点P 的坐标为A (-1,1) B(1,-1) C(0,2) D (2,0) E(1,1)12. 设,,a b c 是小于12的三个不同的质数(素数),且8a b b c c a -+-+-=,则a b c ++=( ) A.10B.12C.14D.15E.1913. 在年底的献爱心活动中,某单位共有100人参加捐款。
