射线追踪方程与程函方程的初至旅行时层析对比

合集下载

地震波初至走时的计算方法综述_赵烽帆

地震波初至走时的计算方法综述
ｗｏｆｔｈｅｔｒａｖｅｌｌｃｕｌａｔｉｏｎｍｅｔｈｏｄｓｏｆｓｅｉｓｍｉｃｆｉｒｓｔｂｒｅａｋＡｒｅｖｉｅｔｉｍｅｃａ－
ＣＥＮＣＢＣ１．ａｋｅｒｋｓｒ，５，ｈｉｎａａｒｔｈｕｅｔｗｏｅｎｔｅｅｉｉｎ０００４ｈｉｎａｑｊｇ１
，ａｔｏｒｓｈｅｒｉｃｔｉｏｎ，ｔｕｔｅｓ，ｓｅｍｃｅｓ，９２．ＳｔａｔｅＫｅＬａｂｏｒｏＬｉｔｈｏＥｖｏｌｕＩｎｓｔｉｏＧｅｏｌｏａｎｄＧｅｏｈｓｉｃＣｈｉｎｅＡｃａｄｅｏＳｃｉｅｎＢｅｉｉｎ０００２Ｃｈｉｎａｙｐｙｙｙｆｆｇｐｙｆｊｇ１３．ＵｎｉｖｅｏＣｈｉｎｅＡｃａｄｅｏＳｃｉｅｎＢｅｉｉｎ０００３Ｃｈｉｎａｒｓｉｔｓｅｍｃｅｓ，９，ｆｆｊｇ１ｙｙ
，ＡｂｓｔｒａｃｔＩｎｔｈｅｓｅｉｓｍｉｃｗａｖｅｆｉｅｌｄｔｈｅｆｉｒｓｔａｒｒｉｖａｌｔｒａｖｅｌｔｉｍｅ－，ｎｉｍｏｒｔａｎｔｒｏｌｅｉｎｔｈｅｆｉｅｌｄｏｆｓｅｉｓｍｏｌｏｗｈｉｃｈｉｓｄｕｅｌａｓａｐｇｙｐｙｔｏｔｈｅｆｉｒｓｔａｒｒｉｖａｌｈａｓｅｓｃａｎｂｅｅａｓｉｌｔｒａｃｅｄａｎｄｉｄｅｎｔｉｆｉｅｄ．ｐｙＴｈｅｓｅｉｓｍｉｃｆｉｒｓｔａｒｒｉｖａｌｔｒａｖｅｌｅｌｄｉｓｗｉｄｅｌｕｓｅｄｉｎｔｉｍｅｆｉ－ｙ，ｖ，ｓｓｅｉｓｍｉｃｒｅｓｔａｃｋｍｉｒａｔｉｏｎｅｌｏｃｉｔａｎａｌｓｉｓｅｉｓｍｉｃｔｒａｖｅｌ－ｐｇｙｙａｎｄｅａｒｔｈｕａｋｅｌｏｃａｔｉｏｎ．Ｔｈｉｓａｅｒｍａｉｎｌｍｏｒａｈｔｉｍｅｔｏｑｐｐｙｇｐｙｉｎｔｒｏｄｕｃｅｓｏｕｒｉｃａｌｅｉｓｍｉｃｉｒｓｔｒｒｉｖａｌｒａｖｅｌｔｉｍｅｆｔｓｆａｔ－ｙｐ，，（ｍｅｔｈｏｄｂａｓｅｄｏｎｌｃｕｌａｔｉｏｎｍｅｔｈｏｄｓｔｈａｔｉｓ１）ｓｅｉｓｍｉｃｒａｃａｙ，ｕｓｅｄｍｅｔｈｏｄｓａｒｏｘｉｍａｔｉｏｎｔｈｅｃｏｍｍｏｎｌｔｈｅｈｉｈｃｆｒｅｕｅｎ－ｐｐｙｇｙｑａｒｅＳｈｏｒｔｅｓｔＰａｔｈＭｅｔｈｏｄ（ＳＰＭ）ａｎｄＭｏｄｉｆｉｅｄＳｈｏｒｔｅｓｔＰａｔｈ；（Ｍｅｔｈｏｄ（ＭＳＰＭ）２）ｔｈｅｍｈｏｄｂａｓｅｄｏｎｔｈｅｎｕｍｅｒｉｃａｌｅｔ，ｗｉｎｃｌｕｄｅＦｉｎｉｔｅｓｏｌｕｔｉｏｎｏｆｅｉｋｏｎａｌｅｕａｔｉｏｎｈｉｃｈｍａｉｎｌｑｙ，Ｍｅｔｈｏｄ（ＦＭＭ）ａｎｄＤｉｆｆｅｒｅｎｃｅＭｅｔｈｏｄ（ＦＤ）ＦａｓｔＭａｒｃｈｉｎｇ；（Ｍｅｔｈｏｄ（ＦＳＭ）３）ＷａｖＦａｓｔＳｗｅｅｉｎｒｏｎｔＣｏｎｓｔｒｕｃｔｉｏｎｅｆｐｇ（；ＷＦＣ）ｍｅｔｈｏｄｂａｓｅｄｏｎｔｈｅＨｕｅｎｓｒｉｎｃｉｌｅａｎｄ（４）ｔｈｅｙｇｐｐｄｏｍａｉｎｗａｖｅｅｕａｔｉｏｎ（ＦＷＱ）．ｍｅｔｈｏｄｂａｓｅｄｏｎｔｈｅｆｒｅｕｅｎｃｑｙｑａｎｄｂｅｔｔｅｒＴｈｅｆｉｒｓｔｏｎｅｈａｓｈｉｈｅｒｃｏｍｕｔａｔｉｏｎａｌａｃｃｕｒａｃｇｐｙ，ｗ，ｗｒｅｓｕｌｔｉｎｈｉｌｅｉｔｎｅｅｄｓｍｏｒｅｒｉｄｏｉｎｔｓｈｉｃｈｍａｓｔａｂｉｌｉｔｇｐｙｙｌｏｗｃｏｍｕｔａｔｉｏｎａｌｅｆｆｉｃｉｅｎｃ．Ｔｈｅｃａｌｃｕｌａｔｉｏｎｏｆｒａａｔｈｓｉｓｐｙｙｐ，ｓｎｏｔｒｅｕｉｒｅｄｉｎｔｈｅｓｅｃｏｎｄｏｎｅｏｉｔｈａｓａｄｖａｎｔａｅｓｉｎｑｇ，ｂ，ｓｃｏｍｕｔａｔｉｏｎａｌｅｆｆｉｃｉｅｎｃｔａｂｉｌｉｔａｎｄｒｅａｌｉｚａｔｉｏｎｕｔｔｈｅｐｙｙ，ｗｉｓｌｏｗｅｒｈｉｃｈｃａｎｂｅｉｍｒｏｖｅｄｂｃｏｍｕｔａｔｉｏｎａｌａｃｃｕｒａｃｐｙｐｙｔｈｅｈｉｈｉｎｔｒｏｄｕｃｉｎｉｎｉｔｅｄｉｆｆｅｒｅｎｃｅｓｃｈｅｍｅ．Ｔｈｅｔｈｉｒｄｏｒｄｅｒｆ－ｇｇ，ｏｎｅｃａｎｃａｌｃｕｌａｔｅｔｒａｖｅｌｔｉｍｅｗｉｔｈｈｉｈａｃｃｕｒａｃａｎｄｓｔａｂｉｌｉｔｙｇｙｗｈｉｌｅｉｔｒｅｕｉｒｅｓｔｈｅｒｉｄｔｒａｎｓｉｔｉｏｎｂｅｔｗｅｅｎｒａｒｉｄａｎｄｒｅｕｌａｒｑｇｙｇｇ，ｗｒｅｓｕｌｔｉｎｌｏｗｃｏｍｕｔａｔｉｏｎａｌｅｆｆｉｃｉｅｎｃ．Ｔｈｅｒｉｄｈｉｃｈｍａｐｙｇｙｌａｓｔｏｎｅｃａｎａｄａｔａｎｃｏｍｌｅｘｍｅｄｉｕｍ，ｂｕｔｔｈｅｃｏｍｕｔａｔｉｏｎａｌｐｙｐｐａｃｃｕｒａｃａｎｄｅｆｆｉｃｉｅｎｃａｒｅｌｏｗｅｒ．ｙｙ；；Ｋｅｗｏｒｄｓｆｉｒｓｔｂｒｅａｋ；ｓｈｏｒｔｅｓｔａｔｈｅｉｋｏｎａｌｅｕａｔｉｏｎｆｉｎｉｔｅｐｑｙ；ｗ；ｆ；ｆｄｉｆｆｅｒｅｎｃｅａｓｔａｒｃｈｉｎａｓｔｗｅｅｉｎａｖｅｆｒｏｎｔｍｓｇｐｇ；ｄｏｍａｉｎｗａｖｅｅｃｏｎｓｔｒｕｃｔｉｏｎｆｒｅｕｅｎｃｎｕａｔｉｏｑｑｙ

【国家自然科学基金】_走时层析_基金支持热词逐年推荐_【万方软件创新助手】_20140803

数值模拟散射条件接收换能器探地雷达成像空间域快速计算快速扫描法庐枞射线追踪射线路径多道互相关技术地震走时层析成像地震反演地幔过渡带地幔上涌地壳上地幔速度结构图像重建发射点南北构造带动力学射线追踪冲击地压兰姆波低速带人工地震勘探中国东部中国东北地区三维速度成像 lax-friedrichs快速扫描算法
推荐指数 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2009年序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34
2008年序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24
科研热词层析成像阿尼玛卿缝合带鄂尔多斯盆地速度分布退火遗传算法走时提取结构混凝土结晶基底混沌变量油气前景沉积建造模拟退火回火算法最佳路径希尔伯特黄变换射线追踪多尺度逐次逼近地震走时层析成像地震层析成像地壳和上地幔速度结构图形理论反投影法华北地区分辨率兰姆波
科研热词层析成像射线龙桥铁矿首都圈首波非对称走时震源深度隐伏矿床速度模型远震波形近地表速度结构走时联合反演等权射线密度灵敏度核波前重建横向变速李代数积分有限频率层析成像最小走时法指数映射折射波投射波庐枞射线追踪射线路径多震相走时多次波射线追踪地震重新定位地震活动性地震层析成像地震噪声敏感性试验同时反演反演策略反演反射地震双差地震层析成像初至波层析成像初至波初始模型假定物理模型京津唐地区不规则界面上地幔速度结构 lsqr

综合地球物理--重点总结

1、能够正确区分普通的水平叠加剖面、偏移剖面与波阻抗反演剖面，并分析说明3种剖面的各自特点及其主要差异。

（1）水平叠加剖面特点：1、在测线上同一点,根据钻井资料得到的地质剖面上的地层分界面,与时间剖面上的反射波同相轴在数量上、出现位置上,常常不是一一对应的。

2、时间剖面的纵坐标是双程旅行时t0 ，而地质剖面或测井资料是以铅垂深度表示的,两者需经时深转换。

3、反射波振幅、同相轴及波形本身包含了地下地层的构造和岩性信息。

4、地震剖面上的反射波是由多个地层分界面上振幅有大有小、极性有正有负、到达时间有先有后的反射子波叠加、复合的结果5、水平叠加剖面上常出现各种特殊如绕射波、断面波、回转波、侧面波等。

（2）偏移剖面特点：正确进行DMO处理及选择最佳的叠加速度下偏移归位的时间剖面。

相对于水平叠加剖面而言，信噪比提高，断层现象清楚，绕射波收敛，反射波归位。

是地下构造形态以及层位信息比较真实的反应。

（3）波阻抗反演剖面波阻抗反演剖面主要反映了波阻抗反演得到的密度、速度信息。

将界面信息转化为层内信息，用以推测地下岩层结构和物性参数的空间分布。

差异：水平叠加剖面和偏移剖面均反映了界面信息，纵轴均为时间轴，而波阻抗反演剖面反映了层内信息，剖面中色谱的信息反映的速度或密度或波阻抗的信息。

水平叠加剖面和偏移剖面比较而言，存在回转波，断面波，绕射波等现象。

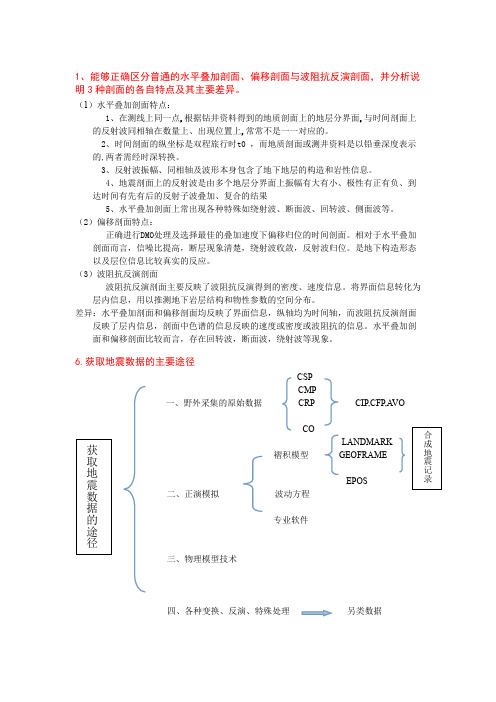
6.获取地震数据的主要途径CSPCMP一、野外采集的原始数据CRP CIP,CFP,A VOCOLANDMARK褶积模型GEOFRAMEEPOS二、正演模拟波动方程专业软件三、物理模型技术四、各种变换、反演、特殊处理另类数据付氏变换（大）（1）小波变换（小尺度）S变换、广义S变换（中）（2）曲波变换C1---互相关（3）相干分析C2---协方差矩阵C3---特征向量AI--波阻抗：s(t)=r(t)*w(t),不使用叠前数据（除零偏移距）；（4）反演井-震联合反演A.佐普利兹方程近似解EI--弹性阻抗 B.佐普利兹方程精确解C.波形反演.（5）各种属性体3D VSP开发地震TLS----时移地震（6）特殊处理成果数据CWS1-3三个角度、三个深度的概念及其相互关系。

基于C++语言实现波前构建射线追踪

维普资讯
２７月０年８０
・
石油址球幽理撂
第４卷２第４期
软件开发与应用・
基于Ｃ＋语言实现波前构建射线追踪＋
韩复兴 ① 孙建国① 杨昊① ② ② ②
（吉林大学地球探测科学与技术学院；国土资源部应用地球物理综合解释理论开放实验室一 ① ② 波动理论与成像技术实验室）
韩复兴。建国，昊．于Ｃ＋＋语言实现波前构建射线追踪．油地球物理勘探，０７４（）４４８孙杨基石２０，２４法射线追踪在实现波前路径计算过程中存在的困难，文提出一种基于ｃ＋＋语言的实现本方法。ｃ＋实现避免了由于射线插值（射线的插入）网格变换（射线网格到矩形网格之问的变换）造＋新和由所成的数据重排和标记等问题，程序的计算过程中，以随时对数据进行插入而不必考虑其定位。从运动学射在可线追踪系统出发，先对波前构建法的基本方程、值计算方法进行简要回顾｝后介绍ｃ＋＋实现中用到的类首数然和函数，出程序的设计思想和实现步骤。实例分析表明，ｃ＋语言实现波前构建法射线追踪能够在很大给用＋

任意速度模型的旅行时计算方法

任意速度模型的旅行时计算方法X赵卫锋,王锡文,张锋军(中原油田分公司物探研究院,河南濮阳　457001) 摘　要:本文介绍了复杂速度模型中旅行时的计算方法。

该方法基于费马原理,并用来进行三维叠前偏移处理。

文中展示了利用该算法所得到的三维叠前深度偏移结果。

与叠后深度偏移相比,其成像效果明显。

关键词:旅行时;模型;费马原理;叠前深度偏移中图分类号:P 631.1+2 文献标识码:A 文章编号:1006—7981(2012)01—0056—01 近年来,任意二维/三维复杂介质中有关旅行时计算的快速算法的发展显得尤为重要。

这些算法主要应用于进行快速的二维/三维叠前深度偏移处理。

众所周知,叠前偏移对速度模型的敏感性促使人们采用迭代过程来提高速度模型的精度。

这个迭代过程利用层析成像(kosl offet.al,1996)来更新叠前深度偏移后的速度模型。

这样可以提高速度模型的精度,进而改善最终深度剖面、切片和数据体的成像质量。

在二维情况下,利用射线追踪可以快速计算旅行时。

但射线追踪方法存在一些缺点。

比如它很难考虑所有的反射和绕射效应,旅行时图上存在所谓的“盲区”。

另外,很难使射线到达指定点。

解决这些问题需要加大算法的复杂程度,从而增加了计算时间。

其它旅行时计算方法是基于程函方程的直接解(Gr ay ,1986,Reshef and Kosloff ,1986,Vidal e ,1988,Van T rier and Symes ,1991,Nichols ,1996),这些方法需要计算密网格上的旅行时。

由于三维处理需要的C P U 时间比较多,因此人们寻找新方法来计算旅行时表。

本文介绍一种基于最短路径的方法。

下面将介绍该方法,并在野外数据例子上进行三维叠前深度偏移来验证该方法。

1　算法利用动态规划求极值问题的解可以计算从一给定炮点或检波点位置到地下的旅行时(Bellman,1957)。

Meshbey et.al (1979和1980年)最先研究这种方法。

地震勘探原理题库

地震勘探原理练习题一一、名词解释（1）波阻抗（2）地震界面（3）速度界面（4）地震子波（5）振动图（6）波剖面（7）视速度（8）正常时差（9）倾角时差（10）地震排列（11）动校正（12）均方根速度（13）调谐振幅（14）调谐厚度（15）地震组合法（16）水平多次叠加法二、说明下列公式的物理意义 1.)cos 1(2)(θλθ+=i K 2.1111----+-=n n n n n n n n n V V V V R ρρρρ 3.21,1,02112===⎪⎪⎭⎫ ⎝⎛=n n n r r A A n4.)(0kz wt i z e e A --=αϕ5.e V V V cos sin *==ε6.V h t 20=7.ψϕαsin sin cos = 8.2022V t x t =∆ 9.20222t V x t NMO +=10.20220)sin (111αββαβ=⎥⎦⎤⎢⎣⎡⎪⎪⎭⎫ ⎝⎛--+⎪⎪⎭⎫ ⎝⎛-z tg x 11.())(111022202t V sh t V ch z x ββββ=⎥⎦⎤⎢⎣⎡--+ 12.t f n t f n V x f n V x f n T t ∆∆=∆∆=⎪⎭⎫ ⎝⎛∆Φππππsin sin /sin /sin ** 三、证明题1.试证明介质的品质因数Q 与介质的吸收系数α成反比关系。

2.试证明地层厚度等于4λ时，调谐振幅达最大值。

3.试证明均匀介质中反射波时距曲线转换到p -τ域内则变成椭圆形状。

4.试证明倾斜地层时共中心点时距曲线按共反射点时距曲线作正常时差校正时有剩余时差。

四、推导公式1.水平层状介质中以均方根速度表示的时距曲线方程。

2.推导单一倾斜界面时反射波时距曲线方程及倾角时差。

3.推导VSP 法中向上一次反射波垂直时距曲线方程。

4.推导VSP 法中向下一次反射波垂直时距曲线方程。

5.推导倾斜地层时折射波相遇时距曲线方程。

FMM射线追踪方法在地震学正演和反演中的应用

ｉｏｈｓｉｉｅｅ，２１ｎＧｅｐｙ．（ｎＣｈｎｓ）００，２（）１９～１０ＤＯＩ１．９９ｊｉｓ．０４２０．０００．０．５４：１７２５，：０３６／．ｓｎ１０ — ９３２１．４０８
ＦＭＭ射线追踪方法在地震学正演和反演中的应用
ＤＯＩ１．９９ｊｉｓ．０４２０．０００．０．：０３６／．ｓｎ１０ —９３２１．４０８
ＺａｇＦＸ，ＷｕＱ，ＬｉＨ，ｅ１ｈｎＪＹｔ．ＡｐｌａｉｎｏＭＭａｒｃｎＯｆｒｒｎｎｅｓｒｂｅｆｅｓｌｇ．ｏｒｓａｐｉｔｆＦｃｏｒｙｔａｉｇｔｏｗａｄａｄｉｖｒｅｐｏｌｍｓｏｉｍｏｏｙＰｒｇｅｓｓ
（ｎｔｕｅｆＧｏｈｓｃ，ｈｎａｔｑａｅＡｍｉｉｒｔｎｅｉｇ１０８，ＣｉａＩｓｉｔｏｅｐｙｉｓＣｉａＥｒｕｋｄｎｓａｉ，Ｂｉｎ００１ｈｎ）ｔｈｔｏｊ
ＡｂｔａｔＦａｓａｃｎｇＭｅｈｓｒｃｔＭｒｈｉｔｏｄ（ＦＭＭ）ｒｙｔａｉｇｉａｒｃｎｅｈｏｓｎｇｔｍｅｉａｏｌｉｓｏｆＥｉｎａａｒｃｎｓａｒｙｔａｉｇｍｔｄｕｉｈｅｎｕｒｃｌｓｕｔｏｎｋｏｌｅａｉ．Ｉｈｉａｒａｎｗａａａｒｙｓｒｔｒｎｄａｄｉｅｔｏｎｐａａｅｅｒｎｒｄｕｅｑｕｔｏｎｎｔｓｐｐｅｅｄｔｒａｔｕｃｕｅａｒｃｉｒｍｔｒａｅｉｔｏｃｄ．ｗｈｉｈａｅｄｆｅｅｒｃｒｉｆｒｎｔｆｏｍｔｅｏｉｉａｈｒｇｎｌＦＭＭｅｈｏ．ＩｉｏｅｅｔＯｇｈｅａｔｒｍｔｄｔｓｃｎｖｎｉｎｔｅｔｔｒｙｐａｈｆｏｍｈｅｅｄａａｒａｙｔｕｔｅＴｈｒｓｌｔｏｎｔｎｗｔａｒｓｒｃｕｒ．ｅｅｏｕｉａｃｒｃａｅｌｏｎｒｌｅｈｄｒｃｉｎａｒｍｅｅ．Ａｔａｔｓｃｕａｙｃｎｂｅｗｌｃｔｏｌｄｂｙｔｅｉｅｔｏｐａｔｒｌｓｏｍｅｅｔｅｕｌｓｒｈｔｓｒｓｔａｅｓｏｗｎｂａｅｏｓｖｒｌｓｄｎｅｅａ

改进的地震模型初值射线追踪方法

（．ｎｒｎｏｉＮ．ＧｏｏｅｎｎｒｌｅｏｒｅＥｐｏａｉｎｘｌｉｔｎＩｓｔｔ，ｈｉＩｎｒｎｏａ１００１ｎｅｇｌｏｅｌＭａｄＭｉａＲｓｕｃｘｌｔｎａｄＥｐｏｔｉｔｕｅＷｕａ，ｎｅＭｏｇｌ６０；ＩＭｏａ８ｏｅｒｏａｏｎｉｉ０
Ｖｏ．．５１２３Ｎｏ０Ｍａ．ｖ２１０ｌ
改进的地震模型初值射线追踪方法
贺中银，阳高
（．１内蒙古第八地质矿产勘查开发院，蒙古乌海０６０；．西省煤田地质局物探测量队．西西安７００）内１００２陕陕１０６摘要：值射线追踪方法是现代射线追踪方法中的一个很重要的理论，克服了两点法射线追踪方法耗时的计算初它效率问题。以程函方程为基础，初值射线追踪方法进行改进，利用平方慢度来替换模型中的速度参数，得程函对即使方程产生解析解，而进一步导出当射线遇到界面时的反射和透射慢度向量的计算表达式，从以及反射、射系数的透函数表达式。过对简单的两层界面向斜模型及复杂的多层盐丘模型的射线追踪，明该初值射线追踪方法的改进通表相比于以往的龙格库塔离散数值解法，但使射线追踪效率得到了大幅度提高（０倍左右）且也扩大了射线法使用不１，

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

射线追踪方程与程函方程的初至旅行时层析对比郭振波;孙鹏远;李培明;任晓乔;钱忠平;唐博文【摘要】初至旅行时层析反演是目前应用最广泛的近地表建模方法.按照反演中正演算子的不同,可将基于射线理论的层析反演方法分为基于射线追踪方程与程函方程两类.本文分别从理论及数值测试上对两种方法在反演精度、计算效率等方面进行了系统的对比分析.结果表明:①两种方法可在统一的反演框架下推导得到,两者主要的差别均是由反演中正演算子的不同引起的;②两者具有相似的反演精度,由于后者的核函数是带限的,在复杂地区的层析反演中更加稳定;③前者的计算效率、内存占用等依赖于检波点个数,后者则依赖于模型大小,检波点稀疏时优选前者,否则优选后者;④前者具有射线密度等质控手段,后者缺少类似的质控手段.【期刊名称】《石油地球物理勘探》【年(卷),期】2019(054)003【总页数】8页(P558-564,576)【关键词】层析;射线追踪;程函方程;近地表建模;地震反演【作者】郭振波;孙鹏远;李培明;任晓乔;钱忠平;唐博文【作者单位】东方地球物理公司物探技术研究中心,河北涿州072751;东方地球物理公司物探技术研究中心,河北涿州072751;东方地球物理公司物探技术研究中心,河北涿州072751;东方地球物理公司物探技术研究中心,河北涿州072751;东方地球物理公司物探技术研究中心,河北涿州072751;东方地球物理公司物探技术研究中心,河北涿州072751【正文语种】中文【中图分类】P6310 引言对于油气地震勘探，需建立较精确的近地表模型以消除地表起伏及近地表速度异常对反射信号的影响，特别是对于山地等复杂探区，近地表模型的精度直接决定了最终的成像效果[1-2]。

由于初至旅行时的稳健性及旅行时层析的高效性，目前利用初至旅行时层析反演进行近地表建模是应用最广泛的方法。

近地表模型通常用于静校正[3]、深度域建模[4]等处理流程。

经典的初至层析反演方法基于射线追踪方程，在反演中需要显式计算炮点到检波点的旅行时及射线路径[5]，本文将这类经典的初至层析反演方法称为基于射线追踪方程的初至层析反演方法。

反演中通常采用两种方式求取旅行时及射线路径：①采用两点射线追踪[6]或类似方法同时求取旅行时及射线路径；②采用波前追踪类方法，如基于程函方程的有限差分类方法[7-8]、基于线性旅行时假设的线性旅行时插值方法[9]、基于图理论的最短路径方法[10]等，该类方法需在求解得到初至时间场的基础上从检波点开始反向追踪得到射线路径[9，11-12]。

反演通常采用反向投影[13]、最小二乘奇异值分解(LSQR)[11]、同时迭代重构(SIRT)[14]等方法。

基于射线追踪方程的层析反演方法已在实际生产中广泛应用，目前主要研究方向是如何与波形反演等精度较高的反演方法相结合[15-16]。

除了上述经典算法外，还存在一类层析反演算法，本文将其称为基于程函方程的层析反演方法。

该类方法仅需要计算初至时间场而不需要计算射线路径，借助伴随状态方法[17]求取模型更新量。

该类方法最早由Sei等[18]于1994年提出，近年来得益于波形反演的兴起，伴随状态方法为地球物理学家所熟知，进而开展了广泛的研究。

Leung等[19]、Taillandier等[20]、谢春等[21]采用快速扫描方法进行初至旅行时层析； Huang等[22]利用该方法进行透射及反射旅行时层析；Benaichouche等[23]、李勇德等[24]讨论了该类层析方法中预处理方法对层析的影响； Waheed等[25]将该类方法用于各向异性介质的初至旅行时层析。

虽然两类方法已得到了广泛研究，但目前还没有从理论及数值测试上进行系统的对比分析。

本文首先基于统一的反演框架从方法原理上对两种方法进行了详细的对比分析，并做了定性的评价；然后通过一个数值测试实例，对两种方法的反演精度、计算效率、内存占用等情况进行了定量的对比分析。

1 方法原理及对比分析1.1 层析反演基本理论旅行时层析通过迭代反演寻找正演旅行时与观测旅行时最优拟合的模型，若不考虑正则化项，L2模的目标函数可写为(1)式中： m为模型介质参数向量； ns为总炮数；为在当前介质模型m下第s炮对应所有检波点处的正演初至时间；为在第s炮观测记录上通过拾取得到的初至时间。

将目标函数在m0处展开且只保留至二阶项，可整理为O(m)≈O(m0)+[|m=m0]Tδm+|m=m0δm(2)通常将目标函数相对于介质参数的一阶导数称为梯度，即(3)将目标函数相对于介质参数的二阶导数称为Hessian矩阵，即(4)由于求取目标函数最小，需要求取目标函数的驻点，即g=0的点。

对式(2)求导并将其设为零，可得H|m0δm=-g|m0(5)δm=-(H|m0)-1g|m0(6)式(6)为在当前模型m0下对应模型更新量的显式表示。

利用δm更新当前模型参数m0并将其作为下次迭代的初始模型，可实现非线性反演。

当目标函数小于给定的阈值时，停止迭代，得到最终的反演模型。

由于Hessian矩阵的逆很难直接求取，通常通过迭代反演的方式求取式(5)所示的线性方程，此时反演方法通常称为高斯—牛顿法。

对于尺度较大的问题，Hessian 矩阵H的求取非常耗时且存储困难，通常需要对其进行近似处理。

若将Hessian 矩阵近似为一单位矩阵，则退化为最速梯度方法；若将Hessian矩阵近似为对角或带限矩阵，则退化为预处理的最速梯度方法。

1.2 基于射线追踪方程的初至层析反演对基于射线追踪方程的初至层析反演，需要求取每个炮检对的射线路径，在得到射线路径之后，可将初至时间表示为(7)式中： nm为模型离散网格总数； mi为第i个网格内的慢度；为第s炮、第r个接收点对应射线在第i个网格内射线段的长度。

可将其写成矩阵的形式式中 Ls(m)为正演算子，包含了不同检波点对应射线路径在网格内的长度。

由于正演算子同样是介质参数m的函数，即计算初至时间与介质参数m为非线性关系。

假设每次迭代的模型更新量不大，不足以引起射线路径的剧烈变化，即∂Ls(m)/∂m=0。

利用该假设，将式(8)代入式(1)，利用式(3)可求得一阶梯度为(9)利用式(4)可求得二阶Hessian矩阵为(10)若利用对角元素近似Hessian矩阵，并将其代入式(6)，通过整理可得到反向投影算法的基本公式(11)式中δts，r为第s炮的第r个检波点处的初至旅行时残差。

将式(9)和式(10)代入式(5)，整理可得(12)式中为第s炮对应的旅行时残差。

式(12)为线性方程，对应式(5)，基于射线追踪方程的初至层析反演通常是在一次非线性迭代的内部通过求解式(12)实现与高斯—牛顿法相同的效果。

根据求取式(12)方法的不同而发展了一系列不同的方法，如LSQR法[11]、SIRT法[14]等，多为数值求解线性方程组算法。

1.3 基于程函方程的初至层析反演基于程函方程的初至层析反演方法直接采用程函方程而不是射线追踪方法作为反演中的正演方法。

各向同性介质中初至旅行时的传播满足程函方程，利用迎风有限差分进行离散之后的形式为(Dxts)(Dxts)+(Dyts)(Dyts)+(Dzts)(Dzts)=diag(m)m(13)满足初始条件ts(is)=0(14)式中：ts为第s炮对应的所有网格点上的初至时间； Dx、Dy、Dz分别为x、y、z方向的迎风差分矩阵；diag(m)为将慢度向量的元素放在对角位置形成的对角矩阵； is为第s炮震源网格序号。

本文利用基于快速匹配方法的迎风差分方法[26]求解式(13)。

对ts作用观测系统算子P后，可提取检波点位置处的初至时间(15)将式(15)代入式(1)，利用式(3)可求得一阶梯度为(16)式中可通过在式(13)两侧对m进行求导、结合式(15)得到diag(Dzts)Dz]-1diag(m)(17)将式(17)代入式(16),可得一阶梯度为(18)由于很难直接求解上式中矩阵的逆，对于单炮梯度可通过有限差分方法求解如下方程得到(19)式(19)是Taillandier等[20]的连续形式偏微分方程式(13)的离散形式。

本文对式(19)采用迎风差分方法求解。

利用式(4)可求取Hessian矩阵为(20)由于式(17)中存在矩阵的逆，通常无法直接求解。

将式(20)代入式(5)，通过整理可获取其等价的形式为(21)若在每次非线性迭代内部迭代求解式(21)即为高斯—牛顿法。

若只保留Hessian 矩阵对角元素，则为预处理的最速下降方法。

1.4 对比分析上文基于相同的目标函数，在统一的反演框架下分别推导了基于射线追踪方程与程函方程初至旅行时层析迭代反演的基础公式。

详细对比两者的理论推导过程，两类方法具有如下共性。

(1)具有相同的理论基础。

理论初至旅行时的计算均采用基于高频近似的射线理论进行；初至旅行时反演采用统一的目标函数，且均可在统一的反演框架下推导迭代反演的基本公式。

(2)具体反演算法之间具有对应性。

基于射线追踪方程方法中的反向投影算法与基于程函方程方法的预处理最速下降方法是对应的；基于射线追踪方程方法中的LSQR、SIRT等与基于程函方程方法中的高斯—牛顿算法是对应的。

对应方法之间可产生相近的效果。

由于两者在理论上的相似性，两者具有相似的分辨率以及处理复杂问题的能力，如两者均无法解决速度反转等复杂探区的问题。

两种方法在理论上具有如下的主要区别。

(1)二者所基于的正演算子不同。

前者基于射线追踪方程，即旅行时为沿射线路径对慢度的积分；后者基于程函方程，即利用有限差分等数值解法通过求解程函方程得到检波点处的初至时间。

(2)二者求取或构造目标函数相对于介质参数一阶梯度及二阶Hessian矩阵的方式不同。

对于前者，可利用不同网格内射线段长度显式地构建一阶及二阶导数所对应的矩阵(式(9)、式(10))，直观且物理意义明确；对于后者，只能通过隐式数值求解偏微分方程(式(19))得到单炮所对应的梯度，对于Hessian矩阵则很难显式地进行构建，只能通过间接的方式考虑Hessian矩阵的影响，物理意义相对不明确。

基于理论上的异同，结合具体实现细节(如图1所示两种方法的反演流程对比)，在实际应用中，基于射线追踪方程的初至层析反演方法具有如下优势。

(1)反演过程中针对性处理更为灵活。

可利用已知的射线路径计算射线角度、射线密度等信息，可利用这些信息在反演的过程中进行针对性处理。

(2)丰富的质控方法。

将射线路径、射线角度、射线密度等利用图形化的方式进行显示，可对最终的反演方法进行有效的质控，如可检查射线是否到达模型边界、根据射线密度判断不同部位反演模型的可靠程度等。

基于程函方程的初至层析反演方法具有如下优势。

(1)避免了射线路径的计算以及由于射线路径计算引入的误差。