线性矩阵不等式
应用线性矩阵不等式解决时滞系统控制问题

( No .9 1 5 5 0 Tr o o p s o f P LA ,Da l i a n 1 1 6 0 2 3 )
Ab s t r a c t I n t h i s p a p e r .h o w t o s o l v e H。 。c o n t r o l p r o b l e m i n a k i n d o f t i me - d e l a y s y s t e m b y u s i n g l i n e a r ma t r i x i n e — q u a l i t y ( LM I )i s s t u d i e d .Ba s e d o n Ly a p u n o v s e c o n d me t h o d,we p r e s e n t t h e Ho o s t a b i l i t y c o n d i t i o n . Th r o u g h s o l v i n g t h e
T P 3 9 1 D O I : 1 0 . 3 9 6 9 / j . i s s n 1 6 7 2 — 9 7 2 2 . 2 0 1 4 . 0 3 . 0 2 0
中 图分 类 号
S o l v i n g Co n t r o l P r o b l e m i n Ti me - d e l a y S y s t e m wi t h L MI
的重视 , 已 成 为 系 统 与 控 制 领 域 的 一 大 热 点 问 题r 1 ] 。本 文介 绍 了一 类 滞 后 型 离 散 时 滞 系 统 的
小 于零 。若下 式成 立
L( z) 一 Lo + 1 L1 +…+x N LⅣ 0
基频约束结构优化设计的线性矩阵不等式方法

基 频 约 束 结 构 优 化 设 计 的
线 性 矩 阵 不 等 式 方 法
张 家 凡
( 汉 工 业 学 院 机 械 工 程 系 , 汉 武 武
4 02 ) 3 0 3 摘 要 : 绍 了半 定 规 划 及 线 性 矩 阵 不 等 式 ( M I 的 基 本 概 念 , 出 具 有 基 频 约 束 的 桁 架 结 构 优 化 问题 的 半 介 L ) 给 定 规 划 形 式 。 半 定 规 划 法 ( 称 线 性 矩 阵 不 等 式 方 法 ) 以有 效 地 求 解 该 问 题 的 全 局 最 优 解 , 后 以 一 个 简 单 桁 架 或 可 最
2 具 有 基 频 约 束 的 桁 架 结 构 优 化 设 计
考 虑 一 个 桁 架 结 构 , 计 向 量 = { } 各 杆 的 横 截 面 设 A, 为 积 , 和 M 分 别 是 结 构 刚 度 矩 阵 及 代 表 杆 件 质 量 部 分 的 结 K 构 质 量 矩 阵 , 。代 表 集 中 质 量 块 等 不 具 有 结 构 刚 度 的 非 结 M
述 上 的 不 同是 前 者 的 约 束 条 件 中 主 要 是 矩 阵 不 等 式 , 后 者 而
为 通 常 的 标 量 不 等 式 ; 如 同 线 性 规 划 一 样 具 有 凸 规 划 的 性 它
质 , 外 还 包 含 一 些 更 广 泛 的 问 题 , 中 重 要 的 如 具 有 二 次 另 其
性 质 ( 对有 限个 L I 集 的交集 也成 立 。 2) M 凸
)
求 解 半 定 规 划 问 题 已 经 有 较 成 熟 和 有 效 的 算 法 , 时 又 同 有 可 靠 的 软 件 如 Si b MAT A 以 及 友 好 的 用 户 界 面 软 件 ca 、 l L B
lmi方法

lmi方法LMI方法(Linear Matrix Inequality)是矩阵不等式约束优化问题的一种方法,通常用于控制系统的设计和分析。
其核心思想是使用线性矩阵不等式来描述系统的约束条件,通过解决矩阵不等式优化问题,提高系统的稳定性和性能。
LMI方法的主要优点是其能够处理非线性系统,并且可以保证优化问题始终是凸优化问题。
同时通过求解矩阵不等式优化问题,可以得到广泛的优化问题解决方法。
LMI方法最常用于研究控制系统的稳定性,特别是在多变量控制系统设计方面。
具体来说,LMI方法用于确定一个线性系统的反馈控制器的参数,以使系统具有所需的稳定性和性能特性。
这包括最大阈值、稳态误差和响应速度等指标。
在LMI方法中,系统的约束条件被表示为矩阵不等式,例如下面给出的矩阵不等式:$$\begin{bmatrix}A & B\\C & D\end{bmatrix} \succeq 0$$其中,$A,B,C,D$分别为矩阵。
上述不等式的意义是:矩阵$\begin{bmatrix}A & B\\C & D\end{bmatrix}$是一个半正定矩阵。
在这个例子中,这个矩阵不等式的应用通常是基于H∞控制设计。
通过应用LMI方法,可以求解这个矩阵不等式的解,并进一步得到系统的反馈控制器的参数。
LMI方法的一般步骤如下:1. 将系统的约束条件表示为矩阵不等式。
2. 将矩阵不等式转换为标准形式,即将其转换为半正定矩阵的形式。
3. 使用数值求解算法求解半正定矩阵的解,并进一步得到系统的控制器参数。
关于步骤2,需要注意的是,将矩阵不等式转换为半正定矩阵的形式可以使用Schur补引理,也可以使用LMI形式。
LMI方法的应用范围非常广泛,一些具体的例子如下:1. 控制系统的设计和分析2. 机器人学中的逆动力学问题3. 路径规划和轨迹规划问题4. 信号处理中的滤波器设计6. 金融工程中的风险控制和投资组合优化问题7. 图像处理和计算机视觉中的图像分割和目标跟踪问题总之,LMI方法为解决各种数学优化问题提供了一个统一的框架,其应用范围越来越广泛。
线性矩阵不等式及其在随机控制中的应用

Ab t a t A n r a e rfr ltd a o v x叩 一 s r c : u e o t t o lmsf m t h si c n ml h o y c n b omuae sc n e O i a p r h o c t e
W ANG i g Z P n , HANG e g li Ch n —e
(col f l t n f m t nadC no E g er gSadn steo Igt nut ,nn205 ,h a Sho oEe r i I o ao n ot l ni en ,hnog ntu fjh IdsyJ a 533 C i ) co cn r i r n i I it r i n
文章编号 :04 4 8 (07 0 —0 1 —0 10 — 2020 ) 1 08 3
线 性 矩 阵不等 式及 其在 随机 控 制 中的应 用
王 平, 张成 磊
( 山东轻工业学 院 电子信息与控制工程学院 , …东 济南 205 ) 533
摘要 : 随机控制理论 中许多重要的问题 , 都可转化为线性矩阵不等式 (M ) L I约束 的凸优化 问题 , 而使其在数值 上 从 易于求解 。本文阐述 了线性矩阵不等式 方法的基本概念和内容 , 并介绍 了有关算法 及计算 软件 , 举例说 明其 最后
问题本 身是有 解 的 , 找 不 出问 题 的解 。这 给 实 际 也
() 1的决策变 量 。 F
已知的实对称阵。显然 F ) ( 是变量 各元素的仿
射 函数 , 外 式 () 味着 F( 是 一 个 负定 矩 阵 , 另 1意 ) 即对 所有 的非零 向量 H , ( u< ∈ u’ ) 0或 F( F ) 的最 大特 征 值 小 于 零 。所 有 满 足 线 性 矩 阵 不 等 式
【江苏省自然科学基金】_线性矩阵不等式(lmi)_期刊发文热词逐年推荐_20140820
2011年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
科研热词 网络控制系统 马尔可夫跳变 量化 脉冲 耦合神经网络 线性矩阵不等式 稳定性 混合时滞 时变时延 故障诊断 广义系统 凸性 全局渐近同步 kalman滤波器 h∞滤波器
推荐指数 3 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2012年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13
科研热词 线性矩阵不等式 测量数据丢失 大系统 h∞控制 鲁棒稳定性 脉冲 耦合神经网络 时延导数相关 变时滞 反应扩散项 全局渐 1 1 1 1 1 1 1 1
2013年 序号 1 2 3 4 5 6 7 8
推荐指数 1 1 1 1 1 1
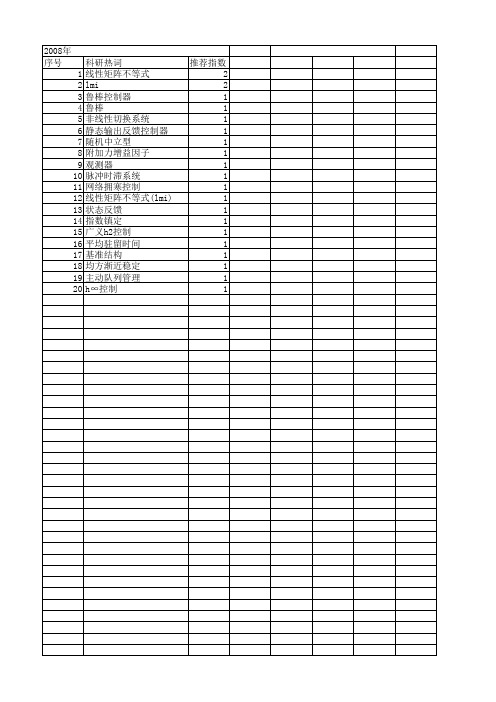
2008年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
科研热词 线性矩阵不等式 lmi 鲁棒控制器 鲁棒 非线性切换系统 静态输出反馈控制器 随机中立型 附加力增益因子 观测器 脉冲时滞系统 网络拥寒控制 线性矩阵不等式(lmi) 状态反馈 指数镇定 广义h2控制 平均驻留时间 基准结构 均方渐近稳定 主动队列管理 h∞控制
推荐指数 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2010年 序号 1 2 3 4 5 6 7 8 9 10 11
科研热词 鲁棒随机稳定 马尔可夫过程 非线性网络控制系统 锥补 量化 耗散控制 线性矩阵不等式 系统辨识 混沌 同步
推荐指数 1 1 1 1 1 1 1 1 1 1 1
2013年 科研热词 间歇过程 线性矩阵不等式(lmi) 线性矩阵不等式 二次型迭代学习控制 主动队列管理 tcp流模型 s-procedure h∞控制 推荐指数 1 1 1 1 1 1 1 1
矩阵的柯西施瓦茨不等式

矩阵的柯西施瓦茨不等式矩阵的柯西施瓦茨不等式是线性代数中一种重要的不等式,它建立了内积空间中向量之间的关系。
柯西施瓦茨不等式的基本思想是通过内积的性质,将向量的长度(模)与向量之间的夹角联系起来。
本文将介绍柯西施瓦茨不等式的定义、证明以及应用。
1. 定义柯西施瓦茨不等式的定义如下:对于实数域上的n维向量x和y,它们的内积满足:|x·y| ≤ ||x|| ||y||其中,x·y表示向量x和y的内积,||x||和||y||分别表示向量x和y的模。
等号成立当且仅当两个向量线性相关。
2. 证明下面给出柯西施瓦茨不等式的证明。
首先,构造一个函数:f(t) = ||tx - y||^2其中,t为实数。
根据内积的定义,有:f(t) = (tx - y)·(tx - y)= (tx)·(tx) - 2(tx)·y + y·y= t^2(x·x) - 2t(x·y) + y·y由于二次函数f(t)≥0,因此它的判别式小于等于0:(2(x·y))^2 - 4(x·x)(y·y) ≤ 0化简得到:(x·y)^2 - (x·x)(y·y) ≤ 0移项后即得到柯西施瓦茨不等式。
3. 应用柯西施瓦茨不等式在许多领域都有广泛的应用。
以下是一些常见的应用示例:3.1. 数值分析在数值分析中,柯西施瓦茨不等式可以用来估计误差。
例如,在数值积分中,我们可以通过柯西施瓦茨不等式来估计数值积分与准确积分之间的误差。
3.2. 泛函分析在泛函分析中,柯西施瓦茨不等式被广泛应用于勒贝格空间、希尔伯特空间等。
它为这些空间的内积定义提供了基础,并且在证明不等式、建立定理时起到了重要作用。
3.3. 物理学在物理学中,柯西施瓦茨不等式被广泛运用于量子力学和统计力学等领域。
它可以用来推导能量的最小值、确定粒子之间的相关性等。
关于矩阵秩的几个重要不等式

关于矩阵秩的几个重要不等式矩阵秩是线性代数中重要的概念,也是其他诸多领域研究的基础。
矩阵秩不仅仅可以用来测量矩阵的复杂性,还可以提供一些重要的不等式,可以用来确定矩阵中特定元素的精确位置,这在很多工程和科学应用中是非常重要的。
首先,对任意有限实矩阵,其秩最大可达到该矩阵维数的较小者。
这一不等式是由埃及学派成员济曼和卡特尔提出的。
它表明,任何矩阵的维数至少可以用它的秩来表示,而不会产生多余的项。
例如,维数可以表示为n×n实矩阵的秩最大为n。
其次,对于任意n×m矩阵A,他的秩不会超过min(m,n)。
这一不等式是由瓦西里科普洛夫于1908年提出的,也是矩阵秩的基本定义。
这一不等式暗示了:当n≤m时,满秩矩阵的秩最大为n;当n >m时,满秩矩阵的秩最大为m。
同样的,如果矩阵的维数n≤m,则秩最大可达n,如果维数n>m,则秩最大可达m。
此外,对任意n阶矩阵A,必有至少一个 n×n子矩阵是满秩矩阵,而且该子矩阵的秩必然等于n。
这一不等式是由瓦西里科普洛夫于1908年提出的,也是矩阵秩的基本定义。
因此,按照科普洛夫定理,任何n阶矩阵都存在至少一个满秩矩阵,且其秩必定等于n。
另外,对任意n×m矩阵A,其主子式的总和的秩的和不会超过m+n。
这一不等式是由洛克菲勒斯教授在1949年提出的,该定理以马尔科夫的名字著称。
他证明了任何有限实矩阵的主子式的总和的秩的和不会超过m+n。
因此,假设矩阵A有m行n列,那么它的主子式的总和的秩最大可达m+n。
最后,对任意矩阵A,它的秩最多只能达到它的行数与列数之和。
这一不等式是由詹姆斯波尔斯阿克特尔在1969年提出的,他提出了一些矩阵分解的概念,以证明该定理。
因此,任何有限实矩阵的秩最多只能达到它的行数与列数之和,超过此限制的结果就无意义了。
以上就是关于矩阵秩的几个重要不等式的内容,它们在线性代数中扮演了重要的角色,也可以用来解决各种工程和科学问题。
矩阵的秩的不等式总结

矩阵的秩的不等式总结矩阵的秩是线性代数中一个重要的概念,它可以描述矩阵的行空间和列空间的维度,也可以用来描述矩阵的奇异性。
在实际应用中,矩阵的秩不仅在理论研究中有重要意义,而且在工程技术和科学计算中也有着广泛的应用。
本文将对矩阵的秩的不等式进行总结,希望能对读者有所帮助。
首先,我们来看矩阵的秩的定义。
对于一个矩阵A,它的秩记作rank(A),定义为矩阵A的行秩和列秩中的较小值。
行秩是指矩阵的行向量组的极大无关组的向量个数,而列秩是指矩阵的列向量组的极大无关组的向量个数。
矩阵的秩可以用来描述矩阵的线性无关性,以及矩阵所表示的线性空间的维度。
接下来,我们来总结矩阵的秩的不等式。
对于一个m×n的矩阵A,它的秩满足以下不等式:1. rank(A) ≤ min(m, n)。
这个不等式表明矩阵的秩不会超过矩阵的行数和列数中的较小值。
这是因为矩阵的秩不会超过矩阵的行空间和列空间的维度,而行空间和列空间的维度最大也不会超过矩阵的行数和列数中的较小值。
2. rank(A) ≤ r。
这里,r代表矩阵A的行秩和列秩中的较小值。
这个不等式说明矩阵的秩不会超过矩阵的行秩和列秩中的较小值,也就是矩阵的行空间和列空间的维度的较小值。
3. rank(AB) ≤ min(rank(A), rank(B))。
对于两个矩阵A和B的乘积AB,它的秩不会超过矩阵A和B的秩中的较小值。
这个不等式可以帮助我们理解矩阵的乘积对秩的影响,以及在实际计算中如何利用矩阵的秩来简化计算。
4. rank(A+B) ≤ rank(A) + rank(B)。
对于两个矩阵A和B的和A+B,它的秩不会超过矩阵A的秩和矩阵B的秩之和。
这个不等式可以帮助我们理解矩阵的和对秩的影响,以及在实际计算中如何利用矩阵的秩来简化计算。
综上所述,矩阵的秩的不等式对于理解矩阵的性质和在实际应用中具有重要的意义。
通过对矩阵的秩的不等式进行总结,我们可以更好地理解矩阵的秩的性质,以及在实际计算中如何利用矩阵的秩来简化计算。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
线性矩阵不等式是一种数学关系,它可以用来描述矩阵之间的线性关系。
它把一个矩阵的元素和另一个矩阵的元素比较,以表达它们之间的线性关系。
它可以用来比较两个矩阵之间的差异,也可以用来比较两个矩阵之间的相似度。
线性矩阵不等式的具体形式是:A,B两个矩阵,其中A和B的元素之间的比较关系可以写成a_ij ≤ b_ij,其中i表示A矩阵的行号,j表示A矩阵的列号,a_ij表示A矩阵第i行第j列的元素,b_ij表示B矩阵第i行第j列的元素。
线性矩阵不等式的应用非常广泛,它可以用来求解矩阵的最大值和最小值,可以用来解决线性规划问题,也可以用来求解矩阵的最优解。
总之,它是一种重要的数学工具,在线性代数中有着重要的应用。
