第二章 交通流基本特性第一节 流量(交通量)Q.
第2章_交通流特性

3.查核线调查——调查是以河流丘陵铁道及地物边界线或 其他人为设立的检查线为分界线,两侧区域互相来往穿过 检查线的交通量。
4.特定地点或专项交通量调查——为满足交通管理与信号 控制的需要而在特定地点进行的交通量调查,为城市出交 通量调查、公共交通调查、综合交通调查、事故调查等。
交通流——道路上的行人或车辆所构成的行人流 或车流的通称。一般情况下,交通流指机动车流 (除特别声明)。
交通流状态: 稳态流动状态
非稳态流动状态
接近或超过道路通行能力 时,交通流受阻,出现排 队或等待。
交通流参数:排队长度、等 待(延误)时间等
18
8
五、交通量调查方法 1.确定调查地点 2.选择调查时间 3.选用调查方法——
1)人工观测法 2)浮动车移动调查法 3)车辆感应器测定法 4)仪器自动计测法:(1)气压式;(2)地磁式;
(3)电磁式;(4)超声波式;(5)红外线式 5)摄影法
9
浮动车移动调查法——
浮动车(Float Car)技术是近年来智能交通系统(ITS) 中所采用的获取道路交通信息的先进技术手段之一。
5
二、交通调查的主要内容 1、交通流要素调查
交通量、车速、密度以及车头间距,占有率等。
2、交通需求调查
土地利用、交通生成等,OD、出行调查
3、交通事故调查
事故发生次数、伤亡、性质等
4、交通环境调查
噪声、废气、振动等。
6
三、交通调查的基本要求
1、交通调查总是在对应于某些条件下进行的,这 些条件在调查中必须予以注明。
掌握交通量随时间推移的变化规律,据此可预测交通 量及其发展趋势。 2、为道路规划、建设及交通营运管理与控制,提供交 通流量流向、车速、延误、停车等数据。 3、为道路几何设计及交通控制设计提供依据交通量。 通过事前、事后的交通量调查,评价道路服务水平与 交通管理措施的效果。 4、在交通研究中通过交通量调查掌握交通实态与变化 的规律。 5、用于推算道路通行能力、预测与计算事故率及道路 运输成本和效益等为制定交通政策法规与科学理论研 究提供基础数据。
交通特性分析—交通量的基本特性

一时间内,路网上各段的交通量有很大不同。一般我们用路网交 通量分布图来表示交通量在路段上的分布。从路网交通量分布 图可以很明显地分辨出路上交通的主要流向、走廊、判断交通 量分布的均匀性。
交通量的空间分布特性
3.交通量的方向分布
一条道路往返两个方向的交通量,在很长时间内,可能是 平衡的,但在某一-短时间内,如一天中某几个小时,两个方向的 交通量会有较大的不同。W为了表示这种方向不平衡,常采用 方向分布系数表示。
(3)
根据使用方面的需要,对断面交通量进 行数据处理后,有断面平均交通量路段 (线)平均交通量及区域交通量等。
(2)
根据观测时间、地点的不同 可分为秒、分、小时或某段 时间的断面或路段交通量。
交通量的定义及分类
3.常见的交通量
1)平均交通量
交通量时刻在变化,在表达方式上通常取某一时间段内的平均值作为 该时间段的代表交通量。按平均值所取得时间段的长度计,常用的平均交 通量又可以分为:年平均日交通量;月平均日交通量;周平均日交通量。
交通量是一个随机数,不同时间、不同地点的交通量都是变化的。交 通量随时间和空间而变化的现象,称为交通量的时空分布特性。研究或观 察交通量的时空变化规律,对于进行交通规划、交通管理、设计方案比较 和经济.交通量的分类
(1)
根据交通物体分类:可分为机动车交 通量、非机动车交通量和行人交通 量等。非机动车交通量可分为自行 车、人力车、畜力车交通量等。
其中年平均日交通量在城市道路与交通工程中是一项极其重要的控制 性指标,用作道路交通设施规划、设计、管理的依据,其他平均交通量仅 供交通量统计分析、求各时段交通量变化系数,以便将各时段平均交通量 进行相互换算之用。
交通流理论第二章
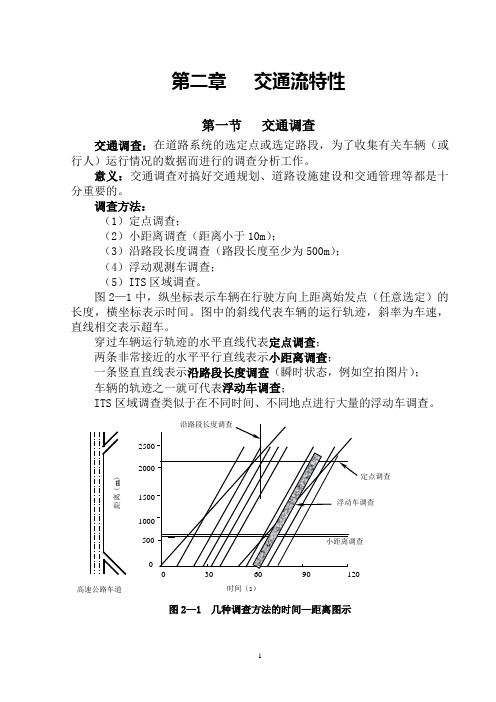
第二章 交通流特性第一节 交通调查交通调查:在道路系统的选定点或选定路段,为了收集有关车辆(或行人)运行情况的数据而进行的调查分析工作。
意义:交通调查对搞好交通规划、道路设施建设和交通管理等都是十分重要的。
调查方法:(1)定点调查;(2)小距离调查(距离小于10m );(3)沿路段长度调查(路段长度至少为500m ); (4)浮动观测车调查; (5)ITS 区域调查。
图2—1中,纵坐标表示车辆在行驶方向上距离始发点(任意选定)的长度,横坐标表示时间。
图中的斜线代表车辆的运行轨迹,斜率为车速,直线相交表示超车。
穿过车辆运行轨迹的水平直线代表定点调查; 两条非常接近的水平平行直线表示小距离调查;一条竖直直线表示沿路段长度调查(瞬时状态,例如空拍图片); 车辆的轨迹之一就可代表浮动车调查;ITS 区域调查类似于在不同时间、不同地点进行大量的浮动车调查。
图2—1 几种调查方法的时间—距离图示时间(s )距离(m )高速公路车道一、定点调查定点调查包括人工调查和机械调查两种。
人工调查方法即选定一观测点,用秒表记录经过该点的车辆数。
机械调查方法常用的有自动计数器调查、雷达调查、摄像机调查等。
自动计数器调查法使用的仪器有电感式、环形线圈式、超声波式等检测仪器,它几乎适用于各种交通条件,特别是需要长期连续性调查的路段。
雷达调查法适用于车速高、交通量密度不大的情况。
摄像机调查法一般将摄像机安装在观测点附近的高空处,将镜头对准观测点,每隔一定的时间,如15s、30s、45s或60s,自动拍照一次,根据自动拍摄的照片上车辆位置的变化,清点出不同流向的交通量。
这种方法可以获得较完全的交通资料,如流量、流向、自行车流及行人流和行驶速度、车头时距及延误等。
除这些方法以外,还有航空摄影调查法、光电管调查法等。
定点调查能直接得到流量、速度和车头时距的有关数据,但是无法测得密度。
二、小距离调查这种调查使用成对的检测器(相隔5m或6m)来获得流量、速度和车头时距等数据。
第2章交通流特性资料

交通参数
1
§2.1 交通流参数
交通流——道路上的行人或车辆所构成的行人流 或车流的通称。一般情况下,交通流指机动车流
(除特别声明)。
交通流状态: 稳态流动状态
非稳态流动状态
车辆在道路上行驶,依次鱼贯 而行,很少受外界因素干扰。
交通流参数:交通流量、速度 和密集度(交通流三要素), 以及车头时距、车头间距等
式中:Qt/3600—到达车辆数概率分布的平均值。 令M为负指数分布的均值,即平均车头时距为:
M=3600/Q=1/λ 负指数分布的方差为:D=1/λ2
32
h≥t 的平均车头时距分布曲线 (M=1s,5s)
h<t 的平均车头时距分布曲线(M=1s)
33
2) 适用条件 车辆到达是随机的、有充分超车机会的单列车
韦布尔分布 概率密度曲线
γ=0 β=1
2.5Leabharlann 38Probability Density Probability Density
4. 爱尔朗分布
爱尔朗分布的概率密度函数为:
p(t) et (t)l1 , l 1, 2, 3,
(l 1)!
0.8
l=1 0.6
0.4
l=2
l=3
0.2
当泊松分布不合适表征,样本方差为:
S 2
1 N 1
N i 1
(ki
m)2
1 N 1
g
(k j
j 1
m)2
fj
25
2. 二项分布
1) 基本公式
P(
x
)
Cnx
(
t
n
)
x
交通理论 第二章 交通流特性

第一节 交通调查
计算公式:
x y q ta tc
y t tc q
tc为观测车与交通流顺向行驶的行程时间
ta为观测车与交通流反向行驶的行程时间 x观测车与交通流反向行驶遇到的车辆数
y观测车与交通流顺向行驶时的净超车数(即
超越观测车的车辆数-被观测车超越的车轮 数) l为路段长度
l us t
NL
NL k L
则可以计算出来密度:
如果用两张相隔很短时间拍摄 的照片可以求出速度和流量。
第一节 交通调查
5、浮动车调查
floating car method 浮动车调查一般由一辆或几辆流动观测车进行交通流的测量。使用这种方法 时候,一辆观测车首先顺着所量测的交通流方向行驶,然后调头与所量 测的交通流反响行驶。车上的一个观测员把每个行驶方向上的行程时间 记录下来。在与测量的交通流顺向行驶中,观测员同时记录超越观测车 和被观测车超越的车辆数。
第二节 交通流参数
举例:假设有长度(单位英尺)分别为17,13,20,40,17和20的6辆汽车,
分布在公路一段长度为1000英尺的单车道上则该公路段上的密度? 解:R1=(17+13+20+40+17+20)/(1000)=0.127 而6辆车的平均长度:21英尺或0.00398英里 则密度:0.127/0.00398=31.91(辆/英里)
第二章 交通流特性
1、交通调查
2、交通流参数 3、交通流参数的统计分布 4、交通流基本参数的关系模型
第一节 交通调查
1、交通调查的方法
在道路系统的选定点或选定路段,为了收集有关车辆运行情况的数据而进行 的调查分析工作称为交通调查。
最初交通调查的工具只有:跑表和手工计数器
交通特性分析—交通流的基本特性及其相互关系

三流量与密度的关系
流量——密度曲线上的其他点的数值以同样的方式求出。点是表示
不拥挤情况的一个典型点。从这图来看,点的流量为1800辆/ℎ,密度为30
辆/及速度(矢径的斜率)为58/ ℎ。
点是表示拥挤情况的一个典型点。从图中看出,点的流量为1224 辆
/ℎ,密度105.6辆/及速度(矢径的斜率)为11.6/ℎ。根据定义,点的流
— — 路段长度()
交通流三参数基本关系
车流密度大小反映一条道路上的交通密集程度。对于同一条道路,可以
不考虑车道数;对于具有不同车道数的道路,为使车流密度具有可比性,
车流密度应按单车道来定义,单位为:辆/( ·车道)。
• 交通流三参数之间的基本关系式为:
=∙
式中:
— — 平均流量(辆/ℎ);
点。从原点 到曲线上点的向量斜率表示那一点的密度的倒
数1/ 。由 点作平行于 轴的一条直线,该直线为(上半部分)
交通流不拥挤的稳定交通流和(下半部分)拥挤路段的不稳定
交通流的分界线。
流量与速度的关系
综上所述,按格林希尔茨的速度——密度模型、流量——密度模型、
速度——流量模型可以看出, 、 、 是划分交通是否拥挤的重要特
密度由大变小时,车速会增大。关于两者之间的关系,已经由各国学者
提出了几种不同的模型。
1934年,格林希尔茨提出了速度一密度线性关系模型:
= (1 − )
式中符号意义同前。
这一模型简单直观如图所示 ,研究表明,刚才的公式表示的模型与实
测数据相关性很好。
速度与密度关系
这一模型简单直观如图所示 ,研究表明,刚才的公式表示的模型与实测数据相
速度与密度关系
第二章交通流特性

交通流参数的统计分布
1. 产生指数分布的随机数
交通流参数的统计分布
由x = FX- 1 ( r)可得
交通流参数的统计分布
2. 产生标准正态分布(N(0,1))的随机数
交通流参数的统计分布
Box-Muller Transformation(1958)
交通流参数的统计分布
验证:
交通流参数的统计分布
(取整)
交通流参数的统计分布
递推公式: P(0)(1p)n
P(x1)nx p P(x) x11p
交通流参数的统计分布
应用条件:
车流比较拥挤、自由行驶机会不多的车流; 当观测数据表明S2/m显著大于1时不适用。
交通流参数的统计分布
3. 负二项分布 基本公式
交通流参数的统计分布
连续型分布 1. 指数分布 • 基本公式 若车辆到达符合泊松分布,则车头时距就是符合指 数分布。 推导:
f(r1,r2)=1
由此,得到z1,z2联合分布概率密度为
f(x1,x2)=
(r1 , r2 ) ( x1, x2 )
雅可比行列式
交通流参数的统计分布
计算雅可比行列式得到:
(r1, r2 ) ( x1, x2 )
可见,X1,X2是两个相互独立的服从标准正态分布 的随机变量。
交通流参数的统计分布
第二章 交通流特性
内容提要
交通调查(交通量的测量) 交通流参数的计算 交通流参数的统计分布 交通流基本参数的关系模型
2.1 交通调查(交通量的量测)(1)
调查对象
反映交通流特征的参数: 流量 速度 密集度
2.1 交通调查(交通量的量测)(2)
调查方法
交通流的特性(课堂PPT)

.
9
.
10
此三参数之间的基本关系为:
QVs K
式中:Q——平均流量(辆/h); V s ——空间平均车速(km/h); K—平均密度(辆/km)。
.
3
能反映交通流特性的一些特征变量:
(1)极大流量Qm,就是Q-V曲线上的峰值。 (2)临界速度Vm,即流量达到极大时的速度。 (3)最佳密度Km,即流量达到极大时的密量。 (4)阻塞密度Kj,车流密集到车辆无法移动(V=0)时的
§4-1 交通流的特性
.
1
一. 交通设施种类
• 交通设施从广义上被分为连续流设施与间断 流设施两大类。
• 连续流主要存在于设置了连续流设施的高速 公路及一些限制出入口的路段。
• 间断流设施是指那些由于外部设备而导致了 交通流周期性中断的设置。
.
2
二. 连续流特征
1. 总体特征
交通量Q、行车速度 V s 、车流密度K是表征交通流 特性的三个基本参数。
密度。
(5)畅行速度Vf,车流密度趋于零,车辆可以畅行无 阻时的平均速度。
.
4
.
5
2. 数学描述
(1)速度与密度关系
格林希尔茨(Greenshields)提出了速度一密度线性
关系模型:
V
Vf
(1
K Kj
)
当交通密度很大时,可以采用格林柏(Grenberg)提出的对数模型:V NhomakorabeaVm
ln
Kj K
式中:Vm—对应最大交通量时速度。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2 2
一、交通量的定义
交通量时刻在变化,在表达方式上通常取某一时 间段内的平均值作为该时间段的代表交通量。如 果以辆/d为单位,平均交通量表达式为: 1 n 平均交通量 Qi n i 1 按平均值所取的时间段的长度计 ,常用的平均交通 量有: 年平均日交通量(AADT); 月平均日交通量(MADT); 周平均日交通量(WADT)。
2018/9/25
19 19
三、时间平均车速与区间平均车速
时间平均速度与区间平均速度之间的互换关系 由时间平均速度可以推算出区间平均速度:
σt2 Vs Vt Vt
式中:σt2 —时间平均速度观测值的方差。 由区间平均速度同样可以推算出时间平均速度:
σ s2 Vt Vs Vs
2 式中: σs —区间平均速度观测值的均方差。
1 n Rs si S i 1 式中: Rs —空间占有率; S —观测路段总长度; si —第i 辆车的长度; n —观测路段内的车辆数。
2018/9/25
24 24
二、车道占有率
空间占有率示意图:
S
s1
s2
s3
s4
2018/9/25
25 25
二、车道占有率
时间占有率: 在道路的任意路段上,车辆通过时 间的累计值与观测总时间之比(%),其表达式 为:
10 10
2018/9/25
四、设计小时交通量
第30位最高小时交通量 所谓第30位最高小时交通量就是将一年中测得的 8700个小时交通量,从大到小按序排列,排在第 30位的那个小时交通量。 研究表明,第30位小时交通量与年平均日交通量 (AADT)之比的K值十分稳定。 据国外观测,按道路类别及所在地区不同K值分 布在12%~18%范围内。
二、交通量的时间分布
时变化:一天24小时中,每个小时的交通量亦在 不断变化。 一天24小时中,流量最大的那个小时的交通量称 为高峰小时交通量。 高峰小时系数:就是高峰小时交通量与高峰小时 内某一时段的交通量扩大为高峰小时的交通量之 比。 高峰小时交通量 PHFt 60 (高峰小时内t时段的交通量) t 一般 t=5min或t=6min或 t=10min,最常用t=15min
2018/9/25 20 20
第三节 密度 k、车道占有率 车头间距 hs 、车头时距 ht
2018/9/25
21 21
一、密度 K交通流车流)密度: 是指某一瞬间内单位道 路长度上的车辆数目。
N K L 式中:N —路段内的车辆数(辆); L —路段长度(km)。
2018/9/25
22 22
2018/9/25
11 11
四、设计小时交通量
设计小时交通量的计算(不考虑方向不均衡性) DHV DHV AADT k n W W1 n C单 式中:DHV—设计小时交通量(辆/h); K —设计小时交通量系数(%); N — 车道数; C单— 每一车道设计通行能力(辆/h); AADT — 规划年的年平均日交通辆量 (辆/d); W —路幅宽度(m); W1 —一条车道宽度(m)。
3 3
2018/9/25
一、交通量的定义
年平均日交通量(AADT):
1 365 1 366 AADT Qi或闰年 : AADT Qi 365 i 1 366 i 1
月平均日交通量(MADT): 1 k MADT Qi k i 1 k:为当月的天数。 周平均日交通量(WADT):
2018/9/25
33 33
二、速度与密度的关系
1933年,格林希尔茨( Green shields )提出了速 度—密度线性关系模型,且模型与实测数据有良 好的吻合性。
K V V f (1 ) Kj
K=0 →V=Vf K=Kj→V=0 K=Km→V=Vm Q→Qmax
2018/9/25 34 34
2018/9/25 12 12
四、设计小时交通量
设计小时交通量的计算(考虑方向不均衡性)
DDHV AADT K KD
式中:DDHV——单向设计小时交通量; K —设计小时交通量系数(%); KD —方向不均匀系数(%)
2018/9/25
13 13
第二节 速度V
2018/9/25
14 14
2018/9/25
29 29
一、交通流三参数基本关系
交通流三参数之间的基本关系式为: Q KV 式中:Q —流量(辆/h); V —速度(区间平均速度)(km/h); K —密度(辆/km)。
2018/9/25
30 30
一、交通流三参数基本关系
流量、密度、速度三者之间的关系见下图:
2018/9/25
2018/9/25 17 17
三、时间平均车速与区间平均车速
时间平均车速:在单位时间内测得通过道路某断 面各车辆的点车速,这些点速度的算术平均值, 即为该断面的时间平均车速,即:
式中: V t —时间平均车速(km/h); v i —第i 辆车的地点车速(km/h); n —单位时间内观测到车辆总数(辆)。
1 n V t vi n i 1
2018/9/25
18 18
三、时间平均车速与区间平均车速
区间平均速度:是指某路段的长度与通过该路 段所有车辆的平均行程时间之比(以后讲到速度 如果不加说明即为区间平均速度)。当观测长度 一定时,其数值为所有车辆行程车速的调和平均 值,计算公式为: s 1 Vs n 1 1 n 1 ti n i 1 n i 1 v i 式中: V s —区间平均速度(km/h) ;s —路段长度 (km);ti —第i辆车的行驶时间(h);n —观 测到的车辆数;vi —第i辆车行程车速(km/h)。
安德伍德模型 的适用范围
2018/9/25
36 36
三、流量与密度的关系
交通流的流量-密度关系是交通流的基本关系,根 据格林希尔茨公式及三参数的基本关系式可得:
K Q KV f (1 ) Kj K2 Vf (K ) Kj
二、交通量的时间分布
周变化:交通量的周变化是指一周内各天的交通 量变化,因此,也称周日变化。 周变系数定义为:年平均日交通量除以某周日的 平均交通量。
K周 日 年平均日交通量 某周日平均交通量
某周日的平均日交通量等于全年所有该周日的交 通量除以全年该周日的总天数。
2018/9/25
6 6
1 n Rt ti T i 1
式中: Rt —时间占有率; T —观测总时间; ti —第i 辆车的长度; n —观测时间内通过该路段的车辆数。
2018/9/25 26 26
三、车头间距 hs 、车头时距 ht
前述Q、K、V(这里V是指什么?)均属于宏观 交通流参数,而车头间距和车头时距属于微观交 通流参数。其定义为: 车头间距:是指一条车道上前后相邻两车(用前 保险杠等具有代表性的点测量)之间的距离。 车头时距:是指连续行驶的前后两辆车(具有代 表性的点)通过行车道上某一点(或某一断面) 的时间差。 对观测路段上所有的车头间距和车头时距取平均 值称为平均车头间距与平均车头时距。
15 15
2018/9/25
一、基本定义
行程车速:行程车速又称区间车速,是车辆行 驶路程与通过该路程所需的总时间(包括停车时 间)之比。行程车速是一项综合性指标,用以评 价道路的通畅程度,估计行车延误情况。要提高 运输效率必须提高车辆的行程车速。 临界车速:这是指道路达到理论通行能力时的 车速,对于选择道路等级具有重要作用。 设计车速:是指在道路交通与气候条件良好的 情况下仅受道路物理条件限制时所能保持的最大 安全车速,用作道路线形几何设计的标准。
27 27
2018/9/25
三、车头间距 hs 、车头时距 ht
平均车头间距与平均车头时距与宏观交通流参数 Q、K存在以下关系:
1000 K hs 3600 Q ht
式中:hs —平均车头间距(m); ht —平均车头时距(s)。
2018/9/25
28 28
第四节
交通流的基本特性 及其相互关系
三、交通量的空间分布
主要包括: 交通量的城乡分布 交通量的路段分布 交通量的方向分布 交通量在车道上的分布
2018/9/25
9 9
四、设计小时交通量
含义及作用: 交通量具有随时间变化和出现高峰小时的特点, 因此,在进行道路设施规划设计时,必须考虑这 个特点。工程上为了保证道路在规划期内满足绝 大多数小时车流能顺利通过,不造成严重阻塞, 同时避免建成后车流量很低,投资效益不高,规 定必须选择适当的小时交通量作为设计小时交通 量。 根据美国的研究、认为第30位最高小时交通量作 为设计小时交通量是最合适的。
二、速度与密度的关系
1959年,格林柏(Greenberg)提出了用于密度很 大时对数模型:
Kj V Vm ln( ) K
格林柏模型 的适用范围
2018/9/25
35 35
二、速度与密度的关系
1961年安德伍德(Underwood)提出了用于密度 很小时的指数模型:
V Vf e
K Km
31 31
一、交通流三参数基本关系
2018/9/25
32 32
一、交通流三参数基本关系
交通流特性的一些特征变量: 极大流量Qm —Q-V曲线上的峰值; 临界速度Vm —即流量达到极大时的速度; 最佳密度km —即流量达到极大时的密度; 阻塞密度Kj —车流密集到所有车辆基本上无法移 动(V=0)时的密度; 畅行速度Vf —车流密度趋于零,车辆可以畅行元阻 时的平均速度。
