0010 第二章 第三节 交通流特性参数的统计分布
合集下载
交通流理论第二章
第二章 交通流特性第一节 交通调查交通调查：在道路系统的选定点或选定路段，为了收集有关车辆（或行人）运行情况的数据而进行的调查分析工作。
意义：交通调查对搞好交通规划、道路设施建设和交通管理等都是十分重要的。
调查方法：（1）定点调查；（2）小距离调查（距离小于10m ）；（3）沿路段长度调查（路段长度至少为500m ）； （4）浮动观测车调查； （5）ITS 区域调查。
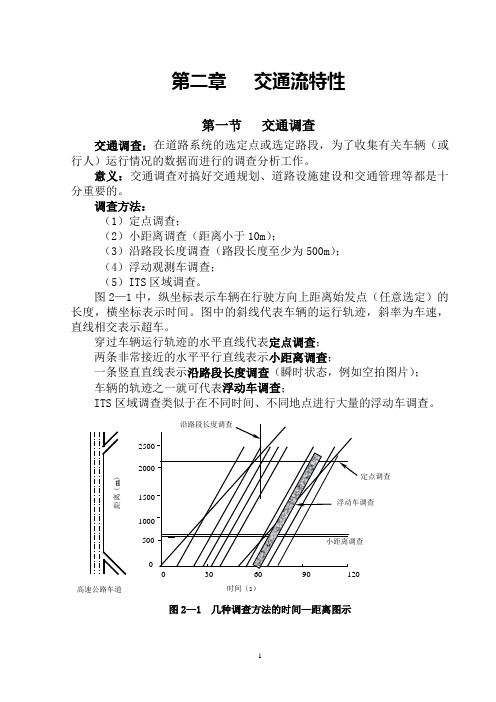
图2—1中，纵坐标表示车辆在行驶方向上距离始发点（任意选定）的长度，横坐标表示时间。
图中的斜线代表车辆的运行轨迹，斜率为车速，直线相交表示超车。
穿过车辆运行轨迹的水平直线代表定点调查； 两条非常接近的水平平行直线表示小距离调查；一条竖直直线表示沿路段长度调查（瞬时状态，例如空拍图片）； 车辆的轨迹之一就可代表浮动车调查；ITS 区域调查类似于在不同时间、不同地点进行大量的浮动车调查。
图2—1 几种调查方法的时间—距离图示时间（s ）距离（m ）高速公路车道一、定点调查定点调查包括人工调查和机械调查两种。
人工调查方法即选定一观测点，用秒表记录经过该点的车辆数。
机械调查方法常用的有自动计数器调查、雷达调查、摄像机调查等。
自动计数器调查法使用的仪器有电感式、环形线圈式、超声波式等检测仪器，它几乎适用于各种交通条件，特别是需要长期连续性调查的路段。
雷达调查法适用于车速高、交通量密度不大的情况。
摄像机调查法一般将摄像机安装在观测点附近的高空处，将镜头对准观测点，每隔一定的时间，如15s、30s、45s或60s，自动拍照一次，根据自动拍摄的照片上车辆位置的变化，清点出不同流向的交通量。
这种方法可以获得较完全的交通资料，如流量、流向、自行车流及行人流和行驶速度、车头时距及延误等。
除这些方法以外，还有航空摄影调查法、光电管调查法等。
定点调查能直接得到流量、速度和车头时距的有关数据，但是无法测得密度。
二、小距离调查这种调查使用成对的检测器（相隔5m或6m）来获得流量、速度和车头时距等数据。
城市道路交通调查与分析
瞬时地点车速行驶车速区间车速临界车速15位车速最低限制速度中位地点车速50位车速85位车速最高限制速度2交通流速度v车速2交通流速度v车速设计车速计算行车速度设计车速是指具有平均驾驶水平的驾驶员在道路交通与气候条件良好的情况下仅受道路条件限制所能保持的最大安全车速是道路线形几何设计的标准
第2章 城市道路交通调查与分析
一、交通流特性
2、三个交通流参数
交通量Q：某一特定时段内，通过道路某一地 点、某一断面或某一条车道的交通体的数量。 交通流速度V（车速） 交通密度K:某一瞬间，单位长度内某一车道、 某一方向或全部车道上的车辆数。
一、交通流特性
2、三个交通流参数
（1）交通量Q：某一特定时段内，通过道路某一 地点、某一断面或某一条车道的交通体的数量。
二、交通流统计分布 2、连续型分布——负指数分布
车头时距服从负指数分布的 车流特性见图，曲线是单调下降 的，说明车头时距愈短，出现的 概率愈大。
二、交通流统计分布 2、连续型分布
当负指数分布用于单车道交通流的车头时距分布时，理 论上会得出大量的0-1s的车头时距，但在实际中这种情 况不可能出现。因为车辆的车头至车头的间距至少为一 个车长加上前车尾部至后车头部的一定间隔。
二、交通流统计分布
交通流的统计分布特性是交通流特性预报的有效手段， 可使交通技术人员用少量的资料得出确切的预测结果。
交通的到达具有随机性，描述这种随机性的统计规律有 两种方法，即概率论中的离散型分布和连续性分布。
离散型分布又称计数分布，考查在一段固定长度的时间 内到达某场所的交通数量的波动性；连续型分布研究上述 事件发生的间隔时间的统计特性，如车头时距、车速和可 穿越空挡等的概率分布。
根据交通类型，可分为机动车交通量和非机动车交通量。
第2章 城市道路交通调查与分析
一、交通流特性
2、三个交通流参数
交通量Q：某一特定时段内，通过道路某一地 点、某一断面或某一条车道的交通体的数量。 交通流速度V（车速） 交通密度K:某一瞬间，单位长度内某一车道、 某一方向或全部车道上的车辆数。
一、交通流特性
2、三个交通流参数
（1）交通量Q：某一特定时段内，通过道路某一 地点、某一断面或某一条车道的交通体的数量。
二、交通流统计分布 2、连续型分布——负指数分布
车头时距服从负指数分布的 车流特性见图，曲线是单调下降 的，说明车头时距愈短，出现的 概率愈大。
二、交通流统计分布 2、连续型分布
当负指数分布用于单车道交通流的车头时距分布时，理 论上会得出大量的0-1s的车头时距，但在实际中这种情 况不可能出现。因为车辆的车头至车头的间距至少为一 个车长加上前车尾部至后车头部的一定间隔。
二、交通流统计分布
交通流的统计分布特性是交通流特性预报的有效手段， 可使交通技术人员用少量的资料得出确切的预测结果。
交通的到达具有随机性，描述这种随机性的统计规律有 两种方法，即概率论中的离散型分布和连续性分布。
离散型分布又称计数分布，考查在一段固定长度的时间 内到达某场所的交通数量的波动性；连续型分布研究上述 事件发生的间隔时间的统计特性，如车头时距、车速和可 穿越空挡等的概率分布。
根据交通类型，可分为机动车交通量和非机动车交通量。
交通理论 第二章 交通流特性
（4）运行速度（Operating Speed ）: 运行速度是指在不超过路段设计车速 的情况下，车辆在给定交通流中能够达到的最大安全车速 。
（5）时间平均速度(Time mean speed －TMS) 和区间平均速度(Space mean speed －SMS)
●时间平均车速是指在特定的时间区间内，通过道路某一地点的所有车辆地 点速度的算术平均值。
量 ●高峰小时系数：高峰小时交通量与高峰小时流率之比
第二节 交通流参数
（3）交通量空间分布特性 ●城乡分布：城市交通量大于乡村交通量 ●路段分布：不同线路或同一线路的不同路段交通量不同 ●方向分布：道路的某一季节或某一时刻，某方向的交通量会比另一方向大，
（早晚上下班方向），但长时间的统计，双向交通量比较接近。 ●车道分布：同一路段同一方向上，不同车道流量不同，通常靠近路中线的
△t ：拍摄照片的时间间隔；
si：△t的时间间隔内，第i车辆行驶的距离
第二节 交通流参数
（4）时间平均速度和空间平均速度的关系
●用区段平均速度计算时间平均速度的关系由沃德洛尔确定：
其中?
2 s
ut
?
us
?
?
2 s
us
是空间平均速度的方差。
●在交通工程实践中，常常要把时间平均速度转化成空间平均速度，公式为：
? ut
?
1 N
N
ui
i?1
第二节 交通流参数
（3）区间平均速度（宏观）
定点 调查
①其中的一个定义：路段的长度与通过该路段所有车辆的平均行驶时间之比
●其计算公式为：
? us ?
D 1N
N
ti
i?1
ti
?
（5）时间平均速度(Time mean speed －TMS) 和区间平均速度(Space mean speed －SMS)
●时间平均车速是指在特定的时间区间内，通过道路某一地点的所有车辆地 点速度的算术平均值。
量 ●高峰小时系数：高峰小时交通量与高峰小时流率之比
第二节 交通流参数
（3）交通量空间分布特性 ●城乡分布：城市交通量大于乡村交通量 ●路段分布：不同线路或同一线路的不同路段交通量不同 ●方向分布：道路的某一季节或某一时刻，某方向的交通量会比另一方向大，
（早晚上下班方向），但长时间的统计，双向交通量比较接近。 ●车道分布：同一路段同一方向上，不同车道流量不同，通常靠近路中线的
△t ：拍摄照片的时间间隔；
si：△t的时间间隔内，第i车辆行驶的距离
第二节 交通流参数
（4）时间平均速度和空间平均速度的关系
●用区段平均速度计算时间平均速度的关系由沃德洛尔确定：
其中?
2 s
ut
?
us
?
?
2 s
us
是空间平均速度的方差。
●在交通工程实践中，常常要把时间平均速度转化成空间平均速度，公式为：
? ut
?
1 N
N
ui
i?1
第二节 交通流参数
（3）区间平均速度（宏观）
定点 调查
①其中的一个定义：路段的长度与通过该路段所有车辆的平均行驶时间之比
●其计算公式为：
? us ?
D 1N
N
ti
i?1
ti
?
2__交通流统计分布
2统计量x2的意义及表达式
3对检验数据的要求
p（x）＝
式中：x为时间段t内通过的车辆数；
m为时间段t内通过车辆数的平均值，即
m＝
Q为交通量(辆/小时)，t为计数时段的时间(秒)，e为自然对数的底。
例题详见p1，每次试验只有两种可能的结果。这就是一个二项式分布的过程。通常用p表示试验成功的概率，二项式分布给出在n次试验中成功x次的概率为p（x）.
则有：
p（x）＝Cxn·px·qn-x
式中，n――试验次数，x――成功次数，p――给定试验中成功的概率，q――失败的概率，q=1－p；
二项式分布可以用来预测违反交通规则的车辆数，在交叉口可能的转弯车辆数以及在路段上超速行驶的车辆数。例题详见p16～17
2.2.2连续型分布
连续型分布是用来描述观测数值的连续随机过程，可假定任何数值的变量。由于在指定的范围内变量可取任何数值，因而连续变量可取某一特定数值的概率为零。几种较常用的连续型分布有负指数分布、移位的负指数分布以及厄朗分布。
p（h∠t）＝1－p（h≥t）＝1－e-m
负指数分布是研究交通流时常用的一种分布，当车流密度较低，车辆行驶较为自由时，车头时距呈负指数分布。国外研究指出，在每个车道每小时的不间断车流量小于或等于500辆小客车时，负指数分布是符合实际的车头时距情况的。
②移位的负指数分布
负指数分布对于较小的事件间隔可得到较大的概率，这在理论上是对的。例如根据p18公式(2—21)可大量得到0～1秒的车头时距，但实际上它们不可能出现，因为前后两车车头之间一般应有不小于1秒的车头时距。为了改正此不合理，可考虑一个最小间隔长度“C”，从分布曲线图上将负指数分布曲线从原点O沿x轴向右移动C值(一般在1．0～1．5秒之间)，此移位的负指数分布曲线则能更好地符合实际交通流状态。
3对检验数据的要求
p（x）＝
式中：x为时间段t内通过的车辆数；
m为时间段t内通过车辆数的平均值，即
m＝
Q为交通量(辆/小时)，t为计数时段的时间(秒)，e为自然对数的底。
例题详见p1，每次试验只有两种可能的结果。这就是一个二项式分布的过程。通常用p表示试验成功的概率，二项式分布给出在n次试验中成功x次的概率为p（x）.
则有：
p（x）＝Cxn·px·qn-x
式中，n――试验次数，x――成功次数，p――给定试验中成功的概率，q――失败的概率，q=1－p；
二项式分布可以用来预测违反交通规则的车辆数，在交叉口可能的转弯车辆数以及在路段上超速行驶的车辆数。例题详见p16～17
2.2.2连续型分布
连续型分布是用来描述观测数值的连续随机过程，可假定任何数值的变量。由于在指定的范围内变量可取任何数值，因而连续变量可取某一特定数值的概率为零。几种较常用的连续型分布有负指数分布、移位的负指数分布以及厄朗分布。
p（h∠t）＝1－p（h≥t）＝1－e-m
负指数分布是研究交通流时常用的一种分布，当车流密度较低，车辆行驶较为自由时，车头时距呈负指数分布。国外研究指出，在每个车道每小时的不间断车流量小于或等于500辆小客车时，负指数分布是符合实际的车头时距情况的。
②移位的负指数分布
负指数分布对于较小的事件间隔可得到较大的概率，这在理论上是对的。例如根据p18公式(2—21)可大量得到0～1秒的车头时距，但实际上它们不可能出现，因为前后两车车头之间一般应有不小于1秒的车头时距。为了改正此不合理，可考虑一个最小间隔长度“C”，从分布曲线图上将负指数分布曲线从原点O沿x轴向右移动C值(一般在1．0～1．5秒之间)，此移位的负指数分布曲线则能更好地符合实际交通流状态。
03.第二、三讲+交通流特性
汽车诞生前的运输
没有车 轮的交 通时代
骆驼编 队运输
汽车诞生前的运输
印度大 象搬运
没有车 轮的交 通时代
爱斯基摩犬 拉雪橇运输
车辆运输和汽车的诞生
马车旅 客搬运
车辆运 输的交 通时代 和汽车 的诞生
德国卡 尔.本茨
一、交通流理论的发展过程
创始阶段
从交通工程（汽车）诞生——第二次世界大战结束
汽车工业发展
交通流理论也是汽车制造、交 通规划与管理、道路设计与建 设、交通环境保护、交通事故 预防等学科的理论基础。
2-2交通流理论的发展
按照时间顺序：可以分为三个阶段（1）萌芽 阶段1930s、（2）发展阶段1950s、（3）形成 阶段1960s； 史称如下三个阶段
创始阶段：从汽车（交通工程）诞生——第二次世 界大战结束 快速发展阶段：第二次世界大战结束——20世纪50 年代末 稳定发展阶段：20世纪50年代末——
按照研究对象可以分为：
（1）单车运动特性； （2）道路多车运动特性（单一路段或单一交叉口 等交通设施）、 （3）路网多车运动特性（一条道路、局部道路网 络）。
（1）传统交通流理论（传统方法）； （2）现代交通流理论（现代方法）。
按照研究手段和方法可以分为：
2-3交通流理论研究的内容
2-5 交通流理论的发展趋势
理论发展——客观需求和支持其发展的客观 环境。 交通流理论——交通运输工程的需求、科学 技术的发展水平。 交通流研究领域：宏观领域（路段交通流； 路网交通流；多模式路网客、货流）。 交通流研究方法：计算机模拟手段与技术； 其他学科现代先进理论与方法。
《交通系统分析》交通参数 ppt课件
《交通系统分析》交通参数
1. 泊松（Poisson）分布
P(k) (t)k et ,
k!
k 0,1, 2,
式中:P(k)——在计数间隔t内到达k辆车或人的概率;
λ——单位时间内的平均到达率(辆/s或人/s)；
t——每个计数间隔持续的时间(s)或距离(m)；
e——自然对数的底，取值为2.71828;
《交通系统分析》交通参数
负二项分布估计波动流合理性分析：观测数据说明合适
车辆数
观测频率
理论拟合频率
泊松分布
负二项分布
0
139
129.6
140.4
1
128
132.4
122.0
2
55
67.7
62.2
3
25
23.1
24.2
4
10
5.9
8.0
5
3
1.2
2.3
>5
0
0.1
0.9
合计
360
360.0
360.0
《交通系统分析》交通参数
3. 负二项（Negative Binomial）分布
P(k)
C 1 k 1
p
(1
p)k
,
k 0,1,2,
p、β为负二项布参数。0＜p＜1，β为正整数。
适用条件：交通流波动性大或以一定的计 算间隔观测到达的车辆数(人数)其间隔长 度一直延续到高峰期间与非高峰期间两个 时段时，所得数据可能具有较大的方差。
解： 可以将400m理解为计算车辆数的空间间隔， 则车辆在空间上的分布服从
泊松分布
t 400m， 60/4000辆/m，m t 6辆，此分布服从m 6的泊松分布
1. 泊松（Poisson）分布
P(k) (t)k et ,
k!
k 0,1, 2,
式中:P(k)——在计数间隔t内到达k辆车或人的概率;
λ——单位时间内的平均到达率(辆/s或人/s)；
t——每个计数间隔持续的时间(s)或距离(m)；
e——自然对数的底，取值为2.71828;
《交通系统分析》交通参数
负二项分布估计波动流合理性分析：观测数据说明合适
车辆数
观测频率
理论拟合频率
泊松分布
负二项分布
0
139
129.6
140.4
1
128
132.4
122.0
2
55
67.7
62.2
3
25
23.1
24.2
4
10
5.9
8.0
5
3
1.2
2.3
>5
0
0.1
0.9
合计
360
360.0
360.0
《交通系统分析》交通参数
3. 负二项（Negative Binomial）分布
P(k)
C 1 k 1
p
(1
p)k
,
k 0,1,2,
p、β为负二项布参数。0＜p＜1，β为正整数。
适用条件：交通流波动性大或以一定的计 算间隔观测到达的车辆数(人数)其间隔长 度一直延续到高峰期间与非高峰期间两个 时段时，所得数据可能具有较大的方差。
解： 可以将400m理解为计算车辆数的空间间隔， 则车辆在空间上的分布服从
泊松分布
t 400m， 60/4000辆/m，m t 6辆，此分布服从m 6的泊松分布
第3章交通流特性
四、交通量-速度-交通密度的关系
通常在交通流中各车辆的速度并不相同。将车 辆按速度分组，对于每组速度的车辆有：
qi kivi
则总的交通量为：
m
m
q kivi k (ki/k)vi kavs
i1
i1
式中：m——速度分组数
—v a—s 平均车速，即各组车速乘以该组车辆的 密度占总密度的比例（权数）。
Time mean speed is defined as the average speed of all the vehicles passing a point on a highway over some specified time period.
Space mean speed(空间平均速度)
对于道路交通，可用线性函数表示为：
va
vf
(1
k kj
)
21
四、交通量-速度-交通密度的关系
2. 交通量-交通密度关系图
qkavk(vk)
The peak of the density flow curve occurs at the theoretical maximum flow (i.e., capacity) of the facility.
k=n/L
Space headway(车头间距s ) is defined as the distance between corresponding points of two successive vehicles at any given time.
sa
s
n
L n
k1/s
16
三、交通密度
Density is an important measure of the quality of traffic flow.
交通流特性(精)
交通量是实测值或预测值，流率是转换后的等效值。
二、交通量的有关概念
1、日交通量 （1）年平均日交通量（AADT） （2）月平均日交通量（MADT） （3）周平均日交通量（WADT） 2、小时交通量 （1）高峰小时交通量 一天内连续60min的最大小时交通量。有整时段和非整时段之分。 （2）第30位（高峰）小时交通量
15%位车速：指所有车辆中，只有15%的车辆在该速度一下行驶。
一般用作最低车速限制标准。
速度观测值的标准差σ（均方差）：
（vi -v）2
n
反映车速分布的离散情况，σ值越大，车速越离散，表明车辆
行驶有很大的自由度。
三、时间平均速度与区间平均速度
1、时间平均速度 Vt
指某一时间段内，通过道路某一断面的所有车辆的地点速度的算
三、交通量在时间上的变化（分布）
1、季节、月份变化 反映交通量在一年内的变化
常用月变系数（又称为月不均匀系数）M表示
2、日变化 反映交通量在一周内的变化
常用周变系数D表示
D=
AADT 某周日的年均日交通量
3、小时变化 反映交通量在一日内的变化，有早、晚高峰 反映交通量在一天内集中程度的参数是高峰小时流量比 ：
3、交通量与密度的关系
由Q=K·V和
K
K2
V=Vf
(1Kj
)
Q=
Vf (K-
Kj
)
说明Q～K呈二次函数（抛物线）关系，其图形为：
对上式进行求导，并令 dQ =0 ，则有：
dK
dQ dK
=
Vf
(1-
2K Kj
)=0
Km
=
Kj 2
K j 2
∴
Qm
=Vf
二、交通量的有关概念
1、日交通量 （1）年平均日交通量（AADT） （2）月平均日交通量（MADT） （3）周平均日交通量（WADT） 2、小时交通量 （1）高峰小时交通量 一天内连续60min的最大小时交通量。有整时段和非整时段之分。 （2）第30位（高峰）小时交通量
15%位车速：指所有车辆中，只有15%的车辆在该速度一下行驶。
一般用作最低车速限制标准。
速度观测值的标准差σ（均方差）：
（vi -v）2
n
反映车速分布的离散情况，σ值越大，车速越离散，表明车辆
行驶有很大的自由度。
三、时间平均速度与区间平均速度
1、时间平均速度 Vt
指某一时间段内，通过道路某一断面的所有车辆的地点速度的算
三、交通量在时间上的变化（分布）
1、季节、月份变化 反映交通量在一年内的变化
常用月变系数（又称为月不均匀系数）M表示
2、日变化 反映交通量在一周内的变化
常用周变系数D表示
D=
AADT 某周日的年均日交通量
3、小时变化 反映交通量在一日内的变化，有早、晚高峰 反映交通量在一天内集中程度的参数是高峰小时流量比 ：
3、交通量与密度的关系
由Q=K·V和
K
K2
V=Vf
(1Kj
)
Q=
Vf (K-
Kj
)
说明Q～K呈二次函数（抛物线）关系，其图形为：
对上式进行求导，并令 dQ =0 ，则有：
dK
dQ dK
=
Vf
(1-
2K Kj
)=0
Km
=
Kj 2
K j 2
∴
Qm
=Vf
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
●二项分布的递推公式：
P(0) (1 p) n nx p P( x 1) P( x) x 1 1 p
一、 离散型分布
（2）举例
车辆数/间隔 <3 3 m=7.469 S2=3.999 S2/m=0.535 4 5 6 观测频率 0 3 0 8 10 理论频率（二 项分布）
0.3 1.0 2.9 6.2 9.8 12.3 12.1 9.4 5.8 2.8 1.0 0.4
上，常常要求计算某一范围事件的概论。
●泊松分布各项可以总起来得出每周期期间少于或多于x辆车的概率。例如：
交通技术人员需要计算在已知的周期期间2辆车或少于2辆车到达的概率？ 解：也就是车辆数0，1，2到达的概率的总和，即：
mi e m P( x 2) i! i 0
2
一、 离散型分布
(t ) e P( x) x!
x
t
me P( x) x!
x m
x 0,1,2,
P(x)为在计数周期t期间x辆车到达的概率
λ为平均到达率（辆/妙）
t为每个计数周期的持续时间（妙） m= λt为在持续时间t周期内平均到达的车辆数
一、 离散型分布
（1）用泊松分布拟合观测数据
当泊松分布拟合到观测数据时，参数m的计算：
e
26 19 16
t / T
值，拟合
车间时距t观测 累积频率，≥t
H，期望的车间时 距数（≥t） 35.7 31.9 28.5
3
4 5 6 7
149
136 125 111 95
153
136.7 122.2 109.4 97.8
19
20 21 22 23
14
11 10 9 8
25.5
22.7 20.3 18.2 16.3
P( h t ) e
Vt / 3600
从该关系可见，在随机车流状况下，大于任何已知值的车间时距数将按指数 曲线分布，为负指数分布，简称为指数分布
二
连续型分布
Vt / 3600
P( h t ) e
上式中m或Vt/3600是到达（计数）概率分布的平均数。如果使m=t/T，T是 间隔（车间时距）概率分布的平均数=3600/V。这样车间时距等于或大于t 的概率可以写成：
一、 离散型分布
●在180个10秒内有111辆车到达,小时交通量:
●第3栏由第1栏乘以第2栏得到; ●理论频率的计算:
222
m xem 理论频率 （总的观测频率） x! 总的车辆到达数量 111 m 总的观测频率 180
x为第一栏中的数值
一、 离散型分布
（2）累积泊松分布
●上面讨论的是对待特定事件（即给定恰好x辆车到达）出现的概论，实际
到达数量至少是l但不超过n的概率：
到达数量大于或等于k的概论：
P( x k ) 1 P( x k )
mi e m 1 i! i 0
i k 1
mi e m P(l x n) i! i l
i n
一、 离散型分布
（3）泊松分布的使用情况
●泊松分布适用于描述离散型随机变量，当交通流量不大并且没有象交通信
理论频率（泊 松分布） 1.3 2.5 4.7 7.1 8.8
7
8 9 10 11 12 >12
11
10 11 9 1 1 0
9.4
8.8 7.3 5.4 3.7 2.3 2.7
合计
64
64
64
一、 离散型分布
3、负二项分布
当交通流计数延续到高峰期间与非高峰期间两个方面时，将会形成一个高方 差。在交通信号的下游会有一个很普遍但不是很明显的情况：信号循环 的前一部分时间，交通流大，信号循环的后一部分时间，交通流很小。 如果计数期间相应于周期的绿灯部分，或相应于整个信号周期，周期影 响会不明显。不过如果计数周期短，会有大流量的时段与小流量的时段， 甚至有居中流的时段，这样形成的计数分布将产生很高的方差。
号这类因素干扰时，交通状况会出现随机性，泊松分布能够提供良好的 成果。
●当交通拥挤或交通流的到达率上有周期干扰时候（如交通信号），用泊松
泊松分布描述交通状况误差会较大。
●具体应用时候，应该注意泊松分布的平均数与方差是相等的，当观测数据
的方差/平均数的比率显著地不等于1.0时候，就是泊松分布不适合的表示。
移位指数分布拟合数据，需要估计参数 T ˆ和
ˆ
是曲线相对于原点的位移
二
举例：与前图对比
连续型分布
二
连续型分布
移位负指数分布适合描述限制超车的单列车流车头时距分布和低流量时多列
有了这些公式就可以 求得相应的概率
一、 离散型分布
●相应的递推公式
P(0) p k
x k 1 P( x) qP( x 1) x
一、 离散型分布
举例：
车辆数/间隔 观测频率
理论频率（负 二项分布）
140.4
122.0 62.2
理论频率（泊 松分布） 129.6
132.4 62.2
总的事件 m 总的观测次数
概率的计算：
观测的总车辆数 总的周期数
P(0) e
m
x
m m e P( x) m x ! x 1 m P( x 1) x m e ( x 1)!
一、 离散型分布
m P( x) P( x 1) x 据此可以得到： P(0) e m m P (1) P (0) 1 m P (2) P (1) 2 m P(3) P(2) 3
通特性是事件之间的时间，即前后车辆到达之间的车间时距。为此需要 用到连续型分布。 负指数分布等
二
1、负指数分布
连续型分布
车辆的到达服从泊松分布，其公式为：
(t ) e P( x) x!
x
t
P(x)为在计数周期t期间x辆车到达的概率 λ为平均到达率（辆/妙） t为每个计数周期的持续时间（妙） m= λt为在持续时间t周期内平均到达的车辆数 令： V 其中V为小时交通量
可拟合观测数据。 （3）在拥挤的交通量计数中，观测数据所得方差/平均值比率事实上小于1， 对观测数据可用二项分布拟合。 （4）在交通量计数中，有流量的周期变化，或在计数周期平均流量在改变， 得出方差/平均值的比率事实上大于1.0，则负二项分布可拟合观测数据。
二
连续型分布
以上分析提出了一定时间间隔内出现离散事件的概率，另外一非常重要的交
重要的分布是离散型分布（描述可数的事件出现率）以及连续型分布 （描述事件之间时间间隙的出现率）。
●本节主要讨论离散分布，主要包括泊松分布、二项分布及负二项分布等，
然后讨论基本的连续型分布，最后讨论了用于交通的几种改进分布。
一、 离散型分布
在一定的时间间隔期间清点车辆到达数，是最老的也是最简单的交通量量测
法。当比较一系列时间间隔相等的计数时，这就形成了一随机序列。这 就引起交通技术人员研究其分布，描述一间隔期间车辆到达的事件。
一、 离散型分布
1、泊松分布
为了描述离散事件完全随机出现，泊松分布是合适的分布。其早期在交通上 的应用有：金蔡于1933年论述了泊松分布应用于交通的可能性，1936年 亚当斯发表了数值例题，1947年格林希尔治在其有关交叉口交通分析中， 采用泊松分布。 泊松分布的公式：
一、 离散型分布
2、二项分布
（1）二项分布的公式 ●对于拥挤的交通（该处观测的方差/平均数比率实际上小于1）时，可以使
用二项分布来描述车辆到达的分布。
●二项分布的表达式：
P( x) C xn p x (1 p) n x
x 0,1,2,, n
n! C x!(n x)!
n x
p 是1辆车到达的概率
C
n 是n个中一次取x的组合数 x
一、 离散型分布
●对于二项分布，m=np，m是平均数；S2=np(1-p)是方差。
如果
ˆ 是拟合中使用的二项分布参数p的估计值， n p ˆ
ˆ (m s 2 ) / m p ˆ m / p m2 /( m s 2 ) n
是拟合中使用的二项
分布参数n的估计值，这些参数可以用下列关系式来估算：
8
9 10 11 12 13 14 15
84
72 61 52 50 34 32 29
87.3
78.1 69.8 62.5 55.8 49.9 44.5 39.8
24
25 26 27 28 29 30 31
8
7 7 6 4 3 1 0
14.6
13.1 11.6 10.5 9.2 8.3 7.5 6.6
●一般情况：
到达数量小于或等于k的概论：
到达数量大于k的概论：
me P( x k ) i! i 0
到达数量小于k的概论：
i k 1
i k
i m
P( x k ) 1 P( x k )
mi e m 1 i! i 0
i k
mi e m P( x k ) i! i 0
二
这样，T=1753/214=8.19秒， 则m=t/T=t/8.19=0.122t
连续型分布
观测数据包含214个时间间隔，总计1753秒。
P( h t ) e
则拟合的结果见上面表格。
0.122t
二
将数据用图来表示：
连续型分布
二
连续型分布
2、改进的负指数分布——移位负指数分布
用于车辆计数的泊松分布及用于前后两车相隔时间的负指数分布，只适用于 低交通量。当交通转为繁忙，车辆随意超车的能力受到限制，车辆间的 相互影响增加。这时车队趋向于成队驾驶，车队的最小车间距明显地大 于0；另外，指数分布描述车间时距越趋于0出现的概率越大，或说指数 分布描述的是车头间距趋于较小时候的概率，或者说指数分布预测的短 车间距太多。