多元回归R案例
多元线性回归模型的案例讲解

多元线性回归模型的案例讲解以下是一个关于房价的案例,用多元线性回归模型来分析房价与其他变量的关系。
假设我们想研究一些城市的房价与以下变量之间的关系:房屋面积、卧室数量、厨房数量和所在区域。
我们从不同的房屋中收集了这些变量的数据,以及对应的房价。
我们希望通过构建多元线性回归模型来预测房价。
首先,我们需要收集数据。
我们找到100个不同房屋的信息,包括房屋的面积、卧室数量、厨房数量和所在区域,以及对应的房价。
接下来,我们需要进行数据处理和探索性分析。
我们可以使用统计软件,如Python的pandas库,对数据进行清洗和处理。
我们可以检查数据的缺失值、异常值和离群点,并对其进行处理。
完成数据处理后,我们可以继续进行变量的选择和模型构建。
在多元线性回归中,我们需要选择合适的自变量,并建立模型。
可以使用统计软件,如Python的statsmodels库,来进行模型的构建。
在本例中,我们使用房屋面积、卧室数量、厨房数量和所在区域作为自变量,房价作为因变量。
我们可以构建如下的多元线性回归模型:房价=β0+β1*面积+β2*卧室数量+β3*厨房数量+β4*所在区域其中,β0、β1、β2、β3和β4是回归模型的系数,表示因变量与自变量之间的关系。
我们需要对模型进行拟合和检验。
使用统计软件,在模型拟合之后,我们可以得到回归模型的系数和统计指标。
常见的指标包括回归系数的显著性、解释方差、调整R方和残差分析等。
根据回归模型的系数,我们可以解释不同自变量对因变量的影响。
例如,如果回归系数β1大于0且显著,说明房屋面积对房价有正向影响。
同理,其他自变量的系数也可以解释其对因变量的影响。
最后,我们可以使用建立的多元线性回归模型进行房价的预测。
通过输入房屋的面积、卧室数量、厨房数量和所在区域等自变量的数值,我们可以预测其对应的房价。
需要注意的是,多元线性回归模型的效果不仅取决于数据的质量,还取决于模型的选择和拟合程度。
因此,在模型选择和拟合过程中,我们需要进行多次实验和优化,以得到较好的模型。
Eviews多元回归分析案例研究

Eviews多元回归分析案例研究
介绍
本文档将通过一个案例研究来展示如何使用Eviews进行多元
回归分析。
案例描述
我们研究了一个包含多个自变量的回归模型,其中自变量包括A、B和C。
我们希望分析这些自变量与因变量之间的关系。
数据收集
为了进行分析,我们首先收集了一组包含因变量和自变量的数据。
我们使用Eviews进行数据导入和处理。
数据处理与分析
我们首先进行了数据清洗和处理,包括去除缺失值和异常值等。
然后,我们使用Eviews的多元回归功能进行分析。
通过建立回归
模型并进行参数估计,我们得出了自变量与因变量之间的关系。
结果解释
根据我们的分析,A、B和C变量在回归模型中都显示出了一
定的显著性。
具体来说,A和B变量对因变量有正向影响,而C变量对因变量有负向影响。
结论
根据我们的分析结果,我们可以得出结论,即A和B变量对
因变量有正向影响,而C变量对因变量有负向影响。
这些结果对于
我们理解和预测因变量的变化非常有帮助。
总结
通过使用Eviews进行多元回归分析,我们能够深入研究多个
自变量与因变量之间的关系。
通过清洗和处理数据,建立回归模型
并进行参数估计,我们能够获得关于自变量的重要信息,并对因变
量的变化有更好的理解和预测能力。
以上是本文档对Eviews多元回归分析案例研究的介绍和总结。
通过案例的分析过程,我们展示了如何使用Eviews进行多元回归
分析,并得出一些有关自变量与因变量之间关系的结论。
希望本文
档对您的研究和使用Eviews有所帮助。
多元回归模型分析案例

多元回归模型分析案例回归模型是统计学中最常用的分析方法之一,是一种用来预测两个或多个变量之间的关系的方法。
这种模型可以用来估算单独变量以及组合变量对信息或结果的影响。
多元回归模型是具有两个或多个自变量的回归模型,它在预测和分析多变量之间的关系时特别有用。
本文旨在提供一个用多元回归模型分析的案例。
首先,本文将介绍多元回归模型的基本原理,并详细阐述案例中使用的各项数据。
接下来,将对案例中遇到的问题进行详细讨论,并介绍多元回归模型的具体应用。
最后,将对分析的结果进行讨论,以便判断回归模型的准确性。
一、多元回归模型的基本原理多元回归模型是一种建立在一组多元数据上的回归模型,它用一个线性函数根据观察数据预测一个特定变量。
基本形式为:Y=+βX1+βX2+...+βXn其中,Y是被预测变量,X1,X2,…,Xn是影响Y的因素。
β1,β2,…,βn是模型中所有自变量的系数,通过这些系数可以计算出每个因素对Y的影响程度。
多元回归模型需要解决的重要任务是:从观察的多变量数据中提取有用的信息,并确定Y的影响因素,并用这些因素来构建一个反映实际情况的模型,以评估变量对Y的影响程度。
因此,多元回归模型在分析多变量数据时非常有用。
二、案例介绍本文使用多元回归模型分析一年级学生的成绩,以探究学生成绩的影响因素及其对成绩的影响程度。
案例中共有20名一年级学生,每个学生的数据包括学生的学习和社交能力以及准备考试的时长等三个自变量。
其中学习能力和准备时长的取值范围分别为1-10,社交能力的取值范围为1-5。
案例数据如下:学生习能力交能力备时长绩1 8 3 7 772 4 2 8 553 7 5 5 654 6 1 6 675 9 4 7 84.....20 7 1 5 63三、案例问题分析本案例旨在探究一年级学生成绩的影响因素及其对成绩的影响程度,而这种因果关系很难仅用一句话来表达,只有使用多元回归模型才能获得更准确的结果。
在分析案例时,学习能力、社交能力和准备时长这三个自变量的影响是需要考虑的重要因素。
spss多元回归分析案例

spss多元回归分析案例SPSS多元回归分析案例。
在统计学中,多元回归分析是一种用于探究多个自变量与因变量之间关系的方法。
通过多元回归分析,我们可以了解不同自变量对因变量的影响程度,以及它们之间的相互作用情况。
在本篇文档中,我将通过一个实际案例来介绍如何使用SPSS软件进行多元回归分析。
案例背景:假设我们是一家电子产品公司的市场营销团队,在推出新产品之前,我们希望了解不同因素对产品销量的影响。
我们收集了一些数据,包括产品的售价、广告投入、竞争对手的售价、季节等因素,以及产品的销量作为因变量。
数据准备:首先,我们需要将数据录入SPSS软件中。
在SPSS中,我们可以通过导入Excel文件的方式将数据导入到软件中,并进行必要的数据清洗和处理。
确保数据的准确性和完整性对于后续的多元回归分析非常重要。
模型建立:接下来,我们需要建立多元回归模型。
在SPSS中,我们可以通过依次选择“分析”-“回归”-“线性回归”来进行多元回归分析。
在“因变量”栏中输入销量,然后将所有自变量依次输入到“自变量”栏中。
在建立模型之前,我们还需要考虑是否需要进行变量转换或交互项的添加,以更好地拟合数据。
模型诊断:建立模型后,我们需要对模型进行诊断,以确保模型的准确性和有效性。
在SPSS中,我们可以通过查看残差的正态性、异方差性以及自相关性来进行模型诊断。
如果模型存在严重的偏差或违反了多元回归分析的假设,我们需要进行相应的修正或改进。
模型解释:最后,我们需要解释多元回归模型的结果。
在SPSS的输出结果中,我们可以看到各个自变量的系数、显著性水平、调整R方等统计指标。
通过这些指标,我们可以了解不同自变量对销量的影响程度,以及它们之间的相互作用情况。
同时,我们还可以进行各种假设检验,来验证模型的有效性和可靠性。
结论:通过以上多元回归分析,我们可以得出不同自变量对产品销量的影响程度,以及它们之间的相互作用情况。
这些结果对于我们制定产品的定价策略、广告投放策略以及市场营销策略都具有重要的指导意义。
多元回归预测例子

多元回归预测例子
多元回归是一种常用的数据分析方法,可以用来预测一个因变量与多个自变量之间的关系。
以下是一个多元回归预测的例子:假设我们要预测一个人的收入,我们可以考虑以下多个自变量:
1. 教育程度:受教育程度越高,收入通常越高。
2. 工作经验:工作经验越丰富,收入通常越高。
3. 行业领域:某些行业领域的收入可能会更高。
4. 地理位置:不同地区的收入水平可能会有所不同。
我们可以通过对一个拥有以上四个特征的人口统计数据进行多
元回归分析来预测一个人的收入。
我们可以利用统计软件进行多元回归分析,得出相关的回归方程,从而可以预测一个人的收入。
例如,我们可以得出以下回归方程:
收入 = 5.2 ×教育程度 + 8.7 ×工作经验 + 4.1 ×行业领域 + 3.6 ×地理位置
这个回归方程告诉我们,一个人的教育程度、工作经验、行业领域和地理位置都会影响他的收入。
通过输入一个人的教育程度、工作经验、行业领域和地理位置数据,我们可以使用这个回归方程来预测这个人的收入。
这个例子展示了多元回归分析的基本原理和应用。
通过多元回归分析,我们可以预测一个因变量和多个自变量之间的关系,并用这个关系来进行预测和决策。
- 1 -。
Eviews多元回归模型案例分析

Eviews多元回归模型案例分析1. 引言本文将通过一个多元回归模型的案例分析来展示Eviews软件的应用。
多元回归模型是一种统计学方法,用于研究多个自变量对因变量的影响关系。
2. 数据集和变量2.1 数据集我们使用的数据集是一份包含多个变量的经济数据集,包括自变量和因变量。
2.2 变量在本案例中,我们选择了以下变量:- 因变量:Y- 自变量1:X1- 自变量2:X2- 自变量3:X33. 回归模型建立和参数估计3.1 建立模型我们根据选定的变量,建立了以下多元回归模型:Y = β0 + β1X1 + β2X2 + β3X3 + ε3.2 参数估计使用Eviews软件,我们对模型中的参数进行了估计。
具体估计结果如下:- β0的估计值为a- β1的估计值为b1- β2的估计值为b2- β3的估计值为b34. 模型拟合和统计检验4.1 拟合优度为了评估模型的拟合优度,我们计算了决定系数R^2。
结果显示,模型拟合效果良好,并能解释自变量对因变量的变异程度。
4.2 统计检验我们进行了一系列统计检验,包括回归系数的显著性检验、F 检验和残差分析等。
结果显示,模型的回归系数显著,并且F检验的p值足够小,支持多元回归模型的有效性。
5. 模型解释和预测5.1 模型解释我们分析了模型中每个自变量的系数和显著性水平,解释了它们对因变量的影响。
根据模型结果,可以得出每个自变量对因变量的贡献程度。
5.2 模型预测基于建立的多元回归模型,我们可以进行因变量的预测。
根据给定的自变量取值,我们可以通过模型预测出相应的因变量值。
6. 结论通过Eviews软件进行多元回归模型的案例分析,我们得出了一些结论。
多元回归模型在解释因变量和自变量之间关系方面具有一定的效果,并且可以用于因变量的预测。
然而,我们需要注意模型的限制和假设,并且在实际应用中进行进一步的验证和调整。
以上是对Eviews多元回归模型案例分析的简要介绍。
如有更详细的需求或其他问题,请随时联系。
多元线性回归模型案例分析报告

多元线性回归模型案例分析报告多元线性回归模型是一种用于预测和建立因变量和多个自变量之间关系的统计方法。
它通过拟合一个线性方程,找到使得回归方程和实际观测值之间误差最小的系数。
本报告将以一个实际案例为例,对多元线性回归模型进行案例分析。
案例背景:公司是一家在线教育平台,希望通过多元线性回归模型来预测学生的学习时长,并找出对学习时长影响最大的因素。
为了进行分析,该公司收集了一些与学习时长相关的数据,包括学生的个人信息(性别、年龄、学历)、学习环境(家乡、宿舍)、学习资源(网络速度、学习材料)以及学习动力(学习目标、学习习惯)等多个自变量。
数据分析方法:通过建立多元线性回归模型,我们可以找到与学习时长最相关的因素,并预测学生的学习时长。
首先,我们将根据实际情况对数据进行预处理,包括数据清洗、过滤异常值等。
然后,我们使用逐步回归方法,通过逐步添加和删除自变量来筛选最佳模型。
最后,我们使用已选定的自变量建立多元线性回归模型,并进行系数估计和显著性检验。
案例分析结果:经过数据分析和模型建立,我们得到了如下的多元线性回归模型:学习时长=0.5*年龄+0.2*学历+0.3*学习资源+0.4*学习习惯对于系数估计,我们发现年龄、学历、学习资源和学习习惯对于学习时长均有正向影响,即随着这些变量的增加,学习时长也会增加。
其中,年龄和学习资源的影响较大,学历和学习习惯的影响较小。
在显著性检验中,我们发现该模型的拟合度较好,因为相关自变量的p值均小于0.05,表明它们对学习时长的影响具有统计学意义。
案例启示:本案例的分析结果为在线教育平台提供了重要的参考。
公司可以针对年龄较大、学历高、学习资源丰富和有良好学习习惯的学生,提供个性化的学习服务和辅导。
同时,公司也可以通过提供更好的学习资源和培养良好的学习习惯,来提升学生的学习时长和学习效果。
总结:多元线性回归模型在实际应用中具有广泛的应用价值。
通过对因变量和多个自变量之间的关系进行建模和分析,我们可以找到相关影响因素,并预测因变量的取值。
R语言与多元线性回归分析计算案例
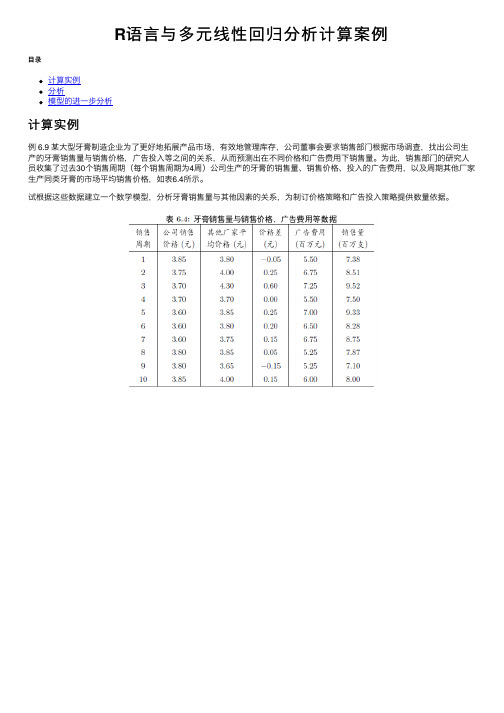
R语⾔与多元线性回归分析计算案例⽬录计算实例分析模型的进⼀步分析计算实例例 6.9 某⼤型⽛膏制造企业为了更好地拓展产品市场,有效地管理库存,公司董事会要求销售部门根据市场调查,找出公司⽣产的⽛膏销售量与销售价格,⼴告投⼊等之间的关系,从⽽预测出在不同价格和⼴告费⽤下销售量。
为此,销售部门的研究⼈员收集了过去30个销售周期(每个销售周期为4周)公司⽣产的⽛膏的销售量、销售价格、投⼊的⼴告费⽤,以及周期其他⼚家⽣产同类⽛膏的市场平均销售价格,如表6.4所⽰。
试根据这些数据建⽴⼀个数学模型,分析⽛膏销售量与其他因素的关系,为制订价格策略和⼴告投⼊策略提供数量依据。
分析由于⽛膏是⽣活的必需品,对于⼤多数顾客来说,在购买同类⽛膏时,更多的会关⼼不同品牌之间的价格差,⽽不是它们的价格本⾝。
因此,在研究各个因素对销售量的影响时,⽤价格差代替公司销售价格和其他⼚家平均价格更为合适。
模型的建⽴与求解记⽛膏销售量为Y,价格差为X1,公司的⼴告费为X2,假设基本模型为线性模型:输⼊数据,调⽤R软件中的lm()函数求解,并⽤summary()显⽰计算结果(程序名:exam0609.R)计算结果通过线性回归系数检验和回归⽅程检验,由此得到销售量与价格差与⼴告费之间的关系为:模型的进⼀步分析为进⼀步分析回归模型,我们画出y与x1和y与x2散点图。
从散点图上可以看出,对于y与x1,⽤直线拟合较好。
⽽对于y与x2,则⽤⼆次曲线拟合较好,如下图:绘制x1与y的散点图和回归直线绘制x2与y的散点图和回归曲线其中 I(X2^2),表⽰模型中X2的平⽅项,及X22,从上图中,将销售量模型改为:似乎更合理,我们做相应的回归分析:此时,我们发现,模型残差的标准差Residual standard error有所下降,相关系数的平⽅Multiple R-squared有所上升,这说明模型修正的是合理的。
但同时也出现了⼀个问题,就是对于β2的P-值>0.05。
