高中历次成绩折线图
高中数学课下能力提升十一频率分布表频率分布直方图与折线图苏教版必修30

课下能力提升(十一) 频率分布表频率分布直方图与折线图一、填空题1.如图是容量为100的样本的频率分布直方图,试根据图形中的数据填空.(1)样本数据在范围[6,10)内的频率为________;(2)样本数据落在范围[10,14)内的频数为________.2.为了调查某厂工人生产某种产品的能力,随机抽查了20名工人某天生产该产品的数量,产品数量的分组区间为[45,55),[55,65),[65,75),[75,85),[85,95],由此得到频率分布直方图如下图,则这20名工人中一天生产该产品数量在[55,75)的人数是________.3.将容量为100的样本数据,按从小到大的顺序分成8个组,如下表:4.为提高公众对健康的自我管理能力和科学认识,某调查机构共调查了200人在一天中的睡眠时间.现将数据整理分组,如下表所示.由于操作不慎,表中A,B,C,D四处数据污损,统计员只记得A处的数据比C处的数据大4,由此可知B处的数据为________.5.图(如图),但是年龄组为[25,30)的数据不慎丢失,则依据此图可得:(1)[25,30)年龄组对应小矩形的高度为________;(2)据此估计该市“四城同创”活动中志愿者年龄在[25,35)的人数为________.二、解答题6.某工厂对一批产品进行了抽样检测,右图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范围是[96,106],样本数据分组为[96,98),[98,100),[100,102),[102,104),[104,106).已知样本中产品净重小于100克的个数是36,则样本中净重大于或等于98克并且小于104克的产品的个数是多少?7.根据空气质量指数API(为整数)的不同,可将空气质量分级如下表:对某城市一年(365天)的空气质量进行监测,获得的API数据按照区间[0,50],(50,100],(100,150],(150,200],(200,250],(250,300]进行分组,得到频率分布直方图如图.(1)求频率分布直方图中x的值;(2)计算一年中空气质量为良和轻微污染的总天数.(提示:结果用分数表示.已知57=78 125,27=128,31 825+2365+71 825+31 825+89 125=1239 125,365=73×5)8.为了了解一个小水库中养殖的鱼的有关情况,从这个水库中多个不同位置捕捞出100条鱼,称得每条鱼的质量(单位:千克),并将所得数据分组,画出频率分布直方图(如图所示).(1)求出各组相应的频率;(2)估计数据落在[1.15,1.30]中的概率为多少;(3)将上面捕捞的100条鱼分别作一记号后再放回水库,几天后再从水库的多处不同位置捕捞出120条鱼,其中还有记号的鱼有6条,请根据这一情况来估计该水库中鱼的总条数.答案1.解析:(1)样本数据在[6,10)内频率为0.08×4=0.32. (2)在[10,14)内的频数为0.09×4×100=36. 答案:(1)0.32 (2)362.解析:由题意得,这20名工人中一天生产该产品数量在[55,75)的人数是20×[(0.040+0.025)×10]=13(人).答案:133.解析:9+14+14+13+12+x +13+10=100,x =15.P =15100=0.15.答案:0.154.解析:设A 处的数据为x ,则C 处的数据为x -4, 则x +x -4+8+52+20+4=200,x =60, 则B 处数据为60200=0.3.答案:0.35.解析:设[25,30)年龄组对应小矩形的高度为h ,则5×(0.01+h +0.07+0.06+0.02)=1,h =0.04.志愿者年龄在[25,35)的频率为5×(0.04+0.07)=0.55,故志愿者年龄在[25,35)的人数约为0.55×800=440.答案:0.04 4406.解:产品净重小于100克的频率为(0.050+0.100)×2=0.300,已知样本中产品净重小于100克的个数是36,设样本容量为n ,则36n=0.300,所以n =120,净重大于或等于98克并且小于104克的产品的频率为(0.100+0.150+0.125)×2=0.750,所以样本中净重大于或等于98克并且小于104克的产品的个数是120×0.750=90.7.解:(1)由图可知50x =1-(31 825+2365+71 825+31 825+89 125)×50=1-1239 125×50,解得x =11918 250;(2)365×(11918 250×50+2365×50)=219.答:一年中空气质量为良和轻微污染的总天数为219天. 8.解:(1)由频率分布直方图和频率=组距×(频率组距)可得下表(2)0.30+0.15+0.02=0.47,所以数据落在[1.15,1.30]中的概率约为0.47.(3)由分层抽样中每个个体被抽到的概率相同知:设水库中鱼的总条数为N,则120 N=6100,即N=2 000,故水库中鱼的总条数约为2 000条.。
高中数学 频率分布表频率分布直方图与折线图课件 苏教版必修3推荐

【变式1】 一个容量为20的样本,已知某组的频率为0.25,
则该组的频数为________.
x 解析 设频数为 x,则 =0.25,∴x=0.25×20=5. 20
答案 5
题型二 画频率分布直方图 【例2】 一个农技站为了考察某种大麦穗生长的分布情况,
在一块试验田里抽取了100株麦穗,量得长度(单位:cm)如下:
频率 提示 小长方形面积=组距× =频率. 组距
2.将样本的数据进行分组的目的是什么? 提示 通过分组,并计算其频率,目的是通过描述样本数据 分布的特征,从而估计总体的分布情况.
名师点睛 1.频率分布表 (1)当总体很大或不便于获得时,可以用样本的频率分布估计 总体的频率分布,我们把反映总体频率分布的表格称为频率分布 表. (2)频率分布表的制作 编制频率分布表可以按下列步骤进行: 第一步:计算数据中最大值与最小值的差,即全距.据此, 全距 决定组数和组距,组距= .要根据数据的多少来确定分组的数 组数 目. 一般来说, 数据越多, 组数越多. 如果取全距时不利于分组(如 不能被组数整除),可适当增大全距,如在左、右两端各增加适当 范围(尽量使两端增加的量相同).
5.6 6.2 6.1 5.3 6.2 6.8 6.6 4.7 5.7 5.7
5.8 5.3 7.0 6.0 6.0 5.9 5.4 6.0 5.2 6.0 6.3 5.7 6.8 6.1 4.5 5.6 6.3 6.0 5.8 6.3
根据上面的数据列出频率分布表、绘制出频率分布直方
图,并估计长度在 5.75~6.05 cm之间的麦穗在这批麦穗中所占
6.5 6.4 6.7 5.8 5.9 5.9 5.2 4.0 5.4 4.6 5.8 5.5 6.0 6.5 5.1 6.5 5.3 5.9 5.5 5.8 6.2 5.4 5.0 5.0 6.8 6.0 5.0 5.7 6.0 5.5 6.8 6.0 6.3 5.5 5.0 6.3 5.2 6.0 7.0 6.4 6.4 5.8 5.9 5.7 6.8 6.6 6.0 6.4 5.7 7.4 6.0 5.4 6.5 6.0 6.8 5.8 6.3 6.0 6.3 5.6 5.3 6.4 5.7 6.7 6.2 5.6 6.0 6.7 6.7 6.0
高二数学频率分布直方图和折线图正式版

高二数学频率分布直方图和折线图正式版文档资料可直接使用,可编辑,欢迎下载第20课时频率分布直方图和折线图【学习导航】知识网络学习要求1.频率分布直方图的作法,频率分布直方图更加直观形象地反映出总体分布的情况; 2.频率分布折线图的作法,优点是反映了数据的变化趋势,如果样本容量足够大,分组的组距足够小,则这条折线将趋于一条曲线,称为总体分布的密度曲线。
【课堂互动】自学评价案例1 下表是某学校一个星期中收交来的失物件数,请将5天中收交来的失物数用条形图(1)在EXCEL 工作表中输入数据,光标停留在数据区中; (2)选择“插入/图表”,在弹出的对话框中点击“柱形图”;(3)点击“完成”,即可看到如下频数条形图.案例2 从某校高一年级的1002名新生中用系统抽样的方法抽取一个容量为100的身高样本,数据如下(单位:cm 。
试作出该样本的频率分布直方图和折线图. 【解】上一课时中, 已经制作好频率分布表,在此基础上, 我们绘制频率分布直方图. (1)作直角坐标系,以横轴表示身高,纵轴表示组距频率;(2)在横轴上标上150.5,153.5,156.5, …,180.5表示的点。
(为方便起见,起始点150.5可适当前移);(3)在上面标出的各点中,分别以连结相邻两点的线段为底作矩形,高等于该组的组距频率至此,就得到了这组数据的频率分布直方图,如下图频率同样可以得到这组数据的折线图. 频率150.5 153.5 156.5 159.5 162.5 165.5 168.5 171.5 174.5 177.5 180.8 【小结】1.利用直方图反映样本的频率分布规律, 这样的直方图称为频率分布直方图(frequencyhistogram, 简称频率直方图。
2. 频率直方图比频率分布表更直观、形象地反映了样本的分布规律。
3.如果将频率分布直方图中相邻的矩形的上底边的中点顺次连结起来,就得到一条折线,我们称这条折线为本组数据的频率折线图(frequency polygon4.频率分布折线图的的首、尾两端如何处理: 取值区间两端点须分别向外延伸半个组距,并取此组距上的x 轴上的点与折线的首、尾分别相连5.如果将样本容量取得足够大,分组的组距取得足够小,则这条折线趋于一条曲线,这一曲线称为总体分布的密度曲线。
高中数学频率分布直方图

频率分布直方图作频率分布直方图的方法为:(1)把横轴分成若干段,每一线段对应一个组的组距;(2)以此线段为底作矩形,它的高等于该组的组距频率,这样得出一系列的矩形;(3)每个矩形的面积恰好是该组上的频率.频率折线图:如果将频率分布直方图中各相邻的矩形的上底边的中点顺次连接起,就得到一条折线,称这条折线为本组数据的频率折线图.作茎叶图的方法是:将所有两位数的十位数字作为“茎”,个位数字作为“叶”,茎相同者共用一个茎,茎按从小到大的顺序从上向下列出,共茎的叶一般按从大到小(或从小到大)的顺序同行列出.知识点1:利用频率分布直方图分析总体分布例题1: 2000辆汽车通过某一段公路时的时速的频率分布直方图如右图所示,时速在[50,60)的汽车大约有 A .30辆 B .60辆 C .300辆 D .600辆变式:某工厂对一批产品进行了抽样检测.右图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范围是 [96,106],样本数据分组为[96,98),[98,100),[100,102),[102,104),[104,106],已知样本中产品净重小于100克的个数是36,则样本中净重大于或等于98克并且小于104克的产品的个数是A.90B.75C. 60D.45变式:某初一年级有500名同学,将他们的身高(单位:cm )数据绘制成频率分布直方图(如图),若要从身高在[)120,130,[)130,140,[]140,150三组内的学生中,用分层抽样的方法选取30人参加一项活动,则从身高在[)130,140内的学生中选取的人数为 .知识点2:用样本分估计总体例题2某市2010年4月1日—4月30日对空气污染指数的监测数据如下(主要污染物为可吸入颗粒物):61,76,70,56,81,91,92,91,75,81,88,67,101,103,95,91,77,86,81,83,82,82,64,79,86,85,75,71,49,45,96 98 100 102 104 106 0.1500.125 0.1000.0750.050 克 频率/组距100 110 120130 140 150 身高频率|组距0.0050.0100.020a0.035(Ⅰ) 完成频率分布表;(Ⅱ)作出频率分布直方图;(Ⅲ)根据国家标准,污染指数在0~50之间时,空气质量为优:在51~100之间时,为良;在101~150之间时,为轻微污染;在151~200之间时,为轻度污染。
高中三年各学年学期成绩单
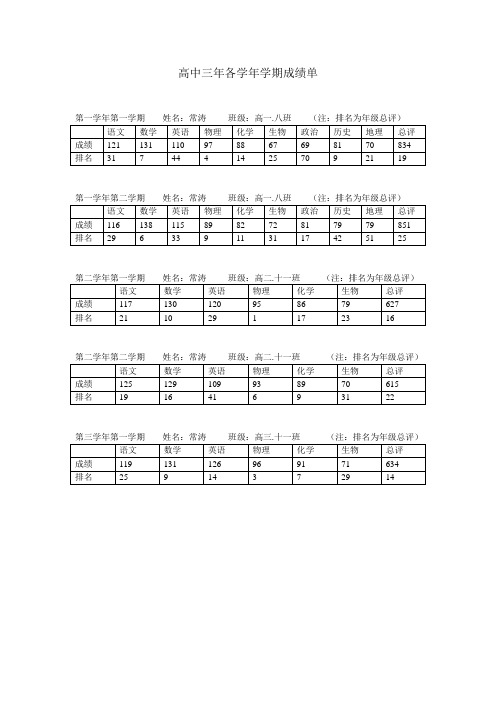
第一学年第一学期姓名:常涛班级:高一.八班(注:排名为年级总评)
语文
数学
英语
物理
化学
生物
政治
历史
地理
总评
成绩
121
1பைடு நூலகம்1
110
97
88
67
69
81
70
834
排名
31
7
44
4
14
25
70
9
21
19
第一学年第二学期姓名:常涛班级:高一.八班(注:排名为年级总评)
语文
数学
英语
物理
化学
语文
数学
英语
物理
化学
生物
总评
成绩
125
129
109
93
89
70
615
排名
19
16
41
6
9
31
22
第三学年第一学期姓名:常涛班级:高三.十一班(注:排名为年级总评)
语文
数学
英语
物理
化学
生物
总评
成绩
119
131
126
96
91
71
634
排名
25
9
14
3
7
29
14
生物
政治
历史
地理
总评
成绩
116
138
115
89
82
72
81
79
79
851
排名
29
6
33
9
11
31
17
42
高中数学第二章统计2.2.2频率分布直方图与折线图二2.2.3茎叶图学案苏教版必修

2.2.2 频率分布直方图与折线图(二) 2.2.3 茎叶图学习目标 1.了解频率折线图和总体密度曲线的定义;2.理解茎叶图的概念,会画茎叶图;3.了解频率分布直方图、频率折线图、茎叶图的各自特征,学会选择不同的方法分析样本的分布,从而作出总体估计.知识点一频率分布折线图和总体密度曲线1.频率分布折线图将频率分布直方图中各个相邻的矩形的______________顺次连结起来,就得到频率分布折线图,简称频率折线图.2.总体密度曲线随着样本容量的增加,作图时所分的________增加,组距减小,相应的频率折线图会越来越接近于一条____________,统计中称这条光滑曲线为总体分布的密度曲线.知识点二茎叶图思考茎叶图是表示样本数据分布情况的一种方法,那么“茎”、“叶”分别指的是哪些数?梳理茎叶图的定义:当数据是两位有效数字时,用中间的数字表示十位数,即第一个有效数字,两边的数字表示个位数,即第二个有效数字,它的中间部分像植物的茎,两边部分像植物茎上长出来的叶子,因此通常把这样的图叫做茎叶图.适用范围:当样本数据较少时,用茎叶图表示数据的效果较好.优点:它不但可以________________,而且可以______________,给数据的记录和表示都带来方便.缺点:当样本数据________时,枝叶就会很长,茎叶图就显得不太方便.类型一频率分布折线图的画法例1 太极拳运动是一项练意、练气、练身三者相结合的运动,它的动作缓慢,柔和自然,心静体松,调和气血,疏通经络,平衡阴阳等特点符合中老年人的运动要求,被大多数中老年人所喜爱.下面是某中老年活动中心选择太极拳项目的人的年龄.57,61,57,57,58,57,61,54,68,51,49,64,50,48,65,52,56,46,54,49,51,47,55,55,54,42,51,56,55,51,54,51,60,62,43,55,56,61,52,69,64,46,54,48(1)将数据进行适当的分组,并画出相应的频率分布直方图和频率分布折线图;(2)用自己的语言描述一下此中老年活动中心选择太极拳项目的人年龄的分布情况.反思与感悟作折线图可以依据直方图,也可以由频率分布表找出折线上各个转折点的坐标从而作出折线图.跟踪训练1 已知50个数据的分组以及各组的频数如下:[153.5,155.5),2,[155.5,157.5),7,[157.5,159.5),9,[159.5,161.5),11,[161.5,163.5),10,[163.5,165.5),6,[165.5,167.5),4,[167.5,169.5],1.试画出频率分布直方图和频率分布折线图.类型二茎叶图的画法及应用例2 某中学甲、乙两名同学最近几次的数学考试成绩情况如下:甲的得分:95,81,75,89,71,65,76,86,91,88,94,110,107;乙的得分:83,86,93,99,88,103,98,114,98,79,88,110,101.画出两人数学成绩的茎叶图,并根据茎叶图对两人的成绩进行比较.反思与感悟茎叶图和频率分布表极为类似,事实上,茎相当于频率分布表中的分组;茎上叶的数目相当于频率分布表中指定区间组的频数.跟踪训练2 某赛季甲、乙两名篮球运动员每场比赛的得分情况如下:甲运动员得分:13,51,23,8,26,38,16,33,14,28,39;乙运动员得分:49,24,12,31,50,31,44,36,15,37,25,36,39.试制作茎叶图来对比描述这些数据.类型三频数(率)分布直方图与茎叶图的比较例3 从甲、乙两个城市所有的自动售货机中随机抽取16台,记录了上午8:00~11:00之间各自的销售情况(单位:元):甲:18,8,10,43,5,30,10,22,6,27,25,58,14,18,30,41;乙:22,31,32,42,20,27,48,23,38,43,12,34,18,10,34,23.试用纵坐标为频数的频数分布直方图与茎叶图的方式分别表示上面的数据,并简要说明各自的优点.反思与感悟茎叶图由所有样本数据构成,没有损失任何样本信息,可以在抽样的过程中随时记录,但样本容量较大,或者需要比较三组以上的数据时,使用茎叶图就不合适;而频率分布表和频率分布直方图可以处理样本容量很大的数据,但损失了样本的原始数据,而且必须在完成抽样后才能制作.跟踪训练3 试比较例3中用到的频数分布直方图和频率分布直方图的区别.1.如图是总体密度曲线,下列说法正确的是________.①组距越大,频率分布折线图越接近于它;②样本容量越小,频率分布折线图越接近于它;③阴影部分的面积代表总体在(a,b)内取值的百分比;④阴影部分的平均高度代表总体在(a,b)内取值的百分比.2.某校为了了解学生的课外阅读情况,随机调查了50名学生,得到他们各自在某一天课外阅读所用时间的数据,结果用下面的条形图表示.根据条形图可得这50名学生平均每天的课外阅读时间为________小时.3.已知某工厂工人在6月份每天加工的零件个数的茎叶图如图所示(以零件个数的百位、十位数字为茎,个位数字为叶),那么该工厂工人在该月内加工的零件个数超过130的天数所占的百分比为________.4.某校举行演讲比赛,9位评委给选手A打出的分数如茎叶图所示,统计员在去掉一个最高分和一个最低分后,算得平均分为91,复核员在复核时,发现有一个数字(茎叶图中的x)无法看清,若统计员计算无误,则数字x应该是________.1.估计总体的分布分两种情况:当总体中的个体取值很少时,用茎叶图估计总体的分布;当总体中的个体取值较多时,将样本数据恰当分组,用各组的频率分布描述总体的分布,方法是用频率分布表或频率分布直方图.2.茎叶图、频率分布表和频率分布直方图都是用来描述样本数据的分布情况的.茎叶图由所有样本数据构成,没有损失任何样本信息,可以在抽样的过程中随时记录;而频率分布表和频率分布直方图则损失了样本的原始信息,必须在完成抽样后才能制作.3.正确利用三种分布的描述方法,都能得到一些有关分布的主要特点(如分布是否具有单峰性、是否具有对称性、样本点落在各分组中的频率等),这些主要特点受样本的随机性的影响比较小,更接近于总体分布相应的特点.答案精析问题导学知识点一1.上底边的中点2.组数光滑曲线知识点二思考茎是指中间的一列数,叶就是从茎的旁边生长出来的数.梳理保留所有信息随时记录较多题型探究例1 解(1)以4为组距,列表如下:频率分布直方图及频率分布折线图如图所示:(2)从频率分布表可以看出,将近60%的选择太极拳的中老年人的年龄在50岁至60岁之间,45岁以下及65岁以上中老年人所占的比例相对较小.跟踪训练1 解频率分布直方图和频率分布折线图如图所示.例2 解甲、乙两人数学成绩的茎叶图如图所示.从这个茎叶图中可以看出,乙同学的得分情况大致是对称的,中位数是98分;甲同学的得分情况除一个特殊得分外,也大致对称,中位数是88分,但分数分布相对于乙来说,趋向于低分阶段.因此乙同学发挥比较稳定,总体得分情况比甲同学好.跟踪训练2 解以十位数字为茎,个位数字为叶,制作茎叶图如下:例3 解方法一用频数分布直方图表示如图.方法二茎叶图如图,两竖线中间的数字表示甲、乙销售额的十位数,两边的数字表示甲、乙销售额的个位数.从方法一可以看出频数分布直方图能直观地反映数据分布的大致情况,并且能够清晰地表示出各个区间的具体数目;从方法二可以看出,用茎叶图表示有关数据对数据的记录和表示都带来方便.跟踪训练3 解首先频数分布直方图的纵坐标为频数,因此其顶点纵坐标是非负整数.频率分布直方图的纵坐标为频率/组距,因此其每个组段的频率就是对应小矩形的面积,且总面积为1.当样本量n增大并且组距越来越小时,相应的小矩形越来越细,其各小矩形上端的中点的连线构成了一条光滑曲线,而这条光滑曲线下的面积为1,这条光滑曲线称为总体分布的密度曲线.当堂训练1.③2.0.9解析由题意可知,50名学生平均每天的课外阅读时间为150×(0.5×20+1.0×10+1.5×10+2.0×5)=0.9(小时).3.10%4.2解析去掉最低分87,去掉最高分94(假设x≤4),则7×91=80×2+9+8+90×5+2+3+2+1+x,所以x=2,符合题意.同理可验证x>4不合题意.。
高中数学必修2《统计》知识点讲义
高中数学必修2《统计》知识点讲义一、引言高中数学必修2中的《统计》部分是我们在日常生活中应用广泛的数学知识。
通过学习统计,我们可以更好地理解世界,做出更明智的决策。
本篇文章将详细讲解统计部分的重要知识点。
二、知识点概述1、描述性统计描述性统计是统计学的基石,它主要研究如何用图表和数值来描述数据的基本特征。
这部分内容将介绍如何制作频数分布表、绘制条形图、饼图和折线图等。
2、概率论基础概率论是统计学的核心,它研究随机事件发生的可能性。
在本部分,我们将学习如何计算事件的概率,了解独立事件与互斥事件的概念。
3、分布论基础分布论是研究随机变量及其分布的数学分支。
本部分将介绍如何计算随机变量的期望和方差,了解正态分布的特点及其在日常生活中的应用。
三、知识点详解1、描述性统计本文1)频数分布表:频数分布表是一种用于表示数据分布情况的表格,其中每一列表示数据的一个取值,每一行表示该取值的频数。
通过频数分布表,我们可以直观地看到数据分布的集中趋势和离散程度。
本文2)图表:图表是描述数据的一种有效方式。
通过绘制条形图、饼图和折线图,我们可以直观地展示数据的数量关系和变化趋势。
2、概率论基础本文1)概率:概率是指事件发生的可能性,通常用P表示。
P(A)表示事件A发生的概率,其值在0和1之间,其中0表示事件不可能发生,1表示事件一定会发生。
本文2)独立事件与互斥事件:独立事件是指两个事件不相互影响,即一个事件的发生不影响另一个事件的概率;互斥事件是指两个事件不包括共同的事件,即两个事件不可能同时发生。
3、分布论基础本文1)期望:期望是随机变量的平均值,通常用E表示。
E(X)表示随机变量X的期望,它是所有可能取值的概率加权平均值。
期望对于预测随机变量的行为非常有用。
本文2)方差:方差是衡量随机变量取值分散程度的指标,通常用D表示。
D(X)表示随机变量X的方差,它是每个取值与期望之差的平方的平均值。
方差越大,随机变量的取值越分散;方差越小,取值越集中。
人教B版高中同步学案数学必修第二册精品课件 第5章 统计与概率 本章总结提升
10
=
+(98-94)2+(102-94)2+(114-94)2]=96.8.所以 s 乙≈9.8.
(2)由(1)知甲 < 乙 ,s 甲>s 乙.
所以乙同学的平均成绩较高且标准差较小,
说明乙同学比甲同学的成绩扎实,稳定.
规律方法
数字特征的应用
样本的数字特征可分为两大类:一类反映样本数据的集中趋势,包括平均数、
2.掌握相互独立事件的概率,提升逻辑推理和数学运算素养.
1 1
【例4】 甲、乙两人破译一密码,他们能破译的概率分别为 3和 4.求:
(1)两人都能破译的概率;
(2)两人都不能破译的概率;
(3)恰有一人能破译的概率;
(4)至多有一人能够破译的概率.
解 设“甲能破译”为事件 A,“乙能破译”为事件 B,则 A,B 相互独立,从而 A 与
则 C=A + B,且 A 与 B 相互独立,A与B 互斥.
又 P(A)=0.7,P(B)=0.6,
所以 P(C)=P(A)+P(B)=0.7×0.4+0.3×0.6=0.46,所以在一轮游戏中,2 人共
投进 1 球的概率为 0.46.
(2)记“在两轮游戏中,2 人共投进 1 球”为事件 D,则 D=C + C,C与
本点.由于每一件产品被取到的机会均等,因此可以确定这些基本事件的出
现是等可能的.用B表示“取出的两件产品中恰有一件次品”,则
4
B={(a1,b),(a2,b),(b,a1),(b,a2)},共包含4个样本点.所以P(B)= 9 .
规律方法
古典概型的应用
古典概型是一种最基本的概率模型,也是学习其他概率模型的基础,在高考
高中数学频率分布折线图与茎叶图课件苏教版必修
乙
0
1
2
25
3
54
4
1 6 1 6 79
5
49
50
甲运动员得分:13,51,23,8,26,38,16,33,14,28,39;
乙运动员得分:49,24,12,31,50,31,44,36,15,37,25,36,
39.
甲
乙
8
0
463 368 389
1
1
2
25
3
54
4
1 6 1 6 79
5
49
50
01 8 23 0 5 4 057
115
3
思考4:一般地,画出一组样本数据的茎叶图的步骤如何?
第一步,将每个数据分为“茎”(高位)和“叶”(低位)两部分; 第二步,将最小的茎和最大的茎之间的数按大小次序排成一列,写在 左(右)侧;
第三步,将各个数据的叶按大小次序写在茎右(左)侧.
思考5:用茎叶图表示数据的分布情况是一种好方法,你认为茎叶图有哪些优 点?
钟跳绳次数测试,将所得数据整理后,画出了频率分布直方图.图中从左
到右各小长方形的面积之比为2:4:17:15:9:3,第二小组的频数为12.
(1)第二小组的频
率是多少?
(2)样本容量是多
少? (3)若次数在110以 上(含110次)为达
0.036
频率/组距
标,试估计该校全体
0.032
高一学生的达标率约
1.00
(2)频率分布直方图:
频率 组距
0.08 0.07 0.06 0.05 0.04 0.03 0.02 0.01
O
122 126 130 134 138 142 146 150 154 158 身高/cm
(初中)学生各学科质量折线图
成绩变化折线图
17
21
25
29
33
1-5六上、5-9六下,9-13七上、13-17七下,17--21八上... 成绩变化折线图
17
21
25
29
33
1-5六上、5-9六下,9-13七上、13-17七下,17--21八上... 成绩变化折线图
17
21
25
29
33
1-5六上、5-9六下,9-13七上、13-17七下,17--21八上... 成绩变化折线图
成绩变化折线图 120 110 100 90 80 70 60 50 40 30 20 10 0 1 5 9 13 17 21 25 29 33 1-5六上、5-9六下,9-13七上、13-17七下,17--21八上... 成绩变化折线图 120 110 100 90 80 70 60 50 40 30 20 10 0 1 5 9 13 17 21 25 29 33 1-5六上、5-9六下,9-13七上、13-17七下,17--21八上... 成绩变化折线图 100 95 90 85 80 75 70 65 60 55 50 45 40 35 30 25 20 15 10 5 0 1 5 9 13 17 21 25 29 33 1-5六上、5-9六下,9-13七上、13-17七下,17--21八上... 成绩变化折线图 100 95 90 85 80 75 70 65 60 55 50 45 40 35 30 25 20 15 10 5 0 1 5 9 13 17 21 25 29 33 1-5六上、5-9六下,9-13七上、13-17七下,17--21八上... 成绩变化折线图 100 95 90 85 80 75 70 65 60 55 50 45 40 35 30 960 900 840 780 720 660 600 540 480 420 360 300 100 95 90 85 80 75 70 65 60 55 50 45 40 35 30 25 20 15 10 5 0 1 5 9 13 100 95 90 85 80 75 70 65 60 55 50 45 40 35 30 25 20 15 10 5 0 1 5 9 13 100 95 90 85 80 75 70 65 60 55 50 45 40 35 30 25 20 15 10 5 0 1 5 9 13 120 110 100 90 80 70 60 50 40 30 20 10 0 1 5 9 13
