2019_2020学年高中数学习题课(二)解析几何初步北师大版必修2
北师大版数学必修2第二章解析几何初步归纳总结课件

得xy′′==3-x-4x45-y5+3y4+,8.
把(x′,y′)代入方程 y=x-2 并整理,得:7x-y-14=0,
即直线 l2 的方程为 7x-y-14=0.
(3)设直线 l 关于点 A(1,1)的对称直线 l′,则直线 l 上任一 点 P(x1,y1)关于点 A 的对称点 P′(x,y)一定在直线 l′上,反 之也成立.
①当直线与圆相离时,圆上的点到直线的最大距离是 d+r, 最小距离是 d-r,其中 d 为圆心到直线的距离.
②当直线与圆相交时,设弦长为 l,弦心距为 d,半径为 r, 则有(2l )2+d2=r2.
③当直线与圆相交时,设弦为 AB,则 |AB|= 1+k2AB·|xA-xB|, |AB|= 1|k+ABk| 2AB·|yA-yB|.
ቤተ መጻሕፍቲ ባይዱ
(2)设 l1:A1x+B1y+C1=0,l2:A2x+B2y+C2=0. ①l1 与 l2 相交⇔A1B2≠A2B1, 特别地 A1A2+B1B2=0 时⇔l1⊥l2; ②l1∥l2⇔A1B2=A2B1,且 A1C2≠A2C1; ③l1 与 l2 重合⇔A1B2=A2B1 且 A1C2=A2C1. 4.两条直线的交点
当|C1C2|=|r1-r2|时,两圆内切; 当|r1-r2|<|C1C2|<r1+r2 时,两圆相交; 当|C1C2|<|r1-r2|时,两圆内含. 10.空间直角坐标系 (1)右手直角坐标系 ∠xOy=∠xOz=135°,∠yOz=90°,x 轴、y 轴、z 轴的正 半轴分别指向右手拇指、食指、中指.
作点 P(x,y,z)的步骤与方法:从原点出发沿 x 轴正(x>0) 或负(x<0)方向移动|x|个单位,再沿 y 轴正(y>0)或负(y<0)方向移 动|y|个单位,最后沿 z 轴正(z>0)或负(z<0)方向移动|z|个单位.
高中数学 第二章 解析几何初步 1.2.2 直线方程的两点式和一般式练习(含解析)北师大版必修2-北
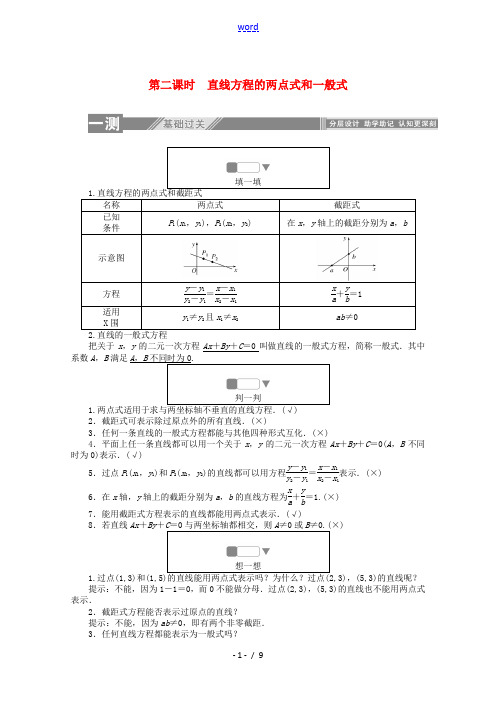
第二课时 直线方程的两点式和一般式填一填1.直线方程的两点式和截距式名称 两点式 截距式已知条件 P 1(x 1,y 1),P 2(x 2,y 2)在x ,y 轴上的截距分别为a ,b示意图方程y -y 1y 2-y 1=x -x 1x 2-x 1 x a +y b=1 适用X 围y 1≠y 2且x 1≠x 2 ab ≠02.直线的一般式方程把关于x ,y 的二元一次方程Ax +By +C =0叫做直线的一般式方程,简称一般式.其中系数A ,B 满足A ,B 不同时为0.判一判1.两点式适用于求与两坐标轴不垂直的直线方程.(√) 2.截距式可表示除过原点外的所有直线.(×)3.任何一条直线的一般式方程都能与其他四种形式互化.(×)4.平面上任一条直线都可以用一个关于x ,y 的二元一次方程Ax +By +C =0(A ,B 不同时为0)表示.(√)5.过点P 1(x 1,y 1)和P 2(x 2,y 2)的直线都可以用方程y -y 1y 2-y 1=x -x 1x 2-x 1表示.(×)6.在x 轴,y 轴上的截距分别为a ,b 的直线方程为x a +y b=1.(×) 7.能用截距式方程表示的直线都能用两点式表示.(√)8.若直线Ax +By +想一想1.过点(1,3)和,(5,3)的直线呢? 提示:不能,因为1-1=0,而0不能做分母.过点(2,3),(5,3)的直线也不能用两点式表示.2.截距式方程能否表示过原点的直线?提示:不能,因为ab ≠0,即有两个非零截距. 3.任何直线方程都能表示为一般式吗?提示:能.因为平面上任意一条直线都可以用一个关于x ,y 的二元一次方程表示. 4.当A ,B 同时为零时,方程Ax +By +C =0表示什么?提示:当C =0时,方程对任意的x ,y 都成立,故方程表示整个坐标平面; 当C ≠0时,方程无解,方程不表示任何图像.故方程Ax +By +C =0,不一定代表直线,只有当A ,B 不同时为零时,即A 2+B 2≠0时才代表直线.思考感悟:练一练1.直线x a +y b=1(ab <0)的图像可能是( )答案:C2.过两点(2018,2019),(2018,2020)的直线方程是( ) A .x =2018 B .x =2019 C .y =2018 D .x +y =2020 答案:A3.直线x -y +5=0的倾斜角为( ) A .45° B.60° C .120° D.135° 答案:A4.在x 轴、y 轴上的截距分别是5,-3的直线的截距式方程为( ) A.x 5+y 3=1 B.x 5-y 3=1 C.y 3-x5=1 D.x 5+y3=0 答案:B5.直线2x +3y -6=0与坐标轴围成的三角形面积为________. 答案:3知识点一 直线的两点式方程1.已知直线l 经过点A (1,-2),B (-3,2),则直线l 的方程为( ) A .x +y +1=0 B .x -y +1=0 C .x +2y +1=0 D .x +2y -1=0解析:由两点式得直线l 的方程为y +22--2=x -1-3-1,即y +2=-(x -1).故选A.答案:A2.过两点(-1,1)和(3,9)的直线在x 轴上的截距为( )A .-32B .-23C.25D .2 解析:由直线的两点式方程可得直线方程为y -19-1=x +13+1,即2x -y +3=0,令y =0得x=-32.故选A.答案:A知识点二 直线的截距式方程3.过点A (4,1)且在两坐标轴上截距相等的直线方程为( ) A .x +y =5 B .x -y =5C .x +y =5或x -4y =0D .x -y =5或x -4y =0解析:当直线过点(0,0)时,直线方程为y =14x ,即x -4y =0;当直线不过点(0,0)时,可设直线方程为x a +y a=1(a ≠0),把(4,1)代入,解得a =5,∴直线方程为x +y =5.综上可知,直线方程为x +y =5或x -4y =0.选C. 答案:C4.两条直线l 1:x a -y b =1和l 2:x b -y a=1在同一平面直角坐标系中的图像可以是( )解析:将两直线方程化成截距式为l 1:x a +y -b =1,l 2:x b +y-a=1,则l 1与x 轴交于(a,0),与y 轴交于(0,-b ),l 2与x 轴交于(b,0),与y 轴交于(0,-a ).结合各选项,先假定l 1的位置,判断出a ,b 的正负,然后确定l 2的位置,知A 项符合.选A.答案:A知识点三直线的一般式方程5.已知直线l 的方程为x -3y +2=0,则直线l 的倾斜角为( ) A .30° B.45° C .60° D .150°解析:设直线l 的倾斜角为θ,则tan θ=13,则θ=30°.答案:A6.设直线l 的方程为(a +1)x +y +2-a =0(a ∈R ),若l 不经过第二象限,则实数a 的取值X 围是________.解析:将直线l 的方程化为y =-(a +1)x +a -2. 则⎩⎪⎨⎪⎧ -a +1>0,a -2≤0或⎩⎪⎨⎪⎧-a +1=0,a -2≤0,∴a ≤-1. 答案:(知识点四 直线方程的应用7.(1)求证:不论a 为何值,直线l 总经过第一象限; (2)为使直线不经过第二象限,求a 的取值X 围.解析:(1)证明:方法一 将直线l 的方程整理为 y -35=a ⎝ ⎛⎭⎪⎫x -15, ∴l 的斜率为a ,且过定点A ⎝ ⎛⎭⎪⎫15,35,而点A ⎝ ⎛⎭⎪⎫15,35在第一象限,故不论a 为何值,l 恒过第一象限.方法二 直线l 的方程可化为(5x -1)a +(3-5y )=0. 当定点为(x ,y )时,上式对任意的a 总成立,必有⎩⎪⎨⎪⎧5x -1=0,3-5y =0,即⎩⎪⎨⎪⎧x =15,y =35,即l 过定点A ⎝ ⎛⎭⎪⎫15,35.以下同方法一.(2)如图,直线OA 的斜率为 k =35-015-0=3. 要使l 不经过第二象限,需它在y 轴上的截距不大于零,即令x =0时,y =-a -35≤0,∴a ≥3.8.已知直线l :y =kx +2k +1.(1)求证:对于任意的实数k ,直线l 恒过一个定点;(2)当-3<x <3时,直线l 上的点都在x 轴的上方,某某数k 的取值X 围. 解析:(1)由y =kx +2k +1, 得y -1=k (x +2).由直线的点斜式方程,可知直线l 恒过定点(-2,1). (2)设函数f (x )=kx +2k +1.若-3<x <3时,直线l 上的点都在x 轴的上方,则⎩⎪⎨⎪⎧f -3≥0,f 3≥0,即⎩⎪⎨⎪⎧-3k +2k +1≥0,3k +2k +1≥0,解得-15≤k ≤1.所以实数k 的取值X 围是⎣⎢⎡⎦⎥⎤-1,1. 综合知识 直线的方程9.(1)经过点(-1,3),且斜率为-3; (2)经过两点A (0,4)和B (4,0);(3)经过点(2,-4)且与直线3x -4y +5=0平行; (4)经过点(3,2),且垂直于直线6x -8y +3=0.解析:(1)根据条件,写出该直线的点斜式方程为 y -3=-3(x +1),即y -3=-3x -3, 整理得其一般式为3x +y =0.(2)根据条件,写出该直线的截距式为x 4+y4=1,整理得其一般式为x +y -4=0.(3)设与直线3x -4y +5=0平行的直线为3x -4y +c =0,将点 (2,-4)代入得6+16+c =0,所以c =-22.故所求直线的一般式为3x -4y -22=0.(4)设与直线6x -8y +3=0垂直的直线为8x +6y +c =0,代入点(3,2)得24+12+c =0,c =-36.从而得8x +6y -36=0,即所求直线的一般式为4x +3y -18=0.10.已知△ABC 的三个顶点为A (0,3),B (1,5),C (3,-5). (1)求边AB 所在的直线方程; (2)求中线AD 所在直线的方程.解析:(1)设边AB 所在的直线的斜率为k ,则k =5-31-0=2.它在y 轴上的截距为3.所以,由斜截式得边AB 所在的直线的方程为y =2x +3.(2)B (1,5)、C (3,-5),1+32=2,5+-52=0,所以BC 的中点D (2,0).由截距式得中线AD 所在的直线的方程为x 2+y3=1.基础达标一、选择题1.下列四个命题中的真命题是( )A .经过定点P 0(x 0,y 0)的直线都可以用方程y -y 0=k (x -x 0)表示B .经过任意两个不同点P 1(x 1,y 1)、P 2(x 2,y 2)的直线都可以用方程(y -y 1)(x 2-x 1)=(x -x 1)(y 2-y 1)表示C .不经过原点的直线都可以用方程x a +yb=1表示D .经过定点A (0,b )的直线都可以用方程y =kx +b 表示解析:当直线与y 轴平行或重合时,斜率不存在,直线方程不能用点斜式、斜截式,选项A 、D 不正确;当直线垂直于x 轴或y 轴时,直线方程不能用截距式表示,选项C 不正确;选项B 正确.故选B.答案:B2.已知直线l :ax +y -2-a =0在x 轴和y 轴上的截距相等,则a 的值是( ) A .1 B .-1 C .-2或-1 D .-2或1解析:①当a =0时,y =2不合题意.②当a ≠0时,令x =0,得y =2+a ,令y =0,得x =a +2a ,则a +2a=a +2,得a =1或a =-2.故选D.答案:D3.直线l 过点P (1,3),且与x ,y 轴正半轴围成的三角形的面积等于6的直线方程是( ) A .3x +y -6=0 B .x +3y -10=0 C .3x -y =0 D .x -3y +8=0 解析:设所求的直线方程为x a +yb=1. 所以⎩⎪⎨⎪⎧1a +3b =1,12|ab |=6,解得a =2,b =6.故所求的直线方程为3x +y -6=0.故选A.答案:A4.如果AB <0,且BC <0,那么直线Ax +By +C =0不通过( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限解析:因为直线Ax +By +C =0可化为y =-A B x -C B ,又AB <0,BC <0,所以-A B >0,-C B>0,所以直线过第一、二、三象限,不过第四象限.故选D. 答案:D5.已知m ≠0,则过点(1,-1)的直线ax +3my +2a =0的斜率为( ) A .3 B .-3 C.13 D .-13解析:由题意,得a -3m +2a =0,所以a =m ,又因为m ≠0,所以直线ax +3my +2a =0的斜率k =-a 3m =-13.故选D.答案:D6.已知两条直线的方程分别为l 1:x +ay +b =0,l 2:x +cy +d =0,它们在坐标系中的位置如图所示,则( )A .b >0,d <0,a <cB .b >0,d <0,a >cC .b <0,d >0,a >cD .b <0,d >0,a <c解析:由题图可知,直线l 1的斜率-1a >0,在y 轴上的截距-ba<0,因此a <0,b <0;直线l 2的斜率-1c >0,在y 轴上的截距-d c >0,因此c <0,d >0.且l 1的斜率大于l 2的斜率,即-1a >-1c,因此a >c ,故选C.答案:C7.若方程(2m 2+m -3)x +(m 2-m )y -4m +1=0表示一条直线,则实数m 满足( )A .m ≠0 B.m ≠-32C .m ≠1 D.m ≠1且m ≠-32且m ≠0解析:∵当2m 2+m -3=0时,m =1或m =-32;当m 2-m =0时,m =0或m =1,要使方程(2m 2+m -3)x +(m 2-m )y -4m +1=0表示一条直线,则2m 2+m -3,m 2-m 不能同时为0,∴m ≠1,故选C.答案:C 二、填空题 8.经过A (1,3)和B (a,4)的直线方程为________________________________________________________________________.解析:当a =1时,直线AB 的斜率不存在,所求直线的方程为x =1;当a ≠1时,由两点式,得y -34-3=x -1a -1,即x -(a -1)y +3a -4=0.这个方程中,对a =1时方程为x =1也满足. 所以,所求的直线方程为x -(a -1)y +3a -4=0. 答案:x -(a -1)y +3a -4=09.过点(5,2),且在x 轴上的截距是在y 轴上的截距的2倍的直线方程是________________。
2019_2020学年高中数学第2章解析几何初步2_1_5平面直角坐标系中的距离公式课件北师大版必修2

[解] (1)直线 y=34x+14化为一般式为 3x-4y+1=0,由点到 直线的距离公式可得
d=|3×3-324+×--422+1|=158. (2)因为直线 y=6 与 y 轴垂直,所以点 P 到它的距离 d=|-2 -6|=8. (3)因为直线 x=4 与 x 轴垂直,所以点 P 到它的距离 d=|3- 4|=1.
[解] 设点 P 的坐标为(x,0),由|PA|=10, 得 x-32+0-62=10, 解得:x=11 或 x=-5. 所以点 P 的坐标为(-5,0)或(11,0).
题型二 点到直线的距离 【典例 2】 求点 P(3,-2)到下列直线的距离: (1)y=34x+14;(2)y=6;(3)x=4. [思路导引] 利用点到直线距离公式时,注意把直线化为一 般式,对于特殊的直线,数列结合,求距离即可.
题型四 距离公式的综合应用 【典例 4】 求过点 M(-1,2),且与点 A(2,3),B(-4,5)距离 相等的直线 l 的方程. [思路导引] 过点 M(-1,2)的直线可以优先考虑点斜式,利 用点 A(2,3),B(-4,5)到直线的距离相等确定斜率,注意斜率不存 在的情况,或者考虑数形结合,过 A(2,3),B(-4,5)的中点或与过 A(2,3),B(-4,5)两点直线平行.
应用点到直线的距离公式应注意的三个问题 (1)直线方程应为一般式,若给出其他形式应化为一般式. (2)点 P 在直线 l 上时,点到直线的距离为 0,公式仍然适用. (3)直线方程 Ax+By+C=0 中,A=0 或 B=0 公式也成立, 但由于直线是特殊直线(与坐标轴垂直),故也可用数形结合求解.
∴l1 的方程为 12x-5y+5=0, l2 的方程为 12x-5y-60=0. 若直线 l1,l2 的斜率不存在,则 l1 的方程为 x=0,l2 的方程 为 x=5, 它们之间的距离为 5,满足条件. 则满足条件的直线方程有以下两组: l1:12x-5y+5=0,l2:12x-5y-60=0; l1:x=0,l2:x=5.
2019-2020学年北师大版高中数学必修二练习:第1章 立体几何初步 1.7.1 Word版含解

姓名,年级:时间:§7简单几何体的再认识7.1柱、锥、台的侧面展开与面积课后篇巩固探究1。
若圆锥的底面直径为6,高是4,则它的侧面积为()A。
12πB。
24πC。
15πD。
30π√32+42=5,于是侧面积S=π×3×5=15π。
2.(2018全国Ⅰ卷,文5)已知圆柱的上、下底面的中心分别为O1,O2,过直线O1O2的平面截该圆柱所得的截面是面积为8的正方形,则该圆柱的表面积为()A.12√2πB。
12πC.8√2πD.10πO 1O2的平面截该圆柱所得的截面为圆柱的轴截面,设底面半径为r,母线长为l,因为轴截面是面积为8的正方形,所以2r=l=2√2,r=√2,所以圆柱的表面积为2πrl+2πr2=8π+4π=12π。
3.若圆台的高为3,一个底面半径是另一个底面半径的2倍,其轴截面的一个底角为45°,则这个圆台的侧面积是()A.27πB.27√2πC.9√2πD。
36√2πr1,下底半径为r2,母线长为l,如图所示,2r2=2r1+6=4r1,∴r 1=3,r2=6。
S圆台侧=π(r1+r2)l=π(6+3)×3√2=27√2π。
4。
《九章算术》中,将底面是直角三角形的直三棱柱称之为“堑堵”,已知某“堑堵”的三视图如图所示,则该“堑堵”的表面积为()A.4 B。
6+4√2 C.4+4√2 D.212×2×1=1,底面周长为2+2×√2=2+2√2,所以棱柱的表面积S=2×1+2×(2+2√2)=6+4√2.故选B。
5。
一个几何体的三视图如图所示,则该几何体的表面积为。
4,3,1,圆柱底面半径为1,高为1,故S=2(3×4+3×1+4×1)—2π+2π×1×1=38。
6.已知正四棱台两底面边长分别为4 cm,8 cm,侧棱长为8 cm,则它的侧面积为cm2。
2019_2020学年高中数学第二章解析几何初步1.5平面直角坐标系中的距离公式课件北师大版必修2

[变式训练1] 已知点 A(5,5),B(1,4),C(4,1),
(1)试判断△ABC 的形状;
(2)求 AB 边上的中线 CM 的长.
解 (1)|AB|= 1-52+4-52= 17,
|AC|= 4-52+1-52= 17,
|BC|= 4-12+1-42= 18,
∵|AB|=|AC|≠|BC|,∴△ABC 为等腰三角形.
[变式训练2] P 点在直线 3x+y-5=0 上,且 P 到直线 x-y-1=0 的 距离为 2,求 P 点的坐标.
解 设点 P 的坐标为(x0,y0), 3x0+y0-5=0,
由题意得|x0-y20-1|= 2, 解得 x0=2,y0=-1 或 x0=1,y0=2. 所以点 P 的坐标为(2,-1)或(1,2).
答案
例 3 已知直线 l1 与 l2 的方程分别为 7x+8y+9=0,7x+8y-3=0,直线
l 平行于 l1,直线 l 与 l1 的距离为 d1,与 l2 的距离为 d2,且dd12=12,求直线 l
提示
4.P,Q 分别为直线 3x+4y-12=0 与 6x+8y+6=0 上任意一点,则|PQ| 的最小值为________.
提示:3 直线 6x+8y+6=0 可变为 3x+4y+3=0,由此可知两直线平 行.它们的距离 d=|-3122+-432|=3,|PQ|最小值为 d=3.
提示
课堂互动探究
1.5 平面直角坐标系中的距离公式
[学习目标] 1.掌握两点间的距离公式并会应用. 2.了解点到直线的距 离公式的推导方法. 3.掌握点到直线的距离公式,并能灵活应用于求平行 线间的距离等问题. 4.初步掌握用解析法研究几何问题的方法.
课前自主学习
2019-2020学年高中数学 第2章 解析几何初步 3 3.3 空间两点间的距离公式学案 北师大版必修2

3.3 空间两点间的距离公式1.长方体的对角线(1)连线长方体两个顶点A ,C ′的线段AC ′称为长方体的对角线.(如图)(2)如果长方体的长、宽、高分别为a ,b ,c ,那么对角线长d 2.空间两点间的距离公式(1)空间任意一点P (x 0,y 0,z 0)与原点的距离 |OP |(2)空间两点A (x 1,y 1,z 1),B (x 2,y 2,z 2)间的距离 |AB |思考:空间两点间的距离公式与平面两间点的距离公式的区别与联系?提示:平面两点间的距离公式是空间两点间的距离公式的特例:①在平面直角坐标系xOy 中,已知两点A (x 1,y 1),B (x 2,y 2),则|AB |=(x 1-x 2)2+(y 1-y 2)2;②在x 轴上的两点A ,B 对应的实数分别是x 1,x 2,则|AB |=|x 2-x 1|.1.空间直角坐标系中,点A (-3,4,0)和点B (2,-1,6)的距离是( ) A .243 B .221 C .9 D.86 D [|AB |=(-3-2)2+(4+1)2+(0-6)2=86.]2.在空间直角坐标系中,设A (1,2,a ),B (2,3,4),若|AB |=3,则实数a 的值是( ) A .3或5 B .-3或-5 C .3或-5D .-3或5A [由题意得|AB |=(1-2)2+(2-3)2+(a -4)2=3,解得a =3或5,故选A.] 3.已知点A (4,5,6),B (-5,0,10),在z 轴上有一点P ,使|PA |=|PB |,则点P 的坐标是________.(0,0,6) [设点P (0,0,z ), 则由|PA |=|PB |,得(0-4)2+(0-5)2+(z -6)2 =(0+5)2+(0-0)2+(z -10)2, 解得z =6,即点P 的坐标是(0,0,6).](1)求△ABC 中最短边的边长; (2)求AC 边上中线的长度. [解] (1)由空间两点间距离公式得 |AB |=(1-2)2+(5-3)2+(2-4)2=3, |BC |=(2-3)2+(3-1)2+(4-5)2=6, |AC |=(1-3)2+(5-1)2+(2-5)2=29, ∴△ABC 中最短边是|BC |,其长度为 6.(2)由中点坐标公式得,AC 的中点坐标为⎝ ⎛⎭⎪⎫2,3,72, ∴AC 边上中线的长度为(2-2)2+(3-3)2+⎝⎛⎭⎪⎫4-722=12.1.求空间两点间的距离问题就是把点的坐标代入距离公式进行计算,其中确定点的坐标或合理设出点的坐标是关键.2.若所给题目中未建立坐标系,需结合已知条件建立适当的坐标系,再利用空间两点间的距离公式计算.1.如果点P 在z 轴上,且满足|PO |=1(O 是坐标原点),则点P 到点A (1,1,1)的距离是________.2或6 [由题意得P (0,0,1)或P (0,0,-1),所以|PA |=(0-1)2+(0-1)2+(1-1)2=2, 或|PA |=(0-1)2+(0-1)2+(1+1)2= 6.]标,并求此时的|AB |.[思路探究] 解答本题可由空间两点间的距离公式建立关于x 的函数,由函数的性质求x ,再确定坐标.[解] 由空间两点的距离公式得|AB |=(1-x )2+[(x +2)-(5-x )]2+[(2-x )-(2x -1)]2=14x 2-32x +19=14⎝ ⎛⎭⎪⎫x -872+57, 当x =87时,|AB |有最小值57=357. 此时A ⎝ ⎛⎭⎪⎫87,277,97,B ⎝⎛⎭⎪⎫1,227,67.解决这类问题的关键是根据点的坐标的特征,应用空间两点间的距离公式建立已知与未知的关系,结合已知条件确定点的坐标.2.在空间直角坐标系中,已知A (3,0,1),B (1,0,-3).在y 轴上是否存在点M ,使△MAB 为等边三角形?若存在,求出点M 的坐标;若不存在,说明理由.[解] 假设在y 轴上存在点M (0,y,0),使△MAB 为等边三角形. 由题意可知y 轴上的所有点都能使|MA |=|MB |成立, 所以只要再满足|MA |=|AB |,就可以使△MAB 为等边三角形. 因为|MA |=32+(-y )2+12=10+y 2, |AB |=2 5.于是10+y 2=25,解得y =±10.故y 轴上存在点M ,使△MAB 为等边三角形,此时点M 的坐标为(0,10,0)或(0,-10,0).【例3】 如图,在棱长为1的正方体ABCD A 1B 1C 1D 1中,以正方体的三条棱所在直线为轴建立空间直角坐标系O xyz .(1)若点P 在线段BD 1上,且满足3|BP |=|BD 1|,试写出点P 的坐标,并写出P 关于y 轴的对称点P ′的坐标;(2)在线段C 1D 上找一点M ,使得点M 到点P 的距离最小,求出点M 的坐标.[思路探究] (1)借助3|BP |=|BD 1|及平面几何的知识求点P 的坐标,利用对称关系求点P ′的坐标;(2)利用空间两点间的距离公式建立点M 到点P 的距离的函数,并用函数的思想求其最小值,及此时的点M 的坐标.[解] (1)由题意知P 的坐标为⎝ ⎛⎭⎪⎫23,23,13. P 关于y 轴的对称点P ′的坐标为⎝⎛⎭⎪⎫-23,23,-13. (2)设线段C 1D 上一点M 的坐标为(0,m ,m ),则有|MP |=⎝ ⎛⎭⎪⎫-232+⎝ ⎛⎭⎪⎫m -232+⎝ ⎛⎭⎪⎫m -132=2m 2-2m +1=2⎝ ⎛⎭⎪⎫m -122+12, 当m =12时|MP |取到最小值,所以点M 为⎝ ⎛⎭⎪⎫0,12,12.与平面直角坐标系中类似,在空间直角坐标系中也常常需要设点的坐标,此时,若注意利用点的特殊性,往往能使求解过程简化,如本例(2)设M (0,m ,m )便是如此.3.如图,在长方体ABCD A 1B 1C 1D 1中,AB =AD =2,AA 1=3,M ,N 分别是AB ,B 1C1的中点,点P 是DM 上的点,DP =a ,当a 为何值时,NP 的长最小?[解] 如图,以点D 为原点,以DA ,DC ,DD 1所在直线分别为x 轴、y 轴、z 轴,建立空间直角坐标系.则D (0,0,0),B 1(2,2,3),C 1(0,2,3),A (2,0,0),B (2,2,0),M (2,1,0),N (1,2,3), 设点P 的坐标为(x ,y,0), 则x =2y (0≤y ≤1).|NP |=(x -1)2+(y -2)2+(0-3)2=(2y -1)2+(y -2)2+(0-3)2=5y 2-8y +14=5⎝ ⎛⎭⎪⎫y -452+545, 所以当y =45时,|NP |取最小值3305,此时a =x 2+y 2=⎝ ⎛⎭⎪⎫852+⎝ ⎛⎭⎪⎫452=455, 所以当a =455时,NP 的长最小.1.学会用类比联想的方法理解空间直角坐标系的建系原则,切实体会空间中点的坐标及两点间的距离公式同平面内点的坐标及两点间的距离公式的区别和联系.2.在导出空间两点间的距离公式的过程中体会转化与化归思想的应用,突出化空间为平面的解题思想.1.思考辨析(1)空间两点间的距离公式与两点顺序有关. ( ) (2)点A (1,1,0)与点B (1,1,1)之间的距离是1.( )[解析] (1)×,空间两点间的距离公式与两点顺序无关. [答案] (1)× (2)√2.已知点A (1,-2,11),B (4,2,3),C (6,-1,4),则△ABC 的形状是( ) A .等腰三角形B .等边三角形C.直角三角形D.等腰直角三角形C [由距离公式得:|AB|=(1-4)2+(-2-2)2+(11-3)2=89,|AC|=(1-6)2+(-2+1)2+(11-4)2=75,|BC|=(4-6)2+(2+1)2+(3-4)2=14,∴|AC|2+|BC|2=|AB|2,∴△ABC为直角三角形.]3.已知A(1,-2,1),B(2,2,2),点P在z轴上,且|PA|=|PB|,则点P的坐标为________.(0,0,3) [∵P在z轴上,可设P(0,0,z),由|PA|=|PB|,∴(1-0)2+(-2-0)2+(1-z)2=(2-0)2+(2-0)2+(2-z)2,解得z=3.]4.点A(1,t,0)和点B(1-t,2,1)的距离的最小值为______.3 [|AB|=t2+(t-2)2+1=2(t-1)2+3,∴当t=1时,|AB|的最小值为 3.]。
2020年高中数学第二章解析几何初步11.2直线的方程(2)课件北师大版必修2
练一练 (2) 在 x 轴、y 轴上的截距分别是 5,-3 的直线的截
距式方程为( )
A.5x+3y=1
B.5x-3y=1
C.3y-5x=1 答案:B
D.5x+3y=0
3.直线方程的一般式:关于 x、y 的二元一次方程A_x_+__B__y+__C__=_ 0 (A、B 不同时为 0)叫做直线方程的一般式.
已知直线 l:5ax-5y-a+3=0.
(1)求证:不论 a 为何值,直线 l 总经过第一象限; (2)为使直线不经过第二象限,求 a 的取值范围. 解:(1)证明:证法一:将直线 l 的方程整理为 y-35=ax-15, ∴直线 l 的斜率为 a,且过定点 A15,35. 而点 A15,35在第一象限,∴不论 a 为何值时,l 恒过第一象 限.
【正解】 若 a2-a-2 与 2-a 同时为 0, 则方程(a2-a-2)x+(2-a)y+5=0 不表示任何直线, 此时 a=2. 所以当 a≠2 时,方程(a2-a-2)x+(2-a)y+5=0 表示某条 直线的方程.
基础知识达标
即学即练 稳操胜券
知识点一 直线的两点式方程
1.过 P(2,1),Q(6,-2)两点的直线的两点式方程为( )
练一练 (3) 斜率为-3,且在 x 轴上截距为 2 的直线方程是
() A.3x+y+6=0 C.3x+y-6=0
B.3x-y+2==-3(x-2),即 3x+y-6=0.
答案:C
用直线方程的两点式或截距式解题时应注意什么? 答:用两点式或截距式表示直线方程时,都有其局限性,不 能表示与坐标轴垂直的直线,截距式还不能表示过原点的直线.平 面内所有直线的方程都可写成一般式,对于所求直线方程,在没 有特殊说明的情况下,应该化为一般式方程.
2019 2020高中数学第二章解析几何初步章末复习学案北师大版必修2
第二章解析几何初步知识网络构建高频考点例析考点一直线的方程lPl的方程.,且与两条坐标轴围成等腰直角三角形,求直线过点 (8,6)1 例直线l与两条坐标轴围成的三角形为等腰直角三角形,直线必须且只需直线解]解法一:[l在两条坐标轴上的截距的绝对值相等且不为0,xyxyal≠0),1(=1或+故设直线=的方程为+aaaa-xyl 1时,当直线=的方程为+aa68aP=14,1把+(8,6)代入得=,解得aalxy-14=∴直线0的方程为;+xyl=1的方程为+时,当直线aa-86Pa=2,1-把(8,6)代入得=,解得aalxy-2∴直线=的方程为0.-lxyxy-2=0综上所述,直线或的方程为0. +--14=lykxbkb≠0),+解法二:设所求直线≠0,的方程为(=bxbyxy. =-==0,得0=,得;令令k∵直线与两条坐标轴围成等腰直角三角形,b????b-.∴|=|k??kb=±1.∵≠0,∴bklyx=1时,直线,的方程为+当=bPb把=-(8,6)代入得6=8+2,解得,xly的方程为2=,-∴直线yx即;-2-=0bxkly+=-=-1时,直线,的方程为当bPb=14=-68+,把,解得(8,6)代入得yxyxl0. =,即-∴直线+的方程为14=-+14yyxlx0. -综上所述,直线-的方程为2+-14=0或=类题通法常用待定系数法求直线方程求直线方程的主要方法是待定系数法,要掌握直线方程五种形式的适用条件及相互转当不能确定某种方程条件具备时要另行讨论条件不满足的情化,能根据条件灵活选用方程,况.1][变式训练yx将直线的方程;-2+6=0y(1)轴上的截距;化成斜截式,并指出它的斜率与在yx轴上的截距.轴、(2)化成截距式,并指出它在1xyxy,因此它的斜率+=将原方程移项得解 (1)22=+6,两边同除以,得斜截式321k,=2y3.在轴上的截距为xyyx由方程可知,61.,得截距式+=,两边同除以-2(2)将原方程移项得-=-63-6yx6,3.轴上的截距分别为-轴、直线在.考点二直线的位置关系laxbylaxyb=0(+-:1)-,求分别满足下列条件+4=0,+:例2 已知两条直线21ab的值.的、lll垂直;,并且直线与直线(-3,-(1)直线1)过点211llll的距离相等.直线(2) 与直线、平行,并且坐标原点到2211llaab)·1=0,-(1)∵1)⊥+,∴((-][解212baa①-=-即0.l在上,-3,-1)又点(1ba 0.②++4∴-3=ba2. ==2,由①②解得alll,的斜率为(2)∵1∥-且221aabla.,即∴的斜率也存在,=1-=1ab-1ll故的方程可分别表示为和21a-yalx=0-1),++:(1aayxla=+1)+:(0. -2a-1ll的距离相等,与∵原点到21aa1-2????????aa. ==∴42=或,解得aa????-132??aa,=2,=??3?因此或?b2=-????b2.=类题通法两条直线位置的判定方法两条直线的位置关系有相交(特例垂直)、平行、重合三种,主要考查两条直线的平行和垂直.通常借助直线的斜截式方程来判断两条直线的位置关系.解题时要注意分析斜率是否存在,用一般式方程来判断,可以避免讨论斜率不存在的情况.22][变式训练aylyxaaxl-1-1)=+已知直线:0+2+6=和直线:0. +(21ll是否平行;与(1)试判断21lla的值.时,求(2) ⊥21ll∥(1)解若,21.aa,0--2×1=?? 则?2aa-6×1≠0.-??aall . ∥=-∴1=-1.∴时,21la =的斜率不存在时,(2)当1. 2lxlxy +62==0,0. 则::+12ll 不垂直.显然 与21la ≠1.当 斜率存在时,2a 1kk =-. 则,=12a 21-a 1????kllk -=-,∴··∵1.⊥= 2211??a 2-12a =.∴ 3考点三 求圆的方程lxyAB (5,2),求此圆的(3,6)6=有一圆与直线0:4相切于点-3,且经过点+例3方程.222CBbrCaCAxayb ,|,=)设圆的方程为(-,)+(由-|)=|,则圆心为|([解] 解法一:CAl ,⊥22222raabb,-+--+-==??? 得b 4-61.×=-?a ?3-39252abr =,=解得,=5, 24925??22y ??x -=-5)+. ∴圆的方程为( ??2422BAlEyFCCAxyDx (5,2)(3,6)=0,圆心为,解法二:设圆的方程为,由+⊥+、++ 在圆上,22FED ,=+3+6+30+6??22FDE +,=052+5+2+D ,=-10???EE ?,9=- 得解得6-- 24???F39.=,=-1×D 3?3--222xyxy +39=-9∴所求圆的方程为:0.+-103CCAlACPCAy -6又设解法三:设圆心为,则⊥,与圆的另一交点为,则方程为=- 4.x -3),(xy -334=即30. +6-2k ==-2, 又AB5-31k =,∴ BP2BPxy -12∴直线=的方程为0. -xxy ,7=-33=30+4,???? 解方程组得??yxy 3.,=-1=0-2????P (7,3).∴95????ACAP ,5|=|∴圆心为.中心,半径为 ??22925??22y ??x -=. 5)+∴所求圆的方程为(- ??24 类题通法求圆的方程常用的方法求圆的方程主要是联想圆系方程、圆的标准方程和一般方程,利用待定系数法解题.采用待定系数法求圆的方程的一般步骤为:abrDEF )的方程(组或),;,(1)选择圆的方程的某一形式;(2)由题意得(3),,解出(abrDEF );(4),(或代入圆的方程.,, ,[变式训练3]Axyxy -1-==0上且与直线 已知圆经过点0(2,-1),圆心在直线2+相切,求圆的方程.22FDxEyxy +0 解解法一:设圆的方程为++,+=DE ????,--. 其圆心为 ??22A (2,-1)∵圆过点, DEF =0-,①+∴5+2xy =0上,+ 又圆心在直线2DE ????????ED -- +②=,即∴2·=020.+ ????22xy -1代入圆方程得将=2FxExDE 0. )2+(+=-2)+(1-+2FDEE 0.+)=③--(Δ=+-2)8(12DD ,0=5)-2-8(1-2)--(将①②代入③中,得.2DDDD 18.或=+360,∴=-=-即2+20DD ,18=-2,=-????EE ??,36==4, 或代入①②,得????FF 67.==322yxxy 0 =-2++4故所求圆的方程为3+22yxyx 0.+67+或36+=-18222rrxayb -()+(.解法二:设圆的方程为(->0))=abyx ∵圆心在直线=-=-22上,∴,aa 2.即圆心为(),-yx ,-(2又圆与直线1)-,-1=0相切,且过点aa 1|+2|-222rara )(2∴-=)+(-1+2=,,2222aaa ),2(-1即(3+-1)=2(2-2)+aa 9. 解得==1或abrrab =338,, ,=-=2或18,∴=9=1,2=-22yx 2,+2)故所求圆的方程为:(=-1)+(22yx 338.+18)或(=-9)+( 考点四 直线与圆、圆与圆的位置关系22ClCxyxyl 截,使以4 已知圆,是否存在斜率为:1+的直线-2被圆+4-4=0例lAB 为直径的圆过原点;若存在,写出直线的方程;若不存在,说明理由.得的弦l 的直线,满足题意,] 假设存在斜率为1[解OBOA ⊥则,yBxAxyBlyxbCA ,((,,的交点)设直线,的方程是的坐标分别为=+,,其与圆)2121yy 21则·=-1,xx 21yyxx =0.即①+2121byx ,+=?? 由?22yyxx ,04=+4+--2??22yxbxbb -44+1)=+消去0. ,得2++2(12xxbxxbb -4),②++4=-(+1), (=所以 212122bxxbbxyybxxx +=(+)()+)=++(211211221222bbbbb 4)(=+4---+ 2.12bb,③=(-+24) 2 把②③式代入①式,得2bbbb 4=0,解得1=或,+3=--4bb且4=1或都使得=-22bbb-4)>0+4Δ=4(成立.+1)-8(xxyly4. 1故存在直线或满足题意,其方程为-==+类题通法开放性题的解题思路再运用直线与圆相交时满足的几何性质或代数关系作解答这类题的思路是先假设存在,转化,求出所涉及的参数,最后通过验证来说明其是否存在.变式训练BPlxMMyA,过点(2,3)且与圆-1)交于=已知圆(:4-1),直线+(lAB 3两点,224][且|,求直线|=的方程.2kkxykllyx=-2+-2)解 (1)当直线存在斜率时,设直线,即的方程为3-3=(-0.CABMC.于⊥作示意图如图,作MBBCMBC=2=3,|,在Rt△|中,||22BCMCMB-|,|故||==|1|kk|1+3-|2-,由点到直线的距离公式得=12k1+3k.=解得4ylx0.6的方程为34-=+所以直线xl当直线(2)2的斜率不存在时,其方程为,=AB,所以适合题意.|=2且|3xlxy2.=或=4综上所述,直线的方程为3-+60思想方法一、数形结合思想.抽象问题具体化,能使复杂问题简单化、数形结合思想通过“以形助数,以数解形”,这是数学的规律性与灵活性的有机有助于把握数学问题的本质,够变抽象思维为形象思维,结合,解析几何本身就是数与形的完美结合.2bxyyxb) ( =1-例1 直线有且仅有一个公共点,则=+的取值范围是与曲线b2|A.|=bb2 .-B1<=-≤1或b.-1≤≤1C .以上结论均不对D2222yxyxbxxyxy,=-[解析]将曲线+=1-=变为与曲线+=1(1≥0).画出直线如下图.b|0+|0-22bbxyyx2.=+|=相切时,满=1当直线,则=+|与曲线2yxxbbby有且仅有+1时,直线与曲线=观察图像,可得当或=-21<-≤=一个公共点.B][答案二、函数与方程思想常把要求的最值或范围表示为某个变量的关系解决有关直线与圆的最值或范围问题时,式,用函数或方程的知识,尤其是配方的方法求出最值或范围.QPyOzyzP1,0,4)(-2 例试在坐标平面,内的直线2使--1=0上确定一点点到点的距离最小.yPyOzy,P∵-在平面内,∴可设点1)的坐标为(0,.由两点间的距离公式,2[解]222yPQy-1++|得-=|+-22yyy6.++26-==520-yPQP 的坐标为(0,2,3),这时点6.取得最小值时,显然当=2||三、分类讨论思想分类讨论思想是数学的基本思想之一,是历年高考的重点.在用二元二次方程表示圆时,在求直线的斜率问题时,用斜率表示直线方程时,都要分类讨论.xPQ轴上的截距之差分别作两条互相平行的直线,(0,2)例3 过点使它们在(-1,0),,求这两条直线的方程.的绝对值为1xx,,0[解](1)当两条平行直线的斜率都不存在时,两条直线的方程分别为==-1x,满足题意.轴上的截距之差的绝对值为1它们在xkky((2)当两条平行直线的斜率都存在时,设其斜率为=,则两条直线的方程分别为kxy2.=+1),+2xxy.令,=0,分别得=-=-1k2????k+-11.==1,即由题意得k??xxyy+1,2=,∴两条直线的方程分别为=+yxyx0.-=0,+即2-+1=yxxxxy0. -+1=-,,=0,或2-=+1=综上可知,所求的两条直线方程分别为0 四、转化与化归思想涉及与圆有关的最值问题,可借助图形的性质,考查所给式子的几何意义,一般地:by- (1)形如的最值问题,可转化为动直线的斜率问题;ax-byax 形如的最值问题,可转化为动直线的截距问题;+(2)22bxay-)+(形如()-的最值问题,可转化为动点到定点的距离问题.(3)y(1)的最大值或最小值;xyx+(2) 22yxxy,求:=+(6例4 如果实数-,满足方程(3)-3)的最大值与最小值;22yx+的最大值与最小值.(3)-22yxPxyPC6. -(,),则点3)的轨迹就是已知圆=:(-3) [解](1)设(+yOOP的斜率,其中而的几何意义就是直线为坐标原点.xyOPykxOPk与圆相切时,斜率取(图略设=),则直线的方程为,当直线=.画图可知x得最值.k3||3-kxyC,的距离为∵圆心到直线=2k1+k3||3-OPk=∴当6与圆相切,时,直线2,即当=3±22k1+y2.22与3-2∴的最大值与最小值分别是3+x2xCyyxybxbxb+-:=-(+与圆,则=-图略+.画图可知(),当直线(2)设3)+=2by取得最值.-3)=6(相切时,截距b||6-byCx,∵圆心到直线+=-的距离为2b|-|6Cbbyx=6±23=-+时,直线相切,,即当∴当=6与圆2yx3. -66+23∴与2+的最大值与最小值分别为2222yyCxx(2,0)的几何意义是圆:(-3)+(代数式(3)-3)=上的点到定点6-+的距离.22C-+3=(2,0)与定点(3,3)∵圆心的距离是10,圆的半径是6,22yx6.-10,最小值是6+∴10的最大值是+-。
2019_2020学年高中数学第二章解析几何初步水平测试北师大版必修2
第二章 解析几何初步水平测试本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.满分150分,考试时间120分钟.第Ⅰ卷(选择题,共60分)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.直线l 经过原点和点(-1,-1),则它的倾斜角是( ) A .45°B .135°C .135°或225°D .0°答案 A解析 本题主要考查直线的倾斜角.由斜率公式得直线l 的斜率k =0--10--1=1,即k =tan α=1,又0°≤α<180°,故倾斜角为45°,故选A.2.斜率为2的直线过(3,5),(a,7),(-1,b )三点,则a +b =( ) A .4 B .-7 C .1 D .-1 答案 C解析 本题考查直线斜率的定义与斜率计算公式.由题意,得2=7-5a -3=b -5-1-3,∴a=4,b =-3,∴a +b =1,故选C.3.直线2x -y +4=0在两坐标轴上的截距之和是( ) A .6 B .4 C .3 D .2 答案 D解析 本题考查直线的截距的定义.令x =0得y =4,即直线在y 轴上的截距为4;令y =0得x =-2,即直线在x 轴上的截距为-2.因此直线在两坐标轴上的截距之和是4+(-2)=2,故选D.4.过点P (3,0)且垂直于直线x -2y +3=0的直线方程为( ) A .2x +y +6=0 B .2x +y -6=0 C .x +2y -6=0 D .x -2y +6=0 答案 B解析 本题考查直线的垂直关系及利用点斜式求直线的方程.∵直线x -2y +3=0的斜率为12,∴其垂线的斜率为-2,∴过点P (3,0)且斜率为-2的直线方程为y =-2(x -3),整理得2x +y -6=0,故选B.5.直线2x -y =7与直线3x +2y -7=0的交点坐标为( ) A .(3,-1) B .(-1,3) C .(-3,-1)D .(3,1)答案 A解析 本题考查两直线的交点坐标的求法.联立两直线的方程,得⎩⎪⎨⎪⎧2x -y =7,3x +2y -7=0,解得⎩⎪⎨⎪⎧x =3,y =-1,即交点坐标为(3,-1),故选A.6.两平行直线5x +12y +3=0与10x +24y +5=0间的距离是( ) A.213 B.113 C.126 D.526答案 C解析 本题考查两平行直线间的距离公式.将直线5x +12y +3=0化为10x +24y +6=0,则d =|6-5|102+242=126,故选C. 7.直线2x +3y -6=0关于点(1,-1)对称的直线方程是( ) A .3x -2y -6=0 B .2x +3y +7=0 C .3x -2y -12=0 D .2x +3y +8=0答案 D解析 本题考查直线的平行关系及对称关系.∵所求直线平行于直线2x +3y -6=0,∴可设所求直线方程为2x +3y +c =0(c ≠-6),由点(1,-1)到两直线的距离相等,得|2-3+c |22+32=|2-3-6|22+32,∴c =8或c =-6(舍去),∴所求直线方程为2x +3y +8=0,故选D.8.如图,在正方体OABC -O 1A 1B 1C 1中,棱长为2,E 是B 1B 上的点,且|EB |=2|EB 1|,则点E 的坐标为( )A .(2,2,1) B.⎝ ⎛⎭⎪⎫2,2,23C.⎝ ⎛⎭⎪⎫2,2,13D.⎝⎛⎭⎪⎫2,2,43 答案 D解析 易知B (2,2,0),B 1(2,2,2), ∴E 点的竖坐标z =23×2=43,∴E 点的坐标为⎝⎛⎭⎪⎫2,2,43. 9.在平面直角坐标系xOy 中,直线3x +4y -5=0与圆x 2+y 2=4相交于A 、B 两点,则弦AB 的长等于( )A .3 3B .2 3 C. 3 D .1 答案 B解析 圆x 2+y 2=4的圆心(0,0)到直线3x +4y -5=0的距离d =1,圆的半径为2,所以弦长|AB |=222-12=2 3.10.若直线x a +y b=1与圆x 2+y 2=1有公共点,则( ) A .a 2+b 2≤1 B .a 2+b 2≥1 C.1a 2+1b 2≤1D.1a 2+1b2≥1答案 D解析 本题考查直线与圆的位置关系的判定.依题意,知圆心(0,0)到直线x a +y b=1的距离不大于圆的半径1,即|-1|⎝ ⎛⎭⎪⎫1a 2+⎝ ⎛⎭⎪⎫1b 2≤1,化简得1a 2+1b 2≥1,故选D.11.如果直线x -my +2=0与圆x 2+(y -1)2=1有两个不同的交点,则( )A .m ≥34B .m >34C .m <34D .m ≤34答案 B解析 本题考查直线与圆的位置关系.圆心为(0,1),半径r =1,圆与直线有两个不同的交点,则圆心到直线的距离d =|-m +2|1+m2<1,得m >34,故选B. 12.圆x 2+y 2-2x -1=0关于直线2x -y +3=0对称的圆的方程是( ) A .(x +3)2+(y -2)2=12B .(x -3)2+(y +2)2=12C .(x +3)2+(y -2)2=2 D .(x -3)2+(y +2)2=2 答案 C解析 本题考查圆的性质.圆x 2+y 2-2x -1=0的圆心为(1,0),半径为2,点(1,0)关于直线2x -y +3=0的对称点为(-3,2),即所求圆的圆心为(-3,2),半径为2,故所求圆的方程为(x +3)2+(y -2)2=2,故选C.第Ⅱ卷(非选择题,共90分)二、填空题(本大题共4小题,每小题5分,共20分.把答案填在题中的横线上) 13.如果圆的方程为x 2+y 2+kx +2y +k 2=0,且圆的面积为π,则圆心坐标为________. 答案 (0,-1)解析 本题考查圆的一般方程及其面积.因为圆x 2+y 2+kx +2y +k 2=0的面积为π,所以圆的半径为1,即12k 2+22-4k 2=124-3k 2=1,所以k =0,所以圆的方程为x 2+y 2+2y =0,得圆心坐标为(0,-1).14.圆心在直线x -2y =0上的圆C 与y 轴的正半轴相切,圆C 截x 轴所得弦的长为23,则圆C 的标准方程为________.答案 (x -2)2+(y -1)2=4解析 本题考查直线与圆的位置关系、圆的方程等基础知识.依题意,设圆心的坐标为(2b ,b )(其中b >0),则圆C 的半径为2b ,圆心到x 轴的距离为b ,所以24b 2-b 2=23,b >0,解得b =1,故所求圆C 的标准方程为(x -2)2+(y -1)2=4.15.已知集合A ={(x ,y )|(x +2)2+(y -2)2=4},B ={(x ,y )|y =kx +3,k ∈R }.若A ∩B 是单元素集,则k =________.答案 -34解析 本题考查直线与圆相切的性质.由A ∩B 是单元素集,知直线y =kx +3与圆(x +2)2+(y -2)2=4相切,所以|-2k -2+3|k 2+1=2,解得k =-34.16.已知两点M (3,-3),N (-3,-5),直线l 过点P (1,1)且与线段MN 相交,则直线l 的斜率k 的取值范围是________.答案 (-∞ ,-2]∪⎣⎢⎡⎭⎪⎫32,+∞解析 本题考查直线斜率的综合应用.如图所示,k PM =1--31-3=-2,k PN =1--51--3=32.过点P 且与x 轴垂直的直线PA 与线段MN相交,但此时直线l 的斜率不存在.直线PN 绕点P 逆时针旋转到PA 处的过程中,l 的斜率始终为正,且逐渐增大,所以此时l 的斜率的范围是k ≥32;直线l 由PA (不包括PA )绕点P逆时针旋转到PM 处的过程中,斜率为负且逐渐增大,此时l 的斜率范围是k ≤-2.综上,k ≤-2或k ≥32.三、解答题(本大题共6小题,共70分.解答应写出必要的文字说明、证明过程或演算步骤)17.(本小题满分10分)已知四边形ABCD 的顶点为A (2,2+22),B (-2,2),C (0,2-22),D (4,2),求证:四边形ABCD 为矩形.证明 由直线的斜率公式计算得k AB =22,k BC =-2,k CD =22,k AD =-2, ∴k AB =k CD ,k BC =k AD ,∴AB ∥CD ,BC ∥AD , ∴四边形ABCD 为平行四边形. 又k AB ·k BC =22×(-2)=-1, ∴AB ⊥BC ,∴四边形ABCD 为矩形.18.(本小题满分12分)求过点P (2,3),且满足下列条件的直线方程: (1)倾斜角等于直线x -3y +4=0的倾斜角的二倍; (2)在两坐标轴上的截距相等.⎝ ⎛⎭⎪⎫参考公式:tan2α=2tan α1-tan 2α解 (1)由题意,设已知直线的倾斜角为α, 可知tan α=13,当所求直线的倾斜角为已知直线的倾斜角的二倍时, k =tan2α=2tan α1-tan 2α=2×131-⎝ ⎛⎭⎪⎫132=34, ∴所求直线的方程为y -3=34(x -2),整理得3x -4y +6=0.(2)当直线过原点时,可设直线方程为y =kx ,又直线过点P (2,3),代入得k =32,∴此时直线的方程为y =32x ,整理得3x -2y =0.当直线不过原点时,可设直线的方程为x m +y m=1, 又直线过点P (2,3),代入得m =5,∴此时直线的方程为x 5+y5=1,整理得x +y -5=0.∴所求直线的方程为3x -2y =0或x +y -5=0.19.(本小题满分12分)已知过点M (-3,-3)的直线l 被圆x 2+y 2+4y -21=0截得的弦长为45,求直线l 的方程.解 圆的方程可化为x 2+(y +2)2=25.由题可知直线l 的斜率存在,故可设直线l 的方程为y +3=k (x +3),即kx -y +3k -3=0.∴圆心(0,-2)到直线l 的距离d =|3k -1|1+k 2, ∵弦长为45,半径r =5,∴d 2+⎝⎛⎭⎪⎫4522=r 2, 整理得2k 2-3k -2=0,∴k =2或-12,∴直线l 的方程为2x -y +3=0或x +2y +9=0.20.(本小题满分12分)设O 点为坐标原点,曲线x 2+y 2+2x -6y +1=0上的P ,Q 两点关于直线x +my +4=0对称,且OP ⊥OQ .(1)求m 的值; (2)求直线PQ 的方程.解 (1)曲线方程为(x +1)2+(y -3)2=9,其表示圆心为(-1,3),半径为3的圆, ∵点P ,Q 在圆上且关于直线x +my +4=0对称, ∴直线x +my +4=0过圆心(-1,3), 代入直线方程得m =-1.(2)由(1)知直线PQ 与直线y =x +4垂直,且直线OP ,OQ 的斜率存在. 设P (x 1,y 1),Q (x 2,y 2),直线PQ 的方程为y =-x +b ,将直线y =-x +b 代入圆的方程,得2x 2+2(4-b )x +b 2-6b +1=0,Δ=4(4-b )2-4×2×(b 2-6b +1)>0,得2-32<b <2+3 2.由根与系数的关系,得x 1+x 2=-(4-b ),x 1x 2=b 2-6b +12,y 1y 2=b 2-b (x 1+x 2)+x 1x 2=b 2-6b +12+4b ,∵OP ⊥OQ ,∴k OP ·k OQ =-1,∴x 1x 2+y 1y 2=0,即b 2-6b +1+4b =0,解得b =1∈(2-32,2+32), ∴直线PQ 的方程为y =-x +1.21.(本小题满分12分)△ABC 的顶点A 的坐标为(1,4),∠B ,∠C 平分线的方程分别为x -2y =0和x +y -1=0,求BC 所在直线的方程.解 该题求直线方程的条件不明显,如果能联想到初中平面几何有关角平分线的知识,就可以发现点A 关于∠B ,∠C 平分线的对称点都在BC 所在直线上,所以只要求出这两个对称点,利用两点式即可求出BC 所在直线的方程.过点A 与直线x -2y =0垂直的直线的斜率为-2,所以其方程为y -4=-2(x -1),将它和x -2y =0联立方程组可求得垂足的坐标为⎝ ⎛⎭⎪⎫125,65, 该垂足是点A 与点A 关于直线x -2y =0的对称点A ′的中点,所以可得点A ′的坐标⎝ ⎛⎭⎪⎫195,-85. 同理可求得点A 关于直线x +y -1=0的对称点A ″的坐标为(-3,0). 由于点A ′⎝⎛⎭⎪⎫195,-85,点A ″(-3,0)均在BC 所在的直线上,∴直线BC 的方程为y -0-85-0=x +3195+3, 即4x +17y +12=0,∴BC 所在直线的方程为4x +17y +12=0.22.(本小题满分12分)在△ABC 中,已知点A (4,-1)、点C (8,3),且AB 的中点为M (3,2). (1)求边BC 所在的直线方程; (2)求△ABC 的外接圆的方程.解 (1)设AC 的中点为N ,利用中点坐标公式得 ⎩⎪⎨⎪⎧x N =4+82=6,y N=-1+32=1,∴N (6,1).∵BC ∥MN ,∴k BC =k MN =2-13-6=-13.故BC 的方程为y -3=-13(x -8),即x +3y -17=0. (2)由条件易得B (2,5).设此三角形的外接圆的方程是x 2+y 2+Dx +Ey +F =0. ∵A ,B ,C 三点在圆上, 故有⎩⎪⎨⎪⎧16+1+4D -E +F =0,4+25+2D +5E +F =0,64+9+8D +3E +F =0,解得D =-9,E =-5,F =14.故所求的外接圆的方程是x 2+y 2-9x -5y +14=0,即⎝ ⎛⎭⎪⎫x -922+⎝ ⎛⎭⎪⎫y -522=252.。
2019-2020高中数学第二章解析几何初步2-2圆与圆的方程学案北师大版必修2
[核心必知] 1.圆的定义1.写出下列各圆的标准方程.(1)圆心在原点,半径为8;=+(y+1)2=5.1.求满足下列条件的圆的标准方程.(1)圆心为(2,-2),且过点(6,3);=+2)2=41.的中点,为(1,-3).=2∴所求圆的标准方程为(x-1)2+(y+3)2=29.(3)由圆的几何意义知圆心坐标(2,-3),=∴圆的方程为(x-2)2+(y+3)2=5.=2-1)2+(y-4)2=8.=5<8,2.已知点A解:∵点A在圆内部,∴(1-3.求圆心在直线[尝试解答]⎨⎩∴圆的方程为(x-2)2+(y-1)2=10.法二:∵圆过A(5,2),B(3,-2)两点,的坐标为(2,1).=∴所求圆的方程为(x-2)2+(y-1)2=10.3.求圆心在直线5解:设所求圆方程为(42+32=答案:75=2 ABCD外接圆的方程为(x-2)2=内部.+(y+4)2=1关于直线x+⎨⎩∴所求圆的方程为(x-4)2+y2=5.法二:∵圆过A(5,2),B(3,-2)两点,=∴所求圆的方程为(x-4)2+y2=5.+y2=5的几何意义,即为动点y )是圆x 2+(y +4)2=4上的任意一点,表示点(1,1)与该圆上点的距离.易知点(1,1)在圆x 2+(y +4)2=4外,结合图易得的最大值为+2=26+2 三、解答题⎩⎨⎧a=1,b=1,1.判断下列方程是否表示圆,若是,化成标准方程.(1)x2+y2+21.求下列圆的圆心和半径.(1)x2+y2-2.已知△ABC 的方程.⎩⎨∴圆的方程为x 2+y 2+4x -4y -2=0.法二:设圆的方程为(x -a )2+(y -b )2⎩⎨⎧ ②-①、③-①得⎩⎨⎧a+2b-2=0,2a-b+6=0,解得a =-2,2.求过点A解:设所求圆的方程为⎩=+y2=10,化成一般方程为:⎩⎨⎧由①、②、③解得D =-4,E =6,∴圆的方程为x 2+y 2-4x +6y +8=-4=0上存在两点关于直线x-y+3=0对称,则实数3=答案:60°7.若直线3x -4y +12=0与两坐标轴交点为⎝ 2+2)2+⎝⎛⎭⎪⎫y-322=⎝ ⎛⎭⎪⎫522,⎩⎨⎧答案:(-∞,1) 三、解答题⎩的几何意义是什么?x1+x22,y1+y21.判断下列直线与圆的位置关系,若有公共点求出公共点的坐标.(1)直线:x∴直线与圆相切,有一个公共点,。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
习题课(二) 解析几何初步
1.若三点A(3,1),B(-2,b),C(8,11)在同一直线上,则实数b等于( )
A.2 B.3
C.9 D.-9
解析:选D 由kAB=kAC,得b=-9.
2.已知直线l1:ax+4y-2=0与直线l2:2x-5y+b=0互相垂直,垂足为(1,c),则
a
+b+c的值为( )
A.-4 B.20
C.0 D.24
解析:选A 垂足(1,c)是两直线的交点,且l1⊥l2,故2a-20=0,∴a=10,l1:10
x
+4y-2=0.将(1,c)代入,得c=-2,将(1,-2)代入l2:2x-5y+b=0,得b=-12.则
a
+b+c=10+(-12)+(-2)=-4.
3.过点M(2,1)的直线l与x轴,y轴分别交于点P,Q两点,且|MP|=|MQ|,则l的方
程是( )
A.x-2y+3=0 B.2x-y-3=0
C.2x+y-5=0 D.x+2y-4=0
解析:选D 由题意可知,M为线段PQ的中点,Q(0,2),P(4,0),可求得直线l的方程
x
+2y-4=0.
4.已知A(-4,2,3)关于xOz平面的对称点为A1,A1关于z轴的对称点为A2,则|AA2|等于
( )
A.8 B.12
C.16 D.19
解析:选A ∵A1(-4,-2,3),A2(4,2,3),∴|AA2|=4+42+2-22+3-32=8.
5.已知圆C与直线x-y=0及x-y-4=0都相切,圆心在直线x+y=0上,则圆C的
方程为( )
A.(x+1)2+(y-1)2=2
B.(x-1)2+(y+1)2=2
C.(x-1)2+(y-1)2=2
D.(x+1)2+(y+1)2=2
解析:选B 由圆心在直线x+y=0上,不妨设为C(a,-a),∴r=|a--a|2=
|a--a-4|
2
,解得a=1,r=2,∴圆C:(x-1)2+(y+1)2=2.
6.(2018·全国卷Ⅲ)直线x+y+2=0分别与x轴,y轴交于A,B两点,点P在圆(x-
2)2+y2=2上,则△ABP面积的取值范围是( )
A.[2,6] B.[4,8]
C.[2,32] D.[22,32]
解析:选A 设圆(x-2)2+y2=2的圆心为C,半径为r,点P到直线x+y+2=0的距离
为d,
则圆心C(2,0),r=2,
所以圆心C到直线x+y+2=0的距离为|2+2|2=22,
可得dmax=22+r=32,dmin=22-r=2.
由已知条件可得|AB|=22,
所以△ABP面积的最大值为12|AB|·dmax=6,
△ABP面积的最小值为12|AB|·dmin=2.
综上,△ABP面积的取值范围是[2,6].
7.若平行直线2x+3y-6=0和4x+6y+a=0之间的距离等于51326,则a的值是
________.
解析:由题意d=51326=-6-a222+32.
∴6+a2=52,解之得a=-7或a=-17.
答案:-7或-17
8.直线l与圆(x+1)2+(y-2)2=5-a(a<3)相交于两点A,B,弦AB的中点为(0,1),
则直线l的方程为________.
解析:圆心为(-1,2),弦中点与圆心连线的斜率为2-1-1-0=-1,由圆的性质知,弦
AB
所在直线即l的斜率为k=1.
故l的方程为x-y+1=0.
答案:x-y+1=0
9.已知直线l:x+my+4=0,若曲线x2+y2+2x-6y+1=0上存在两点P,Q关于直线
l对称,则m
的值为________.
解析:因为曲线x2+y2+2x-6y+1=0是圆(x+1)2+(y-3)2=9,若圆(x+1)2+(y-3)
2
=9上存在两点P,Q关于直线l对称,则直线l:x+my+4=0过圆心(-1,3),所以-1+3
m
+4=0,解得m=-1.
答案:-1
10.已知两直线l1:ax+2y+6=0和l2:x+(a-1)y+(a2-1)=0.
(1)若l1⊥l2,求实数a的值;
(2)试判断l1与l2是否平行.
解:法一:(斜截式方程)
(1)由直线l1的方程知其斜率为-a2,
当a=1时,直线l2的斜率不存在,l1与l2不垂直;
当a≠1时,直线l2的斜率为-1a-1.
由-a2·-1a-1=-1⇒a=23.
故所求实数a的值为23.
(2)由(1)知,当a=1时,l1,l2相交,
当a≠1时,直线l1的斜率为-a2,直线l2的斜率为-1a-1.
由l1∥l2可得-a2=-1a-1,
解得a=-1或a=2.
当a=2时,l1的方程为x+y+3=0,
l2的方程为x+y+3=0,显然l1与l
2
重合.
当a=-1时,l1的方程为x-2y-6=0,l2的方程为x-2y=0,显然l1与l2平行.
所以,当a=-1时,l1∥l2;
当a≠-1时,l1与l2不平行.
法二:(一般式方程)
(1)由已知条件得a·1+2·(a-1)=0⇒a=23,
故所求实数a的值为23.
(2)由A1B2-A2B1=0,得a(a-1)-1×2=0,
即a2-a-2=0,解得a=-1或a=2.
当a=-1时,l1的方程为x-2y-6=0,
l2的方程为x-2y
=0,显然两直线平行.
当a=2时,l1的方程为x+y+3=0,l2的方程为x+y+3=0,显然两直线重合.
所以,当a=-1时,l1∥l2;
