台州书生中学初一分档测试B1卷
平行线的性质与判定 解答题培优专练(原卷)

平行线的性质与判定解答题培优专练1.(2022春·浙江温州·七年级校考期中)如图1,直线AB∥CD,△ABE的顶点E在AB与CD 之间.(1)若∠ABE=150°,∠BAE=20°.△当△CDE=2△EDM时,求△BED的度数.△如图2,作出△CDE的角平分线DF,当DF平行于△ABE中的一边时,求△BED的度数.(2)如图3,△CDE的角平分线DF交EB的延长线于点H,连结BF,当△ABH=2△HBF,1 2∠BED+13∠F=40°时,求△CDE的度数.2.(2022春·浙江金华·七年级校联考期中)如图,直线PQ∥MN,一副直角三角板△ABC、△DEF 中,△ACB=△EDF=90°,△ABC=△BAC=45°,△DFE=30°,△DEF=60°.(1)若△DEF如图1摆放,当ED平分△PEF时,则△DFM=.(2)若图2中△ABC固定,将△DEF沿着AC方向平移,边DF与直线PQ相交于点G,作△FGQ 和△GF A的角平分线GH、FH相交于点H(如图3),求△GHF的度数.(3)若图2中△DEF固定,(如图4)将△ABC绕点A顺时针旋转,1分钟转半圈,旋转至AC 与直线AN首次重合的过程中,当线段BC与△DEF的一条边平行时,请直接写出旋转的时间.(单位必须化成秒)3.(2022春·浙江金华·七年级校联考阶段练习)如图1,已知MN∥PQ,,B在MN上,C在PQ上,A在B的左侧,D在C的右侧,DE平分△ADC,BE平分△ABC,直线DE,BE交于点E,△CBN=120°.(1)若△ADQ=100°,求△BED的度数;(2)在图1中过点D作△ADQ的角平分线与直线BE相交于点F,如图2,试探究△DEB与△DFE 的关系;(3)若改变线段AD的位置,使得点D在点C的左侧,其他条件不变,若△ADQ=n°,过点D 作△PDA的角平分线与直线BE相交于点G,求△BED+△DGE的和是多少度?(用含n的代数式表示)4.(2022春·浙江湖州·七年级统考期末)长江汛期即将来临,为了便于夜间查看江水及两岸河堤的情况,防汛指挥部在一危险地带两岸各安置了一探照灯(如图1),假定这一带长江两岸河堤是平行的,即PQ∥MN,连结AB,且∠ABN=45°.灯A射线自AQ顺时针旋转至AP便立即回转,灯B射线自BM顺时针旋转至BN便立即回转,两灯不停交叉照射巡视.若灯A转动的速度是1度/秒,灯B转动的速度是3度/秒.(1)若两灯同时转动,在灯B射线第一次转到BN之前,两灯射出的光线交于点C.△如图1,当两灯光线同时转动50秒时,求∠ABC的度数.△如图2,过C作CD⊥BC交PQ于点D,则在转动过程中,求∠ABC与∠ACD的比值,并说明理由.(2)若灯A射线先转动30秒,灯B射线才开始转动,在灯A射线第一次转到AP之前,B灯转动几秒,两灯的光线互相平行?5.(2021春·浙江衢州·七年级校考期中)如图1,将一副直角三角板放在同一条直线AB上,它们的一边分别与直线AB重合,其中△ONM=30°,△OCD=45°,将图1中的三角板OMN 绕点O按每秒15°的速度沿逆时针方向旋转α°.(0°<α°<180°).(1)当△AOM=105°时,求旋转角的度数.(2)当两块三角板中至少有一组边互相平行时,求旋转的时间.(3)将图1中的三角板OMN绕点O按逆时针方向旋转得到图2,MN与CD相交于点E,若△CEN=β°时,试探究α与β的数量关系,并直接写出结论.6.(2022春·浙江金华·七年级统考期末)如图,已知AB∥CD,直线MN交AB于点M,交CD于点N.点E是线段MN上一点,P,Q分别在射线MA,NC上,连接PE,QE,PF平分△MPE,QF平分△CQE.(1)如图1,若PE△QE,△EQN=64°,则△MPE=°,△PFQ=°.(2)如图2,求△PEQ与△PFQ之间的数量关系,并说明理由.(3)如图3,当PE△QE时,若△APE=150°,△MND=110°,过点P作PH△QF交QF的延长线于点H.将直线MN绕点N顺时针旋转,速度为每秒5°,直线MN旋转后的对应直线为M′N,同时△FPH绕点P逆时针旋转,速度为每秒10°,△FPH旋转后的对应三角形为△F′PH′,当直线MN首次落到CD上时,整个运动停止.在此运动过程中,经过t秒后,直线M′N恰好平行于△F′PH′的一条边,请直接写出所有满足条件的t的值.7.(2022春·浙江嘉兴·七年级校考期中)如图1,点O为直线AB上一点,过点O作射线OC,使△AOC=60°.将一把直角三角尺的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方,其中△OMN=30°.(1)将图1中的三角尺绕点O顺时针旋转至图2,使一边OM在△BOC的内部,且恰好平分△BOC,求△CON的度数;(2)将图1中的三角尺绕点O按每秒6°的速度绕点O沿顺时针方向旋转一周,OC也以每秒1°的速度绕点O顺时针方向旋转,当三角尺停止运动时,OC也停止运动.△在旋转的过程中,问运动几秒时,边MN恰好与射线OC平行;△将图1中的三角尺绕点O顺时针旋转至图3,使ON在△AOC的内部,请探究△AOM与△NOC 之间的数量关系(直接写出结果).8.(2022春·浙江台州·七年级校联考阶段练习)如图1,已知两条直线AB,CD被直线EF所截,分别交于点E,点F,EM平分△AEF交CD于点M,且△FEM=△FME.(1)判断直线AB与直线CD是否平行,并说明理由;(2)如图2,点G是射线MD上一动点(不与点M,F重合),EH平分△FEG交CD于点H,过点H作HN△EM于点N,设△EHN=α,△EGF=β.△当点G在点F的右侧时,若β=56°,求α的度数;△当点G在运动过程中,α和β之间有怎样的数量关系?请写出你的猜想,并加以证明.9.(2021春·浙江绍兴·七年级校考阶段练习)已知直线l1∥l2,直线l3,l4分别与l1,l2交于点B,F和A,E,点P是直线l3上一动点(不与点B,F重合),设△BAP=△1,△PEF=△2,△APE=△3.(1)如上图,当点P在B,F两点之间运动时,试确定△1,△2,△3之间的关系,并给出证明;(2)当点P在B,F两点外侧运动时,试探究△1,△2,△3之间的关系,画出图形,给出结论,不必证明.10.(2022春·浙江衢州·七年级统考期末)已知△ABC与△ADE共顶点A,∠BAC=∠DAE=90∘,顶点B和C在直线l1上(点B在点C的左侧),顶点D和E在直线l2上(点D在点E的左侧),且直线l1∥l2.(1)如图1,顶点A在l1与l2之间,判断△BAD与∠ABC+∠ADE是否相等,并说明理由.(2)如图2,顶点A在l1与l2之间,△ABC的外角平分线与△AED的角平分线交于点F,若∠BAD=70∘,求△BFE的度数.(3)若顶点A在直线l2的下方,且顶点B、A、D不在一条直线上,△ABC的外角平分线与△AED 的角平分线交于点F,记∠BAD=α,∠BFE=β,请探究α与β的数量关系,并直接写出结论.11.(2022春·浙江金华·七年级统考期末)如图,AB、CD被AC所截,AB∥CD,△CAB=108°,点P为直线AB上一动点(不与点A重合),连CP,作△ACP和△DCP的平分线分别交直线AB于点E、F.(1)当点P在点A的右侧时△若△ACP=36°,则此时CP是否平分△ECF,请说明理由.△求△ECF的度数.(2)在点P运动过程中,直接写出△APC与△AFC之间的数量关系.12.(2022春·浙江湖州·七年级统考期末)如图1,已知直线AB∥CD,∠CMN=60∘,射线ME 从MD出发,绕点M以每秒a度的速度按逆时针方向旋转,到达MC后立即以相同的速度返回,到达MD后继续改变方向,继续按上述方式旋转;射线NF从NA出发,绕点N以每秒b度的速度按逆时针方向旋转,到达NB后停止运动,此时ME也同时停止运动.其中a,b满足方程组{4a+b=173a−2b=10.(1)求a,b的值;(2)若NF先运动30秒,然后ME一起运动,设ME运动的时间为t,当运动过程中ME∥NF时,求t的值;(3)如图2,若ME与NF同时开始转动,在ME第一次到达MC之前,ME与NF交于点P,过点P 作PQ⊥ME于点P,交直线AB于点Q,则在运动过程中,若设∠NME的度数为m,请求出∠NPQ 的度数(结果用含m的代数式表示).13.(2022春·浙江绍兴·七年级统考期末)已知AB△CD,(1)如图1,若△ABE=160°,△CDE=120°,求△BED的度数;(2)如图2,若BF平分△ABE,DF平分△CDE,则△BFD与△BED有怎样的数量关系,并说明理由;(3)如图3,若BF平分△ABE,DF平分△CDE,则△BFD与△BED有怎样的数量关系,并说明理由.14.(2022春·浙江宁波·七年级校考期中)如图,直线PQ∥MN,一副三角尺(∠ABC=∠CDE= 90°,∠ACB=30°,∠BAC=60°,∠DCE=∠DEC=45°)按如图△放置,其中点E在直线PQ 上,点B,C均在直线MN上,且CE平分∠ACN.(1)求∠DEQ的度数.(2)如图△,若将三角形ABC绕点B以每秒2度的速度按逆时针方向旋转(A,C的对应点分别为F,G),设旋转时间为t(s)(0≤t≤90).△在旋转过程中,当BG∥CD时,求t的值.△若在三角形ABC绕点B旋转的同时,三角形CDE绕点E以每秒1度的速度按顺时针方向旋转(C,D的对应点为H,K),请直接写出当BG∥HK时t的值.15.(2022春·浙江金华·七年级校考期中)(1)如图1,点E在BC上,△A=△D,△ACB=△CED.请说明AB∥CD的理由.(2)如图2,AB∥CD,BG平分△ABE,与△EDF的平分线交于H点,若△DEB比△DHB大60°.求△DEB的度数.(3)保持(2)中所求的△DEB的度数不变,如图3,AB∥CD,BM平分△EBK,DN平分△CDE,作BP∥DN,则△PBM的度数是否改变?若不变,请直接写出△PBM的度数;若改变,请说明理由.16.(2022春·浙江湖州·七年级校联考阶段练习)(1)【问题】如图1,若AB∥CD,∠BEP=25°,∠PFC=150°,求∠EPF的度数;(提示:过点P作PQ∥AB)(2)【问题迁移】如图2,AB∥CD,点P在AB的上方,∠PEA,∠PFC,∠EPF之间有何数量关系?请说明理由;(3)【联想拓展】如图3所示,在(2)的条件下,已知∠EPF=α,∠PEA的平分线和∠PFC的平分线交于点G,用含有α的式子表示∠G的度数.17.(2022春·浙江宁波·七年级校联考期末)如图△,AB,BC被直线AC所截,点D是线段AC 上的点,过点D作DE∥AB,连接AE,∠B=∠E=60°.(1)请说明AE∥BC;(2)将线段AE沿着直线..AC平移得到线段PQ,连接DQ.△.如图△,当DE⊥DQ时,则∠Q的度数=_____________;△.在整个运动中,当∠Q=2∠EDQ时,∠Q=_____________.18.(2022春·浙江宁波·七年级校考期中)如图,直线CD//EF,点A、B分别在直线CD、EF上(自左向右分别为点C、A、D和点E、B、F),△ABF=60°,射线AM自射线AB的位置开始,绕点A以每秒1°的速度沿逆时针方向旋转,同时,射线BN自射线BE开始以每秒5°的速度绕点B沿顺时针方向旋转,当射线BN旋转到BF的位置时,两者均停止运动,设旋转时间为x秒.(1)如图1,直接写出下列答案:△△BAD的度数是;△当旋转时间x= 秒时,射线BN过点A.(2)如图2,若AM∥BN,求此时对应的旋转时间x的值.(3)若两条射线AM和BN所在直线交于点P,△如图3,若点P在CD与EF之间,且△APB=126°,求旋转时间x的值;△若旋转时间x<24,求△APB的度数(用含x的代数式表示).19.(山西省忻州市代县2021-2022学年七年级下学期期末数学试题)如图1,AB∥CD,点E 为直线AB,CD外一点.(1)若AE⊥AB,∠C=65°,求出△E的度数.(2)如图2,点F在BA的延长线上,连接BE,EF,若CE⊥CD,EF平分∠AEC,∠B=∠AEB,求∠BEF的度数:(3)如图3,在(2)的条件下,过点F作∠BFG=∠BFE,交EC的延长线于点G,延长EF 交CD于点H,过点F作FI∥BE交CD于点I.当FH平分∠IFG时,请直接写出∠CHF的度数.20.(山东省日照市岚山区2021-2022学年七年级下学期期末考试数学试题)(1)阅读下面材料:已知:如图1,AB∥CD,E为AB,CD之间一点,连接AE,CE,得到∠AEC.求证:∠AEC+∠A+∠C=360°.解答过程如下,并请你在括号内填写推理的依据:过点E作EF∥AB,则有∠AEF+∠A=180°(______).△AB∥CD,△EF∥CD(______).△∠FEC+∠C=180°(______).△∠AEF+∠A+∠FEC+∠C=360°,又△∠AEC=∠AEF+∠FEC△∠AEC+∠A+∠C=360°.假若将具有图1特征的图形称为“平行凸折线”,“平行凸折线”的性质可以表述如下:若AB∥CD,E为AB,CD之间一点,则有∠AEC+∠A+∠C=360°(2)已知:直线m∥n,点A,B在直线m上,点C,D在直线n上,连接AD,BC,BE平分∠ABC,DE平分∠ADC,且BE,DE所在的直线交于点E.△如图2,当点D在点C的左侧时,若∠ADC=80°,∠BED=160°,请你结合(1)中“平行凸折线”的性质,求∠ABC的度数;△如图3,当点D在点C的右侧时,设∠ABC=α,∠ADC=β,请直接写出∠BED的度数(用含有α,β的式子表示).21.(江苏省江阴市周庄中学2021-2022学年七年级下学期3月限时作业数学试题)(1)光线从空气中射入水中会产生折射现象,同时光线从水中射入空气中也会产生折射现象,如图1,光线a从空气中射入水中,再从水中射入空气中,形成光线b,根据光学知识有△1=△2,△3=△4,请判断光线a与光线b是否平行,并说明理由.(2)光线照射到镜面会产生反射现象,由光学知识,入射光线与镜面的夹角与反射光线与镜面的夹角相等,如图2有一口井,已知入射光线a与水平线OC的夹角为42°,问如何放置平面镜MN,可使反射光线b正好垂直照射到井底?(即求MN与水平线的夹角)(3)如图3,直线EF上有两点A、C,分别引两条射线AB、CD.△BAF=110°,△DCF=60°,射线AB、CD分别绕A点,C点以1度/秒和3度/秒的速度同时顺时针转动,设时间为t,在射线CD转动一周的时间内,是否存在某时刻,使得CD与AB平行?若存在,求出所有满足条件的时间t.22.(2021春·浙江·七年级阶段练习)如图1,已知AB△CD,△B=30°,△D=120°;(1)若△E=60°,则△F=;(2)请探索△E与△F之间满足的数量关系?说明理由;(3)如图2,已知EP平分△BEF,FG平分△EFD,反向延长FG交EP于点P,求△P的度数.23.(2022春·浙江台州·七年级台州市书生中学校考期中)“一带一路”让中国和世界更紧密,“中欧铁路”为了安全起见在某段铁路两旁安置了两座可旋转探照灯,便于夜间查看道路安全情况,如图,灯A射线AM′自AM顺时针旋转至AN便立即回转,灯B射线BQ′自BQ顺时针旋转至BP便立即回转,两灯不停交叉照射巡视.若灯A转动的速度是a°/秒,灯B转动的速度是b°/秒,且a、b满足√5−a+|b−a+3|=0,假定主道路的两边是平行的,即PQ△MN.(1)求a、b的值;(2)若灯B的射线BQ′先转动30秒,灯A的射线AM′才开始转动,在射线BO′到达BP之前,射线AM′转动几秒,两灯的光束互相平行?(3)若灯A、B的射线AM′,BQ′同时转动t秒,在射线BQ′到达BP之前,记射线AM′与BQ′交于点H,若两束光束垂直,求t的值.24.(2021春·浙江·七年级专题练习)问题情境在综合与实践课上,老师让同学们以“两条平行线AB,CD和一块含60°角的直角三角尺EFG (△EFG=90°,△EGF=60°)”为主题开展数学活动.操作发现(1)如图(1),小明把三角尺的60°角的顶点G放在CD上,若△2=2△1,求△1的度数;(2)如图(2),小颖把三角尺的两个锐角的顶点E、G分别放在AB和CD上,请你探索并说明△AEF与△FGC之间的数量关系;结论应用(3)如图(3),小亮把三角尺的直角顶点F放在CD上,30°角的顶点E落在AB上.若∠AEG=α,则△CFG等于______(用含α的式子表示).25.(2021春·浙江衢州·七年级浙江省衢州市衢江区实验中学校考开学考试)将一副三角板中的两个直角顶点C叠放在一起(如图△),其中△A=30°,△B=60°,△D=△E=45°.(1)猜想△BCD与△ACE的数量关系,并说明理由;(2)若△BCD=4△ACE,求△BCD的度数;(3)若按住三角板ABC不动,绕顶点C转动三角DCE,试探究△BCD等于多少度时CE△AB,并简要说明理由.26.(2022春·浙江金华·七年级义乌市绣湖中学教育集团校联考阶段练习)如图,直线MN//PQ,将一副三角板中的两块直角三角板如图1放置,△ACB=△EDF=90°,△ABC=△BAC=45°,△DFE=30°,△DEF=60°,此时点A与点E重合.(1)对于图1,固定△ABC的位置不变,将△DEF绕点E按顺时针方向进行旋转,旋转至DE与BC首次平行,如图2所示,求此时△F AC的度数.(2)对于图1,固定△ABC的位置不变,将△DEF沿AC方向平移至点F正好落在直线MN上,再将△DEF绕点F按顺时针方向进行旋转,如图3所示.△若边EF与边BC交于点G,试判断△BGF﹣△EFN的值是否为定值,若是定值,则求出该定值,若不是定值,请说明理由;△对于图3,固定△ABC的位置不变,将△DEF绕点F顺时针方向以每秒10°的速度进行旋转,当EF与直线MN首次重合时停止运动当经过t秒时,线段DE与△ABC的一条边平行,求满足条件的t的值.27.(2020春·浙江杭州·七年级统考期末)问题情境:如图1,已知AB△CD,∠APC=108°.求∠PAB+∠PCD的度数.经过思考,小敏的思路是:如图2,过P作PE△AB,根据平行线有关性质,可得∠PAB+∠PCD=360°−∠APC=252°.问题迁移:如图3,AD△BC,点P在射线OM上运动,∠ADP=∠α,∠BCP=∠β.(1)当点P在A、B两点之间运动时,∠CPD、∠α、∠β之间有何数量关系?请说明理由.(2)如果点P在A、B两点外侧运动时(点P与点A、B、O三点不重合),请你直接写出∠CPD、∠α、∠β之间的数量关系.(3)问题拓展:如图4,MA1△NA n,A1−B1−A2−⋯−B n−1−A n是一条折线段,依据此图所含信息,把你所发现的结论,用简洁的数学式子表达为.28.(2020春·浙江宁波·七年级统考期中)已知AM∥CN,点B为平面内一点,AB⊥BC于B.(1)如图,直接写出∠A和∠C之间的数量关系.(2)如图,过点B作BD⊥AM于点D,求证:∠ABD=∠C.(3)如图,在(2)问的条件下,点E,F在DM上,连接BE,BF,CF,BF那平分∠DBC,BE平分∠ABD,若∠FCB+∠NCF=180°,∠BFC=3∠DBE,求∠EBC的度数.29.(2021春·浙江金华·七年级统考期末)如图1,在△ABC中,△B=65°,△BAC=75°,D 为AC边上一点,分别过点A、D作BC、AB的平行线交于点E.(1)求△E的度数.(2)点P为直线AC上的一个动点,过点P作PF△AE,且PF=AE,连DF.△如图2,当点P在点C的右侧,且△PFD=25°时,判断DE与DF的位置关系,并说明理由.△在整个运动中,是否存在点P,使得△PFD=2△EDF?若存在,请求出△PFD的度数,若不存在,请说明理由.30.(2021春·浙江宁波·七年级统考期末)如图,直线CD//EF,点A,B分别在直线CD,EF上(自左向右分别为点C,A,D和点E,B,F),∠ABF=60°.射线AM自射线AB的位置开始,绕点A以每秒1°的速度沿逆时针方向旋转,同时,射线BN自射线BE开始以每秒5°的速度绕点B沿顺时针方向旋转,当射线BN旋转到BF的位置时,两者均停止运动,设旋转时间为x秒.(1)如图1,直接写出下列答案:△∠BAD的度数是______.△当旋转时间x=______秒时,射线BN过点A.(2)如图2,若AM//BN,求此时对应的旋转时间x的值.(3)若两条射线AM和BN所在直线交于点P.△如图3,若点P在CD与EF之间,且∠APB=126°,求旋转时间x的值.△若旋转时间x<24,求∠APB的度数(直接写出用含x的代数式表示的结果).。
人教版七年级下册数学重点知识点练习及答案解析——命题、定理及平移测试

人教版七年级下册数学重点知识点练习及答案解析——命题、定理及平移测试一、选择题(本大题共14个小题,每题2分,共28分,在每个小题的四个选项中只有一项是符合题目要求的)1.(2019·江苏初一月考)在以下现象中:①温度计中,液柱的上升或下降;②打气筒打气时,活塞的运动;③钟摆的摆动;④传送带上,瓶装饮料的移动,属于平移的是()A.①,②B.①,③C.②,③D.②,④【答案】D【解析】①温度计中液柱的上升或下降改变图形的大小,不属于平移;②打气筒打气时,活塞的运动属于平移;③钟摆的摆动是旋转,不属于平移;④传送带上瓶装饮料的移动符合平移的性质,属于平移,故选D.2.(2019·重庆市忠县拔山中学校初一期中)下列语句不是命题的是()A.熊猫没有翅膀B.点到直线的距离C.若|a|=|b| ,则a=b D.小明是七年级二班的学生【答案】B【解析】熊猫没有翅膀、若|a|=|b|,则a=b和小明是七年级(2)班的学生都是命题,而点到直线的距离为一个名称,它不是命题.故选B.3.(2019·浙江初一期中)如图,A,B,C,D中的哪幅图案可以通过图案①平移得到()A.B.C.D.【答案】D【解析】通过图案①平移得到必须与图案①完全相同,角度也必须相同,观察图形可知D可以通过图案①平移得到.故答案选:D.4.(2019·邓州市张村乡中学初一期末)下面给出的结论中,说法正确的有()①最大的负整数是﹣1;②在同一个平面内,经过一个已知点只能画一条直线和已知直线垂直;③当a≤0时,|a|=﹣a;④若a2=9,则a一定等于3;⑤邻补角的两条角平分线构成一个直角;⑥同旁内角相等,两直线平行.A.2个B.3个C.4个D.5个【答案】C【解析】①最大的负整数是﹣1,正确;②在同一个平面内,经过一个已知点只能画一条直线和已知直线垂直,正确;③当a≤0时,|a|=﹣a,正确;④若a2=9,则a=±3,错误;⑤邻补角的两条角平分线构成一个直角,正确;⑥同旁内角互补,两直线平行,错误.故选C.5.(2019·嵊州市谷来镇中学初二期中)在下列命题中,为真命题的是()A.两个锐角的和是锐角B.相等的角是对顶角C.同旁内角互补D.同角的补角相等【答案】D【解析】解:A、错误.两个锐角的和可能是锐角或直角或钝角;B、错误.相等的角不一定是对顶角;C、错误,两直线平行时同旁内角互补;D、正确.故选:D.6.(2019·河北初三期中)在图示的四个汽车标志图案中,能用平移变换来分析其形成过程的图案是()A.B.C.D..【答案】D【解析】解:A.可以通过轴对称变换得到;B.不能通过平移变换得到;C. 可以通过旋转得到;D. 可以通过平移变换得到,故选:D.7.(2019·上海市江宁学校初一期中)一辆汽车在笔直的公路上,两次拐弯后,仍在原来的方向上平行前进,则这两次拐弯的角度应是()A.第一次向左拐40°,第二次向右拐40°B.第一次向右拐40°,第二次向左拐140°C.第一次向左拐40°,第二次向左拐140°D.第一次向右拐40°,第二次向右拐140°【答案】A【解析】如图,第一次拐的角是∠1,第二次拐的角是∠2,由于平行前进,可以得到∠1=∠2.故选A.8.(2019·重庆市两江育才中学校初二开学考试)如图,已知直角△ABC中,∠B=90°,AB=8,BC=6,把斜边AC 分成n段,以每段为对角线作小长方形,则所有这些小长方形的周长的和是()A.14B.28C.14nD.28n【答案】B【解析】∵∠B=90°,AB=8,BC=6,且斜边AC平均分成n段,∴小矩形的长为ABn=8n,宽为BCn=6n,∴一个小矩形的周长为:2(86n n)=28n,∴这些小矩形的面积和是n•28n=28.故选:B.9.(2019·浙江初二期中)能说明命题“若|a|=|b|,则a=b”是假命题的反例为()A.a=2,b=-2B.a=1,b=0C.a=1,b=1D.a=-3,b= 1 3【答案】A【解析】解:若a,b互为相反数,则|a|=|b|,a≠b,命题“若|a|=|b|,则a=b”是假命题,则a ,b 互为相反数即可, a=2,b=-2时,a ,b 互为相反数,故答案为A.10.(2019·呼伦贝尔市海拉尔区铁路第三中学初一期末)将一副三角板按如图放置,则下列结论中,正确的有( ) ①∠1=∠3;②如果∠2=30°则有AC ∥DE ;③如果∠2=30°,则有BC ∥AD ;④如果∠2=30°,必有∠4=∠CA .①②③B .①②④C .③④D .①②③④【答案】B【解析】 解:∵∠1+∠2=90°,∠3+∠2=90°,∴∠1=∠3,①正确;∵∠2=30°,∴∠1=60°,又∵∠E =60°,∴∠1=∠E ,∴AC ∥DE ,②正确;∵∠2=30°,∴∠1+∠2+∠3=150°,又∵∠C =45°,∴BC 与AD 不平行,③错误;∵∠2=30°∴AC ∥DE ,∴∠4=∠C ,④正确.故选:B .11.(2019·浙江初二期中)能说明命题“若22a b =,则a b =”是假命题的一个反例可以是( )A .2,2a b ==-B .2,3a b ==C .2,2a b =-=-D .2,3a b =-=-【答案】A【解析】若22a b =,则a=b”是假命题的一个反例可以是a=2,b=-2.故选A.12.(2019·昆明市呈贡区实验学校初二期末)某同学在研究传统文化“抖空竹”时有一个发现:他把它抽象成数学问题,如图所示:已知//AB CD ,87BAE ∠=︒,121DCE ∠=︒,则E ∠的度数是( )A .28︒B .34︒C .46︒D .56︒【答案】B【解析】解:如图,延长DC 交AE 于F ,//AB CD Q ,87BAE ∠=︒,87CFE ∴∠=︒,又121DCE ∠=︒Q ,1218734E DCE CFE ∴∠=∠-∠=︒-︒=︒,故选:B .13.(2017·内蒙古初一期末)如图,将半径为2cm 的半圆水平向左平移2cm ,则半圆所扫过的面积(阴影部分)为( ).A .2cm πB .24cmC .2ππ⎛⎫- ⎪⎝⎭ cm 2D .2ππ⎛⎫+ ⎪⎝⎭cm 2【答案】B【解析】 根据图形可知阴影面积为:2×2=4;故选B.14.(2019·浙江初二月考)某校八年级四个班的代表队准备举行篮球赛.甲、乙、丙三位同学预测比赛的结果如下:甲说:“802班得冠军,804班得第三”;乙说:“801班得第四,803班得亚军”;丙说:“803班得第三,804班得冠军”赛后得知,三人都只猜对了一半,则得冠军的是( )A .801班B .802班C .803班D .804班【答案】B【解析】解:假设甲说的“802班得冠军”是正确的,那么丙说的“804班得冠军”是错误的,“803班得第三”就是正确的,那么乙说的“803班得亚军”是错误的,“801班得第四”是正确的,这样三人都猜对了一半,且没矛盾.故猜测是正确的.故选:B.二、填空题(本题共4个小题;每个小题3分,共12分,把正确答案填在横线上)15.(2018·浙江初二期中)把命题“在一个三角形中,等角对等边”改写成“如果……那么……”的形式为.【答案】如果在一个三角形中有两个角相等,那么这两个角所对的边也相等【解析】因为条件是:在同一个三角形中有两个角相等,结论为:这两个角所对的边也相等.所以改写后为:如果在同一个三角形中有两个角相等,那么这两个角所对的边也相等.16.(2019·上海尚德实验学校初一月考)如图,在长方形ABCD中,AB=7cm,BC=10cm,现将长方形ABCD向右平移3m,再向下平移4cm后到长方形A'B'C'D'的位置,A'B'交BC于点E,A'D'交DC于点F,那么长方形A'ECF 的周长为_____cm.【答案】20【解析】解:由题意得到BE=3cm,DF=4cm,∵AB=DC=7cm,BC=10cm,∴EC=BC-BE=10cm-3cm=7cm,FC=DC-DF=7cm-4cm=3cm,∴长方形A'ECF的周长=2×(7+3)=20(cm),故答案为20.17.(2019·山东初二期末)如图,直线AB∥CD,∠C=44°,∠E为直角,则∠1=_____.134【答案】0【解析】如图,过E作EF∥AB,根据平行于同一直线的两直线互相平行,求出AB∥CD∥EF,根据平行线的性质得出∠C=∠FEC=44°,∠BAE=∠FEA,求出∠BAE=90°-44°=46°,即可求出∠1=180°-46°=134°.18.(2018·辽宁初二期末)如图,直线a∥b,△ABC是等边三角形,点A在直线a上,边BC在直线b上,把△ABC 沿BC方向平移BC的一半得到△A′B′C′(如图①);继续以上的平移得到图②,再继续以上的平移得到图③,…;请问在第100个图形中等边三角形的个数是___.【答案】301.【解析】∵△ABC是等边三角形,∴AB=BC=AC,∵A′B′∥AB,BB′=B′C=12 BC,∴B′O=12AB,CO=12AC,∴△B′OC是等边三角形,同理阴影的三角形都是等边三角形.观察图可得,第1个图形中大等边三角形有2个,小等边三角形有2个,第2个图形中大等边三角形有3个,小等边三角形有4个,第3个图形中大等边三角形有4个,小等边三角形有6个,…依次可得第n个图形中大等边三角形有n+1个,小等边三角形有2n个.故第100个图形中等边三角形的个数是:100+1+2×100=301.故答案是301.三、解答题(本题共8道题,19-21每题6分,22-25每题8分,26题10分,满分60分)19.(2019·全国初二课时练习)下列句子中哪些是命题?(1)动物需要水;(2)玫瑰花是动物;(3)美丽的天空;(4)相等的角是对顶角;(5)负数都小于0;(6)你的作业做完了吗?【答案】(1)(2)(4)(5)是命题【解析】根据命题的定义(1)(2)(4)(5)都对一件事情做出了判断,因此属于命题,(3)“美丽的天空”不是判断语句,因此不是命题,(6)是疑问句,因此不是命题。
七年级数学下学期第一次月考试题新人教版

浙江省台州市书生中学 七年级数学下学期第一次月考试题1. 在平面直角坐标系中,点P )1,1(2+-m 必然在【 】A .第一象限B .第二象限C .第三象限D .第四象限 2. 以下实数33,9,15.3,2,0,87,3--π中,无理数有【 】 A .1个 B .2个 C .3个 D .4个3.如图1,三条直线1l ,2l ,3l 相交于点E ,那么123++=∠∠∠【 】A .3600B .1800C .1200D .9004.已知点A (2,2-),若是把点A 向上平移4个单位,再向左平移4个单位取得点C,那么C 点的坐标是【 】 A .(2-,2) B .(2,2) C .(1-,1-) D .(2-,2-) 5.如图,图中∠1与∠2是同位角的是【 】⑴ ⑵ ⑶ ⑷ A .⑵⑶ B .⑵⑶⑷ C .⑴⑵⑷ D .⑶⑷ 6. 以下各式正确的选项是【 】A .5)5(2-=- B . 15)15(2-=-- C .5)5(2±=- D .2121= 7.下面两点中,关于x 轴对称的是【 】A .(3,5-)和(3-,5-);B .(1-,3)和(1,3-);C .(2-,4)和(2,4-);D .(5,3-)和(5,3). 8.如图,AB ∥EF ,∠C=90°,那么α、β和γ的关系是【 】A .α+γ=βB .α+β-γ=90°C .β+γ-α=90°D .α+β+γ=180°9.平面直角坐标系xoy 中,有两点A (m ,0),B (5,8),请你求出线段AB 的最小值, 及现在m 的值( )A. AB 最小值为5,m =8B. AB 最小值为3,m =0C. AB 最小值为5,m =5D. AB 最小值为8,m =510.如图①,一张四边形纸片ABCD ,∠A =50°,∠C =150°.假设将其依照图②所示方式折叠后,恰好MD ′∥AB ,ND ′∥BC ,那么∠D 的度数为 ( ).A. 70°B. 75°C. 80°D. 85°第3题图1 2 1 22 1 12第8题图序号 座位号----------------线---------------------------------10题图 图① 图② 二、填空题:(此题6小题,每题3分,共18分) 11.21-的相反数是_________.依照以上变换有:[(3)](3)(3)g f g -=--=-,4,4,4,那么[(5)]f g ,2等于 . 14.已知点P 的坐标为(2a -,36a +),且点P 到两坐标轴的距离相等,那么点P 坐标 是________ . 15.如图,已知,AB B AOC ∠OE AB 75,A C ︒∠+∠=7.5,ABE ︒∠=C ∠=° 16.如图,在平面直角坐标系中,有假设干个横坐标和纵坐标都是整数的点,其顺序排列规律如下:(1,0),(2,0),(2,1),(3,2),(3,1),(3,0),…,依照那个规律探讨可得,第100个点的坐标为__________;第2015个点的坐标为__________.台州市书生中学二、填空题:(此题6小题,每题3分,共18分)11. 12. ____________________________________________________.13. 14.________ .15. 题号 1 2 3 4 5 6 7 8 9 10 答案第19题EAOCB三、解答题:(此题8小题,共52分)17.计算(此题6分):(1)412743+- (2)32332327)21()4()2()2(---⨯-+-⨯-18.(6分) 已知:如图,点A 、B 、C 在一条直线上, AD ∥BE ,∠1=∠2.将求证:∠A =∠E 的进程填空完整.证明:∵AD ∥BE ∴∠A = ( ), 又∵∠1=∠2∴ED ∥ ( ),∴∠E = ( ),∴∠A =∠E19.(5分)如图,已知CD ∥AF ,BAF CDE ∠=∠,BC AB ⊥,︒=∠124C ,︒=∠80E ,求F ∠的大小.20.(此题8分)如图,在平面直角坐标系中,B 点坐标为(2-,1).(1)请在图中画出将四边形ABCD 先向右平移6个单位长度,再向上平移2个单位长度后的四边形C DBDBECA21第18题D C B A '''';并写出点A '、B '、C '、D '的坐标. (2)求四边形ABCD 的面积.21.(此题6分)已知:如图, AE ⊥BC 于M , FG ⊥BC 于N , ∠1=∠2, ∠D =∠3+60︒, ∠CBD =70︒ . (1)求证:AB ∥CD ;(2)求∠C 的度数.DC E G22.(本小题6分)如图,长方形OABC 中,O 为平面直角坐标系的原点,点A 、C 的坐标别离为A (3,0)、 C (0,2),点B 在第一象限。
浙江省台州市书生中学2013-2014学年下学期初中八年级期中考试科学试卷 有答案
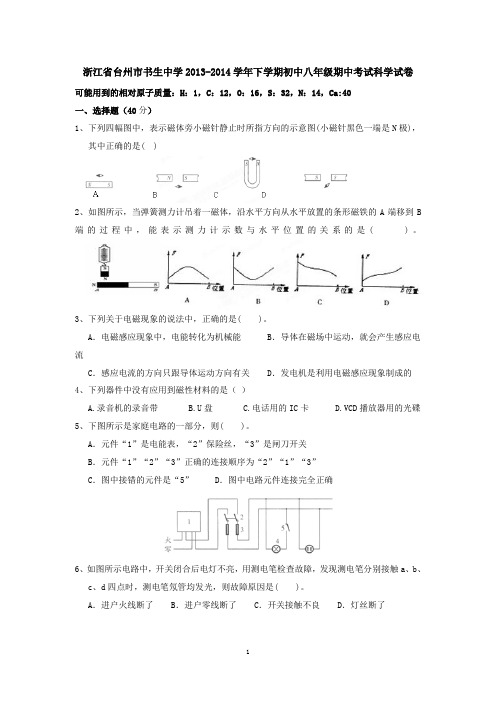
浙江省台州市书生中学2013-2014学年下学期初中八年级期中考试科学试卷可能用到的相对原子质量:H:1,C:12,O:16,S:32,N:14,Ca:40一、选择题(40分)1、下列四幅图中,表示磁体旁小磁针静止时所指方向的示意图(小磁针黑色一端是N极),其中正确的是( )2、如图所示,当弹簧测力计吊着一磁体,沿水平方向从水平放置的条形磁铁的A端移到B 端的过程中,能表示测力计示数与水平位置的关系的是( )。
3、下列关于电磁现象的说法中,正确的是( )。
A.电磁感应现象中,电能转化为机械能 B.导体在磁场中运动,就会产生感应电流C.感应电流的方向只跟导体运动方向有关 D.发电机是利用电磁感应现象制成的4、下列器件中没有应用到磁性材料的是()A.录音机的录音带B.U盘C.电话用的IC卡D.VCD播放器用的光碟5、下图所示是家庭电路的一部分,则( )。
A.元件“1”是电能表,“2”保险丝,“3”是闸刀开关B.元件“1”“2”“3”正确的连接顺序为“2”“1”“3”C.图中接错的元件是“5” D.图中电路元件连接完全正确6、如图所示电路中,开关闭合后电灯不亮,用测电笔检查故障,发现测电笔分别接触a、b、c、d四点时,测电笔氖管均发光,则故障原因是( )。
A.进户火线断了 B.进户零线断了 C.开关接触不良 D.灯丝断了7、一只小鸟落在11万伏的高压输电线上,虽然通电的高压线是裸露的电线,但小鸟仍安然无恙,这是因为( )。
A.鸟有耐高压的天性 B.鸟脚是干燥的,鸟的身体不导电C.鸟两脚间的电压几乎为零 D.乌体电阻极大所以无电流通过小鸟8、下列四幅图中,哪幅图是表示研究电磁感应现象的实验装置()A. B. C. D.9、以下属于模型的是()10、1932年,美国化学家H.C尤里等发现了一种质子数与氢原子相同,但中子数比氢原子多一个的新原子,关于这种原子的说法中,正确的是()。
A.是与氢原子相同的原子 B.是氢元素的另一种原子C.是一种新元素 D.是与氢元素不同类的原子11、如图,α粒子是一种带正电荷的粒子,卢瑟福用α粒子轰击金属箔,发现小部分α粒子发生偏转,极少的α粒子甚至像碰到硬核似地反弹回来,大部分α粒子却能通过原子,这一实验不能说明的是( )A、原子核极其微小B、原子并不是一个实心球体,大部分空间是空的C、粒子发生偏转是因为原子核质量很大且同种电荷之间互相排斥D、电子围绕着核作高速运动12、下列符号中,同时表示一种单质、一种原子和一种元素的是()。
浙江省台州市书生中学2021学年下学期高二年级开学考试语文试卷

浙江省台州市书生中学2020-2021学年下学期高二年级开学考试语文试卷(满分:150分考试时间:150 分钟)1.下列加点字的注音正确的一项是()(3分)A.创痕(chuāng)晕车(yùn)老妪(yù)悄无声息(qiǎo)B.症结(hēng)攒射(cuán)间(jiān)断菲薄(fěi)C.矜持(jīn)乳媪(ǎo)泠然(líng)笑靥儿(yàn)D.绯闻(fěi)谂知(shěn)强颜(qiǎng)呱呱而泣(gū)2.下列各句中,没有错别字的一项是()(3分)A.苻坚的人生剽悍而无奈,他前期安邦定国,文治武功,彪炳一时,最后却在淝水之战中遭遇人生最大败迹,身死国灭,只留后人空嗟叹。
B.科教片《美丽星球》为我们捕捉到地球的许多瞬间,从清晨形如金色弹丸的美丽星球,到夜晚人世间的斑斓灯火,无不美得慑人心魄。
C.下雨的日子,平时紧张忙碌得快要绷断了的那一根根弦,这会儿全放松下来,心绪便开始信马由缰、一无羁勒地恣意驰骋。
D.在阅读浩如烟海的经典作品时,切勿把大师的思想奉为圭皋,不知不觉画地为牢,让自己变成面目可憎的教条主义者。
3.下列句中加点词语的运用,不正确...的一项是()(3分)A.有的放矢....的批评和自我批评是我们党保持肌体健康,不断增强战斗力的锐利武器。
B.名为“海贝斯”的强大台风正在靠近,当地民众人心惟危....,纷纷采购食品作为储备。
C.当今世界,一些国家之间战火不绝,人类能否化干戈为玉帛......,最终达到和谐共生呢D.九层之台....,起于累土....。
要把十九大描绘的蓝图变为现实,必须从最基础的工作做起。
A.网络谣言,不仅损害了公民权益,而且扰乱了社会秩序,事实表明,网络谣言的泛滥和滋生,会使许多人成为受害者。
B.望着玉苍山上密布的形态各异的奇石,形成石的海洋,场面十分壮观,无不使游览者感受到大自然的壮美雄奇和神功伟力。
C.中国古代文学中发展得最为成熟的样式是以抒情为主要功能的诗歌,而抒情性质使中国古代文学在总体上具有诗的光辉。
台州书生中学初中招生条件

台州书生中学初中招生条件
台州书生中学初中招生条件如下:
一、户籍条件
1.在台州市区范围内或台州市台州开发区、临海市中心城区、温岭市中心城区居住三年及以上,有常住户口的适龄未入学的初中学生均可报名。
2.在温岭市其他城镇和县区,可以报名参加考试,但需要参加温岭市中考并且成绩合格后才能录取。
二、学业表现条件
1.学习成绩优秀,品学兼优的学生优先被录取。
2.没有考试作弊和违纪违规行为,有良好的学习和生活习惯。
三、体育艺术条件
1.具有一定的体育或艺术特长者,可在招生时优先录取。
2.体育文化素质高,身体素质较好的学生也会得到优先录取的机会。
四、其他条件
1.符合国家和地方相关规定的义务教育入学资格条件。
2.未患有传染性疾病或其他有影响入学的身体疾病。
台州书生中学招生条件严格,但对于优秀的学生来说,一定会给予相应的机会和录取资格。
希望有志于进入该校的学生在报名和考试准备过程中,请勤奋学习,保持好的态度,争取更好的成绩和表现。
2025届浙江省台州市温岭市书生中学高考临考冲刺语文试卷含解析
2025届浙江省台州市温岭市书生中学高考临考冲刺语文试卷考生请注意:1.答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内,不得在试卷上作任何标记。
2.第一部分选择题每小题选出答案后,需将答案写在试卷指定的括号内,第二部分非选择题答案写在试卷题目指定的位置上。
3.考生必须保证答题卡的整洁。
考试结束后,请将本试卷和答题卡一并交回。
1、阅读下面的文字,完成下面小题中医药学包含着中华民族几千年的健康养生理念及其实践经验,是中国古代科学的瑰宝也是打开中华文明宝库的钥匙。
国之所需、民之所急,是中医药创新发展的方向。
随着疾病谱的变化,“第二次卫生革命”面临挑战,慢性病成为难解方程式。
如何破解这些难题,大家把目光聚焦在了中医药学上。
当前,我们看到,()。
能不能处理好传承与创新的关系①是中医药发展的关键②可以说③不善于传承,创新就没有基础④不善于创新,传承就缺乏动力。
青蒿素的发现,就是屠呦呦等科研人员从祖国传统医药学得到启示,进而进行创新的成果。
“单打独斗”式的科研已经难以适应时代的要求,中医药的发展离不开集智攻关。
我们要发挥中医药原创优势,建成以围绕国家中医医学中心、区城中医医疗中心为龙头,融预防保健、康复和疾病治疗于一体的中医药服务体系。
广大中医药工作者应当胸怀祖国、敢于担当、团结协作,共同答好中医药高质量发展的时代考题,促进中医药传承创新发展。
1.下列填入文中括号内的语句,衔接最恰当的一项是A.越来越多的人接受中医药,这体现出它虽古老,但却历久弥新B.古老的中医药历久弥新,是因为越来越多的人正在接受它C.古老的中医药历久弥新,正在被越来越多的人接受D.越来越多的人认可古老的中医药,这使它历久弥新2.依次填入文中空处的标点,下列表中最恰当的一项是A.A B.B C.C D.D3.文中画横线的句子有语病,下列修改最恰当的一项是A.建成以围绕国家中医医学中心、区域中医医疗中心为龙头,融预防保健、疾病治疗和康复于一体的中医药服务体系B.建成围绕国家中医医学中心、区域中医医疗中心,融预防保健、康复和疾病治疗于一体的中医药服务体系C.建成以国家中医医学中心、区域中医医疗中心为龙头,融预防保健、疾病治疗和康复于一体的中医药服务体系D.建成围绕国家中医医学中心、区域中医医疗为中心,融预防保健、康复和疾病治疗于一体的中医药服务体系。
浙江省台州市书生中学2015-2016学年高一下学期起始数学试卷Word版含解析
2015-2016学年浙江省台州市书生中学高一(下)起始数学试卷一、选择题(每题3分,共42分)1.的值是( )A .B .C .D .2.已知集合A={α|α=2k π±,k ∈Z },B={β|β=4k π±,k ∈Z },C={γ|γ=k π±,k ∈Z },则这三个集合之间的关系为( )A .A ⊆B ⊆C B .B ⊆A ⊆C C .C ⊆A ⊆BD .B ⊆C ⊆A3.把函数y=sinx (x ∈R )的图象上所有点向左平行移动个单位长度,再把所得图象上所有点的横坐标缩短到原来的倍(纵坐标不变),得到的图象所表示的函数是( )A .,x ∈RB .,x ∈RC .,x ∈RD .,x ∈R4.已知向量=(4,﹣2),向量=(x ,5),且∥,那么x 的值等于( )A .10B .5C .D .﹣105.下列函数中,在区间上为减函数的是( )A .y=cosxB .y=sinxC .y=tanxD .6.sin20°cos40°+cos20°sin40°的值等于( )A .B .C .D .7.已知,且,那么sin2A 等于( )A .B .C .D .8.若tan α=3,,则tan (α﹣β)等于( )A .﹣3B .C .3D .9.在△ABC 中,cosAcosB >sinAsinB ,则△ABC 为( )A .锐角三角形B .直角三角形C .钝角三角形D .无法判定10.已知tan θ+=2,则sin θ+cos θ等于( )A .2B .C .﹣D .±11.若向量的夹角为60°,,则向量的模为()A.2 B.4 C.6 D.1212.设向量=(m,n),=(s,t),定义两个向量,之间的运算“⊗”为⊗=(ms,nt).若向量=(1,2),⊗=(﹣3,﹣4),则向量等于()A.(﹣3,2)B.(3,﹣2)C.(﹣3,﹣2)D.(﹣2,﹣3)13.若=1,则的值为()A.3 B.﹣3 C.﹣2 D.﹣14.若0<α<<β<π,且cosβ=﹣,sin(α+β)=,则sinα的值是()A.B.C.D.二、填空题(每题3分,共18分)15.cos43°cos77°+sin43°cos167°的值为.16.给定两个向量=(3,4),=(2,﹣1),且(+m)⊥(﹣),则实数m=.17.已知函数,则f(x)的值域是.18.对函数y=f(x)=4sin(2x+)(x∈R)有下列命题:①函数y=f(x)的表达式可改写为y=4cos(2x﹣)②函数y=f(x)是以2π为最小正周期的周期函数③函数y=f(x)的图象关于点(﹣,0)对称④函数y=f(x)的图象关于直线x=﹣对称其中正确的命题是.19.已知点A(2,3),B(5,4),C(7,10),若点P满足=+λ(λ∈R),且点P 在第三象限,则λ的取值范围是.20.已知向量,向量,则的最大值为最小值为.三、解答题(每题8分,共40分)21.如图,已知正方形ABCD的边长为2,E,F分别为BC,CD的中点.求:(1)的值;(2)与夹角的余弦值.22.若sin α=,sin β=,且α,β均为钝角,求cos(α+β)的值以及α+β的值.23.已知函数f(x)=(sinx+cosx)2+cos2x﹣1(Ⅰ)求f(x)最小正周期;(Ⅱ)求f(x)在区间[0,]上的最大值和最小值.24.在平面直角坐标系xOy中,已知向量=(,﹣),=(sinx,cosx),x∈(0,).(1)若⊥,求tanx的值;(2)若与的夹角为,求x的值.25.已知函数y=2sin2x+mcosx﹣.(1)当m=﹣1且﹣≤x≤时,求函数值域;(2)当x∈R时,试讨论函数最大值.2015-2016学年浙江省台州市书生中学高一(下)起始数学试卷参考答案与试题解析一、选择题(每题3分,共42分)1.的值是()A.B.C.D.【考点】诱导公式的作用.【分析】原式三个因式中的角度变形后,利用诱导公式化简,计算即可得到结果.【解答】解:原式=sin(π+)•cos(π﹣)•tan(﹣π﹣)=﹣sin•(﹣cos)•(﹣tan)=﹣×(﹣)×(﹣)=﹣.故选A2.已知集合A={α|α=2kπ±,k∈Z},B={β|β=4kπ±,k∈Z},C={γ|γ=kπ±,k∈Z},则这三个集合之间的关系为()A.A⊆B⊆C B.B⊆A⊆C C.C⊆A⊆B D.B⊆C⊆A【考点】集合的表示法.【分析】将集合C中的k取偶数就得到了集合A,从而集合A是集合C的子集,将集合A 中的k取偶数就得到了集合B,从而集合B是集合A的子集,根据集合的性质可知集合A、B、C的包含关系.【解答】解:C={γ|γ=kπ±,k∈Z}中的k取偶数就是集合A,故A⊊CA={α|α=2kπ±,k∈Z},中的k取偶数就是集合B,故B⊊A所以B⊊A⊊C,故选B.3.把函数y=sinx(x∈R)的图象上所有点向左平行移动个单位长度,再把所得图象上所有点的横坐标缩短到原来的倍(纵坐标不变),得到的图象所表示的函数是()A.,x∈R B.,x∈RC.,x∈R D.,x∈R【考点】函数y=Asin(ωx+φ)的图象变换.【分析】根据左加右减的性质先左右平移,再进行ω伸缩变换即可得到答案.【解答】解:由y=sinx的图象向左平行移动个单位得到y=sin(x+),再把所得图象上所有点的横坐标缩短到原来的倍得到y=sin(2x+)故选C4.已知向量=(4,﹣2),向量=(x,5),且∥,那么x的值等于()A.10 B.5 C. D.﹣10【考点】平行向量与共线向量;平面向量的正交分解及坐标表示.【分析】由题中向量的坐标结合向量平行的坐标表示公式,列出关于x的方程并解之,即可得到实数x的值.【解答】解:∵=(4,﹣2),=(x,5),且∥,∴4×5=﹣2x,解之得x=﹣10故选:D5.下列函数中,在区间上为减函数的是()A.y=cosx B.y=sinx C.y=tanx D.【考点】正切函数的单调性;余弦函数的单调性.【分析】根据正弦函数、余弦函数、正切函数的单调性,得出结论.【解答】解:由于y=tanx 在区间上为增函数,y=tanx 在区间上为增函数,故排除B、C.在区间上,﹣≤x﹣≤,故在区间上为增函数,故排除D.故只有y=cosx在区间上为减函数.故选:A.6.sin20°cos40°+cos20°sin40°的值等于()A.B.C.D.【考点】两角和与差的正弦函数.【分析】利用正弦的两角和公式即可得出答案【解答】解:sin20°cos40°+cos20°sin40°=sin60°=故选B.7.已知,且,那么sin2A等于()A.B.C.D.【考点】二倍角的正弦.【分析】根据角A的范围及同角三角函数的基本关系,求出sinA=,再由二倍角公式求出sin2A的值.【解答】解:∵已知,且,∴sinA=,∴sin2A=2 sinA cosA=2×=,故选D.8.若tanα=3,,则tan(α﹣β)等于()A.﹣3 B. C.3 D.【考点】两角和与差的正切函数.【分析】根据两角和与差的正切公式,代入即可得到答案.【解答】解:∵tanα=3,∴故选D9.在△ABC中,cosAcosB>sinAsinB,则△ABC为()A.锐角三角形B.直角三角形C.钝角三角形D.无法判定【考点】三角形的形状判断.【分析】利用余弦的两角和公式整理题设不等式求得cos(A+B)>0进而判断出cosC<O,进而断定C为钝角.【解答】解:依题意可知cosAcosB﹣sinAsinB=cos(A+B)>0,﹣cosC>O,cosC<O,∴C为钝角故选C10.已知tanθ+=2,则sinθ+cosθ等于()A.2 B.C.﹣D.±【考点】同角三角函数基本关系的运用;三角函数的化简求值.【分析】先求出tanθ,再求出sinθ=cosθ=±,即可得出结论.【解答】解:∵tanθ+=2,∴tanθ=1,∴sinθ=cosθ=±,∴sinθ+cosθ=.故选:D.11.若向量的夹角为60°,,则向量的模为()A.2 B.4 C.6 D.12【考点】向量的模;平面向量数量积的运算.【分析】分解(a+2b)•(a﹣3b)得|a|2﹣|a||b|cos60°﹣6|b|2,因为向量的夹角、已知,代入可得关于的方程,解方程可得.【解答】解:(a+2b)•(a﹣3b)=|a|2﹣|a||b|cos60°﹣6|b|2=|a|2﹣2|a|﹣96=﹣72,∴|a|2﹣2|a|﹣24=0.∴(|a|﹣6)•(|a|+4)=0.∴|a|=6.故选C12.设向量=(m,n),=(s,t),定义两个向量,之间的运算“⊗”为⊗=(ms,nt).若向量=(1,2),⊗=(﹣3,﹣4),则向量等于()A.(﹣3,2)B.(3,﹣2)C.(﹣3,﹣2)D.(﹣2,﹣3)【考点】平面向量的坐标运算.【分析】设向量=(x,y),由=(x,2y)=(﹣3,﹣4),解方程求得x,y的值.【解答】解:设向量=(x,y),=(x,2y)=(﹣3,﹣4),∴x=﹣3,y=﹣2,故向量=(﹣3,﹣2 ),故选C.13.若=1,则的值为()A.3 B.﹣3 C.﹣2 D.﹣【考点】三角函数中的恒等变换应用;同角三角函数间的基本关系.【分析】利用二倍角的三角函数公式,结合弦化切化简得=,由=1解之得tan θ=﹣,代入前面式子即可得出所求.【解答】解:∵cos2θ=cos 2θ﹣sin 2θ,1+sin2θ=sin 2θ+2sin θcos θ+cos 2θ∴=分子、分母都除以cos 2θ,得=∵=1,解之得tan θ=﹣∴代入=得==3故选:A14.若0<α<<β<π,且cos β=﹣,sin (α+β)=,则sin α的值是( )A .B .C .D .【考点】两角和与差的正弦函数.【分析】先根据已知条件分别求得sin β和cos (α+β)的值,最后利用正弦的两角和公式求得答案.【解答】解:由0<α<<β<π,知<α+β<π且cos β=﹣,sin (α+β)=,得sin β=,cos (α+β)=﹣.∴sin α=sin [(α+β)﹣β]=sin (α+β)cos β﹣cos (α+β)sin β=. 故选:C .二、填空题(每题3分,共18分)15.cos43°cos77°+sin43°cos167°的值为 ﹣ .【考点】两角和与差的正弦函数.【分析】先根据三角函数的诱导公式将cos167°化为﹣sin77°,再根据两角和的余弦公式可得答案.【解答】解:cos43°cos77°+sin43°cos167° =cos43°cos77°﹣sin43°sin77°=cos120°=﹣.故答案为:﹣16.给定两个向量=(3,4),=(2,﹣1),且(+m)⊥(﹣),则实数m=.【考点】平面向量的坐标运算.【分析】根据向量的坐标运算和向量垂直得到关于m的方程,解得即可.【解答】解:两个向量=(3,4),=(2,﹣1),∴+m=(3+2m,4﹣m),﹣=(1,5),∵(+m)⊥(﹣),∴(+m)(﹣)=0.即3+2m+5(4﹣m)=0,解得m=,故答案为:.17.已知函数,则f(x)的值域是.【考点】正弦函数的定义域和值域;余弦函数的定义域和值域.【分析】讨论sinx与cosx的大小,把函数化简可得f(x)=,结合函数的图象可求函数的值域.【解答】解:=画图可得f(x)的值域是故答案为:18.对函数y=f(x)=4sin(2x+)(x∈R)有下列命题:①函数y=f(x)的表达式可改写为y=4cos(2x﹣)②函数y=f(x)是以2π为最小正周期的周期函数③函数y=f(x)的图象关于点(﹣,0)对称④函数y=f(x)的图象关于直线x=﹣对称其中正确的命题是①③.【考点】正弦函数的对称性.【分析】利用诱导公式化简①,判断正误;求出周期判断②;求出函数的对称中心判定③;对称直线方程判断④的正误;即可得到解答.【解答】解:①f(x)=4sin(2x+)=4cos(﹣2x﹣)=4cos(2x+﹣)=4cos(2x﹣)②最小正周期T===π,②不正确;③f(x)=4sin(2x+)的对称点满足(x,0)2x+=kπ,x=()k∈Z(﹣,0)满足条件④f(x)=4sin(2x+)的对称直线满足2x +=(k +)π;x=(k +)x=﹣不满足 故答案为:①③19.已知点A (2,3),B (5,4),C (7,10),若点P 满足=+λ(λ∈R ),且点P 在第三象限,则 λ的取值范围是 (﹣∞,﹣1) .【考点】向量的线性运算性质及几何意义.【分析】设P (x ,y ),由点P 满足=+λ(λ∈R ),且点P 在第三象限,列出不等式组,由此能求出λ的取值范围.【解答】解:∵A (2,3),B (5,4),C (7,10),点P 满足=+λ(λ∈R ),且点P 在第三象限,∴设P (x ,y ),则,∴,且x <0,y <0,∴,解得λ<﹣1.∴λ的取值范围是(﹣∞,﹣1).故答案为:(﹣∞,﹣1).20.已知向量,向量,则的最大值为 4 最小值为 0 .【考点】两角和与差的正弦函数.【分析】由已知中向量,坐标,求出向量的坐标,代入向量模的计算公式,结合同角三角函数的基本关系,和差角公式,余弦型函数的图象和性质,可得答案.【解答】解:∵向量,向量,向量=,===当=1时,有最大值4当=﹣1时,有最小值0故答案为:4,0三、解答题(每题8分,共40分)21.如图,已知正方形ABCD的边长为2,E,F分别为BC,CD的中点.求:(1)的值;(2)与夹角的余弦值.【考点】平面向量数量积的运算.【分析】(1)利用两个向量的加减法的法则,以及其几何意义,以及两个向量的数量积的定义,求得的值.(2)利用两个向量的数量积的定义,求得与夹角的余弦值.【解答】解:(1)已知正方形ABCD的边长为2,E,F分别为BC,CD的中点.∴=(+)•(+)=++=++0=4.(2)设与夹角为θ,则cosθ===.22.若sin α=,sin β=,且α,β均为钝角,求cos(α+β)的值以及α+β的值.【考点】两角和与差的余弦函数.【分析】利用同角三角函数的基本关系求得α,β的范围,以及cosα和cosβ的值,再利用两角和的余弦公式求得cos(α+β)的值以及α+β的值.【解答】解:∵sin α=<,sin β=<,且α,β均为钝角,∴α∈(,π)、β∈(,π)∴cosα=﹣=﹣,cosβ=﹣=﹣,∴α+β∈(,2π),cos(α+β)=cosαcosβ﹣sinαsinβ=﹣•(﹣)﹣=,∴α+β=.23.已知函数f(x)=(sinx+cosx)2+cos2x﹣1(Ⅰ)求f(x)最小正周期;(Ⅱ)求f(x)在区间[0,]上的最大值和最小值.【考点】三角函数中的恒等变换应用;正弦函数的图象.【分析】(Ⅰ)利用二倍角公式及辅助角公式将f(x)化简,根据周期公式即可求得f(x)最小正周期;(Ⅱ)由x的取值范围,求得2x+∈[,],根据正弦函数图象即可求得f(x)在区间[0,]上的最大值和最小值.【解答】解:(Ⅰ)f(x)=(sinx+cosx)2+cos2x﹣1,=1+sin2x+cos2x﹣1,=sin(2x+),由T===π,f(x)最小正周期π;(Ⅱ)x∈[0,],2x+∈[,],由正弦函数图象及性质可知:sin(2x+)∈[﹣,1],f(x)在区间[0,]的值域为[﹣1,]f(x)在区间[0,]上的最大值和最小值﹣1.24.在平面直角坐标系xOy中,已知向量=(,﹣),=(sinx,cosx),x∈(0,).(1)若⊥,求tanx的值;(2)若与的夹角为,求x的值.【考点】平面向量数量积的运算;数量积表示两个向量的夹角.【分析】(1)若⊥,则•=0,结合三角函数的关系式即可求tanx的值;(2)若与的夹角为,利用向量的数量积的坐标公式进行求解即可求x的值.【解答】解:(1)若⊥,则•=(,﹣)•(sinx,cosx)=sinx﹣cosx=0,即sinx=cosxsinx=cosx,即tanx=1;(2)∵||=,||==1,•=(,﹣)•(sinx,cosx)=sinx﹣cosx,∴若与的夹角为,则•=||•||cos=,即sinx﹣cosx=,则sin(x﹣)=,∵x∈(0,).∴x﹣∈(﹣,).则x﹣=即x=+=.25.已知函数y=2sin2x+mcosx﹣.(1)当m=﹣1且﹣≤x≤时,求函数值域;(2)当x∈R时,试讨论函数最大值.【考点】三角函数的最值.【分析】(1)当m=﹣1时y=﹣2(cosx+)2+2,由﹣≤x≤可得﹣≤cosx≤1,由二次函数区间的最值可得;(2)可得y=﹣2(cosx﹣)2+,cosx∈[﹣1,1],由二次函数区间的最值分类讨论可得.【解答】解:(1)当m=﹣1时,y=2sin2x+mcosx﹣=2sin2x﹣cosx﹣=2(1﹣cos2x)﹣cosx﹣=﹣2cos2x﹣cosx+=﹣2(cosx+)2+2∵﹣≤x≤,∴﹣≤cosx≤1,由二次函数可知当cosx=﹣时,y取最大值2,当cosx=1时,y取最小值﹣,故函数的值域为:[﹣,1];(2)配方可得y=﹣2cos2x+mcosx+=﹣2(cosx﹣)2+,∵x∈R,∴cosx∈[﹣1,1],由二次函数区间的最值可知:当<﹣1即m<﹣4时,在cosx=﹣1时,y取最大值﹣m﹣;当>1即m>4时,在cosx=1时,y取最大值m﹣;当﹣1≤≤1即﹣4≤m≤4时,在cosx=时,y取最大值.2016年10月25日。
浙江省台州市书生中学2020-2021学年七年级科学寒假作业一(无答案)
七年级科学寒假作业一一、科学并不神秘1.有下列现象:A.夏天雨后美丽的彩虹;B.火山爆发;C.海岛附近看到美丽的“海市蜃楼”;D.含羞草开花;E.伊拉克战争;F.“神舟六号”上天;G.种子发芽;H.大雁南飞;I.昆虫蜕皮,青蛙冬眠。
其中属于自然现象的有。
2.小明在家中做饭时发现他家的菜刀生锈了。
小明仔细观察发现,菜刀上的锈斑大都在水滴的边缘,呈圆形,而水滴的中间大多(选填“有”或“没有”)生锈。
请提出一个问题:?并根据生活经验探究一下钢铁生锈的条件。
二、走进科学实验室3.下列仪器中,取用少量固体药品的是________,滴加少量液体的是________,用作少量物体反应的容器的是________(填序号)。
a.烧杯b.滴管c.酒精灯 d.试管e.药匙4.下列仪器中,用来取用少量粉末状固体药品的是________(填序号,下同),用作少量物质反应的容器的是____ ____,用来给物质加热的是__ ______。
5.请指出下列实验操作行为的错误之处。
A.________;B.________;C.________。
6.按下列要求将仪器对应字母填在横线上:(1)用于测量液体体积的仪器是________;(2)用于取用固体粉末的仪器是________;(3)用于少量试剂的反应容器是________;(4)用于加热其他装置的仪器是________。
7.下列是科学实验中常见的基本操作。
据图回答下列问题:(1)如图A 所示,手握细口瓶倾倒液体时,细口瓶标签的一面要________,细口瓶的塞子要________在桌面上;(2)如图B 所示,用完酒精灯后,必须用________盖灭。
(3)如图C 所示,用酒精灯加热试管里的液体时:①试管里的液体不应超过试管容积的________;②先对试管进行________,然后用酒精灯的外焰对准药品所在部位加热;(4)如图D 所示,如果试管不干净时,需要________,然后倒放在试管架上晾干。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2016年台州书生中学初一分档测试B1卷
一、 填空题(每题2分,共40分)
1、地球的表面积五亿一千零六万七千八百六十平方千米,横线上的数写作( )平方
千米,四舍五入“亿位”约是( )平方千米。
2、2.05时=( )时( )分
3、在下面的括号里填上合适的单位名称
一块橡皮的体积约是6( ) 一个西瓜的质量约为5( )
4、三个数的平均数是90,他们的比是1:2:3.其中最大的数是( ),最小的数是最大的
数的( )%。(百分数前保留整数)
5、如果(均不为0),那么=( ):( )。
6、mn=60,m÷n=,那么m=( ),n=( )。
7、一个等腰三角形(三条边都是整厘米)周长是36厘米,其中一条边长16厘米,另两条的长
是( )厘米和( )厘米或( )厘米和( )厘米。
8、有一个长方体,它的地面为正方形,如果把它的高增加5厘米就是正方体,而且表面积就增
加200平方厘米,这个长方体的表面积是( )平方厘米,体积是( )立方厘米。
9、统计病人一昼夜提问变化情况,应选用( )统计图;统计班级各项兴趣小组人数与班级
总人数之间的关系,选用( )统计图比较合适。
10、把5米长的钢筋锯成每段一样长的小段,共锯6此,则每段长( )米。如果把这条钢筋
锯成两段需2分钟,锯成6段共需( )分钟。
11、一个二位小数精确到十分位后是10.0,这个数最大是( )。
12、一个分数,分子加上1可约成,分母减去1可约成,这个分数是( )。
13、有两列火车,一列长102米,每秒行20米;另一列长83米,每秒行17米。两车在双轨线
上相向而行,从两车相遇到车尾离开一共用了( )秒。
14、一个圆的面积是62.8平方厘米,在圆内画一个最大的正方形,这个正方形的面积是( )
平方厘米。
15、一个两位数,个位上和十位上的数字是最大公因数为1的两个合数,这个两位数最大数
( )。
16、一个圆柱的底面半径是4分米,把它的侧面展开正好是一个正方形,那么这个圆柱的体积
是( )立方分米。(精确到0.01)
17、一个钟面显示的时间为6时15分,再经过( )分,分针和时针刚好重合在一起。
yx4131
yx、xy:
3
2
415
1
18、小明新买一支净含量为45立方厘米的牙膏,牙膏的图形出口的直径是6毫米,他早晚各刷
一次牙,每次挤出的牙膏约20毫米。这支牙膏估计能( )天。(圆周率取3)
19、长方形ABCD的长为8cm,宽6cm,对角线10cm。将它的宽边BC对折AC重叠,重叠后的
三角形即阴影的面积是( )平方厘米
20、把3千克水加到盐水中,得到浓度10%的盐水,再把1千克盐加到所得到的盐水中,这时
盐水的浓度为20%,原来盐水的浓度是( )。
二、判断题(对的打"√",错的打"╳",每题2分,共10分)
1、一个精密零件长5毫米,把它画在纸上是5厘米,它的比例尺是1:10。
2、半圆的周长不等于圆的周长的一半。
3、3个工人3个小时加工3个零件,照这样计算4个工人4个小时可以加工4个零件
4、一批布,全做上衣可以做15件,全做裤子可以做10条,如果成套加工,可以做6套。
5、三个连续奇数的和是m(m为正整数),那么其中最小的奇数
2
3
m
三、选择题(把正确答案的序号填在括号里,每题2分,共10分)
1、把一条绳子对折后再对折,再对折,这时每一份的长度是全长的( )。
(A) (B) (C) (D)
2、把三个1立方米的正方体拼成一个长方体后,它的棱长总和是( )米。
(A)32 (B)28 (C)24 (D)42
3、五个连续自然数,其中第三个数比第一、五个数之和的少2,第三个数是
(A)9 (B)18 (C)36 (D)42
4、 从左面看到的形状是( )
(A) (B) (C) (D)
5、甲、乙、丙、丁在比较他们的身高,甲说:“我最高。”乙说:“我不是最矮。”丙说:“我没有
甲高但还有人比我矮。”丁说:“我最矮。”实际测量表明,只有一个人说错了。那么身高从高
到低排在第二位的是( )
(A)甲 (B)乙 (C)丙 (D)丁
418112116
1
9
5
四、计算题
1、用递等式计算,能简便的要写出简算过程(每题3分,共18分)
(1)3600÷15-2.5 1.6 (2)(+-)×72
(3)×÷+ (4) 5.4-+4.6-62.5%
(5) (0.75-)÷(+) (6)×[÷(-)]
2、求未知数(3分)。
16:=0.75:
3、已知有图半圆的直径是8厘米,计算图中阴影部分的面积。(3分)
125918
3
3510332618
3
16521518398455
6
x
8
15
x
五、应用题
1、水果店运回桔子390千克,比运回的香蕉的2倍少10千克。如果每筐香蕉重25千克,运
回香蕉多少筐?
2、甲乙两人拿出同样多的钱合买一筐水果,甲分去12千克,乙分去18千克。结果乙要付给
甲5.70元。苹果每千克的价格是多少元?
3、两个筑路队合修一条长47.52千米的路,甲队每天比乙队多修20%。两队合修16天后,还
剩下全长的。乙队每天修路多少千米?
4、甲加工组与乙加工组的人数比为5:3,从甲组调14人到乙组的人数比是1:2,
。两个组原来
各有几人?
5、有一块宽为16厘米的长方形铁皮,在它的四角上分别剪去边长为4厘米正方形,将它焊成
一个无盖的盒子。已知这个盒子的体积是768立方厘米,求这块铁皮原来的面积。
6、甲、乙两种商品,成本共2200元,甲商品按20%的利润定价,乙商品按15%的利润定价
后。后来都按定价的90%打折出售,结果仍获利131元。甲种商品的成本是多少元?
9
1
