psd谱的平均频率
PSD-功率谱密度软件

USA – 222 Vista Ave., Pasadena, CA 91107 / Tel (626) 795-2220 / Fax (626) 795-0868Switzerland – Z.I. Le Trési 3, 1028 Préverenges / Tel (21) 803-2829Visit us on the web at PSD 软件包旨在帮助Aitus 系列仪器(K2, Etna , Mt.Whitney)的用户进行这些仪器记录数据的频率分析。
该软件以EVT 格式的文件为输入文件,具有获得以下分析结果:1) 信噪比:以信号的头1024个点作为噪声,而以从触发点开始的1024个点作为信号,计算信噪比。
2) 功率谱密度:采用单边自谱密度函数计算功率谱密度。
用户可以设定诸如滤波器拐点频率、滤波器阶数和窗等参数。
3) 相干函数:计算用户所选定的两个信号的相干函数(一般的)。
用户可以设定滤波器拐点频率和窗参数4) 传递函数:采用与相干函数相关的算法计算传递函数。
计算给出信号的增益和相位。
用户可以设定滤波器拐点频率和窗参数。
PSD K I N E M ET R IC S PSD 功率谱密度软件 PSD 功率谱密度软件对工程师们来说是一个很有用数据处理工具。
可以在现场轻而易举的对所采集数据的质量进行评估。
该软件能对1.50以上版本的(.EVT )格式的事件文件进行读取和处理,并得到下列结果:♦ 功率谱密度;♦ 信噪比;♦ 两个通道间的相干性;♦ 两个通道间的传递函数。
PSD 的主对话界面结构简单,且具有在线帮助,十分便于理解和使用。
所有结果均可以图形方式显示,图形任何一个坐标轴均可单独设定为线性/对数坐标。
可选项包括:♦ 选择感兴趣的通道;♦ 选择所处理数据的范围;♦ 以对数-对数、对数-线性、线性-对数或线性-线性方式显示数据图形。
Figure 1 - Signal to Noise Ratio PlotFigure 3 - Coherence DialogFigure 2 – Power Spectral Density Figure 4 - Transfer Function Plot。
功率谱密度psd计算公式

功率谱密度psd计算公式功率谱密度(Power Spectral Density,简称 PSD)是在信号处理领域中一个非常重要的概念,它用于描述信号在不同频率上的功率分布情况。
那咱就来好好聊聊功率谱密度 PSD 的计算公式。
咱先从一个简单的例子说起哈。
就比如说,你在操场上跑步,你跑的速度不是一直不变的,有时候快,有时候慢。
那如果我们想知道你在不同“速度频率”下的能量消耗情况,这时候功率谱密度的概念就派上用场啦。
功率谱密度 PSD 的计算公式呢,通常可以通过傅里叶变换来推导。
对于一个连续的随机信号 x(t) ,它的自相关函数R(τ) 定义为R(τ) =E[x(t)x(t + τ)] ,其中 E 表示数学期望。
然后通过傅里叶变换,把自相关函数R(τ) 变换到频域,就得到了功率谱密度 S(f) 。
具体的公式就是S(f) = ∫_{-∞}^{+∞} R(τ) e^{-j2πfτ} dτ 。
这里面涉及到的傅里叶变换可能听起来有点复杂,但其实咱们可以把它想象成一个魔法工具,能把一个在时间域里看起来很复杂的信号,变到频率域里,让我们更清楚地看到不同频率成分的“力量”有多大。
再比如说,想象一下你听音乐的时候,那些高音低音,其实就相当于不同的频率成分。
功率谱密度就是告诉我们高音和低音分别有多大的“能量”。
在实际应用中,比如在通信系统里,我们需要知道信号在不同频率上的功率分布,来评估系统的性能。
如果功率谱密度在某些频率上太高,可能就会造成干扰;如果太低,可能信号就传不远。
还有在地震学中,通过分析地震波的功率谱密度,我们可以了解地震的能量在不同频率上的分布,从而更好地研究地震的特性和预测可能的危害。
对于工程师们来说,计算功率谱密度就像是在解谜。
他们得处理一堆复杂的数据,运用各种数学工具和算法,才能得到准确的结果。
总之,功率谱密度 PSD 的计算公式虽然有点复杂,但它在很多领域都有着极其重要的作用,帮助我们更好地理解和处理各种信号。
各种谱计算,频响函数,传递率

各种谱计算,频响函数,传递率阅读:22802006-05-25 22:01A.信号与谱的分类由于时域信号有不同的分类, 变换后对应的频域也有不同的谱信号可分为模拟(连续)信号和数字(离散)信号, 连续信号变换后称为谱密度, 离散信号变换后称为谱.连续信号又可分为绝对可积,平方可积(能量有限),均方可积(功率有限)绝对可积信号有傅里叶谱(线性谱)和傅里叶谱密度(线性谱密度),如时域信号单位为电压V,则前者单位为V,后者单位为V/Hz.均方可积信号有功率谱PS(单位为V2)和功率谱密度PSD(单位为V2/ Hz.).平方可积信号有能量谱密度ESD(单位为V2 s / Hz.).注1 平方量称为功率,平方量乘秒称为能量,谱分量除以频率称为谱密度.注2 功率谱密度另一定义(离散信号的功率谱密度)见下述, 连续信号的功率谱密度.为连续(光滑)曲线, 离散信号的功率谱密度为不连续的阶梯形..注3 随机信号求功率谱密度时为减少方差,可采用平均,重叠和加窗处理(Welch法).数字信号又可分为绝对可和,平方可和,均方可和.B.各种谱计算1. 线性谱Linear Spectrum: 对时域离散信号作DFT(离散傅里叶变换)得到,采用方法为FFT(快速傅里叶变换)法.X(f)=FFT(x(t))2. 自功率谱APS=Auto Power Spectrum: 离散信号的线性谱乘其共轭线性谱APS(f)=X(f)*conj(X(f)), conj=conjugate共轭(实部不变,虚部变符号).3. 互功率谱CPS=Cross Power Spectrum::x(t)的线性谱乘y(t)的共轭线性谱互功率谱是复数,可表示为幅值和相位或实部和虚部等.CPS(f)=X(f) *conj(Y(f)) Y(f)=FFT(y(t))4. (自)功率谱密度PSD(=Power Spectrum Density):PSD(f)=APS(f)/Δf Δf—频率分辨率(Hz),自功率谱密度与自相关函数成傅立叶对应关系故功率谱密度也称为规一化的功率谱.5. 互功率谱密度CSD=CPS(f)/ΔfA.频响函数FRF, 传递率A1.频响函数.FRF为响应的傅里叶变换与力的傅里叶变换之比或力和响应的互谱与力的自谱之比后者可通过平均减少噪声,故较常用.H(f)=X(f ) / F(f)=X(f)*conj(F(f)) / F(f)*conj(F(f))=CPS / APS.A2. 频响函数有三种表达形式频响函数表达成分子多项式与分母多项式(特征多项式)之比,也称有理分式.(两多项式求根后) 频响函数表达成极点,零点和增益ZPK形式.频响函数表达成部分分式,也称极点留数形式,( 部分分式的分子项称为留数.),例如:最常见的单自由度(位移)频响函数H(ω)=X(ω)/F(ω)H = 1 / (k+(jω) 2*m+jωC) 有理分式(多项式之比)= (1 /m )* 1/(jω-p1)(jω-p2) 极点,零点和增益ZPK形式= R1/(jω-p1) + R2/(jω-p2). 部分分式(极点和留数形式)本例特殊, 分子非多项式,无根(无零点),留数为共轭虚数(一般为共轭复数)a.共轭极点( 分母多项式的根) p: p1=σ+jωd, p2=σ-jωd, J=√-1ωd--有阻尼固有频率, ωd=ωn *√1-ζ2b.共轭留数R: R1=1/2j*ωd R2= -1/2j*ωdc.增益K: K = 1/m计算留数可用待定系数法或(复变函数中的)留数定理.多自由度系统中留数包含振型信息.A3. 频响矩阵: 当N点测力,N点测响应时, 频响函数为N x N矩阵,但独立元素只有N个, 测试时既可只测一行(如H11,H12,H13,…H1N, 即激多点,测一点);也可只测一列(如H11,H21,H31,…HN1,即激一点,测多点)B. 传递率(Transmissibility)传递率为同量纲物理量傅里叶变换之比,如电压传递率,力传递率,位移传递率等,以位移传递率为例: Tij=Xi(f)/Xj(f)= Xj(f)*conj(Xj(f)) / Xj(f)*conj(Xj(f))=CPSij / APSjj式中: Xi(f)-- 位移xi的傅里叶变换, Xj(f)-- 位移xj的傅里叶变换,(不测力法无频响函数,只能用传递率求振型,此时xj位置保持不变,称为参考(基准)位移.。
psd功率谱密度的理解

PSD功率谱密度的奥秘揭秘
PSD功率谱密度是一种针对信号的频谱特征分析方法。
所谓PSD,即Power Spectral Density,中文意为功率谱密度。
在频域中,信号的特征通过频率分量来表示,而PSD则能够提供更多的有用信息。
它能够明确地反映信号在不同频率下的功率分布情况。
通常情况下,PSD都是通过傅里叶变换来计算的。
PSD与信号的相关性非常高。
对于不同的信号特征,PSD的形式也不同。
例如,对于白噪声信号,PSD呈均匀分布;对于周期性信号,PSD会在其频率处呈现出峰值;对于复杂的非周期性信号,PSD会出现较高的峰值和较低的峰值,并随着频率的变化而变化。
PSD分析在多个领域有着广泛应用。
在通信领域,PSD分析用于信号编码和解码、信道估计、多信道信号分离等;在机械领域,PSD分析用于机械振动信号处理、故障诊断等;在生物学领域,PSD分析用于生物信号的处理和分析等。
总的来说,PSD功率谱密度是一种非常重要的信号分析工具。
在实际应用中,通过合理地计算PSD,可以更好地了解不同信号的特征,并精确地进行处理和识别。
psd曲线有效加速度

psd曲线有效加速度
PSD(Power Spectral Density,功率谱密度)曲线描述了信号的频率分布,通常在振动分析和信号处理领域中使用。
有效加速度(Effective Acceleration)则是描述振动信号对结构或系统产生的影响的参数。
在振动分析中,可以通过PSD曲线来获取有效加速度。
有效加速度与PSD 曲线的关系可以通过下面的公式表示:
其中,Sa(f) 是频率�f处的加速度谱密度,积分范围是从00 到无穷大。
在实际应用中,通常使用有限数量的离散频率点来估计这个积分。
对于离散频率的情况,上述积分可以通过数值方法(如梯形法则或Simpson 法则)来近似计算。
这可以通过对PSD 曲线上的离散数据点进行数值积分来实现。
在MATLAB 等工具中,也可以使用相关的函数来计算PSD 曲线的积分,从而得到有效加速度。
例如,MATLAB 中的trapz函数可以用于数值积分。
需要注意的是,对于具体的工程应用,可能还需要根据具体的振动分析标准和要求进行修正或调整。
随机振动-试验人员必须了解的参数及设置
随机振动-试验人员必须了解的参数及设置江苏省电子信息产品质量监督检验研究院谢杰一.简述近年来,随机振动试验在我院所有振动试验中的比例越来越高,原因有三:1、科学进步,此类设备的软件大量普及,一般只需在原来的电磁振动台加上一套控制软件及配套设备就可实行。
2、企业随着国际标准的大量采用,许多振动试验都采用随机振动。
3、随机振动相对传统的正弦振动有着无法比拟的优点,它能模拟各种实际运输条件下可能遇到的振动情况,如模拟公路运输,模拟铁路运输,模拟海运运输等等。
本文主要介绍对于试验人员来说必须了解的随机振动参数及设置要求。
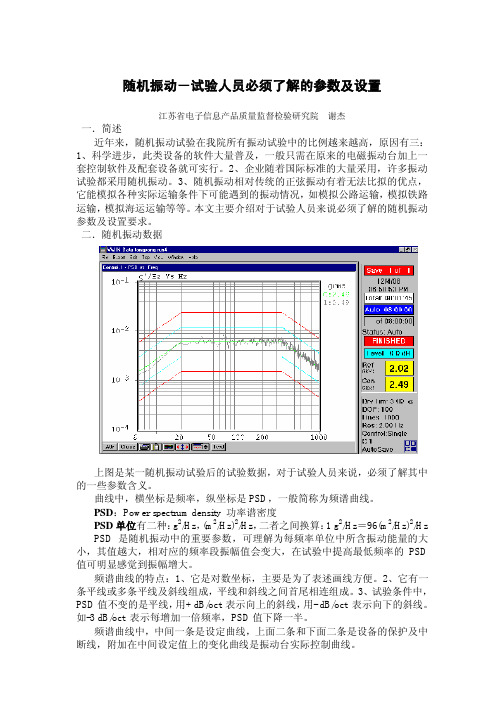
二.随机振动数据上图是某一随机振动试验后的试验数据,对于试验人员来说,必须了解其中的一些参数含义。
曲线中,横坐标是频率,纵坐标是PSD,一般简称为频谱曲线。
PSD:Power spectrum density 功率谱密度PSD单位有二种:g2/Hz,(m2/Hz)2/Hz,二者之间换算:1 g2/Hz=96(m2/Hz)2/Hz PSD是随机振动中的重要参数,可理解为每频率单位中所含振动能量的大小,其值越大,相对应的频率段振幅值会变大,在试验中提高最低频率的PSD 值可明显感觉到振幅增大。
频谱曲线的特点:1、它是对数坐标,主要是为了表述画线方便。
2、它有一条平线或多条平线及斜线组成,平线和斜线之间首尾相连组成。
3、试验条件中,PSD值不变的是平线,用+dB/oct表示向上的斜线,用- dB/oct 表示向下的斜线。
如-3 dB/oct 表示每增加一倍频率,PSD值下降一半。
频谱曲线中,中间一条是设定曲线,上面二条和下面二条是设备的保护及中断线,附加在中间设定值上的变化曲线是振动台实际控制曲线。
三.频率的选择频率是随机振动的另一个重要参数,其单位是Hz,频率的选择一般与实践使用范围有关。
例如:海运试验条件频率较低,一般从1~100Hz,而且低频PSD 值较大,随机振动的感觉像乘海轮,振幅大,频率低。
功率谱密度

功率谱密度功率谱密度是信号处理中的重要概念,它描述了信号的频率成分在功率上的分布。
在工程领域中,功率谱密度广泛应用于信号分析、通信系统设计以及噪声分析等方面。
本文将介绍功率谱密度的定义、性质、计算方法以及在实际应用中的重要性。
1. 定义功率谱密度(Power Spectral Density,PSD)是描述信号功率在频域上的分布情况的密度函数。
在时域中,信号的功率通常被定义为信号的能量在单位时间内的平均值,而功率谱密度则描述了信号功率在不同频率上的分布。
功率谱密度通常用单位频率范围内的功率值表示,是信号频谱特性的重要指标之一。
2. 性质功率谱密度具有以下几个重要性质:•非负性:功率谱密度始终大于等于零,表示信号中的功率都是非负的。
•互相关函数和功率谱密度之间的关系:两个信号的自相关函数的傅里叶变换是它们的功率谱密度的乘积。
•窄带信号:窄带信号的功率谱密度在窄频段内集中,而宽带信号的功率谱密度分布更广。
3. 计算方法计算功率谱密度可以通过信号的自相关函数或者信号的傅里叶变换来实现。
常用的计算方法包括:•周期图法:通过对信号进行周期图分析,可以得到信号的功率谱密度。
•傅里叶变换法:对信号进行傅里叶变换,然后计算幅度谱的平方即可得到功率谱密度。
•Welch方法:对信号进行分段处理,然后对各段信号的功率谱密度进行平均,可以获得更加准确的估计。
4. 应用功率谱密度在通信系统、雷达系统、生物医学工程等领域具有重要应用价值,例如:•在通信系统中,功率谱密度可以帮助分析信道的频率选择性,设计滤波器以及优化调制方案。
•在雷达系统中,功率谱密度可以帮助分析雷达回波信号的频率特性,识别目标特征。
•在生物医学工程中,功率谱密度可用于分析生物信号的频率特征,帮助诊断疾病。
5. 总结功率谱密度作为描述信号频率特性的重要参数,在信号处理和通信系统设计中扮演着重要角色。
了解功率谱密度的定义、性质、计算方法以及应用领域,有助于更深入地理解信号处理中的功率谱密度的重要性和作用。
功率信号的功率谱密度

功率信号的功率谱密度
功率信号的功率谱密度是描述信号频域特性的一个重要概念。
功率谱密度是一个信号在频率域上的功率分布,通常用于分析信号的频谱特性。
功率信号的功率谱密度(Power Spectral Density,PSD)通常用符号S(f)表示,其中"f" 代表频率。
PSD可以根据信号的周期或持续时间来定义。
对于一个连续时间信号x(t),其功率谱密度S(f)可以通过傅立叶变换来计算,具体公式如下:
其中,S(f) 表示在频率f处的功率谱密度,X(f) 是信号x(t)的傅立叶变换,T 表示信号x(t)的时间长度。
该公式的意义在于,它表示了信号在频率域上的功率分布,即信号在不同频率成分上的能量。
对于离散时间信号x[n],其功率谱密度S(f)可以通过离散傅立叶变换(DFT)来计算,具体公式如下:
其中,S(f) 表示在频率f处的功率谱密度,N 表示信号x[n]的长度。
功率谱密度的计算可以帮助分析信号在频域上的特性,例如查找信号的主要频率成分、识别信号中的谐波或噪声成分等。
在实际应用中,功率谱密度常常用于信号处理、通信系统分析、频谱分析以及噪声分析等领域。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
psd谱的平均频率
PSD谱的平均频率是指信号的功率能量与频率的关系的物
理量的平均值。
PSD谱是表征信号的功率能量与频率的关系的物理量,通常
用来研究随机振动信号。PSD通常根据频率分辨率做归一化,对
于振动数据,PSD的单位通常是g^2/Hz。这个单位看起来不很直
观,但它有助于确保随机数据可以独立于数据的频率分辨率进行
比较。
