zjq勾股定理和四边形表格
14勾股定理

第14章勾股定理§14.1勾股定理1. 直角三角形三边的关系2. 直角三角形的判定阅读材料勾股定理史话美丽的勾股树§14.2勾股定理的应用小结复习题课题学习勾股定理的“无字证明”第14章勾股定理还记得2002年在北京召开的国际数学家大会(ICM2002)吗?在那个大会上,到处可以看到一个简洁优美的图案在流动,那个远看像旋转的纸风车的图案就是大会的会标.那是采用了1700多年前中国古代数学家赵爽用来证明勾股定理的弦图.§14.1 勾股定理1. 直角三角形三边的关系本章导图中的弦图隐含着直角三角形三边之间的一种奇妙的关系,让我们首先观察经常使用的两块直角三角尺.试一试测量你的两块直角三角尺的三边的长度,并将各边的长度填入下表:三角尺直角边a直角边b斜边c 关系12根据已经得到的数据,请猜想三边的长度a、b、c之间的关系.图14.1.1是正方形瓷砖拼成的地面,观察图中用阴影画出的三个正方形,很显然,两个小正方形P、Q的面积之和等于大正方形R的面积.即AC2+BC2=AB2,图14.1.1这说明,在等腰直角三角形ABC中,两直角边的平方和等于斜边的平方.那么在一般的直角三角形中,两直角边的平方和是否等于斜边的平方呢?试一试观察图14.1.2,如果每一小方格表示1平方厘米,那么可以得到:正方形P的面积=平方厘米;正方形Q的面积=平方厘米;(每一小方格表示1平方厘米)图14.1.2正方形R的面积=平方厘米.我们发现,正方形P、Q、R的面积之间的关系是.由此,我们得出直角三角形ABC的三边的长度之间存在关系.做一做在图14.1.3的方格图中,用三角尺画出两条直角边分别为5cm、12cm的直角三角形,然后用刻度尺量出斜边的长,并验证上述关系对这个直角三角形是否成立.(每一小格代表1平方厘米)图14.1.3概括数学上可以说明:对于任意的直角三角形,如果它的两条直角边分别为a、b,斜边为c,那么一定有a2+b2=c2,这种关系我们称为勾股定理.勾股定理直角三角形两直角边的平方和等于斜边的平方.勾股定理揭示了直角三角形三边之间的关系.例1如图14.1.4,将长为5.41米的梯子AC斜靠在墙上,BC长为2.16米,求梯子上端A到墙的底边的垂直距离AB.(精确到0.01米)图14.1.4解如图14.1.4,在Rt△ABC中,BC=2.16米,AC=5.41米,根据勾股定理可得AB=-BCAC22=2216.5≈4.96(米).41.-2答:梯子上端A到墙的底边的垂直距离AB约为4.96米.练习1. 在Rt△ABC中,AB=c,BC=a,AC=b,∠B=90°.(1)已知a=6,b=10,求c;(2)已知a=24,c=25,求b.2. 如果一个直角三角形的两条边长分别是3厘米和4厘米,那么这个三角形的周长是多少厘米?试一试剪四个与图14.1.5完全相同的直角三角形,然后将它们拼成如图14.1.6所示的图形.大正方形的面积可以表示为,又可以表示为.对比两种表示方法,看看能不能得到勾股定理的结论.图14.1.5 图14.1.6用上面得到的完全相同的四个直角三角形,还可以拼成如图14.1.7所示的图形,与上面的方法类似,也能说明勾股定理是正确的. 读一读我国古代把直角三角形中较短的直角边称为勾,较长的称为股,斜边称为弦.图14.1.7称为“弦图”,最早是由三国时期的数学家赵爽在为《周髀算经》作注时给出的.图14.1.8是在北京召开的2002年国际数学家大会(ICM2002)的会标,其图案正是“弦图”,它标志着中国古代的数学成就.图14.1.7 图14.1.8 例2如图14.1.9,为了求出位于湖两岸的两点A 、 B 之间的距离,一个观测者在点C 设桩,使三角形ABC恰好为直角三角形.通过测量,得到AC 长160米,BC长128米.问从点A 穿过湖到点B 有多远?图14.1.9解 如图14.1.9,在直角三角形ABC中,AC =160米, BC=128米,根据勾股定理可得AB=22BC AC -=22128160-=96(米).答: 从点A 穿过湖到点B 有96米.练习1. 如图,小方格都是边长为1的正方形,求四边形ABCD的面积与周长.2. 假期中,王强和同学到某海岛上去探宝旅游,按照探宝图(如图),他们登陆后先往东走8千米,又往北走2千米,遇到障碍后又往西走3千米,再折向北走到6千米处往东一拐,仅走1千米就找到宝藏,问登陆点A到宝藏埋藏点B的直线距离是多少千米?(第1题)(第2题)2. 直角三角形的判定古埃及人曾经用下面的方法画直角:将一根长绳打上等距离的13个结,然后如图14.1.10那样用桩钉钉成一个三角形,他们认为其中一个角便是直角.你知道这是什么道理吗?图14.1.10试一试试画出三边长度分别为如下数据的三角形,看看它们是一些什么样的三角形:(1)a=3,b=4,c=5;(2)a=4,b=6,c=8;(3)a=6,b=8,c=10.可以发现,其中按(1)、(3)所画的三角形都是直角三角形,而按(2)所画的不是直角三角形.在这三组数据中,(1)、(3)两组都满足a2+b2=c2,而组(2)不满足.以后我们会证明一般的结论:如果三角形的三边长a、b、c有关系:a2+b2=c2,那么这个三角形是直角三角形.古埃及人所画的三角形的三边长恰好满足这样的关系,所以其中一个角是直角.例 3 设三角形三边长分别为下列各组数,试判断各三角形是否是直角三角形:(1)7,24,25;(2)12,35,37;(3)13,11,9.解因为252=242+72,372=352+122,132≠112+92,所以根据前面的判定方法可知,以(1)、(2)两组数为边长的三角形是直角三角形,而以组(3)的数为边长的三角形不是直角三角形.练习1. 设三角形的三边长分别等于下列各组数,试判断各三角形是否是直角三角形.若是,指出哪一条边所对的角是直角.(1)12,16,20;(2)8,12,15;(3)5,6,8.2. 有哪些方法可以判断一个三角形是直角三角形?习题14.11. 将图14.1.6沿中间的小正方形的对角线剪开,得到如图所示的梯形.利用此图的面积表示式验证勾股定理.(第1题)2. 已知△ABC中,∠B=90°,AC=13cm,BC=5cm,求AB的长.3. 已知等腰直角三角形斜边的长为2cm,求这个三角形的周长.4. 如图,分别以直角三角形的三边为边长向外作正方形,然后分别以三个正方形的中心为圆心、正方形边长的一半为半径作圆.试探索这三个圆的面积之间的关系.(第4题)(第5题)5. 如图,已知直角三角形ABC的三边分别为6、8、10,分别以它的三边为直径向上作三个半圆,求图中阴影部分的面积.6. 试判断以如下的a、b、c为边长的三角形是不是直角三角形?如果是,那么哪一条边所对的角是直角?(1)a=25,b=20,c=15;(2)a=1,b=2,c=3;(3)a=40,b=9,c=40;(4)a∶b∶c=5∶12∶13.阅读材料勾股定理史话勾股定理从被发现到现在已有五千年的历史.远在公元前三千年的巴比伦人就已经知道和应用它了.我国古代也发现了这个定理.据《周髀算经》记载,商高(公元前1120年)关于勾股定理已有明确的认识,《周髀算经》中有商高答周公的话:“勾广三,股修四,径隅五.”同书中还有另一位学者陈子(公元前六七世纪)与荣方(公元前六世纪)的一段对话:“求邪(斜)至日者,以日下为勾,日高为股,勾、股各自乘,并而开方除之,得邪至日”(如图所示),即邪至日=勾2+股2.这里陈子已不限于“三、四、五”的特殊情形,而是推广到一般情形了.人们对勾股定理的认识,经历过一个从特殊到一般的过程,其特殊情况,在世界很多地区的现存文献中都有记载,很难区分这个定理是谁最先发明的.国外一般认为这个定理是毕达哥拉斯(Pythagoras)学派首先发现的,因而称为毕达哥拉斯定理.勾股定理曾引起很多人的兴趣,世界上对这个定理的证明方法很多.1940年卢米斯(E.S. Loomis)专门编辑了一本证明勾股定理的小册子——《毕氏命题》,作者收集了这个著名定理的370种证明,其中包括大画家达·芬奇和美国第20任总统詹姆士·阿·加菲尔德(James Abram Garfield,1831~1881)的证法.美丽的勾股树你可能去过森林公园,看到过许许多多千姿百态的植物.可是你是否见过如下的勾股树呢?你知道这是如何画出来的吗?仔细看看,你就会发现那一个个细小的部分正是我们学过的勾股图,一个一个连接在一起,构成了多么奇妙美丽的勾股树!动手画画看,相信你也能画出其他形态的勾股树.§14.2 勾股定理的应用勾股定理能解决直角三角形的许多问题,因此在现实生活和数学中有着广泛的应用.例1如图14.2.1,一圆柱体的底面周长为20cm ,高AB为4cm ,BC是上底面的直径.一只蚂蚁从点A 出发,沿着圆柱的侧面爬行到点C ,试求出爬行的最短路程.图14.2.1 分析 蚂蚁实际上是在圆柱的半个侧面内爬行,如果将这半个侧面展开(如图14.2.2),得到矩形 ABCD ,根据“两点之间,线段最短”,所求的最短路程就是侧面展开图矩形对角线AC 之长.(精确到0.01cm )图14.2.2解 如图14.2.2,在Rt △ABC中,BC=底面周长的一半=10cm ,∴ AC =22BC AB +=22104+=229≈10.77(cm )(勾股定理).答: 最短路程约为10.77cm .例2一辆装满货物的卡车,其外形高2.5米,宽1.6米,要开进厂门形状如图14.2.3的某工厂,问这辆卡车能否通过该工厂的厂门?图14.2.3分析由于厂门宽度足够,所以卡车能否通过,只要看当卡车位于厂门正中间时其高度是否小于CH .如图14.2.3所示,点D 在离厂门中线0.8米处,且CD ⊥AB, 与地面交于H .解 在Rt △OCD 中,由勾股定理得CD=22OD OC -=228.01-=0.6米,C H=0.6+2.3=2.9(米)>2.5(米).因此高度上有0.4米的余量,所以卡车能通过厂门.做一做图14.2.4如图14.2.4,以直角三角形ABC的三边为边分别向外作正方形,其中一个正方形划分成四个形状与大小都一样的四边形.试将图中5个带色的图形拼入到大正方形中,填满整个大正方形. 练习1. 如图,从电杆离地面5米处向地面拉一条7米长的钢缆,求地面钢缆固定点A到电杆底部B的距离.2. 现准备将一块形为直角三角形的绿地扩大,使其仍为直角三角形,两直角边同时扩大到原来的两倍,问斜边扩大到原来的多少倍?(第1题)例3如图14.2.5,在5×5的正方形网格中,每个小正方形的边长都为1,请在给定网格中按下列要求画出图形:(1)从点A出发画一条线段AB,使它的另一个端点B在格点(即小正方形的顶点)上,且长度为22;(2)画出所有的以(1)中的AB为边的等腰三角形,使另一个顶点在格点上,且另两边的长度都是无理数.分析只需利用勾股定理看哪一个矩形的对角线满足要求.图14.2.5 图14.2.6解(1)图14.2.6中AB长度为22.(2)图14.2.6中△ABC、△ABD就是所要画的等腰三角形.例4如图14.2.7,已知CD=6m,AD=8m,∠ADC=90°,BC =24m,AB=26m.求图中阴影部分的面积.图14.2.7解在Rt△ADC中,AC2=AD2+CD2=62+82=100(勾股定理),∴AC=10m.∵AC2+BC2=102+242=676=AB2,∴△ACB为直角三角形(如果三角形的三边长a、b、c有关系:a2+b2=c2,那么这个三角形是直角三角形),∴S阴影部分=S△ACB-S△ACD=1/2×10×24-1/2×6×8=96(m2).练习1. 若直角三角形的三边长分别为2、4、x,试求出x的所有可能值.2. 利用勾股定理,分别画出长度为3和5厘米的线段.习题14.21. 若等腰直角三角形的斜边长为2cm,试求出它的直角边和斜边上的高的长度.2. 下图由4个等腰直角三角形组成,其中第1个直角三角形腰长为1cm,求第4个直角三角形斜边长度.(第2题) (第3题)3. 如图,为了加固一个高2米、宽3米的大门,需在相对角的顶点间加一块木条.求木条的长度.4. 在△ABC中,AB=2, BC=4, AC=23, ∠C =30°, 求∠B 的大小.5. 已知三角形的三边分别是n +1、 n +2、 n +3,当n 是多少时,三角形是一个直角三角形?6. 如图,AD ⊥CD , AB=13,BC=12,CD=4,AD=3, 若∠C AB=55°,求∠B 的大小.(第6题)小结一、 知识结构二、 概括直角三角形 勾股定理应用判定直角三角形的一种方法本章研究了揭示直角三角形三条边之间关系的勾股定理和由此产生的一种判定直角三角形的方法.如果知道了直角三角形任意两边的长度,那么应用勾股定理可以计算出第三边的长度;如果知道了一个三角形的三边的长,也可以判断这个三角形是否是直角三角形.勾股定理可以解决直角三角形中的许多问题,在现实生活中有许多重要的应用.复习题A组1. 求下列阴影部分的面积:(1)阴影部分是正方形;(2)阴影部分是长方形;(3)阴影部分是半圆.(第1题)2. 如图,以Rt△ABC的三边为直径分别向外作三个半圆,试探索三个半圆的面积之间的关系.(第2题)3. 试判断下列三角形是否是直角三角形:(1)三边长为m2+n2、mn、m2-n2(m>n>0);(2)三边长之比为1∶1∶2;(3)△ABC的三边长为a、b、c,满足a2-b2=c2.4. 一架2.5米长的梯子靠在一座建筑物上,梯子的底部离建筑物0.7米,如果梯子的顶部滑下0.4米,梯子的底部向外滑出多远?5. 如图所示的图形中,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为7cm,求正方形A、B、C、D的面积和.(第5题)B组6. 在△ABC中,AB=AC=10,BD是AC边的高,DC=2,求BD的长.(第7题)7. 有一块四边形地ABCD(如图),∠B=90°,AB=4m,BC=3m,CD=12m,DA=13m,求该四边形地ABCD 的面积.8. 能够成为直角三角形三条边长的正整数,称为勾股数.请你写出5组勾股数.9. 已知△ABC中,三条边长分别为a=n2-1,b=2n,c=n2+1(n>1).试判断该三角形是否是直角三角形,若是,请指出哪一条边所对的角是直角.C组10. 如图,四边形ABCD中,AB=BC=2,CD=3,DA=1,且∠B=90°,求∠DAB的度数.(第10题)(第11题)11. 如图,在矩形ABCD中,AB=5cm,在边CD上适当选定一点E,沿直线AE把△ADE折叠,使点D恰好落在边BC上一点F 处,且△ABF的面积是30cm2.求此时AD的长.(第12题)12. 折竹抵地(源自《九章算术》):今有竹高一丈,末折抵地,去本三尺.问折者高几何?意即:一根竹子,原高一丈,虫伤有病,一阵风将竹子折断,其竹梢恰好抵地,抵地处离原长竹子处3尺远.问原处还有多高的竹子?课题学习勾股定理的“无字证明”在勾股定理的学习过程中,我们已经学会运用以下图形,验证著名的勾股定理:整个大正方形的面积可以表示为里面小正方形的面积与四边上的4个直角三角形的面积之和,即为(a+b) 2=c2+4·(1/2ab),由此可以推出勾股定理a2+b2=c2.这种根据图形可以极其简单地直观推论或验证数学规律和公式的方法,简称为“无字证明”.对于勾股定理,我们还可以找到一些用于“无字证明”的图形.现在请你和大家一起,查阅课本和其他有关书籍,上网查询各种相应的资料,相信你一定能够发现更多的有趣图形,验证勾股定理.实际上你还可以发现“无字证明”也可以用于验证数与代数、空间与图形等领域中的许多数学公式和规律!。
(完整版)勾股定理知识点、经典例题,推荐文档
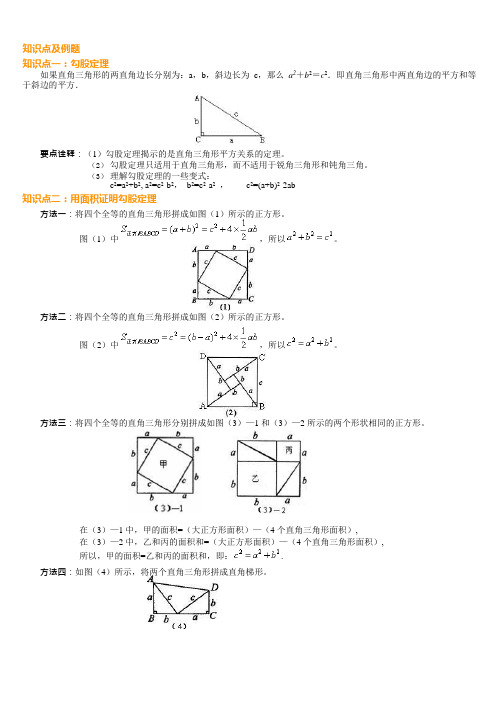
知识点及例题知识点一:勾股定理如果直角三角形的两直角边长分别为:a,b,斜边长为c,那么a2+b2=c2.即直角三角形中两直角边的平方和等于斜边的平方.要点诠释:(1)勾股定理揭示的是直角三角形平方关系的定理。
(2)勾股定理只适用于直角三角形,而不适用于锐角三角形和钝角三角。
(3)理解勾股定理的一些变式:c2=a2+b2, a2=c2-b2,b2=c2-a2 ,c2=(a+b)2-2ab知识点二:用面积证明勾股定理方法一:将四个全等的直角三角形拼成如图(1)所示的正方形。
图(1)中,所以。
方法二:将四个全等的直角三角形拼成如图(2)所示的正方形。
图(2)中,所以。
方法三:将四个全等的直角三角形分别拼成如图(3)—1 和(3)—2 所示的两个形状相同的正方形。
在(3)—1 中,甲的面积=(大正方形面积)—(4 个直角三角形面积),在(3)—2 中,乙和丙的面积和=(大正方形面积)—(4 个直角三角形面积),所以,甲的面积=乙和丙的面积和,即:.方法四:如图(4)所示,将两个直角三角形拼成直角梯形。
知识点三:勾股定理的作用,所以。
1.已知直角三角形的两条边长求第三边;2.已知直角三角形的一条边,求另两边的关系;3.用于证明平方关系的问题;4.利用勾股定理,作出长为的线段。
2.在理解的基础上熟悉下列勾股数满足不定方程x2+y2=z2 的三个正整数,称为勾股数(又称为高数或毕达哥拉斯数),显然,以x,y,z 为三边长的三角形一定是直角三角形。
熟悉下列勾股数,对解题是会有帮助的:①3、4、5②5、12、13;③8、15、17;④7、24、25;⑤10、24、26;⑥9、40、41.如果(a,b,c)是勾股数,当t>0 时,以at,bt,ct 为三角形的三边长,此三角形必为直角三角形。
经典例题透析类型一:勾股定理的直接用法1、在Rt△ABC 中,∠C=90°(1)已知a=6,c=10,求b,(2)已知a=40,b=9,求c;(3)已知c=25,b=15,求a.思路点拨: 写解的过程中,一定要先写上在哪个直角三角形中,注意勾股定理的变形使用。
勾股定理 课件

请大家仿照老师的书写格式做第二题
1.求下列直角三角形中未知边的长:来自8x17
16
20
x
12
5
x
2.已知Rt△ABC的三边分别为a,b,c 若a:b=3:5,b=5,则a=( ) ,c=( )
3:将长为5米的梯子AC斜靠在墙上, BC长为2米,求梯子上端A到墙的底端 B的距离.
第十七章 勾股定理
勾股定理
A的面积
B的面积
C的面积
左图
右图
4 9
16 9
13
25
(2)根据表中数据,你得到了什么?
(3)你能用直角三角形的两直角边的长a、b和斜边长c来表示图中正方形的面积吗?
(4)你能发现直角三角形三边长度之间存在什么关系吗?
C
A
B
解:在Rt△ABC中,∠ABC=90° ∵BC=2 ,AC=5 ∴AB2= AC² - BC² = 5²-2² =21 ∴ AB= (米) AB= (不合题意,舍去)
-
答:梯子上端A到墙的底端B的距离为 米。
1.成立条件: 在直角三角形中;
3.作用:已知直角三角形任意两边长, 求第三边长.
2.公式变形:
a
b
c
如果直角三角形两直角边长分别为a、b,斜边长为c,那么
勾 股 定 理
(注意:哪条边是斜边)
图1-1
图1-2
在Rt△ABC中,∠C=900,∠A、∠B、∠C所对的边分别为a、b、c (1)已知a=1,b=2,求c (2) 已知a=10,c=15,求b
A
C
B
b
a
c
解:(1.)在Rt△ABC中,∠C=900, ∴a2+b2=c2 ∴C= = =
勾股定理ppt课件

学校名称 “赵爽弦图”体现了我国古代人民对数学的钻研精神和
聪明才智,它是我国古代数学的骄傲,所以,这个图案
被选为2002年在北京召开的国际数学大会的会徽
勾股定理是几何中比较重 要的重要定理之一,应用十分 广泛,迄今为止,它的证明方 法已经有600多种,其中,美 国第二十任总统伽菲尔德的证 法在数学史上被传为佳话。下 面让我们一起来探索这个证明 方法吧。
学校名称 我们通过这个图形就证明了以上命题中直角三角形三边的关系
成立。我们知道经过证明被确认为正确的命题叫做定理。因此, 这就是我们今天要学习的内容:勾股定理。中国古代称直角三 角形为勾股形,并且直角边中较小者为勾,另一长直角边为股, 斜边为弦,所以称这个定理为勾股定理。即如果直角三角形的 两条直角边分别为a和b,斜边长为c,那么a2+b2=c2
学校名称
等腰三角形的直角边的平方之和=斜边的平方
a2+b2=c2
这种转化的思想在今后的学习中还会经 常用到,希望同学们Leabharlann 很好掌握学校名称再见
学校名首称先画出直角三角形AEC,其中CE=a AE=b, AC=c.
继续做一个跟它全等的直角三角形BDC,其中BD=a CD=b BC=c,要求E、C、D三点共线,点C在ED之间,连接AB, 就形成了梯形ABDE。
我们发现三角形ABC是等腰直角三角形,那么梯形面积 等于这三个直角三角形的面积之和。利用梯形面积公 式来计算。S梯ABDE=1/2(上底+下底)×高=1/2(a+b) (a+b)
ab+2ab+b2=ab+ab+c2
a2+b2=c2
这个证明方法我们称之为“总统证法”,该证法简 单、直观易懂,即通过计算出三个直角三角形面积 之和与梯形的面积相等,建立等式并进行推导,得 到勾股定理的表达式,为我们展现了数学的美妙之 处。
第四讲 勾股定理(解析版)

第四讲 勾股定理目录必备知识点........................................................................................................................................1考点一 勾股定理的证明................................................................................................................1考点二 勾股定理的逆定理............................................................................................................4考点三 勾股定理的基础应用.. (6)必备知识点1.勾股定理直角三角形两直角边a 、b 的平方和等于斜边c 的平方。
(即:a 2+b 2=c 2)【注意】勾股定理反映了直角三角形三边之间的关系,是直角三角形的重要性质之一,其主要应用:(1)已知直角三角形的两边求第三边(2)已知直角三角形的一边与另两边的关系,求直角三角形的另两边(3)利用勾股定理可以证明线段平方关系的问题2.勾股定理的逆定理如果三角形的三边长:a 、b 、c ,则有关系a 2+b 2=c 2,那么这个三角形是直角三角形。
【注意】勾股定理的逆定理是判定一个三角形是否是直角三角形的一种重要方法,它通过“数转化为形”来确定三角形的可能形状,在运用这一定理时应注意:(1)首先确定最大边,不妨设最长边长为:c (2)验证c 2与a 2+b 2是否具有相等关系:若c 2=a 2+b 2,则△ABC 是以∠C 为直角的直角三角形 ;若c 2>a 2+b 2,则△ABC 是以∠C 为钝角的钝角三角形;若c 2<a 2+b 2,则△ABC 为锐角三角形。
勾股定理四边形计算
2.如图所示,在Rt△ABC中,∠ABC=90°.将 Rt△ABC绕点C顺时针方向旋转60°得到△DEC,点E 在AC上,再将Rt△ABC沿着AB所在直线翻转180°得 到△ABF.连接AD. (1)求证:四边形AFCD是菱形; (2)连接BE并延长交AD于G,连接CG,请问:四 边形ABCG是什么特殊平行四边形,为什么?
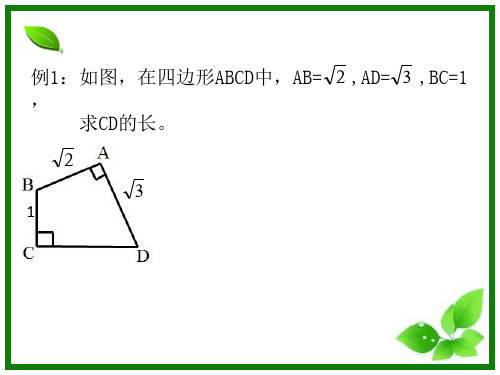
例1:如图,在四边形ABCD中,AB= 2 ,AD= 3 ,BC=1 ,
求CD的长。
2
3
1
例2:在△ABC中,∠C=45°,AB=5,AC= 4 2 ,
求BC的长。
5
42
练习:在△ABC中,∠C=135°,AC= 2 ,BC=2,
求AB的长。
2
2
D
• ——四边形中的计算
试一试,都能做对吗? 1.十边形共有 条对角线。 2.已知一个多边形的每一个内角都是156°, 则它的边数为__. 3.一个正多边形的每个内角都比相邻外角大 36°则这个多边形的边数______。
矩形
如图,四边形ABCD是矩形,△PBC和△QCD都 是等边三角形,且点P在矩形上方,点Q在矩形 内. 求证:(1)∠PBA=∠PCQ=30°;
(2)PA=PQ.PADQBC
菱形
1.如图,已知菱形ABCD的对角线AC,BD的 长分别为6cm, 8cm,AE⊥BC于点E,则AE的 长是_______.
训练:
1. 如图,点M是□ABCD的边AD上任意一点,
则S□ABCD =16cm2,则S△MBC =____
A.8 cm2 B. 10cm2
AM
D
C. 12cm2 D. 16cm2
B
C
2. 如图,在□ABCD中,对角线AC、BD
勾股定理(精品)
新冠肺炎传播途径主要为飞沫传播和接触传播. 若假设一个人的唾沫飞扬距离为50米.如下图所示:假设有一个新冠肺炎 患者在A地打电话,A地距离水平公路l的距离为40米,行人小王从较远 的B地向左一直走,速度为3分米/秒,问小王是否会接触到患者的飞沫? 如果接触到了,受影响的时间为?
1、总结 2、回忆 3、猜想
勾股定理——东西方数学交相辉映 勾股定理的证明 勾股定理的简单应用
《周髀算经》 我国在公元前 1000多 ቤተ መጻሕፍቲ ባይዱ前发现勾股定理
古希腊的数学家 毕达哥拉斯(约 公元前 580~前 500年)
赵爽(东汉末 至三国时代吴 国人,约182--250年)
欧几里得 (约公元前 330年—公元 前275年)
勾股定理的证明
如右图所示,如右图所示:图 中所有的三角形都是直角三角 形,四边形都是正方形.已知正 方形A,B,C,D的面积分别 是4,16,1,4.求正方形E的面 积.
如图,在一次冰雪灾害中,一棵 大树在离地面3米处折断,树的 顶端落在离树杆底部4米处,那 么这棵树折断之前的高度是 ________米.
如图,一根垂直于地面的旗杆 在离地面5m处撕裂折断,旗杆 顶部落在离旗杆底部12m处, 旗杆折断之前的高度是 ________.
如果一个直角三角形两直角边分别 为3和4,求斜边长______________.
如果一个直角三角形两条边长分别 为3和4,求第三条边长__________.
如果一个直角三角形两条边长分别 为3和4,求斜边上的高__________.
如右图所示,字母B所代表的正方 形的面积是( )
A.12 B.13 C.144 D.194
等腰直角三角形的三边之间 有一种特殊的关系:
斜边的平方等于两直角边的 平方和.
勾股定理教案表格版
XX市XXX中学统一备课用纸科目数学年级八班级授课时间年月日课题17.1.1 勾股定理课型新授课教学目标1.探索直角三角形三边关系,学习数学定理的论证过程,运用勾股定理解决简单的问题;2.让学生经历观察、猜想、推理、论证等过程,探索勾股定理,体会数形结合的思想,体验从特殊到一般的逻辑推理过程;3.通过了解勾股定理的历史,激发学生学习数学的兴趣,培养学生严谨的数学学习态度,体验数学的探索性和创造性,感受数学之美,探究之趣。
教学重点勾股定理的证明与运用教学难点勾股定理的探索及论证教具准备多媒体及课件教学内容及过程教学方法和手段一、创设情境,导入新课引入2002年国际数学家大会的会徽的图案,从而导出勾股定理观察猜想:2500年前,毕达哥拉斯在一次朋友家做客时,发现朋友家用砖铺成的地面中反映了直角三角形三边的某种数量关系。
1、A、B、C的面积有什么关系?为什么?2、等腰直角三角形三边有什么关系?结论:等腰直角三角形两直角边的平方和等于斜边的平方。
网格中对于一般直角三角形是否也具有这种性质?(网格中每个小方格的面积都是1)然后通过数格子的形式求出正方形A,B的面积,对于正方形C的面积通过学生回答以割、补、拼三种形式求出面积。
从而得出猜想:如果直角三角形的两直角边长分别为a、b,斜边为c,那么a2+b2=c2二、合作探究,形成知识然后开展学生动动手活动,证明勾股定理成立。
要求: 1、两个同学用四个全等的直角三角形和一个小正方形拼出左边图形,并用a,b,c 求出左边图形的面积。
2、另外两名同学用同样的图形拼出一个大正方形,并用正方形求面积 的方法求出图形的面积。
勾股定理:如果直角三角形的两直角边长分别为a 、b ,斜边为c ,那么a 2+b 2=c 2 即直角三角形两直角边的平方和等于斜边的平方. 几何语言:在Rt △ABC 中,∠C= 90° ∴a 2+b 2=c 2 结论变形:22ca b 22a c b 22b c a三、初步应用,巩固知识例:在△ABC 中,∠C =90°,BC =a ,AC =b ,AB =c.(1)已知a =1,b =2,求c ;(2)已知a =15,c =17,求b ;(3)已知a =53,b=54,求c ; 变式:若一个直角三角形的两边长分别是3、4,则第三边长是 . (4)已知c =34,a ∶b =8∶15,求a ,b.变式1:在Rt △ABC 中,∠C =90°,∠A =45° ,则BC ∶AC ∶AB =_______________; 变式2:在Rt △ABC 中,∠C =90°,∠A =30°, 则BC ∶AC ∶AB =_______________.变式3:如图,AD 是Rt △ABC 中BC 边上的高,若AB=6,AC=8,则BC= ,AD= .拓展提升:如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形7的边长为7cm,求正方形1,2,3,4的面积的和.四、课堂小结 教学反思。
冀教版八年级数学上册17.3《勾股定理》 (共33张PPT)
C D
B A
7cm
1
ቤተ መጻሕፍቲ ባይዱ
1
1、如图,一个高3 米,宽4 米的大门,需在相 对角的顶点间加一个加固木条,则木条的长 为( )C
A.3 米 B.4 米 C.5米 D.6米
3
4
试一试:
2、已知:Rt△ABC中,AB=4,AC=3,则
BC的长为____5__或_____7
a
经过证明被确认正确的命题叫做定理.
勾股命定题1理如: 果如直果角直三角角三形角的形两的直角两边直长角分边长分 别为别a为,ba,,斜b, 斜边边长长为为c,c那, 那么么aa22 b2 cc22..
用赵爽弦图证明勾股定理
b
a
a2 b2 =
c b
a
c2
勾股定理(gou-gu法则)
如果直角三角形两直角边分别为a、b,
径隅(就是弦)则为5。以后人们就简单地把这个事实说
成“勾三股四弦五”,所以在我国人们就把这个定理叫作
“商高定理”。
毕达哥拉斯定理:
“勾股定理”在国外,尤其在西 方被称为“毕达哥拉斯定理”或“百 牛定理”.
毕达哥拉斯
相传这个定理是公元前500多年时 古希腊数学家毕达哥拉斯首先发现的 。他发现勾股定理后高兴异常,命令 他的学生宰了一百头牛来庆祝这个伟 大的发现,因此勾股定理又叫做“百 牛定理”.
A
130
?
C
120 B
1、判断题: 1)直角三角形三边分别为 a, b, c ,则一定满足下面的
式子: a2+b2 =c2( × )
2) 直角三角形的两边长分别是3和4,则第三边长是5.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
教学方案
教学方案
谈谈你的学习收获【检测反馈】:
教学方案
教学方案
教学方案
教学方案
教学方案
教学方案
教学方案
教学方案
教学方案
教学方案
教学方案
在
.在
.已知
是
.
教学方案
活动二运用矩形的性质解决问题
1.自学课本95页的例
(1)还能用什么方法求出对角线的长?
【检测反馈】 (每题101.如图,矩形ABCD 中,对角线图中有 个直角三角形,有 于F ,且BAE DAE ∠=∠3.求
教学方案
教学方案
教学方案
教学方案
活动二:探究正方形的判定方法,并进行相应的证明和计算
.怎样判定一个四边形是正方形?把你所想的判定方法写出来
教学方案
教学方案
教学方案
教学方案
教学方案
.
⊥BC于G.。
