基于细观方法的颗粒增强复合材料弹塑性分析
界面强度对柔颗粒增强复合材料破裂特性的影响
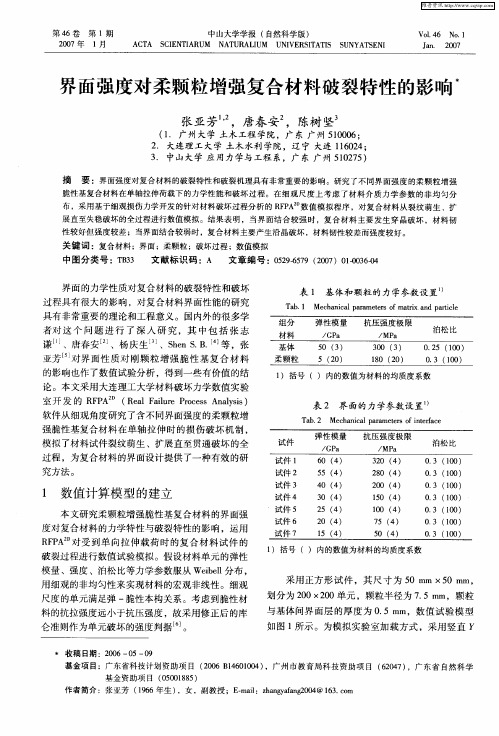
表 1 基体 和颗粒 的 力学参 数设 置 ’
T b 1 Me h nc lp r mee s o t x a d p r ce a . c a ia a a tr fma r n a t l i i
者对 这 个 问题 进 行 了 深 入 研 究 ,其 中 包 括 张 志 谦 ¨ 、唐 春安 J 、杨 庆生 J hnS B [ ,张 、S e . . 等
Jn 2 o a. O7
界面强度对柔颗粒增强复合材料破裂特性的影响
张亚芳 ,唐春安 ,陈树 坚
( . 广 州大学 土木 工程 学 院 ,广 东 广州 5 0 0 ; 1 10 6 2 大连 理 工 大学 土木水 利 学院 ,辽 宁 大连 16 2 . 10 4; 3 中山大 学 应 用力 学与 工程 系,广 东 广 州 507 ) . 125
1 )括号 () 内的数值为材料的均质度系数
表 2 界 面的 力学参数 设 置 ’
T . Me h n c l a a tr fi tr c b a 2 c a ia rmee so ef e p n a
软 件从细 观角度 研究 了含 不 同界 面强度 的柔 颗粒 增 强脆 性基 复合材 料 在 单轴 拉 伸 时 的损 伤 破 坏 机制 ,
模量 、强度 、泊 松 比等力 学参数 服从 Webl分 布 , ie 1
用 细观 的非 均匀 性来 实现材 料 的宏观非 线性 。细 观
1 )括号 () 内的数值为材料的均质度系数
采用正方形试件 ,其 尺寸为 5 m x 0m 0m m, 5
划分 为 20X 0 元 ,颗粒 半径 为 7 5m 0 20单 . m,颗粒 与基 体 问界 面层 的厚 度 为 0 5mm,数 值试 验 模 型 . 如 图 1所示 。为模拟 实验 室加 载 方式 ,采 用 竖直 y
编织复合材料弹性性能的细观力学模型

编织复合材料弹性性能的细观力学模型1)1)国家自然科学基金和航空科学基金资助项目. 1996205220收到第一稿,1996211228收到修改稿.燕 瑛(北京航空航天大学飞行器设计与应用力学系,北京100083)摘要 提出了编织复合材料弹性性能分析的细观力学模型,这个力学模型考虑了实际编织结构中的纬向和经向纤维束的曲屈,相邻纤维束之间的间隙和纤维束的横截面尺寸对编织复合材料弹性性能的影响,并探讨了在纤维束间纯树脂区内孔隙的含量和两种叠层结构对材料弹性性能的影响.理论计算结果与实测值的比较,表明所提出的细观力学模型是合理的.根据理论分析的结果,提出了优化单层和叠层编织结构的结构参数选择方法.关键词 编织复合材料,弹性性能,纤维束的曲屈,结构参数引 言与单向纤维增强的复合材料层合板相比,编织复合材料层板一方面对改进层间、层内强度和损伤容限等方面具有巨大潜力,另一方面,由于它更易于成型,减轻了因铺层所带来的繁琐劳动,制造费用较低,因此具有更强的竞争性.编织复合材料的弹性性能和强度取决于织物的细观结构,采用细观力学的分析方法,预测编织复合材料的细观结构形式对其宏观性能的影响,是实现其性能优化的重要基础.从公开发表的论文看,国内外学术界对编织复合材料细观力学的研究还较少,所提出的分析模型从根本上分为应用层合板理论和有限元分析法[1,2].Ishikawa 和Chou 提出了3个模型来分析编织复合材料,它们是镶嵌模型[3]、纤维曲屈模型[3]和桥式模型[4].这些模型的基本假设是经典层合板理论适用于编织复合材料单层的每一个极微小的基本单元上,因此这些模型被称为层合板理论模型.镶嵌模型和纤维曲屈模型把织物细观结构看成一条一维的织物带,因此不能代表真实的织物结构.为分析缎纹织物结构复合材料的单层所提出的桥式模型,仅仅在受载方向上考虑了纤维束的曲屈和连续性,忽略了垂直载荷方向上纤维束的曲屈对材料性能的影响.Naik 和G anesh 所提出的二维模型[5]是对纤维曲屈模型的发展,考虑了织物结构的二维性和织物结构中存在的间隙,并探讨了织物几何参数对材料面内弹性模量的影响,但此二维模型的应用局限在平纹织物复合材料分析上.Ishikawa 和Chou [3]将有限元理论应用到二维和三维镶嵌模型和纤维曲屈模型中.White 2comb [6]采用三维有限元分析平纹织物复合材料,他研究了纤维束的波纹度对弹性模量、泊松比和应变分布的影响.Zhang 和Harding [7]在假设织物结构单向直波纹情况下,根据应变能等效原理,利用有限元分析方法,给出了一组平纹织物复合材料单层弹性常数的估算结果.本文中所提出的二维波纹细观力学模型在以下这些方面比前面所提到的模型有所改进:(1)这个模型建立了编织复合材料弹性常数随织物结构参数———纤维束曲屈率和相邻纤维束间间第29卷第4期力 学 学 报Vol.29,No.41997年7月ACTA MECHAN ICA SIN ICA J uly ,1997隙的变化关系;(2)考虑了沿纬向和经向纤维束波纹对复合材料弹性性能的影响;(3)探讨了纤维束之间的间隙、层合结构状态和纯树脂区内孔隙的含量对编织复合材料弹性性能的影响.1二维波纹细观力学模型1.1细观几何结构为了便于掌握编织复合材料的力学性能,首先应确定一个用于力学分析的结构体积代表元素.合理地建立编织复合材料力学模型的一个重要方面是建立一个合理的几何构造来描述编织复合材料的细观结构,这里根据编织复合材料的显微照片来确定它的细观几何结构.图1是一典型的T 2300碳纤维平纹织物/环氧树脂复合材料的横截面显微照片.从图中可以看出其细观结构的复杂性.纤维束由于编织形式而纵横交错、波纹起伏,纤维束横截面呈椭圆形,并且展平填满大部分空间,很少量的纯树脂区存在.整个复合材料从体积上由三个区域所组成:浸有树脂的纬向和经向纤维束、纯树脂和孔隙.图1 碳纤维平纹织物/环氧树脂复合材料横截面显微照片Fig.1 Photomicrograph of a section of plain weave carbon fabric/epoxy composite 图2给出了根据显微照片所确定的编织复合材料的体积代表元素.纤维束的宽度和厚度分别用wy 和ty 表示,两相邻纤维束之间间隙用gy 表示,沿x 和y 方向的几何尺寸相等.设x 和y 方向分别为纬向和经向纤维束的方向.纤维束上下波动的几何性可以它的中心线来描述,纬向纤维束的中心线在xz面内的波动图2 编织复合材料的体积代表元素Fig.2 Volume representative element for a woven com posite034力 学 学 报1997 年 第 29 卷以下面的函数表示(图3)z =ty 2sin πxw y +gy (1)其中ty 2和2(w y +gy )分别是波动纤维束的幅度和波长.图3纤维束中心线波动示意图Fig.3The sinusoidal centre line of the yarn 纤维束中心线上某点的切线与x 轴之间的夹角θ是x 的函数tan θ=d z d x =πty 2(w y +gy )cos πx w y +gy =δcos πx w y +gy(2)其中δ=πty/[2(w y +gy )]定义为纤维束波纹度.θmax =cot πty2(w y +gy )(3)在x 与x +d x 之间纤维束的长度ds 可由下式求出d s =d x 2+d z 2=d x 1+c cos 2πxw y +gypr 其中c =πty2(w y +gy )292=δ2(4)在x =0和2(w y +gy )之间曲屈的纤维总长s 可由积分获得s 2(w y +gy )=1+2κ28曲屈+13κ28面内2+90κ28ou 3+644κ284+4708.5κ28影响5+ (5)其中κ2=c1+c (6)根据体积代表元素的几何形状,浸脂纤维束的体积含量由下式确定V y =π(w y )s8(gy +w y )2(7)134第4期燕 瑛:编织复合材料弹性性能的细观力学模型浸脂纤维束是由体积含量为V t f 的纤维束和树脂组成,因此纤维的体积含量为V f =V y V t f (8)根据纤维束曲屈率的定义[8],曲屈率由下式表示CF =s -2(w y +gy )2(w y +gy )(9)1.2应力2应变的关系纵向、横向纤维束和树脂的线性本构关系为σL x σL yy =Q L x xQ L xy Q L xy Q L yy y εx εy y (, σT x σT yy =Q T x x Q T xy Q T xy Q T yy 2εx εy 2πσm x σm y=Q m x xQ m xy Q m xy Q m yy 和2w y εx εy s (10)其中L ,T 和m 分别表示纵向、横向纤维束和树脂.使用矢量转换式,建立偏轴刚度系数和正轴刚度系数的关系Q L x x =Q 11cos 4θx +2(Q 12+2Q 66)cos 2θx sin 2θx +Q 22sin 4θxQ L xy =Q 12cos 2θx +Q 23sin 2θxQ L yy =Q 22Q T x x =Q 22Q T xy =Q 12cos 2θy +Q 23sin 2θy Q T yy =Q 11cos 4θy +2(Q 12+2Q 66)cos 2θy sin 2θy +Q 22sin 4θy 65(11)式中θy 是横向纤维束中线上某点的切线与y 轴的夹角,它的计算方法与公式(2)相似.1.2.1同相状态从图1的光学显微照片可以看出,各织物层间相互错位,无一定组成规律.图4(a )给出织物叠层构造的极限情况,各层之间处于同相状态,因为织物层的排列具有重复性,仅需分析一层的性能,认为垂直于载荷方向的截面保持不变形,因此应变由下式表示εx =εx (x ),εy =εy (y )(12)234力 学 学 报1997 年 第 29 卷这时应力2应变关系由下式表示σLx(x,y)σTx(x,y)σmx (x,y)维束=Q L x x Q L xy Q T x x Q T xy Q m x x Q m xyσεx(x)ε2σLy(x,y)σTy(x,y)σmy(x,y)=Q L xy Q L yyQ T xy Q T yyQ m xy Q m yyε1εy(y)(13)式中ε1和ε2分别表示在体积代表元素内εx(x)和εy(y)的平均值,因此沿x方向作用在横截面上的力为F1(x)=A T(x)σT x(x)+A L(x)σL x(x)+A m(x)σm x(x)(14)式中A T和A L分别是横向和纵向纤维束的横截面积,它们的数值可近似由下式表示A L=π8tyw yA T=1+14δ2x1-2xw ys2x 1/2ty(w y+gy), -w y/2ΦxΦw y/2(15)A m为树脂所占的横截面积.根据公式(11),(13)和(14),作用在x方向上的力可表示为F1=α1(x)εx(x)+α2(x)ε2(16)由对称性,作用在y方向上的力为F2=α2(y)ε1+α1(y)εy(y)(17)式中系数α1(x)和α2(x)为α1(x)=2ty(w y+gy)1+14δ2()1-2xw y方法211/2Q22+ π2tyw y(Q11cos3θx+2(Q12+2Q66)cosθx sin2θx+Q22sin4θx cos-1θx)+ ηQ m11ty4(w y+gy)-π2w ycos-1θx-2(w y+gy)1+14δ2建议1-2xw y件(21/2α2(x)=2ty(w y+gy)1+14δ2121-2xw y21/2Q12+12δ2Q23++ π2tyw y(Q12cosθx+Q23sin2θx cos-1θx)+ ηQ m12ty4(w y+gy)-π2w ycos-1θx-2(w y+gy)1+14δ2ua1-2xw y……2……1/2(18)334第4期燕 瑛:编织复合材料弹性性能的细观力学模型式中0ΦηΦ1是一个反映纤维束间树脂含量的系数,当η=0意味着纯树脂区域完全是空的,当η=1时表明区域内充满树脂.将公式(18)中的所有x 换为y 就可得到α1(y )和α2(y )的表达式.根据公式(16)和(17),在体积代表元素上的平均应变为ε1=C 11-C 22F 1-C 1C 21-C 22F 2, ε2=C 11-C 22F 2-C 1C 21-C 22F 1(19)其中C 1=12(w y +gy )∫w y +gy-(w y +gy )1α1(x )d x , C 2=12(w y +gy )∫w y +gy-(w y +gy )α2(x )α1(x )d x由公式(17),编织复合材料的弹性模量和泊松比为E x =1-C 224ty (w y +gy )C 1, νxy =C 2(20)1.2.2无规则相状态图4(b )给出了另一织物叠层的极限情况,即无规则状态.图4织物叠层结构Fig.4Fabric stacking configuration在这种状态下,假设在任意横截面上的平均刚度相等,应变是均匀的,即εx (x ,y ,z )=ε1,εy (x ,y ,z )=ε2(21)式中ε1和ε2是常数,根据公式(10)可得材料的应力,类似公式(14)可得在这种状态下力的表达式,它是x 的函数,在体积代表元素内的平均力为F 1=12(w y +gy )∫(w y +gy )-(w y +gy )F 1(x )d x (22)也可进一步写为F 1=α11ε1+α12ε2(23)式中α11=πtyw y 2Q 111-34δ2)+(Q 12+2Q 66)δ2+Q 221+14δ212Q +ηQ m 11ty 4(w y +gy )-πw y 1+14δ22os α12=πtyw y 22Q 12+12Q 23δ2+ηQ m 12ty 4(w y +gy )-πw y 1+14δ2y 14(24)434力 学 学 报1997 年 第 29 卷用类似的方法可求出作用在y 方向上的力,又因 F 1=4ty (w y +gy )σ1,F 2=4ty (w y +gy )σ2,σ1和σ2是远端作用的应力,因此编织复合材料的刚度和泊松比可表示为E x =α11(1-ν2xy )4ty (w y +gy ), νxy =α12α112结果与讨论通过对几个编织复合材料构造参数的分析确定纤维束的曲屈率、孔隙的含量对纤维体积含量、弹性模量和泊松比的影响.图5给出了纤维体积含量与纤维束曲屈率及ty/gy 比值间的关系.可以看出,对编织复合材料具有小间隙(ty/gy =10)的细观结构,纤维体积含量随着纤维束曲屈率的增大而增加,而对于具有中等间隙(ty/gy =1)和大间隙(ty/gy =0.1)的细观结构,纤维体积含量随着纤维束曲屈率的增大而减小;另一方面,图中的数据也说明了随着间隙的增加,纤维体积含量将减小,这是由于随着间隙的增大而增加了树脂所占的比例.图5纤维体积含量与纤维束曲屈率及ty/gy 比值间的关系Fig.5Variation of fibre volume fraction with yarn crimp percentage 图6给出了编织复合材料弹性模量与纤维束曲屈率及ty/gy 比值间的变化关系.可以看出,弹性模量随着纤维束曲屈率的增加而减小,具有同相叠层构造状态的编织复合材料提供了比较高的弹性性能,弹性模量随着间隙的增加而降低.这个结果与Shembekar 和Naik 所得结论相一致[9].纤维束之间的间隙的影响是两方面的,随着间隙的增大,很明显纤维的体积含量将降低,因而弹性模量也将降低;另一方面,间隙的存在将减小纤维束的曲屈程度而使弹性模量增加.从这个分析知,通过织物结构设计,选取合理的间隙值,可使弹性模量取最大值.另外,具有间隙的织物,有较好的浸润性,因而易获得较好性能的编织复合材料.图7给出了弹性模量与纤维体积含量及ty/gy 比值间的变化关系.对具有中等间隙细观结构的编织复合材料,弹性模量随纤维体积含量的增加而增大;对具有小间隙细观结构的编织复合材料,弹性模量随纤维体积含量的增加而减小.这个图说明具有中等间隙细观结构的材料比具有小间隙细观结构的材料更为合理,因为这种结构在相对低的纤维体积含量下提供同等程度高的弹性性能.图8给出了泊松比与纤维束曲屈率及ty/gy 比值间的变化关系.随着纤维束曲屈率的增534第4期燕 瑛:编织复合材料弹性性能的细观力学模型加,泊松比显著的增大,对具有中等间隙和同相叠加状态的复合材料,泊松比随纤维束曲屈率的增高而增大得极为显著.另外,随着间隙的增加,泊松比的数值有所增大.图8泊松比与纤维束曲屈率及ty/gy 比值间的关系Fig.8Variation of major Poisson ’s ratio with yarn crimp percentage (wy =2,void content =0.2)634力 学 学 报1997 年 第 29 卷 图9给出了泊松比与纤维体积含量及ty/gy 比值间的变化关系.对具有小间隙的材料,泊松比随纤维体积含量的增高而增大;而对中等间隙的编织复合材料,泊松比随纤维体积含量的增高而减小.此图进一步说明了中等间隙的编织复合材料的结构较为合理,因为在相对低的纤维体积含量下,具有同等低的泊松比.图9泊松比与纤维体积含量及ty/gy 比值间的关系Fig.9Variation of major Poisson ’s ratio with fibre volume fraction (wy =2,void content =0.2) 在同相和无规则相状态下确定的纯树脂区内孔隙的含量对复合材料刚度和泊松比的影响在表1中列出.从表中数据知,随着孔隙含量的增加(从η=1到η=0),弹性模量和泊松比都有所降低,弹性模量的变化范围在1.8%~1.9%,而泊松比的变化范围为17%.表1 树脂区内孔隙的含量对弹性模量和泊松比的影响Table 1 E ffect of void content on the elastic modulus and Poisson ’s ratio Void content Iso 2phase mode (IPM )Random 2phase mode (RPM )ηE x νxy E x νxy 061.2350.035857.880.0380.261.460.03758.10.03940.461.680.038458.330.040.661.90.039758.550.0420.862.120.04158.770.043162.350.0422590.0447V ariation (%)1.8171.917 表2给出了弹性模量和泊松比的理论预测值与实验值的比较.从表中数据可以看出预测值与实测值很接近.表2 弹性模量和泊松比的理论预测值与实验值的比较Table 2Predicted elastic modulus and Poisson ’s ratio in comparison with experimental dataE x /GPav xy E x /GPa v xy E x [10]v xy ty/gy =10IPM ty/gy =10IPM ty/gy =10RPM ty/gy =10R PM Experimental Data Experimental Dada61.460.037158.10.039461±3.60.0533结论1)通过理论计算结果与实测值的比较,证明所提出细观力学模型的正确性;2)纤维体积含量与编织几何形状有关.对纤维束之间具有小间隙的情况下,随着纤维曲734第4期燕 瑛:编织复合材料弹性性能的细观力学模型834力 学 学 报1997 年 第 29 卷屈率的增大,纤维体积含量增大;而对具有中等间隙和大间隙时,会产生相反的结果;3)复合材料叠层结构为同相状态时所具有的刚度比无规则相状态时要高些;4)纯树脂区中孔隙含量的大小对泊松比有很大的影响;5)在理论分析的基础上,提出了优化编织复合材料性能的结构参数的选择.参 考 文 献1Raju IS,Wang J T.Classical laminate theory models for woven fabric com posites.Journal of Com posites Technolo2 gy&Research,1994,16(4):289~3032Whitcomb J,Woo K,Gundapaneni S.Macro finite element for analysis of textile composites.Journal of Com pos2 ite M aterials,1994,28(7):607~6173Ishikawa T,Chou TW.One2dimensional micromechanical analysis of woven fabric composites.A IA A Journal, 1983,21:1714~17214Ishikawa T,Chou TW.Stiffness and strength behaviour of woven fabric com posites.Journal of M aterial Science, 1982,17:3211~32205Naik N K,G anesh V K.Prediction of on2axes elastic properties of plain weave fabric posites Science and Technology,1992,45:135~1526Whitcomb JD.Three2dimensional stress analysis of plain weave posite Materials:Fatigue and Fracture(Third Volume),ASTM STP1110,T K O’Brien Ed.,American S ociety for Testing and Materials, Philadelphia,1991.417~4387Zhang YC,Harding J.A numerical micromechanics analysis of the mechanical properties of a plain weave compos2 puters and S t ructures,1990,36:839~8448燕瑛,丁逸强.纺织结构复合材料强度性能的研究.北京航空航天大学学报,1996,22(6)9Naik N K,Shembekar PS.Elastic behaviour of woven fabric com posites:I2lamina analysis.Journal of Composites Materials,1992,26:2196~222510Ding YQ.Structural characterization and mechanical properties of32Dwoven composites.SAMPE,Birmingham, 1993.1~9A MICR OMECHANICAL MODE L FOR E LASTIC BEHAVIOURANALYSIS OF WOVEN FABRIC COMPOSITESY an Y ing(Instit ute of A ircraf t Design and Research,BeijingU niversity ofAeronautics and Ast ronautics,Beijing100083,China)Abstract A micromechanical model for elastic behaviour analysis of woven fabric composites is proposed in this paper.This model takes into account the actual fabric structure by considering the fibre undulation and continuity along both the warp and weft directions,the gaps between adjacent yarns and the actual cross2sec2 tional geometry of the yarn.The effect of the voids in the interyarn space and two cases of fabric stacking arrangements to the composite elastic properties have been investigated.A comparison of the resulting ana2 lytical predictions with experimental results shows that the proposed model is valid.K ey w ords woven fabric composites,elastic behaviour,fibre undulation。
考虑颗粒形状的复合固体推进剂细观损伤分析

考虑颗粒形状的复合固体推进剂细观损伤分析侯宇菲;许进升;陈雄;周长省;朱亮【摘要】HTPB复合固体推进剂作为一种多颗粒填充的含能材料,其损伤过程复杂.为更直观地分析其受损过程,从细观角度出发,通过分子动力学方法建立圆形颗粒填充模型与多边形颗粒填充模型.在颗粒/基体界面嵌入了零厚度的内聚力单元,分别采用双线性内聚力模型与指数型内聚力模型的分离位移关系对其进行数值仿真,并通过了Hooke-Jeeves反演方法得到了内聚力模型参数.通过对5组加载速率下不同模型的试验结果与仿真结果对比,发现多边形颗粒模型更符合推进剂的细观结构;指数型内聚力模型更适合粘弹性材料的损伤;载荷速率的提高,使得材料的模量下降率升高.【期刊名称】《固体火箭技术》【年(卷),期】2019(042)004【总页数】8页(P440-446,475)【关键词】复合固体推进剂;零厚度内聚力单元;指数型内聚力模型;Hooke-Jeeves 反演方法;脱湿【作者】侯宇菲;许进升;陈雄;周长省;朱亮【作者单位】南京理工大学机械工程学院,南京 210094;南京理工大学机械工程学院,南京 210094;南京理工大学机械工程学院,南京 210094;南京理工大学机械工程学院,南京 210094;南京理工大学机械工程学院,南京 210094【正文语种】中文【中图分类】V5120 引言复合固体推进剂材料的力学性能在固体火箭发动机药柱的结构完整性中起着重要作用。
若想达到固体推进剂在工作过程中的力学指标,必须提前对推进剂的力学性能进行预测,保证固体推进剂的结构完整性。
在过去的几十年中,许多研究人员从连续介质力学角度对固体推进剂本构关系进行了大量的探索与研究[1],这些理论研究均将固体推进剂视为一种连续均匀的介质。
然而,复合固体推进剂是一种多颗粒填充的非均匀含能材料,上述方法不能从本质上解释造成固体推进剂力学性能非线性的原因。
因此,采用细观方法对复合固体推进剂的力学性能进行研究成为一种有效途径。
复合材料的细观力学研究进展

复合材料的细观力学研究进展作者:刘克明, 金莹, 康林萍, 谌昀, 付青峰, LIU Ke-ming, JIN Ying, KANG Lin-ping , CHEN Yun, FU Qing-feng作者单位:刘克明,LIU Ke-ming(江西省科学院江西省铜钨新材料重点实验室,江西,南昌,330029;中南大学材料科学与工程学院,湖南,长沙,410083), 金莹,康林萍,谌昀,付青峰,JIN Ying,KANGLin-ping,CHEN Yun,FU Qing-feng(江西省科学院江西省铜钨新材料重点实验室,江西,南昌,330029)刊名:江西科学英文刊名:JIANGXI SCIENCE年,卷(期):2010,28(3)被引用次数:0次1.Tekoglu C.Pardoen T A micromechanics based damage model for composite materials 20102.胡丽娟.张少睿.李大永.苌群峰.彭颖红细观参数对纤维增强金属基复合材料宏细观力学性能的影响 2008(3)3.吕毅.吕国志.孙龙生基于有限元计算细观力学的RVE库的建立与应用 2009(5)4.Segurado J.Llorca J Computational micromechanics of composites:The effect of particle spatial distribution 20065.陈增涛.王铎动态延性损伤的细观力学研究现状 1994(5)6.王俊.G M Birman V Micromechanics and structural response of functionally graded,particulate-matrix,fiber-reinforced composites 20097.Axelrad D R.Basu S Mechanical relaxation theory of fibrous structures 1977(3-4)8.Aghdam M M.Dezhsetan A Micromechanics based analysis of randomly distributed fiber reinforced composites using simplified unit cell model 20059.陈玮.赵清杰.马艳红细观力学理论在氧化铝陶瓷材料中的应用进展 2004(S)10.Kontou E Micromechanics model for particulate composites 200711.曾庆敦复合材料的细观破坏与强度 200212.Xiaz.Okabe T.Curtia W A Shear-lag versus finite element models for stress transfer in fiber-reinforced composites 200213.Okabe T.Takeda N Estimation of strength distribution for a fiber embedded in single-fiber composite:experiments and statistical simulation based on the elastoplastic shear-lag approach 2001 14.Okabe T.Takeda N Elastoplastic shear-lag analysis of single-fiber composites and strength prediction of unidirectional multi-fiber composites 200215.Xiza.Curtin W A.Okabe T Green's function vs shear-lag models of damage and failure in fiber composites 200216.Hui C Y.Phoenis S L.Shia D The single filament composite test:application of new statistical theory for estimating and Weibull parameters for composite design 199717.李红周.贾玉玺.姜伟纤维增强复合材料的细观力学模型以及数值模拟进展 200618.宋迎东.雷友锋.孙志刚.高德平一种新的纤维增强复合材料细观力学模型 2003(4)19.刘波.雷友锋.宋迎东纤维增强复合材料宏观与细观统一的细观力学模型 2007(3)20.方岱宁.周储伟有限元计算细观力学对复合材料力学行为的数值分析 1998(2)21.Sun H Y.Di S L.Zhang N Micromechanics of composite materials using multivariable finite element method and homogenization theory 200122.Zhang S Q.Jang B Z.Valaire B T A new criterion for composite materials mixed mode fracture analysis 198923.Sih G.C Energy-density concept in fracture mechanics 197324.张少琴.杨维阳.张克颢复合材料的Z-断裂准则及专家系统 200325.雷友锋.魏德明.高德平细观力学有限元法预测复合材料宏观有效弹性模量 2003(3)1.会议论文杨庆生.马连华含流体夹杂复合材料的细观力学2008含有流体夹杂复合材料具有广泛的实际背景,生物组织、饱和岩土、胶体材料等都是由固体骨架与间隙流体组成的复合材料。
《纳米复合材料的弹性性能的多尺度建模分析》

《纳米复合材料的弹性性能的多尺度建模分析》一、引言随着科技的不断进步,纳米复合材料因其在强度、硬度、耐热性及弹性等多方面的卓越性能,已成为现代工程领域的研究热点。
特别是其弹性性能,在众多应用中如橡胶、塑料、生物材料等均具有重要价值。
然而,为了更好地理解和利用这些特性,我们有必要在多个尺度上建立数学模型来模拟其性能。
本文将对纳米复合材料的弹性性能进行多尺度建模分析,深入探讨其内在机制。
二、多尺度建模方法多尺度建模是一种将不同尺度的物理现象和过程进行整合的建模方法。
在纳米复合材料的弹性性能研究中,我们主要关注的是微观和宏观两个尺度。
微观尺度主要涉及分子、原子和纳米结构的行为,而宏观尺度则关注材料整体的行为和性能。
在微观尺度上,我们通常使用分子动力学模拟、量子力学等方法来研究材料的结构和性质。
在宏观尺度上,我们则使用连续介质力学、有限元分析等方法来描述材料的整体行为。
通过将这两个尺度的模型进行连接和整合,我们可以得到一个全面的多尺度模型。
三、纳米复合材料的弹性性能多尺度建模对于纳米复合材料的弹性性能多尺度建模,我们首先需要建立微观尺度的模型。
这包括确定材料的组成、结构和相互作用等。
例如,我们可以使用分子动力学模拟来研究纳米粒子和基体之间的相互作用,以及这些相互作用如何影响材料的弹性性能。
在宏观尺度上,我们使用连续介质力学和有限元分析等方法来描述材料的整体行为。
这包括建立材料的本构关系、边界条件等。
通过将微观尺度的模拟结果与宏观尺度的模型进行连接,我们可以得到一个完整的弹性性能多尺度模型。
四、结果与分析通过多尺度建模分析,我们可以得到纳米复合材料在不同尺度上的弹性性能表现。
在微观尺度上,我们可以观察到纳米粒子和基体之间的相互作用如何影响材料的弹性性能。
在宏观尺度上,我们可以看到材料在不同条件下的整体行为和性能。
这些结果为我们理解和利用纳米复合材料的弹性性能提供了重要的理论依据。
五、结论通过多尺度建模分析,我们可以更好地理解和利用纳米复合材料的弹性性能。
《纳米复合材料的弹性性能的多尺度建模分析》

《纳米复合材料的弹性性能的多尺度建模分析》篇一一、引言随着纳米科技的飞速发展,纳米复合材料因其独特的物理和化学性质在众多领域展现出巨大的应用潜力。
弹性性能作为纳米复合材料重要的性能指标之一,对其实际应用具有重要的指导意义。
多尺度建模方法作为一种有效的分析工具,能够帮助我们更深入地理解纳米复合材料的弹性性能。
本文旨在探讨纳米复合材料的弹性性能的多尺度建模分析,以期为相关研究提供理论支持。
二、纳米复合材料概述纳米复合材料是由纳米尺度的组分构成的复合材料,其组成可以是无机物、有机物或生物材料等。
由于纳米尺度的组分具有独特的物理和化学性质,使得纳米复合材料在力学、热学、电学等方面表现出优异的性能。
弹性性能作为纳米复合材料的基本性能之一,对于其在实际应用中的表现具有重要意义。
三、多尺度建模方法多尺度建模方法是一种综合利用不同尺度下的物理和化学信息,对材料性能进行模拟和分析的方法。
在纳米复合材料的弹性性能研究中,多尺度建模方法能够从微观到宏观的多个尺度上揭示材料的弹性行为。
其中,微观尺度主要关注原子和分子的相互作用,中观尺度关注纳米尺度的组分间的相互作用,宏观尺度则关注材料整体的力学性能。
四、多尺度建模分析1. 微观尺度建模:在微观尺度上,通过量子力学和分子动力学等方法,研究原子和分子的相互作用以及力学行为。
这些研究能够帮助我们了解纳米复合材料中各组分的相互作用机制,从而为提高材料的弹性性能提供理论依据。
2. 中观尺度建模:在中观尺度上,通过建立纳米尺度的组分间的相互作用模型,研究各组分对材料整体性能的影响。
这有助于我们理解纳米复合材料的微观结构和弹性性能之间的关系,为优化材料设计提供指导。
3. 宏观尺度建模:在宏观尺度上,通过连续介质力学等方法,研究材料整体的力学性能。
这能够让我们从整体上了解纳米复合材料的弹性性能,为实际应用的可行性提供理论支持。
五、结果与讨论通过多尺度建模分析,我们可以更深入地理解纳米复合材料的弹性性能。
哈工大——复合材料细观力学-1
50年代----70年代
80年代快速发展 90年代不可缺少
参考教程
杜善义、王彪 《复合材料细观力学》科学出版社 1997 Mura T. Micromechanics of defects in solids. 1987 杨卫 《宏微观断裂力学》国防工业出版社 1995 基础教程 《弹性力学》、《复合材料力学》
out
pq C pqmn { Cijkl * Gmk ,ln ( x, x' )dV} ji
得到各向同性介质椭球体中,存在
ij S
* ijkl kl
S是四阶Eshelby张量,与材料性能和夹杂形状 有关,具有椭圆积分形式,并可推广到各向异 性介质和本征应变不均匀情况。对于特殊形状 夹杂,可以写出解析表达式:
第二章 复合材料有效性能
第一节
Eshelby等效夹杂理论
1957年Eshelby在英国皇家学会会刊 发表了关于无限大体内含有椭球夹杂弹性 场问题的文章,证明了在均匀外载作用时, 椭球夹杂内部弹性场亦均匀。(椭圆积分 形式)
2.1Eshelby相变问题
将应变分解为两部分
ij eij
复合材料有效性能
有效弹性模量的影响因素 组分材料的弹性常数
基体 -各向同性 纤维 -横观各向同性
微结构特征
夹杂形状(纤维、颗粒、晶须、孔洞、裂纹) 几何尺寸、分布 体积含量 等等
成熟的细观力学方法
Eshelby 等效夹杂理论
自洽理论(自相似理论) Mori-Tanaka方法(背应力法) 微分法 Hashin 变分原理求解上下限方法 其他方法
复合材料有效弹性性质分析方法
复合材料有效弹性性质分析方法
胡更开;郑泉水;黄筑平
【期刊名称】《力学进展》
【年(卷),期】2001(031)003
【摘要】建立复合材料的有效性质与微结构参数的关联,是复合材料优化设计的基础.本文具体针对有效弹性性质,重点介绍了建立有效性质的基本思路和主要分析方法.首先讨论了代表单元的概念,然后分别从复合材料有效性质的普适关系、界限理论和近似方法三个不同的视角较全面地介绍了建立非均质材料有效性质的方法、主要结果和最新进展.重点从构型的概念和微结构分布形式上分析了各种模型间及分析方法之间的联系与差别.最后还就建立非均质材料有效性质中存在的问题和研究热点做了简单的介绍.
【总页数】33页(P361-393)
【作者】胡更开;郑泉水;黄筑平
【作者单位】北京理工大学应用力学系;清华大学工程力学系;北京大学力学与工程科学系
【正文语种】中文
【中图分类】TB383
【相关文献】
1.应用数字岩心和有效介质模型研究岩石弹性性质 [J], 张晋言;孙建孟
2.复合材料夹层板壳一种有效分析方法 [J], 晏麓晖;曾首义
3.损伤体有效弹性性质的细观分析和不变性描述:一个考虑微缺陷相互?… [J], 高蕴昕;郑泉水
4.空心球复合材料热弹性性质的一些精确结果 [J], 何陵辉;成振强;刘人怀
5.高体积百分比颗粒增强聚合物材料的有效粘弹性性质 [J], 李丹;胡更开
因版权原因,仅展示原文概要,查看原文内容请购买。
颗粒增强复合材料的强度预测
复合材料的增强原理在复合材料中,由于增强体的形态不同,其增强原理也有很大差别,以下简要介绍几种复合材料的增强原理。
(1)弥散强化原理弥散增强复合材料是由弥散颗粒与基体复合而成。
其增强机理与析出强化机理相似,可用Orowan 机理及位错绕过理论来解释,见图1。
此时,载荷主要由基体承担,弥散微粒阻碍基体的位错运动。
微粒阻碍基体位错运动的能力越大,增强的效果越大。
在剪切应力的作用下,位错的曲率半径R 为i m b G R τ2/= (1)式中,G m 是基体的剪切模量,b 是柏氏矢量。
若微粒之间的距离为D f ,当剪切应力τi 大到使位错的曲率半径R=D f /2时,基体发生位错运动,复合材料产生塑性变形,此时剪切应力即为复合材料的屈服强度f m c D b G /=τ (2)假设基体的理论断裂应力为G m /30,基体屈服强度为G m /100,它们分别为发生位错运动所需剪应力的上、下限。
代入式(2)中得出微粒间距的上、下限分别为0.3μm 和0.01μm 。
当微粒间距在0.01~0.3μm 之间时,微粒具有增强作用。
若微粒直径为d ,体积分数为V p 、微粒弥散且均匀分布,根据体视金相学,有如下关系:)1()/32(2/12p p p p V V d D -= (3)代入式(2)即得:⎥⎦⎤⎢⎣⎡-=)1()/32(/2/12p p p m c V V d b G τ (4)显然,微粒尺寸越小,体积分数越高,强化效果越好:一般V p =0.01%~0.15%,d=0.01~0.1μm 。
(2)颗粒增强原理颗粒增强复合材料是由尺寸较大(>1μm )的坚硬颗粒与基体复合而成。
其增强原理与弥散增强有区别,在颗粒增强复合材料中,虽然载荷主要由基体承担,但颗粒也承受载荷并与约束基体的变形、颗粒阻止基体位错运动的能力越大,增强效果越好。
在外载荷的作用下,基体内位错的滑移在基体-颗粒界面上受到阻滞,并在颗粒上产生应力集中,其值为:σσn i = (5)根据位错理论,应力集中因子为:b G D n m p /σ= (6)将上式代入式(5)得:b G D m p i /2σσ= (7)如果p i σσ=时,颗粒开始破坏,产生裂纹,引起复合材料变形,并令C G p p /=σ,则有: b G D c G m p pp i /2σσσ=== (8)式中,σp 为颗粒强度,c 为常数。
SiC颗粒增强Al基复合材料及其性能研究
SiC颗粒增强Al基复合材料及其性能研究杨雅静;李付国;袁战伟【摘要】SiC颗粒的加入使SiC增强铝基复合材料拥有了优异的综合性能,从而成为具有广泛使用价值的先进复合材料.本文综述了SiC颗粒增强铝基复合材料的第二相特征及其对使用性能的影响规律.特别是对近年来倍受关注的SiC颗粒形状、尺寸、体积分数、颗粒分布和界面特征等对复合材料宏、微观性能的影响进行了详细论述.%The second phase characteristics of Silicon carbide particles reinforced Al matrix composites and its influence law on the performance have been overviewed in the text. The influence of silicon carbide particle factors, including particle shape, particle size, volume fraction, particles distribution and interface characteristics between particjle and matrix, on macro and micro performance of matrix composites have been expounded in detail.【期刊名称】《锻压装备与制造技术》【年(卷),期】2012(000)006【总页数】7页(P82-88)【关键词】复合材料;SiCp/Al;性能;综述【作者】杨雅静;李付国;袁战伟【作者单位】西北工业大学凝固技术国家重点实验室,陕西西安 710072;西北工业大学凝固技术国家重点实验室,陕西西安 710072;西北工业大学凝固技术国家重点实验室,陕西西安 710072【正文语种】中文【中图分类】TG146.2+11 前言SiCp/Al基复合材料由于具有高比强度、高刚度、耐疲劳、耐磨损、热膨胀系数低、优良的尺寸稳定性、较强的可设计性等优异的综合性能,已成为具有广泛使用价值的先进复合材料。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第33卷第6期2001年12月南 京 航 空 航 天 大 学 学 报Jo urnal o f Nanjing Univ ersity o f Aerona utics &Astronautics V ol.33N o.6 Dec.2001文章编号:1005-2615(2001)06-0512-04基于细观方法的颗粒增强复合材料弹塑性分析周储伟 王鑫伟(南京航空航天大学航空宇航学院 南京,210016)摘要 针对高体积含量的颗粒增强复合材料,提出了一种细观结构模型:将颗粒简化为同质、同尺寸的弹性圆球,两颗粒之间的连接基体简化为一弹塑性短圆柱体,并假设细观应力、应变和塑性区均为轴对称分布。
基体和颗粒的变形行为分别简化为类似于弹性地基和弹性半空间,以此为基础,建立了反映一对颗粒法向和切向变形协调关系的两个积分方程。
数值求解这两个方程,可得到一对颗粒间基体中细观应力的分布形式,从而建立颗粒对的细观弹塑性本构,采用平均化方法,进一步推导出材料宏观的应力-应变关系。
本文利用该模型对一种金属基复合材料的拉伸实验进行了模拟,理论预测与实验结果吻合较好。
关键词:复合材料;颗粒增强复合材料;本构关系;细观力学;平均化方法中图分类号:T B333;O 343.7;O 344.1 文献标识码:A 基金项目:中国博士后基金及江苏省博士后基金资助项目。
收稿日期:2000-11-07;修订日期:2001-07-18 作者简介:周储伟,男,副教授,1964年2月生;王鑫伟,男,教授,博士生导师,1948年2月生。
引 言颗粒增强复合材料的力学性能与颗粒体和基体的模量、强度、颗粒的体积含量、颗粒/基体的粘合强度等细观参数有关,从这些细观参数出发,预测出材料的宏观力学性能,是材料设计和使用中所关心的问题。
当颗粒体积含量较高时,颗粒间的相互作用效应很强,这种效应对于材料的模量、屈服、损伤等力学性能都有很大的影响,此时适用于较小颗粒体积含量的基于Eshelby 方法的各种细观力学模型不再适用[1~2]。
本文以高体积含量的颗粒增强复合材料为背景,通过对其细观结构的简化和引入类似文[3~5]中对细观应力、变形及塑性区域的一些假设,提出了一种适用于高体积含量的颗粒复合材料的细观结构模型,并给出了细观应力和一个颗粒对的拉压、剪切模量的求法。
在此基础上,采用平均化的方法,求出了材料宏观的应力-应变关系。
1 材料细观结构的简化模型本文假设颗粒是同质、同尺寸的弹性圆球,连接两颗粒的基体部分简化为一段圆柱体,该圆柱体与颗粒球心的连线共轴,如图1所示。
圆柱半径r c的选取具有一定的人为性,本文采用的方法为:设一个颗粒与N 个颗粒相邻,则就有N 个连接柱体,这N 个连接柱体在该颗粒球面上的投影圆相切。
圆柱形基体中的应力、应变及塑性等均假设为轴对称分布,基体材料的屈服从两颗粒相距的最近处,即圆柱体的轴线处萌生,并以轴对称的方式向外扩展。
对于颗粒体积含量较高的情况,圆柱形基体的轴向长度远小于其半径,故假设其应力、应变及塑性变形沿轴向为均匀分布,圆柱体的径向应变也远小于轴向及剪切应变,分析中忽略不计。
颗粒的弹性变形用空间半无限体的变形来模拟。
图1 颗粒通过基体相连接的模型2 一对颗粒的细观弹塑性分析对于两相邻颗粒组成的颗粒对,取图2所示的图2 一个颗粒对的坐标系坐标系,n 和t 分别为沿球心连线和垂直球心连线方向上的单位向量,h 0表示基体轴心处的厚度,h c 表示圆柱体最外圈的厚度,h (r )=h 0+r 2/R 表示圆柱体至轴心距离为r 处的厚度,R 为颗粒的半径。
由于XO Y 平面为对称面,可只取一个颗粒半个圆柱形基体的构型来研究。
设两颗粒之间相互作用力的合力为P ,颗粒球心之间的相对位移为2w ,记变形后颗粒表面相对于该颗粒变形前球心位置的位移为u P ,相对于X OY 平面的位移为u M ,则w =u P +u M 。
颗粒和基体接触面中的应力记为e 。
根据第1节中的假设,基体中的应变可以近似为X n =2u nM (r )h (r ) V nt =2u t M(r )h (r )(1)式中:u nM(r ),u t M(r )分别为u M的法向和切向的位移分量;而基体中的应力分量为e n (r )=4G M 1-v M 1-2v M u n M (r )h (r )e r (r )=e θ(r )=4G Mv M 1-2v M u n M (r )h (r )f nt (r )=4G Mu tM (r )h (r )(2)式中:G M ,v M 分别为基体的剪切模量和泊松比。
位移协调条件可以写为[3~10]w n =(1-2v M )4(1-v M )G Mh (r )e n (r )+(1-v P )2G P π∫π0d θ∫r cos θ+r 2c-r 2sin 2θ×e n (r 2+s 2-2rs cos θ)d sw t =12G Mh (r )f nt (r )+14G P π∫π0d θ∫r cos θ+r 2c-r 2sin 2θ×f nt (r 2+s 2-2rs cos θ)(1-v M sin 2θ)d s (3)其中:G P ,v P 为颗粒的剪切模量和泊松比,式(3)右端第一项为基体变形的贡献,第二项为颗粒变形的贡献,颗粒的变形认为近似于弹性半空间的变形[4~5],其中坐标参数θ,s 的意义见图3。
颗粒表面图3 计算颗粒表面一点变形的积分区域任一点A 处的变形,可视为AB 线段上每一点上的面力对A 点变形贡献的积分,同时AB 线段绕A 点从-π到π旋转(由对称性,实际旋转范围为0~π),而AB 线段的长度,就是式(3)中d s 的积分区域。
可采用数值方法求解积分方程(3),如可将e n (r ),f nt (r )设为多项式,其系数通过配点法来确定,与w n ,w t 成比例。
设基体为理想弹塑性材料,并且满足V on-Mises 屈服准则,则弹、塑性区域交界面处的应力应满足下式1-2v M 1-v M2e 2n (r y )+3f 2nt (r y )=e 2s (4)式中:e s 为屈服应力,r y 为塑性区域的半径。
设塑性加载条件下,塑性区内(0≤r ≤r y )应力分量的值保持不变,由应力连续要求,塑性区内的应力分量等于弹塑性交界面处的应力分量:e Pn =e (r y ),f Pnt =f nt(r y )。
弹性区域内的应力分布仍可通过式(3)表示的位移协调条件求解。
对于本文的模型,塑性区分布在圆柱状基体的中心处,所以材料中某点处基体塑性区半径r y 随空间取向的变化,就反映了该点的塑性程度。
颗粒对之间作用力的合力可以由基体中的分布应力积分得到P n =2π∫rc0e n r d r d θ P t =2π∫rc0f nt r d r d θ(5) 一对颗粒的法向和切向的切线模量由下式给出K n = P n w n K t = P tw t(6)3 宏观等效力学性能与算例图4所示材料中一颗粒m ,半径为r ,n 为另一513第6期周储伟,等:基于细观方法的颗粒增强复合材料弹塑性分析个与之相邻的颗粒,两颗粒之间的距离为h 0,颗粒中心连线方向上的单位矢量为I nm =(X n -X m )/(2R +h 0)。
设在颗粒直径尺度上,宏图4 空间一对相邻颗粒观的应变场可视为均匀,则两颗粒球心间的相对位移可用该处的宏观应变场X-表示[11,12]W n =(2R +h 0)I nm X- I nm I nmW t =(2R +h 0)I nm X -(l -I nm I nm )(7)式中l 为二阶单位张量。
两颗粒之间的作用力用宏观应变表示,其分量形式为P nm i =R +h 02[(K n -K t )X -kl I nm k I nm l I nm i +K t X -i j I nm j ](8) 空间X m点处的宏观应力可取包含该点的一个小区域中细观应力的平均值,现令该区域包含颗粒m ,而且其边界包含由该颗粒组成的每一个颗粒对的对称面,这样该区域中颗粒的体积含量等同于该材料的颗粒体积含量。
利用GU ASS 公式,该点的平均应力可以表示为e-ij =1V m∫V me mij d V =1V m∑M n =1∫Snm(Fnm ix j +F nmj x i )d S(9)式中:V m为该区域的体积;e mi j 为该区域中的应力;M 为每个颗粒平均组成的颗粒对数目;S nm为颗粒n ,m 之间连接圆柱体在颗粒表面的投影面积;Fnm=e nm n +f nm nt 为基体中的应力分布。
可用分布力的合力P nm 来进一步简化并代替分布力的积分,合力的作用点为颗粒对轴线的中点,以颗粒m 的中心为新的坐标原点,则式(9)可改写为e -ij =12V m ∑M n =1[P n m i (X m j -X n j )+P nm j (X m i -X ni )](10) 由颗粒体积含量的表达式f V =4πR 3/3V m,并利用式(8),上式可改写为e -ij =3f V (2R +h 0)216πR 3∑Mn =1[2(K n -K t )I nm k I nm l I nm i I nmj +K t (W jl I n m k I nm i +W il I nm k I nm j )]X -kl=∑Mn =1e ~ij(Inm1,I nm 2,I nm3)(11)式中,W ij 为Kronecker 符号。
当材料为各向同性时,颗粒对在空间各方向上取向的概率相同。
将平均应力在以单位长度为半径的球面上平均化,并将I nm在图4所示的坐标系中分解,式(11)可以写为e -i j =M 4π∫2π0∫2π0e ~i j (sin θcos h ,sin θsin h ,co s θ)sin θd h d θ(12)M ,h 0和r c 的取值由颗粒的排布方式与体积含量决定,例如颗粒为立方排列时M =6,为体心排列时M =8,由于几何上的限制,M 的最大取值为12。
本文对某种无压浸渗工艺制造的Al 2O 3/Al 颗粒复合材料进行了单轴拉伸实验,用以验证理论模型。
该材料颗粒体积含量为48%,颗粒和基体的弹性模量分别为E P =400GPa 和E M =70GPa,泊松比分别为v P =0.2和v M =0.33,基体的屈服应力es =E M /200,并设每个颗粒平均有8个相邻的颗粒(颗粒按体心排布),可计算出相应的颗粒间距h 0=0.246R ,基体圆柱半径r c =0.707R 。
当颗粒对法向发生相对位移0.006R 时,用多项式拟合得到的基体中的法向应力分布如图5所示,图6为该材料单轴拉伸时的宏观平均应力应变曲线,可见理论结果与实验相吻合。
