拉伸法测弹性模量实验数据
东南大学物理实验 静态拉伸法测弹性模量的误差分析

2011大学生物理实验研究论文静态拉伸法测弹性模量的误差分析(东南大学 自动化学院,南京 211100 )摘 要: 用Mathematica 处理数据,得到一条拟合线。
对实验过程中存在的系统误差,提出改进方法,减少实验误差。
关键词: 数据处理;系统误差;改进方法Analysis on the Result Error s of Measuring ElasticModulus by Static Stretching Method(College of Automation, nanjing 211100)Abstract: Through using computer software Mathematica to process experimental data, we can get fitting curve.Discusseing thefactors which may influence measurement results in the experiment and raises some improvements in order to obtain a more accurate measurement result.key words: Data processing; System error;Improvement弹性模量是工程材料重要的性能参数,从宏观角度来说,弹性模量是衡量物体抵抗弹性变形能力大小的尺度,从微观角度来说,则是原子、离子或分子之间键合强度的反映。
静态拉伸法测弹性模量是一种传统的测量方法,但是实验过程中,存在金属丝拉伸不均匀的现象,而且由于金属丝拉伸过程变化较小,对于画图存在一定的误差,我考虑用Matlab 画出图像,进行分析。
1 实验原理胡克定律指出,对于有拉伸压缩形变的弹性形作者简介:王丽,女,1993,自动化,yx-wangli@.体,在弹性范围内,应力与应变成正比,即F式中比例系数E 称为材料的弹性模量,它是描写材料自身弹性的物理量.改写上式则有、(1)① 可见,只要测量外力F 、材料(本实验用金属丝)的长度L 和截面积S ,以及金属丝的长度变化弹性 量,就可以计算出弹性模量E 。
静态拉伸法测材料的弹性模量实验报告

静态拉伸法测材料的弹性模量实验报告
静态拉伸法测材料的弹性模量实验报告实验日期:2012年12月1日—4日,2012年11月24日9点20分
试样编号:12实验者姓名:胡超祥所在班级:08机电2班实验目的:1.学习与掌握静态拉伸法测定钢材弹性模量;2.了解钢材弹性模量的实际意义。
3.巩固理论知识。
实验原理:静态拉伸法测定钢材的弹性模量是将被测试样放入试样夹中并施以拉伸负荷后,通过测定试样开始破坏前单位面积上的变形来确定试样的弹性模量,即为弹性模量。
一般钢铁材料具有良好的塑性和韧性,其弹性模量比较大,因此可采用这种方法测得它们的弹性模量。
主要仪器:1、金属丝线材。
- 1 -。
用拉伸法测钢丝杨氏模量——实验报告
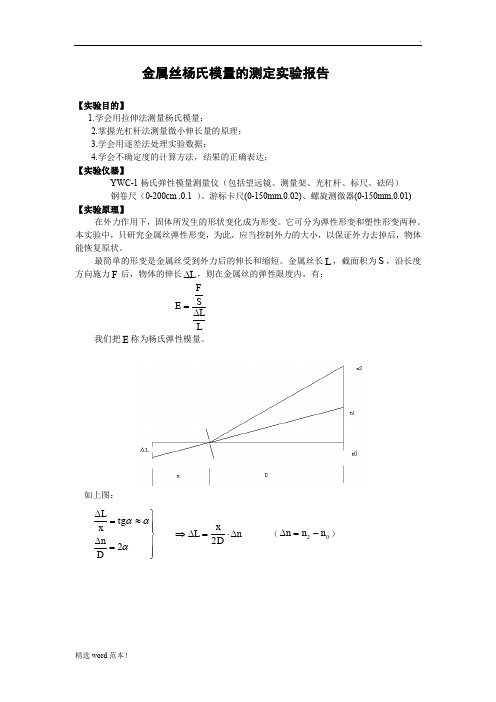
金属丝杨氏模量的测定实验报告【实验目的】1.学会用拉伸法测量杨氏模量;2.掌握光杠杆法测量微小伸长量的原理;3.学会用逐差法处理实验数据;4.学会不确定度的计算方法,结果的正确表达;【实验仪器】YWC-1杨氏弹性模量测量仪(包括望远镜、测量架、光杠杆、标尺、砝码) 钢卷尺(0-200cm ,0.1 )、游标卡尺(0-150mm,0.02)、螺旋测微器(0-150mm,0.01)【实验原理】在外力作用下,固体所发生的形状变化成为形变。
它可分为弹性形变和塑性形变两种。
本实验中,只研究金属丝弹性形变,为此,应当控制外力的大小,以保证外力去掉后,物体能恢复原状。
最简单的形变是金属丝受到外力后的伸长和缩短。
金属丝长L ,截面积为S ,沿长度方向施力F 后,物体的伸长L ∆,则在金属丝的弹性限度内,有:FS E LL=∆ 我们把E 称为杨氏弹性模量。
如上图:⎪⎪⎭⎪⎪⎬⎫=∆≈=∆ααα2D n tg x L n D x L ∆⋅=∆⇒2 (02n n n -=∆)n x d FLD Ln Dx d FL L S F E ∆⋅=∆=∆=228241ππ 真实测量时放大倍数为4倍,即E=2E【实验内容】<一> 仪器调整1、杨氏弹性模量测定仪底座调节水平;2、平面镜镜面放置与测定仪平面垂直;3、将望远镜放置在平面镜正前方1.5-2.0m 左右位置上;4、粗调望远镜:将镜面中心、标尺零点、望远镜调节等高,望远镜的缺口、准星对准平面镜中心,并能在望远镜外看到尺子的像;5、调节物镜焦距能看到尺子清晰的像,调节目镜焦距能清晰的看到叉丝;6、调节叉丝在标尺cm 2±以内,并使得视差不超过半格。
<二>测量1、 记下无挂物时刻度尺的读数0n ;2、依次挂上100g 的砝码,8次,计下7654321,,,,,,n n n n n n n ;3、依次取下100g 的砝码,8次,计下n 0‘,'7'65'4'3'2'1,,,,,,'n n n n n n n ; 4、用米尺测量出金属丝的长度L (两卡口之间的金属丝)、镜面到尺子的距离D ;5、用游标卡尺测量出光杠杆x 、用螺旋测微器测量出金属丝直径d 。
用拉伸法测金属丝的杨氏模量(显微镜直读法)-试验报告(含数据)

用拉伸法测金属丝的杨氏模量(显微镜直读法)-试验报告(含数据)大学物理实验讲义实验4.2.1 拉伸法测金属丝的杨氏模量杨氏模量是描述固体材料抵抗形变能力的物理量,是工程技术上常用的参数,是工程技术人员选择材料的重要依据之一。
条形物体(如钢丝)沿纵向的弹性模量叫杨氏模量。
测量材料杨氏模量方法很多,其中最基本的方法有伸长法和弯曲法。
伸长法一般采用拉伸法,其采用的具体测量方法有光杠杆放大法和显微镜直读法;弯曲法包括静态弯曲法和动态弯曲法。
本实验采用拉伸法当中的显微镜直读法。
【实验目的】1. 熟悉米尺和千分尺的使用,掌握读数显微镜的使用方法;2. 学习用逐差法处理数据;3. 了解CCD 成像系统。
【实验仪器】YWC-III 杨氏模量测定仪、钢卷尺、千分尺、水准仪和0.1kg 、0.2kg 的砝码若干。
杨氏模量测定仪的结构如图4-2-1所示。
(a)学生实验配置 (b)教学演示配置图4-2-1 杨氏模量测定仪1. 金属丝支架S 为金属丝支架,高约1.30m ,可置于实验桌上,支架顶端设有金属丝夹持装置,金属丝长度可调,约77cm ,金属丝下端的夹持装置连接一小方块,方块中部的平面上有细十字线供读数用,小方块下端附有砝码盘。
支架下方还有一钳形平台,设有限制小方块转动的装置(未画出),支架底脚螺丝可调。
2. 读数显微镜读数显微镜M 用来观测金属丝下端小圆柱中部平面上细横线位置及其变化,目镜前方装有分划板,分划板上有刻度,其刻度范围0-8mm, 分度值0.01mm ,每隔1mm 刻一数字。
H 1为读数显微镜支架。
D 成像、显示系统(作为示教仪)CCD 黑白摄像机:灵敏度:最低照度≤0.2Lux;CCD 接在显微镜目镜与电视显示器上。
H 2为CCD 黑白摄像机支架。
【实验原理】物体在外力作用下,总会发生形变。
当形变不超过某一限度时,外力消失后形变随之消失,这种形变称为弹性形变。
发生弹性形变时,物体内部产生恢复原状的内应力。
用拉伸法测杨氏模量

用拉伸法测杨氏模量实验报告【一】实验目的及实验仪器实验目的1. 用金属丝的伸长测杨氏弹性模量。
2. 学习光杠杆镜尺法测量做小长度变化的原理和调节方法。
3. 学习处理数据的一种方法——逐差法。
实验仪器光杠杆,游标卡尺,螺旋测微器,卷尺,杨氏模量仪,望远镜(附标尺)。
实验原理及过程简述实验原理在外力作用下,固体所发生的形状变化成为形变。
它可分为弹性形变和塑性形变两种。
本实验中,只研究金属丝弹性形变,为此,应当控制外力的大小,以保证外力去掉后,物体能恢复原状。
最简单的形变是金属丝受到外力后的伸长和缩短。
金属丝长L,截面积为S,沿长度方向施力F后,物体的伸长,则在金属丝的弹性限度内,有:Y=我们把Y称为杨氏弹性模量。
实验证明,杨氏弹性模量与外力F、物体的长度L和截面积S无关,它仅决定于金属丝的材料,是表征固体性质的一个物理量。
根据上式,测出等号右边各量就可以计算出杨氏弹性模量,式中的F、S和L用通常的方法可以测出, L是一个很小的长度变化,很难用普通测量长度的仪器将它测准,因此,我们采用光杠杆来测量长度变化量。
实验仪器装置如图所示,一段粗细均匀的金属丝,长度为L,截面积为S,将其上端固定于架A上,下端装有一个小环,环上挂着砝码钩。
C为中间有一个小孔的圆柱体,金属丝可从其中穿过。
实验时应将圆柱体一端用螺旋卡头夹紧,使其能随金属丝的伸缩而移动。
G是一个固定平台,中间开有一孔,圆柱体C可以在孔中自由地上下移动。
光杠杆M下面的两尖脚放在平台的沟内,主杆尖脚放在圆柱体C的上端,将水平仪放置在平台G上。
调节支架底部的3个调节螺丝H可使平台成水平,望远镜R和标尺S是测伸长量用的测量装置。
金属丝受力F的作用而发生形变,伸长了,光杠杆的主杆尖脚也随之下降。
使主杆转过一个角度,同时平面镜的法线也转过相同角度,由光杠杆的原理可得=/b=/D由于很小,很小,,,所以=Y=式中d为金属丝的直径,b为光杠杆臂的长度,D为标尺到镜面的距离,L为金属丝的原长。
大学物理实验《用拉伸法测金属丝的杨氏弹性模量》

三、实验中注意:实验测量中,发现增荷和减荷时读数相关差较大,当荷重按比例增加时,?n不按比例增加,应找出原因,重新测量。这种情况可能发生的原因有:
1、金属丝不直,初始砝码太轻,没有把金属丝完全拉直。
2、杨氏弹性模量仪支柱不垂直,使金属丝下端的夹头不能在金属框内上下自由滑动,摩擦阻力太大。
1
3、加减砝码时动作不够平衡,导致光杠杆足尖发生移动。
1、万能试验机法:在万能试验机上做拉伸或压缩试验,自动记录应力和应变的关系图线,从而计算出杨氏弹性模量。
2、静态拉伸法(本实验采用此法),它适用于有较大形变的固体和常温下的测量,它的缺点是:①因为载荷大,加载速度慢,含有驰豫过程。所以它不能很真实地反映出材料内部结构的变化。②对脆性材料不能用拉伸法测量;③不能测量材料在不同温度下的杨氏弹性模量。
8LD?n??F?KF 2?dbE
8LD
?d2bE由此式作?n?F图线,应得一直线。从图线中计算出直线的斜率K,再由K?
即可计算出E。
3
篇二:大学物理实验用拉伸法测金属丝的杨氏模量
用拉伸法测金属丝的杨氏模量
材料在外力作用下产生形变,其应力与应变的比值叫做弹性模量,它是反映材料抵抗形变能力的物理量,杨氏模量是固体材料的纵向弹性模量,是选择机械构件的依据之一,也是工程技术中研究材料性质的常用参数。测定弹性模量的方法很多,如拉伸法、振动法、弯曲法、光干涉法等,本实验采用拉伸法测定金属丝的杨氏弹性模量,研究拉伸正应力与应变之间的关系。
拉伸法测量钢丝的弹性模量

可把(3)式改写为
Δni
=
ni
− n0
=
8DLg πd 2IE
mi
=
Kmi
在弹性限度内,K应为常量,可在坐标纸上作mi-Δni关系曲线,则其斜率为K,然 后可由下式计算E值:
E = 8DLg πd 2IK
[数据记录与处理]
本实验要求用两种方法处理数据,分别求出杨氏模量。
1.用逐差法计算杨氏模量 E(关于逐差法,参见第四章§3)。
(1)首先求出 Δ4n 的平均值 Δ4n ,然后将其代替(3)式中的 Δn,即按下式计 算 E 值:
E = 8DLg m πd 2I Δ4n
在计算时应注意: a.在用(4)式计算 E 值时,m 应该取 4 个砝码的质量(为什么?); b.重力加速度g的值,在北京地区应取为 9.80m/s2; c.要统一用国际单位制。 (2)求出E的不确定度σE。
由(4)式可导出 E 的不确定度的传递公式如下:
(4)
σE
=
⎢⎡⎜⎛ ⎢⎣⎝
∂E ∂D
⎟⎞ ⎠
2
σ
2 DБайду номын сангаас
+
⎜⎛ ⎝
∂E ∂L
⎟⎞ ⎠
2
σ
2 L
+
⎜⎛ ⎝
∂E ∂m
⎟⎞ ⎠
2
σ
2 m
+
⎜⎛ ⎝
∂E ∂I
⎟⎞ ⎠
2
σ
2 I
1
+
⎜⎛ ⎝
∂E ∂d
⎟⎞ ⎠
2
σ
拉伸法测金属丝杨氏弹性模量

(2)调节平台的上下位置,使随金属丝伸长的夹具B 上端与沟槽在同一水平面上(为什么?)。
(3)加1Kg砝码在砝码托盘上,将金属丝拉直,检查 夹具B是否能在平台的孔中上下自由地滑动,金属丝 是否被上下夹子夹紧.
2.光杠杆及望远镜尺组的调节
(1)外观对准——调节光杠杆与望远镜、标尺中部 在同一高度上。 (2)镜外找像——缺口、准星、平面镜中标尺 像.三者在一条水平 线上。 (3)镜内找像 ——先调节目镜使叉丝清晰,再调节 调焦距看清标尺像,直到无视差为准。 (4)细调对零——对准标尺像零刻线附近的任一刻
4 n4 9 n9
n7 n2
5 n5 10 n10
n8 n3
n9 n4
n10 n5
5
2
A t0 .9 55i 1
N iN 5 1
,
B仪,
因 n1N
5
所 以 n5 1N
N
2 2
AB
nnn
返回
实验内容
1.杨氏模量测定仪的调整
i1
31
B 仪
nnn
n 2A2B
杨氏模量 E计 8FL算D
d2bn
不确定度计算:
EEFF2LL2D D24dd2bb2nn2
E
E E
E
用拉伸法测量金属丝杨氏模量
1. 实验简介 2. 实验目的 3. 实验原理 4. 逐差法处理数据 5. 实验内容 6. 注意事项 7. 数据记录与处理 8. 课后思考题
实验简介
材料受外力作用时必然发生形变,杨氏模量(也称弹性模量)是 反映固体材料弹性形变的重要物理量,在一般工程设计中是一个 常用参数, 是选定机械构件材料的重要依据之一。常用金属材
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
拉伸法测弹性模量实验数据
拉伸法是一种测量材料弹性行为的方法。
通过施加拉力,并对材料的应变进行测量,
可以计算出材料的弹性模量。
本实验旨在通过拉伸法测量不同材料的弹性模量,并分析影
响弹性模量的因素。
实验中使用了两种不同的材料:钢和铜。
首先,我们测量了每种材料的截面积和长度,以计算出它们的初始横截面积和初始长度。
然后,将样品固定在仪器上,施加拉力,同时
记录材料的应变。
当拉伸达到一定程度时,停止拉伸并记录最终长度和应力值。
根据应变-应力曲线,我们计算出材料的弹性模量。
为了比较两种材料,我们将它们
的应变-应力曲线画在同一张图上,并绘制各自的弹性区域。
经过计算,得出钢的弹性模
量为200 GPa,铜的弹性模量为110 GPa。
这表明钢比铜更具弹性,因为它需要更大的力
来使其发生应变。
此外,在实验中还测试了其他因素对弹性模量的影响。
我们发现,当拉伸速度较快时,材料的弹性模量较小。
这是因为快速的拉伸会导致更多的约束力和能量散失,并使其失去
一些弹性能。
此外,当样品在高温下拉伸时,弹性模量也会降低。
这是因为高温会使分子
变得更具活性,从而使分子内部更容易滑动。
综上,拉伸法是一种简单而有效的测量材料弹性模量的方法。
通过实验,我们可以深
入了解不同材料弹性模量的差异以及各种因素对其的影响。
这对于工程应用和材料选择至
关重要。
