高斯光束
合集下载
高斯光束 通俗
高斯光束通俗
（最新版）
目录
1.高斯光束的定义和特点
2.高斯光束的生成原理
3.高斯光束的应用领域
正文
一、高斯光束的定义和特点
高斯光束，又称高斯光束束腰，是指在传播过程中，光束的横截面上光强分布呈现高斯分布的光束。
高斯光束具有很多特点，例如，光束的束腰位置光强分布最为集中，呈高斯分布，离束腰越远，光强分布逐渐减弱。
此外，高斯光束的光学传输特性较好，光束的指向性和稳定性都相对较高。
二、高斯光束的生成原理
高斯光束的生成原理主要基于光的传播规律和高斯光束的聚焦特性。
一般来说，高斯光束可以通过两种方法生成：一种是通过透镜或反射镜等光学元件对光束进行调制，使得光束在传播过程中满足高斯分布；另一种是通过激光器等光源产生的光束，在传播过程中自然形成高斯分布。
三、高斯光束的应用领域
高斯光束在许多领域都有广泛的应用，例如在光通信、光学测量、激光加工、光学成像等方面。
高斯光束的光强分布特点使其在光通信领域具有很高的信噪比和传输速率；在光学测量领域，高斯光束的聚焦性能和指向稳定性使其成为理想的测量工具；在激光加工领域，高斯光束的优异光学性能使其在激光切割、打标等方面具有很高的加工精度和效率；在光学成像领域，高斯光束的成像质量高，可以提高成像系统的分辨率和成像质量。
综上所述，高斯光束以其独特的光学性能和广泛的应用领域，在光学领域具有重要的研究价值和实用意义。
激光原理-(9)-高斯光束
ω ( z ) ω 0，z ⇒ R( z ) θ 0 2. 任一 坐标 z 处的光斑半径 ω ( z )及等相面曲率半径 R( z )
ω 0（或共焦参量 f ）与腰位置 z
ω ( z )
ω 0 ⇒ R( z ) z
NJUPT
高斯光束的 q 参数（复曲率半径）
x2 + y2 ω0 x2 + y2 exp − 2 ) − ϕ ( z ) u00 ( x , = y, z ) c exp − i k ( z + 2 R( z ) ω(z) ω (z)
第4章 高斯光束
NJUPT
高斯光束
高斯光束：所有可能存在的激光波型的概称。 理论和实践已证明，在可能存在的激光束形式中， 最重要且最具典型意义的就是基模高斯光束。 无论是方形镜腔还是圆形镜腔，基模在横截面上的光 强分布为一圆斑，中心处光强最强，向边缘方向光强 逐渐减弱，呈高斯型分布。因此，将基模激光束称为 “高斯光束”。
1 A B TF = = 1 C D − F 0 1
F
AR1 + B R2 = CR1 + D
（遵循ABCD变换法则） NJUPT
高斯光束q参数的变换规律——ABCD公式
在自由空间的传播 束腰处：
1 自由空间变换矩阵： TL = 0
πω 0 2 = = if = i z 0，q(0) λ
πω λ
2
1
B A+ R 1 R2 = B A+ C + R1
πω1 2 B + λ 2 2 D πω1 + BD R1 λ
高斯光束
为光波波前的曲率半径 ；
束宽： 对于在自由空间传播的高斯光束，其腰斑位置的半径在光轴方向总大于一个 最小值 ，这个最小值被称为束腰。波长为 的光波的腰斑位置在轴上的分 布为 这里将 定为束腰位置。 被称为瑞利长度。
瑞利距离和共Байду номын сангаас参数：与束腰轴向距离等于瑞利距离 处的束宽为 这两点之间的距离称作是共焦参数或光束的焦深
高斯光束
钱朝阳
在光学中，高斯光束（Gaussian beam）是 横向电场以及辐照度分布近似满足高斯函数 的电磁波光束，所以称为高斯光束。是激光 在光学谐振腔里基模条件下发出的光，许多 激光都近似满足高斯光束的条件。
麦克斯韦方程组 （1）
物质方程 （5）
（2）
（3） （4）
（6）
（7）
对光频电磁场, 主要关心电场E,我们所讲的光场均指电 磁场的电场分量。
谢谢观赏
曲率半径： 光束偏移：当
是光束波前的曲率半径，它是轴向距离的函数 ，参数 趋于一条直线。这条直线与中央光轴的夹角被称为 光束的偏移，即远场发散角。
综上所述，可知高斯光束在其轴线附近可以看做是一种非均匀高 斯球面波，周期传输过程中曲率中心不断改变，其振幅在横截面 内为一高斯函数，强度集中在轴线及其附近，且等相面为球面 （特殊范围内为平面）。
（13）
式（13）为在近轴近似下的波动方程，高斯光束就是缓变振幅 近似下的一个特解。
高斯光束作为电磁波，其电场的振幅为：
r为场点距离光轴中的径向距离；z为光轴上光波最狭窄位置束腰的位置坐标 为激光的束腰宽度 为波数 ； 为电磁场振幅降到轴向的1/e、强度降到轴向的1/e2的点的半径 为轴对称光波的Gouy相位，对高斯光束的相位 也有影响，在近轴条件下可以忽略。
光学谐振腔理论-第8节-高斯光束的传输
05 高斯光束的未来发展与应 用
高斯光束在光学通信中的应用
高速光通信
高斯光束在光学通信中具有较高的传输速度和较低的信号衰减，有助于实现高 速、大容量的光通信系统。
远程通信
高斯光束具有较好的光束质量和传输稳定性，适用于长距离的光纤通信，有助 于实现远程、稳定的通信连接。
高斯光束在光学传感中的应用
03 高斯光束的调制与控制
高斯光束的相位调制
01
相位调制是指通过改变高斯光束的相位分布来改变其波前的状 态。
02
常见的相位调制方法包括利用液晶空间光调制器、光栅或其他
光学元件对高斯光束进行相位调制。
相位调制在光学通信、光学传感和光学计算等领域有广泛应用，
03
可以实现光束的聚焦、散焦、波形转换等功能。
高斯光束的波前测量
波前测量概述
波前是描述光束相位变化的物理量，高斯光束的波前测量有助于 了解光束的传播特性和干涉、衍射等光学现象。
波前测量方法
常用的波前测量方法有干涉法、散斑法、剪切干涉法等，可以根据 高斯光束的特点和测量精度要求选择合适的方法。
测量误差来源
波前测量误差主要来源于光束的聚焦、光束截面分布、光学元件的 误差等因素。
高斯光束的聚焦特性
聚焦原理
高斯光束经过透镜聚焦后，其横截面 上的强度分布会发生变化，形成明暗 相间的干涉条纹。
干涉条纹
干涉条纹的形状取决于透镜的焦距和 光束的束腰半径。当透镜焦距一定时 ，束腰半径越小，干涉条纹越密集； 反之，则越稀疏。
02 高斯光束在光学谐振腔中 的应用
光学谐振腔对高斯光束的影响
偏振态调制是指通过改变高斯光 束的偏振状态来改变其电磁场分
布。
常见的偏振态调制方法包括利用 偏振片、电光晶体或液晶等对高
高斯光束的聚焦和准直课件
高斯光束的参数如束腰半径、波长等 也会影响准直效果。
光学元件质量
透镜、反射镜等光学元件的质量对准 直效果有重要影响，如光学元件的加 工精度、表面质量等。
04
高斯光束聚焦和准直的应用
光学通信
总结词
高斯光束的聚焦和准直技术在光学通信领域具有广泛应用，能够实现高速、高效 、远距离的光信号传输。
详细描述
实时处理能力
对于动态变化的光束，需要具备实 时处理能力，以便快速响应和调整 。
研究方向
新型光学元件研究
研究新型的光学元件，以提高光 束的聚焦和准直精度。
光束质量提升技术
研究提高光束质量的方法和技术 ，以满足各种应用需求。
实时控制系统
研究实时的光学控制系统，以快 速响应和调整光束。
发展前景
应用领域拓展
比较不同聚焦透镜和不同输入光束参 数对聚焦效果的影响，得出结论和建 议。
06
高斯光束聚焦和准直的未来 发展
技术挑战
高精度控制
高斯光束的聚焦和准直需要高精 度的光学元件和控制系统，以实
现光束的稳定和精确控制。
光束质量提高
目前的高斯光束聚焦和准直技术受 到光束质量的限制，如何提高光束 质量是未来的一个重要挑战。
减小。
高斯光束的应用
1 2
3
激光加工
高斯光束可被用于激光切割、打标和焊接等加工领域。
光学测量
高斯光束可被用于光学测量领域，如干涉仪、光谱仪和全息 术等。
光学通信
高斯光束在光纤通信中用作信号传输的光源，具有传输损耗 低、信号稳定等优点。
02
高斯光束的聚焦
聚焦原理
高斯光束的聚焦是指将发散的高 斯光束通过透镜或反射镜系统， 使其在空间上形成一个能量集中
3.8高斯光束
第八节 高斯光束
一、高斯光束的基本性质
1.基模高斯光束
沿z轴传播的基模高斯光束的表达式
x2 + y2 ⎡ z k x2 + y2 ⎤ −i ⎢ kz − arctg + ⎥ zR 2 R(z ) ⎥ ⎢ ⎣ 14444244443 4 4⎦
相位因子
(
)
C 00 − w2 ( z ) ψ 00 ( x, y , z ) = e e w( z ) 14243
U ( x, y , z ) ∝ 1 −ikR 1 e ≈ e R R
⎛ x2 + y2 −ik ⎜ z + ⎜ 2z ⎝ ⎞ ⎟ ⎟ ⎠
=
1 e R
⎛ x2 + y2 −ik ⎜ z + ⎜ 2R ⎝
⎞ ⎟ ⎟ ⎠
因此，q(z)称为高斯光束的复曲率半径，也称为q参数
q(z)将w(z)和R(z)统一起来，已知q(z)可求出w(z) 和R(z)
Q 高斯光束的q的变换规律同球面波R的变换规律相同 ∴ Aq1 + B q2 = Cq1 + D
（1）高斯光束q参数在自由空间的传播 由
⎧ 1 1 λ ⎪ = −i q( z ) R( z ) πω 2 ( z ) ⎪ ⎪ ⎡ ⎛ πω 2 ⎞ 2 ⎤ ⎪ 0 ⎨ R( z ) = z ⎢1 + ⎜ ⎟ ⎜ λz ⎟ ⎥ ⎢ ⎝ ⎠ ⎥ ⎪ ⎦ ⎣ ⎪ ⎡ ⎛ λz ⎞ 2 ⎤ ⎪ω 2 ( z ) = ω 2 ⎢1 + ⎜ 0 ⎟ ⎜ πω 2 ⎟ ⎥ ⎪ ⎢ ⎝ 0⎠ ⎥ ⎦ ⎣ ⎩
（3）普通球面波的ABCD定律
光学系统 R1
θ1
P1 R2
r1
r2
θ2
P2
一、高斯光束的基本性质
1.基模高斯光束
沿z轴传播的基模高斯光束的表达式
x2 + y2 ⎡ z k x2 + y2 ⎤ −i ⎢ kz − arctg + ⎥ zR 2 R(z ) ⎥ ⎢ ⎣ 14444244443 4 4⎦
相位因子
(
)
C 00 − w2 ( z ) ψ 00 ( x, y , z ) = e e w( z ) 14243
U ( x, y , z ) ∝ 1 −ikR 1 e ≈ e R R
⎛ x2 + y2 −ik ⎜ z + ⎜ 2z ⎝ ⎞ ⎟ ⎟ ⎠
=
1 e R
⎛ x2 + y2 −ik ⎜ z + ⎜ 2R ⎝
⎞ ⎟ ⎟ ⎠
因此，q(z)称为高斯光束的复曲率半径，也称为q参数
q(z)将w(z)和R(z)统一起来，已知q(z)可求出w(z) 和R(z)
Q 高斯光束的q的变换规律同球面波R的变换规律相同 ∴ Aq1 + B q2 = Cq1 + D
（1）高斯光束q参数在自由空间的传播 由
⎧ 1 1 λ ⎪ = −i q( z ) R( z ) πω 2 ( z ) ⎪ ⎪ ⎡ ⎛ πω 2 ⎞ 2 ⎤ ⎪ 0 ⎨ R( z ) = z ⎢1 + ⎜ ⎟ ⎜ λz ⎟ ⎥ ⎢ ⎝ ⎠ ⎥ ⎪ ⎦ ⎣ ⎪ ⎡ ⎛ λz ⎞ 2 ⎤ ⎪ω 2 ( z ) = ω 2 ⎢1 + ⎜ 0 ⎟ ⎜ πω 2 ⎟ ⎥ ⎪ ⎢ ⎝ 0⎠ ⎥ ⎦ ⎣ ⎩
（3）普通球面波的ABCD定律
光学系统 R1
θ1
P1 R2
r1
r2
θ2
P2
thorlabs 高斯光束公式
高斯光束公式是描述高斯光束的光学特征的数学公式。
它是基于高斯光束的波前形状和光强分布的特征参数，是光学研究和应用中常用的重要工具。
Thorlabs是一家知名的光学仪器和设备供应商，他们提供了广泛的高斯光束公式相关的产品和技术支持。
本文将探讨高斯光束公式的基本原理和应用，以及Thorlabs在这一领域的贡献和影响。
一、高斯光束的基本原理1. 高斯光束的定义高斯光束是一种特殊的光束模式，其波前形状和光强分布都服从高斯函数的特征。
在光学系统中，高斯光束具有重要的理论和实际意义，可以用来描述激光束、光纤等光学器件的光学特性。
2. 高斯光束公式高斯光束的波前形状和光强分布可以用数学公式来描述。
一般而言，高斯光束的波前形状可以由二次相位曲面和一次振幅曲面共同确定，而光强分布则由波前形状和物质透过能力共同决定。
二、高斯光束的应用领域1. 激光器高斯光束是激光器输出光束的典型模式，其特征参数和稳定性对激光器的性能和输出功率有重要影响。
在激光器设计和优化中，高斯光束公式是理论分析和仿真的重要工具。
2. 光通信光通信系统中常使用光纤作为传输介质，而高斯光束是光纤中常见的传输模式。
通过高斯光束公式的分析和计算，可以优化光通信系统的传输性能和带宽利用率。
三、Thorlabs在高斯光束公式领域的贡献1. 产品和技术支持Thorlabs提供了丰富的高斯光束公式相关的产品和技术支持，包括激光器、光学器件、光纤等。
这些产品和技术支持为科研机构和工程实践提供了重要的工具和资源。
2. 应用案例和实验验证Thorlabs在高斯光束公式的应用领域做了大量的实验研究和案例验证，为高斯光束公式的理论基础和工程应用提供了有力的支撑。
四、结语高斯光束公式是描述高斯光束的重要数学工具，对光学研究和应用具有广泛的影响和意义。
Thorlabs作为光学仪器和设备供应商，在高斯光束公式领域做出了重要的贡献，为光学领域的科研和工程应用提供了有力的支持。
希望通过今后的持续努力，高斯光束公式的理论和应用能够得到进一步的发展和完善。
第4章高斯光束
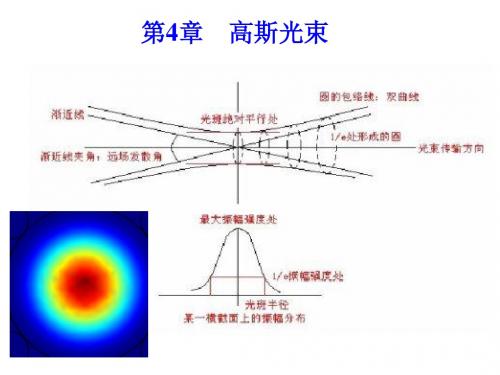
2、普通球面波经过薄透镜的变换规律
R1 O
R2 O’ F
物
l
像
l`
1 1 1 R2 R1 F
0 1 1/ F 1
3、普通球面波的ABCD定律
若一条入射光线 r1 ,1 ，经过一个光学系统后 ，变成 A B 出射光线 r2 , 2 ，则可用矩阵 C D 描述光学系统对光线 的变换作用 r2 A B r1 C D 1 2
x2 y2 x2 y 2 A0 Emn x, y, z exp 2 exp ik z i z wz w ( z) 2 Rz
A0 x2 y2 E mn x, y, z exp ik z wz 2
2
2
2、等相位面分布
2 2 0 f R z z z 1 z z 2
总结：
高斯光束既不是平面波，也不是一般的球面波，在其传输 轴线附近可以看作是一种非均匀球面波。它在共焦中心处是强 度为高斯分布的平面波，在其他地方则是强度为高斯分布的球
2d z 2 0 lim z dz 0
f 0
2、任一z坐标处的光斑半径及等相位面曲率半径
2 z 0 z 1 R z
2
1 2
Rz z Rz 1 2 z
2
1
可以用任一z处的ω(z)和R (z)表征高斯光束。
3、高斯光束的q参数
1 1 i qz Rz z 2
q(z)将ω(z)和R (z)联系起来。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
若有解
( x, y, z) 则为一个正确的波束解，这个解与
x, y有关部分完全含于高斯函数中，其他因子仅为z的函数。
解第一式：
1 f ( z) 2i z k
积分常数
2 f 2 ikf 比较 两式 2 fg ikg
因此，得解
g c f
(c const )
g ( z)
讨论内容：
一、高斯光束的定义 二、高斯光束波函数的解（亥姆霍兹方程的波束解）
1.高斯光束的纵向相位因子
三、高斯光束的传播特性
2.高斯光束的等相面曲率半径
3.高斯光束的束宽与远场发射角
高斯光束
定义：在光学中，高斯光束（Gaussian
分布近似满足高斯函数的电磁波光束。 beam）是横向电场以及辐照度
基本应用：许多激光都近似满足高斯光束的条件，在这种情况里，激光
在光谐振腔里以TEM00波模传播。当它在镜片发生衍射，高斯光束会变换成 另一种高斯光束，这时若干参数会发生变化。这解释了高斯光束是激光光学 里一种方便、广泛应用的原因。
描述：高斯光束的数学函数是亥姆霍兹方程的一个近轴近似解（属于小角
近似的一种）。这个解具有高斯函数的形式，表示电磁场的复振幅。电磁波 的传播包括电场和磁场两部分。研究其中任一个场，就可以描述波在传播时 的性质。
2 0
2i (1 z) k
令
4z 2 2z 2 2 ( z ) (1 2 2 ) 0 [1 ( 2 ) ] k k0
2
f ( z)
同理，可得
1 2iz (1 ) 2 2 ( z) k0
g ( z)
0
2z 1 ( 2 ) k0
e
i
表示各点处的波振幅
e
x2 y 2
2
限制波束宽度的因子
0 0
Z轴上波的振幅
k ( x2 y 2 ) kz 2 k 2 z[1 ( 0 ) 2 ] 2z 讨论
当z 0时=0
z 0 平面是一个波阵面（光束腰部）
2
z 远处时（腰部远处） z k0
亥姆霍兹方程的波束解
波束场强在横截面上的分布形式是由具体激发条件决定的
x2 y2 exp 2
（高斯函数）
此函数具有描某种波束能量在横截面上分布的性质，而所描 述的这种波束能量分布具有轴对称性。在中部场强最大，靠 近边缘处强度迅速减弱。
假设某波束对称轴为z轴，则上式中：
令：
( x, y, z) g ( x) exp( f ( z)( x2 y 2 ))
( x, y, z) : z的缓变函数（相对于eikz）
当z 时 eikz （已有显著变化）
其中：
因此，设
当z~时， ( x, y, z)变化很小，对z的展开可忽略其高次项
电磁场的任一直角分量u( x, y, z)满足亥姆霍兹方程
x y :场点到波束中心轴（z轴）的距离
2
2
: 波束的宽度
由于波动的特点，波束在传播过程中一般不能保持截面不 变，因而波束宽度一般是传播距离的函数。
当 时 或 ，因此波幅也一般为z的函数
以u x, y, z 代表电磁场的任一直角分量，我们设解u具有如下形式：
u x, y, z =g ( z ) exp f z ( x 2 y 2 ) exp(ikz )
( x2 y 2 )[2gf ikgf ] [2 fg ikg ] 0
上式中的撇号表示对z的一阶导数
( x2 y 2 )[2gf ikgf ] [2 fg ikg ] 0
由于上式方程对任意x,y成立，因此两方程括号内的量都应为零 所以，整理得
2 f 2 ikf 2 fg ikg
波束的发散角
tan(
( z)
z
)
2 k0
利用公式
tan(
( z)
z
)
分析：
远场发散角
– 从高斯光束的等相位面半径以及光束半径的分布规律可以知道， 在瑞利长度之外，高斯光束迅速发散，定义当 z 时高斯光 束振幅减小到最大值1/e处与z轴夹角为高斯光束的远场发散角 （半角）：
lim
2 当z k0 时
2z ( z) （波束宽随z的变化） k0
分析
z 0时，R( z) 此时的等相面是平面 （R为等相位面曲率半径）
z z0时，R( z) 2z0此时的等相位面曲率半径最小
z 时，R( z) z 此时等相面也是平面
注意
球面的球心位置随着光束的传播不断变化
0 i 0 e
( g ( z)
0
2i 1 z k
)
2z arctan( 2 ) 纵向相位因子 k0
1 2iz 由已知解 f ( z ) 2 (1 2 ) ( z) k0
g ( z)
0
1 ( 2z ) 2 k0
ei 0
0 i e
0
2i 1 z k
0 为积分常数
2i z0 k
注意
此处的 一般为复数，它的虚数部分可以用一项 抵消，使得 为实数，即
f ( z ) 可以改写为：
f ( z)
1 4z2 (1 2 2 ) k
2i (1 z) k
由 f ( z)
1 4z2 (1 2 2 ) k
x2 y 2 1 2 z (1 ) const 2 z
或
r ( x 2 y 2 z ) const
1 2 2
结论： 在远处波阵面变为以腰部中心为球心的球面，波阵面从腰部的 平面逐渐过渡到远处的球面形状
2 4 z 2z 2 2 2 ( z) (1 2 2 ) 0 [1 ( 2 ) ] k k0
arctan(
2
2z ) 2 k0
因此在讨论远处等相面时可以忽略这一项
因此，上式 在远处等相面方程为：
x2 y 2 z const 2z
由于当
z 2 x2 y 2
2 2 x2 y 2 1 x y 2 (1 ) 1 2 z 2z2
等相面方程可写为：
z
( z)
z
0 z0
– 包含在全远场发散角内的光束功率占 – 高斯光束总功率的86.5% 高斯光束在轴线附近可以看成一种非均匀高斯球面波，在传播过 程中曲率中心不断改变，其振幅在横截面内为一高斯分布，强度 集中在轴线及其附近，且等相位面保持球面。
其中：
eikz：沿z方向的传播因子
g ( z)和f ( z) : 对z的缓变函数
e
f ( x )( x 2 y 2 )
: 限制波束空间宽度的因子
由于射束不能有完全确定的波矢量，因此束的宽度 应为z的缓变函数，因子g ( z )主要表示波的振幅，同时也 含有传播因子中与纯平面波因子eikz 偏离的部分
2 2 u x , y , z = g ( z ) exp f z ( x y ) exp(ikz ) 代入
0 i u x, y, z 0 e e
整理上式，得
x2 y 2
2
(z)
(1
2iz
2 k0
)
eikz
0 u x, y, z 0 e
其中
x2 y 2
2
ei
波束的 相位
k ( x2 y 2 ) kz 2 0 k 2 2 z[1 ( ) ] 2z
高斯光束的传播特性
0 u x, y, z 0 e
x2 y 2
2
ei
e
i
相位因子
x2 y 2
0 0 e
2
uk u 0
2 2
(k )
将 u x, y, z =g ( z ) exp f z ( x 2 y 2 ) exp(ikz )代入上式方程
2u 忽略 2 项 z
2 2 2 ik 0 x 2 y 2 z
2 2 （ 2 2 2ik 0） 将 x, y, z 代入上式方程 x y z
( x, y, z) 则为一个正确的波束解，这个解与
x, y有关部分完全含于高斯函数中，其他因子仅为z的函数。
解第一式：
1 f ( z) 2i z k
积分常数
2 f 2 ikf 比较 两式 2 fg ikg
因此，得解
g c f
(c const )
g ( z)
讨论内容：
一、高斯光束的定义 二、高斯光束波函数的解（亥姆霍兹方程的波束解）
1.高斯光束的纵向相位因子
三、高斯光束的传播特性
2.高斯光束的等相面曲率半径
3.高斯光束的束宽与远场发射角
高斯光束
定义：在光学中，高斯光束（Gaussian
分布近似满足高斯函数的电磁波光束。 beam）是横向电场以及辐照度
基本应用：许多激光都近似满足高斯光束的条件，在这种情况里，激光
在光谐振腔里以TEM00波模传播。当它在镜片发生衍射，高斯光束会变换成 另一种高斯光束，这时若干参数会发生变化。这解释了高斯光束是激光光学 里一种方便、广泛应用的原因。
描述：高斯光束的数学函数是亥姆霍兹方程的一个近轴近似解（属于小角
近似的一种）。这个解具有高斯函数的形式，表示电磁场的复振幅。电磁波 的传播包括电场和磁场两部分。研究其中任一个场，就可以描述波在传播时 的性质。
2 0
2i (1 z) k
令
4z 2 2z 2 2 ( z ) (1 2 2 ) 0 [1 ( 2 ) ] k k0
2
f ( z)
同理，可得
1 2iz (1 ) 2 2 ( z) k0
g ( z)
0
2z 1 ( 2 ) k0
e
i
表示各点处的波振幅
e
x2 y 2
2
限制波束宽度的因子
0 0
Z轴上波的振幅
k ( x2 y 2 ) kz 2 k 2 z[1 ( 0 ) 2 ] 2z 讨论
当z 0时=0
z 0 平面是一个波阵面（光束腰部）
2
z 远处时（腰部远处） z k0
亥姆霍兹方程的波束解
波束场强在横截面上的分布形式是由具体激发条件决定的
x2 y2 exp 2
（高斯函数）
此函数具有描某种波束能量在横截面上分布的性质，而所描 述的这种波束能量分布具有轴对称性。在中部场强最大，靠 近边缘处强度迅速减弱。
假设某波束对称轴为z轴，则上式中：
令：
( x, y, z) g ( x) exp( f ( z)( x2 y 2 ))
( x, y, z) : z的缓变函数（相对于eikz）
当z 时 eikz （已有显著变化）
其中：
因此，设
当z~时， ( x, y, z)变化很小，对z的展开可忽略其高次项
电磁场的任一直角分量u( x, y, z)满足亥姆霍兹方程
x y :场点到波束中心轴（z轴）的距离
2
2
: 波束的宽度
由于波动的特点，波束在传播过程中一般不能保持截面不 变，因而波束宽度一般是传播距离的函数。
当 时 或 ，因此波幅也一般为z的函数
以u x, y, z 代表电磁场的任一直角分量，我们设解u具有如下形式：
u x, y, z =g ( z ) exp f z ( x 2 y 2 ) exp(ikz )
( x2 y 2 )[2gf ikgf ] [2 fg ikg ] 0
上式中的撇号表示对z的一阶导数
( x2 y 2 )[2gf ikgf ] [2 fg ikg ] 0
由于上式方程对任意x,y成立，因此两方程括号内的量都应为零 所以，整理得
2 f 2 ikf 2 fg ikg
波束的发散角
tan(
( z)
z
)
2 k0
利用公式
tan(
( z)
z
)
分析：
远场发散角
– 从高斯光束的等相位面半径以及光束半径的分布规律可以知道， 在瑞利长度之外，高斯光束迅速发散，定义当 z 时高斯光 束振幅减小到最大值1/e处与z轴夹角为高斯光束的远场发散角 （半角）：
lim
2 当z k0 时
2z ( z) （波束宽随z的变化） k0
分析
z 0时，R( z) 此时的等相面是平面 （R为等相位面曲率半径）
z z0时，R( z) 2z0此时的等相位面曲率半径最小
z 时，R( z) z 此时等相面也是平面
注意
球面的球心位置随着光束的传播不断变化
0 i 0 e
( g ( z)
0
2i 1 z k
)
2z arctan( 2 ) 纵向相位因子 k0
1 2iz 由已知解 f ( z ) 2 (1 2 ) ( z) k0
g ( z)
0
1 ( 2z ) 2 k0
ei 0
0 i e
0
2i 1 z k
0 为积分常数
2i z0 k
注意
此处的 一般为复数，它的虚数部分可以用一项 抵消，使得 为实数，即
f ( z ) 可以改写为：
f ( z)
1 4z2 (1 2 2 ) k
2i (1 z) k
由 f ( z)
1 4z2 (1 2 2 ) k
x2 y 2 1 2 z (1 ) const 2 z
或
r ( x 2 y 2 z ) const
1 2 2
结论： 在远处波阵面变为以腰部中心为球心的球面，波阵面从腰部的 平面逐渐过渡到远处的球面形状
2 4 z 2z 2 2 2 ( z) (1 2 2 ) 0 [1 ( 2 ) ] k k0
arctan(
2
2z ) 2 k0
因此在讨论远处等相面时可以忽略这一项
因此，上式 在远处等相面方程为：
x2 y 2 z const 2z
由于当
z 2 x2 y 2
2 2 x2 y 2 1 x y 2 (1 ) 1 2 z 2z2
等相面方程可写为：
z
( z)
z
0 z0
– 包含在全远场发散角内的光束功率占 – 高斯光束总功率的86.5% 高斯光束在轴线附近可以看成一种非均匀高斯球面波，在传播过 程中曲率中心不断改变，其振幅在横截面内为一高斯分布，强度 集中在轴线及其附近，且等相位面保持球面。
其中：
eikz：沿z方向的传播因子
g ( z)和f ( z) : 对z的缓变函数
e
f ( x )( x 2 y 2 )
: 限制波束空间宽度的因子
由于射束不能有完全确定的波矢量，因此束的宽度 应为z的缓变函数，因子g ( z )主要表示波的振幅，同时也 含有传播因子中与纯平面波因子eikz 偏离的部分
2 2 u x , y , z = g ( z ) exp f z ( x y ) exp(ikz ) 代入
0 i u x, y, z 0 e e
整理上式，得
x2 y 2
2
(z)
(1
2iz
2 k0
)
eikz
0 u x, y, z 0 e
其中
x2 y 2
2
ei
波束的 相位
k ( x2 y 2 ) kz 2 0 k 2 2 z[1 ( ) ] 2z
高斯光束的传播特性
0 u x, y, z 0 e
x2 y 2
2
ei
e
i
相位因子
x2 y 2
0 0 e
2
uk u 0
2 2
(k )
将 u x, y, z =g ( z ) exp f z ( x 2 y 2 ) exp(ikz )代入上式方程
2u 忽略 2 项 z
2 2 2 ik 0 x 2 y 2 z
2 2 （ 2 2 2ik 0） 将 x, y, z 代入上式方程 x y z