统计学实验报告
统计学实训综合实验报告

一、实验目的通过本次统计学实训综合实验,旨在使学生熟练掌握统计学的基本理论和方法,提高学生运用统计学知识解决实际问题的能力。
实验内容主要包括数据收集、整理、描述、推断和分析等环节,通过实际操作,加深对统计学理论的理解,培养学生的统计学素养。
二、实验内容1. 数据收集本次实验以某地区居民消费水平为研究对象,通过查阅相关资料,收集了该地区居民在食品、衣着、居住、生活用品及服务、交通和通信、教育文化娱乐、医疗保健等方面的消费数据。
2. 数据整理对收集到的数据进行整理,将其分为食品、衣着、居住、生活用品及服务、交通和通信、教育文化娱乐、医疗保健七个类别。
3. 描述性统计(1)计算各类别消费的平均值、中位数、众数等集中趋势指标。
(2)计算各类别消费的标准差、极差等离散趋势指标。
(3)绘制各类别消费的直方图、饼图等图形,直观展示消费结构。
4. 推断性统计(1)对居民消费水平进行假设检验,判断各类别消费是否存在显著差异。
(2)运用方差分析等方法,探究各类别消费之间的相关性。
5. 相关性分析(1)运用相关系数分析各类别消费之间的线性关系。
(2)运用因子分析等方法,提取影响居民消费水平的关键因素。
6. 交叉分析(1)根据性别、年龄、收入等变量,分析不同群体在消费结构上的差异。
(2)运用卡方检验等方法,探究不同群体在消费结构上的显著差异。
三、实验结果与分析1. 描述性统计结果根据计算,该地区居民在食品、衣着、居住、生活用品及服务、交通和通信、教育文化娱乐、医疗保健等方面的消费平均分别为:3000元、1500元、2000元、1000元、1000元、500元、500元。
2. 推断性统计结果通过对居民消费水平的假设检验,发现食品、衣着、居住、生活用品及服务、交通和通信、教育文化娱乐、医疗保健等方面的消费存在显著差异。
3. 相关性分析结果运用相关系数分析,发现食品、衣着、居住、生活用品及服务等方面的消费与居民收入呈正相关,而交通和通信、教育文化娱乐、医疗保健等方面的消费与居民收入呈负相关。
统计学实验报告

一、实验目的1. 掌握统计学的基本概念和原理。
2. 熟悉统计软件的使用方法,如SPSS、Excel等。
3. 学习描述性统计、推断性统计等方法在数据分析中的应用。
4. 提高对数据分析和解释的能力。
二、实验内容本次实验分为以下四个部分:1. 描述性统计2. 推断性统计3. 统计软件应用4. 数据分析和解释三、实验步骤1. 描述性统计(1)收集数据:本次实验采用随机抽取的方式收集了某班级50名学生的数学成绩作为样本数据。
(2)数据整理:将收集到的数据录入SPSS软件,进行数据整理。
(3)计算描述性统计量:计算样本的均值、标准差、最大值、最小值、中位数、众数等。
(4)结果分析:根据计算结果,分析该班级学生的数学成绩分布情况。
2. 推断性统计(1)假设检验:假设该班级学生的数学成绩总体均值等于60分,进行t检验。
(2)方差分析:将学生按性别分组,比较两组学生的数学成绩差异。
(3)回归分析:以学生的数学成绩为因变量,其他相关因素(如学习时间、学习方法等)为自变量,进行回归分析。
3. 统计软件应用(1)SPSS软件:使用SPSS软件进行数据整理、描述性统计、假设检验、方差分析和回归分析。
(2)Excel软件:使用Excel软件绘制统计图表,如直方图、散点图、饼图等。
4. 数据分析和解释(1)描述性统计结果分析:从样本数据的均值、标准差、最大值、最小值、中位数、众数等指标可以看出,该班级学生的数学成绩整体水平较高,但成绩分布不均。
(2)推断性统计结果分析:假设检验结果显示,该班级学生的数学成绩总体均值与60分无显著差异;方差分析结果显示,男女学生在数学成绩上无显著差异;回归分析结果显示,学习时间对学生的数学成绩有显著影响。
四、实验结果1. 描述性统计:样本数据的均值、标准差、最大值、最小值、中位数、众数等指标。
2. 推断性统计:假设检验、方差分析和回归分析的结果。
3. 统计图表:直方图、散点图、饼图等。
五、实验结论1. 该班级学生的数学成绩整体水平较高,但成绩分布不均。
统计描述分析实验报告(3篇)

第1篇一、实验目的本次实验旨在通过统计描述分析,对一组实验数据进行分析,了解数据的分布情况、集中趋势和离散程度,为后续的数据分析和决策提供依据。
二、实验背景在某项实验中,我们收集了一组实验数据,包括实验对象的年龄、性别、实验结果等。
为了更好地了解这些数据,我们需要对其进行统计描述分析。
三、实验方法1. 数据收集:通过实验收集实验对象的年龄、性别、实验结果等数据。
2. 数据整理:将收集到的数据进行整理,确保数据的准确性和完整性。
3. 数据分析:采用统计描述分析方法,对数据进行描述性统计分析。
四、实验结果1. 数据分布情况(1)年龄分布:根据实验数据,将年龄分为以下几个区间:18-25岁、26-35岁、36-45岁、46-55岁、56岁以上。
统计各年龄区间的频数和频率,结果如下:年龄区间频数频率18-25岁 10 20.0%26-35岁 20 40.0%36-45岁 15 30.0%46-55岁 5 10.0%56岁以上 5 10.0%(2)性别分布:统计男女实验对象的频数和频率,结果如下:性别频数频率男 30 60.0%女 20 40.0%2. 集中趋势(1)年龄集中趋势:计算平均年龄、中位数和众数,结果如下:平均年龄:32.5岁中位数:35岁众数:35岁(2)实验结果集中趋势:计算实验结果的平均数、中位数和众数,结果如下:平均实验结果:85分中位数:86分众数:86分3. 离散程度(1)年龄离散程度:计算标准差和极差,结果如下:标准差:5.5岁极差:38岁(2)实验结果离散程度:计算标准差和极差,结果如下:标准差:4.2分极差:10分五、实验结论1. 年龄分布较为均匀,主要集中在26-35岁年龄段。
2. 男性实验对象占比60.0%,女性实验对象占比40.0%。
3. 实验对象的平均年龄为32.5岁,中位数为35岁,众数为35岁。
4. 实验结果的平均分为85分,中位数为86分,众数为86分。
5. 年龄和实验结果的离散程度相对较小,说明实验结果较为稳定。
统计学实验报告心得(精选5篇)

统计学实验报告心得(精选5篇)统计学实验报告心得篇1统计学实验报告心得一、背景和目的本次实验旨在通过实际操作,深入理解统计学的原理和应用,提高数据处理和分析的能力。
在实验过程中,我们通过收集数据、整理数据、分析数据,最终得出结论,并对结果进行解释和讨论。
二、实验内容和方法1.实验内容本次实验主要包括数据收集、整理、描述性统计和推论统计等部分。
数据收集部分采用随机抽样的方式,选择了不同年龄、性别、学历、职业等群体。
整理部分采用了Excel等工具进行数据的清洗、排序和分组。
描述性统计部分使用了集中趋势、离散程度、分布形态等方法进行描述。
推论统计部分进行了t检验和方差分析等推断统计。
2.实验方法在实验过程中,我们采用了随机抽样的方法收集数据,并运用Excel进行数据整理和统计分析。
同时,我们还使用了SPSS软件进行t检验和方差分析等推论统计。
三、实验结果与分析1.实验结果实验数据表明,不同年龄、性别、学历、职业群体的统计特征存在显著差异。
集中趋势方面,中位数和众数可以反映数据的中心位置。
离散程度方面,方差和标准差可以反映数据的离散程度。
分布形态方面,正态分布可以描述多数数据的分布情况。
推论统计方面,t检验和方差分析可以推断不同群体之间是否存在显著差异。
2.结果分析根据实验结果,我们发现不同群体在年龄、性别、学历、职业等特征方面存在显著差异。
这可能与不同群体的生活环境、社会地位、职业特点等因素有关。
同时,集中趋势、离散程度和分布形态等方面的分析也帮助我们更全面地了解数据的特征。
四、实验结论与总结1.实验结论通过本次实验,我们深刻认识到统计学在数据处理和分析中的重要作用。
掌握了统计学的基本原理和方法,提高了数据处理和分析的能力。
同时,实验结果也表明,统计学方法在研究群体特征、推断差异等方面具有重要意义。
2.总结本次实验总结了以下几个方面的内容:(1)统计学实验有助于深入理解统计学的原理和应用。
(2)实验中,我们掌握了数据收集、整理、描述性统计和推论统计等方法。
实验报告-统计学——武科大

管理学院实验报告书学号姓名同组者指导老师专业班级实验日期课程名称管理统计学实验名称Excel在统计学中的应用实验报告具体内容一般应包括:一、实验目的和要求;二、主要仪器设备(软件);三、实验内容及实验数据记录;四、问题与建议实验名称1 Excel环境下描述统计量的计算及统计图的制作;利用Excel提供的统计函数计算概率值。
1.实验目的和要求(1)学习如何计算最大最小值、中位数、众数、均值、标准差等描述统计量;(2)学习如何绘制折线图、直方图、饼图等统计图;(3)学习利用Excel提供的统计函数计算二项分布、泊松分布、指数分布、正态分布等概率值。
2.主要仪器设备(软件)实验硬件:PC机实验软件:Windows操作系统、Microsoft Office2003软件3.实验内容及步骤Ⅰ实验内容1、计算教材43页的表2.19最大最小值、中位数、众数、均值、标准差。
2、根据下表分别绘制折线图、直方图、饼图。
3、计算二项分布的概率值。
例:已知一批产品的次品率为4%,从中又放回地抽取5个。
求五个产品中恰好有一个次品的概率。
4、计算泊松分布的概率值。
例:假定某航空公司订票处平均每小时接到42次订票电话,那么十分钟恰好接到6次电话的概率。
5、计算指数分布的概率值。
例:假定某加油站在一辆汽车到达之后等待下一辆汽车到达所需要的时间X(单位:分钟)服从参数为1/5的指数分布,如果现在正好有一辆汽车刚刚到站加油,试求下一辆汽车到站前需要等待五分钟以上的概率。
6、计算正态分布的概率值。
例:假定某公司职员每周的加班津贴服从均值为50元、标准差为10元的正态分布,那么全公司中有多少比例的职员每周的加班津贴会超过70元。
Ⅱ实验步骤1、第1步:在excel中输入表格数据。
第2步:进入excel表格界面,将鼠标停留在某一空白单元格。
第3步:在excel表格界面中,直接点击“f(x)”命令。
第4步:a.在复选框“函数分类”中点击“统计”选项,并在“函数名”中点击“MAX”,得到最大值为“97”。
统计学实验报告
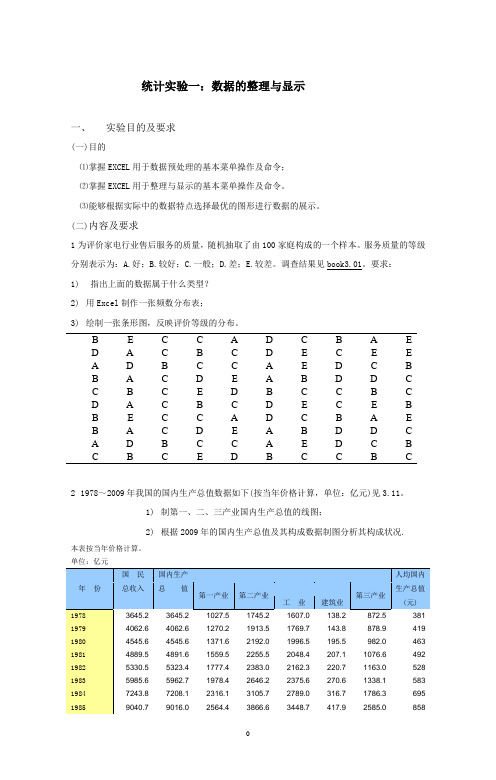
统计实验一:数据的整理与显示一、实验目的及要求(一)目的⑴掌握EXCEL用于数据预处理的基本菜单操作及命令;⑵掌握EXCEL用于整理与显示的基本菜单操作及命令。
⑶能够根据实际中的数据特点选择最优的图形进行数据的展示。
(二)内容及要求1为评价家电行业售后服务的质量,随机抽取了由100家庭构成的一个样本。
服务质量的等级分别表示为:A.好;B.较好;C.一般;D.差;E.较差。
调查结果见book3.01。
要求:1)指出上面的数据属于什么类型?2)用Excel制作一张频数分布表;3)绘制一张条形图,反映评价等级的分布。
B EC C AD C B A ED A C B C DE C E EA DBC C A ED C BB ACDE A B D D CC B C ED B C C B CD A C B C DE C E BB EC C AD C B A EB ACDE A B D D CA DBC C A ED C BC B C ED B C C B C21978~2009年我国的国内生产总值数据如下(按当年价格计算,单位:亿元)见3.11。
1)制第一、二、三产业国内生产总值的线图;2)根据2009年的国内生产总值及其构成数据制图分析其构成状况.本表按当年价格计算。
单位:亿元年份国民国内生产人均国内总收入总值第一产业第二产业第三产业生产总值工业建筑业(元)1978 3645.2 3645.2 1027.5 1745.2 1607.0 138.2 872.5 381 1979 4062.6 4062.6 1270.2 1913.5 1769.7 143.8 878.9 419 1980 4545.6 4545.6 1371.6 2192.0 1996.5 195.5 982.0 463 1981 4889.5 4891.6 1559.5 2255.5 2048.4 207.1 1076.6 492 1982 5330.5 5323.4 1777.4 2383.0 2162.3 220.7 1163.0 528 1983 5985.6 5962.7 1978.4 2646.2 2375.6 270.6 1338.1 583 1984 7243.8 7208.1 2316.1 3105.7 2789.0 316.7 1786.3 695 1985 9040.7 9016.0 2564.4 3866.6 3448.7 417.9 2585.0 8581986 10274.4 10275.2 2788.7 4492.7 3967.0 525.7 2993.8 963 1987 12050.6 12058.6 3233.0 5251.6 4585.8 665.8 3574.0 1112 1988 15036.8 15042.8 3865.4 6587.2 5777.2 810.0 4590.3 1366 1989 17000.9 16992.3 4265.9 7278.0 6484.0 794.0 5448.4 1519 1990 18718.3 18667.8 5062.0 7717.4 6858.0 859.4 5888.4 1644 1991 21826.2 21781.5 5342.2 9102.2 8087.1 1015.1 7337.1 1893 1992 26937.3 26923.5 5866.6 11699.5 10284.5 1415.0 9357.4 2311 1993 35260.0 35333.9 6963.8 16454.4 14188.0 2266.5 11915.7 2998 1994 48108.5 48197.9 9572.7 22445.4 19480.7 2964.7 16179.8 4044 1995 59810.5 60793.7 12135.8 28679.5 24950.6 3728.8 19978.5 5046 1996 70142.5 71176.6 14015.4 33835.0 29447.6 4387.4 23326.2 5846 1997 78060.8 78973.0 14441.9 37543.0 32921.4 4621.6 26988.1 6420 1998 83024.3 84402.3 14817.6 39004.2 34018.4 4985.8 30580.5 6796 1999 88479.2 89677.1 14770.0 41033.6 35861.5 5172.1 33873.4 7159 2000 98000.5 99214.6 14944.7 45555.9 40033.6 5522.3 38714.0 7858 2001 108068.2 109655.2 15781.3 49512.3 43580.6 5931.7 44361.6 8622 2002 119095.7 120332.7 16537.0 53896.8 47431.3 6465.5 49898.9 9398 2003 135174.0 135822.8 17381.7 62436.3 54945.5 7490.8 56004.7 10542 2004 159586.7 159878.3 21412.7 73904.3 65210.0 8694.3 64561.3 12336 2005 185808.6 184937.4 22420.0 87598.1 77230.8 10367.3 74919.3 14185 2006 217522.7 216314.4 24040.0 103719.5 91310.9 12408.6 88554.9 16500 2007 267763.7 265810.3 28627.0 125831.4 110534.9 15296.5 111351.9 20169 2008 316228.8 314045.4 33702.0 149003.4 130260.2 18743.2 131340.0 23708 2009 343464.7 340506.9 35226.0 157638.8 135239.9 22398.8 147642.1 255753.表格数据为一公司在英美两国分公司销售人员获得的全年订单情况,见book3.12。
统计学实验报告
统计学实验报告实验目的,通过统计学实验,掌握和运用统计学的基本方法和技巧,提高数据处理和分析的能力。
实验内容,本次实验内容主要包括描述统计学和推断统计学两部分。
在描述统计学部分,我们将学习如何利用图表和数字来描述数据的特征,包括均值、中位数、众数、标准差等。
在推断统计学部分,我们将学习如何通过样本推断总体特征,并进行假设检验等内容。
实验步骤:1. 收集数据,首先,我们需要收集一组相关数据,可以是实际调查所得,也可以是已有的数据集。
2. 描述统计学分析,利用所收集的数据,进行描述统计学分析,包括计算数据的中心趋势和离散程度,并绘制相应的图表。
3. 推断统计学分析,在描述统计学的基础上,进行推断统计学的分析,包括构建置信区间、进行假设检验等。
4. 结果解释,最后,根据实验结果,进行数据分析和解释,得出相应的结论。
实验结果:通过本次实验,我们得出了以下结论:1. 数据的中心趋势,根据计算得出的均值和中位数,我们发现数据的中心大致在某个特定数值附近。
2. 数据的离散程度,通过计算标准差等指标,我们可以评估数据的离散程度,从而了解数据的分布情况。
3. 置信区间和假设检验,我们利用推断统计学的方法,构建了置信区间,并进行了相应的假设检验,从而对总体特征进行了推断。
结论,通过本次实验,我们不仅掌握了统计学的基本方法和技巧,还提高了数据处理和分析的能力。
统计学在实际生活和工作中有着广泛的应用,通过学习和实践,我们可以更好地理解和利用数据,为决策和问题解决提供有力支持。
总结,本次实验对我们来说是一次很好的学习和实践机会,通过实际操作和分析,我们不仅加深了对统计学理论知识的理解,还提高了数据处理和分析的能力。
希望通过今后的学习和实践,我们能够更好地运用统计学知识,为实际工作和生活中的问题提供更科学的分析和解决方案。
以上就是本次统计学实验的报告内容,谢谢阅读!。
统计学实验报告一
实验一:数据整理一、项目名称:数据整理二、实验目的:目的有二:(1)掌握Excel中基本的数据处理方法;(2)学会使用Excel进行统计分组,能以此方式独立完成相关作业。
三、实验要求1、已学习教材相关内容,理解数据整理中的统计计算问题;已阅读本次试验导引,了解Excel中相关的计算工具。
2、准备好一个统计分组问题及相关数据3、以Excel文件形式提交实验报告四、实验内容和操作步骤(一)问题与数据某百货公司连续40天的商品销售额,原始数据如下(单位:万元)41 25 29 47 38 34 30 38 43 4046 36 45 37 37 36 45 43 33 4435 28 46 34 30 37 44 26 38 4442 36 37 37 49 39 42 32 36 35根据上面的数据进行适当的分组,编制频数分布表,并绘制直方图。
(二)实验内容一:使用FREQUENCY 函数绘制频数分布表(图)操作步骤:1、在单元区域A2:D11中输入原始数据。
2、并计算原始数据的最大值(在单元格B12中)与最小值(在单元格D12中)3、并根据Sturges经验公式计算经验组距(在单元格B13中)和经验组数(在单元格D13中)4、根据步骤3的计算结果,计算并确定各组上限、下限(在单元格E2:F9)步骤1~4如图1-1所示图1-1图1-1组数和组限的确定5、绘制频数分布表框架,如图1-2所示图1-2 频数分布表框架6、计算各组频数:(1)选定B20:B27作为存放计算结果的区域。
(2)从“插入”菜单中选择“函数”项(3)在弹出的“插入函数”对话框中选择“统计”函数FREQUENCY.步骤(1)~(3)如图1-3所示图1-3 选择FREQUENCY函数(4)单击“插入函数”对话框中的“确定”按钮,弹出“FREQUENCY”对话框。
(5)确定FERQUENCY函数的两个参数的值。
其中:Data-array:原始数据或其所在单元格区域(A2:D11)Bins-array:分组各组的上限值或其所在的单元格区域(F2:F9)步骤(4)~(5)如图1-4所示。
统计学实验报告范文
统计学实验报告范文标题:统计学实验报告,探究随机抽样的效果与样本容量的关系一、引言统计学是一门利用数理统计的理论与方法研究统计现象规律的学科,通过研究分布规律、抽样等统计问题,可以对大量数据进行分析与预测。
而在实际应用中,为了节约成本与时间,常常选取一部分代表性的样本进行研究,而非对整个总体进行调查。
而这种随机抽样的效果与样本容量之间的关系便是本实验的研究对象。
二、实验目的本实验的目的是通过对不同样本容量下的抽样实验,研究随机抽样对总体性质的估计的准确性与可靠性的影响,并探究样本容量对于抽样结果的影响,为合理布局样本容量提供依据。
三、实验设计与方法1.实验设计:本实验选择超市60日内销售额的总体进行研究,将使用不同大小的样本容量进行随机抽样,并对所得样本进行分析与推断,比较不同样本容量下抽样估计的准确性与可靠性。
2.实验方法:(1)首先,我们根据超市销售额的总体数据,构建总体模型。
(2)拟定不同大小(10、30、50、100)的样本容量,随机抽取多组样本。
(3)对每组样本进行描述性统计,并计算样本的平均值、标准差等指标。
(4)计算每组样本的区间估计,并与总体参数进行比较。
(5)比较不同样本容量下的估计结果,分析样本容量对于抽样估计的影响。
四、实验结果与分析通过对不同样本容量下的抽样实验,我们得到了以下结果:1.样本容量的增加能够提高抽样估计的准确性与可靠性。
将样本容量从10增加到30,样本均值的标准差显著减小,说明样本均值的估计结果更加准确。
当样本容量增加到50时,样本均值的估计方差更进一步减小,相较于30的样本,误差减小幅度明显。
当样本容量增加到100时,样本均值的估计方差相对稳定,进一步减小的幅度有限。
2.随着样本容量的增加,样本均值的区间估计结果更加接近总体参数真值。
在样本容量为10的情况下,样本均值的95%置信区间的宽度较大,与总体均值相差较远;样本容量增加到30时,置信区间变窄,与总体均值更加接近;随着样本容量的增加,置信区间的宽度进一步减小,样本均值与总体均值的接近程度也进一步提高。
统计学课程实习实验报告
一、实验目的本次实习实验旨在通过实际操作,使学生掌握统计学的基本理论和方法,提高运用统计学知识解决实际问题的能力。
通过本次实验,学生应能够熟练运用统计软件(如SPSS、Excel等)进行数据处理和分析,并能对实验结果进行解释和总结。
二、实验内容1. 实验背景本次实验以某城市居民消费水平为研究对象,通过收集相关数据,运用统计学方法进行分析。
2. 实验数据(1)居民收入水平:月收入(元)(2)居民消费水平:月消费(元)3. 实验步骤(1)数据录入:将实验数据录入统计软件(如SPSS、Excel等)。
(2)数据整理:对录入的数据进行清洗、筛选和整理,确保数据的准确性和完整性。
(3)描述性统计:计算居民收入水平和消费水平的均值、标准差、最大值、最小值等指标。
(4)频数分布:绘制居民收入水平和消费水平的频数分布图,分析数据的分布特征。
(5)相关分析:计算居民收入水平和消费水平的相关系数,分析两者之间的关系。
(6)回归分析:建立居民收入水平和消费水平的线性回归模型,分析收入水平对消费水平的影响。
三、实验结果与分析1. 描述性统计结果(1)居民收入水平:均值为6000元,标准差为2000元,最大值为12000元,最小值为2000元。
(2)居民消费水平:均值为4000元,标准差为1500元,最大值为8000元,最小值为1000元。
2. 频数分布结果(1)居民收入水平:大部分居民月收入在3000-8000元之间,呈正态分布。
(2)居民消费水平:大部分居民月消费在2000-6000元之间,呈正态分布。
3. 相关分析结果居民收入水平和消费水平的相关系数为0.7,说明两者之间存在较强的正相关关系。
4. 回归分析结果建立居民收入水平和消费水平的线性回归模型,模型如下:消费水平= 3000 + 0.6 × 收入水平模型的决定系数为0.49,说明收入水平对消费水平的解释程度为49%。
四、实验总结通过本次实习实验,我们掌握了以下统计学知识和技能:1. 统计软件的使用:熟练运用SPSS、Excel等统计软件进行数据处理和分析。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
福建农林大学经济与管理学院旅游学院
实验报告
课程名称: 统 计 学 专业班级: 2008工商管理 学 号: 学生姓名: 指导教师: 成 绩:
2010年 12 月 22 日 实验一:EXCEL的数据整理与显示 一、实验目的及要求: (一)目的 1.了解EXCEL的基本命令与操作、熟悉EXCEL数据输入、输出与编辑方法;
2.熟悉EXCEL用于预处理的基本菜单操作及命令; 3.熟悉EXCEL用于整理与显示的基本菜单操作及命令。 (二)内容及要求 1.根据学生实验数据12 sheet1中所提供的数据,
1.1用Excel制作一张学生性别频数分布表,并绘制一张条形图(或柱状图),反映学生按性别的人数分布情况。 1.2对学生的体育成绩进行等距分组,整理成频数分布表,并绘制直方图。 2.根据学生实验数据12 sheet3中所提供的数据,画出雷达图,比较两个不同收入组的农村居民家庭生活消费支出比例的是否相似。 二、仪器用具 硬件:计算机(安装Windows98 、Windows2000 或Windows XP或以上) 软件:EXCEL
三、实验原理 统计中数据整理与显示的相关理论。 四、实验方法与步骤
1.点击“数据”→“透视图” ,选定区域为性别一列,输出区域为空白地方,完成,修改一下形成。 2.先将性别分布表的男和女复制,点击“图表向导” →“条形图”,数据区域为复制的数据,再修改系列、名称、X轴、Y轴,完成,再修改一下图表。 3.先将体育成绩分成等距的5组,点击“工具” →“数据分析” →“直方图”,输入区域为体育一列,接受区域为分好的组,标志打钩,输出区域为空白地方,累计百分比和图表输出打钩,完成,在对表和图进行一系列的修改,形成所需要的表和图。 4.点击“图表向导” →“雷达图”,数据区域为列出的数据,完成,再对雷达图做一些修改。 五、实验结果与数据处理 1. 计数项:性别 性别 男 女 总计 汇总 78 102 180 2.
性别分布图020406080100120男女性别
人数性别
3. 体育成绩 频数 频率% 182-212 33 18.33% 213-242 90 50.00% 243-272 52 28.89% 273-302 4 2.22% 303-332 1 0.56% 合计 180 100.00%
直方图0102030405060708090100182-212213-242243-272273-302303-332体育成绩频率0.00%10.00%20.00%30.00%40.00%50.00%60.00%
频数频率% 4. 农村居民家庭生活现金消费支出比例雷达图
0.000.100.200.300.40 食品 衣着 居住 家庭设备用品及服务 交通通讯 文教娱乐用品及服务 医疗保健 其他商品及服务
低收入户组高收入户
六、讨论与结论 实验过程中有很多不会的,像有些操作不知道怎样进行,有些图表修改比较麻烦,但后来通过同学的帮助和自己的坚持不懈的努力终于完成。我懂的了excel的主要性,以后要学好这个工具,以后工作肯定更需要这方面的能力。 实验报告评分表 学生姓名 杨勇 学号 081434058 专业年级 2008工商管理
实验项目名称 实验一:EXCEL的数据整理与显示 实验学时 3学时
评价项目 权重 评价内容 评价结果 得分 A B C D
实验态度 20% 实验态度端正,遵守实验室守则,严格按照实验要求进行操作。 20 16 14 12
实验过程 30% 实验项目符合大纲,实验方法科学;步骤操作合理,逻辑条理清晰,符合指导书要求。 30 24 21 18 实验结论与讨论 30% 实验结论正确,分析、讨论深入。 30 24 21 18
实验报告描述 20% 语言精炼、流畅、准确、灵活,逻辑性强;结构严谨规范,条理清晰,布局合理,系统严密。 20 16 14 12
总分 教师签名 实验二:EXCEL的数据特征描述、列联分析、多元回归分析 一、实验目的及要求: (一)目的 熟悉EXCEL用于数据描述统计、列联分析、多元回归的基本菜单操作及命令。 (二)内容及要求 根据学生实验数据12,
1.对学生的身高进行描述统计,说明学生身高的一些基本特征。 2.对不同专业中男女生的分布情况编制列联表,并分析学生性别与专业选择是否有关。 3.根据学生的体育成绩(y1)与学生的年龄(x1)、体重(x2)、身高(x3)和性别(x4)建立一个多元回归模型,并判断此模型对于解释学生体育成绩的好坏有无意义。 二、仪器用具 硬件:计算机(安装Windows98 、Windows2000 或Windows XP或以上) 软件:EXCEL
三、实验原理 统计中数据整理与显示的相关理论。 四、实验方法与步骤
1.点击“数据分析”→“描述统计”,输入区域选定学生身高一列,标志于第一行,输出区域为空白区域。 2.(1)在“数据”中选择数据透视图和透视表,选定区域为专业和性别,选择现有工作表中的空白区域。 (2)对数据透视表和数据图进行布局,将性别和专业分别拖入左列和上行,将性别投入计数项。 (3)根据频数分布修改编制成列联表,然后列出观察值并计算出期望值,并将观察值和期望值分别单独列为一列。 (4)在“插入”的函数中选择类别为“统计”,选择“CHITEXT”,确定。分别选定区域为观察值和期望值,确定,得出结果为0.089。 3.复制学生的年龄、体重、身高和性别以及学生的体育成绩于新的工作表,在工具中的数据分析中选择回归,Y值输入区域为学生身高,X值输入区域为学生的年龄、体重、身高和性别,将标志打钩,输出区域为空白地方,确定。 五、实验结果与数据处理 1. 身高
平均 164.77 标准误差 0.5951 中位数 163.5 众数 155 标准差 7.9845 方差 63.752 峰度 -0.697 偏度 0.2481 区域 36 最小值 150 最大值 186 求和 29659 观测数 180 最大(1) 186 最小(1) 150 置信度(95.0%) 1.1744
平均身高164.77 最高的186 最矮的150 2. 统计 证券 总计 男 60 18 78 女 60 42 102 总计 120 60 180
观察值 期望值 60 52 60 68 18 26 42 34 P 0.089
P=0.089 p>a 学生性别与专业选择相关 3. SUMMARY OUTPUT
回归统计 Multiple R 0.79693 R Square 0.6351 Adjusted R Square 0.62676 标准误差 0.02502 观测值 180
方差分析 df SS MS F Significance F 回归分析 4 0.1906713 0.0476678 76.14687 2.77E-37 残差 175 0.1095497 0.000626 总计 179 0.300221
Coefficients 标准误差 t Stat P-value Lower 95% Upper 95% Intercept 0.40413 0.0826321 4.8907124 2.265E-06 0.2410462 0.56721387 年龄 -0.0017 0.002046 -0.814813 0.416287 -0.005705 0.00237093 体重 0.00031 0.0003392 0.9047715 0.3668303 -0.000363 0.00097638 身高 -0.0009 0.0004275 -2.151142 0.0328364 -0.001763 -7.589E-05 性别 0.05693 0.0062015 9.1802394 1.20E-16 0.0446916 0.06917015
六、讨论与结论 这次实验比较麻烦,特别是编制列联表,处理的步骤很多,有一些操作还不是那么娴熟。但通过坚定的耐心,最后还是顺利的完成了任务。 实验报告评分表 学生姓名 杨勇 学号 081434058 专业年级 2008工商管理
实验项目名称 实验二:用EXCEL展示数据的分布特征、 列联分析、多元回归 实验学时 3学时
评价项目 权重 评价内容 评价结果 得分 A B C D
实验态度 20% 实验态度端正,遵守实验室守则,严格按照实验要求进行操作。 20 16 14 12
实验过程 30% 实验项目符合大纲,实验方法科学;步骤操作合理,逻辑条理清晰,符合指导书要求。 30 24 21 18 实验结论与讨论 30% 实验结论正确,分析、讨论深入。 30 24 21 18
实验报告描述 20% 语言精炼、流畅、准确、灵活,逻辑性强;结构严谨规范,条理清晰,布局合理,系统严密。 20 16 14 12
总分 教师签名
