宿迁市2013届高三年级第二次模拟考试

合集下载

江苏省宿迁市2013届高三年级摸底调研测试政治试题.

x y高三年级摸底调研测试政治一、单项选择题：本大题共33小题，每小题2分，共计66分。

在每题给出的四个选项中，只有一个选项是最符合题意的。

1．有些品牌白酒注重窖藏环节，根据窖藏时间的长短制定不同的价格。

“白酒按年论价”，说明白酒价格的决定性因素是A ．使用价值B ．价值C ．供求关系D ．存放时间2．假定其他条件不变，在一般情况下，下列选项中与右图反映的变动关系相一致的是①y 为人民币汇率 x 为商品进口量②y 为货币流通速度 x 为实际需要的货币量③y 为个别劳动时间 x 为商品价值总量④y 为某种商品价格 x 为该商品替代品需求量A ．①②B ．②③C ．①④D ．②④3．2012年上半年，我国民营企业进出口总值同比增长19%，快于同期我国总体进出口总增速11个百分点；外商投资企业、国有企业进出口总值分别占同期我国进出口总值的49.5%、20.6%。

这表明A ．民营企业是社会主义经济的重要组成部分B ．民营企业、外资经济是我国国民经济的主体C ．在市场竞争中，多种所有制经济能够共同发展D ．必须把坚持对外开放作为我国发展的根本立足点4．今年中秋夜过后，三亚大东海景区3公里海滩遍布50吨生活垃圾，严重污染了海洋环境。

这启发我们要坚持A ．绿色消费B ．适度消费C ．理性消费D ．紧缩消费注意事项考生在答题前请认真阅读本注意事项及各题答题要求1.本试卷共8页，包含选择题（第1题-第33题，共33题）、非选择题（第34题-第37题，共4题）两部分。

本卷满分120分，考试时间为100分钟。

考试结束后，请将答题卷和答题卡一并交回。

2.答题前，请您务必将自己的姓名、准考证号、座位号用0.5毫米黑色字迹签字笔填写在答题卷及答题卡上。

3.作答选择题必须用2B 铅笔把答题卡对应题目的答案标号涂黑。

如需改动，请用橡皮擦干净后，再选涂其它答案。

作答非选择题必须用书写黑色字迹的0.5毫米的签字笔写在答题卷上的指定位置，在其它位置作答一律无效。

宿迁市2013届高三年级模拟测试一

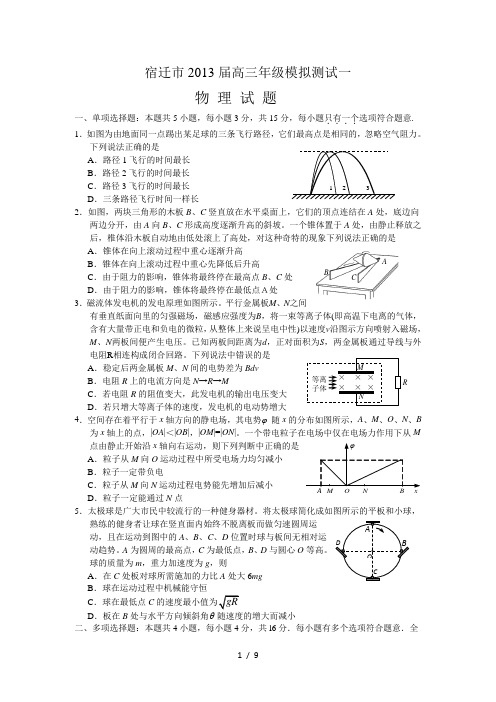
宿迁市2013届高三年级模拟测试一物理试题一、单项选择题：本题共5小题，每小题3分，共15分，每小题只有一个．．．．选项符合题意. 1．如图为由地面同一点踢出某足球的三条飞行路径，它们最高点是相同的，忽略空气阻力。

下列说法正确的是A ．路径1飞行的时间最长B ．路径2飞行的时间最长C ．路径3飞行的时间最长D ．三条路径飞行时间一样长2．如图，两块三角形的木板B 、C 竖直放在水平桌面上，它们的顶点连结在A 处，底边向两边分开，由A 向B 、C 形成高度逐渐升高的斜坡。

一个锥体置于A 处，由静止释放之后，椎体沿木板自动地由低处滚上了高处，对这种奇特的现象下列说法正确的是 A ．锥体在向上滚动过程中重心逐渐升高B ．锥体在向上滚动过程中重心先降低后升高C ．由于阻力的影响，锥体将最终停在最高点B 、C 处D ．由于阻力的影响，锥体将最终停在最低点Ａ处3．磁流体发电机的发电原理如图所示。

平行金属板M 、N 之间有垂直纸面向里的匀强磁场，磁感应强度为B ，将一束等离子体(即高温下电离的气体，含有大量带正电和负电的微粒，从整体上来说呈电中性)以速度v 沿图示方向喷射入磁场，M 、N 两板间便产生电压。

已知两板间距离为d ，正对面积为S ，两金属板通过导线与外电阻R 相连构成闭合回路。

下列说法中错误的是A ．稳定后两金属板M 、N 间的电势差为BdvB ．电阻R 上的电流方向是N →R →MC ．若电阻R 的阻值变大，此发电机的输出电压变大D ．若只增大等离子体的速度，发电机的电动势增大4．空间存在着平行于x 轴方向的静电场，其电势ϕ 随x 的分布如图所示，A 、M 、O 、N 、B为x 轴上的点，|OA |＜|OB |，|OM |=|ON |。

一个带电粒子在电场中仅在电场力作用下从M点由静止开始沿x 轴向右运动，则下列判断中正确的是 A ．粒子从M 向O 运动过程中所受电场力均匀减小B ．粒子一定带负电C ．粒子从M 向N 运动过程电势能先增加后减小D ．粒子一定能通过N 点5．太极球是广大市民中较流行的一种健身器材。

安徽省宿州市泗县二中2013届高三上学期第二次月考数学(理)试题

宿州市泗县二中2013届高三上学期第二次月考数学（理）试题一、选择题（每小题5分，共60分。

下列每小题所给选项只有一项符合题意，请将正确答案的序号填涂在答题卡上）1、已知集合R ，若集合{||23},{|21|1},()x R A x x B x C A B =-≤=->⋂则为A ．{x | 1< x ≤5}B ．{x | x ≤或x> 5}C ．≤—1或x> 5}D ．—1≤ x ≤ 5} 2．命题 P ：若∈R, 则|a|+|b|>1 是|a+b|>1 的充分不必要条件；命题 q ：不等式||11x x x x >--的解集为 {x |0<x<1}，则A ．“p 或 q” 为假命题B ．“p 且 q” 为真命题 A ．“⌝p 或 q” 为假命题 B ．“⌝p 且 q” 为真命题3．已知{}n a 为等比数列，若4617373910,2a a a a a a a a +=++则的值为 A ．10B ．20C ．60D ．100 4．已知直线 α和平面α，β，α∩β=l ，a ⊄α,a ⊄β,a 在α，β内的射影分别为直线 b和 c ,则 b 和 c 的位置关系是 A ．相交或平行 B ．相交或异面C ．平行或异面D ．相交﹑平行或异面 5．已知sin()cos()2tan 2,sin()sin()2πθπθθπθπθ+--=---则等于 A ．2 B ．—2 C ．0 D ．236．一个几何体的三视图如图所示,且其侧视图是一个等边三角形,实数解，则这个几何的体积为AB．(4π+ CD7．函数32(0,1)x y a a a a +=->≠的图像恒过定点 A ，若点 A 在直线1,x y m n+=-上且m,n>0则的最小值为（） A ．13 B ．16C ．11+ D ．28 8．若函数21()log ()2a f x x ax =++有最小值，则实数a 的取值范围是A ．（0，1）B ．（0，1）（1，2）C ．（1，2）D ．[2,)+∞ 9．在△ABC 中，∠C =90°，∠B =30°，AC=1，M 为 AB 中点，将△ACM 沿 CM 折起，使 A 、B 间的距离为，则 M 到面 ABC 的距离为A ．12 BC ．1D ．3210．若函数()sin ,,()2,()0,f x x x x R f a f ωωβ=+∈=-=又且|α-β|的最小值为3,4πω则正数的值为 A ．13 B ．23 C ．43 D ．32 11．已知 A 、 B 、 C 是平面上不共线的三点， O 是三角形 ABC 的重心，动点 P 满足111(2)322OP OA OB OC =++，则点 P 一定为三角形的A ．AB 边中线的中点 B ．AB 边中线的三等分点（非重心）C ．重心D ．AB 边的中点12．已知函数21,0()21,0x x f x x x x +≤⎧=⎨-+>⎩，若关于x 的方程2()()0f x af x ==恰有5个不同的实数解，则a 的取值范围是A ．（0，1）B ．（0，2）C ．（1，2）D ．（0，3）二．填空题：本大题共 4 小题，每题 5 分，共 20 分 13．若点 P （x ，y ）满足线性约束条件020,0y x A y -≤-+≥⎨⎪≥⎪⎩点，O 为坐标原点，则OA OP ⋅的最大值_________．14．如图，四边形 ABCD 为菱形，四边形 CEFB 为正方形，平面 ABCD ⊥平面CEFB,CE=1,∠AED=30°，则异面直线BC 与AE 所成角的大小_________．15．已知数列1{}331(*,2)n n n n a a a n N n -=+-∈≥满足，且115,()(*)3n n na b a t n N ==+∈若且{}n b 的等差数列，则t=_________． 16．已知函数()f x 的定义域为-1，5]，部分对应值如下表，()f x 的导函数 ()f x '的图像如图所示，给出关于()f x 的下列命题：①函数()y f x =在x=2时，取极小值 ②函数()f x 在[0，1]是减函数，在[1，2]是增函数，③当12a <<时，函数()y f x a =-有4个零点④如果当[1,]x t ∈-时，()f x 的最大值是2，那么t 的最大值为5，其中所有正确命题序号为_________．三、解答题：本大题共 6 个小题，共 70 分，解答应写出文字说明、证明过程或演算步骤．17．（本小题满分 10 分）在△ABC 中，角 A, B, C 的对边分别为 a, b, c ，且满足(2)cos 0.c a cosB b A --=（1）若7,13b a c =+=求此三角形的面积;（2()6A sin C π+-的取值范围。

【解析版】江苏省宿迁市泗阳中学、盱眙中学2013届高三联考数学试卷

江苏省宿迁市泗阳中学、盱眙中学2013届高三联考数学试卷一、填空题：本大题共14小题，每小题5分，共计70分．请把答案填写在答题卡相应位置上．1．（5分）（2013•泗阳县模拟）已知全集I={1，2，3，4，5，6}，集合A={1，3，4，5}，集合B={1，4}，则A∩C I B={3，5}．2．（5分）（2013•泗阳县模拟）某校高中生共有900人，其中高一年级300人，高二年级200人，高三年级400人，现采用分层抽样的方法抽取容量为45的样本，那么高三年级应抽取的人数为20．=×=203．（5分）（2013•泗阳县模拟）若复数（a+i）（1﹣2i）（i是虚数单位）是纯虚数，则实数a=﹣2．4．（5分）（2013•泗阳县模拟）以如图所示伪代码：根据以上伪代码，则f（﹣e）+f（e）= 2+2e．5．（5分）（2013•泗阳县模拟）函数的定义域是（2，+∞）∪（﹣∞，0）．（6．（5分）（2013•泗阳县模拟）若随机向一个边长为2的正方形内丢一粒豆子，则豆子落在此正方形内切圆内的概率为．P=故答案为：．7．（5分）（2013•泗阳县模拟）设α，β为两个不重合的平面，l，m，n为两两不重合的直线，给出下列四个命题：①若α∥β，l⊂α，则l∥β；②若m⊂α，n⊂α，m∥β，n∥β，则α∥β；③若l∥α，l⊥β，则α⊥β；④若m、n是异面直线，m∥α，n∥α，且l⊥m，l⊥n，则l⊥α．其中真命题的序号是①③④．8．（5分）（2013•泗阳县模拟）两个正数a，b的等差中项是，等比中项是，且a＞b，则双曲线的离心率为．，等比中项是为，由此能求出双曲线的离心率．，等比中项是，且∴双曲线为，双曲线e=．故答案为：9．（5分）（2013•泗阳县模拟）已知函数y=sinωx在上是减函数，则实数ω的取值范围是﹣≤ω＜0．上是减函数，可得，且≥上是减函数，且≥，∴≥，≤ω≤ω10．（5分）（2013•泗阳县模拟）在等差数列{a n}中，＜﹣1，若它的前n项和S n有最大值，则使S n取得最小正数的n=19．可将＜﹣转化为：有最大值，＜﹣⇔＜=10=19a＜11．（5分）（2013•泗阳县模拟）在直角△ABC中，两条直角边分别为a、b，斜边和斜边上的高分别为c、h，则的取值范围是（1，]．根据勾股定理和三角形面积公式，将＞．再设，则可将表示成关于，）．由此即可得到c==，=∵=∴，即=，则，=+t）上）上是增函数，可得当t时，）综上所述，的取值范围是（，]12．（5分）（2013•泗阳县模拟）直线与圆x2+y2=1相交于A，B两点（其中a，b是实数），且△AOB是直角三角形（O是坐标原点），则点P（a，b）与点（0，1）之间距离的最大值为．，即==1）的距离最大为故答案为：13．（5分）（2013•泗阳县模拟）如图，△ABC中，AB=4，AC=8，∠BAC=60°，延长CB到D，使BA=BD，当E点在线段AB上移动时，若，当λ取最大值时，λ﹣μ的值是．，，求出=4．又∵，∴=====故答案为：14．（5分）（2013•泗阳县模拟）在平面直角坐标系中，点集A={（x，y）|x2+y2≤1}，B={（x，y）|﹣1≤x≤1，﹣1≤y≤1}，则点集Q={（x，y）|x=x1+x2，y=y1+y2，（x1，y1）∈A，（x2，y2）∈B}所表示的区域的面积为12+π．，，二、解答题：本大题共6小题，共计90分．请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤．15．（14分）（2013•泗阳县模拟）在△ABC中，内角A，B，C的对边分别为a，b，c，已知a，b，c成等比数列，．（1）若ac=2，求a+c的值；（2）求的值．=16．（14分）（2013•泗阳县模拟）直三棱柱ABC﹣A1B1C1中，AC=BC=BB1=1，AB1=（1）求证：平面AB1C⊥平面B1CB；（2）求三棱锥A1﹣AB1C的体积．=17．（15分）（2013•泗阳县模拟）某生产旅游纪念品的工厂，拟在2010年度将进行系列促销活动．经市场调查和测算，该纪念品的年销售量x万件与年促销费用t万元之间满足3﹣x 与t+1成反比例．若不搞促销活动，纪念品的年销售量只有1万件．已知工厂2010年生产纪念品的固定投资为3万元，每生产1万件纪念品另外需要投资32万元．当工厂把每件纪念品的售价定为：“年平均每件生产成本的150%”与“年平均每件所占促销费一半”之和时，则当年的产量和销量相等．（利润=收入﹣生产成本﹣促销费用）（1）求出x与t所满足的关系式；（2）请把该工厂2010年的年利润y万元表示成促销费t万元的函数；（3）试问：当2010年的促销费投入多少万元时，该工厂的年利润最大？．由题知，有∴分）∴，进一步化简，得年的年利润）知，18．（15分）（2013•泗阳县模拟）设椭圆C：+=1（a＞b＞0）的左焦点为F，上顶点为A，过点A与AF垂直的直线分别交椭圆C与x轴正半轴于点P、Q，且=．（1）求椭圆C的离心率；（2）若过A、Q、F三点的圆恰好与直线l：x+y+3=0相切，求椭圆C的方程．的坐标表示出，根据）根据∵，∴得在椭圆上，所以．，a Q的外接圆圆心为（a r=|FQ|=ab=19．（16分）（2013•泗阳县模拟）已知数列{a n}的首项a1=2a+1（a是常数，且a≠﹣1），a n=2a n +n2﹣4n+2（n≥2），数列{b n}的首项b1=a，b n=a n+n2（n≥2）．﹣1（1）证明：{b n}从第2项起是以2为公比的等比数列；（2）设S n为数列{b n}的前n项和，且{S n}是等比数列，求实数a的值；（3）当a＞0时，求数列{a n}的最小项．进而可求得时，∴，即，时，最小项为20．（16分）（2013•泗阳县模拟）已知函数（a∈R）．（Ⅰ）当a≥0时，讨论f（x）的单调性；（Ⅱ）设g（x）=x2﹣2bx+4．当时，（i）若对任意x1∈（0，2），存在x2∈[1，2]，使f（x1）≥g（x2），求实数b取值范围．（ii）对于任意x1，x2∈（1，2]都有，求λ的取值范围．，，）的结论，我们可得当，可转化为上是增函数，函数，构造函数，可得函，，令时，，所以此时函数时，令，解得）在，令，解得，）在，由于，令，解得）当，又已知存在，使，即，，解得取值范围是上是增函数，函数在（∴上恒成立，即，进而根。

江苏13大市2013年高三历次考试数学试题分类汇编16：复数

[推荐]##省13大市20##高三历次考试数学试题分类汇编16：复数一、填空题1 ．〔##市2012-2013学年度第一学期高三期末考试数学试卷〕已知i 为虚数单位,复数z 满足<1-i>z =2,则z =_________.[答案]1+i;2 ．〔##省##市2013届高三年级第二次模拟考试数学试卷〕若复数z 满足2)1(=-z i <i 为虚数单位>,则=z ________.[答案3 ．〔##省##、##、##、宿迁、##五市2013届高三第三次调研测试数学试卷〕设复数z 满足(34i)50z ++=<i 是虚数单位>,则复数z 的模为______.[答案]14 ．〔##市、##市2013届高三第二次模拟考试数学试卷〕若复数12mi z i-=+<是虚数单位>是纯虚数,则实数m 的值为____.[答案]25 ．〔##市2013届高三第一次调研测试数学试卷〕已知复数z =32i i-<i 是虚数单位>,则复数z 所对应的点位于复平面的第________象限.[答案] 答案:三.考查复数的基本概念与几何意义.对复数的概念宜适当疏理,防止出现知识盲点6 ．〔##省##市2012-2013学年度第一学期期末考试高三数学试题〕设复数122z i =+,222z i =-,则12z z =__________ [答案]i7 ．〔##市、##市2013届高三年级第一次模拟考试数学试题〕复数2(12)i -的共轭复数是 .[答案]34i -+8 ．〔2012-2013学年度苏锡常镇四市高三教学情况调研〔二〕数学试题〕已知i 是虚数单位,复数31i z i+=+对应的点在第____象限. [答案]四9 ．〔苏北三市〔##、##、宿迁〕2013届高三第二次调研考试数学试卷〕已知i 是虚数单位,实数b a ,满足,10))(43(i bi a i =++则=-b a 43_____.[答案]010．〔##省苏锡常镇四市2013届高三教学情况调研<一>数学试题〕若实数a 满足221ai i i+=-,其中是虚数单位,则a =_____.[答案]211．〔##市2012-2013学年度第一学期高三期末考试数学试卷〕设复数z 满足(2)12z i i +=-<为虚数单位>,则z =____________.[答案]112．〔##市2013届高三教学期末调研测试数学试题〕已知复数1i z =-+<为虚数单位>,计算:z z z z⋅-=______. [答案]i -13．〔##市、##市2013届高三第三次模拟考试数学试卷〕已知复数z 满足<z +1>i=3+5i,其中i 为虚数单位,则|z |=________.[答案]514．〔##、##、##、宿迁四市2013届高三第二次调研测试数学试卷〕设复数z 满足| z | = |z -1 | = 1,则复数z 的实部为____.[答案]1215．〔##、宿迁市2013届高三年级第三次模拟考试数学试卷〕已知i 是虚数单位,若3i i(,)ia b a b =∈++R ,则ab 的值为____. [答案]3-;16．〔##省##市2013届高三上学期期末考试数学试卷〕已知i是虚数单位,则122ii-+等于______________. [答案]i-。

江苏省13大市2013年高三历次考试数学试题分类汇编3：函数的应用汇总

江苏省13大市2013年高三历次考试数学试题分类汇编3：函数的应用一、解答题1 ．（南通市2013届高三第一次调研测试数学试卷）某公司为一家制冷设备厂设计生产一种长方形薄板,其周长为4米,这种薄板须沿其对角线折叠后使用.如图所示,()ABCD AB AD >为长方形薄板,沿AC 折叠后,AB '交DC 于点P .当△ADP 的面积最大时最节能,凹多边形ACB PD '的面积最大时制冷效果最好.(1)设AB =x 米,用x 表示图中DP 的长度,并写出x 的取值范围; (2)若要求最节能,应怎样设计薄板的长和宽? (3)若要求制冷效果最好,应怎样设计薄板的长和宽?2 ．（南京市、盐城市2013届高三年级第一次模拟考试数学试题）近年来,某企业每年消耗电费约24万元, 为了节能减排, 决定安装一个可使用15年的太阳能供电设备接入本企业电网, 安装这种供电设备的工本费(单位:万元)与太阳能电池板的面积(单位: 平方米)成正比, 比例系数约为0.5. 为了保证正常用电, 安装后采用太阳能和电能互补供电的模式. 假设在此模式下, 安装后该企业每年消耗的电费C (单位:万元)与安装的这种太阳能电池板的面积x (单位:平方米)之间的函数关系是()(0,20100kC x x kx =≥+为常数). 记F 为该村安装这种太阳能供电设备的费用与该村15年共将消耗的电费之和. (1)试解释(0)C 的实际意义, 并建立F 关于x 的函数关系式; (2)当x 为多少平方米时, F 取得最小值?最小值是多少万元?3 ．（苏州市2012-2013学年度第一学期高三期末考试）在路边安装路灯,灯柱AB 与地面垂直,灯杆BC 与灯柱AB 所在平面与道路垂直,且120ABC ∠=,路灯C 采用锥形灯罩,射出的光线如图中阴影部分所示,已知60ACD ∠=,路宽24AD =米,设灯柱高AB h =(米),ACB θ∠=(3045θ≤≤)(1)求灯柱的高h (用θ表示);(2)若灯杆BC 与灯柱AB 所用材料相同,记此用料长度和为S ,求S 关于θ的函数表达式,并求出S 的最小值.CD（第17题）B 'PCBAD4 ．（江苏省泰州市2012-2013学年度第一学期期末考试高三数学试题）如图,一个半圆和长方形组成的铁皮,长方形的边AD 为半圆的直径,O 为半圆的圆心,1,2AB BC ==,现要将此铁皮剪出一个等腰三角形PMN ,其底边MN BC ⊥.(1)设备30MOD ∠=︒,求三角形铁皮PMN 的面积; (2)求剪下的铁皮三角形PMN 面积的最大值.5 ．（苏北三市（徐州、淮安、宿迁）2013届高三第二次调研考试数学试卷）如图,两座建筑物CD AB ,的底部都在同一个水平面上,且均与水平面垂直,它们的高度分别是9cm 和15cm ,从建筑物AB 的顶部A 看建筑物CD 的视角︒=∠45CAD . (1) 求BC 的长度; (2) 在线段BC 上取一点(P 点P 与点C B ,不重合),从点P 看这两座建筑物的视角分别为,,βα=∠=∠DPC APB 问点P 在何处时,βα+最小?6 ．（江苏省无锡市2013届高三上学期期末考试数学试卷）要制作一个如图的框架(单位:米),要求所围成的总面积为19.5(米2),其中ABCD 是一个矩形,EFCD 是一个等腰梯形,梯形高h=12AB, tan ∠FED=34,设AB=x 米,BC=y 米. (Ⅰ)求y 关于x 的表达式;(Ⅱ)如何设计x,y 的长度,才能使所用材料最少?ABDCPβα 第17题图7 ．（南京市、淮安市2013届高三第二次模拟考试数学试卷）如图,某广场中间有一块扇形绿地OA B,其中O 为扇形所在圆的圆心,60AOB ∠=︒,广场管理部门欲在绿地上修建观光小路:在AB 上选一点C,过C 修建与OB 平行的小路CD,与OA 平行的小路CE,问C 应选在何处,才能使得修建的道路CD 与CE 的总长最大,并说明理由.8 ．（江苏省苏锡常镇四市2013届高三教学情况调研(一)数学试题）某部门要设计一种如图所示的灯架,用来安装球心为O ,半径为R (米)的球形灯泡.该灯架由灯托、灯杆、灯脚三个部件组成,其中圆弧形灯托EA ,EB ,EC ,ED 所在圆的圆心都是O 、半径都是R (米)、圆弧的圆心角都是θ(弧度);灯杆EF 垂直于地面,杆顶E 到地面的距离为h (米),且h R >;灯脚1FA ,1FB ,1FC ,1FD 是正四棱锥1111F A B C D -的四条侧棱,正方形1111A B C D 的外接圆半径为R (米),四条灯脚与灯杆所在直线的夹角都为θ(弧度).已知灯杆、灯脚的造价都是每米a (元),灯托造价是每米3a(元),其中R ,h ,a 都为常数.设该灯架的总造价为y (元) .(1)求y 关于θ的函数关系式;(2)当θ取何值时,y 取得最小值?119 ．（江苏省泰州、南通、扬州、宿迁、淮安五市2013届高三第三次调研测试数学试卷）某单位设计的两种密封玻璃窗如图所示:图1是单层玻璃,厚度为8 mm;图2是双层中空玻璃,厚度均为4 mm,中间留有厚度为x 的空气隔层.根据热传导知识,对于厚度为d 的均匀介质,两侧的温度差为T ∆,单位时间内,在单位面积上通过的热量T Q k ∆=⋅,其中k 为热传导系数.假定单位时间内,在单位面积上通过每一层玻璃及空气隔层的热量相等.(注:玻璃的热传导系数为3410 J mm/C -⨯⋅,空气的热传导系数为42.510 J mm/C -⨯⋅.)(1)设室内,室外温度均分别为1T ,2T ,内层玻璃外侧温度为1T ',外层玻璃内侧温度为2T ',且1122T T T T ''>>>.试分别求出单层玻璃和双层中空玻璃单位时间内,在单位面积上通过的热量(结果用1T ,2T 及x 表示); (2)为使双层中空玻璃单位时间内,在单位面积上通过的热量只有单层玻璃的4%,应如何设计x 的大小?10．（江苏省盐城市2013届高三年级第二次模拟考试数学试卷）如图,在海岸线l 一侧C 处有一个美丽的小岛,某旅游公司为方便游客,在l 上设立了A 、B 两个报名点,满足A 、B 、C 中任意两点间的距离为10千米.公司拟按以下思路运作:先将A 、B 两处游客分别乘车集中到AB 之间的中转点D 处(点D 异于A 、B 两点),然后乘同一艘游轮前往C 岛.据统计,每批游客A 处需发车2辆,B处需发车4辆,每辆汽车每千米耗费2元,游轮每千米耗费12元.设∠α=CDA ,每批游客从各自报名点到C 岛所需运输成本S 元.⑴写出S 关于α的函数表达式,并指出α的取值范围; ⑵问中转点D 距离A 处多远时,S 最小?11．（2012-2013学年度苏锡常镇四市高三教学情况调研（二）数学试题）如图所示,有两条道路OM 与ON ,060MON ∠=,现要铺设三条下水管道OA ,OB ,AB (其中A ,B 分别在OM ,ON 上),若下水管道的总长度为3km ,设()OA a km =,()OB b km =.(1)求b 关于a 的函数表达式,并指出a 的取值范围;(2)已知点P 处有一个污水总管的接口,点P 到OM 的距离PH为,到点O 的距离PO,问下水管道AB 能否经过污水总管的接口点P ?若能,求出a 的值,若不能,请说明理由.12．（扬州、南通、泰州、宿迁四市2013届高三第二次调研测试数学试卷）为稳定房价,某地政府决定建造一批保障房供给社会.计划用1 600万元购得一块土地,在该土地上建造10幢楼房的住宅小区,每幢楼的楼层数相同,且每层建筑面积均为1 000平方米,每平方米的建筑费用与楼层有关,第x 层楼房每平方米的建筑费用为(kx +800)元(其中k 为常数) .经测算,若每幢楼为5层,则该小区每平方米的平均综合费用为1 270元. (每平方米平均综合费用=购地费用+所有建筑费用所有建筑面积).(1)求k 的值;(2)问要使该小区楼房每平方米的平均综合费用最低,应将这10幢楼房建成多少层?此时每平方米的平均综合费用为多少元?13．（连云港市2012-2013学年度第一学期高三期末考试数学试卷）某单位决定对本单位职工实行年医疗费用报销制度,拟制定年医疗总费用在2万元至10万元(包括2万元和10万元)的报销方案,该方案要求同时具备下列三个条件:①报销的医疗费用y (万元)随医疗总费用x (万元)增加而增加;②报销的医疗费用不得低于医疗总费用的50%;③报销的医疗费用不得超过8万元.(1)请你分析该单位能否采用函数模型y =0.05(x 2+4x +8)作为报销方案;(2)若该单位决定采用函数模型y =x -2ln x +a (a 为常数)作为报销方案,请你确定整数a 的值.(参考数据:ln2≈0.69,ln10≈2.3)14．（徐州、宿迁市2013届高三年级第三次模拟考试数学试卷）已知一块半径为r 的残缺的半圆形材料ABC ,O 为半圆的圆心,12OC r =,残缺部分位于过点C 的竖直线的右侧.现要在这块材料上截出一个直角三角形,有两种设计方案:如图甲,以BC 为斜边;如图乙,直角顶点E 在线段OC 上,且另一个顶点D 在AB 上.要使截出的直角三角形的面积最大,应该选择哪一种方案?请说明理由,并求出截得直角三角形面积的最大值.15．（常州市2013届高三教学期末调研测试数学试题）第八届中国花博会将于2013年9月在常州举办,展览园指挥中心所用地块的形状是大小一定的矩形ABCD ,BC a =,CD b =.a ,b 为常数且满足b a <.组委会决定从该矩形地块中划出一个直角三角形地块AEF 建游客休息区(点E ,F 分别在线段AB ,AD 上),且该直角三角形AEF 的周长为(2l b >),如图.设AE x =,△AEF 的面积为S . (1)求S 关于x 的函数关系式;(2)试确定点E 的位置,使得直角三角形地块AEF 的面积S 最大,并求出S 的最大值.（第17题甲图）（第17题乙图）16．（南京市、盐城市2013届高三第三次模拟考试数学试卷）将一张长8cm,宽6cm的长方形的纸片沿着一条直线折叠,折痕(线段)将纸片分成两部分,面积分别为S1cm2,S2cm2,其中S1≤S2.记折痕长为l cm.(1)若l=4,求S1的最大值;(2)若S1∶S2=1∶2,求l的取值范围.参考答案1．（南通市2013届高三第一次调研测试数学试卷）解:(1)由题意,AB x =,2BC x =-.因2x x >-,故12x << 设DP y =,则PC x y =-. 因△ADP ≌△CB P ',故PA PC x y ==-.由222PA AD DP =+,得 2221()(2)2(1)x y x y y x-=-+⇒=-,12x <<(2)记△ADP 的面积为1S ,则 11(1)(2)S x x =--23()2x x=-+≤-,当且仅当x =,S 1取得最大值米,宽为2-米时,节能效果最好 (3)记△ADP 的面积为2S ,则 221114(2)(1)(2)3()22S x x x x x x=-+--=-+,12x << 于是,3222142(2)02x S x x x x-+'=--==⇒= 关于x 的函数2S在上递增,在上递减.所以当x =时,2S 取得最大值米,宽为2米时,制冷效果最好本题主要考查应用所学数学知识分析问题与解决问题的能力.试题以常见的图形为载体,再现对基本不等式、导数等的考查.讲评时,应注意强调解决应用问题的一般步骤与思维规律,教学中应帮助学生克服解决应用题时的畏惧心理,在学生独立解决应用问题的过程中不断增强他们的自信心.在使用基本不等式应注意验证取等号的条件,使用导数时应谨慎决断最值的取值情况.2 ．（南京市、盐城市2013届高三年级第一次模拟考试数学试题）】解: (1) (0)C 的实际意义是安装这种太阳能电池板的面积为0时的用电费用, 即未安装电阳能供电设备时全村每年消耗的电费 [来源:学科网ZXXK]由(0)24100k C ==,得2400k = 所以24001800150.50.5,0201005F x x x x x =⨯+=+≥++(2)因为18000.5(5)0.250.2559.755F x x =++-≥-=+当且仅当18000.5(5)5x x =++,即55x =时取等号，所以当x 为55平方米时, F 取最小值为59.75万元 (说明:第(2)题用导数可最值,类似给分)3 ．（苏州市2012-2013学年度第一学期高三期末考试数学试卷）BCD（第17题）B 'P4 ．(1)设MN 交AD 交于Q 点∵∠MQD =30°,∴MQ =21,OQ =23(算出一个得2分) S △PMN =21MN ·AQ =21×23×(1+23)=8336+ (2)设∠MOQ =θ,∴θ∈[0,2π],MQ =sin θ,OQ =cos θ ∴S △PMN =21MN ·AQ =21(1+sin θ)(1+cos θ)=21(1+sin θcos θ+sin θ+cos θ) 令sin θ+cos θ=t ∈[1,2],∴S △PMN =21(t +1+212-t ) θ=4π,当t =2,∴S △PMN 的最大值为4223+ 5 ．⑴作AE ⊥CD ,垂足为E ,则9CE =,6DE =,设BC x =,则tan tan tan tan()1tan tan CAE DAE CAD CAE DAE CAE DAE ∠∠∠=∠∠=-∠⨯∠++ 961961x x x x==-⋅+,化简得215540x x --=,解之得,18x =或3x =-(舍) 答:BC 的长度为18m⑵设BP t =,则18(018)CP t t =-<<, 2291516266(27)18tan()9151813518135118t t t t t t t t t tαβ-===-----⋅-++++++设227()18135tf t t t =--++,222542723()(18135)t t f t t t -⨯'=-++,令()0f t '=,因为018t <<,得27t =,当27)t ∈时,()0f t '<,()f t 是减函数;当27,18)t ∈ 时,()0f t '>,()f t 是增函数,所以,当27t =时,()f t 取得最小值,即tan()αβ+取得最小值, 因为2181350t t --<+恒成立,所以()0f t <,所以tan()0αβ<+,(,)2αβπ∈π+, 因为tan y x =在(,)2ππ上是增函数,所以当27t =时,αβ+取得最小值. 答:当BP 为27)m 时,αβ+取得最小值 67 ．（南京市、淮安市2013届高三第二次模拟考试数学试卷）【答案】8 ．（江苏省苏锡常镇四市2013届高三教学情况调研(一)数学试题）9 ．（江苏省泰州、南通、扬州、宿迁、淮安五市2013届高三第三次调研测试数学试卷）解:(1)设单层玻璃和双层中空玻璃单位时间内,在单位面积上通过的热量分别为1Q ,2Q ,则312121410T T T T Q ---=⨯⋅=, 3431112222410 2.51041044T T T T T T Q x ---''''---=⨯⋅=⨯⋅=⨯⋅ 11122234344410 2.510410T T T T T T x ---''''---===⨯⨯⨯ 11122234344410 2.510410T T T T T T x ---''''-+-+-=++⨯⨯⨯12T T -=(2)由(1)知21121Q Q x =+, 当1=4%时,解得12x =(mm). 答:当12x =mm 时,双层中空玻璃通过的热量只有单层玻璃的4%10．（江苏省盐城市2013届高三年级第二次模拟考试数学试卷）【答案】解: (1)由题在ACD ∆中,2,,10,333CAD ADC AC ACD πππα∠=∠==∠=-. 由正弦定理知102sin sin sin 33CD AD ππαα==⎛⎫- ⎪⎝⎭,得210sin 3sin CD AD πα⎛⎫- ⎪⎝⎭==240sin 348121248080sin S AD BD CD CD AD παα⎛⎫- ⎪⎝⎭∴=++=-+=+26033x ππ⎛⎫=+<< ⎪⎝⎭(2)'S =,令'0S =,得1cos 3α= 当1cos 3α>时,'0S <;当1cos 3α<时,'0S >,∴当1cos 3α=时S 取得最小值此时5sin sin 53sin 4AD αααα+===+∴中转站距A处204+千米时,运输成本S 最小 11．（2012-2013学年度苏锡常镇四市高三教学情况调研（二）数学试题）12．（扬州、南通、泰州、宿迁四市2013届高三第二次调研测试数学试卷）【解】(1)如果每幢楼为5层,那么所有建筑面积为10×1 000×5平方米,所有建筑费用为[(k +800)+(2k +800)+(3 k +800)+(4k +800)+(5k +800)]×1 000×10,所以,1270=16 000 000+［(k +800)+(2k +800)+(3k +800)+(4k +800)+(5k +800)］×1 000×1010×1 000×5,解之得:k =50(2)设小区每幢为n (n ∈N*)层时,每平方米平均综合费用为f (n ),由题设可知f (n ) =16 000 000+［(50 +800)+(100 +800)+…+(50n +800)］×1 000×1010×1 000×n=1 600n+25n +825≥2 1 600×25+825=1225(元)当且仅当1 600n=25n ,即n =8时等号成立答:该小区每幢建8层时,每平方米平均综合费用最低,此时每平方米平均综合费用为1 225元13．【答案】【解】(1)函数y =0.05(x 2+4x +8)在[2,10]上是增函数,满足条件①,当x =10时,y 有最大值7.4万元,小于8万元,满足条件③ 但当x =3时,y =2920<32,即y ≥x2不恒成立,不满足条件②,故该函数模型不符合该单位报销方案(2)对于函数模型y =x -2ln x +a ,设f (x )= x -2ln x +a ,则f ´(x )=1-2x =x －2x≥0.所以f (x )在[2,10]上是增函数,满足条件①,由条件②,得x -2ln x +a ≥x 2,即a ≥2ln x -x2在x ∈[2,10]上恒成立,令g (x )=2ln x -x 2,则g ´(x )=2x －12=4－x2x,由g ´(x )>0得x <4,∴g (x )在(0,4)上增函数,在(4,10)上是减函数.∴a ≥g (4)=2ln4-2=4ln2-2由条件③,得f (10)=10-2ln10+a ≤8,解得a ≤2ln10-2另一方面,由x -2ln x +a ≤x ,得a ≤2ln x 在x ∈[2,10]上恒成立, ∴a ≤2ln2,综上所述,a 的取值范围为[4ln2-2,2ln2], 所以满足条件的整数a 的值为114．（徐州、宿迁市2013届高三年级第三次模拟考试数学试卷）【答案】如图甲,设DBC α∠=, 则3cos 2r BD α=,3sin 2r DC α=, 所以29sin 216BDC S r α=△ 2916r ≤, 当且仅当π4α=时取等号, 此时点D 到BC 的距离为34r ,可以保证点D 在半圆形材料ABC 内部,因此按照图甲方案得到直角三角形的最大面积为2916r如图乙,设EOD θ∠=,则cos OE r θ=,sin DE r θ=, 所以21(1cos )sin 2BDE S r θθ=+△,ππ[,]32θ∈设21()(1cos )sin 2f r θθθ=+,则21()(1cos )(2cos 1)2f r θθθ'=+-,当ππ[,]32θ∈时,()0f θ'≤,所以π3θ=时,即点E 与点C 重合时,BDE △222916r >,所以选择图乙的方案,截得的直角三角形面积最大,215．（常州市2013届高三教学期末调研测试数学试题）解:(1)设AF y =,则x y l +=,整理,得222()l lx y l x -=- 2(2)4(12)l l x S lx x xy --==,](0,x b ∈（第17题甲图）（第17题乙图）(2)()()]22'22242,(0,44l x lx l l S x x x b x l x l ⎛⎫⎛⎫-+=⋅=⋅-∈ ⎪ ⎪ ⎪ ⎪--⎝⎭⎝⎭∴当b ≤时,'0S >,S 在](0,b 递增,故当x b =时,()()max 24bl b l S b l -=-;当b >时,在x ⎛⎫∈ ⎪ ⎪⎝⎭上,'0S >,S 递增,在,x b ⎫∈⎪⎪⎭上,'0S <,S 递减,故当x =时,2max S =. 16．（南京市、盐城市2013届高三第三次模拟考试数学试卷）解如图所示,不妨设纸片为长方形ABCD ,AB =8cm,AD =6cm,其中点A 在面积为S 1的部分内. 折痕有下列三种情形:①折痕的端点M ,N 分别在边AB ,AD 上;②折痕的端点M ,N 分别在边AB ,CD 上; ③折痕的端点M ,N 分别在边AD ,BC 上.(1)在情形②､③中MN ≥6,故当l =4时,折痕必定是情形①.设AM =x cm,AN =y cm,则x 2+y 2=16因为x 2+y 2≥2xy ,当且仅当x =y 时取等号,所以S 1=12xy ≤4,当且仅当x =y =22时取等号.即S 1的最大值为4(2)由题意知,长方形的面积为S =6×8=48. 因为S 1∶S 2=1∶2,S 1≤S 2,所以S 1=16,S 2=32.当折痕是情形①时,设AM =x cm,AN =y cm,则12xy =16,即y =32x .由⎩⎪⎨⎪⎧0≤x ≤8，0≤32x≤6，得163≤x ≤8.所以l =x 2＋y 2=x 2＋322x 2,163≤x ≤8设f (x )=x 2+322x 2,x >0,则f ′(x )=2x -2×322x 3=2(x 2＋32)(x ＋42)(x －42)x3,x >0.故 x 163 (163,42) 4 2 (42,8)8 f ′(x )-+ f (x )6449↘ 64↗80所以f (x )的取值范围为[64,80],从而l 的范围是[8,45]; 当折痕是情形②时,设AM =x cm,DN =y cm,则12(x +y )×6=16,即y =163-x .由⎩⎪⎨⎪⎧0≤x ≤8，0≤163－x ≤8，得0≤x ≤163.所以l =62＋(x －y )2=62＋4(x －83)2,0≤x ≤163.ABCD （情形①）MNABCD （情形②）MNABCD （情形③）MN所以l 的范围为[6,21453];当折痕是情形③时,设BN =x cm,AM =y cm,则12(x +y )×8=16,即y =4-x .由⎩⎨⎧0≤x ≤6，0≤4－x ≤6，得0≤x ≤4.所以l =82＋(x －y )2=82＋4(x －2)2,0≤x ≤4. 所以l 的取值范围为[8,45].综上,l 的取值范围为[6,45]。

安徽省宿州市泗县二中2013届高三上学期第二次月考数学理试题Word版含答案

宿州市泗县二中2013届高三上学期第二次月考数学（理）试题一、选择题（每小题5分，共60分。

【解析版】江苏省盐城市2013届高三第二次模拟(3月)考试数学试题

名师远程辅导互动平台网址：
1
一、填空题：本大题共14小题，每小题5分，计70分．不需写出解题过程，请把答案写在答题纸的指定
位置上． 1．（5分）（2013•盐城二模）若集合A={1，m ﹣2}，且A ∩B={2}，则实数m 的值为 4 ．
2．（5分）（2013•盐城二模）若复数z 满足（1﹣i ）z=2（i 为虚数单位），则|z|= ．
故答案为．3．（5分）（2013•盐城二模）现有在外观上没有区别的5件产品，其中3件合格，2件不合格，从中任意抽检2件，则一件合格，另一件不合格的概率为
．
有另一件不合格的抽法有
P=故答案为．4．（5分）（2013•盐城二模）已知正六棱锥的底面边长是3，侧棱长为5，则该正六棱锥的体积是．
名师远程辅导互动平台
网址：
2 ××故棱锥的高为=4
V=
=
故答案为：5．（5分）（2013•盐城二模）若，
是两个单位向量，
，
，且⊥，则
，
的夹角为
．
＜
，﹣，）﹣，
＞﹣，
＞．再由＜，
，可得＜，
，．6．（5分）（2013•盐城二模）如图，该程序运行后输出的结果为 16 ．
名师远程辅导互动平台网址：
3
7．（5分）（2013•盐城二模）函数
，x ∈[﹣π，0]的单调递增区间为．
∈，﹣
，﹣﹣﹣
，﹣
，则，﹣
﹣，﹣
∴由﹣≤≤得：≤）在﹣
，8．（5分）（2013•盐城二模）若等比数列{a n }满足a m ﹣3=4且
（m ∈N *
且m ＞4），则a 1a 5的值
为 16 ．。

2010-2023历年江苏省宿豫中学高三第二次模拟考试物理试卷

2010-2023历年江苏省宿豫中学高三第二次模拟考试物理试卷第1卷一.参考题库(共20题)1.总质量为M的火箭被飞机释放时的速度为，方向水平。

释放后火箭立即向后以相对于地面的速率u喷出质量为m的燃气，火箭相对于地面的速度变为多大？2.近年来，酒驾几乎成为一种“社会公害”。

2011年2月25日十一届全国人大常委会在京闭幕，会议通过了刑法修正案，将醉酒驾车列为犯罪。

交警用来检测酒驾的酒精测试仪的工作原理如图所示，其中P是半导体型酒精气体传感器，该传感器的电阻的倒数与酒精气体的浓度C成正比，为定值电阻。

以下关于电流表的示数与酒精气体浓度C之间关系的图象，正确的是( )3.如图甲所示，光滑且足够长的平行金属导轨MN、PQ固定在同一水平面上，两导轨间距L＝0.30 m．导轨电阻忽略不计，其间连接有固定电阻R＝0.40 Ω.导轨上停放一质量m＝0.10 kg、电阻r＝0.20Ω的金属杆ab，整个装置处于磁感应强度B＝0.50T的匀强磁场中，磁场方向竖直向下．用一外力F沿水平方向拉金属杆ab，使之由静止开始运动，电压传感器可将R两端的电压U即时采集并输入电脑，获得电压U随时间t变化的关系如图乙所示．(1)利用上述条件证明金属杆做匀加速直线运动，并计算加速度的大小；(2)求第2 s末外力F的瞬时功率；(3)如果水平外力从静止开始拉动杆2 s所做的功W＝0.35J,求金属杆上产生的焦耳热．4.以下说法正确是▲A．满足能量守恒定律的宏观过程都是可以自发进行的B．熵是物体内分子运动无序程度的量度C．若容器中用活塞封闭着刚好饱和的一些水汽，当保持温度不变向下缓慢压活塞时，水汽的质量减少，密度不变D．当分子间距离增大时，分子间引力增大，而分子间斥力减少5.如图，一集热箱里面封闭着一定量的气体，集热板作为箱的活塞且始终正对着太阳，其面积为S，在t时间内集热箱里气体膨胀对外做功数值为W，其内能增加了△U，不计封闭气体向外散的热，已知照射到集热板上太阳光的能量有5 0%被箱内气体吸收求：①这段时间内集热箱里气体共吸收的热量；②太阳光照在集热板单位面积上的辐射功率。

【推荐】江苏省13大市2013年高三历次考试数学试题分类汇编8立体几何

【推荐】江苏省13大市2013年高三历次考试数学试题分类汇编8：立体几何一、填空题1 ．（苏州市2012-2013学年度第一学期高三期末考试数学试卷）如图,在长方体1111ABCD A B C D -中,3AB AD cm ==,12AA cm =,则三棱锥11A B D D -的体积为_______3cm .A 1B 1DC B AD 1C 1【答案】3 2 ．（江苏省盐城市2013届高三年级第二次模拟考试数学试卷）已知正六棱锥的底面边长是3,侧棱长为5,则该正六棱锥的体积是________.【答案】3 ．（扬州、南通、泰州、宿迁四市2013届高三第二次调研测试数学试卷）若将一个圆锥的侧面沿一条母线剪开,其展开图是半径为2 cm 的半圆,则该圆锥的高为____cm.【答案】4 ．（南京市、淮安市2013届高三第二次模拟考试数学试卷）已知圆锥的侧面展开图是一个半径为3cm,圆心角为23π的扇形,则此圆锥的高为___cm.【答案】5 ．（徐州、宿迁市2013届高三年级第三次模拟考试数学试卷）已知三棱锥P ABC -的所有棱长都相等,现沿PA ,PB ,PC 三条侧棱剪开,将其表面展开成一个平面图形,若这个平面图形外接圆的半径为则三棱锥P ABC -的体积为____.【答案】9;6 ．（江苏省泰州市2012-2013学年度第一学期期末考试高三数学试题）在空间中,用a,b,c 表示三条不同的直线,γ表示平面,给出下列四个命题:(1)若,a b b c ,则a c (2)若,a b b c ⊥⊥,则a c ⊥(3) 若a γ,b γ,则a b (4)若a γ⊥,b γ⊥,则a b【答案】①④7 ．（江苏省苏锡常镇四市2013届高三教学情况调研(一)数学试题）已知,m 是两条不同的直线,α,β是两个不同的平面,有下列四个命题:①若l β⊂,且αβ⊥,则l α⊥;②若l β⊥,且//αβ,则l α⊥;③若l β⊥,且αβ⊥,则//l α;④若m αβ=,且//l m ,则//l α.则所有正确命题的序号是_________.【答案】②8 ．（扬州市2012-2013学年度第一学期期末检测高三数学试题）设a b 、是两条不同的直线,α、β是两个不同的平面,则下列四个命题①若,a b a α⊥⊥,则//b α,②若,a βαβ⊥⊥,则//a α, ③若βαβα⊥⊥则,,//a a④若,,a b a b αβ⊥⊥⊥,则αβ⊥, 其中正确的命题序号是____.【答案】③④;9 ．（常州市2013届高三教学期末调研测试数学试题）给出下列命题:(1)若一个平面经过另一个平面的垂线,那么这两个平面相互垂直;(2)若一个平面内的两条直线与另一个平面都平行,那么这两个平面相互平行;(3)若两条平行直线中的一条垂直于直线m ,那么另一条直线也与直线m 垂直;(4)若两个平面垂直,那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直. 其中,所有真命题的序号为______.【答案】()1、()3、()410．（苏北三市（徐州、淮安、宿迁）2013届高三第二次调研考试数学试卷）若一个长方体的长、宽、高分别为3、2、1,则它的外接球的表面积是_____.【答案】6π11．（连云港市2012-2013学年度第一学期高三期末考试数学试卷）已知正方形ABCD 的边长为2,E ,F 分别为BC ,DC 的中点,沿AE ,EF ,AF 折成一个四面体,使B ,C ,D 三点重合,则这个四面体的体积为_________.【答案】13;12．（连云港市2012-2013学年度第一学期高三期末考试数学试卷）二维空间中,圆的一维测度(周长)l =2πr ,二维测度(面积)S =πr 2;三维空间中,球的二维测度(表面积)S =4πr 2,三维测度(体积)V =43πr 3.应用合情推理,若四维空间中,“超球”的三维测度V =8πr 3,则其四维测度W =____.【答案】2πr 4;13．（南京市、盐城市2013届高三年级第一次模拟考试数学试题）现有如下命题:①过平面外一点有且只有一条直线与该平面垂直;②过平面外一点有且只有一条直线与该平面平行;③如果两个平行平面和第三个平面相交, 那么所得的两条交线平行;④如果两个平面相互垂直, 那么经过第一个平面内一点且垂直于第二个平面的直线必在第一个平面内.则所有真命题的序号是 .【答案】①③④14．（南京市、盐城市2013届高三第三次模拟考试数学试卷）已知m ,n 是两条不同的直线,α,β是两个不同的平面.①若m ⊂α,m ⊥β,则α⊥β; ②若m ⊂α,α∩β=n ,α⊥β,则m ⊥n ;③若m ⊂α,n ⊂β,α∥β,则m ∥n ; ④若m ∥α,m ⊂β,α∩β=n ,则m ∥n .上述命题中为真命题的是________(填写所有真命题的序号).【答案】①④15．（南通市2013届高三第一次调研测试数学试卷）已知正四棱锥的底面边长是6,这个正四棱锥的侧面积是________.【答案】答案:48.考查常见几何体的表面积与体积的计算.应熟练掌握常见几何体的表面积的计算,灵活应用等体积法计算点面距16．（2012-2013学年度苏锡常镇四市高三教学情况调研（二）数学试题）在矩形ABCD 中,对角线AC 与相邻两边所成的角为α,β,则22cos cos 1αβ+=.类比到空间中一个正确命题是:在长方体1111ABCD A B C D -中,对角线1AC 与相邻三个面所成的角为α,β,γ,则有__________.【答案】222cos cos cos 2αβγ++=二、解答题17．（连云港市2012-2013学年度第一学期高三期末考试数学试卷）【答案】以O点为原点,OB为x轴,OC为y轴,OS为z轴建立空间直角坐标系.由题意知∠SBO=45°,SO=3.∴O(0,0,0),CA(0,,0),S(0,0,3),B(3,0,0).(1)设BD=λBS(0≤λ≤1),则BD=(1-λ)OB+λOS=(3(1-λ),0,3λ),所以CD=(3(1-λ),,3λ).因为ABCD⊥AB,所以CD AB⋅=9(1-λ)-3=0,解得λ=23.故SDDB=12时, CD⊥AB(2)平面ACB 的法向量为n 1=(0,0,1),设平面SBC 的法向量n 2=(x ,y ,z ),则⎩⎨⎧3x -3z =03y -3z =0,解得⎩⎨⎧x =z y =3z,取n 2所以cos<n 1,n 2=又显然所求二面角的平面角为锐角,18．（苏州市2012-2013学年度第一学期高三期末考试数学试卷）三棱柱111ABC A B C -在如图所示的空间直角坐标系中,已知2AB =,4AC =,13AA =.D 是BC 的中点.(1)求直线1DB 与平面11AC D 所成角的正弦值;(2)求二面角111B A D C --的大小的正弦值.【答案】-的底面19．（2012-2013学年度苏锡常镇四市高三教学情况调研（二）数学试题）已知四棱锥S ABCD ABCD是边长为2的正方形,侧面SAB是等边三角形,侧面SCD是以CD为斜边的直角三角形,E 为CD的中点,M为SB的中点.CM平面SAE;(2)求证:SE⊥平面SAB;(1)求证://-的体积.(3)求三棱锥S AEDB【答案】20．（南京市、盐城市2013届高三第三次模拟考试数学试卷）如图,三棱锥P-ABC中,已知PA⊥平面ABC,△ABC是边长为2的正三角形,D,E分别为PB,PC中点.(1)若PA=2,求直线AE与PB所成角的余弦值;(2)若平面ADE⊥平面PBC,求PA的长.ABC EDP（第22题）【答案】解(1)如图,取AC 的中点F ,连接BF ,则BF ⊥AC .以A 为坐标原点过A 且与FB 平行的直线为x 轴,AC 为y 轴,AP 为z 轴,建立空间直角坐标系. 则A (0,0,0),B (3,1,0),C (0,2,0),P (0,0,2),E (0,1,1),从而→PB =(3,1,-2), →AE =(0,1,1).设直线AE 与PB 所成角为θ,则cos θ=|→PB ·→AE |→PB |×|→AE ||=14. 即直线AE 与PB 所成角的余弦值为14(2)设PA 的长为a ,则P (0,0,a ),从而→PB =(3,1,-a ),→PC =(0,2,-a ).设平面PBC 的法向量为n 1=(x ,y ,z ),则n 1·→PB =0,n 1·→PC =0, 所以3x +y -az =0,2y -az =0.令z =2,则y =a ,x =33a . 所以n 1=(33a ,a ,2)是平面PBC 的一个法向量. 因为D ,E 分别为PB ,PC 中点,所以D (32,12,a 2),E (0,1,a 2), 则→AD =(32,12,a 2),→AE =(0,1,a 2). 设平面ADE 的法向量为n 2=(x ,y ,z ),则n 2·→AD =0,n 2·→AE =0.（第22题）所以32x +12y +a 2z =0,y +a 2z =0. 令z =2,则y =-a ,x =-33a . 所以n 2=(-33a ,-a ,2)是平面ADE 的一个法向量因为面ADE ⊥面PBC ,所以n 1⊥n 2,即n 1·n 2=(33a ,a ,2)·(- 33a ,-a ,2)=-13a 2-a 2+4=0, 解得a =3,即PA 的长为 321．（扬州市2012-2013学年度第一学期期末检测高三数学试题）如图,在四棱锥P ABCD -中,PA ⊥平面ABCD , AC BD ⊥于O .(Ⅰ)证明:平面PBD ⊥平面PAC ;(Ⅱ)设E 为线段PC 上一点,若AC BE ⊥,求证://PA 平面BED【答案】(Ⅰ)证:因为PA ⊥平面ABCD ,BD ⊂平面ABCD ,PA BD ∴⊥又AC BD ⊥,,PA AC 是平面PAC 内的两条相交直线,BD ∴⊥平面PAC ,而BD ⊂平面PBD ,所以平面PBD ⊥平面PAC(Ⅱ)证:AC BE ⊥,AC BD ⊥,BE 和BD 为平面BED 内两相交直线,AC ∴⊥平面BED ,连接EO ,EO ⊂平面BED ,AC EO ∴⊥,PA ⊥平面ABCD ,AC ⊂平面ABCD ,AC PA ∴⊥,又,,AC PA EO 共面,//EO PA ∴,又PA ⊄平面BED ,EO ⊂平面BED ,//PA ∴平面BED22．（江苏省苏锡常镇四市2013届高三教学情况调研(一)数学试题）如图,圆锥的高4PO =,底面半径2OB =,D 为PO 的中点,E 为母线PB 的中点,F 为底面圆周上一点,满足EF DE ⊥.(1)求异面直线EF 与BD 所成角的余弦值; (2)求二面角O DF E --的正弦值.【答案】OED A F BP23．（连云港市2012-2013学年度第一学期高三期末考试数学试卷）如图,在直三棱柱ABC -A 1B 1C 1中,AB =AC ,点D 为BC 中点,点E 为BD 中点,点F 在AC 1上,且AC 1=4AF .(1)求证:平面ADF ⊥平面BCC 1B 1;(2)求证:EF //平面ABB 1A 1.【答案】证明:(1) 因为直三棱柱ABC -A 1B 1C 1,所以CC 1⊥平面ABC ,而AD ⊂平面ABC , 所以CC 1⊥AD又AB =AC ,D 为BC 中点,所以AD ⊥BC ,因为BC ⋂CC 1=C ,BC ⊂平面BCC 1B 1,CC 1⊂平面BCC 1B 1,所以AD ⊥平面BCC 1B 1,因为AD ⊂平面ADF ,所以平面ADF ⊥平面BCC 1B 1(2) 连结CF 延长交AA 1于点G ,连结GB .因为AC 1=4AF ,AA 1//CC 1,所以CF =3FG ,又因为D 为BC 中点,点E 为BD 中点,所以CE =3EB ,所以EF //GB ,而EF ⊄平面ABBA 1,GB ⊂平面ABBA 1,所以EF //平面ABBA 1A BCC 1A 1B 1FE D (第16题图)24．（江苏省泰州、南通、扬州、宿迁、淮安五市2013届高三第三次调研测试数学试卷）如图,在四棱锥P ABCD -中,底面ABCD 是矩形,四条侧棱长均相等.(1)求证:AB //平面PCD ; (2)求证:平面PAC ⊥平面ABCD .【答案】证明:(1)在矩形ABCD 中,//AB CD ,又AB ⊄平面PCD ,CD ⊂平面PCD ,所以AB //平面PCD(2)如图,连结BD ,交AC 于点O ,连结PO ,在矩形ABCD 中,点O 为 AC BD ，的中点,又PA PB PC PD ===,故PO AC ⊥,PO BD ⊥,又AC BD O =I ,AC BD ，⊂平面ABCD ,所以PO ⊥平面ABCD ,又PO ⊂平面PAC ,所以平面PAC ⊥平面ABCD25．（江苏省无锡市2013届高三上学期期末考试数学试卷）如图,四棱锥P-A BCD 中,底面ABCD 为菱形,BD⊥面PAC,A C=10,PA=6,cos∠PCA=45,M 是PC 的中点. (Ⅰ)证明PC⊥平面BMD; ABC （第15题）PD O A BCC 1A 1B 1 FE D G(Ⅱ)若三棱锥M-BCD 的体积为14,求菱形ABCD 的边长.【答案】26．（扬州、南通、泰州、宿迁四市2013届高三第二次调研测试数学试卷）必做题, 本小题10分.解答时应写出文字说明、证明过程或演算步骤.如图,在三棱柱111ABC A B C -中,1A B ABC ⊥平面,AB AC ⊥,且12AB AC A B ===.(1)求棱1AA 与BC 所成的角的大小;(2)在棱11B C 上确定一点P ,使二面角1P AB A --.【答案】【解】(1)如图,以A 为原点建立空间直角坐标系,则 ()()()()11200020022042C B A B ，，，，，，，，，，，, （第22题） B ACA 1B 1C 1()1022AA =，，,()11220BC B C ==-，，. 1111cos 28AA BCAA BC AA BC ⋅〈〉===-⋅，, 故1AA 与棱BC 所成的角是π3(2)P 为棱11B C 中点,设()111220B P B C λλλ==-，，,则()2422P λλ-，，.设平面PAB 的法向量为n 1(),,x y z =,()=2422AP λλ-，，, 则1103202000AP x y z z x y y AB λ⎧⋅=++==-⎧⎧⎪⇒⇒⎨⎨⎨==⋅=⎩⎩⎪⎩，，，．n n 故n 1()10λ=-，，而平面1ABA 的法向量是n 2=(1,0,0),则121212cos ,⋅〈〉===⋅n n n n n n 解得12λ=,即P 为棱11B C 中点,其坐标为()132P ，，．27．（南京市、淮安市2013届高三第二次模拟考试数学试卷）如图,在四棱锥P-ABCD中,底面ABCD 是直角梯形,AD//BC,PB ⊥平面ABCD,CD ⊥BD,PB=AB=AD=1,点E 在线段PA 上,且满足PE=2EA.(1)求三棱锥E-BAD 的体积; (2)求证:PC//平面BDE.【答案】C 128．（江苏省泰州市2012-2013学年度第一学期期末考试高三数学试题）在三棱锥S-ABC中,SA⊥平面(1)求证:BC⊥AM(2)若AM⊥平面SBC,求证:EM平面ABS【答案】(1)∵AB =AC ,D 是BC 的中点,∴AD ⊥BC ,AM BC SAD AM SAD BC A SA AD BC SA ABC BC ABC SA ⊥⇒⎭⎬⎫⊂⊥⇒⎭⎬⎫=⋂⊥⇒⎭⎬⎫⊂⊥面平面面面 (证到SA⊥平面SAD 得5分)(2)∵AM ⊥面SAB , ⇒AM ⊥SD ,⇒⎭⎬⎫==DE AE MD SM 44⎪⎭⎪⎬⎫⊆⊄平面平面SA ABS //ME SAME ⇒EM ∥面ABS (证到SM =4MD 得10分,得到ME ‖SA 得12分.)29．（徐州、宿迁市2013届高三年级第三次模拟考试数学试卷）如图,AB ,CD 均为圆O 的直径,CE ⊥圆O 所在的平面,BF CE .求证:⑴平面BCEF ⊥平面ACE ;⑵直线DF 平面ACE .F（第15题图）【答案】⑴因为CE ⊥圆O 所在的平面,BC ⊂圆O 所在的平面,所以CE BC ⊥,因为AB 为圆O 的直径,点C 在圆O 上,所以AC BC ⊥,因为AC CE C =,,AC CE ⊂平面ACE ,所以BC ⊥平面ACE ,因为BC ⊂平面BCEF ,所以平面BCEF ⊥平面ACE⑵由⑴AC BC ⊥,又因为CD 为圆O 的直径,所以BD BC ⊥,因为,,AC BC BD 在同一平面内,所以AC BD ,因为BD ⊄平面ACE ,AC ⊂平面ACE ,所以BD 平面ACE因为BF CE ,同理可证BF 平面ACE ,因为BD BF B =,,BD BF ⊂平面BDF ,所以平面BDF 平面ACE ,因为DF ⊂平面BDF ,所以DF 平面ACE30．（扬州、南通、泰州、宿迁四市2013届高三第二次调研测试数学试卷）如图,在四棱锥P ABCD -中,平面PAB ⊥平面ABCD ,BC //平面PAD ,PBC ∠90=,90PBA ∠≠.求证:(1)//AD 平面PBC ; (2)平面PBC ⊥平面PAB .【答案】【证】(1)因为BC //平面PAD ,而BC ⊂平面ABCD ,平面ABCD I 平面PAD = AD ,所以BC //AD因为AD ⊄平面PBC ,BC ⊂平面PBC ,所以//AD 平面PBCA B P（第16题）D(2)自P 作PH ⊥AB 于H ,因为平面PAB ⊥平面ABCD ,且平面PAB I 平面ABCD =AB ,所以PH ⊥平面ABCD因为BC ⊂平面ABCD ,所以BC ⊥PH .因为PBC ∠90=,所以BC ⊥PB ,而90PBA ∠≠,于是点H 与B 不重合,即PB I PH = H .因为PB ,PH ⊂平面PAB ,所以BC ⊥平面PAB因为BC ⊂平面PBC ,故平面PBC ⊥平面A B31．（徐州、宿迁市2013届高三年级第三次模拟考试数学试卷）【必做题】本小题10分.解答时应写出文字说明、证明过程或演算步骤.如图,在正三棱柱111ABC A B C -中,已知16AA =,2AB =,,M N 分别是棱1BB ,1CC 上的点,且4BM =,2CN =.⑴求异面直线AM 与11A C 所成角的余弦值;⑵求二面角1M AN A --的正弦值.【答案】⑴以AC 的中点为原点O ,分别以,OA OB 所在直线为,x z 轴,建立空间直角坐标系O xyz -(如图). 则(0,0,0)O ,(1,0,0)A ,(1,0,0)C -,B ,(1,2,0)N -,M ,1(1,6,0)A ,1(1,6,0)C -.所以(AM =-,11(2,0,0)A C =-.（第22题图） A BC A 1B 1C 1 M N AB PDH所以111111cos ,2AM A CAM A C AM A C <>===所以异面直线AM 与11A C⑵平面1ANA 的一个法向量为(0,0,1)=m .设平面AMN 的法向量为(,,)x y z =n ,因为(AM =-,(2,2,0)AN =-, 由,,AM AN ⎧⊥⎪⎨⊥⎪⎩n n 得40,220,x y x y ⎧-=⎪⎨-=⎪⎩+++令1x =,则(1,1,=n . 所以3cos,-<>===m n m n m n , 所以二面角1M AN A --的正弦值为532．（常州市2013届高三教学期末调研测试数学试题）如图,在四棱锥P -ABCD 中,PD ⊥底面ABCD ,AD ⊥AB ,CD ∥AB , 2AB ==,3CD =,直线PA 与底面ABCD 所成角为60°,点M 、N 分别是PA ,PB 的中点.(1)求证:MN ∥平面PCD ;(2)求证:四边形MNCD 是直角梯形;(3)求证:DN ⊥平面PCB .【答案】证明:(1)因为点M ,N 分别是P A ,PB 的中点,所以MN ∥AB因为CD ∥AB ,所以MN ∥CD .又CD ⊂平面PCD , MN ⊄平面PCD ,所以MN ∥平面PCD(2)因为AD ⊥AB ,CD ∥AB ,所以CD ⊥AD ,又因为PD ⊥底面ABCD ,CD ⊂平面ABCD ,所以CD ⊥PD ,又AD PD D =,所以CD ⊥平面PAD因为MD ⊂平面PAD ,所以CD ⊥MD ,所以四边形MNCD 是直角梯形(3)因为PD ⊥底面ABCD ,所以∠PAD 就是直线PA 与底面ABCD 所成的角,从而∠PAD = 60在Rt △PDA 中,AD =,PD =,PA =,MD =在直角梯形MNCD 中,1MN =,ND =3CD =,CN ==,从而222DN CN CD +=,所以DN ⊥CN在Rt △PDB 中,PD = DB, N 是PB 的中点,则DN ⊥PB 又因为PBCN N =,所以DN ⊥平面PCB33．（南京市、盐城市2013届高三第三次模拟考试数学试卷）如图,在正三棱柱ABC -A 1B 1C 1中,A 1A =2AC ,D ,E ,F 分别为线段AC ,A 1A ,C 1B 的中点.(1)证明:EF ∥平面ABC ;(2)证明:C 1E ⊥平面BDE .【答案】证明(1)如图,取BC 的中点G ,连结AG ,FG .因为F 为C 1B 的中点,所以FG ＝∥12C 1C . 在三棱柱ABC -A 1B 1C 1中,A 1A ＝∥C 1C ,且E 为A 1A 的中点, 所以FG ＝∥EA . 所以四边形AEFG 是平行四边形. （第16题） AB C DEC 1A 1B 1 F G A BC DEC 1A 1B 1 F（第16题）所以EF ∥AG因为EF ⊄平面ABC ,AG ⊂平面ABC , 所以EF ∥平面ABC(2)因为在正三棱柱ABC -A 1B 1C 1中,A 1A ⊥平面ABC ,BD ⊂平面ABC , 所以A 1A ⊥BD .因为D 为AC 的中点,BA =BC ,所以BD ⊥AC .因为A 1A ∩AC =A ,A 1A ⊂平面A 1ACC 1,AC ⊂平面A 1ACC 1,所以BD ⊥平面A 1ACC 1. 因为C 1E ⊂平面A 1ACC 1,所以BD ⊥C 1E根据题意,可得EB =C 1E =62AB ,C 1B =3AB , 所以EB 2+C 1E 2=C 1B 2.从而∠C 1EB =90°,即C 1E ⊥EB因为BD ∩EB =B ,BD ⊂平面BDE , EB ⊂平面BDE , 所以C 1E ⊥平面BDE34．（南通市2013届高三第一次调研测试数学试卷）如图,在正三棱柱ABC -A 1B 1C 1中,E 是侧面AA 1B 1B 对角线的交点,F 是侧面AA 1C 1C 对角线的交点,D 是棱BC 的中点.求证: (1)//EF 平面ABC ;(2)平面AEF ⊥平面A 1AD .【答案】解:(1)连结11A B A C 和.因为E F 、分别是侧面11AA B B 和侧面11AA C C 的对角线的交点, 所以E F 、分别是11A B A C 和的中点. 所以//EF BC又BC ⊂平面ABC 中,EF Ø平面ABC 中, 故//EF 平面ABC(2)因为三棱柱111ABC A B C -为正三棱柱,ABCDEF A 1B 1C 1(第15题)ABC DEF A 1B 1C 1(第15题)所以1A A ⊥平面ABC ,所以1BC A A ⊥. 故由//EF BC ,得1EF A A ⊥又因为D 是棱BC 的中点,且ABC ∆为正三角形,所以BC AD ⊥. 故由//EF BC ,得EF AD ⊥ 而1A AAD A =,1,A A AD ⊂平面1A AD ,所以EF ⊥平面1A AD又EF ⊂平面AEF ,故平面AEF ⊥平面1A AD \本题主要考查空间点线面的位置关系,考查逻辑推理能力以及空间想象能力.讲评时应注意强调规范化的表达.注意所用解题依据都应来自于课本的有关定义、公理、定理等.35．（苏州市2012-2013学年度第一学期高三期末考试数学试卷）如图,在三棱锥P ABC -中,BC ⊥平面PAB .已知PA AB =,点D ,E 分别为PB ,BC 的中点.(1)求证:AD ⊥平面PBC ;(2)若F 在线段AC 上,满足//AD 平面PEF ,求AFFC的值. APBCD EF【答案】36．（南京市、盐城市2013届高三年级第一次模拟考试数学试题）在直三棱柱111C B A ABC -中, AB BC ⊥,D 为棱1CC 上任一点.(1)求证:直线11A B ∥平面ABD ;(2)求证:平面ABD ⊥平面11BCC B .【答案】(1)证明:由直三棱柱111C B A ABC -,得11//A B AB而,EF ABD AB ABD ⊄⊂面面,所以直线EF ∥平面ABD(2)因为三棱柱111C B A ABC -为直三棱柱,所以1AB BB ⊥,又AB BC ⊥,而1BB ⊂面11BCC B ,BC ⊂面11BCC B ,且1BB BC B =,所以AB ⊥面11BCC B又AB ABD ⊂面,所以平面ABD ⊥平面11BCC B37．（江苏省盐城市2013届高三年级第二次模拟考试数学试卷）正三棱柱111C B A ABC -的所有棱长都为4,D 为的1CC 中点.(1)求证:1AB ⊥平面BD A 1;(2)求二面角B D A A --1的余弦值.【答案】解:取BC 中点O,连AO,∵ABC ∆为正三角形,∴BC AO ⊥,∵在正三棱柱111C B A ABC -中,平面ABC ⊥平面11B BCC ,∴⊥AD 平面11B BCC ,取11C B 中点为1O ,以O 为原点,,1OO ,的方向为,x y ,z 轴的正方向,建立空间直角坐标系,则)0,4,2(),32,0,0(),32,4,0(),0.2,2(),0,0,2(11B A A D B -.∴)32,4,2(),0,2,4(),32,4,2(11-=-=-BA AB ,∵00881=++-=⋅AB ,01216411=-+-=⋅AB . ∴BD AB ⊥1,11BA AB ⊥,∴⊥1AB 面BD A 1(2)设平面AD A 1的法向量为),,(z y x n =,)0,4,0(),32,2,2(1=--=AA AD .1,AA ⊥⊥,∴⎪⎩⎪⎨⎧=⋅=⋅01AA n AD n ,∴⎩⎨⎧==-+-0403222y z y x ,⇒⎩⎨⎧-==z x y 30,令1=z ,得)1,0,3(-=n 为平面AD A 1的一个法向量,由(1)知⊥1AB 面BD A 1,∴1AB 为平面AD A 1的法向量,462423232,cos 1-=⨯--=⋅>=<AB n , ∴二面角B D A A --1的余弦值为46-38．（江苏省苏锡常镇四市2013届高三教学情况调研(一)数学试题）如图,在三棱柱111A B C ABC -中,已知E ,F ,G 分别为棱AB ,AC ,11A C 的中点,090ACB ∠=,1A F ⊥平面ABC ,CH BG ⊥,H 为垂足.求证:(1)1//A E 平面GBC ; (2)BG ⊥平面ACH .C 1B1BHEF GC AA 1【答案】39．（扬州市2012-2013学年度第一学期期末检测高三数学试题）在四棱锥P ABCD -中,侧面PCD ⊥底面ABCD ,PD CD ⊥,底面ABCD 是直角梯形, //AB CD ,2ADC π∠=,1AB AD PD ===,2CD =.设Q 为侧棱PC 上一点,PQ PC λ=,试确定λ的值,使得二面角Q BD P --为45°.【答案】解:因为侧面PCD ⊥底面ABCD ,平面PCD平面ABCD CD =,PD CD ⊥,所以PD ⊥平面ABCD ,所以PD ⊥AD ,即三直线,,DA DC DP 两两互相垂直. 如图,以D 为坐标原点,,,DA DC DP 分别为,,x y z 轴建立直角坐标系, 则平面PBD 的一个法向量为(1,1,0)=-n , (0,2,1),,(0,1)PC PQ PC λλ=-=∈,所以(0,2,1)Q λλ-,设平面QBD 的一个法向量为(,,)a b c =m ,由0BD ⋅=m ,0DQ ⋅=m ,得⎧⎨⎩02(1)0a b b c λλ+=+-=,所以2(1,1,)1λλ=--m 所以||cos 45||||⋅=⋅m n m n ,= 注意到(0,1)λ∈,解得1λ=-40．（苏北三市（徐州、淮安、宿迁）2013届高三第二次调研考试数学试卷）如图,在四棱柱1111D C B A ABCD -中,已知平面⊥C C AA 11平面,ABCD 且3===CA BC AB ,1==CD AD .(1) 求证:;1AA BD ⊥(2) 若E 为棱BC 的中点,求证://AE 平面11D DCC .【答案】⑴在四边形ABCD 中,因为BA BC =,DA DC =,所以BD AC ⊥,又平面11AAC C ⊥平面ABCD ,且平面11AAC C平面ABCD AC =,BD ⊂平面ABCD ,所以BD ⊥平面11AA C C ,又因为1AA ⊂平面11AA C C ,所以1BD AA ⊥⑵在三角形ABC 中,因为AB AC =,且E 为BC 中点,所以BC AE ⊥, 又因为在四边形ABCD 中,AB BC CA ===1DA DC ==, 所以60ACB ∠=︒,30ACD ∠=︒,所以BC DC ⊥,所以AE DC ,因为DC ⊂平面11D DCC ,AE ⊄平面11D DCC ,所以AE平面11D DCC41．（江苏省盐城市2013届高三年级第二次模拟考试数学试卷）如图,在四棱锥P-ABCD中,PA=PB=PD=AB=BC=CD=DA=DB=2,E 为的PC 中点.⑴求证:PA∥平面BDE; ⑵求证:平面PBC⊥平面PDC.【答案】证明(1)连接AC 交BD 于O ,连接PO EO ,∵四边形ABCD 是菱形, ∴O 是AC 中点, 又E 为PC 中点.∴PA ∥EO又BDE EO 面⊂,BDE PA 面⊄∴PA ∥平面BDE (2)在△PAC 中,易得3===PO CO AO ∴ 90=∠APC ,∴22=PC1AEC D BA1D1B1C第16题∴在△PDC 中可求得2=DE ,同理在△PBC 中可求得2=BE∴在△BDE 中可得90=∠BED ,即BE ⊥DE 又BC PB =,E 为PC 中点, ∴BE ⊥PCBE ⊥面PDC ,又⊂BE 面PBC ∴平面⊥PBC 平面PDC。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

宿迁市2013届高三年级第二次模拟考试学生答题分析与教学建议

宿迁市中小学教学研究室 2013年4月2日

语文一、命题意图：模拟高考，指导复习，查漏明缺，提升能力。本次考试，试卷命题以2013年江苏省高考语文《考试说明》为依据，参照2012年江苏高考语文试卷的考查内容和试卷结构，在全面考查的基础上，考查学生一轮复习的效果，同时查找在一轮复习中存在的漏洞，进一步明晰二轮复习的着力点与提升点。整个试卷共七大题18小题，满分为160分，考试时间为150分钟。第一大题是语言文字运用，15分，考查内容包括字音、字形，病句的辨析，材料概括，画外音拟写。第二大题为文言文阅读，文言文阅读选自宋代曾巩的《元丰类稿》，考查对文言知识的理解能力，对文章信息的筛选、分析综合能力，对重要语句的翻译能力；第三大题为古诗鉴赏，诗歌阅读选用的是唐代杜甫的《悲陈陶》，考点在景与技法，考查的是理解、分析综合、鉴赏评价能力；第四大题为名句名篇默写，内容选自《考试说明》中规定的背诵的初高中篇目及课外名句，考查的是识记能力。第五大题为文学类文本阅读，选文为美国作家斯考特•奥洛期基的《朋友》，主要考查对文学作品的阅读鉴赏能力——品味语言，领悟内涵，分析艺术表现力；理解作品反映的社会生活和情感世界，探索作品蕴含的民族心理和人文精神。第六大题为论述类文章阅读，选的是王蒙的《文化瑰宝与文化泡沫》，以主观题的形式，重点考查学生对文章的思路梳理，筛选并整合文中信息的能力。第七大题是作文，考查学生语文综合能力。二、各题答题情况分析及复习建议选择题

题目平均分难度% 正确答案选作人数正答率 A B C D 选择题1 2 66.81 B 38316 0.67 939 25600 4181 7482 选择题2 1.06 35.18 D 38316 0.35 5618 5380 13716 13479 选择题3 2.27 75.73 B 38316 0.76 2920 29015 2375 3890 选择题4 1.84 61.49 D 38316 0.61 8558 2570 3494 23560 选择题5 1.28 42.75 B 38316 0.43 501 16382 10179 11105 第３题平均得分2.79 难度系数0.69. 总体评价：就答题而言，三点原因中，第一、三点绝大多数考生能基本了解并作出回答（缺核心技术、无安全机制等）。但在第二点上，则表现为概括盲目，扣不住关键内容，大多是提取其中一个小点，以偏概全（如只答“不明”或“盗版”等）。典型问题：１．学生在答此类问题时，有相当部分是采用提取法，即从原材料（文本）中摘取语句或词语，导致答案不够准确、鲜明。２．电脑处理此答案时，只注重关键词或中心词，综合批改带来阻碍，在宽松和严准上有一定差距，这是批改过程“产生无效果批改”的主要原因。３．正确运用“概括”和“摘取（提取）”两种答题要求和技巧的区别在学生中再强化。教学建议：注重审题，关注题干中“根本原因”关键字眼；要读懂文本，学会正确分层概括。第4题均分3.48分。难度系数0.69 总体评价：1、试题所选时鲜性材料，可读性强，便于学生阅读，对学生精神品质的升华有潜移默化的影响。 2．本题考查“画外音”的叙写，要求使用修辞手法，兼以抒情意味浓郁的句子表达，有字数限制，基本符合高考考纲的要求。典型问题：1．对画外音的考查，各地模拟题都不曾出现，学生对这一考点较陌生。 2．学生使用修辞错误或使用不当，这影响得分。 3．许多学生对材料进行简单地缩写，不符合题干的要求。 4、少数学生用第一人称。 5．个别学生批评李文波的行为。教学建议：1、引导学生关注时鲜素材，关注社会热点问题。2、强化审题意识，加强审题训练。3、帮助学生树立正确的世界观、人生观。 8—1题本题共4分，均分1.67，难度系数0.42，得分率较低。总体评价： “侃然”无一考生译出，体现命题的难点，其余翻译点体现基础。典型问题： 1．译句缺乏整体意识，不能结合语境准确规范的译句，如不知补出主语；介词“于”多译为“在”“把”；“顾计”多译成“顾忌”“算计”等；“自任”多译为“上任”“任务”等； 2．译句缺乏灵活性，需直译却意译，需意译却直译，如“及”多译成“像他一样”“和他相比”“和他相提并论”等；“义所在”多直译成“道义所在的地方”； 3．文言基础掌握不牢固。“莫”译成“没有”“不”等。教学建议：1．回归基础，巩固掌握文言基础知识； 2．直译为主的基础上，能结合上下文语境灵活译句。 8—2题平均分0.9 难度系数0.30 总体评价:考点贴近课本,“所以”、“具”、“预”都是教材中学过的，此题重在引导学生注重对书本上重要实词的积累。典型问题：1．“所以”解释不对，有较多学生解释为“„„的原因”；还有的直接没有解释。 2．“具”解释错误，或解释为“工具”，或解释为“农具”。 3．语句不通，存在病句现象。教学建议:1．梳理课本中的重点实词的不同义项。2．译文时培养学生的整体意识，避免出现前后搭配不当现象。

8—3 平均分1.39 难度系数0.46. 总体评价：难度适中，区分度适中，能考出学生的水平。典型问题：“陈枢”没能补出来；判断句没能翻译出来；“致仕、报”翻译不准。教学建议：加强文言文翻译训练；在文言翻译的基本方法上做文章；注意核查译句后的完整性和通顺性。 9-1题平均分1.68 难度系数0.42. 总体评价:本题满分4分，试题难度较大,学生总体答题情况不太好,但学生和学生之间的答题情况差别较大,有不少满分,也有不少零分典型问题:1．很多学生缺乏答题思路,没有题型思路,有不少同学将它当成了普通的炼字题作答,更有不少同学没有任何答题思路,只是跟着感觉走. 2．学生答题严重欠缺规范意识,例如答成:首联写了„„此为一悲,颔联写了„„ 此为二悲；等.语言表达很不到位;或者答成:作者从1,2,3等方面表达了自已的悲伤之情„„ 教学建议:1．对于一字或一词统领全诗的诗眼题,是典型的诗歌鉴赏题型,但对于这种传统题型,许多同学已经记不清答题思路,什么是诗眼?分为哪几种类型?如何鉴赏诗眼?在接下来的教学中,老师可以选择典型诗题,有的放矢地进行复习 2．在教学中要进一步加强学生规范答题的意思. 9—2 平均分1.42 难度系数0.47. 总体评价：难易适中，学生无审题难度，有话可说；有答题步骤；衬托、借景抒情、渲染是多数学生的答案。典型问题：答反衬、乐景衬哀情的较多；第2小点，学生容易忽视；技法名称错字不少。教学建议：重视学生读懂诗歌的训练；答题要结合诗句，少一些大而化之的内容。 9—3 平均分1.01 难度系数0.33. 总体评价：审题难度较大，得分率较低。典型问题：学生对“史”的界定不清，与情感评价糅合在一起；很多学生不能紧扣诗句内容作概括；不看题目具体设问角度有针对性作答。教学建议：注意审题训练；把握评价此类诗歌题型的解答角度。 10题分值：8分均分：5 难度系数0.62. 总体评价：本题考察学生对名言名句的掌握，难度适中。典型问题：1．错字别字现象严重。如：言笑晏晏（宴宴），吾尝（长）跂而望矣，庶（恕）竭驽（奴）钝（顿），猿猱（揉）欲度（渡）愁攀援（缘、岩），官盛（胜）则近谀，酒酣胸（凶）胆尚（敞）开张，其利(力)断金（筋），其臭（嗅）如兰。其中“晏”“ 跂”“猱”“攀”有不少同学写了错字。 2．书写不认真、不清楚。笔画不清楚和偏旁不规范。教学建议：巩固背诵的基础上，加强对默写的检查力度，着重针对易错的字。 11题：平均分1.67 难度系数0.42. 总体评价：题型典型，学生能从多角度作答，得分较高。典型问题：1．答题多用套话，内容不具体、不完整。 2．错别字较多，如“渲染”写成“宣染”或“喧染”；“铺垫”写成“辅堑”；“基调”写成“激调”等。 3．卷面不清洁，涂改现象严重。教学建议：1．强调要从多方面考虑问题，不能使用套话作答。 2．加强基本功训练，杜绝错别字的出现。 3．保持卷面的整洁，书写的规范。 12题：平均分1.75 难度系数0.44. 总体评价：本小题分值为4分，全市均分为1.88分左右，难易度适中，考查涉及小说主旨理解的重点词语的理解。典型问题： 1．答非所问，未能扣住题干，联系语境，解释第一处“平静”含义，表述失当； 2．未能正确理解讳饰手法，未能理解小说结尾部分的内容，对亚当的死亡及死因理解错误，导致对第二处“平静”理解错误。教学建议：1．加强阅读指导，提高学生理解文本的能力；2．指点理解文中重要词语含义的方法；3．强化训练，培养题感。 13题分值：6分，均分：1.55分。难度系数0.26. 总体评价：基本掌握答题步骤，对点答题，前两点涉及较细。典型问题：1．“欧亨利式结尾”特点不明。2．缺少“分点”意识。3．作用分析不到位。4．字迹不整。教学建议：有针对性地了解中外文学名人特色；加强审题要求，此题第三点基本无人答出；字迹、卷面问题仍需强调。第14题，分值6分，均分1.05 难度系数0.18. 总体评价：1．书写较差，答案无条理。2．把题目理解成作用题，情节梳理题。3．总分6分，均分1.3，得分太低。典型问题：1．本题目为意蕴探究题，很多考生却答“朋友为全文线索，有力的刻画了人物形象”等离谱答案。2．主旨错误理解成“对空巢老人的漠视、战争给人带来心灵的创伤、如何交友”等。3．对情节把握错误，认为是雷直接或间接杀死了亚当。4．答案混乱，不分点作答，只笼统对“朋友”定义大加评述。教学建议：1．多阅读，提高对作品的理解力。2．培养能根据文本相关情节的交代抓住文章主题的能力。3．加大意蕴探究题型的练习力度，答题要求规范工整。4．要细审题。第15题，分值6分，均分3.75 难度系数0.62. 总体评价：本题紧贴考纲，符合教与学的实际，具有很强的针对性；参考答案设计巧妙而规范，特别是第三个答案点：“通过对比”的要求提示很好。典型问题：1．有相当数量的学生答题时没有表示论述思路的关联词语，从而导致扣分。 2．第三个答案点，部分学生没有概括出要点，而是运用文本中的具体内容。教学建议：1．教育学生，平时答题时要有规范答题的意识。2．教育学生如何划分层次，学会概括内容。 16题分值6分，均分1.87 难度系数0.31. 总体评价：难度系数大，学生得分不理想。典型问题： 1．审题不准。题目问“为什么说有时文化符号到文化泡沫，只有一步之遥”，需要回答到“文化符号”与“文化泡沫”两方面的内容及二者转换原因，但学生基本只谈及“文化泡沫”的特征或产生原因。 2．信息筛选不准确或提炼不准确。 3．不分点作答，也有的将相同角度的答案分成两点作答。教学建议： 1．加强审题指导，指导学生学会从题干的字里行间寻找答题的角度、要点。 2．加强对学生分点作答的指导，既要强化学生分点作答的意识，也要训练学生对筛选到的信息分类合并、提炼、概括的能力。 17题: 此题分值6分，平均分2.38 难度系数为0.39. 总体评价：答案要点为三点，第一点答对的同学较多，答出寻找措施加强管理的人也较多，但二三两点答出来的较少典型问题：1．学生从文中寻找原文,但是不会概括.2．审题不清,导致答题思路不清。3．没有全篇意识,往往只想从一节中概括出全部答案。教学建议：1．高考论述类文本概括能力要求很高,在平常的教学中要加以锻炼,不能只做一些原文找出答案的题目,多做概括性较强的文本。 2、文本意识要加强,不能脱离文本胡乱作答。 18题此题分值70分，平均分45.22 难度系数0.64. 总体评价：这次作文为材料作文，是一则寓言故事。关键句是“我懂得如何对待别人的光芒”，“它的光芒甚至比星光更闪亮、更耀眼”。由此可得出“借鉴”“欣赏”“认识自我”“取长补短”“善于借鉴并转化自己的东西”等。从阅卷过程来看，本次作文能考查出学生的作文水平，对学生在审题、立意、构思、选材、文体选择方面都有所考查。在评分方面基本遵循江苏省的阅卷标准进行，判分上拉开了优生和差生之间的距离，对优秀的作文敢于给分、给高分，对态度不端正、抄袭、思想不健康的敢于打低分。典型问题： 1．审题不准，如尊重、看待、奉献、感恩、回报等 2．文章立意不深，流于肤浅。 3．学生使用材料单一，不够丰富，泛泛而谈，空洞无物。 4．文体单一，以议论文为主，少有记叙文。 5．标题不当，题目过长或含糊不清。 6．书写不认真。字体太大或太小，潦草、不清洁、错别字等情况严重，尤其是标题中的错别字。教学建议： 1．加强训练，强化审题意识。 2．规范文体，议论文与记叙文同时推进。