武汉理工大学量子力学2010A卷标答
量子力学教程课后习题答案

量子力学教程课后习题答案量子力学习题及解答第一章量子理论基础1.1 由黑体辐射公式导出维恩位移定律:能量密度极大值所对应的波长与温度T成反比,即T=b(常量);并近似计算b的数值,准确到二位有效数字。
解根据普朗克的黑体辐射公式,(1)以及,(2),(3)有这里的的物理意义是黑体内波长介于λ与λ+dλ之间的辐射能量密度。
本题关注的是λ取何值时,取得极大值,因此,就得要求对λ的一阶导数为零,由此可求得相应的λ的值,记作。
但要注意的是,还需要验证对λ的二阶导数在处的取值是否小于零,如果小于零,那么前面求得的就是要求的,具体如下:如果令x= ,则上述方程为这是一个超越方程。
首先,易知此方程有解:x=0,但经过验证,此解是平庸的;另外的一个解可以通过逐步近似法或者数值计算法获得:x=4.97,经过验证,此解正是所要求的,这样则有把x以及三个物理常量代入到上式便知这便是维恩位移定律。
据此,我们知识物体温度升高的话,辐射的能量分布的峰值向较短波长方面移动,这样便会根据热物体(如遥远星体)的发光颜色来判定温度的高低。
1.2 在0K附近,钠的价电子能量约为3eV,求其德布罗意波长。
解根据德布罗意波粒二象性的关系,可知E=h,如果所考虑的粒子是非相对论性的电子(),那么如果我们考察的是相对性的光子,那么E=pc 注意到本题所考虑的钠的价电子的动能仅为3eV,远远小于电子的质量与光速平方的乘积,即,因此利用非相对论性的电子的能量——动量关系式,这样,便有在这里,利用了以及最后,对作一点讨论,从上式可以看出,当粒子的质量越大时,这个粒子的波长就越短,因而这个粒子的波动性较弱,而粒子性较强;同样的,当粒子的动能越大时,这个粒子的波长就越短,因而这个粒子的波动性较弱,而粒子性较强,由于宏观世界的物体质量普遍很大,因而波动性极弱,显现出来的都是粒子性,这种波粒二象性,从某种子意义来说,只有在微观世界才能显现。
1.3 氦原子的动能是(k为玻耳兹曼常数),求T=1K时,氦原子的德布罗意波长。
2010大学物理试卷A+答案
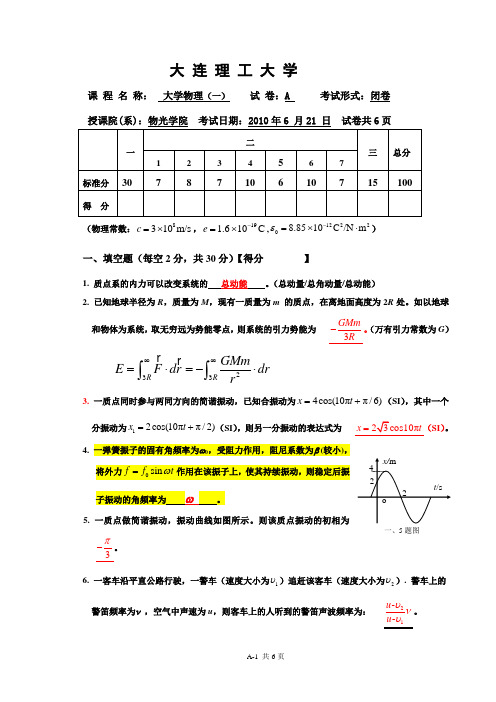
大 连 理 工 大 学课 程 名 称: 大学物理(一) 试 卷:A 考试形式:闭卷 授课院(系):物光学院 考试日期:2010年6 月21 日 试卷共6页(物理常数:8310m/s c =⨯,C 106.119-⨯=e ,122208.8510C /N m ε-=⨯⋅)一、填空题(每空2分,共30分)【得分 】1. 质点系的内力可以改变系统的 总动能 。
(总动量/总角动量/总动能)2. 已知地球半径为R ,质量为M ,现有一质量为m 的质点,在离地面高度为2R 处。
如以地球和物体为系统,取无穷远为势能零点,则系统的引力势能为3-GMmR。
(万有引力常数为G ) 233R R GMmE F dr dr r∞∞=⋅=-⋅⎰⎰ 3. 一质点同时参与两同方向的简谐振动,已知合振动为4cos(10ππ/6)x t =+(SI ),其中一个分振动为12cos(10ππ/2)x t =+(SI ),则另一分振动的表达式为 SI )。
4. 一弹簧振子的固有角频率为ω0,受阻力作用,阻尼系数为β (较小), 将外力0sin f f t ω=作用在该振子上,使其持续振动,则稳定后振5. 一质点做简谐振动,振动曲线如图所示。
则该质点振动的初相为 3π-。
6. 一客车沿平直公路行驶,一警车(速度大小为1υ)追赶该客车(速度大小为2υ). 警车上的警笛频率为ν ,空气中声速为u ,则客车上的人听到的警笛声波频率为:21--υνυu u 。
一、5题图7. 实验室测得一粒子的总能量是205m c (0m 为其静止质量,c 为真空中的光速),则实验室测得该粒子的动能为 204m c ;实验室测得该粒子的质量为 05m 。
8.9. 由狭义相对论原理可知:设两个惯性系彼此运动,在其中任意一个惯性系内部做电磁学实验 都 不能 测出这两个惯性系的相对运动速度。
10. 一均匀带电的正方形薄板,沿其中一个边长方向以0.6c υ=的速度运动,与该物体静止时的状态相比较,电荷密度是静止时的 5/4 倍。
2010双语力学试题A卷及答案(定稿)

6. If a man moves, with a speed equal to 0.5 that of sound, away from a stationary organ(风琴) producing a sound of frequency f , he will probably hear a sound of frequency7. If the angular momentum of the system remains constant, the net external torque acting on a system is8. The distance between the adjacent two nodes isⅡ.Choose the Correct Answer (3 10=30marks )1. A 0.20kg puck slides across a frictionless floor with a speed of 10 m/s. The net work done on the puck is ( ) A-20J B -10J C 0J D20J2. Two objects A and B, as shown in Fig.2, both with mass m are placed inside an elevator whose acceleration is 4g , the masses of the rope and the pulley are negligible. If the frictional forces of the pulley axis and the table are also negligible, and the resistance of the air can be neglected, the tension in the rope is ( ) A mg B 14mg C 34mg D 58mg3. The magnitude of the force of gravity between two identical objects is given by 0F . If the mass of each object is doubled but the distance between them is halved, then the new force of gravity between the objects will be ( ) A 160F B 40F C 0F D 80F4. A point mass m is undergoing uniform circular motion with an angularFigure 2frequency ω in a horizontal circle of radius r. Which of the following is arepresentation of the angular momentum of the mass? ( ) A. ωmr B. m r /2ω C. ω2mr D. ω/2mr5. When a mass point is in a circular motion then ( ) A The tangential acceleration definitely change, the normal acceleration also change.B The tangential acceleration may not change, the normal acceleration definitely change.C The tangential acceleration may not change, the normal acceleration does not change.D The tangential acceleration definitely change, the normal acceleration does not change.6. The expression of mechanical wave is 0.05cos(60.06)y t x ππ=+, where the unit of y and x is meter and the unit of the t is second, then( )A the wavelength is 5mB the wave speed is 110m s -⋅C the period is 13s D the wave travels along the positive direction of x axis7. A standing wave as shown in figure3, the phase difference of the points a and b is ( )A πB 2πC 54πD 08. An uniform thin rod OA is pivoted on a frictionless hinge at one end O, as shown in Fig4. The rod is held at rest horizontally and then released. When it reaches the vertical position which one is correct of following statements ( ) A Angular velocity varies from small to big, angular acceleration remains unchanged.B Both angular velocity and angular acceleration varyFigure 3from small to big.C Angular velocity varies from small to big, while angular acceleration varies from big to small.D Angular velocity remains unchanged, angular acceleration equals zero.9.Which of the following relationships between the force F on a particle and the particle’s position x implies simple harmonic motion ( ) A 5x - B 240x - C 10x D 23x10. Kepler’s second law of planetary motion is a consequence of the law of conservation of ( ) A linear momentum B mechanical energy C kinetic energy D angular momentumⅢ.(10 marks )A 40g bullet is fired along a horizontal direction with the velocity 500/m s . Itcomes to a stop 20cm within a solid wall.(a) What is thechange in the bullet’s mechani cal energy?(b) What isthe magnitude of the average force from the wall stopping it?Ⅳ.(15 marks ) A block of mass 5.4M kg =, at rest on a horizontal frictionless table, is attached to a rigidsupport by a spring of constant k=6000N/m. A bullet of mass 9.5m g =andvelocity v of magnitude 630/m s strikes and is embedded in the block (Fig5). Assuming the compression of the spring is negligible until the bullet is embedded, determine (a) the speed of the block immediately after the collision and (b) the amplitude of the resulting simple harmonic motion.Ⅴ.(15 marks)In Fig.6, a small 50g block slidesdown a frictionless surface through height 20h cm=andthen sticks to a uniform rod of mass 100g and length 40cm.The rod pivots about point O through angleθbefore momentarily stopping. Findθ.Figure 5Figure 6Ⅵ.(10 marks) A bat is flitting about in a cave, Array navigating via ultrasonic bleeps(哔哔声). Assume thatthe sound emission frequency of the bat is 39000Hz. During one fast swoop (猛扑)directly toward a flat wall surface, the bat is moving at 0.025 times the speed of sound in air. What frequency does thebat hear reflected off the wall?Figure 72010─2011学年 第一学期《力学》(双语) 课程考试试卷(A 卷)参考答案及评分标准一、 Fill in the Blanks. (2 ⨯10=20 marks)1. No 7.00 6.00()i j N +2. 22rod com com c I I mh I I md =+=+或3. 122m m F Gr = 4. 114.kg m s -⋅ 5.2112m m g m m -+ , 21122m m g m m +6. 0.5f7. 08. 2λ二、Choose the Correct Answer. (3⨯10=30 marks)三.(10 marks )Solution: (a) The key idea here is that when the bullet stops within a solid wall, the speed of the bullet is zero. The bullet’s mechanical energy changes occur between the initial state and the final state, the change2102mec i E K mv ∆=∆=-Substituting known data gives us232114010(500)500022mec i E mv J -∆==⨯⨯⨯= (5 marks)(b) The key idea is that the work F W done on the bullet by the solid wall is equal the kinetic energy change of the bullet, which has an initial value of212i K mv =and a value of zero when the bullet stops. So we can write the work-kinetic energy theorem for the bullet as f i K K Fs -=-Substituting known data, we can yield5000250000.20i K J F N s m=== (5 marks)四.(15 marks )Solution:(a) When the bullet strikes the block which is on the horizontal frictionless table, the momentum of the system1 composed with the bullet and the block is conservative. So we can obtain the speed of the block immediately after the collision1()mv m M v =+ So the speed of the block immediately after the collision is19.5630 1.11/()9.55400mv v m s m M ⨯===++(5 marks)(b) Then we can get the kinetic energy of the system122221211()()()22()2()K m v m v E m M v m M m M m M =+=+=++ (3 marks) Next, we consider the bullet 、the block and the spring as the system2, themechanic energy of the system2 is conserved. When the kinetic energy is zero, the spring potential energy is max and we can get the amplitude of the resulting SHM222122()K m K m v U kx E m M ===+ (5 marks)Then we can get amplitude of the resulting simple harmonic motion20.00953.3210 3.32m x m cm-==⨯=⨯= (2 marks)五.(15 marks )Solution: The whole process can be divided into three parts :(1) The small block slides down the frictionless surface through height h , In this part only the gravitational force , being a conservative force, does work, so the law of conservation of mechanic energy holds211121v m gh m = (2 marks)where 1v is the speed of the block before it collides with the rod.The small block collides with the rod and sticks to it. During this interaction there is no net torque acting on the block –rod system relative to the point O , the angular momentum of the system is conserved (Note: since is a net force acting on the rod at point O by the pivot, the law of conservation of linear momentum does not hold! )ωI L v m =11 (2 marks)where ωis the angular speed of the system about point O just after the collision. I is the rotational inertia of the block-rod system about point O , which is222113I m L m L =+ (2 marks)The block-rod system swings up until it momentarily stops, During this process the mechanic energy of the system is conserved, we thus writecom h g m m I ∆+=)(21212ω (2 marks) Where com h ∆ is the height change of the center of mass of the block-rod system in the swing up process. In the vertical position the center of mass of the system is below point O at1212(0.5)(0.05)(0.4)(0.1)(0.2)0.26670.050.10com m L m L kg m kg m L m m m kg kg++===++So )c o s 1(θ-=∆c o m c o m L h (2 marks)Substituting all the known values into Eq.1~Eq.5, we can then get the answer as the following steps: Form Eq.1s m m s m gh v /98.1)2.0)(/8.9(2221===From Eq.32222110.1()(0.05)(0.4)0.013333kg I m m L kg m kgm =+=+=From Eq.2 we have211(0.05)(1.98/)(0.4)/(0.0133)m v L I kg m s m kgm ω==2.97/rad s =Combine Eq4 and Eq.5, we have)cos 1()(21212θω-+=com gL m m I cos 0.85θ=Thus the angle θ we look for is31.8θ=︒ (5marks)六.(10 marks )Solution: There are two Doppler shifts in this situation. First, the emitted wave strikes the wall, so the sound wave of frequency is113900040000100251s f f Hz v .v'===-- (5 marks)which means source moves toward the stationary wall.Second, the wall reflects the wave of frequency f 'and reflects it, so the frequency detected f '', will be given1400001002541000ov f f ()(.)Hz v'''=+=+= (5 marks) which means observer moves toward the stationary source.。
【北航2010】量子力学课代表答案

2010量子力学
(chap1)设一维自由粒子在t=0时的状态为0
i p x x e ψ (,0),求t 时刻粒子的状态,x t ψ()。
1
√2πℏexp ii ℏ(p 0x −EEt ), EE =p 022m
(chap2)设质量为m 的粒子处于势场()V x Kx =−中,其中K 为非零常数。
在动量表象....下,求与能量E 对应的本征波函数()E p Φ。
ΦE (p )=exp �−ii ℏ�p 36Km −EEp K
��
(chap6) 出现在()θϕ,方向立体角元的概率。
(注: )。
(chap7&4)在ˆx S 表象上,求出y ˆS 的本征态的表示,求出并验证ˆy S 表象到ˆz
S 表象的表象变换矩阵。
ℏ2�0110� 1√2�−ii 1ii 1�
(chap7)设电子处于某自旋态,在该态中,电子自旋的y S 自旋向上,求该态中电子自旋x S 的可能值、测量概率和平均值。
ℏ2,−ℏ2 12,12 0
(chap8)一体系未受微扰作用时只有三个能级,0102033,,2;E E E εεε===−哈密顿为(0)3000
0002H εεε = − ,当有微扰时的哈密顿为300
002a H a a εεεεεε = −+ ,其中a ε和都是实数,用微扰
公式求能量至二级..
修正。
EE 1=3εε+aa 22εε EE 2=εε−aa 2εε EE 3=−2εε+aaεε。
量子力学课后习题答案

Wnl (r)dr Rnl2 (r)r 2dr
例如:对于基态 n 1, l 0
W10 (r) R102 (r)r 2
4 a03
r e2 2r / a0
求最可几半径
R e 2 r / a0
10
a03 / 2
dW10 (r) 4 (2r 2 r 2 )e2r / a0
x)
k
2
2
(
x)
0
其解为 2 (x) Asin kx B cos kx
根据波函数的标准条件确定系数A、B,由连续性条件,得
2 (0) 1(0) B 0
2 (a) 3 (a) Asin ka 0
A0
sin ka 0
ka n
(n 1, 2, 3,)
[1 r
eikr
r
(1 r
eikr )
1 r
eikr
r
(1 r
eikr )]er
i1 1 11 1 1
2
[ r
(
r2
ik
) r
r
(
r2
ik
r )]er
k
r2
er
J1与er 同向。 1 表示向外传播的球面波。
习题
(2)
J2
i
2
(
2
* 2
2*
解:U (x)与t 无关,是定态问题
薛定谔方程为
2
2
d2 dx2
(x) U (x) (x)
E (x)
在各区域的具体形式为:
x0
量子力学教程课后习题答案

量子力学教程课后习题答案量子力学习题及解答第一章量子理论基础1.1 由黑体辐射公式导出维恩位移定律:能量密度极大值所对应的波长与温度T成反比,即T=b(常量);并近似计算b的数值,准确到二位有效数字。
解根据普朗克的黑体辐射公式,(1)以及,(2),(3)有这里的的物理意义是黑体内波长介于λ与λ+dλ之间的辐射能量密度。
本题关注的是λ取何值时,取得极大值,因此,就得要求对λ的一阶导数为零,由此可求得相应的λ的值,记作。
但要注意的是,还需要验证对λ的二阶导数在处的取值是否小于零,如果小于零,那么前面求得的就是要求的,具体如下:如果令x= ,则上述方程为这是一个超越方程。
首先,易知此方程有解:x=0,但经过验证,此解是平庸的;另外的一个解可以通过逐步近似法或者数值计算法获得:x=4.97,经过验证,此解正是所要求的,这样则有把x以及三个物理常量代入到上式便知这便是维恩位移定律。
据此,我们知识物体温度升高的话,辐射的能量分布的峰值向较短波长方面移动,这样便会根据热物体(如遥远星体)的发光颜色来判定温度的高低。
1.2 在0K附近,钠的价电子能量约为3eV,求其德布罗意波长。
解根据德布罗意波粒二象性的关系,可知E=h,如果所考虑的粒子是非相对论性的电子(),那么如果我们考察的是相对性的光子,那么E=pc 注意到本题所考虑的钠的价电子的动能仅为3eV,远远小于电子的质量与光速平方的乘积,即,因此利用非相对论性的电子的能量——动量关系式,这样,便有在这里,利用了以及最后,对作一点讨论,从上式可以看出,当粒子的质量越大时,这个粒子的波长就越短,因而这个粒子的波动性较弱,而粒子性较强;同样的,当粒子的动能越大时,这个粒子的波长就越短,因而这个粒子的波动性较弱,而粒子性较强,由于宏观世界的物体质量普遍很大,因而波动性极弱,显现出来的都是粒子性,这种波粒二象性,从某种子意义来说,只有在微观世界才能显现。
1.3 氦原子的动能是(k为玻耳兹曼常数),求T=1K时,氦原子的德布罗意波长。
2010级大学物理AI试卷A答案
石家庄铁道大学2010-2011学年第二学期10级本科班期末考试试卷A 答案(大学物理AI)一 选择题 (每题3分,共30分) 1-10 B C C C D , C D D B B 二 填空题 (共30分)11 0321=++v v v3分12 )1(2122212121-r r mr ω 3分13 2 m/s 3分14 速率区间0 ~ v p 的分子数占总分子数的百分率; 2分⎰⎰∞∞=ppf f v v vv v v v v d )(d )( 2分15 ||1W - 2分 ||2W - 2分 16 不变 1分 增加 2分17 不变 2分减小 2分 18E Sgε202 3分19d 211λλλ+ 3分三 计算题 (每题10分,共40分)1 解:两自由质点组成的系统在自身的引力场中运动时,系统的动量和机械能均守恒.设两质点的间距变为l /2时,它们的速度分别为v 1及v 2,则有02211=-v v m m ① 2分lm Gm m m l m Gm 212222112122121-+=-v v ② 4分 联立①、②,解得)(22121m m l G m +=v ,)(22112m m l Gm +=v 4分2解:受力分析如图. 2分mg -T 2 = ma 2 1分 T 1-mg = ma 1 1分 T 2 (2r )-T 1r =9mr 2β / 2 2分 2r β = a 2 1分 r β = a 1 1分 解上述5个联立方程,得: rg192=β 2分3解:(1) 过程ab 与bc 为吸热过程, 吸热总和为 Q 1=C V (T b -T a )+C p (T c -T b ) )(25)(23b b c c a a b b V p V p V p V p -+-==800 J 4分 (2) 循环过程对外所作总功为图中矩形面积 W = p b (V c -V b )-p d (V d -V a ) =100 J 2分(3)T a =p a V a /R ,T c = p c V c /R , T b = p b V b /R ,T d = p d V d /R ,T a T c = (p a V a p c V c )/R 2=(12×104)/R 2 T b T d = (p b V b p d V d )/R 2=(12×104)/R 2∴ T a T c =T b T d 4分aa 14解: 由高斯定理可知空腔内E =0,故带电球层的空腔是等势区,各点电势均 为U . 2分 在球层内取半径为r →r +d r 的薄球层.其电荷为d q = ρ 4πr 2d r该薄层电荷在球心处产生的电势为 ()00/d 4/d d ερεr r r q U =π= 2分 整个带电球层在球心处产生的电势为()212200002d d 21R R r r U U R R -===⎰⎰ερερ 3分 因为空腔内为等势区所以空腔内任一点的电势U 为()2122002R R U U -==ερ 3分 若根据电势定义⎰⋅=l E Ud 计算同样给分.。
2010级大学物理A(A卷)
――――――――――――――――――――――――――装订线―――――――――――――――――――――――――――教学班号 自然班 姓名 学号-―――――――――――――――――――――――――密封线―――――――――――――――――――――――――――2010级大学物理A (A 卷)一、单项选择题(在每小题的四个备选答案中,选出一个正确答案,并将其代码填入答题纸的对应位置,每小题3分,共45分) 1、 以下关系正确的是:(A ) |v |=v ,|v |= v (B ) |v |≠v ,|v|≠ v (C ) |v |=v ,|v |≠ v (D ) |v |≠v ,|v|= v2、 一物体作斜上抛运动,初速度为200=v m/s 与水平方向夹角为︒60.物体轨道最高点处的曲率半径ρ为(A ) 5m (B ) 10m (C ) 17.3m (D ) 20m3、 如图所示,一轻绳跨过一个定滑轮,两端各系一质量分别为m 1和m 2的重物,且m 1>m 2.滑轮质量及轴上摩擦均不计,此时重物的加速度的大小为a .今用一竖直向下的恒力g m F 2=代替质量为m 2的物体,可得质量为m 1的重物的加速度为的大小a ′,则(A ) a ′< a (B ) a ′> a (C ) a ′= a (D ) 不能确定.4、 如图所示,圆锥摆的摆球质量为m ,速率为v ,圆半径为R ,当摆球在轨道上运动半周时,绳子对摆球拉力冲量的大小为 (A ) 0. (B ) v /Rmg π (C ) 2m v .(D )22)/()2(v v R mg m π+.5、 对质点系以哪种说法是正确的:(A ) 质点系总动量的改变与内力无关; (B ) 质点系总动能的改变与内力无关; (C ) 质点系机械能的改变与保守内力有关. (D ) 质点系总势能的改变与保守内力无关6、 质量为m 1 的子弹A ,以1v 的速度水平地射入一静止在水平面上的质量为m 2的木块B 内,A 射入B 后,B 向前移动了s 后而停止.以地面为参考系,下列说法中正确的说法是 (A ) 木块与子弹共同运动的过程中,木块对子弹不作功 (B ) 整个过程中木块对子弹所作的功等于子弹对木块所作的功 (C ) 子弹对木块所作的功等于木块动能的改变量 (D ) 木块对子弹所作的功等于子弹动能的改变量 7、 下列说法中不正确的是(A ) 一对作用力和反作用力对同一轴的力矩之和必为零; (B ) 作用在定轴转动刚体上的合力矩越大,刚体转动的角速度越大 (C ) 作用在定轴转动刚体上的合力矩越大,刚体转动的角加速度越大 (D ) 对某个定轴转动刚体而言,内力矩不会改变刚体的角加速度8、 质量相同、半径相同的匀质圆盘A 、匀质圆环B 和匀质圆柱体C ,以相同的角速度ω 绕其对称轴旋转,若从某时刻起,它们受到相同的阻力矩,则 (A ) A 先停转. (B ) B 先停转. (C ) C 先停转.(D ) A 、C 同时停转.9、 一个圆盘在水平面内绕一竖直固定轴转动的转动惯量为J ,初始角速度为0ω,后来变为021ω,在上述过程中,阻力矩的冲量矩为(A ) 0ωJ (B ) 041ωJ -(C ) 021ωJ - (D ) 021ωJ 10、 一个质点作简谐振动,振辐为A ,在起始时刻质点的位移为A /2,且向x 轴的负方向运动,代表此简谐振动的旋转矢量图为图中哪一图?11、 两个同方向同频率的简谐振动,其振动表达式分别为)5c o s (10621π/2+⨯=-t x (SI ) , )52c o s (10222t x -π⨯=- (SI )它们的合振动的初相为(A )2π-(B )0 (C )2π(D ) π12、 当机械波在媒质中传播时,一媒质质元的最小变形量发生在(A 是振动振幅)(A ) 媒质质元离开其平衡位置最大位移处 (B ) 媒质质元离开其平衡位置2/2A 处 (C ) 媒质质元在其平衡位置处 (D ) 媒质质元离开其平衡位置2/A 处13、 在真空中波长λ为的单色光,在折射率为n 的透明介质中从A 沿某路径传播到B ,若A 、B 两点相位差为3π,则此路径AB 的长度为(A )(A ) λ5.1 (B )n /5.1λ (C ) λn 5.1 (D ) λ314、 在图所示的三种透明材料构成的牛顿环装置中,用单色光垂直照射,在反射光中看到干涉条纹,则在接触点P 处形成的圆斑为 (A )右半部暗,左半部明 (B )右半部明,左半部暗 (C )全暗 (D )全明15、 单缝夫琅和费衍射实验中,波长为λ的单色光垂直入射在宽度λ6=a 的单缝上,对应于衍射角为︒30的方向,单缝处波阵面可分成的半波带数目为(A ) 2个 (B ) 4个 (C ) 6个 (D ) 8个 二、填空题(请按每空的标号将答案写在答题纸上,共10分) 1、 一质点沿半径为R 的圆周运动,运动学方程为221bt s =,其中b 是常数,则t 时刻质点的加速度矢量=a (1) ;2、 宇宙飞船关闭发动机返回地球的过程,可以认为是仅在地球万有引力作用下运动.若用m 表示飞船质量,M 表示地球质量,G 表示引力常量,则飞船从距地球中心r 1 处下降到r 2 处的过程中,动能的增量为 (2) 。
量子力学试卷A(2007级)
武汉理工大学教务处试题标准答案及评分标准用纸| 课程名称—量子力学—— ( A 卷) | 一、选择题(每题3分,共15分) 装 1.B 2.C 3. A 4.D 5.B | 二、填空题 (每空2分,共20分)1. 单值的,平方可积的2. 线性算符,厄米算符3. 平均值 几率分布4. 4 200ψ,211ψ,210ψ,211ψ-5. 平均场 积三、 证明题(共15分)证明:(1)[][]ˆˆ,1111ˆˆˆˆ2222ˆˆˆˆ,,122a a p p p p p p i i x p p x +⎡⎤⎫⎫⎡⎤=-⎥⎪⎪⎣⎦⎪⎪⎥⎭⎭⎦⎤⎡⎤⎡⎤⎤=+--⎥⎥⎥⎥⎥⎥⎥⎦⎦⎦⎦=-=-其中利益[]ˆˆ,xp i = (6分) (2)[],,,a a a a a a a a a a +++⎡⎤⎡⎤=+=-⎣⎦⎣⎦ ,,,a a a a a a a a a a +++++++⎡⎤⎡⎤⎡⎤=+=⎣⎦⎣⎦⎣⎦(4分) (3)可以求得:)ˆxa a +=+)ˆpa a +=-系统Hamilton 为()()()()22222ˆ1111ˆˆ2222211121222p H xa a a a a a aa a a a a μωωμωωω++++++⎡⎤=+=--++⎢⎥⎣⎦⎛⎫=+=+=+ ⎪⎝⎭ (5分)四 计算题(第1、2题各15分,第3、4题各10分,要求有具体计算步骤)1、解:(1)一维无限深势阱的本征态波函数是()n n xx aπψ=(2分) 利用三角函数积化和、差,将()x ψ改写 ()2cos x x x a a ππψ=21cos x x a a ππ⎡⎤=+⎢⎥⎣⎦22sin 2sin cos x x x a a a πππ⎤=+⎥⎦3sin sin xx a a ππ⎤=+⎥⎦3x x a a ππ⎤=+⎥⎦()()13x x ψψ=+⎤⎦ (4分) ()x ψ是非本征态,它可以有二种本征态,部分处在()1xx aπψ=出现几率为12,能量为22122E ma π=部分处在()33xx aπψ=,出现几率为12,能量为223292E ma π= (2分) (2)处于这种状态下粒子的能量平均值22132115222E E E ma π=+= (3分)(3)粒子随时间变化的波函数为 ()229223,n i i iE t t t ma ma nnx x x t C ee e a a ππππψψ---⎫⎫==⎪⎪⎪⎪⎭⎭∑(4分) 2、解:(1)在z σ表象中,0110x σ⎛⎫=⎪⎝⎭ 00y i i σ-⎛⎫= ⎪⎝⎭ 1001z σ⎛⎫= ⎪-⎝⎭(3分)cos sin sin cos i x x y y z z i e n n n n eϕϕθθσσσσθθ-⎛⎫=++= ⎪-⎝⎭,其本征方程为cos sin cos sin 0sin cos sin cos i i i i a a a e e b b b ee ϕϕϕϕθθθλθλθθθθλ--⎛⎫⎛⎫-⎛⎫⎛⎫⎛⎫=⇒= ⎪ ⎪ ⎪ ⎪ ⎪---⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭ 有非零解的条件为cos sin 01sin cos i i e eϕϕθλθλθθλ--=⇒=±-- (4分)当1λ=时,对应的本征态为()()1cos /2sin /2i e ϕθψθ-⎛⎫=⎪⎝⎭ 当1λ=-时,对应的本征态为()()2sin /2cos /2i e ϕθψθ-⎛⎫=⎪-⎝⎭ (2分) (2)在ˆz s本征态1/2χ下,n σ的可能测值为1± 故n σ的可能测值为1+的几率为()()()()22211/21cos /2,sin /2cos /20i e ϕψχθθθ⎛⎫== ⎪⎝⎭(3分)故n σ的可能测值为1-的几率为()()()()22221/21sin /2,cos /2sin /20i e ϕψχθθθ-⎛⎫=-= ⎪⎝⎭(3分)3、解:微扰算符的的矩阵是'''111213'''212223'''31323300'000H H H b H H H H a H H H ba **⎡⎤⎡⎤⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦ (1) 根据无简并微扰论,一级能量修正量是: kk H从(1)中看出,对角位置的矩阵元全是零,因此一级修正量0)0(3)0(2)0(1===E E E (2分)又二级能量公式是: 2'(2)(0)(0)nkknk nn kH E E E ≠=-∑(2分)所需的矩阵元'nk H 已经直接由式(1)表示出,毋需再加计算,因而有:2222'''12131(2)1(0)(0)(0)(0)(0)(0)(0)(0)1121313n nnH H H b E EEEEEEEE ==+=----∑(2分)2222'''21232(2)2(0)(0)(0)(0)(0)(0)(0)(0)2312123n n n H H H aE EE E E E E E E ==+=----∑ (2分)22222'''32313(2)3(0)(0)(0)(0)(0)(0)(0)(0)(0)(0)332313132n nnH H H b a E EEEEEEEEEE==+=+-----∑(2分)4.解:(1)利用21ˆˆ2q H P A q c φμ⎛⎫=-+ ⎪⎝⎭可得系统的哈密顿量为222222211ˆˆˆˆˆ221ˆˆˆ2x x y y zz x y z q q q q H P A q P A P A P A q y c c c c q P By P P q yc φεμμεμ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫=-+=-+-+--⎢⎥ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎢⎥⎣⎦⎡⎤⎛⎫=+++-⎢⎥ ⎪⎝⎭⎢⎥⎣⎦(4分)(2)证明:2222221ˆˆˆˆˆˆ,,2111ˆˆˆˆˆˆˆ,,,,0222x x y z x x x y x z x x q H P P By P P q y P c q P By P P P P P q y P c εμεμμμ⎡⎤⎡⎤⎛⎫⎡⎤=+++-⎢⎥⎢⎥ ⎪⎣⎦⎝⎭⎢⎥⎢⎥⎣⎦⎣⎦⎡⎤⎛⎫⎡⎤⎡⎤⎡⎤=+++-=⎢⎥ ⎪⎣⎦⎣⎦⎣⎦⎝⎭⎢⎥⎣⎦2222221ˆˆˆˆˆˆ,,2111ˆˆˆˆˆˆˆ,,,,0222z x y z z x z y z z z z q H P P By P P q y P c q P By P P P P P q y P c εμεμμμ⎡⎤⎡⎤⎛⎫⎡⎤=+++-⎢⎥⎢⎥ ⎪⎣⎦⎝⎭⎢⎥⎢⎥⎣⎦⎣⎦⎡⎤⎛⎫⎡⎤⎡⎤⎡⎤=+++-=⎢⎥ ⎪⎣⎦⎣⎦⎣⎦⎝⎭⎢⎥⎣⎦ˆx P 的本征函数为()/x x ip x P x ψ= ,本征值为x p -∞<<∞ ˆz P 的本征函数为()/z zip z P x ψ= ,本征值为z p -∞<<∞ (4分) (3)选守恒量完全集为()ˆˆˆ,,x zH P P (2分)。
量子力学复习题及答an答案比较全
量子力学期末考试辅导一、简答题1. 束缚态、非束缚态及相应能级的特点。
答:束缚态:粒子在一定范围内运动,∞→r 时,0→ψ。
能级分立。
非束缚态:粒子的运动范围没有限制,∞→r 时,ψ不趋于0。
能级分立。
2. 简并、简并度。
答:量子力学中,把处于不同状态、具有相同能量、对应同一能级的现象称为简并。
把对应于同一能级的不同状态数称为简并度。
3. 用球坐标表示,粒子波函数表为 ()ϕθψ,,r ,写出粒子在立体角Ωd 中被测到的几率。
解:()⎰∞Ω=022,,dr r r d P ϕθψ4. 用球坐标表示,粒子波函数表为 ()ϕθψ,,r ,写出粒子在球壳()dr r r +,中被测到的几率。
解:()ϕϕθψθθππd r d dr r P ⎰⎰=2022,,sin5. 用球坐标表示,粒子波函数表为()ϕθψ,,r 。
写出粒子在),(ϕθ方向的立体角Ωd 中且半径在a r <<0范围内被测到的几率。
解: ()⎰Ω=adr r r d P 022,,ϕθψ6. 一粒子的波函数为()()z y x r ,,ψψ=,写出粒子位于dx x x +~间的几率。
解:()⎰⎰+∞∞-+∞∞-=2,,z y x dz dy dx P ψ7. 写出一维谐振子的归一化波函数和能级表达式。
解:!2,)()(2/22n A x H eA x nn n x n n ⋅==-πααψα,2,1,0,21=⎪⎭⎫⎝⎛+=n n E n ω8. 写出三维无限深势阱⎩⎨⎧∞<<<<<<=其余区域,0,0,0,0),,(cz b y a x z y x V中粒子的能级和波函数。
解:能量本征值和本征波函数为 ⎪⎪⎭⎫ ⎝⎛=++222222222c n b n a n mE z yx n n n zy x π,3,2,1,00,0,0,sin sin sin 8),,(=⎪⎩⎪⎨⎧<<<<<<=n c z b y a x czn b y n a x n abc z y x z y x n n n z y x 其余区域πππψ 9. 粒子在一维δ势阱 )0()()(>-=γδγx x V中运动,波函数为)(x ψ,写出)(x ψ'的跃变条件。
