九年级上期末数学试卷4(含答案)
浙江省宁波市余姚市2023-2024学年九年级上学期期末数学试题(含答案)

余姚市2023学年第一学期初中期末考试九年级数学试题卷温馨提示:1.本试卷分试题卷和答题卷两部分,试题卷6页,满分120分,考试时间120分钟.2.所有答案都必须做在答题卷规定的位置上,务必注意试题序号和答题序号相对应.3.考试期间不能使用计算器.一、选择题(每小题3分,共30分,在每小题给出的四个选项中,只有一项符合题目要求)1.抛物线的顶点坐标是( )A .B .C .D .2.若线段,,则a 和b 的比例中项线段等于( )A .1B .2C .4D .83.任意抛掷一枚均匀的骰子,骰子停止转动后,发生可能性最大的事件是( )A .朝上一面的点数大于3B .朝上一面的点数小于3C .朝上一面的点数是3的倍数D .朝上一面的点数是3的因数4.已知点A 是外一点,且的半径为5,则的长可能为()A .3B .4C .5D .65.在中,,,,则边的长为( )A .3B .4CD6.如果一个正多边形的内角是,那么这个正多边形的边数为( )A .5B .6C .7D .87.下列命题中,错误的是()A .直径是圆中最长的弦B .直径所对的圆周角是直角C .平分弦的直径垂直于弦D .垂直平分弦的直线必定经过圆心8.若二次函数的图象经过和两点,则m 的值为( )A .1B .C .D .9.如图,矩形的内部有5个全等的小正方形,小正方形的顶点E ,F ,G ,H 分别落在边,,,上,若,,则小正方形的边长为( )()212y x =-+()1,2()2,1()1,2-()2,1-1a =4b =O O OA Rt ABC △90C ∠=︒5AB =3sin 5A =AC 135︒()2215y x =-+(),m n ()3,n 1-5252-ABCD AB BC CD DA 20AB =16BC =A .B .5C .D .10.如图,在中,点D 是上一点(不与点A ,B 重合),过点D 作交于点E ,过点D 作交于点F ,点G 是线段上一点,,点H 是线段上一点,,若已知的面积,则一定能求出()A .的面积B .的面积C .的面积D .的面积二、填空题(每小题4分,共24分)11.若两个相似多边形的相似之比是,则它们的周长之比是______.12.技术变革带来产品质量的提升.某企业技术变革后,抽检某一产品5000件,欣喜发现产品合格的频率已达到,若在相同条件下,我们可以用频率估计该产品合格的概率约为______.(结果保留两位小数)13.把函数的图象向上平移1个单位后所得图象的函数表达式是______.14.如图所示的图形叫弧三角形,又叫莱洛三角形,是机械学家莱洛首先进行研究的.弧三角形是这样画的:先画正三角形,然后分别以点A ,B ,C 为圆心,长为半径画弧.若正三角形的边长为2cm ,则弧三角形的周长为______cm .15.如图,一段抛物线:,记为,它与x 轴交于点O ,,将绕点顺时针旋转得到……,如此进行下去,得到一条连续的曲线,若点在这条曲线上,则m 的值为______.16.如图,在四边形中,,点E 是上一点,连结,,,ABC △AB DE BC ∥AC DF AC ∥BC AE AG GE =DF DH HF =BGH △ADE △BDF △ABG △CEF △2:50.991523y x =ABC AB ABC ()()505y x x x =--≤≤1C 1A 1C 1A 180︒2C ()2023,P m ABCD AD BC ∥AB AC CE ED,,,将沿翻折得到,若点恰好落在的延长线上,则______,______.三、解答题(第17、18、19题各6分,第20、21、22各8分,第23题10分,第24题12分,共66分)17.计算:(1)(2)已知,求18.在一个不透明的袋子中装有4个只有颜色不同的球,其中1个白球,3个红球.(1)从袋中随机摸出一个球,求摸出的球是白球的概率.(2)从袋中随机摸出一个球,放回,摇匀,再随机摸出一个球,请用树状图或列表法求两次摸出的球颜色相同的概率.19.如图,在6×6的正方形网格中,点A ,B ,C 均在格点上,请按要求作图.(1)在图1中,将绕点A 顺时针方向旋转,作出经旋转后的.(其中点D ,E 分别是点B ,C 的对应点).(2)在图2中,请用无刻度直尺找出过A ,B ,C 三点的圆的圆心,标出圆心O 的位置.20.如图,在中,是角平分线,点E 是边上一点,且.(1)求证:.(2)若,,求的长.BEC ADC ∠=∠10AB AC ==12BC =ACD △CD A CD '△A 'EDCE =BE =2sin 302cos30 tan 60︒-︒+︒12a b =2a b b+ABC △90︒ADE △ABC △AD AC ADE B ∠=∠ADB AED ∽△△3AE =5AD =AB21.如图,二次函数的图象与x 轴交于A 、B 两点,与y 轴交于点C ,连结,.(1)求点A 和点C 的坐标.(2)若在第一象限的二次函数图象上存在点D ,使,求点D 的坐标.22.如图,四边形内接于,延长,交于点E ,.(1)求证:是等腰三角形.(2)若点C 是中点,,,求的长.23.平面直角坐标系中,点,在函数(b ,c 是常数)的图象上.(1)若,,求该函数的表达式,(2)若,求证:该函数的图象经过点.(3)已知点,,在该函数图象上,若,,试比较,的大小,并说明理由.24.如图,内接于,是的直径,,过点A 作,交于点E ,点F 是上一点,连结交于点G ,连结交于点H.211322y x x =--AC CD ACO DCO ∠=∠ABCD O AB DC DE DA =BCE △ BD11AB =4BC =AD ()1,m ()2,n 2y x bx c =++2m =1n =2m n =()3,2()3,0()12,y -()25,y 0m >0n <1y 2y ABC △O BC O tan 2ACB ∠=AD BC ⊥OAB EF BC CF AD(1)求证:.(2)若,,求的长.(3)设,,求y 关于x 的函数表达式.2023学年第一学期初中期末考试九年级数学参考答案及评分参考一、选择题(每小题3分,共30分,在每小题给出的四个选项中,只有一项符合题目要求)题号12345678910答案ABADBDCBBB二、填空题(每小题4分,共24分)题号111213141516答案0.99610,4.4三、解答题(第17、18、19题各6分,第20、21题各8分,第22、23题10分,第24题12分,共66分)注:1.阅卷时应按步计分,每步只设整分.2.如有其它解法,只要正确,可参照评分标准,各步相应给分.17.解:(1)原式.(2)设,,原式.18.解:(1),(2)记三个红球为,,,摸两次球的所有可能结果如下:.19.解:(1)如图1,就是所求作的三角形.(2)如图2,点O 就是所求作的圆心.AFC HFE ∽△△10BC =8CF =EF OG x OC =AHy AD=2:5231y x =+2π1222=⨯-+1=1=a k =()20b k k =≠2255222k k k k k +⨯===1()4P =白球1红2红3红()105168P ∴==两次摸出的球颜色相同ADE △20.解:(1)在中,是角平分线,,,.(2),,,21.解:(1)二次函数的图象与x 轴交于点A 和B 两点,当时,,,,点,二次函数的图象与y 轴交于点C ,当时,,点.(2)如图,设与x 轴交于点E ,,,,,,点,设直线的函数表达式为.点,点直线的函数表达式为. ABC △AD BAD DAE ∴∠=∠B ADE ∠=∠ ADB AED ∴∽△△ADB AED ∽ △△AB ADAD AE ∴=3AE = 5AD =253AB ∴=211322y x x =-- 0y =2113022x x --=12x =-23x =∴()2,0A - 211322y x x =-- 0x =3y =-∴()0,3C -CD ACO DCO ∠=∠ 90AOC EOC ∠=∠=︒ CO CO =COA COE ∴≌△△2OE OA ∴==∴()2,0E CD )0(y kx b k =+≠ ()0,3C -()2,0E ∴CD 332y x =-令,得,当时,,点.22.解:(1),,四边形内接于,,,,,,是等腰三角形.(2)点C 是中点,,,,,,,,,,,,.23.解:(1)点,在函数(b ,c 为常数)的图象上,,,,该函数的表达式为.(2),,,,时,,该函数的图象经过点.(3),当时,,,当时,,抛物线经过点,抛物线的对称轴在直线的右侧,在直线的左侧,点到对称轴的距离大于点到对称轴的距离,而抛物线开口向上,.211333222x x x --=-10x =24x = 4x =3y =∴()4,3D DE DA = A E ∴∠=∠ ABCD O 180A DCB ∴∠+∠=︒180BCE DCB ∠+∠=︒ BCE A ∴∠=∠BCE E ∴∠=∠BE BC ∴=BCE ∴△ BD4CD BC ∴==4BE BC ∴==11415AE AB BE ∴=+=+=BCE A ∠=∠ E E ∠=∠BCE DAE ∴∽△△BE CEDE AE∴=4DE DC CE CE =+=+ 4415CECE ∴=+6CE ∴=10DE CD CE ∴=+=10AD ∴= ()1,m ()2,n 2y x bx c =++1,42,b c m b c n ++=⎧∴⎨++=⎩2m = 1n =12,421,b c b c ++=⎧∴⎨++=⎩4,5.b c =-⎧∴⎨=⎩∴245y x x =-+2m n = ()1242b c b c ∴++=++37c b ∴=--()237y x bx b ∴=++--3x = ()233372y b b =++--=∴()3,20m > ∴1x =0y >0n < ∴2x =0y < ()3,0∴2x =3x =∴()12,y -()25,y 12y y ∴>24.解:(1)是的直径,,,,和是所对圆周角,,.(2)如图,连结,是的直径,,,,,,,,,,,,,,,是的直径,,,,,,,,,,,,,BC O AD BC ⊥ CACE ∴=AFC CFE ∴∠=∠ACF ∠ AEF ∠ AF ACF AEF ∴∠=∠AFC HFE ∴∽△△BF BC O 90BAC ∴∠=︒tan 2ACB ∠= 2AB AC ∴=222AB AC BC += 10BC =AC ∴=AD BC ⊥ 90ADC ∴∠=︒tan 2ACB ∠= 2AD CD ∴=222AD CD AC += 2CD ∴=4AD ∴=4ED AD ∴==BC O 90BFC ∴∠=︒10BC = 8CF =6BF ∴=90BFC HDC ∠=∠=︒ FCB DCH ∠=∠BFC HDC ∴∽△△BF CFHD CD∴=1.5HD ∴= 5.5HE ED HD ∴=+=AFC HFE ∽ △△AC CFHE EF∴=EF ∴=(3)设,则,,,,,,①如图,当点G 在线段上时,,,,,过点G 作于点M ,,,,,,,,.,,即,又,,,,,.②如图,当点G 在线段上时,同理可求得.OC r =2BC r =tan 2ACB ∠= 2AD CD ∴=2BD AD =25CD r ∴=45AD r =OD OG x OC= OG xr ∴=()1CG x r =-()1BG x r =+GM CF ⊥90GMF ∴∠=︒ 90ADC ∠=︒CAE CFE ∠=∠FGM ACB ∴∠=∠tan tan 2FGM ACB ∴∠=∠=2FM GM ∴=90GMC BFC ∠=∠=︒ GM BF ∴∥CG CM GB MF ∴=2CG CMGB GM∴=2CG CM GB GM =CM CD GM HD =2CD CGHD GB∴=(1)5(1)x r HD x +∴=-4(1)3555(1)55r x r x AH AD HD r x x +-∴=-=-=--3544AH xAD x-∴=-3544x y x -∴=-OB 3544x y x+=+。
2023-2024学年重庆市渝北区九年级(上)期末数学试卷及答案解析

2023-2024学年重庆市渝北区九年级(上)期末数学试卷一、选择题:(本大题10个小题,每小题4分,共40分)在每个小题的下面,都给出了代号为A,B,C,D的四个选项,其中只有一个选项是正确的,请在答题卡上把你认为是正确的选项对应的方框涂黑.1.(4分)2的相反数是()A.B.C.﹣2D.22.(4分)下列4个汉字中可以看成是轴对称图形的是()A.中B.国C.繁D.华3.(4分)已知反比例函数的图象经过点(2,﹣3),则k的值是()A.B.6C.D.﹣64.(4分)下列调查中,适合普查的是()A.调查全国中学生的视力情况B.调查遭受积石山地震损坏的房屋数量C.调查一批电池的使用寿命D.调查市场上某种饮料的质量情况5.(4分)估计的值在()A.3与4之间B.4与5之间C.5与6之间D.6与7之间6.(4分)如图,已知AB∥CD,∠BAP=33°,∠DCP=21°,则∠P的度数为()A.52°B.53°C.54°D.55°7.(4分)周日上午,小张跑步去公园锻炼身体,到达公园后原地锻炼了一会之后散步回家,下面能反映小张离公园的距离y与时间x的函数关系的大致图象是()A.B.C.D.8.(4分)如图,⊙O是等边△ABC的外接圆,连接AO并延长交⊙O于点D,连接CD,,则△ADC的面积为()A.B.C.D.9.(4分)如图,点M是正方形ABCD边AB上一点,DN⊥CM于N,DN=2CN=2,则BN的长度为()A.2B.C.D.10.(4分)关于x的二次三项式M=2x2+ax+b,关于x的三次三项式N=3x3﹣5x2﹣7=c(x ﹣1)3+d(x﹣1)2+e(x﹣1)+f,下列说法中正确的个数为()①当多项式M•N乘积不含x3时,则5a=3b;②当M能被2x+1整除时,a﹣2b=1;③c﹣d+e=2.A.0B.1C.2D.3二、填空题:(本大题8个小题,每小题4分,共32分请将每小题的答案直接填写在答题卡中对应题号的横线上.11.(4分)()﹣1+()0=.12.(4分)一个多边形的内角和为900°,则这个多边形的边数为.13.(4分)有三张背面完全一样,正面分别写有数字1,0,﹣1的卡片,若将它们背面朝上并洗匀,从中随机抽取一张,记下卡片上的数字后放回洗匀,再从中随机抽取一张,则抽取的两张卡片上的数字的乘积为负数的概率是.14.(4分)若a2+2ab=4,b2﹣3ab=﹣2,则2a2+b2+ab=.15.(4分)如图,在菱形ABCD中,AB=4,∠BAD=60°,连接AC,取AC中点O,以点A为圆心,AO长为半径画弧,分别交边AD,AB于点E,F,则图中阴影部分的面积是.16.(4分)若关于x的一元一次不等式组有解且最多4个整数解,且关于y 的分式方程的解为整数,则符合条件的所有整数m的和为.17.(4分)如图,在菱形ABCD中AC交BD于点O,点M为OB的中点,连接AM并延长交BC于点N,若AC=12,BN=,则AN=.18.(4分)对于一个两位数,(0≤b≤a≤9,1≤a+b≤9),记F(m)=a+b,将m的十位数字与个位数字的和、十位数字与个位数字的差分别作为m'的十位数字和个位数字,新形成的两位数m'叫做m的伴生和差数,把m放置于m'十位数字与个位数字之间,就可以得到一个新的四位数M,最小的M为,若M能被7整除,则的最小值为.三、解答题:(本大题8个小题,第19小题8分,第20-26小题每小题8分,共78分)解答时每小题必须给出必要的演算过程或推理步骤,画出必要的图形(包括辅助线),请将解答过程书写在答题卡中对应的位置上.19.(8分)计算.(1)x(x+2)﹣(x+1)(x﹣1);(2).20.(10分)如图,在平行四边形ABCD中,BM⊥AC于点M.(1)用尺规完成以下基本作图:过点D作DN⊥AC于点N,并连接BN,DM.(保留作图痕迹,不写作法,不下结论)(2)求证:BN=DM.(请补全下面证明过程)证明:∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD.∴①.∵BM⊥AC,DN⊥AC,∴②.在△ABM 和△CDN 中,,∴△ABM ≌△CDN (AAS ).∴③.又∵BM ⊥AC ,DN ⊥AC ,∴BM ∥DN .∴④.∴BN =DM .21.(10分)宪法是我国的根本法,是治国安邦的总章程,是党和人民意志的集中体现.2023年12月4日是我国第十个国家宪法日,在这一天某学校开展了宪法知识竞答比赛.现从该校七、八年级中各随机抽取20名学生的比赛成绩进行整理分析(成绩用x 表示,满分100分,共分成四组:D 组0≤x <60,C 组60≤x <80,B 组80≤x <100,A 组x =100)下面给出了部分信息:七年级抽取的学生比赛成绩在B 组的数据是:98,88,89,90,95,86;八年级抽取的学生比赛成绩的数据是:50,52,52,59,63,66,78,78,78,87,89,92,96,100,100,100,100,100,100,100.七、八年级抽取的学生比赛成绩的统计表年级平均数众数中位数满分率七年级81.5100a m %八年级82b8835%根据以上信息,解答下列问题:(1)直接写出a ,b ,m 的值;(2)根据上述数据,你认为该校七、八年级中哪个年级学生对宪法知识掌握更好?请说明理由(写出一条理由即可);(3)该校七年级有400人,八年级有600人参加此次宪法知识竞答比赛,估计该校七、八年级参加此次比赛成绩满分的学生人数有多少人?22.(10分)2023年9月23日,第19届亚运会开幕式在杭州奥体中心体育场盛大开幕,潮起东方惊艳世界.奥体中心体育场的设计也同样令人赞叹,以莲花为原型,由28片大“莲花瓣”和27片小“莲花瓣”组成,宛如一朵绽放的莲花,栩栩如生.建设初期,计划由甲、乙两工程队承包完成其中一个小项目,若乙队单独施工,则恰好在计划工期完成;若甲队单独施工,可提前8天完成;若甲、乙两队先同时施工6天,剩下的由乙队单独施工,也可以提前8天完成.(1)求甲、乙两队单独完成该项目所需的时间;(2)实际施工时,甲队先单独施工若干天,剩下的工程由乙队单独施工完成.甲队每天施工费用为2万元,乙队每天施工费用为1.25万元,为了控制预算,该项目支付给工程队的施工总费用不超过45万元,则甲队至多施工多少天?23.(10分)如图,在矩形ABCD中,AB=3,BC=4,点Q为边BC上的中点.动点M从点A出发,沿折线AD﹣DC以每秒1个单位长度的速度向点C运动,到点C时停止.设为y.(y≠0)运动的时间为t秒,记S△MDQ(1)请直接写出y关于t的函数表达式以及对应的t的取值范围;(2)在给定的平面直角坐标系中画出这个函数的图象,并写出该函数的一条性质;(3)结合图象,当y≥2时,直接写t的取值范围.(保留一位小数,误差不超过0.2)24.(10分)如图,A,B,C是我国南部的三个岛屿,已知岛屿C在岛屿A的东北方向,岛屿B在岛屿A的正东方向,A,C两岛的距离为km,A,B两岛的距离为68km.(1)求出B,C两岛的距离;(2)在岛屿B产生了台风,风力影响半径为25km(即以台风中心B为圆心,25km为半径的圆形区域都会受到台风影响),台风中心以20km/h的速度由B向A移动,请判断岛屿C是否会受到台风的影响,若不会受到影响,请说明理由;若会受到影响,请求出台风影响岛屿C持续时间有多长?25.(10分)二次函数y=ax2+bx+4经过点A(﹣1,0),点B(4,0),点C,点D分别为二次函数与y轴的交点和顶点,点M为二次函数图象上第一象限内的一个动点.(1)求二次函数的解析式;(2)如图1,连接BC,过点A作BC的平行线交二次函数于点E,连接CM,BM,BE,CE.求四边形CMBE面积的最大值以及此时点M的坐标;(3)如图2,过点M作MN∥y轴,交BC于点N(点M不与点D重合),过点D作DH ∥y轴,交BC于点H,当DM=HN时,直接写出点M的坐标.26.(10分)已知△ABC,AB=AC.(1)如图1,∠BAC=60°,点D是线段BC上一点,将线段AD绕点A逆时针旋转60°到AM,连接DM,CM.若BD=2,CD=1,求△CDM的面积;(2)如图2,若∠BAC=90°,点D在边AB上,将线段AD绕点A顺时针旋转90°得到线段AM,连接MD并延长交BC于点H,连接AH,CD,猜想AH与CD存在的数量关系,并证明你的猜想;(3)如图3,若∠BAC=60°,AB=3,点D是线段BC上的一动点,连接AD,将线段AD绕点A逆时针旋转90°得到线段AQ,过点C作CE⊥AQ于点E交BA的延长线于点M,过点E分别作EN⊥AB于点N,作EH⊥AB于点H,连接NH,当NH取最大值时,请直接写出△NHE的面积.2023-2024学年重庆市渝北区九年级(上)期末数学试卷参考答案与试题解析一、选择题:(本大题10个小题,每小题4分,共40分)在每个小题的下面,都给出了代号为A,B,C,D的四个选项,其中只有一个选项是正确的,请在答题卡上把你认为是正确的选项对应的方框涂黑.1.【分析】根据相反数的概念解答即可.【解答】解:2的相反数是﹣2,故选:C.【点评】本题考查了相反数的意义,一个数的相反数就是在这个数前面添上“﹣”号;一个正数的相反数是负数,一个负数的相反数是正数,0的相反数是0.2.【分析】根据如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,这条直线叫做对称轴进行分析即可.【解答】解:选项B、C、D的汉字不能找到一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以不是轴对称图形.选项A的汉字能找到一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以是轴对称图形.故选:A.【点评】此题主要考查了轴对称图形,关键是正确确定对称轴位置.3.【分析】把点(2,﹣3)代入即可求解.【解答】解:∵反比例函数的图象经过点(2,﹣3),∴k=2×(﹣3)=﹣6.故选:D.【点评】本题考查了反比例函数图象上点的坐标特征,熟知待定系数法是解题的关键.4.【分析】根据普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似解答.【解答】解:A.调查全国中学生的视力情况,适合抽样调查,故本选项不符合题意;B.调查遭受积石山地震损坏的房屋数量,适合全面调查,故本选项符合题意;C.调查一批电池的使用寿命,适合抽样调查,故本选项不符合题意;D.调查市场上某种饮料的质量情况,适合抽样调查,故本选项不符合题意.故选:B.【点评】本题考查了抽样调查和全面调查的区别,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.5.【分析】先运用二次根式知识进行计算,再进行比较,即可得出答案.【解答】解:=4+,∵1<<2,∴5<4<6,∴的值在5与6之间.故选:C.【点评】此题考查了二次根式和无理数的估算能力,掌握二次根式的混合运算法则和无理数的估算是解题的关键.6.【分析】过点P作PE∥AB,则∠BAP=∠APE,再由AB∥CD可知PE∥CD,故∠DCP =∠EPC,据此可得出结论.【解答】解:过点P作PE∥AB,∵∠BAP=33°,∠DCP=21°,∴∠BAP=∠APE=33°,∵AB∥CD,∴PE∥CD,∴∠DCP=∠EPC=21°,∴∠P=∠APE+∠EPC=33°+21°=54°.故选:C.【点评】本题考查的是平行线的性质,熟知两直线平行,内错角相等是解题的关键.7.【分析】根据在每段中,离家的距离随时间的变化情况即可进行判断.【解答】解:图象应分三个阶段,第一阶段:跑步到公园,在这个阶段,离公园的距离随时间的增大而减小;第二阶段:在公园锻炼了一会,这一阶段公园的距离不随时间的变化而改变,即为0;第三阶段:散步回家,这一阶段,离公园的距离随时间的增大而增大,并且这段的速度小于第一阶段的速度.故选:C.【点评】本题主要考查函数图象,理解每阶段中,离家的距离与时间的关系,根据图象的斜率判断运动的速度是解决本题的关键.8.【分析】根据圆周角定理、垂径定理的推论得到∠ACD=90°,AD⊥CB,∠CAD=∠CAB,根据余弦的定义求出AD,再根据三角形的面积公式计算,得到答案.【解答】解:∵△ABC为等边三角形,AB=3,∴AC=BC=AB=3,∠CAB=60°,∵AD是⊙O的直径,∴∠ACD=90°,AD⊥CB,∠CAD=∠CAB=30°,∴CE=EB,在Rt△ACE中,∠CAD=30°,AC=3,∴CE=AC=,在Rt△ACD中,∠CAD=30°,AC=3,∴AD==6,=××6=,∴S△ADC故选:C.【点评】本题考查的是三角形的外接圆与外心、等边三角形的性质、垂径定理的推论、圆周角定理,掌握相关的性质定理是解题的关键.9.【分析】过点B作BE⊥CM于E,可证得△DCN≌△CBE(AAS),再证得△BNE是等腰直角三角形,即可求得答案.【解答】解:如图,过点B作BE⊥CM于E,∵DN⊥CM,BE⊥CM,∴∠DNC=∠CEB=90°,∴∠DCN+∠CDN=90°,∵四边形ABCD是正方形,∴DC=CB,∠ABC=∠BCD=90°,∴∠DCN+∠BCE=90°,∴∠CDN=∠BCE,∴△DCN≌△CBE(AAS),∴DN=CE,CN=BE,∵DN=2CN=2,∴CN=BE=1,CE=2,∴EN=CE﹣CN=2﹣1=1,∴EN=BE=1,∵∠BEN=90°,∴△BNE是等腰直角三角形,∴BN=BE=.故选:B.【点评】本题考查了正方形的性质,等腰直角三角形的性质,全等三角形的判定和性质等,添加辅助线构造全等三角形是解题关键.10.【分析】①根据多项式乘以多项式的运算法则展开,再由题意可得5a﹣3b=0;②由题意可知(2x2+ax+b)÷(2x+1)=x+b,则2x2+2bx+x+b=2x2+ax+b,即可求得a﹣2b=1;③由题意可得3x3﹣5x2﹣7=c(x3﹣3x2+3x﹣1)+d(x2﹣2x+1)+e(x﹣1)+f,从而得到c=3,d﹣3c=﹣5,3c﹣2d+e=0,分别求出c、d、e的值即可判定.【解答】解:①M•N=(2x2+ax+b)(3x3﹣5x2﹣7)=6x5﹣10x4﹣14x2+3ax4﹣5ax3﹣7ax+3bx3﹣5bx2﹣7b=6x5﹣(10﹣3a)x4﹣(14+5b)x2﹣(5a﹣3b)x3﹣7ax﹣7b,∵多项式M•N乘积不含x3,∴5a﹣3b=0,故①符合题意;②(2x2+ax+b)÷(2x+1)=x+b,∴2x2+2bx+x+b=2x2+ax+b,∴2b+1=a,即a﹣2b=1;故②符合题意;∵3x3﹣5x2﹣7=c(x﹣1)3+d(x﹣1)2+e(x﹣1)+f,∴3x3﹣5x2﹣7=c(x3﹣3x2+3x﹣1)+d(x2﹣2x+1)+e(x﹣1)+f,∴c=3,d﹣3c=﹣5,3c﹣2d+e=0,解得d=4,e=﹣1,∴c﹣d+e=3﹣4﹣1=﹣2,故③不符合题意;故选:C.【点评】本题考查多项式,熟练掌握多项式乘以多项式的运算法则是解题的关键.二、填空题:(本大题8个小题,每小题4分,共32分请将每小题的答案直接填写在答题卡中对应题号的横线上.11.【分析】利用负整数指数幂,零指数幂计算即可.【解答】解:原式=3+1=4,故答案为:4.【点评】本题考查实数的运算,熟练掌握相关运算法则是解题的关键.12.【分析】本题根据多边形的内角和定理和多边形的内角和等于900°,列出方程,解出即可.【解答】解:设这个多边形的边数为n,则有(n﹣2)×180°=900°,解得:n=7,∴这个多边形的边数为7.故答案为:7.【点评】本题主要考查多边形的内角和定理,解题的关键是根据已知等量关系列出方程从而解决问题.13.【分析】列表可得出所有等可能的结果数以及抽取的两张卡片上的数字的乘积为负数的结果数,再利用概率公式可得出答案.【解答】解:列表如下:10﹣11(1,1)(1,0)(1,﹣1)0(0,1)(0,0)(0,﹣1)﹣1(﹣1,1)(﹣1,0)(﹣1,﹣1)共有9种等可能的结果,其中抽取的两张卡片上的数字的乘积为负数的结果有:(1,﹣1),(﹣1,1),共2种,∴抽取的两张卡片上的数字的乘积为负数的概率为.故答案为:.【点评】本题考查列表法与树状图法,熟练掌握列表法与树状图法以及概率公式是解答本题的关键.14.【分析】把原式整理后,再代入化简即可.【解答】解:由b2﹣3ab=﹣2得:b2=﹣2+3ab,由a2+2ab=4得:a2=4﹣2ab.2a2+b2+ab=2a2﹣2+3ab+ab=2(4﹣2ab)﹣2+3ab+ab=8﹣4ab﹣2+3ab+ab=6.故答案为:6.【点评】本题考查了代数式的化简,熟练进行整理化简是解题的关键.15.【分析】阴影部分的面积=菱形ABCD的面积﹣扇形AEF的面积.【解答】解:连接BD,∵∠BAD=60°,四边形ABCD是菱形,∴∠BAC=∠DAC=30°,AC⊥BD,∵AB=4,∴AO=AB•cos∠BAC=2,BO=AB•sin∠BAC=2,AC=4,BD=4,阴影部分的面积=×AC×BD﹣=8﹣2π,故答案为:8﹣2π.【点评】本题考查了菱形、扇形的面积,关键是掌握菱形、扇形的面积公式.16.【分析】求出一元一次不等式组的解集,根据它有解且最多4个整数解,求得m的取值范围;解分式方程,根据其解为整数,求得所有符合条件的m的值,将这些值相加即可.【解答】解:不等式组的解集为﹣4<x<m,∵原不等式组有解且最多4个整数解,∴﹣4<m≤1.分式方程的解为y=,∵y=1是原分式方程的增根,∴m≠﹣1.∴﹣1<m+3≤4,且m+3≠2,∵y=为整数,∴m+3=0或4,当m+3=0时,m=﹣3;当m+3=4时,m=1,﹣3+1=﹣2,故答案为:﹣2.【点评】本题考查分式方程的解和解一元一次不等式组,熟练掌握它们的解法是本题的关键.17.【分析】通过证明△ADM∽△NBM,可得=3,可得AD=3BN=6,AM =3MN,由勾股定理可求DO的长,AM的长,即可求解.【解答】解:∵四边形ABCD是菱形,∴AC⊥BD,AO=CO=AC=6,BO=DO,∵点M为OB的中点,∴OM=BM,∴DM=3OM=3BM,∵AD∥BC,∴△ADM∽△NBM,∴=3,∴AD=3BN=6,AM=3MN,∴DO===12,∴MO=BM=6,∴AM===6,∴MN=2,∴AN=AM+MN=8,故答案为:8.【点评】本题考查了相似三角形的判定和性质,菱形的性质,勾股定理,证明三角形相似是解题的关键.18.【分析】根据题意用a、b写出四位数M的表达式,根据a、b的范围,可得最小的M,因为M能被7整除,所以可知a和b的取值,即得的最小值.【解答】解:∵两位数m的十位数字是a,个位数字是b,两位数m′的十位数字是(a+b),个位数字是(a﹣b),∴四位数M=1000(a+b)+100a+10b+(a﹣b)=1101a+1009b,∴a=1,b=0时,M最小,M=1101,∵M能被7整除,1≤a+b≤9,∴a=3,b=1时,M=4312,a=5,b=4时,M=9541,a=6,b=2时,M=8624,a=7,b=0时,M=7707,==+最小,即最小,∴a=7,b=0时,=,故答案为:1101,.【点评】本题考查了整式的加减,关键是计算正确.三、解答题:(本大题8个小题,第19小题8分,第20-26小题每小题8分,共78分)解答时每小题必须给出必要的演算过程或推理步骤,画出必要的图形(包括辅助线),请将解答过程书写在答题卡中对应的位置上.19.【分析】(1)直接利用单项式乘多项式以及平方差公式计算,进而得出答案;(2)直接将括号里面通分运算,再利用分式的混合运算法则计算得出答案.【解答】解:(1)原式=x2+2x﹣(x2﹣1)=x2+2x﹣x2+1=2x+1;(2)原式=[+]•=•=.【点评】此题主要考查了分式的混合运算、整式的混合运算,正确掌握相关运算法则是解题关键.20.【分析】(1)利用基本作图,过D点作AC的垂线即可;(2)先根据平行四边形的性质得到AB∥CD,AB=CD.则∠BAM=∠DCN,再证明△ABM≌△CDN得到BM=DN,然后判断四边形BMDN为平行四边形,从而得到BN=DM.【解答】(1)解:如图,DN为所作;(2)证明:∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD.∴∠BAM=∠DCN,∵BM⊥AC,DN⊥AC,∴∠AMB=∠CND,在△ABM和△CDN中,,∴△ABM≌△CDN(AAS),∴BM=DN,又∵BM⊥AC,DN⊥AC,∴BM∥DN.∴四边形BMDN为平行四边形,∴BN=DM.故答案为:∠BAM=∠DCN,∠AMB=∠CND,BM=DN,四边形BMDN为平行四边形.【点评】本题考查了作图﹣基本作图:熟练掌握5种基本作图是解决问题的关键.也考查了全等三角形的判定与性质、平行四边形的判定与性质.21.【分析】(1)根据中位数和众数的定义解答即可求出a、b的值,用“1”分别减去其它三个等级所占百分比可得m的值;(2)根据平均数、中位数和满分率进行判断即可;(3)分别求出七、八年级学生竞赛成绩的满分率即可求解.【解答】解:(1)七年级学生竞赛成绩从小到大排列后,处在中间位置的两个数的平均数为(86+88)÷2=87(分),因此中位数是87分,即a=87;八年级学生竞赛成绩的100出现的次数最多,故众数为100,即b=100;m%=1﹣25%﹣20%﹣=25%,即m=25.(2)八年级学生对宪法知识掌握更好,理由如下:因为八年级学生的平均数、中位数和满分率都高于七年级,所以八年级学生对宪法知识掌握更好;(3)400×25%+600×35%=100+210=310(人),答:估计该校七、八年级参加此次比赛成绩满分的学生人数大约有310人.【点评】本题考查扇形统计图、中位数、众数、平均数以及用样本估计总体,理解中位数、众数的计算方法是正确求解的前提.22.【分析】(1)设甲队单独完成该项目所需的时间为x天,则乙队单独完成该项目所需的时间为(x+8)天,根据若甲、乙两队先同时施工6天,剩下的由乙队单独施工,也可以提前8天完成.列出分式方程,解方程即可;(2)设甲队施工y天,则乙队施工=(32﹣y)天,根据该项目支付给工程队的施工总费用不超过45万元,列出一元一次不等式,解不等式即可.【解答】解:(1)设甲队单独完成该项目所需的时间为x天,则乙队单独完成该项目所需的时间为(x+8)天,由题意得:+=1,解得:x=24,经检验,x=24是原方程的解,且符合题意,∴x+8=24+8=32,答:甲队单独完成该项目所需的时间为24天,乙队单独完成该项目所需的时间为32天;(2)设甲队施工y天,则乙队施工=(32﹣y)天,由题意得:2y+1.25(32﹣y)≤45,解得:y≤15,答:甲队至多施工15天.【点评】本题考查了分式方程的应用以及一元一次不等式的应用,解题的关键是:(1)找准等量关系,正确列出分式方程;(2)找出数量关系,正确列出一元一次不等式.23.【分析】(1)分为:当0<t<4时,y=DM•AB=(4﹣t)=﹣;当4<t≤7时,y==t﹣4;(2)取(0,6),(4,0)及(7,3)作出图象,根据函数图象写增减性;(3)当y=2时,由﹣和t﹣4=2分别求出t的值,进而得出结果.【解答】解:(1)如图1,当0<t<4时,y=DM•AB=(4﹣t)=﹣,如图2,当4<t≤7时,y==t﹣4,综上所述:y=;(2)如图3,在4<t≤7范围内,y随着t的增大而增大;(3)当y=2时,由﹣得,t=≈2.7,由t﹣4=2得,t=6,∴当y≥2时,0<t≤2.7或6≤t≤7.【点评】本题考查了求一次函数的解析式,根据解析式画一次函数的图象,一次函数及其图象的性质等知识,解决问题的关键是熟练掌握有关基础知识.24.【分析】(1)过点C作CD⊥AB于点D,在Rt△ACD中,利用勾股定理可求出AD,CD,再在Rt△BCD中,利用勾股定理即可求出BC,从而解决问题;(2)由25>20,可知会受影响.以点C为圆心,25km长为半径画弧与AB交于点E,F,利用勾股定理求出DE,进而得到EF的长,再除以台风移动速度即可求出台风影响岛屿C持续时间.【解答】解:(1)过点C作CD⊥AB于点D,由题意知:∠ACD=45°,∴∠A=∠ACD=45°,∴CD=AD,在Rt△ACD中,AC=km,由勾股定理,得AD2+CD2=AC2,∴2AD2=()2,解得AD=20km(负值已舍),∴CD=20km,在Rt△BCD中,BD=AB﹣AD=68﹣20=48(km),由勾股定理,得BC===52(km),答:B,C两岛的距离为52km;(2)会受影响,以点C为圆心,25km长为半径画弧与AB交于点E,F,则EF=2DE,在Rt△CDE中,由勾股定理,得DE===15(km),∴EF=30km,30÷20=1.5(h),答:台风影响岛屿C持续时间为1.5h.【点评】本题考查勾股定理的应用,理解题意,通过作CD⊥AB构造直角三角形是解题的关键.25.【分析】(1)用待定系数法求函数的解析式即可;(2)求出直线BC的解析式,再由平行线的性质求出直线AE的解析式从而确定E点坐标,再由直线CE的解析式求出直线CE与x轴的交点坐标,从而求出三角形BCE的面积,过点M作MG∥y轴交直线BC于点G,设M(t,﹣t2+3t+4),则G(t,﹣t+4),可=﹣2(t﹣2)2+8,从而求出四边形面积的最大值及点M的坐标;得S△BCM(3)求出D(,),H(,),设M(x,﹣x2+3x+4),则N(x,﹣x+4),则DM =,HN=,再由DM=HN,求出x=(舍)或x=或x=,即可求M点坐标.【解答】解:(1)将点A(﹣1,0),点B(4,0)代入y=ax2+bx+4,∴,解得,∴二次函数的解析式为y=﹣x2+3x+4;(2)当x=0时,y=4,∴C(0,4),∴OC=OB=4,∴直线BC的解析式为y=﹣x+4,∵AE∥BC,∴直线AE的解析式为y=﹣x﹣1,当﹣x﹣1=﹣x2+3x+4时,解得x=﹣1或x=5,∴E(5,﹣6),设CE的直线解析式为y=kx+4,∴5k+4=﹣6,解得k=﹣2,∴直线CE的解析式为y=﹣2x+4,∴直线CE与x轴的交点为(2,0),=(4﹣2)×(4+6)=10,∴S△BCE过点M作MG∥y轴交直线BC于点G,设M(t,﹣t2+3t+4),则G(t,﹣t+4),∴MG=﹣t2+3t+4+t﹣4=﹣t2+4t,=4×(﹣t2+4t)=﹣2(t﹣2)2+8,∴S△BCM+S△BCM=10﹣2(t﹣2)2+8,∴四边形CMBE的面积=S△BCE∵0<t<4,∴当t=2时,四边形CMBE的面积有最大值18,此时M(2,6);(3)∵y=﹣x2+3x+4=﹣(x﹣)2+,∴D(,),∵DH∥y轴,∴H(,),设M(x,﹣x2+3x+4),则N(x,﹣x+4),∴DM=,HN=,∵DM=HN,∴=,解得x=(舍)或x=或x=,∴M(,)或(,).【点评】本题考查二次函数的图象及性质,熟练掌握二次函数的图象及性质,两点间距离公式,平行线的性质,铅锤法求面积是解题的关键.26.【分析】(1)可证明△BAD≌△CAM,从而得出∠ACM=∠AB=60°,CM=BD=2,进一步得出结果;(2)作AG⊥MH于G,可证明△AGH∽△DAC,进一步得出结果;(3)可证得四边形BCEN内接于以BE为直径的圆,从而得出NH=BE•sin∠ABC=BE,故当BE最大时,NH最大,可证得E在以AC为直径的圆O上运动,连接BO 并延长,交⊙O于点E,此时BE最大,NH最大,NH交BE于X,进一步得出结果.【解答】解:(1)如图1,作ME⊥BC,交BC的延长线于点E,∵AB=AC,∠BAC=60°,∴△ABC是等边三角形,∴∠B=∠ACB=60°,∵线段AD绕点A逆时针旋转60°到AM,∴∠AD=AM,∠DAM=60°,∴∠BAC=∠DAM,∴∠BAD=∠CAM,∴△BAD≌△CAM(SAS),∴∠ACM=∠AB=60°,CM=BD=2,∴∠MCE=180°﹣∠ACB﹣∠ACM=60°,∴EM=CM=,=;∴S△CDM(2)如图2,CD=AH,理由如下:作AG⊥MH于G,∵∠BAC=90°,线段AD绕点A顺时针旋转90°得到线段AM,∴AD=AM,∠DAM=90°,M、A、C共线,∴∠BDH=∠ADM=∠M=45°,∵AB=AC,∠BAC=90°,∴∠B=∠ACB=45°,∴∠DHC=∠BHD=90°,∴∠DHC+∠BAC=180°,∴点A、D、H、C共圆,∴∠AHG=∠ACD,∵∠AGH=∠BAC=90°,∴△AGH∽△DAC,∴,∴CD=AH;(3)如图3,∵EN⊥AB,EH⊥BC,∴∠ENB=∠EHB=90°,∴四边形BCEN内接于以BE为直径的圆,∵∠ABC=60°,∴NH=BE•sin∠ABC=BE,∴当BE最大时,NH最大,∵∠AEC=90°,AC=AB=3,∴E在以AC为直径的圆O上运动,连接BO并延长,交⊙O于点E,此时BE最大,NH最大,NH交BE于X,此时BE=OB+OE=AB+AC=AB=,∴EN=EH=BE=,∴NX=HX=EN=,EX=EN=,=NH•EX=NX•EX=.∴S△NHE【点评】本题考查了全等三角形的判定和性质,相似三角形的判定和性质,确定圆的条件,等腰三角形的判定和性质,解直角三角形等知识,解决问题的关键是将条件转化。
河南省平顶山市2023-2024学年九年级上学期期末数学试题(含答案)
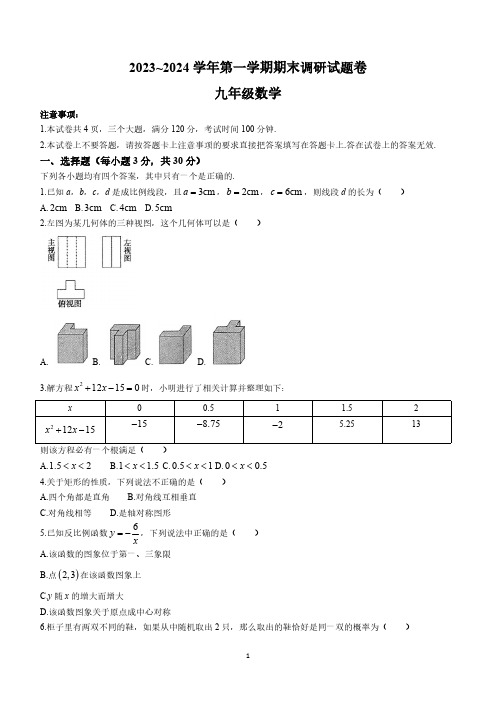
2023~2024学年第一学期期末调研试题卷九年级数学注意事项:1.本试卷共4页,三个大题,满分120分,考试时间100分钟.2.本试卷上不要答题,请按答题卡上注意事项的要求直接把答案填写在答题卡上.答在试卷上的答案无效.一、选择题(每小题3分,共30分)下列各小题均有四个答案,其中只有一个是正确的.1.已知a ,b ,c ,d 是成比例线段,且,,,则线段d 的长为( )A. B. C. D.2.左图为某几何体的三种视图,这个几何体可以是()A.B. C. D.3.解方程时,小明进行了相关计算并整理如下:x0.511.525.2513则该方程必有一个根满足()A. B. C. D.4.关于矩形的性质,下列说法不正确的是()A.四个角都是直角B.对角线互相垂直C.对角线相等D.是轴对称图形5.已知反比例函数,下列说法中正确的是()A.该函数的图象位于第一、三象限B.点在该函数图象上C.y 随x 的增大而增大D.该函数图象关于原点成中心对称6.柜子里有两双不同的鞋,如果从中随机取出2只,那么取出的鞋恰好是同一双的概率为()3cm a =2cm b =6cm c =2cm 3cm 4cm 5cm212150x x +-=21215x x +-15-8.75-2-1.52x <<1 1.5x <<0.51x <<00.5x <<6y x=-()2,3A.B. C.D.7.如图,四边形为平行四边形,E ,F 为边的三等分点,连接,,交点为G ,则等于()A. B. C. D.8.某商品原价为100元,连续两次降价后为81元,设平均每次降价的百分率为x ,则下列方程正确的是( )A. B.C. D.9.如图,矩形的四个顶点分别在直线,,,上,若直线且相邻两直线间距离相等.若,,则,之间的距离为()A.5B.C. D.10.如图,一组等腰三角形的底边均在x 轴的正半轴上,两腰的交点在反比例函数的图象上,且它们的底边都相等.若记,,…的面积分别为则的值为()13141516ABCD CD AF BE :EFG BAG S S △△1:91:41:31:2()2811100x +=()2100181x -=()1001281x -=()8112100x +=ABCD 1l 3l 4l 2l 1234l l l l ∥∥∥6AB =4BC =2l 3l 65125245()10y x x=>11OA B △122A A B △233A A B △101110121012A A B △1231012,,S S S S 1012SA.B. C. D.二、填空题:(每小题3分,共15分)11.如果,那么_______.12.已知关于x 的一元二次方程的一个根是1,则_______.13.一个口袋中装有红球和白球共10个,这些球除颜色外都相同,将口袋中的球摇匀,从中随机摸出一个球,记下它的颜色后再放回口袋中.不断重复这一过程,共摸了100次球,发现共有70次摸到红球,估计这个口袋中自球的个数为_______.14.如图,菱形中,对角线,相交于点O ,点E 为的中点,连接,若,则菱形的周长为_______.15.如图,已知点E ,F 分别为三角形纸片的边,上的点,将三角形纸片沿所在直线折叠,点B 的对应点恰好落在边上.已知,.若以,F ,C 为顶点的三角形与相似,则的长是______.三、解答题(本大题共8个小题,共75分)16.(10分)解方程:(1)(用因式分解法)(2)(用公式法)17.(9分)如图,一转盘被等分为三个区城,上面分别标有数字1,0,,转动转盘,指针停止后指向哪个区域,就得到该区域上的数字.(指针停在分界线上时,重新转动转盘,直到指向一个区域内部)(1)小明转动转盘一次,得到的数字是非负数的概率为_____;(2)小明和小红分别转动转盘一次,用树状图或列表的方法求两人得到相同数字的概率.1101211013120231202412a b =aa b=+22340x kx -+=k =ABCD AC BD AB OE 3.5OE =ABCD ABC AB BC ABC EF B 'AC 3AB AC ==4BC =B 'ABC △BF ()5454x x x +=+22980x x -+=1-18.(9分)已知点E 是边的中点,连接并延长交的延长线于点F ,连接,,且.(1)求证:四边形为矩形;(2)若,请直接写出的长.19.(9分)已知,关于x 的一元二次方程.(1)试说明:不论m 取何值时,该方程总有实数根;(2)若这个一元二次方程的一根大于2,另一根小于2,求m 的取值范围.20.(9分)如图,白鹭洲国家湿地公园广场有一灯柱,M 为光源.某兴趣小组为了测量灯柱的高度,在灯柱同侧竖立两根长度均为的标杆和.测得的影长等于,且点N ,B ,C 在同一条直线上.(1)请画出标杆的影子;(2)若,求灯柱的高度.21.(9分)据统计,摩托车、电动自行车、小汽车是导致交通事故死亡最多的车辆,摩托车、电动自行车驾乘人员死亡事故中约80%为颅脑损伤致死.为确保安全出行,交警提醒骑车出行必须佩戴头盔.某头盔品牌厂商在各大电商平台共有100个网店,一个网店平均每月销售1000个头盔.现准备多开一些网店以提高销售量,试验发现,每多开1个网店,每个网店头盔月销售量就会减少2个,但随着网店数量增加,运营成本也会增加,如果要使每月总销售量增加15.2%,且尽可能减少运营成本,那么应多开几个网店?22.(10分)已知一次函数与反比例函数的图象交于A ,B 两点,且点A 的坐标为.(1)求m 的值及反比例函数的解析式;(2)连接,,求的面积;(3)观察图象,请直接写出的解集.ABCD AD BE CD BD AF AD BF =ABDF 3CD ED ==BD ()2430x m x m -+++=MN MN 1.6m AB CD AB BC 3m CD CE 4m CE =MN 5y x =-+ky x=()4,m OA OB AOB △5kx x-+>23.(10分)如图1,四边形和四边形均为正方形,点E ,G 分则在,上,,分别为两正方形的对角线.(I )猜想:图1中的值为_______;(2)探究:将正方形绕点A 旋转到图2位置,连接,,判断的值是否保持不变?并说明理由.(3)延伸:若将正方形绕点A 旋转到图3位置,其中G ,E ,B 三点在一条直线上,延长交边于点H ,若,请直接写出正方形与正方形的边长.2023~2024学年第一学期期末调研试题九年级数学参考答案一、选择题(每题3分,共30分)题号12345678910答案CDBBDAABCC二、填空题(每小题3分,共15分)题号1112131415答案2328或2三、解答题(本大题共8个小题,共75分)ABCD AEFG AB AD AC AF FCEBAEFG BE FC FCEBAEFG AF CD BE =FH =AEFG ABCD 1312716.(1)解:原方程可变形为或,.(2)解:这里,,即,17.(9分)解:(1)(2)第一次第二次110共9种等可能的结果,其中两次数字相同的结果有3个,所以二人得到相同数字的概率.18.(9分)(1)证明:四边形是平行四边形,,,点E 为的中点,,又,四边形是平行四边形,又是矩形.()()54540x x x +-+=()()5410x x +-=540x +=10x -=∴145x =-21x =2a =9b =-8c = ()2249428170b ac -=--⨯⨯=>∴x =1x =2x =231-()1,1()0,1()1,1-()1,0()0,0()1,0-1-()1,1-()0,1-()1,1--13ABCD ∴AB DC ∥AB DC =∴EAB EDF∠=∠ AD ∴AE DE = AEB DEF ∠=∠∴()AEB DEF ASA ≌△△∴BE FE= AE DE=∴ABDF BF AD=∴ABDF(2)19.(9分)解:(1)由题可知:,,.即不论m 取何值,原方程有两个实数根.(2)解方程得,因为,,即.所以m 的取值范围是.20.(9分)解:(1)如图所示的影子为;(2)由题意可知,,.即设灯柱的高度为x m ,根据题意,得由,得即代入数据,化简得由,得即BD =1a =()4b m =-+3c m =+()()224443b ac m m -=-+-⨯+⎡⎤⎣⎦()220m =+≥∴()2430x m x m -+++=()422m m x +±+=∴11x =23x m =+12<∴32m +>1m >-1m >-CD CE MN NE ⊥AB NE ⊥CD NE ⊥90MNE ABC DCE ∠=∠=∠=︒MN ABC MNE ∠=∠MCN MCN ∠=∠ABC MNC △∽△AB BCx BC BN=+331.6xBN =-DCE MNE ∠=∠MEN MEN ∠=∠DCE MNE △∽△CD ECx EC BC BN=++代入数据,化简得,(m )答:灯柱的高度为.21.解:设应增加x 个网店,根据题意,得解得,,因为网店越多,运营成本增加越多,为减少运营成本x 取20 答:应增加20个网店.22.(10分)解:(1)点是直线与的交点,把,,代入得.,.(2)设一次函数的图象分别与x 轴,y 轴交于M ,N 两点由得,.由与得B 的坐标为(3)x 的取值范围为或.23.(10分)解:(1);471.6x BN =-∴34371.6 1.6x x -=-∴ 6.4x =MN 6.4m ()()()100021001001000115.2%x x -+=⨯⨯+120x =2380x = ()4,A m 5y x =-+ky x=∴4x =y m =5y x =-+451m =-+=∴414k =⨯=∴1m =4y x=5y x =-+5OM =5ON =5y x =-+4y x=()1,4AOB MON AOM BONS S S S =--△△△△111555151222=⨯⨯-⨯⨯-⨯⨯152=0x <14x <<FCEB=(2)①四边形与四边形是正方形,,即②正方形的边长为3,正方形的边长为.ABCD AEFG ∴45EAF BAC ∠=∠=︒FA ACAE AB==∴EAF CAE BAC CAE∠+∠=∠+∠CAF BAE∠=∠∴CAF BAE △∽△∴FC AC FAEB AB AE===AEFGABCD。
2023-2024学年安徽省合肥市中国科大附中高新中学九年级(上)期末考试数学试卷(含答案)

2023-2024学年合肥市中国科大附中高新中学九年级(上)期末考试数学试卷一、选择题:本题共10小题,每小题4分,共40分。
在每小题给出的选项中,只有一项是符合题目要求的。
1.下列图形中,既是轴对称图形又是中心对称图形的是( )A. B. C. D.2.反比例函数y =−4x 的图象一定经过的点是( )A. (1,4)B. (−1,−4)C. (−2,2)D. (2,2)3.若x +y y =53,则x y 等于( )A. 32B. 83C. 23D. 584.下列关于抛物线y =−x 2−9的说法,正确的是( )A. 抛物线开口向上B. 抛物线过点(−1,−8)C. 抛物线的对称轴是直线x =0D. 抛物线与x 轴有两个交点5.如图,直线l 1 // l 2 // l 3,直线AC 分别交直线l 1、l 2、l 3于点A 、B 、C ,直线DF 分别交直线l 1、l 2、l 3于点D 、E 、F ,直线AC 、DF 交于点P ,则下列结论错误的是( )A. AB BC =DE EFB. PA PC =PD PFC. PA PB =PE PFD. PB PE =AC DF6.如图,在正方形网格中,点A,B,C都在格点上,则sin A的值为( )A. 1010B. 31010C. 13D. 557.如图,是直立在高速公路边水平地面上的交通警示牌,经测量得到如下数据:AM=4米,AB=8米,∠MAD=45°,∠MBC=30°,则警示牌的高CD为( )A. 43米B. (23+2)米C. (42−4)米D. (43−4)米8.如图,四边形ABCD内接于⊙O,AD=DC,∠CBE=45∘,∠AOD的大小为( )A. 130∘B. 100∘C. 145∘D. 135∘9.如图,将一个小球从斜坡的点O处抛出,小球的抛出路线可以用二次函数y=4x−12x2刻画,斜坡可以用一次函数y=12x刻画.下列结论错误的是( )A. 小球距O点水平距离超过4米呈下降趋势B. 当小球水平运动2米时,小球距离坡面的高度为6米C. 小球落地点距O点水平距离为7米D. 当小球拋出高度达到8m时,小球距O点水平距离为4m10.如图,点A,B的坐标分别为A(2,0),B(0,2),点C为坐标平面内一点,BC=1,点M为线段AC的中点,连接OM,则OM的最大值为( )A. 2+1B. 2+12C. 22+1 D. 22−12二、填空题:本题共4小题,每小题5分,共20分。
2023-2024学年安徽省阜阳市颍州区九年级(上)期末数学试卷(含答案)

2023-2024年度(上)九年级期末学情调研数学卷注意事项:1.数学试卷满分150分,考试时间为120分钟.2.本试卷包括“试题卷”和“答题卷”两部分,“试题卷”共4页,“答题卷”共6页.3.请务必在“答题卷”上答题,在“试题卷”上答题无效.4.考试结束后,请将“试题卷”和“答题卷”一并交回.一、选择题(本大题共10小题,每小题4分,满分40分,每小题都给出A ,B ,C ,D 四个选项,其中只有一个是符合题目要求的)1.我国传统文化中的“福禄寿喜”图(如图)由四个图案构成,这四个图案中是中心对称图形的是()A .B .C .D .2.若是关于x 的一元二次方程的一个根,则( )A .6B .9C .D .3.在平面直角坐标系中,已知点M 的坐标为,则下列说法不正确的是( )A .点M 在第四象限B .点M 关于x 轴的对称点的坐标为(6,5)C .点M 关于y 轴的对称点的坐标为D .点M 关于原点的对称点的坐标为4.下列函数中,当时,y 随x 的增大而减小的是( )A .B .C .D .5.有数字4,5,6的三张卡片,将这三张卡片任意摆成一个三位数,摆出的三位数是2的倍数的概率是( )A.B .C .D .6.如图,五边形ABCDE 为⊙O 的内接正五边形,点P 为劣弧上的任意一点(不与D ,E 重合),则∠EPD的度数是()第6题图A .136°B .144°C .145°D .150°7.如图,边长为1的正方形ABCD 绕点A 顺时针旋转30°到正方形AB 'C 'D ',则图中阴影部分的面积为()20x c +=c =6-9-()6,5-()6,5--()5,6-0x <1y x=-()211y x =-++21y x =--3y x=56342312»DE 3x =-第7题图A .1BC .D .8.已知一次函数和反比例函数的图象如图所示,则二次函数的图象大致可能是()第8题图A .B .C .D .9.如图,在矩形ABCD 中,,点E ,F 分别为BC ,CD 的中点,BF ,DE 相交于点G ,过点E 作,交BF 于点H ,则线段GH 的长是()第9题图A .B .1C .D .10.如图,点A ,B 是半径为2的⊙O 上的两点,且)第10题图A .圆心O 到AB 的距离为12-2y ax b =+c y x=2y ax bx c =++6,4AB AD ==EH CD ∥565453AB =B .在圆上取异于A ,B 的一点C ,则△ABC 面积的最大值为C .以AB 为边向上作矩形ABPQ ,交⊙O 于点P ,Q ,则扇形OPQ 的面积为πD .取弦AB 的中点D ,当AB 绕点O 旋转一周时,点D 运动的路线长为2π二、填空题(本大题共4小题,每小题5分,满分20分)11.如果将抛物线向下平移2个单位长度,那么所得新抛物线的函数解析式是______.12.已知等腰三角形的两边长为方程的两根,则这个等腰三角形的周长为______.13.如图,点A 在x 轴的正半轴上,点C 在反比例函数的图象上,AC 交y 轴于点B .若点B是AC 的中点,△AOB 的面积为2,则k 的值为______.第13题图14.如图,在边长为4的正方形ABCD 中,P 为BC 的中点,点Q 在射线AD 上,过点Q 作于点E ,连接PQ .请解决下列问题:第14题图(1)______;(2)当△ABP 与△PEQ 相似时,______.三、(本大题共2小题,每小题8分、满分16分)15.解方程:.16.如图,OC 为⊙O 的半径,弦AB 垂直平分半径OC ,垂足为E .若AB 的长为6,求⊙O 的半径.四、(本大题共2小题,每小题8分,满分16分)17.如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点)和点2y x =2680x x -+=()0k y x x=<QE AP⊥AP =PQ =()()3112x x +-=D ,点D 在网格的格点上.(1)以点D 为位似中心,在网格内点D 上方画出△ABC 的位似图形且使得它们的相似比为2:1;(2)将(1)中的绕点D 顺时针旋转90°得到,画出.18.【观察】,,,…,,,,,,…,,,.【发现】根据以上材料,回答下列问题:(1)设参与上述运算的第一个因数为a ,第二个因数为b ,用等式表示a 与b 的数量关系是______.【类比】观察下列两数的积:,,,,…,,…,,,,.(2)猜想mn 的最大值为______,并用你学过的知识加以证明.五、(本大题共2小题,每小题10分,满分20分)19.如图,已知反比例函数的图象与直线相交于,B (3,n )两点.(1)求反比例函数与一次函数的解析式;(2)求△AOB 的面积;(3)直接写出当时,对应的x 的取值范围.20.定远池河大桥,原名太平桥,位于安徽省定远县池河镇西官驿道上,雄跨于蜿蜒的池河之上,如图,拱桥的拱形是抛物线形状,在拱桥中,当水面宽度米时,水面离桥洞最大距离为1米,以水平面为x 轴,点O为原点建立平面直角坐标系.111A B C △111A B C △222A B C △222A B C △15959⨯=258116⨯=357171⨯=2832896⨯=2931899⨯=3030900⨯=3129899⨯=3228896⨯=573171⨯=582116⨯=59159⨯=179⨯278⨯377⨯476⨯m n ⨯764⨯773⨯782⨯791⨯11ky x=22y k x b =+()1,3A-12y y >8OA=(1)求该拱桥所在抛物线的解析式;(2)当水面离桥洞最大距离为3米时,求此时拱桥内水面的宽度.六、(本题满分 12 分)21.如图,⊙O 是△ABC 的外接圆.AB 是⊙O 的直径,过点O 作于点E ,延长OE 至点D ,连接CD ,使.(1)求证:CD 是⊙O 的切线;(2)若,求AC 的长.七、(本题满分12分)22.如图,过等边三角形ABC 的顶点A 作AC 的垂线l ,点P 为l 上一点(不与点A 重合),连接CP ,将线段CP 绕点C 逆时针旋转60°得到线段CQ ,连接QB .(1)求证:;(2)连接PB 并延长交直线CQ 于点D ,且.①试猜想BC 和BQ 的数量关系,并证明;②若PB 的长.八、(本题满分14分)23.如图1,已知抛物线与x 轴交于A ,B 两点,与y 轴交于点C .(1)求线段AB 的长;(2)若点P 为直线BC 上方抛物线上的一点,当△BCP 的面积最大时,求点P 的坐标;OE AC ⊥D A ∠=∠AB CD ==AP BQ =PD CQ ⊥AC =223y x x =-++(3)如图2,若点M 为该抛物线的顶点,直线轴于点D ,在直线MD 上是否存在点N ,使点N 到直线MC 的距离等于点N 到点A 的距离?若存在,求出点N 的坐标;若不存在,请说明理由.2023-2024年度(上)九年级期末学情调研数学卷参考答案及评分标准一、选择题(本大题共10小题,每小题4分,满分40分)1.B 2.D 3.D 4.D 5.C 6.B 7.C 8.B 9.A10.C 【解析】如图1,过点O 作于点H ,连接OA ,则.在Rt△AOH 中,由勾股定理得,∴圆心O 到AB 的距离为1,故选项A 正确;如图1,延长HO 交⊙O 于点C ,此时△ABC 的面积最大.∵,∴,∴△ABC 面积的最大值为B 正确;如图2,连接PA ,QB .∵四边形ABPQ 是矩形,∴,∴PA ,QB 是⊙O 的直径,∴.在Rt △ABP 中,由勾股定理得.∵,∴,∴△POB 是等边三角形,∴,∴,∴,故选项C 错误;取弦AB 的中点D ,连接OD ,OA ,OB .∵,∴,∴,∴当AB 绕点O 旋转一周时,点D 运动的路线是以O 为圆心,半径长是1的圆,∴点D 运动的路线长为,故选项D 正确.二、填空题(本大题共4小题,每小题5分,满分20分)11. 12.10 13.14.(1)2分) (2)4或5(3分) 【解析】(1)∵四边形ABCD 是正方形,∴,∵点P 为BC 的中点,∴,∴.(2)∵四边形ABCD 是正方形,∴.∵,∴,∴.①MD x ⊥OH AB ⊥1122AH BH AB ===⨯=1HO ===213CH OC OH =+=+=11322ABC S AB CH =⋅=⨯=△90QAB PBA ∠=∠=︒224AP =⨯=2BP ===2PO BO ==PO BO BP ==60POB ∠=︒180120POQ POB ∠=︒-∠=︒2120π24π3603OPQS ⨯==扇形OA OB =OD AB ⊥1OD ===2π12π⨯=22y x =-8-4AB BC ==2BP CP ==AP ===90ABP ∠=︒EQ AP ⊥90PEQ ∠=︒ABP PEQ ∠=∠当时,.∵,∴,∴,∴.∵,∴.∵,∴;当时,.∵,∴,∴,∴四边形ABPQ 是矩形,∴.综上所述,PQ 的长为4或5.三、(本大题共2小题,每小题8分,满分16分)15.解:整理,得,因式分解,得,∴或,解得,.16.解:如图,连接OA .∵OC 为⊙O 的半径,AB 垂直平分半径OC ,,∴,.设⊙O 的半径为r ,则.在Rt △OAE 中,由勾股定理得(负值舍去).∴⊙O 的半径为.四、(本大题共2小题,每小题8分,满分16分)17.解:(1)如图,即为所作.ABP EPQ ∠=∠ABP QEP △△∽AD BC ∥APB PAQ ∠=∠EPQ PAQ ∠=∠AQ PQ =EQ AP ⊥12AE EP AP ===BP AP EP QP ==5PQ =BAP APQ ∠=∠ABP PEQ △△∽90BAD PAQ BAP ∠=∠+∠=︒90PAQ APQ ∠+∠=︒90AQP ∠=︒4PQ AB ==22150x x +-=()()530x x +-=50x +=30x -=15x =-23x =6AB =12OE OC =132AE BE AB ===12OE r =AE =3=r =111A B C △(2)如图,即为所作.18.解:(1)(2)1600证明:由题意,得.将代入mn ,得,∴当时,mn 的最大值为1600.五、(本大题共2小题,每小题10分,满分20分)19.解:(1)将代入,得,∴反比例函数的解析式为;∵点B (3,n )在反比例函数的图象上,∴,∴点B 的坐标为.将,代入,得解得∴一次函数的解析式为.(2)设直线AB 与y 轴交于点C .由,得点C 的坐标为(0,2),∴.(3)根据函数图象可知,当时,对应的x 的取值范围为或.20.解:(1)∵,∴该抛物线的对称轴为直线,A (8,0).222A B C △60a b +=80m n +=80n m =-()2280401600mn m m m =-+=--+40m =()1,3A -11k y x=()1133k =-⨯=-13y x=-13y x=-1n =-()3,1-()1,3A -()3,1B -22y k x b =+223,31,k b k b -+=⎧⎨+=-⎩21,2,k b =-⎧⎨=⎩2y x =-+2y x =-+()1124422AOB AOC BOC B A S S S OC x x =+=⋅-=⨯⨯=△△△12y y >10x -<<3x >8OA =842x ==∵水面离桥洞最大距离为1米,∴该抛物线顶点坐标为(4,1).设该抛物线解析式为,把A (8,0)代入,得,解得,∴该拱桥所在抛物线的解析式为.(2)由题意,得.把代入,得,解得.答:此时拱桥内水面的宽度为六、(本题满分12分)21.(1)证明:如图,连接OC .∵,∴,∴.∵,∴.∵,∴,∴,∴,即.∵OC 是⊙O 的半径,∴CD 是⊙O 的切线.(2)解:∵,∴.在Rt △COD 中,由勾股定理得.∵,∴∵,∴.七、(本题满分12分)22.(1)证明:∵△ABC 是等边三角形,∴,.由旋转,得,,∴,∴,即.()241y a x =-+()20841a =-+116a =-()214116y x =--+132-=-2y =-()214116y x =--+()2124116x -=--+14x =+24x =-((44+--=OE AC ⊥90DEC ∠=︒90D DCE ∠+∠=︒A D ∠=∠90A DCE ∠+∠=︒OA OC =A ACO ∠=∠90ACO DCE ∠+∠=︒90DCO ∠=︒OC CD ⊥AB CD ==OC =OD ===1122COD S OC CD OD CE =⋅=⋅△OC CD CE OD⋅===OE AC ⊥2AC CE ==AC BC =60ACB ∠=︒CP CQ =60PCQ ∠=︒60ACB PCQ ∠=∠=︒ACB PCB PCQ PCB ∠-∠=∠-∠ACP BCQ ∠=∠在△ACP 和△BCQ 中,∴,∴.(2)解:①.证明如下:如图,连接PQ .由旋转,得,,∴△CPQ 是等边三角形.∵,∴,∴PD 是CQ 的垂直平分线.∵点B 在PD 上,∴.②由(1)知,∴,,∴∵,∴,∴,∴.在Rt △CDP 中,,∴,∴.∵,,∴.∵,∴.∴,∴.八、(本题满分14分)23.解:(1)令,得,解得,,即,B (3,0),∴.(2)由抛物线知,点C 的坐标为(0,3).如图1,连接OP ,设,,,,AC BCACP BCQ CP CQ =⎧⎪∠=∠⎨⎪=⎩()ACP BCQ SAS ≌△△AP BQ =BC BQ =CP CQ =60PCQ ∠=︒PD CQ ⊥CD DQ =BC BQ =ACP BCQ≌△△AP BQ =CBQ CAP ∠=∠AC BC BQ AP ====CA AP ⊥90CAP ∠=︒90CBQ CAP ∠=∠=︒4CP ==9030CPD PCQ ∠=-∠=︒︒122CD CP ==PD ==90CBQ CAP ∠=∠=︒BC BQ =45BCQ ∠=︒90CDB ∠=︒45CBD BCQ ∠=︒=∠2BD CD ==2PB PD BD =-=-0y =2230x x -++=11x =-23x =()1,0A -()314AB =--=223y x x =-++()2,23P m m m -++则.∵,∴当时,,此时,,∴当△BCP 的面积最大时,点P 的坐标为.(3)存在满足条件的点N .如图2,过点N 作于点H ,连接NA .由抛物线可知,抛物线的顶点为M (1,4),与y 轴的交点为C (0,3).设直线MC 的解析式为,把M (1,4)代入,得,解得,∴直线MC 的解析式为,∴,∴.当时,.设N (1,n ),则,∴,解得∴点N 的坐标为或.BCP OCP OBP BOC S SS S =+-△△△△()2111332333222m m m =⨯⨯+⨯⨯-++-⨯⨯()23327228m =--+302-<32m =278S =最大()2233152323224m m -++=-+⨯+=()315,24NH MC ⊥223y x x =-++3y ax =+43a =+1a =3y x =+45CMN ∠=︒MN =NH AN =MN =4MN n =-AN =4n -=4n =-±(1,4-+(1,4--。
河南省商丘市2023-2024学年九年级上学期期末数学试题(含答案)

永城2023—2024学年上学期期末学业评价卷九年级数学(人教版)注意事项:1.本试卷共4页.三个大题.满分120分.考试时间100分钟.2.本试卷上不要答题,请按答题卡上注意事项的要求直接把答案填写在答题卡上,答在试卷上的答案无效一、选择题(每小题3分,共30分)下列各小题均有四个选项,中只有一个是正确的.1.下列关系式中,是x 的反比剑函数的是()A .B .C .D .2.下面是4个有关航天领域的图标.中既是轴对称图形又是中心对称图形的是( )A .B .C .D .3.在一个不透明的袋子里装有红球.黄球共20个,其中红球有2个.这些球除颜色外其他都相同,随机摸出1个球.摸出的是红球的概率是()A.B .C .D .4.下列四条线段中.能与,,这三条线段组成比例线段的是()A .B .C .D .5.下列图象中.有可能是函数的图象的是()A .B .C .D .6.“绿色电力.与你同行”",我国新能源汽车销售量逐年增加,据统计,2022年新能源汽车年销售量为690万辆.预计2024年新能源汽车手销售量将达到1166万辆,设这两年新能源汽车销售量年平均增长率为x ,则所列方程正确的是()A .B .C .D .7.若关于x 的一元二次方程有实数根,则实数k 的取值范围是()A .B .C .D .1y x =-3y x =-35y x =22y x =-12151101202a =3b =c =11d =2d =36d =4d =2)0(y ax a a =+≠()269011166x +=()211661690x -=()269069011166x ++=()116612690x -=2420x x k -+=2k >2k ≥2k <2k ≤8.对于反比例函数,下列结论中错误的是( )A .图象位于第二,四象限B .图象关于y 轴对称C .当时,y 随x 的增大而增大D .若点在图象上,则点也一定在图象上9.如图,一个隧道的横截面是以O 为圆心的圆的一部分,点D 是中弦AB 的中点,CD 经过圆心O 交于点C ,若路面AB =6m ,此圆的半径OA 的长为5m ,则净高CD 的长为( )A .5mB .6m C.m D .9m10.如图,在△ABC 中,AC =BC ,AB =12,把△ABC 绕点A 逆时针旋转60°得到△ADE ,连接CD ,当时,AC 的长为( )A .B .10C .D 二、填空题(每小题3分,共15分)11.“海日生残夜,江春入旧年”.如图所记录的日出美景中,太阳与海天交界处可看成圆与直线,它们的位置关系是______.12.图1是装满了液体的高脚杯(数据如图),用去部分液体后,放在水平的桌面上如图2所示,此时液体AB =______.13.抛物线的部分图象如图所示,当时,x 的取值范围是______.()0k y k x=≤0x >(),a b (),a b --O O 133CD =2y ax bx c =++5y >14.小诚和爸爸搭乘长途汽车回老家过年,在小程序上购票时,系统自动将两人分配到同一排(如图是长途汽车座位示意图),则小诚和爸爸分配的座位恰好是邻座(过道两侧也视为邻座)的概率是______.15.如图,已知反比例函数,.点A 在y 轴的正半轴上,过点A 作直线轴,且分别与两反比例函数的图象交于点C 和点B ,连接OC ,OB .若△BOC 的面积为9,AC :AB =4:5,则______.三、解答题(本大题共8个小题,共75分)16.(10分)用适当的方法解下列一元二次方程:(1);(2).17.(8分)如图.在平面直角坐标系中,△ABC 的顶点均在正方形网络的格点上,已知点C 的坐标为.(1)以点O 为位似中心,在给出的网格内曲使与位似,并且点的坐标为;(2)与的相似比是______.18.(9分)如图.文文应用所学的三角形相关知识测量河南广播电视塔的高度,她站在距离塔底A 点120m 处的D 点.测得自己的影长DE 为0.4m ,此时该塔的影子为AC ,她测得点D 与点C 的距离为23m ,已知文文的身高DF 为1.6m .求河南广播电视塔AB 的高.(图中各点都在同一平面内.点A ,C ,D .E 在同一直线上)111(0)k y k x =≥222(0)k y k x=<BC x ∥12k k =()419x x x -=-26160x x --=()4,1-111A B C △111A B C △ABC △1C ()8,2-ABC △111A B C △19.(9分)如图,在平面直角坐标系中,直线与反比例函数在第一象限内的图象交于点.(1)求反比例函数的表达式;(2)直接写出当时,关于x的不等式的解集.20.(9分)掷实心球是2024年郑州巿高中阶段学校招生体育考试的抽考项目,如图1是一名男生投实心球,实心球的行进路线是—条抛物线,行进高度y (m )与水平距离x (m )之间的函数关系如图2所示,掷出时起点处高度为m ,当水平距离为5m 时,实心球行进至最高点4m 处.(1)求y 关于x 的函数表达式(不写x 的取值范围);(2)根据郑州市高中阶段学校招生体育考试评分标准(男生).在投掷过程中.实心球从起点到落地点的水平距离大于等于11.4m 时,此项考试得分为满分10分.请判断该男生在此项考试中是否能得满分,并说明理由.21.(10分)如图,AB 是的直径,点C ,D 是上位于直线AB 异侧的两点,,交CB 的延长线于点E .且BD 评分.(1)求证:DE 为的切线;213y x =-()0k y k x=≠()6,A a 0x >213k x x >-9649O O DE BC ⊥ABE ∠O(2)若,,①求DE 的长;②图中阴影部分的面积为______.22.(10分)如图,抛物线交x 轴于,两点,与y 轴交干点C .(1)求此抛物线的解析式;(2)已知P 为抛物线上一点(不与点B 重合),若点P 关于x 轴对称的点恰好在直线BC 上,求点P 的坐标.23.(10分)已知△ABC 与△DEC 都为等腰三角形,AB =AC ,DE =DC ,.(1)当n =60°时,①如图1,当点D 在AC 上时,BE 与AD 的数量关系是______;②如图2,当点D 不在AC 上时,BE 与AD 的数量关系是______.(2)如图3(点B 位于△CDE 的内部).当n =90°时,①探究线段BE 与AD 的数量关系,并说明理由;②当,时.请直接写出CE 的长.永城2023—2024学年上学期期未学业评价卷九年级数学(人教版)参考答案一、选择题(每小题3分,共30分)1.B 2.C 3.C 4.D 5.A 6.A 7.D 8.B 9.D 10.C二、填空题(每小题3分,共15分)11.相交12.4cm 13. 14. 15.-80三、解答题(本大题共8个小题,共75分)16.解:(1).60ABC ∠=︒4AB =2c y x bx =-++()1,0A -()2,0B 2y x b c =-++P 'BAC EDC n ∠=∠=AD BC ∥AB =7AD =04x <<12249x x x -=-,.,.(2).,.由此可得,,.17.解:(1)如图所示.(2)1:2.18.解:太阳光是平行光线,因此.由题意得,.,.m ,m ,(m ).m ,m ,,m .河南广播电视塔的高度为388m .19.解:(1)∵点在直线上,.249x =294x =132x =-232x =2616x x -=269169x x -+=+()2325x -=35x -=±18x =22x =-111A B C △BCA FED ∠=∠AB AC ⊥DF AC ⊥ABC DFE ∴△△∽AB DF AC DE∴=120AD = 23CD =97AC AD CD ∴=-=0.4DE = 1.6DF =1.6970.4AB ∴=388AB ∴=∴()6,A a 213y x =-26133a ∴=⨯-=即点A 的坐标为.点A 在反比例函数的图象上,.反比例函数的表达式为.(2)当时,关于x 的不等式的解集为.20.解:(1)设y 关于x 的函数表达式为.把代入表达式,得,解得..(2)该男生在此项考试中能得满分.理由:令,即,解得,(舍去).,该男生在此项考试中能得满分.21.(1)证明:连接OD .∵BD 平分,.,...,.∵点D 在上,DE 为的切线.(2)解:①如图,过点O 作,垂足为F .()6,3k y x=6318k =⨯=∴∴18y x=0x >213k x x >-06x <<()254y a x =-+960,49⎛⎫ ⎪⎝⎭()29605449a =-+449a =-24(5)449y x ∴=--+0y =()2454049x --+=112x =22x =-1211.4> ∴ABE ∠ABD DBE ∴∠=∠OD OB = ODB ABD ∴∠=∠ODB DBE ∴∠=∠OD BC ∴∥DE BC ⊥ OD DE ∴⊥O ∴O OF BC ⊥,.,..在Rt △OBF 中,由(1)得,,.四边形OFED 为矩形..②.22.解:(1)将,代入,得解得lc =2.抛物线的解析式为.(2)设直线BC 的解析式为.由(1)中得,点C 的坐标为.将,代入,得,解得,直线BC 的解析式为.设点的坐标为,∵点P 与点关于x 轴对称,点P 的坐标为.∵点P 在抛物线上,.解得,.又∵点P 不与点B 重合,..点P 的坐标为.4AB = 122B OB A ==∴60ABC ∠=︒ 30BOF ∴∠=︒112BF OB ∴==OF ===OD DE ∥DE BC ⊥90ODE E OFE ∴∠=∠=∠=︒∴DE OF ∴==2π3()1,0A -()2,0B 2y x bx c =-++10,420.b c b c --+=⎧⎨-++=⎩12b c =⎧⎨=⎩∴22y x x =-++y kx m =+22y x x =-++()0,2()2,0B ()0,2C y kx m =+202h m m +=⎧⎨=⎩12k m =-⎧⎨=⎩∴2y x =-+P '(),2a a -+P '∴(),2a a -222a a a -=-++∴12a =22a =-2a ∴=-2224a ∴-=--=-∴()2,4--23.解:(1)①,②(2)①.理由如下:当时,,∵,.△ABC 与△DEC 为等腰直角三角形..则,.,,....②CE 的长为.BE AD =BE AD=BE =90n =︒90BAC EDC ∠=∠=︒AB AC =DE DC =∴45ACB ABC DCE DEC ∴∠=∠=∠=∠=︒BC ==EC ==DC AC EC BC ∴==45DCE DCB ECB ∠=∠+∠=︒45ACB ACD DCB ∠=∠+∠=︒DCA ECB ∴∠=∠DCA ECB ∴△△∽AD DC BE EC ∴==BE ∴=。
山东省济宁市曲阜市、鱼台县2023-2024学年九年级上学期期末数学试卷(含解析)
2023-2024学年山东省济宁市曲阜市、鱼台县九年级(上)期末数学试卷一、选择题:本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项符合题目要求.1.(3分)下面用数学家名字命名的图形中,既是轴对称图形,又是中心对称图形的是( )A .赵爽弦图B .笛卡尔心形线C .科克曲线D .斐波那契螺旋线2.(3分)下列函数中,y 是x 反比例函数的是( )A .B .C .D .3.(3分)二次函数y =(x ﹣2)2﹣8的顶点坐标为( )A .(2,﹣8)B .(2,8)C .(﹣2,8)D .(﹣2,﹣8)4.(3分)某小组做“用频率估计棍率”的试验时,统计了某一结果出现的频率,绘制了如图所示的折线统计图,则符合这一结果的试验最有可能的是( )A .掷一枚一元硬币,落地后正面朝上B .在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀”C .一副去掉大小王的扑克牌洗匀后,从中任抽一张牌的花色是红桃D .任意写一个整数,它能被2整除2xy =-21y x =+2y x =2y x=-5.(3分)关于的方程mx2+2x+1=0有两个实数根,则m的取值范围是( )A.m<1B.m≤1C.m<1且m≠0D.m≤1且m≠06.(3分)如图,AB为⊙O的直径,弦CD⊥AB,E为上一点,若∠CEA=28°,则∠BDC的度数为( )A.62°B.52°C.28°D.56°7.(3分)如图,反比例函数的图象经过▱ABCD对角线的交点P,已知点A,C,D在坐标轴上,BD⊥DC,▱ABCD的面积为6,则k的值是( )A.3B.﹣3C.2D.﹣28.(3分)如图,△ABC的顶点都是正方形网格中的格点,则cos∠ACB等于( )A.B.C.D.9.(3分)如图,在△ABC中,DE∥BC,AE:BE=3:4,BD与CE交于O,下列结论:①=;②=;③=;④=.其中正确结论的个数是( )A.1B.2C.3D.410.(3分)如图,一段抛物线y=﹣x2+4x(0≤x≤4),记为抛物线C1,它与x轴交于点O,A1;将抛物线C1绕点A1旋转180°得抛物线C2,交x轴于点A2;将抛物线C2绕点A2旋转180°得抛物线C3,交x轴于点A3.…如此进行下去,得到一条“波浪线”,若点M(2023,m)在此“波浪线”上,则m的值为( )A.﹣3B.3C.﹣4D.4二、填空题:本大题共5小题,每小题3分,共15分.11.(3分)点P(﹣1,2)关于原点对称的点P′的坐标是 .12.(3分)若a、b是方程x2+2x﹣2023=0的两实数根,则a2+3a+b= .13.(3分)如图,一次函数y1=k1x+b与反比例函数的图象相交于A,B两点,点A的横坐标为2,点B的横坐标为﹣1,则不等式的解集是 .14.(3分)如图,在Rt△ABC中,∠BAC=90°,AB=3,BC=5,点P为BC边上任意一点,连接PA,以PA,PC为邻边作平行四边形PAQC,连接PQ,则PQ长度的最小值为 .15.(3分)如图所示,扇形AOB中,∠AOB=140°,点C为OA中点,OA=8,CD⊥AO交于D,以OC 为半径画交OB于E,则图中阴影部分面积为 .三、解答题:本大题共7小题,共55分.16.(6分)(1)解方程:x2+6x﹣7=0;(2)计算:4sin45°﹣+(﹣1)0﹣tan30°.17.(6分)如图,在直角坐标系中,边长为1的小正方形组成的网格中,给出了格点△ABC(顶点为网格线的交点),在给定的网格中,解答下列问题:(1)以A为位似中心,将△ABC按相似比2:1放大,得到△AB1C1,画出△AB1C1.(2)以C1为旋转中心,将△AB1C1顺时针旋转90°,得到△A1B2C1.①画出△A1B2C1;②求点A的运动路径长.18.(6分)2018年9月,第24届山东省运动会在青岛举行,有20名志愿者参加某分会场的工作,其中男生8人,女生12人.(1)若从这20人中随机选取一人作为联络员,求选到女生的概率;(2)若该分会场的某项工程只在甲、乙两人选一人,他们准备以游戏的方式决定由谁参加,游戏规则如下:将四张牌面数字分别为2,3,4,5的扑克牌洗匀后,数字朝下放于桌面,从中任取1张,不放回,再取1张,若牌面数字之和为偶数,则甲参加;否则乙参加,试问这个游戏公平吗?请用树状图或列表法说明理由.19.(8分)曲阜尼山圣境孔子像,背山面湖,面南而立,为世界最高最大的孔子像,成为儒客和游人朝拜、瞻仰必到之处.一游客想知道孔子像AB的高度.如图,AB与水平面BD垂直,在点D处测得顶部A的仰角是37°,向前走了24米至点E处,测得此时顶部A的仰角是45°,请聪明的你帮他求出孔子像AB的高度.(参考数据:,,)20.(9分)如图,AB为⊙O的直径,D、E是⊙O上的两点,延长AB至点C,连接CD,∠BDC=∠BAD.(1)求证:CD是⊙O的切线.(2)若tan∠BED=,AC=9,求⊙O的半径.21.(8分)正方形ABCD的边长为4,AC,BD交于点E.在点A处建立平面直角坐标系如图所示.(1)如图1,双曲线过点E,求点E的坐标和反比例函数的解析式;(2)如图2,将正方形ABCD向右平移m(m>0)个单位长度,使过点E的双曲线与AB交于点P.当△AEP为等腰三角形时,求m的值.22.(12分)如图,抛物线y=﹣x2+bx+c与x轴交于点A和点B,与y轴交于点C,点B坐标为(6,0),点C坐标为(0,6),点D是抛物线的顶点,过点D作x轴的垂线,垂足为E,连接BD.(1)求抛物线的解析式及点D的坐标;(2)点F是抛物线上的动点,当∠FBA=∠BDE时,求点F的坐标;(3)若点M是抛物线上的动点,过点M作MN∥x轴与抛物线交于点N,点P在x轴上,点Q在坐标平面内,以线段MN为对角线作正方形MPNQ,请写出点Q的坐标.2023-2024学年山东省济宁市曲阜市、鱼台县九年级(上)期末数学试卷参考答案与试题解析一、选择题:本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项符合题目要求.1.(3分)下面用数学家名字命名的图形中,既是轴对称图形,又是中心对称图形的是( )A .赵爽弦图B .笛卡尔心形线C .科克曲线D .斐波那契螺旋线【解答】解:A .是中心对称图形,不是轴对称图形,故此选项不合题意;B .不是中心对称图形,是轴对称图形,故此选项不合题意;C .既是中心对称图形,也是轴对称图形,故此选项符合题意;D .不是中心对称图形,也不是轴对称图形,故此选项不合题意;故选:C .2.(3分)下列函数中,y 是x 反比例函数的是( )A .B .C .D .【解答】解:A 、y =﹣不符合y =的形式,不是反比例函数,不符合题意;B 、y =不符合y =的形式,不是反比例函数,不符合题意;C 、y =是反比例函数,符合题意;D 、y =﹣x 2不符合y =的形式,不是反比例函数,不符合题意.故选:C .3.(3分)二次函数y =(x ﹣2)2﹣8的顶点坐标为( )A .(2,﹣8)B .(2,8)C .(﹣2,8)D .(﹣2,﹣8)【解答】解:已知二次函数顶点式:y =a (x ﹣h )2+k 的顶点为(h ,k ),∴y =(x ﹣2)2﹣8的顶点坐标为(2,﹣8).故选:A .4.(3分)某小组做“用频率估计棍率”的试验时,统计了某一结果出现的频率,绘制了如图所示的折线统计图,则符合这一结果的试验最有可能的是( )2xy =-21y x =+2y x =2y x=-A.掷一枚一元硬币,落地后正面朝上B.在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀”C.一副去掉大小王的扑克牌洗匀后,从中任抽一张牌的花色是红桃D.任意写一个整数,它能被2整除项不符合题意;此选项符合题意;近于0.33不符,此选项不符合题意;故选:B.5.(3分)关于的方程mx2+2x+1=0有两个实数根,则m的取值范围是( )A.m<1B.m≤1C.m<1且m≠0D.m≤1且m≠0【解答】解:∵关于的方程mx2+2x+1=0有两个实数根,∴m≠0且△≥0,即22﹣4×m×1≥0,解得m≤1且m≠0.故选:D.6.(3分)如图,AB为⊙O的直径,弦CD⊥AB,E为上一点,若∠CEA=28°,则∠BDC的度数为( )A.62°B.52°C.28°D.56°【解答】解:∵AB为⊙O的直径,弦CD⊥AB,∴=,∠BFD=90°,∴∠ABD=∠CEA=28°,∴∠BDC=90°﹣28°=62°.故选:A.7.(3分)如图,反比例函数的图象经过▱ABCD对角线的交点P,已知点A,C,D在坐标轴上,BD⊥DC,▱ABCD的面积为6,则k的值是( )A.3B.﹣3C.2D.﹣2【解答】解:设点B(a,b),∴OD=﹣a,BD=b,∵四边形ABCD为平行四边形,∴AB∥CD,点P为BD的中点,∵BD⊥CD,∴BD⊥AB,又∵∠DOA=90°,∴四边形ABDO为矩形,∴AB=OD,∴OD=CD=﹣a,∵▱ABCD的面积为6,∴CD•BD=6,即﹣ab=6,∵点P为BD的中点,∴点P的坐标为(a,b),∵反比例函数的图象经过点P,∴k=ab=﹣3.故选:B.8.(3分)如图,△ABC的顶点都是正方形网格中的格点,则cos∠ACB等于( )A.B.C.D.【解答】解:∵AB=5,BC==5,AC==,∴BA=BC,∴∠ACB=∠CAB,∴cos∠ACB=cos∠CAB==,故选:D.9.(3分)如图,在△ABC中,DE∥BC,AE:BE=3:4,BD与CE交于O,下列结论:①=;②=;③=;④=.其中正确结论的个数是( )A.1B.2C.3D.4【解答】解:∵AE:BE=3:4,∴,∵DE∥BC,∴△AED∽△ABC,∴,=,则①,②错误;∵DE∥BC,∴△EOD∽△COB,∴=,则③正确;∵△EOD∽△COB,∴,∴,∴,则④正确;故选:B.10.(3分)如图,一段抛物线y=﹣x2+4x(0≤x≤4),记为抛物线C1,它与x轴交于点O,A1;将抛物线C1绕点A1旋转180°得抛物线C2,交x轴于点A2;将抛物线C2绕点A2旋转180°得抛物线C3,交x轴于点A3.…如此进行下去,得到一条“波浪线”,若点M(2023,m)在此“波浪线”上,则m的值为( )A.﹣3B.3C.﹣4D.4【解答】解:∵y=﹣x2+4x=﹣x(x﹣4)(0≤x≤4),∴A1(4,0),∴整个函数图象,每隔4×2=8个单位长度,函数值就相等,∵2023÷8=252……7,∴m的值与x=7时的函数值相同,∵x=7在C2上,∵将抛物线C1绕点A1旋转180°得抛物线C2,交x轴于点A2,∴OA1=A1A2,∴A2(8,0),∴C2:y=(x﹣4)(x﹣8),当x=7时,y=m=(7﹣4)×(7﹣8)=﹣3;故选:A.二、填空题:本大题共5小题,每小题3分,共15分.11.(3分)点P(﹣1,2)关于原点对称的点P′的坐标是 (1,﹣2) .【解答】解:点P(﹣1,2)关于原点对称的点P′的坐标是(1,﹣2).故答案为:(1,﹣2).12.(3分)若a、b是方程x2+2x﹣2023=0的两实数根,则a2+3a+b= 2021 .【解答】解:∵a是方程x2+2x﹣2023=0的根,∴a2+2a﹣2023=0,即a2+2a=2023,∵a,b是方程x2+2x﹣2023=0的两个实数根,∴a+b=﹣2,∴a2+3a+b=a2+2a+a+b=2023﹣2=2021.故答案为:2021.13.(3分)如图,一次函数y1=k1x+b与反比例函数的图象相交于A,B两点,点A的横坐标为2,点B的横坐标为﹣1,则不等式的解集是 ﹣1<x<0或x>2 .【解答】解:由题意得,不等式的解集即为一次函数图象在反比例函数图象下方时自变量的取值范围,∴不等式的解集是﹣1<x<0或x>2.故答案为:﹣1<x<0或x>2.14.(3分)如图,在Rt△ABC中,∠BAC=90°,AB=3,BC=5,点P为BC边上任意一点,连接PA,以PA,PC为邻边作平行四边形PAQC,连接PQ,则PQ长度的最小值为 .【解答】解:方法一:∵∠BAC=90°,AB=3,BC=5,∴AC===4,∵四边形APCQ是平行四边形,∴PO=QO,CO=AO=2,∵PQ最短也就是PO最短,∴过O作BC的垂线OP′,∵∠ACB=∠P′CO,∠CP′O=∠CAB=90°,∴△CAB∽△CP′O,∴,∴,∴OP′=,∴则PQ的最小值为2OP′=,方法二:过点A作AE⊥BC垂足为E当PQ⊥BC时,符合题意,则四边形AEPQ是矩形,∴PQ=AE=2.4.故答案为:.15.(3分)如图所示,扇形AOB中,∠AOB=140°,点C为OA中点,OA=8,CD⊥AO交于D,以OC为半径画交OB于E,则图中阴影部分面积为 8π+8 .【解答】解:如图,连接OD.∵点C为OA中点,OA=8,∴OC=OA=4,∵OD=OA=8,CD⊥AO,∴∠CDO=30°,∴∠COD=60°,∴S阴=S扇形OAB﹣S扇形OCE﹣(S扇形OAD﹣S△OCD)=﹣﹣(﹣×4×4)=8π+8,故答案为:8π+8.三、解答题:本大题共7小题,共55分.16.(6分)(1)解方程:x2+6x﹣7=0;(2)计算:4sin45°﹣+(﹣1)0﹣tan30°.【解答】解:(1)∵x2+6x﹣7=0,∴(x+7)(x﹣1)=0,∴x1=﹣7,x2=1(2)原式=17.(6分)如图,在直角坐标系中,边长为1的小正方形组成的网格中,给出了格点△ABC(顶点为网格线的交点),在给定的网格中,解答下列问题:(1)以A为位似中心,将△ABC按相似比2:1放大,得到△AB1C1,画出△AB1C1.(2)以C1为旋转中心,将△AB1C1顺时针旋转90°,得到△A1B2C1.①画出△A1B2C1;②求点A的运动路径长.【解答】解:(1)如图所示,△AB1C1即为所求;(2)①如图所示,△A1B2C1即为所求;②由图形可知,AC1==2,∴点A的运动路径为==π.18.(6分)2018年9月,第24届山东省运动会在青岛举行,有20名志愿者参加某分会场的工作,其中男生8人,女生12人.(1)若从这20人中随机选取一人作为联络员,求选到女生的概率;(2)若该分会场的某项工程只在甲、乙两人选一人,他们准备以游戏的方式决定由谁参加,游戏规则如下:将四张牌面数字分别为2,3,4,5的扑克牌洗匀后,数字朝下放于桌面,从中任取1张,不放回,再取1张,若牌面数字之和为偶数,则甲参加;否则乙参加,试问这个游戏公平吗?请用树状图或列表法说明理由.【解答】解:(1)∵共20名志愿者,女生12人,∴选到女生的概率是:=;(2)不公平,根据题意画图如下:∵共有12种情况,和为偶数的情况有4种,∴牌面数字之和为偶数的概率是=,∴甲参加的概率是,乙参加的概率是,∴这个游戏不公平.19.(8分)曲阜尼山圣境孔子像,背山面湖,面南而立,为世界最高最大的孔子像,成为儒客和游人朝拜、瞻仰必到之处.一游客想知道孔子像AB的高度.如图,AB与水平面BD垂直,在点D处测得顶部A的仰角是37°,向前走了24米至点E处,测得此时顶部A的仰角是45°,请聪明的你帮他求出孔子像AB的高度.(参考数据:,,)【解答】解:由题意得DE=24米,在Rt△ABE中,∠AEB=45°,∴∠BAE=45°,∴AB=BE.设AB=BE=x米,在Rt△ABD中,tan∠ADB=,∴tan37°=,∴≈,解得x=72,经检验x=72是原方程的解,∴AB=72米.答:孔子像AB的高度为72米.20.(9分)如图,AB为⊙O的直径,D、E是⊙O上的两点,延长AB至点C,连接CD,∠BDC=∠BAD.(1)求证:CD是⊙O的切线.(2)若tan∠BED=,AC=9,求⊙O的半径.【解答】(1)证明:连接OD,∵AB为⊙O的直径,∴∠ADB=90°,∴∠A+∠ABD=90°,∵OB=OD,∴∠ABD=∠ODB,∵∠BDC=∠A,∴∠BDC+∠ODB=90°,∴∠ODC=90°,∴OD⊥CD,∵OD是⊙O的半径,∴CD是⊙O的切线;(2)解:∵∠ADB=90°,tan∠BED=,∴,∵∠DCB=∠ACD,∠BDC=∠BAD,∴△BDC∽△DAC,∴=,∵AC=9,∴,∴CD=6,∴,∴BC=4,∴AB=AC﹣BC=9﹣4=5.∴⊙O的半径为.21.(8分)正方形ABCD的边长为4,AC,BD交于点E.在点A处建立平面直角坐标系如图所示.(1)如图1,双曲线过点E,求点E的坐标和反比例函数的解析式;(2)如图2,将正方形ABCD向右平移m(m>0)个单位长度,使过点E的双曲线与AB交于点P.当△AEP为等腰三角形时,求m的值.【解答】解:(1)∵正方形ABCD的边长为4,AC,BD交于点E,∴C(4,4),∵点E是OC的中点,∴E(2,2),将E点坐标代入双曲线,得2=,解得k1=4,∴双曲线的解析式为y=;(2)∵正方形边长为4,由(1)知E(2,2),∴AE=2,①当AP=AE=2时,∵P(m,2),E(m+2,2),点P、E在反比例函数图象上,∴2m=2(m+2),∴m=2+2;②当EP=AE时,点P与点B重合,∵P(m,4),E(m+2,2),点P、E在反比例函数图象上,∴4m=2(m+2),∴m=2;③当EP=AP时,点P、E不可能都在反比例函数图象上,故此情况不存在;综上所述,满足条件的m的值为2或2+2.22.(12分)如图,抛物线y=﹣x2+bx+c与x轴交于点A和点B,与y轴交于点C,点B坐标为(6,0),点C坐标为(0,6),点D是抛物线的顶点,过点D作x轴的垂线,垂足为E,连接BD.(1)求抛物线的解析式及点D的坐标;(2)点F是抛物线上的动点,当∠FBA=∠BDE时,求点F的坐标;(3)若点M是抛物线上的动点,过点M作MN∥x轴与抛物线交于点N,点P在x轴上,点Q在坐标平面内,以线段MN为对角线作正方形MPNQ,请写出点Q的坐标.【解答】解:(1)把B、C两点坐标代入抛物线解析式可得,解得,∴抛物线解析式为y=﹣x2+2x+6,∵y=﹣x2+2x+6=﹣(x﹣2)2+8,∴D(2,8);(2)如图1,过F作FG⊥x轴于点G,连接FB,设F(x,﹣x2+2x+6),则FG=|﹣x2+2x+6|,∵∠FBA=∠BDE,∠FGB=∠BED=90°,∴△FBG∽△BDE,∴=,∵B(6,0),D(2,8),∴E(2,0),BE=4,DE=8,OB=6,∴BG=6﹣x,∴=,当点F在x轴上方时,有=,解得x=﹣1或x=6(舍去),此时F点的坐标为(﹣1,);当点F在x轴下方时,有=﹣,解得x=﹣3或x=6(舍去),此时F点的坐标为(﹣3,﹣);综上可知F点的坐标为(﹣1,)或(﹣3,﹣);(3)如图2,设对角线MN、PQ交于点O′,∵点M、N关于抛物线对称轴对称,且四边形MPNQ为正方形,∴点P为抛物线对称轴与x轴的交点,点Q在抛物线的对称轴上,设Q(2,2n),则M坐标为(2﹣n,n),∵点M在抛物线y=﹣x2+2x+6的图象上,∴n=﹣(2﹣n)2+2(2﹣n)+6,解得n=﹣1+或n=﹣1﹣,∴满足条件的点Q有两个,其坐标分别为(2,﹣2+2)或(2,﹣2﹣2).。
2023-2024学年江苏省南京市建邺区九年级(上)期末数学试卷(含解析)
2023-2024学年江苏省南京市建邺区九年级(上)期末数学试卷一、选择题(共6小题,每小题2分,共12分.在每小题所给出的四个选项中,恰有一项是符合题目要求的,请将正确选项前的字母代号填涂在答题卡相应位置上)1.一元二次方程的根是 A .B .C .,D .2.一组数据:7,5,9,3,9,15,关于这组数据说法错误的是 A .极差是12B .众数是9C .中位数是7D .平均数是83.如图,是的外接圆,若,则的度数等于 A .B .C .D .4.对于二次函数的图象,下列说法正确的是 A .对称轴为直线B .最低点的坐标为C .与轴有两个公共点D .与轴交点坐标为5.如图,直线,直线、与、、分别交于点、、和点、、,若,,则的长为 A .2B .3C .4D .56.下列四个命题中,正确的是 (1)各角相等的圆内接五边形是正五边形;(2)各边相等的圆内接五边形是正五边形;29x =()123x x ==123x x ==-13x =23x =-12x x =()O ABC ∆50OCA ∠=︒ABC ∠()30︒40︒50︒60︒2(2)2y x =-+()2x =-(2,2)x y (0,2)123////l l l a b 1l 2l 3l A B C D E F :1:2AB BC =6DF =EF ()()(3)各角相等的圆内接六边形是正六边形;(4)各边相等的圆内接六边形是正六边形.A .(1)(2)(3)B .(1)(2)(4)C .(1)(3)(4)D .(2)(3)(4)二、填空题(共10个小题,每小题2分,共20分.不需写出解答过程,请把正确答三、案直接填写在答题卡相应位置上)7.若关于的方程有两个相等的实数根,则 .8.设,是一元二次方程的两个根,则的值是 .9.已知点是线段的黄金分割点,.若.则 (结果保留根号).10.某农场的粮食产量在两年内从3000吨增加到3630吨,若设平均每年增产的百分率为,则所列方程为 .11.把二次函数的图象先向右平移3个单位长度,再下平移1个单位长度,所得图象对应的函数表达式是 .12.如图,一块飞镖游戏板由除颜色外都相同的9个小正方形构成.假设飞镖击中每1块小正方形是等可能的(击中小正方形的边界或没有击中游戏板,则重投一次).任意投掷飞镖一次,击中黑色区域的概率是 .13.如图,在中,,,,以边所在的直线为轴旋转一周得到一个圆锥,则这个圆锥的面积是 .14.已知二次函数、、是常数,且,函数值与自变量的部分x 220x x m -+=m =1x 2x 240x x +-=12x x +P AB AP PB >10AB =AP =x 22y x =ABC ∆90ACB ∠=︒4AC cm =3BC cm =AC 2cm 2(y ax bx c a =++b c 0)a ≠y x对应值如下表:01234102125当时,自变量的取值范围是 .15.如图,在四边形中,、、分别与相切于、、三点,为的直径.若,,则的半径为 .16.如图,在正方形中,,点为上动点,点在的延长线上,且,、相交于点.当点从点运动到点时,点运动的路线长度为 .三、解答题(本人题共11小题,共88分,请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤)17.(8分)解方程:(1);(2).18.(8分)某校从甲、乙两名同学中选拔一名代表学校参加《喜迎二十大奋进新征程》演讲比赛,如图是甲、乙两名学生在五次选拔比赛中的成绩情况:根据以上信息,整理分析数据如下:学生平均数(分中位数(分方差(分x⋯1-⋯y⋯1y ⋯1y y <x ABCD BC CD DA O B E A AB O 4BC cm =3AD cm =O cm ABCD 3AB cm =P AB Q AB 2BP BQ =CP DQ E P A B E cm 2420x x --=3(2)24x x x --=))2)甲8 3.6乙8(1) , , ;(2)根据五次选拔比赛的成绩,你认为选谁较为合适?请说明理由.19.(8分)一个不透明的口袋中有三个完全相同的小球,把它们分别标号为1,2,3.随机摸出一个小球后放回,再随机摸出一个小球.(1)第二次摸到1号小球的概率是 ;(2)求两次摸出的小球标号和为3的概率.20.(7分)如图,学校打算用长的篱笆围成一个一面靠墙且面积是的矩形生态园饲养小兔,求生态园的长和宽.21.(8分)如图,二次函数图象顶点坐标为,与轴一个交点坐标为.(1)该函数图象与轴的另一个交点坐标为 ;(2)求这个二次函数的表达式;(3)当时,的取值范围为 .b aca =b =c =16m 230m (1,4)--x (1,0)x 40x -<<y22.(8分)如图,在中,的垂直平分线分别交,于点,,交于点,.(1)判断与是否相似,并说明理由.(2)与相等吗?为什么?23.(8分)某种服装,平均每天可销售20件,每件盈利44元.若每件降价1元,则每天可多售5件,降价幅度不超过10元,那么每件应降价多少元,可获得最大利润?最大利润是多少?24.(7分)在四边形中,用无刻度的直尺和圆规完成下列作图(保留作图痕迹,不写作法,写出必要的文字说明).(1)如图①,连接,在边上作点,使得;(2)如图②,在边上作点,使得.25.(8分)如图,在的内接四边形中,,直径,垂足为点.(1)当时,求的度数;(2)当,时,求的长.ABC ∆BC BC AC D E BE AD F AB AD =FDB ∆ABC ∆AF DF ABCD BD CD M AMB ADB ∠=∠CD N BND A ∠=∠O ABCD AB BC =AE CD ⊥F BCCD =D ∠5AB =8AD =CD26.(8分)已知二次函数的图象经过,两点.(1)求的值;(2)求证该二次函数的图象与轴的总有两个公共点;(3)设该函数图象与轴的两个公共点分别为、.当时,直接写出的取值范围.27.已知的半径为,是外一点,,点、在上,在中,.(1)如图①,是的切线,当时,求证:是的切线;(2)如图②,、分别交于点、,当点为中点时,求的长;(3)线段的取值范围是 .2y ax bx c =++(1,3)-(1,1)-b x x (,0)m (,0)n 0mn <a O 2cm P O 4PO cm =A B O PAB ∆BP BA =PB O PA PB =PA O PA PB O C D C PA PD PA2023-2024学年江苏省南京市建邺区九年级(上)期末数学试卷参考答案与试题解析一、选择题(共6小题,每小题2分,共12分.在每小题所给出的四个选项中,恰有一项是符合题目要求的,请将正确选项前的字母代号填涂在答题卡相应位置上)1.一元二次方程的根是 A .B .C .,D .【分析】两边直接开平方得:,进而可得答案.解:,两边直接开平方得:,则,.故选:.【点评】此题主要考查了直接开平方法解一元二次方程,解这类问题要移项,把所含未知数的项移到等号的左边,把常数项移项等号的右边,化成的形式,利用数的开方直接求解.2.一组数据:7,5,9,3,9,15,关于这组数据说法错误的是 A .极差是12B .众数是9C .中位数是7D .平均数是8【分析】根据众数、极差、平均数、中位数的含义和求法,逐一判断即可.解:,5,9,3,9,15这组数据的最大值是15最小值是3这组数据的极差是:,选项正确,不符合题意;这组数据中9出现了2次,最多,众数为9,选项确,不符合题意;,5,9,3,9,15这组数据的中位数是8选项不正确,符合题意;据的平均数是:29x =()123x x ==123x x ==-13x =23x =-12x x =3x =±29x =3x =±13x =23x =-C 2(0)x a a =…()7 ∴15312-=A ∴∴B 7 ∴C (7593915)6+++++÷486=÷.选项正确,不符合题意;故选:.【点评】此题主要考查了众数、极差、平均数、中位数的含义和求法,要熟练掌握.3.如图,是的外接圆,若,则的度数等于 A .B .C .D .【分析】连接,根据等腰三角形的性质得到,根据三角形内角和定理求得,由圆周角定理即可求出的度数.解:连接,,,,,故选:.【点评】本题主要考查了三角形的外接圆与外心,圆周角定理,等腰三角形的性质,正确作出辅助线,熟练掌握圆周角定理是解决问题的关键.4.对于二次函数的图象,下列说法正确的是 A .对称轴为直线B .最低点的坐标为C .与轴有两个公共点D .与轴交点坐标为【分析】根据二次函数的性质对各选项进行判断.解:,8=∴D C O ABC ∆50OCA ∠=︒ABC ∠()30︒40︒50︒60︒OA 50OAC OCA ∠=∠=︒80AOC ∠=︒ABC ∠OA OA OC = 50OAC OCA ∴∠=∠=︒180()80AOC OAC OCA ∴∠=︒-+∠=︒1402ABC AOC ∴∠=∠=︒B 2(2)2y x =-+()2x =-(2,2)x y (0,2)2(2)2y x =-+抛物线开口向上,对称轴为直线,与轴有两个公共点,顶点坐标为,则最低点的坐标为;其当时,,即与轴交点坐标为,与轴没有交点,故选项、、说法错误,选项说法正确,故选:.【点评】本题考查的是抛物线与轴的交点,主要考查函数图象上点的坐标特征,要求学生非常熟悉函数与坐标轴的交点、顶点等点坐标的求法,及这些点代表的意义及函数特征.5.如图,直线,直线、与、、分别交于点、、和点、、,若,,则的长为 A .2B .3C .4D .5【分析】根据平行线分线段成比例定理解答即可.解:直线,,,,,故选:.【点评】本题主要考查了平行线分线段成比例的性质,能够熟练运用其性质是解题的关键.6.下列四个命题中,正确的是 (1)各角相等的圆内接五边形是正五边形;(2)各边相等的圆内接五边形是正五边形;(3)各角相等的圆内接六边形是正六边形;∴2x =x (2,2)(2,2)0x =6y =y (0,2)x A C D B B x 123////l l l a b 1l 2l 3l A B C D E F :1:2AB BC =6DF =EF ()123////l l l ∴12AB DE BC EF ==6DF = ∴162EF EF-=4EF ∴=C ()(4)各边相等的圆内接六边形是正六边形.A .(1)(2)(3)B .(1)(2)(4)C .(1)(3)(4)D .(2)(3)(4)【分析】根据正多边形的性质一一判断即可.解:(1)各角相等的圆内接五边形是正五边形,因为圆内接五边形的角度都是相等的,所以是正五边形,说法正确;(2)各边相等的圆内接五边形是正五边形,因为圆内接五边形的边长都相等,所以是正五边形,说法正确;(3)各角相等的圆内接六边形,因为圆内接六边形的角度相等,但各边不一定相等,所以不一定是正六边形,说法错误;(4)各边相等的圆内接六边形是正六边形,因为圆内接六边形的边长都是相等的,所以是正六边形,说法正确.故选:.【点评】本题考查正多边形的性质等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.二、填空题(共10个小题,每小题2分,共20分.不需写出解答过程,请把正确答三、案直接填写在答题卡相应位置上)7.若关于的方程有两个相等的实数根,则 1 .【分析】根据判别式的意义得到,然后解关于的方程即可.解:根据题意得△,解得.故答案为1.【点评】本题考查了根的判别式:利用一元二次方程根的判别式△判断方程的根的情况.8.设,是一元二次方程的两个根,则的值是 .【分析】根据根与系数的关系得出即可.解:,是一元二次方程的两个根,,故答案为:.B x 220x x m -+=m =2(2)40m --=m 2(2)40m =--=1m =(24)b ac =-1x 2x 240x x +-=12x x +1-1x 2x 2410x x +-=12111x x ∴+=-=-1-【点评】本题考查了根与系数的关系,能熟记根与系数的关系的内容是解此题的关键.9.已知点是线段的黄金分割点,.若.则 (结果保留根号).【分析】根据黄金分割点的定义,知是较长线段;则,代入数据即可得出的长.解:由于为线段的黄金分割点,且是较长线段;则,故答案为:.【点评】本题考查黄金分割点的概念.应该识记黄金分割的公式:较短的线段原线段的,较长的线段10.某农场的粮食产量在两年内从3000吨增加到3630吨,若设平均每年增产的百分率为,则所列方程为 .【分析】此题是平均增长率问题,一般用增长后的量增长前的量增长率),参照本题,如果设平均每年增产的百分率为,根据“粮食产量在两年内从3000吨增加到3630吨”,即可得出方程.解:设平均每年增产的百分率为;第一年粮食的产量为:;第二年粮食的产量为:;依题意,可列方程:;故答案为:.【点评】本题考查了由实际问题抽象出一元二次方程中求平均变化率的方法.若设变化前的量为,变化后的量为,平均变化率为,则经过两次变化后的数量关系为.11.把二次函数的图象先向右平移3个单位长度,再下平移1个单位长度,所得图P AB AP PB >10AB =AP =5-AP AP =AP P 10AB =AP 105AP AB ===-5==x 23000(1)3630x +==(1⨯+x x 3000(1)x +23000(1)(1)3000(1)x x x ++=+23000(1)3630x +=23000(1)3630x +=a b x 2(1)a x b ±=22y x =象对应的函数表达式是 .【分析】利用二次函数平移规律进而求出即可.解:把二次函数的图象先向右平移3个单位长度,再下平移1个单位长度,所得图象对应的函数表达式是:.故答案为.【点评】本题考查的是二次函数的图象与几何变换,熟知函数图象平移的法则是解答此题的关键.12.如图,一块飞镖游戏板由除颜色外都相同的9个小正方形构成.假设飞镖击中每1块小正方形是等可能的(击中小正方形的边界或没有击中游戏板,则重投一次).任意投掷飞镖一次,击中黑色区域的概率是 .【分析】用黑色小正方形的个数除以小正方形的总个数可得.解:共有9种小正方形,其中黑色正方形的有3个,小刚任意投掷飞镖一次,刚好击中黑色区域的概率是,故答案为:.【点评】本题考查几何概率:如果一个事件有种可能,而且这些事件的可能性相同,其中事件出现种可能,那么事件的概率(A ).13.如图,在中,,,,以边所在的直线为轴旋转一周得到一个圆锥,则这个圆锥的面积是 .22(3)1y x =--22y x =22(3)1y x =--22(3)1y x =--13∴3193=13n A m A P m n=ABC ∆90ACB ∠=︒4AC cm =3BC cm =AC 24π2cm【分析】利用勾股定理易得圆锥母线长,那么圆锥的侧面积底面周长母线长.解:由勾股定理易求得.旋转后的圆锥母线为,长度为,底面半径为,长度为,则底面圆的周长,即侧面展开图的弧长是.圆锥的侧面积是:.圆锥的底面积是,圆锥的面积是.【点评】本题从圆锥的形成过程中,考查其侧面积公式,明确为底面半径,为母线长.14.已知二次函数、、是常数,且,函数值与自变量的部分对应值如下表:01234102125当时,自变量的取值范围是 .【分析】根据题意确定二次函数的开口方向、对称轴和顶点坐标,根据二次函数的性质解答即可.解:由题意得,抛物线的顶点坐标为,对称轴是直线,开口向上,当时的函数值与时的函数值相等,当时,自变量的取值范围是,故答案为:.【点评】本题考查的是二次函数的图形和性质,根据表格确定二次函数的开口方向、对称轴和顶点坐标是解题的关键.=⨯2÷5AB cm === AB 5cm BC 3cm 6cm π∴2165152cm ππ⨯⨯=2239cm ππ=∴215924cm πππ+=BC AB 2(y ax bx c a =++b c 0)a ≠y x x⋯1-⋯y⋯1y ⋯1y y <x 04x <<(2,1)2x =∴0x =4x =∴1y y <x 04x <<04x <<15.如图,在四边形中,、、分别与相切于、、三点,为的直径.若,,则的半径为 .【分析】过作于,由切线长定理得到,,由切线的性质定理得到直径,直径,推出四边形是矩形,得到,,求出,,由勾股定理求出,得到,即可得到圆的半径长.解:过作于,、、分别与相切于、、三点,,,直径,直径,四边形是矩形,,,,,,,为的直径,的半径为.故答案为:.ABCD BC CD DA O B E A AB O 4BC cm =3AD cm =Ocm D DH BC ⊥H 3DE AD cm ==4CE BC cm ==AB AD ⊥AB BC ⊥ABHD DH AB =3BH AD cm ==431()CH BC BH cm =-=-=347()DC DE CE cm =+=+=)DH cm ==)AB cm =D DH BC ⊥H BC CD DA O B E A 3DE AD cm ∴==4CE BC cm ==AB AD ⊥AB BC ⊥∴ABHD DH AB ∴=3BH AD cm ==431()CH BC BH cm ∴=-=-=347()DC DE CE cm =+=+=)DH cm ∴==)AB cm ∴=AB O O ∴【点评】本题考查切线的性质,切线长定理,勾股定理,矩形的判定和性质,关键是由切线长定理得到的长,由矩形的性质得到的长,由勾股定理求出的长.16.如图,在正方形中,,点为上动点,点在的延长线上,且,、相交于点.当点从点运动到点时,点运动的路线长度为 .【分析】先画出点运动的路线,过作,交于点,根据,可得,设,则,,再根据,可求得、,利用勾股定理可得.解:当点在点处时,如图,,,,,当点运动到点时,如图,CD CH DH ABCD 3AB cm =P AB Q AB 2BP BQ =CP DQ E P A B E E EE 'E EF AQ ⊥AQ F EAF CAB ∆∆∽EF AF =EF xcm =(3)BF x cm =-(4.5)QF x cm =-EQF DQA ∆∆∽EF E F 'EE 'P A 2BP BQ = 3BP cm =1.5BQ cm ∴=P B,所以点运动的路线,如图,,过作,交于点,即,四边形为正方形,,在中,,,,,,,,设 ,则,,,,,,即,解得:,,,E EE 'E EF AQ ⊥AQ F 90AFE EFQ ∠=∠=︒ ABCD 3BC AD cm ∴==Rt ABC ∆AC ==90AFE ABC ∠=∠=︒ CAB EAF ∠=∠EAF CAB ∴∆∆∽∴EF AFCB AB=AB BC = EF AF ∴=EF x =cm (3)BF x cm =-(4.5)QF x cm =-EQF DQA ∠=∠ 90EFQ DAQ ∠=∠=︒EQF DQA ∴∆∆∽∴EF QF DA QA =(4.5)3 4.5x x -=95x =95EF cm ∴=65E F BF cm '==在中,,.【点评】本题考查了正方形的综合题,关键是借助相似三角形对应边成比例解决问题.三、解答题(本人题共11小题,共88分,请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤)17.(8分)解方程:(1);(2).【分析】(1)利用配方法求解;(2)利用公式法求解.解:(1),,,,;(2),,,,,,△,,【点评】本题考查解一元二次方程公式法,配方法,解题的关键是掌握公式法,配方法解一元二次方程.18.(8分)某校从甲、乙两名同学中选拔一名代表学校参加《喜迎二十大奋进新征程》演讲比赛,如图是甲、乙两名学生在五次选拔比赛中的成绩情况:Rt EFE ∆')EE cm '==2420x x --=3(2)24x x x --=242x x -=24424x x -+=+2(2)6x -=2x ∴-=12x ∴=+22x =3(2)24x x x --=23624x x x --=23840x x --=3a =8b =-4c =-6443(4)1120=-⨯⨯-=>x ∴===1x ∴=2x =-根据以上信息,整理分析数据如下:学生平均数(分中位数(分方差(分甲8 3.6乙8(1) 8 , , ;(2)根据五次选拔比赛的成绩,你认为选谁较为合适?请说明理由.【分析】(1)根据平均数,中位数,方差的定义解决问题即可;(2)利用方差小成绩稳定判断即可.解:(1)由题意,,.故答案为:8,8,0.8;(2)从方差看,乙的成绩比较稳定,选乙比较合适.【点评】本题考查折线统计图,条形统计图,中位数,平均数,方差等知识,解题的关键是掌握中位数,平均数,方差的定义,属于中考常考题型.19.(8分)一个不透明的口袋中有三个完全相同的小球,把它们分别标号为1,2,3.随机摸出一个小球后放回,再随机摸出一个小球.(1)第二次摸到1号小球的概率是 . ;(2)求两次摸出的小球标号和为3的概率.【分析】(1)直接利用概率公式可得答案.))2)baca =b =c =1(27829)85a =⨯++⨯=8b =2221[2(78)(88)2(98)]0.85c =⨯-+-+⨯-=13(2)列表可得出所有等可能的结果数以及两次摸出的小球标号和为3的结果数,再利用概率公式可得出答案.解:(1)由题意得,第二次摸到1号小球的概率是.故答案为:.(2)列表如下:123123共有9种等可能的结果,其中两次摸出的小球标号和为3的结果有:,,共2种,两次摸出的小球标号和为3的概率为.【点评】本题考查列表法与树状图法、概率公式,熟练掌握列表法与树状图法以及概率公式是解答本题的关键.20.(7分)如图,学校打算用长的篱笆围成一个一面靠墙且面积是的矩形生态园饲养小兔,求生态园的长和宽.【分析】设生态园的宽为,则长为,根据生态园的面积是的矩形,列出一元二次方程,解方程即可.解:设生态园的宽为,则长为,由题意得:,解得:,,当时,;当时,.答:生态园的长为,宽为或长为,宽为.【点评】本题考查了一元二次方程的应用,找准等量关系,正确列出一元二次方程是解题的1313(1,1)(1,2)(1,3)(2,1)(2,2)(2,3)(3,1)(3,2)(3,3)(1,2)(2,1)∴2916m 230m ?x m (162)x m -230m ?x m (162)x m -(162)30x x -=13x =25x =3x =162162310x -=-⨯=5x =16216256x -=-⨯=10m 3m 6m 5m关键.21.(8分)如图,二次函数图象顶点坐标为,与轴一个交点坐标为.(1)该函数图象与轴的另一个交点坐标为 ;(2)求这个二次函数的表达式;(3)当时,的取值范围为 .【分析】(1)根据函数的对称性可得结论;(2)用待定系数法可求解析式即可;(3)根据函数的性质结合函数图象求的取值范围.解:(1)二次函数的对称轴为直线,与轴一个交点坐标为,二次函数图象与轴的另一交点为,故答案为:;(2)设二次函数的表达式为,把代入解析式得:,解得,二次函数的表达式表达式为;(3)抛物线开口向上,顶点坐标为,抛物线的最小值为,,当时,,当时,的取值范围为,故答案为:.【点评】本题考查了抛物线与轴的交点,二次函数图象的性质,用待定系数法求二次函数解析式,熟练掌握二次函数图象的性质是本题的关键.(1,4)--x (1,0)x (3,0)-40x -<<y y 1x =-x (1,0)∴x (3,0)-(3,0)-2(1)4y a x =+-(1,0)440a -=1a =∴2(1)4y x =+- (1,4)--∴4-1(4)30(1)1---=>--= ∴4x =-5y =∴40x -<<y 45y -<...45y -< (x)22.(8分)如图,在中,的垂直平分线分别交,于点,,交于点,.(1)判断与是否相似,并说明理由.(2)与相等吗?为什么?【分析】(1)根据相似三角形的判定即可求出答案.(2)由相似三角形的性质即可知道,由于,所以,从而可知解:(1)是垂直平分线,,,,,;(2),,,,.【点评】本题考查相似三角形的性质,涉及相似三角形的判定与性质,等腰三角形的性质,垂直平分线的性质等知识,综合程度较高.23.(8分)某种服装,平均每天可销售20件,每件盈利44元.若每件降价1元,则每天可多售5件,降价幅度不超过10元,那么每件应降价多少元,可获得最大利润?最大利润是多少?【分析】设每件应降价元,利润为元,则每天的销量为件,每件的利润为ABC ∆BC BC AC D E BE AD F AB AD =FDB ∆ABC ∆AF DF 2AB FD =AB AD =2AD FD =DF AF=DE BC BE CE ∴=EBC ECB ∴∠=∠AB AD = ABC ADB ∴∠=∠FDB ABC ∴∆∆∽FDB ABC ∆∆ ∽∴12FD BD AB BC ==2AB FD ∴=AB AD = 2AD FD ∴=DF AF ∴=x y (205)x +(44)x -元;再根据“降价后每件的盈利降价后每天的销量”可列式配方后可求解,注意降价幅度不超过10元.解:设每件应降价元,利润为元,根据题意得:,,当时,随的增大而增大,,当时,有最大值是:,答:每件应降价10元,可获得最大利润,最大利润是2380元.【点评】此题考查了二次函数的应用,其中根据每件降价1元,则每天可多售5件表示出每件的利润及卖的件数是列函数解析式的关键.24.(7分)在四边形中,用无刻度的直尺和圆规完成下列作图(保留作图痕迹,不写作法,写出必要的文字说明).(1)如图①,连接,在边上作点,使得;(2)如图②,在边上作点,使得.【分析】(1)作的外接圆交于点,则根据圆周角定理得到;(2)先作点关于的对称点,则,再作△的外接圆交于点,则根据圆周角定理得到,所以.解:(1)如图①,作和的垂直平分线,它们相交于点,然后以点为圆心,为半径作圆交于点,则点为所作;y =⨯x y 22(44)(205)52008805(20)2880y x x x x x =-+=-++=--+50-< ∴20x <y x 10x …∴10x =y 25(1020)28802380--+=ABCD BD CD M AMB ADB ∠=∠CD N BND A ∠=∠ABD ∆CD M AMB ADB ∠=∠A BD A 'BAD BA D ∠=∠'A BD 'CD N BND BA D ∠=∠'BND A ∠=∠AB AD O O OA CD M M(2)如图②,作点关于的对称点,再作和的垂直平分线,它们相交于点,然后以点为圆心,为半径作圆交于点,则点为所作.【点评】本题考查了作图复杂作图:解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.也考查了圆周角定理.25.(8分)如图,在的内接四边形中,,直径,垂足为点.(1)当时,求的度数;(2)当,时,求的长.【分析】(1)根据题意得到关于和的二元一次方程组求解即可,(2)根据题意,利用勾股定理及两个三角形相似的判定定理求解即可.解:(1)连接,,,,所以,,,,,,在同一个圆上,,A BD A 'DA 'BD O O OB CD N N -O ABCD AB BC =AE CD ⊥F BCCD =D ∠5AB =8AD =CD CAD ∠ACD ∠AC OC OD BDBAC CAD ∠=∠AB BC = BCA BAC CAD ∴∠=∠=∠A B C D 180BAD BCD ∴∠+∠=︒,,且,,为等腰三角形,,,联立,解得:,.(2)延长,过作,于,设,由(1)知,,,在中,,在中,,,解得:,,,,,又,,,180BCA ACD BAC CAD ∴∠+∠+∠+∠=︒3180CAD ACD ∠+∠=︒OC OD = OF CD ⊥CF FD ∴=ACD ∴∆ACD ADC ∴∠=∠2180CAD ACD ∴∠+∠=︒31802180CAD ACD CAD ACD ∠+∠=︒⎧⎨∠+∠=︒⎩3672CAD ACD ∠=︒⎧⎨∠=︒⎩72D ACD ∴∠=∠=︒CB A AG CB ⊥G BG x =8AC AD ==5BC AB ==Rt ABG ∆222AG AB BG =-Rt ACG ∆222AG AC CG =-222268(5)x x ∴-=-+75x =180ABG ABC ∠+∠=︒ 180ABC ADC ∠+∠=︒ADC ACD ∠=∠ABG ACD ∴∠=∠90AGB AFC ∠=∠=︒ ABG ACF ∴∆∆∽∴AC AB CF BG=,,,的长为.【点评】本题考查的是圆内接四边形的性质及圆周角定理,熟知圆内接四边形的对角互补是解题的关键.26.(8分)已知二次函数的图象经过,两点.(1)求的值;(2)求证该二次函数的图象与轴的总有两个公共点;(3)设该函数图象与轴的两个公共点分别为、.当时,直接写出的取值范围.【分析】(1)依据题意,由二次函数图象经过,两点,进而代入计算得①,②,再由②①得,,从而求出的值;(2)依据题意,由(1)得,,又,从而,最后,进而△,进而可以判断得解;(3)依据题意,由该函数图象与轴的两个公共点分别为、,进而求得,又,再依据的值进行分类讨论即可判断得解.解:(1)由题意,二次函数图象经过,两点,①,②.②①得,..(2)由(1)得,,又,..△∴8575CF =5625CF =56112222525CD CF ∴==⨯=CD ∴112252y ax bx c =++(1,3)-(1,1)-b x x (,0)m (,0)n 0mn <a (1,3)-(1,1)-3a b c -+=1a b c ++=--24b =-b 2b =-3a b c -+=1a c +=1c a =-22444(1)(21)3b ac a a a =-=--=-+x (,0)m (,0)n 1c a mn a a-==0mn <a (1,3)-(1,1)-3a b c ∴-+=1a b c ++=-∴-24b =-2b ∴=-2b =-3a b c -+=1a c ∴+=1c a ∴=-∴2444(1)b ac a a =-=--.对于任意的都有,△.该二次函数的图象与轴的总有两个公共点.(3)由题意,该函数图象与轴的两个公共点分别为、,.又,.①当时,...②当时,..综上,或.【点评】本题主要考查了图象与性质,解题时要熟练掌握并能灵活运用是关键.27.已知的半径为,是外一点,,点、在上,在中,.(1)如图①,是的切线,当时,求证:是的切线;(2)如图②,、分别交于点、,当点为中点时,求的长;(3)线段的取值范围是 .2444a a =-+2(21)3a =-+ a 2(21)0a -…∴2(21)330a =-+>…∴x x (,0)m (,0)n 1c a mn a a-∴==0mn <∴10a a-<0a <10a ∴->1a ∴<0a ∴<0a >10a ∴-<1a ∴>0a <1a >O 2cm P O 4PO cm =A B O PAB ∆BP BA =PB O PA PB =PA O PA PB O C D C PA PDPA 6PA …【分析】(1)连接,,证明得到即可得证;(2)连接,,,先根据圆的有关性质求出,再证明,根据相似比求出即可解答;(3)先确定的运动轨迹,当,,三点共线时,最大,求出此时的,当最小时最小,根据勾股定理求出此时的几颗解答.解:(1)连接,,是的切线,,在与中,,,,是的半径,是的切线;(2)连接,,,如图:OA OB PBO PAO ∆≅∆90PAO PBO ∠=∠=︒BC AD OD 4BA BP cm ==OBD POB ∆∆∽BD P P O A PA PA BP PA PA OA OB PB O 90PBO ∴∠=︒PBO ∆PAO ∆PB PA OB OA PO PO =⎧⎪=⎨⎪=⎩()PBO PAO SSS ∴∆≅∆90PAO PBO ∴∠=∠=︒OA O OA ∴O BC AD OD,点为中点,,是的直径,设圆心为,连接,的半径为,,,,,,,,即,,;(3),的运动轨迹为以为圆心,半径为的圆,如图:BA BP = C PA BC AP ∴⊥AB ∴O O OP O 2cm 4BA BP cm ∴==OB OD = PO PB =OBD ODB ∴∠=∠OBP POB ∠=∠OBD POB ∴∆∆∽∴OD BD PO BO =242BD =1BD ∴=413PD PB BD cm ∴=-=-=4OP cm = P ∴O 4cm,,三点共线时,最大,此时,,,即,当最小时,最小,如图:此时,,共线,,,作于,则,,,,.故答案为:.【点评】本题考查与圆有关的性质和概念,全等三角形的判定和性质,相似三角形的判定和P ∴O A PA 426PA PO OA cm =+=+=BP AB = PA BP AP <+2PA BP <∴BP PA P B O 422PB PO OB =-=-=2PB AB OA OB cm ∴====AH OB ⊥H 112BH OB ==AH ∴===3PH PB BH cm =+=PA ∴==6PA ∴…6PA …性质,正确作出辅助线是解题关键.。
重庆市巴蜀中学2023-2024学年九年级上学期期末数学试题(含答案)
数学一、选择题:(本大题共10个小题,每小题4分,共40分)在每个小题的下面,都给出了代号为A 、B 、C 、D 的四个答案,其中只有一个是正确的,请将答题卡上题号右侧正确答案所对应的方框涂黑.1.若数a 的平方等于16,那么数a 可能是()A .2B .-4C .D .2.如图,该几何体由5个大小相同的正方体组成,从正面看到该几何体的形状图是()A .B .C .D .3.下列运算正确的是()A .B .C .D .4.已知一次函数,y 随着x 的增大而减小,且,则在直角坐标系内它的图象大致是()A .B .C .D .5.如图,反比例函数的图象经过矩形OABC 的对角线AC 的中点D ,若矩形OABC 的面积为12,则k 的值为()(5题图)A .2B .3C .4D .66.如图,在中,,若,,则为()4±8±325x x x +=32x x x-=326x x x ⋅=32x x x÷=y kx b =+0kb <()0,0ky k x x=≠>ABC △DE BC ∥:1:2ADE BDE S S =△△3ADE S =△ABC S △(6题图)A .9B .12C .24D .277.平面直角坐标系中,A 、B 、C 三点坐标分别为,,,以这三点为平行四边形的三个顶点,则第四个顶点不可能在()A .第一象限B .第二象限C .第三象限D .第四象限8.如图,过上一点P 的切线与直径AB 的延长线交于点C ,点D 是圆上一点,且,则的度数为()(8题图)A .32°B .33°C .34°D .35°9.菱形ABCD ,,E ,F 分别是CB ,CD 上两点,连接AE ,AF ,EF ,且,如果,则下列说法错误的是()(9题图)A .B .C .D .10.对于以下式子:,,,,下列说法正确的有()(1)如果,则无论y 取何常数,A ,B ,C ,D 调整顺序后可组成一列数,这列数后项减去前项的差均相等;(2)代数式一定是非负数;(3)如果A 为第1项,B 为第2项,C 为第3项,第1项与第2项的和减去第3项的结果为第4项,第2项()0,0()0,4-()3,3-O e 29BDP ∠=︒C∠60B ∠=︒60EAF ∠=︒BAE α∠=CEF α∠=60FAD α∠=︒-60EFC α∠=︒-90AFD α∠=︒-A x y =+B x y =-2C x y =-D xy =0x =222A B C D ⋅--与第3项的和减去第4项的结果为第5项,……,依此类推,则第2024项为.A .0个B .1个C .2个D .3个二、填空题(本大题共8个小题,每小题4分,共32分)请将每小题的答案直接填在答题卡中对应的横线上.11______.12.一个正多边形的内角和是1080°,则这个正多边形有______条边.13.已知当时,整式的值等于10,则当时,则的值为______.14.某次车展活动设计了一种有奖竞猜游戏,游戏规则如下:在5个相同商标牌中,有3个商标牌的背面贴有一个笑脸,其余2张商标牌的背面贴一张哭脸,每个人每次翻两张牌,只有两张都是笑脸才得奖,则观众每次获奖的概率是______.15.如图,已知,,,B 、D 、E 在同一直线上,则的度数为______.(15题图)16.如图,扇形AOB ,点O 为圆心,半径OB 长为2,,再以点B 为圆心,OB 为半径作弧,交弧AB 于点C ,则阴影部分的面积是______.(16题图)17.若整数a 使关于x 的不等式组无解,且使关于y 的分式方程有非负整数解,则满足条件的a 的值之和为______.18.一个四位正整数M ,如果千位数字与十位数字之和的两倍等于百位数字与个位数字之和,则称M 为“共进退数”,并规定等于M 的前两位数所组成的数字与后两位数所组成的数字之和,等于M 的前两位数所组成的数字与后两位数所组成的数字之差,如果,那么M 各数位上的数字之和为3032x y +0122⎛⎫--= ⎪⎝⎭2x =35bx cx +-2x =-37bx cx ++AB AC =AD AE =52BAC DAE ∠=∠=︒BEC ∠90AOB ∠=︒232x a x a ->⎧⎨-<-⎩5355ay y y -=---()F M ()G M ()60F M =______;有一个四位正整数(,,,且为整数)是一个“共进退数”,且是一个平方数,是一个整数,则满足条件的数N 是______.三.解答题(本大题共8个小题,第19题8分,其余每题各10分,共78分)解答时每小题必须给出必要的演算过程或推理步骤,画出必要的图形(包括辅助线),请将解答过程书写在答题卡中对应的位置上.19.(本小题满分8分)计算:(1)(2)20.(本小题满分10分)如图:正方形ABCD 中,直线经过点D ,与AB 交于点E ,(1)用直尺和圆规作图:过点C 作DE 的垂线,垂足为G ,交AD 于点F ,(请保留作图痕迹,不要求写作图过程)(2)同学们作图完成后,通过测量发现,并且推理论证了该结论,请你根据他们的推理论证过程完成以下证明:如图:已知正方形ABCD 中,DE 、CF 分别是直线,直线被一组对边截得的线段,当时,求证:.证明:∵正方形ABCD ,∴,∴,∴,∵,∴,∴ ② ,∴,在和中,1101100010N x y z =+++08x ≤≤09y ≤≤08z ≤≤()F N ()7G N ()()()212141a a a a -+--211121xx x x ⎛⎫-÷ ⎪+++⎝⎭1l 2l DE CF =1l 2l DE CF ⊥DE CF =AD DC =90EAD CDF ∠=∠=︒90+∠=︒AED ①DE CF ⊥90FGD ∠=︒AED DFG ∠=∠DAE △CDF △,∴,∴.同学们进一步研究发现,一条直线被正方形的一组对边所截得的线段与另一条直线被正方形的另一组对边所截得的线段垂直时均具备此特征,请你依据题目中的相关描述,完成下列命题:两条直线分别被正方形的一组对边所截,若所截得的线段④.21.(本小题满分10分)为了激发同学们对古诗词学习的兴趣,2023年9月我市某中学开展了“课外古诗词赏析比赛”.为了解学生课外古诗词的学习情况,现从该校七、八年级中各随机抽取10名学生的比赛成绩(成绩为百分制,学生得分均为整数且用x 表示,)进行整理、描述和分析,并将其共分成四组:A :,B :,C :,D :)下面给出了部分信息:七年级10名学生的比赛成绩是:84,85,86,88,89,95,96,99,99,99.八年级10名学生的比赛成绩在C 组中的数据是:90,94,94.七、八年级抽取的学生比赛成绩统计表年级七年级八年级平均数9292中位数92b 众数c100根据以上信息,解答下列问题:(1)______,______,______;(2)根据以上数据,你认为该校七、八年级中哪个年级学生古诗词掌握得较好?请说明理由(一条理由即可);(3)该校七年级有1420名学生、八年级有1300名学生参加了此次“课外古诗词赏析比赛”,请估计参加此次比赛成绩不低于90分的学生人数是多少?22.列方程解应用题(本小题满分10分)中国最重要的传统节日之一春节,除了有热烈的庆祝活动和丰盛的美食外,长辈发压岁钱给晚辈表达美好的祝福也是春节习俗的重要组成部分.为迎接2024年龙年春节的到来,某工厂计划安排甲车间生产16000个龙年布艺红包袋.根据现有设备和工艺,甲车间每天可生产360个布艺红包袋,甲车间单独先工作4天后,工厂安排乙车间加入一起赶工,且乙车间每天可生产680个布艺红包袋,EAD CDF AED DFG⎧∠=∠⎪⎨⎪∠=∠⎩③DAE CDF △≌△DE CF =85x <8590x ≤<9095x ≤<95100x ≤≤a =b =c =(1)从开始加工到完成这批布艺红包袋一共需要多少天?(2)由于市场需求增大,甲车间按原生产效率单独生产4天后,工厂改进了两个车间的生产工艺,并将剩下的生产任务平均分给了甲、乙两车间.改进后甲、乙两车间每天生产的布艺红包袋数量之比为,且改进工艺后两个车间完成剩下生产任务的天数之和为10天,问改进工艺后甲车间每天生产多少个布艺红包袋?23.(本小题满分10分)如图,平行四边形ABCD 中,,,连接AC ,,动点P 以每秒1个单位的速度从点C 出发沿折线运动,设点P 运动时间为x 秒,的面积为,(1)请直接写出关于x 的函数表达式,并注明自变量x 的取值范围;(2)在给定的平面直角坐标系中画出这个函数图象,并写出该函数的一条性质;(3)的函数图象如图所示,当时请直接写出x 的取值范围.(结果保留一位小数,误差小于0.2)24.(本小题满分10分)今年10月“愉悦创造营”的同学们积极参加劳动实践,在校园“耕读园”里播种了近百粒萝卜种子.某周日下午返校时涵涵和静静约好一起去“耕读园”看看萝卜的生长情况.如图,已知“耕读园”在点A 处,涵涵家位于点A 正南方一条东西走向的街道BD 上,且在耕读园西南方向800米的C 处;静静家位于点D 正北方米且位于“耕读园”南偏西60°方向上的点E 处,图中点A 、B 、C 、D 、E 在同一平面内,(1)求静静家离耕读园的距离是多少?(结果保留根号)7:133AB =5BC =90BAC ∠=︒C A D →→ABP △1y 1y 24y x=12y y ≥(2)涵涵周日下午5:40出门,先以80米/分钟的速度从C 出发,往正西方向走到点D 处后再向正北方向到静静家楼下两人碰面,然后两人以此速度一起前往“耕读园”,请问她们能在5:55前到达耕读园吗?(参考数据:,结果精确到十分位)25.(本小题满分10分)如图1:平面直角坐标系中,抛物线与x 轴交于点和点B ,与y轴交于点C ,点是抛物线上一点,图1图2 图3(1)求抛物线表达式;(2)如图2:点是y 轴上一点,连接AD ,点P 是直线AD 上方抛物线上一个动点,过点P 作轴交直线AD 于点E ,在射线ED 上取一点F ,使得,求周长的最大值及此时点P 的坐标.(3)如图3:将原抛物线沿射线AD 方向平移4个单位长度,平移后抛物线的对称轴与x 轴交于点N ,射线AD 上有一点G ,连接GN ,过点G 作GN 的垂线与抛物线交于点M ,连接MN ,若,请直接写出点M 的坐标.26.(本小题10分)已知,中,,,交BC 于点D ,.图1 图2 图3(1)如图1,将BD 绕点B 逆时针旋转得线段BE ,且点E 在DA 的延长线上,求BE 的长.(2)如图2,在(1)的条件下,连接CE ,F 为AB 上一点,且满足:,作于点G ,求证:.(3)如图3,在(1)的条件下,P 、Q 分别为线段BA 、EB 上的两个动点,且满足,当1.414≈ 2.449≈292y ax bx =++()A -()()0,3D PE y ∥PE PF =PEF △292y ax bx =++1y 1y 30GMN ∠=︒ABC △AB AC =120BAC ∠=︒AD AB ⊥6AD =BEF AFG ∠=∠FG CE ⊥CG =BP EQ =PD QD+最小时,M 为平面内一动点,将沿EM 翻折得,请直接写出的最大值.BEM △B EM '△PB '参考答案一、选择题(每题4分,共48分)1-5:CADAB6-10:DAADB二、填空题(每题4分,共32分)19.计算:(1)解:原式.(2)解:原式.20.①②③④互相垂直,那么这两条线段相等21.(1)40,94,99;(2)解:八年级学生的古诗词掌握得较好.从平均数看,七年级平均分92分=八年级平均分92分,从中位数看,七年级92分<八年级中位数94分,所以八年级学生的古诗词掌握得较好.(3)(人)答:估计参加本次比赛成绩不低于90分的学生约为1620人.22.解:(1)设从开始加工到完成这批布艺红包袋一共需要x 天.答:从开始加工到完成这批布艺红包袋.一共需要18天.()()()212141a a a a -+--224141a a a a =--+=-211121xx x x ⎛⎫-÷ ⎪+++⎝⎭2(1)11x x x x x+=⨯=++ADE ∠90ADE DFG ∠+∠=︒AD CD =571420130016201010⨯+⨯=()()3603603204160003604x ++-=-⨯⎡⎤⎣⎦18x =(2)设甲车间每天生产7m 个,乙车间每天生产13m 个布艺红包袋.(个)经检验:是原分式方程的解,且符合题意.∴改进后甲每天产量:(个).答:改进工艺后,甲车间每天生产1120个布艺红包袋.23.(1)(2)当时,随x 增大而减小,当时,随x 增大而增大.(3)或(结果保留一位小数,误差不超过0.2).24.解:(1)过E 作于H ,,,∵中,,,∴,∴,∴,∴∵,EDBH 为矩形.∴,,∵,,,∴(米),答:静静家离耕读园距离为米.(2)∵,,∴∵矩形EDBH ,,∴,16000360472802-⨯=7280728010713m m+=160m =160m =16071120⨯=()()360426244955x x y x x ⎧-+≤<⎪⎪=⎨⎪-<≤⎪⎩04x <<1y 49x <<1y 0.8 3.2x ≤≤ 4.79.0x ≤≤EH AB ⊥90EHA BHE ∠==︒800AC =ABC △90B ∠=︒45BAC ∠=︒9045ACB BAC BAC ∠=︒-∠=︒=∠BA BC =222AC AB BC =+AB BC ==90D B BHE ∠=∠=∠=︒ED =HE BD =ED HB ==90AHE ∠=︒60EAH ∠=︒AH =cos AH AE EAH ===∠90AHE ∠=︒60EAH ∠=︒AE =sin EH AE EAH =⋅∠==BD EH ==CD BD BC =-=-∴总用时:(分),∵5:50-5:40=15(分),∴,∴她们能在5:55前到达耕读园.25.解:(1),代入,,∴.(2)过P 作于点H ,则,设,,,∴,,∴,∴,∴PE最大时,最大,直线AD :,,,,开口向下,对称轴直线,,∴时,,.14.4814.580CD DE EA ++=≈≈14.515<()A -()927029362a a ⎧-+=⎪⎪⎨⎪-+=⎪⎩12a b ⎧=-⎪⎨⎪=⎩21922y x =-+PH EF ⊥90PHE ∠=︒219,22P p p ⎛⎫-+ ⎪⎝⎭∠=∠PHE DOA EPH DAO ∠=∠EPH DAO △∽△PH AO PE AD ==PH PE =()(22PEF C PE PH PE =+=+△PEF C △3y x =+3E p p ⎛⎫+ ⎪ ⎪⎝⎭212526PE p ⎛=-++ ⎝102-<x =0p -<<x =PEF C △356P ⎛⎫ ⎪ ⎪⎝⎭(3),,.26.解:(1).(2)延长EF 至M ,使得,连接BM 、CM 、CF ,,∴,∴,,∴,,,∴,,∴,,,∴,∴,∴,∴,,∴(3)1223M ⎫⎪⎪⎭)2M ()316M --12BE =EM CM =BEF AFG ∠=∠AFE EBF BEF EFG AFG ∠=∠+∠=∠+∠30EBF EFG ∠=∠=︒FG CE ⊥60FEG ∠=︒EM CM BEM DEC EB EC =⎧⎪∠=∠⎨⎪=⎩()SAS BEM DEC △≌△BM CD =120EAM EDC ∠=∠=︒180EBM AEB ∠+∠=︒BM AE ∥CD AD AE ==BM AE =()ASA AEF BMF △≌△FE FM =CF EM ⊥30FCG ∠=︒CG =()max 12PB '=+-。
2023-2024学年河南省洛阳市九年级(上)期末数学试卷(含解析)
2023-2024学年河南省洛阳市九年级(上)期末数学试卷一、选择题:本题共10小题,每小题3分,共30分。
在每小题给出的选项中,只有一项是符合题目要求的。
1.下列根式中,不是最简二次根式的是( )A. 2B. 3C. 4D. 52.某商家搞营销活动,顾客买商品后抽奖券,中奖概率为0.2.对“中奖概率为0.2.”这句话,下列理解正确的是( )A. 抽1张奖券肯定不会中奖B. 抽100张奖券肯定会中2张奖C. 抽1张奖券也可能会中奖D. 抽100张奖券至少中1张奖3.下列计算正确的是( )A. 23+22=25B. 18÷2=3C. 53×23=103D. 413=2334.方程x(x+5)=x的根是( )A. x=−5B. x1=−5,x2=0C. x1=−4,x2=0D. x1=−6,x2=05.已知一个袋子中装有2个红球和x个黄球,这些球除颜色外其余都相同.若从该袋子中任意摸出一个球是红球的概率为13,则x等于( )A. 3B. 4C. 5D. 66.在Rt△ABC中,∠C=90°,若cosB=35,则sinB的值得是( )A. 45B. 35C. 34D. 437.关于x的一元二次方程2x2+4mx+2m2=0的根的情况为( )A. 有两个不相等的实数根B. 有两个相等的实数根C. 没有实数根D. 无法确定8.水果店花1000元进了一批水果,按50%利润定价,无人购买,决定打折出售,但仍无人购买,于是又一次打折后才售完,经结算,这批水果共盈利400元若两次打折的折扣相同,设每次打x折,(打x折,即按原价的十分之x出售.)根据题意列方程为( )A. 1000×(1+50%)×(1+x10)2=1000+400B. 1000×(1+50%)×(1+x)2=1000+400C. 1000(1+x10)2=1000+400D. 1000×(1+50%)×(x10)2=1000+4009.在如图每个小方格均为小正方形的网格中,点A、B、C都在格点上,则∠ABC的正切值是( )A. 23B. 12C. 33D. 2131310.如图,在△ABC中,E、F分别是AB和AC上的中点,P是BC所在直线上任一点,当点P在BC所在直线上移动时,下列结论不正确的( )A. △PEF的周长总等于△AEF的周长B. PE+PF可能等于12(AB+AC)C. S△EFP=14S△ABC D. S△EFP=S△AEF二、填空题:本题共5小题,每小题3分,共15分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第1页 共21页 九年级上期末数学试卷4(含答案) 一、选择题(本题共8小题,每小题3分,共24分) 1.一元二次方程x2﹣4=0的解是( )
A.x=2 B.x1=,x2=﹣ C.x=﹣2 D.x1=2,x2=﹣2 2.下列图形中既是中心对称图形又是轴对称图形的是( )
A. B. C. D.
3.若甲、乙两个样本的方差分别为0.4、0.6,则下列说法正确的是( )
A.甲比乙稳定 B.乙比甲稳定
C.甲、乙一样稳定 D.无法比较
4.关于x的一元二次方程x2﹣kx﹣1=0的根的情况是( )
A.没有实数根 B.有一个实数根
C.有两个相等的实数根 D.有两个不相等的实数根
5.如图,⊙O的直径AB=10,CD是⊙O的弦,CD⊥AB,垂足为M,若OM:OB=3:5,则CD的长为( )
A.8 B.6 C.4 D.
6.如图,小正方形的边长均为1,则图中三角形(阴影部分)与△ABC相似的是( )
A. B. C. D.
7.正六边形的周长为6,则它的面积为( )
A.9 B.3 C. D. 8.两个相似三角形的最短边分别是5cm和3cm,它们的周长之差为12cm,那么小三角形的
周长为( ) 第2页 共21页
A.14cm B.16cm C.18cm D.30cm 二、填空题(本题有8小题,每小题3分,共24分) 9.在Rt△ABC中,∠C=90°,sinA=,则∠A= 度.
10.将抛物线y=﹣3x2向上平移1个单位长度,所得抛物线的函数表达式为 .
11.若⊙O的半径为4cm,圆心O到直线l的距离为5cm,则直线l与⊙O的位置关系是 .
12.口袋内装有一些除颜色外完全相同的红球、白球和黑球,从中摸出一球,摸出红球的概率
是0.2,摸出白球的概率是0.5,那么摸出黑球的概率是 . 13.用一个圆心角为120°,半径为4的扇形作一个圆锥的侧面,这个圆锥的底面圆的半径
为 . 14.如图,AB、AC是⊙O的两条弦,∠A=30°,过点C的切线与OB的延长线交于点D,则∠
D= °.
15.如图,点B、C都在x轴上,AB⊥BC,垂足为B,M是AC的中点.若点A的坐标为(3,
4),点M的坐标为(1,2),则点C的坐标为 .
16.如图,在平面直角坐标系中,点A在抛物线y=x2﹣2x+3上运动,过点A作AB⊥x轴于点
B,以AB为斜边作Rt△ABC,则AB边上的中线CD的最小值为 .
三、解答题(本题有9小题,共72分) 第3页 共21页
17.(1)计算:(3+1)0﹣()﹣1+2cos60° (2)解方程:x2﹣4x﹣5=0. 18.一只箱子里共有3个球,其中2个白球,1个红球,它们除颜色外均相同.
(1)从箱子中任意摸出一个球是白球的概率是多少? (2)从箱子中任意摸出一个球,不将它放回箱子,搅匀后再摸出一个球,求两次摸出球的都是白球的概率,并画出树状图. 19.九年级某班部分同学利用课外活动时间,积极参加篮球定点投篮的训练,训练后的测试成
绩如下表所示: 进球数(个) 8 7 6 5 4 3
人数 2 1 4 7 8 2 回答下列问题: (1)训练后篮球定点投篮进球数的众数是 个,中位数是 个; (2)若训练后的人均进球数比训练前增加25%,求训练前的人均进球数. 20.如图,在平面直角坐标系中,△ABC中的三个顶点坐标分别为A(1,4)、B(﹣1,2)、C(3,3).在x轴上方,请画出以原点O为位似中心,相似比为2:1.将△ABC放大后得到的△A1B1C1,并写出△A1B1C1各顶点的坐标.
21.如图,AB是⊙O的直径,CD是⊙O的切线,切点为C,BE⊥CD,垂足为E,连接AC、BC.
(1)求证:BC平分∠ABE; (2)若∠A=60°OA=4,求CE的长. 第4页 共21页
22.如图,在∠A=30°的等腰三角形ABC中,AB=AC,若过点C作CD⊥AB于点D,则∠BCD=15°.根
据图形,计算tan15°的值.
23.如图,平面直角坐标系中,矩形ABCO的边OA,OC分别在坐标轴上,OA=2,OC=1,以
点A为顶点的抛物线经过点C (1)求抛物线的函数表达式; (2)将矩形ABCO绕点A旋转,得到矩形AB′C′O′,使点C′落在x轴上,抛物线是否经过点C′?请说明理由.
24.某商店销售一种成本为40元/kg的水产品,若按50元/kg销售,一个月可售出500kg,售
价毎涨1元,月销售量就减少10kg. (1)写出月销售利润y(元)与售价x(元/kg)之间的函数表达式; (2)当售价定为多少元时,该商店月销售利润为8000元? (3)当售价定为多少元时会获得最大利润?求出最大利润. 25.将三角尺的直角顶点P放在矩形ABCD的对角线BD上,使其一条直角边经过点A,另一
条直角边和CD交于点E. (1)如图①,分别过点P作PM⊥AD、PN⊥CD,垂足分别为点M、N.
①求证△PMA∽△PNE; ②求证:tan∠ADB=. (2)如图②,若AB=4,BC=3,过点E作EF⊥BD于点F,连接AF,则随着点P取不同的位置,△PAF的面积是否发生变化?若不变,求出其面积;若改变,请说明理由. 第5页 共21页 九年级(上)期末数学试卷
参考答案与试题解析 一、选择题(本题共8小题,每小题3分,共24分) 1.一元二次方程x2﹣4=0的解是( )
A.x=2 B.x1=,x2=﹣ C.x=﹣2 D.x1=2,x2=﹣2 第6页 共21页
【考点】解一元二次方程-直接开平方法. 【分析】移项后直接开平方求解可得. 【解答】解:∵x2﹣4=0, ∴x2=4, ∴x1=2,x2=﹣2, 故选:D.
2.下列图形中既是中心对称图形又是轴对称图形的是( )
A. B. C. D.
【考点】中心对称图形;轴对称图形. 【分析】根据轴对称图形与中心对称图形的概念求解. 【解答】解:A、不是轴对称图形,也不是中心对称图形; B、是轴对称图形,也是中心对称图形;
C、不是轴对称图形,是中心对称图形;
D、是轴对称图形,不是中心对称图形.
故选B.
3.若甲、乙两个样本的方差分别为0.4、0.6,则下列说法正确的是( )
A.甲比乙稳定 B.乙比甲稳定
C.甲、乙一样稳定 D.无法比较
【考点】方差. 【分析】首先比较出甲、乙两个样本的方差的大小关系,然后根据方差越大,波动性越大,判断出哪个稳定即可. 【解答】解:因为0.4<0.6, 所以甲样本的方差小, 所以甲比乙稳定. 故选:A.
4.关于x的一元二次方程x2﹣kx﹣1=0的根的情况是( )
A.没有实数根 B.有一个实数根 第7页 共21页
C.有两个相等的实数根 D.有两个不相等的实数根
【考点】根的判别式. 【分析】先计算判别式的值得到△=k2+4,从而可判断△>0,则根据判别式的意义可判断方程根的情况. 【解答】解:∵△=(﹣k)2﹣4×(﹣1)=k2+4>0, ∴方程有两个不相等的两个实数根. 故选D.
5.如图,⊙O的直径AB=10,CD是⊙O的弦,CD⊥AB,垂足为M,若OM:OB=3:5,则CD的长为( )
A.8 B.6 C.4 D.
【考点】垂径定理;勾股定理. 【分析】直接利用垂径定理得出MC=DM,再利用勾股定理得出CM的长,进而得出出DC的长. 【解答】解:连接CO, ∵⊙O的直径AB=10, ∴BO=CO=5, ∵OM:OB=3:5, ∴OM=3, ∴在直角三角形COM中, MC==4,
∵CD⊥AB, ∴MC=MD=4, ∴DC=8. 故选:A. 第8页 共21页
6.如图,小正方形的边长均为1,则图中三角形(阴影部分)与△ABC相似的是( )
A. B. C. D.
【考点】相似三角形的判定. 【分析】利用△ABC中,∠ACB=135°,AC=2,BC=,然后根据两组对应边的比相等且夹角对应相等的两个三角形相似可对各选项进行判定. 【解答】解:在△ABC中,∠ACB=135°,AC=2,BC=, 在A、C、D选项中的三角形都没有135°,而在B选项中,三角形的钝角为135°,它的两边分别为1和,
因为=,所以B选项中的三角形与△ABC相似. 故选B.
7.正六边形的周长为6,则它的面积为( )
A.9 B.3 C. D. 【考点】正多边形和圆. 【分析】首先根据题意画出图形,即可得△OBC是等边三角形,又由正六边形ABCDEF的周长为6,即可求得BC的长,继而求得△OBC的面积,则可求得该六边形的面积. 【解答】解:如图,连接OB,OC,过O作OM⊥BC于M,
∴∠BOC=×360°=60°, ∵OB=OC, ∴△OBC是等边三角形, ∵正六边形ABCDEF的周长为6, ∴BC=6÷6=1,
