人大附中华杯赛资料:《对应计数》配套练习题
第12章 图形的计数

第5讲 图形的计数赛点突破计数是组合数学的重要内容,计数的方法有分类法,分步法,递推法和与对应法等。
1.分类计数在计数时,为了做到不重复也不遗漏,可以先将图形按某个标准分类,然后将其每一类相的方法数加,便得到了总数。
这种方法叫做分类法。
2.分步计数在计数时,为了有序地思维,我们常将其分成若干步,然后将其每一步的方法数相乘,便得到了总数。
这种方法叫做分步法。
3.递推计数为了求出计数的总数,当所研究的对象数目较大时,我们常常对较小数量的对象进行观察,计算。
如果对研究对象的个数n 观察,计算后,发现由n=1的结果可以算出n=2的结果,由n=2的结果可以算出n=3的结果,等等,我们就找到了计数的规律。
这种方法叫做递推法。
4.对应计数在解决某些计数问题时,为了解决某个问题A ,我们将其中的研究对象和另一个问题B 中的研究对象配成对,通过解决B 问题来达到解决A 问题的目的。
这种方法叫做对应法范例解密例1.如图,直线上有6个点:A ,B ,C ,D ,E ,F ,以这些点为端点的线段有多少条?A C D E F解1 对于两条线段,只要有一个端点不同,就是不同的线段,我们以左端点为标准,将线段分5类分别计数:(1)以A 为左端点的线段有AB ,AC ,AD ,AE ,AF 共5条;(2)以B 为左端点的线段有BC ,BD ,BE ,BF 共4条;(3)以C 为左端点的线段有CD ,CE ,CF 共3条;(4)以D 为左端点的线段有DE ,DF 共2条;(5)以E 为左端点的线段只有EF 一条.所以,不同的线段一共有5+4+3+2+1=15(条).解2 因为每两点可以连一条线段,我们先取一点,有6种取法;再取第二点,有5种取法。
故一共有6×5=30种取法。
但因先取A 点再取B 点和先取B 点再取A 点得到的是同一条线段,在上述计数中被重复计算了,故实际上是30÷2=15种取法,即一共可以连45条线段。
职高 分步计数原理与分类计数原理基础练习练习题复习.doc

两个计数原理练习题1.有不同颜色的四件上衣与不同颜色的三件长裤,如果一条长裤与一件上衣配成一套,则不同的配法有种.2.从3名女同学和2名男同学中选1人主持本班的某次主题班会,则不同的选法有种.3.一个乒乓球队里有男队员5人,女队员4人,从中选出男、女队员各一名组成混合双打,共有种不同的选法.4.现有三位数密码锁,各位上数字由0—9组成,可以组成多少种密码?其中首位数字不为0的密码有多少个?5.某学校学生会由高一年级5人,高二年级6人,高三年级4人组成。
(1)选其中1人为学生会主席,有多少种不同的选法?(2)若每年级选1人为校学生会常委,有多少种不同的选法?(3)若需选出不同年级的两人参加市里组织的活动,有多少种不同的选法?6.某班共有男生28名、女生20名,从该班选出学生代表参加校学代会。
(1)若学校分配给该班1名代表,有多少种不同的选法?(2)若学校分配给该班2名代表,且男、女生代表各1名,有多少种不同的选法?7.已知集合M={-3,-2,-1,0,1,2},P(a,b)表示平面上的点(a,b∈M),问:(1)P可表示平面上多少个不同的点?(2)P可表示平面上多少个第二象限的点?8.在一次读书活动中,有5本不同的政治书,10本不同的科技书,20 本不同的小说书供学生选用,(1)某学生若要从这三类书中任选一本,则有多少种不同的选法?(2)若要从这三类书中各选一本,则有多少种不同的选法?(3)若要从这三类书中选不属于同一类的两本,则有多少种不同的选法?9.将3封信投入4个不同的信箱,共有种不同的投法。
11.现有0,1,2,3,4,,5六个数字,(1)能组成不可重复的四位数多少个?(2)能组成多少个不可重复的四位奇数?。
2020年第十八届华杯赛决赛小高年级(B)卷-试题及解析word版

总分 第十八届华罗庚金杯 少年邀请赛 决赛试题B (小学高年级组) (时间2013年4月20日10:00~11:30)一、填空题(每小题 10分, 共80分)1.计算: 19×0.125+281×81+12.5=________. 解析:原式=(19+281+100)×0.125=400×0.125=502.农谚‘逢冬数九’讲的是, 从冬至之日起, 每九天分为一段, 依次称之为一九, 二九, ……, 九九, 冬至那天是一九的第一天. 2012年12月21日是冬至, 那么2013年的2月10日是________九的第________天.解析:31-21+1+31+10=52,52÷9=5…7,2013年的元旦是六九的第7天.3.某些整数分别被131********,,,除后, 所得的商化作带分数时, 分数部分分别是112927252,,,, 则满足条件且大于1的最小整数是________.解析:设整数为A, 分别被131********,,,除后, 所得的商分别为A A A A 11139117957,,,; )1(111311211113)1(911921911)1(7972179)1(5752157-++=-++=-++=-++=A A A A A A A A ,,,显然,当A-1是[5,7,9,3]的时候满足题意。
所以A-1=3465,A=3466。
4.如图所示, P, Q 分别是正方形ABCD 的边AD 和对角线 AC 上的点, 且PD:AP =4:1, QC:AQ =2:3, 如果正方形ABCD 的面积为25, 那么三角形PBQ 的面积是 .解析:连接QD,做QE ⊥BC 于E, QF ⊥AD 于F, QG ⊥CD 于G, 正方形ABCD 的面积为25,所以AD=EF=5, QC: AQ =2:3,根据正方形对称性,所以QE=QG=2,QF=3, PD:AP =4:1, AP=1,PD=4。
对应分析练习题
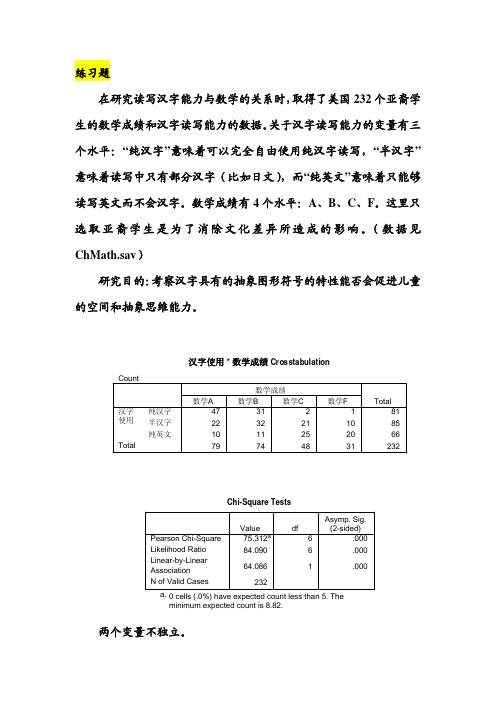
练习题在研究读写汉字能力与数学的关系时,取得了美国232个亚裔学生的数学成绩和汉字读写能力的数据。
关于汉字读写能力的变量有三个水平:“纯汉字”意味着可以完全自由使用纯汉字读写,“半汉字”意味着读写中只有部分汉字(比如日文),而“纯英文”意味着只能够读写英文而不会汉字。
数学成绩有4个水平:A、B、C、F。
这里只选取亚裔学生是为了消除文化差异所造成的影响。
(数据见ChMath.sav)研究目的:考察汉字具有的抽象图形符号的特性能否会促进儿童的空间和抽象思维能力。
两个变量不独立。
那么,两个变量各个类别之间存在什么关系呢?在对应分析中,可以找到行和列的若干有意义的代表,分别称为行记分(row score)和列记分(column score),它们互为对方的加权均值,而且它们之间有不同程度的相关性。
Inertia:惯量(也就是特征根),为每一维到其重心的加权距离的平方。
它度量的是行列关系的强度。
Singular Value:奇异值,是惯量的平方根,反映的是行与列各水平在二维图中分量的相关程度,是对行与列进行因子分析产生的新的综合变量的典型相关系数。
Chi Square:列联表行列独立性的2 检验值。
Proportion of Inertia:惯量比例,是各维度(公因子)分别解释总惯量的比例及累积百分比,类似于因子分析中公因子解释能力的说明。
从该表可以看出,由于第一维的惯量比例占了总比例的93.9%,因此,其他维的重要性可以忽略(虽然画图时需要两维,但主要看第一维,即横坐标的大小)。
Mass:行与列的边缘概率(各类别的百分比)。
Score in Dimension:各维度的分值(二维图中的坐标)纯汉字的点与最好的数学成绩A最接近,而不会汉字只会英文的点与最差的数学成绩F最接近,半汉字的和数学成绩B最接近。
三年级下册数学竞赛试题- 对应法解题 北师大版(含答案) (1)

三年下册奥数试题- 用对应法解题姓名得分【名师解析】小朋友在解答应用题时,经常会碰到这样一类题,给定的数量和所对应的数量关系是在变化的,为了使变化的数量看得更清楚,可以把已知条件按照他它们之间的对应关系排列出来,进行观察和分析,从而找到答案,这种解题的思维方法叫对应法。
在用对应法解题时,通常先把题目中的数量关系转化为等式,并把这些等式按顺序编号,然后认真观察,比较对应关系的变化,以便寻找解题的突破口。
【例题精讲】例1小进去商店买学习用品,如果买了4本笔记本,3支2元钱一支的笔,一共用去18元钱。
一本练习本多少钱?练习:妈妈在超市里用了40元钱,买了4把牙刷和2条毛巾,她只记得牙刷是3元钱一把,忘记了毛巾的价钱。
你知道吗?能不能帮她算一算?例2平价水果店的水果,若买1千克苹果和2千克梨子需18元,若买2千克苹果和2千克梨子则需要24元。
梨子、苹果每千克各多少元钱?练习:某车间工人,拧1个螺丝和2个螺帽需4分钟,拧1个螺丝和4个螺帽需6分钟。
拧一个螺丝需要多长时间?例3奶奶去买水果,如果她买4千克梨和5千克荔枝,需花58元;如果她买6千克梨和5千克荔枝,那么需花62元,问1千克梨和1千克荔枝各多少元?练习:3筐苹果和5筐橘子共重270千克,3筐苹果和7筐橘子共重342千克,一筐苹果和一筐橘子各重多少千克?例4学校买足球和排球,买3个足球和4个排球共需要190元,如果买6个足球和2个排球需要230元,一个足球和一个排球各需要多少元?练习:4本练习本和5枝圆珠笔共14元,2本练习本和4枝圆珠笔共10元,一本练习本和一枝圆珠笔各多少元?例5商店里有一些气球,其中红气球和蓝气球共21只,蓝气球和黄气球共28只,黄气球和红气球共29只,红气球、蓝气球和黄气球各有多少只?练习:1、小明和小红共12岁,小红和小丽共17岁,小明和小丽共13岁,三人各多少岁?2、新华书店有批书,故事书和连环画共70本,连环画和科技书共82本,科技书和故事书共76本,三种书各多少本?例6三年级三个班参加兴趣小组。
人大附中 华杯赛资料--运动与区域

例1.一条直线上放着一个长和宽分别为4cm和3cm的长方形Ⅰ(如图).它的对角线长恰好是5cm.让这个长方形绕顶点B顺时针旋转90°后到达长方形Ⅱ的位置,这样连续做三次,A点到达E点的位置.求A点走过的路程的长(圆周率按3计算).
[答疑编号505721460101]
【答案】18cm.
【解答】2π×(3+4+5)× =18cm。
4×(18+16+16)+2×2+4π+π+π×16× =28.07平方厘米
例5.如下左图,半径为25厘米的小铁环沿着半径为50厘米的大铁环的内侧作无滑动的滚动,当小铁环沿大铁环滚动一周回到原位时,问:小铁环绕自身转了几圈?
思考:如果小铁环在圆外滚动一周回到原位,到底自身滚动几圈呢?
[答疑编号505721460105]
因为硬币相互间滚过的圆弧长是相等的,
所以这时它与两枚硬币的交点分别是C和D.
当到达阴影所示的部分时,硬币又滚过了三分之一的圆弧长,
所以与X点重合的是F点.
例2.如图是一个直径为3cm的半圆,让这个半圆以A点为轴沿逆时针方向旋转60°,此时B点移动到B′点,求阴影部分的面积.
[答疑编号505721460102]
【答案】4.71cm2.
【解答】S阴影+S扇=S扇+S扇BAB’
所以 S阴影=S扇BAB’
S=π×r2× =π×9× =4.71cm2
例3.如图,将长方形ABCD绕顶点C顺时针旋转90度,若AB=4,BC=3,AC=5,求AD边扫过部分的面积.
[答疑编号505721460104]
【答案】228.07平方厘米.
【解答】
我们逐段画出小圆板的运动轨迹,
可以看到:圆板经过的区域可以分成几个部分求解,
而且每部分的主要组成都是长方形,
2020版人教A版数学选修2-3同步配套练习:第一章 计数原理 1.2.1 Word版含解析
姓名,年级:时间:1.2 排列与组合1。
2。
1 排列课时过关·能力提升基础巩固1下列问题属于排列问题的是( )①从10个人中选2人分别去种树和扫地; ②从10个人中选2人去扫地;③从班上30名男生中选出5人组成一个篮球队; ④从数字5,6,7,8中任取两个不同的数作幂运算。
A.①④ B 。
①② C 。
③④ D.①③④①④是排列问题,故选A 。
2从5本不同的书中选两本送给2名同学,每人一本,则不同的送书方法的种数为( ) A.5 B.10 C 。
20 D.605个不同元素中取出2个元素的排列数,即共有A 52=20种不同的送书方法.3若要在某跨海大桥上建造风格不同的3个报警电话亭和3个观景区,要求它们各自互不相邻,则不同的排法种数为( ) A.144 B.72 C 。
36 D 。
9有A 33种方法.则观景区插入电话亭所形成的空时,只有△○△○△○或○△○△○△两类,观景区有2A 33种排法.故共有2A 33·A 33=72种排法. 答案:B4设m ∈N *,则乘积m (m+1)(m+2)…(m+20)可表示为 ( )A .A 20A m 21C.A m+2020D.A m+2021式,A m+2021=(m +20)(m +19)(m +18)…(m+1)m.5要排一个有5个独唱节目和3个舞蹈节目的节目单,若舞蹈节目不排在开头,并且任意两个舞蹈节目不排在一起,则不同的排法种数是()A.A3A5B.A55A33C.A55A53D.A55A835个独唱节目共A55种;第二步排舞蹈,不相邻则用插空法,且保证不放到开头,从剩下5个空中选3个插空共有A53种,故一共有A55A53种.6某年级一天有6节课,需要安排6门课程,则该年级一天的课程表的排法有()A。
66种B。
36种C.A66种D.12种6个元素进行全排列,故有A66种排法.7某会议室共有8个座位,现有3人就座,若要求每人左右均有空位,则不同的坐法有()A.12种B。
高斯小学奥数六年级上册含答案第04讲 对应计数
详解:由对称性,只需求出常昊获胜的比赛过程有多少种,再乘以2即可.比赛最多进行7场,其中常昊一定胜4场,而且比赛一定是在常昊获得第4场胜利时结束的,因此常昊获胜的那4场比赛的编号就决定了整个比赛流程.
例题6.答案:
详解:本题从题面上看,是要从18盏灯中选出7盏来熄灭.但实际解决的时候,需要换一个角度:如何把灭掉的7盏灯,插入另外11盏亮着的灯之间.如下图所示,在11盏亮灯之间插入熄灭的灯时,每个空隙最多插1盏,否则灭灯就相邻了,因此必须挑7个空隙,每个空隙插一盏,而可供插入的空隙有12个(两端也可),因此答案为 .
例6.海淀大街上一共有18盏路灯,区政府为了节约用电,打算熄灭其中的7盏.但为了行路安全,任意相邻的两盏灯不能同时被熄灭,请问:一共有多少种熄灯方案?
「分析」你能用插板法求解这道题吗?
作业
1.一部电视连续剧共8集,电视台要在周一到周四这4天内按顺序播完,其中可以有若干天不播,共有多少种安排播出的方法?165
对应法最早的应用是结绳计数.最早期的时候,人类还没有发明数字.因而用枚举等其他方法来记录数量的多少是不可能办到的.这时,人们的计数方法是在绳子上打结或者在树上刻痕.用绳子上的结的数目或者树上划痕的道数来记录补获了多少猎物,采集了多少花果.这个时期持续了很长时间,因为人类的历史已经有几百万年,而数字的发明距今还不到1万年,在人类历史上的大部分时间,使用的计数方法是对应法——结绳计数.
结绳记数这种方法,不但在远古时候使用,而且一直在某些民族中沿用下来.宋朝人在一本书中说:“鞑靼无文字,每调发军马,即结草为约,使人传达,急于星火.”这是用结草来调发军马,传达要调的人数呢!其他如藏族、彝族等,虽都有文字,但在一般不识字的人中间都还长期使用这种方法.中央民族大学就收藏着一副高山族的结绳,由两条绳组成:每条上有两个结,再把两条绳结在一起.
三年级下册数学竞赛试题-对应法解题北师大版(含答案)
用对应法解题【名师解析】小朋友在解答应用题时,经常会碰到这样一类题,给定的数量和所对应的数量关系是在变化的,为了使变化的数量看得更清楚,可以把已知条件按照他它们之间的对应关系排列出,进行观察和分析,从而找到答案,这种解题的思维方法叫对应法。
在用对应法解题时,通常先把题目中的数量关系转化为等式,并把这些等式按顺序编号,然后认真观察,比较对应关系的变化,以便寻找解题的突破口。
【例题精讲】例1小进去商店买学习用品,如果买了4本笔记本,3支2元钱一支的笔,一共用去18元钱。
一本练习本多少钱?练习:妈妈在超市里用了40元钱,买了4把牙刷和2条毛巾,她只记得牙刷是3元钱一把,忘记了毛巾的价钱。
你知道吗?能不能帮她算一算?例2平价水果店的水果,若买1千克苹果和2千克梨子需18元,若买2千克苹果和2千克梨子则需要24元。
梨子、苹果每千克各多少元钱?练习:某车间工人,拧1个螺丝和2个螺帽需4分钟,拧1个螺丝和4个螺帽需6分钟。
拧一个螺丝需要多长时间?例3奶奶去买水果,如果她买4千克梨和5千克荔枝,需花58元;如果她买6千克梨和5千克荔枝,那么需花62元,问1千克梨和1千克荔枝各多少元?练习:3筐苹果和5筐橘子共重270千克,3筐苹果和7筐橘子共重342千克,一筐苹果和一筐橘子各重多少千克?例4学校买足球和排球,买3个足球和4个排球共需要190元,如果买6个足球和2个排球需要230元,一个足球和一个排球各需要多少元?练习:4本练习本和5枝圆珠笔共14元,2本练习本和4枝圆珠笔共10元,一本练习本和一枝圆珠笔各多少元?例5商店里有一些气球,其中红气球和蓝气球共21只,蓝气球和黄气球共28只,黄气球和红气球共29只,红气球、蓝气球和黄气球各有多少只?练习:1、小明和小红共12岁,小红和小丽共17岁,小明和小丽共13岁,三人各多少岁?2、新华书店有批书,故事书和连环画共70本,连环画和科技书共82本,科技书和故事书共76本,三种书各多少本?例6三年级三个班参加兴趣小组。
北京中国人民大学附属外国语中学高中数学选修2-3第一章《计数原理》测试卷(有答案解析)
一、选择题1.从0,1,2,3,…,9中选出三个不同数字组成一个三位数,其中能被3整除的三位数个数为( ) A .252 B .216 C .162 D .228 2.5个人排成一排,其中甲与乙不相邻,而丙与丁必须相邻,则不同的排法种数为( ) A .72 B .48 C .24 D .60 3.把4个不同的小球全部放人3个不同的盒子中,使每个盒子都不空的放法总数为( )A .1333C AB .3242C AC .132442C C CD .2343C A4.某地政府召集5家企业的负责人开会,其中甲企业有2人到会,其余4家企业各有1人到会,会上有3人发言,则这3人来自3家不同企业的可能情况的种数为 A .14B .16C .20D .485.设()22201221nn n x x a a x a x a x ++=++++,则022n a a a 的值是( )A .()1312n- B .1312nC .3nD .31n +6.甲乙和其他2名同学合影留念,站成两排两列,且甲乙两人不在同一排也不在同一列,则这4名同学的站队方法有( ) A .8种B .16种C .32种D .64种7.有5位同学参加青少年科技创新大赛的3个不同项目,要求每位同学参加一个项目且每个项目至少有一位同学,则不同的参加方法种数为( ) A .80B .120C .150D .3608.3450(1)(1)(1)x x x ++++++的展开式中3x 的系数是( )A .351CB .450C C .451CD .447C9.现有甲、乙、丙、丁、戌5人参加社区志愿者服务活动,每人从事团购、体温测量、进出人员信息登记、司机四项工作之一,每项工作至少有一人参加.若甲、乙不会开车但能从事其他三项工作,丙、丁、戌都能胜任四项工作,则不同安排方案的种数是( ) A .234B .152C .126D .10810.我省5名医学专家驰援湖北武汉抗击新冠肺炎疫情现把专家全部分配到A ,B ,C 三个集中医疗点,每个医疗点至少要分配1人,其中甲专家不去A 医疗点,则不同分配种数为( ) A .116B .100C .124D .9011.2101()x x+的展开式中含5x 项的系数为( ) A .160B .210C .120D .25212.若()5211x a x ⎛⎫+- ⎪⎝⎭的展开式中常数项为-1,则a 的值为( ) A .1B .9C .-1或-9D .1或9二、填空题13.若9m x x ⎛⎫- ⎪⎝⎭的展开式中3x 的系数为84,则m =_________. 14.某学校安排5名高三教师去3个学校进行交流学习,且每位教师只去一个学校,要求每个学校至少有一名教师进行交流学习,则不同的安排方式共有______种. 15.设2122101221(1)x a a x a x a x -=+++,则1011a a += .16.北京《财富》全球论坛期间,某高校有8名志愿者参加接待工作.若每天排早、中、晚三班,每班至少2人,每人每天必须值一班且只值一班,则开幕式当天不同的排班种数为______.17.6人排成一排合影,甲乙相邻但乙丙不相邻,共有____(用数字)种不同的排法. 18.有4位同学和2位教师一起合影.若教师不能坐在两端,也不坐在一起,则有_________种坐法.19.把6张不同的充值卡分给4位同学,每人至少1张,有_________种分法20.将编号为1,2,3,4,5,6,7的七个小球放入编号为1,2,3,4,5,6,7的七个盒中,每盒放一球,若有且只有三个盒子的编号与放入的小球的编号相同,则不同的放法种数为______.三、解答题21.已知()22nn N x +⎫∈⎪⎭的展开式中第二项与第三项的二项式系数之和为36.(1)求n 的值;(2)求展开式中二项式系数最大的项.22.在二项式n的展开式中,前三项系数的绝对值成等差数列. (1)求n 的值;(2)求展开式中系数最大的项.23.现有2位男生和3位女生共5位同学站成一排.(用数字作答) (1)若2位男生相邻且3位女生相邻,则共有多少种不同的排法? (2)若男女相间,则共有多少种不同的排法?(3)若男生甲不站两端,女生乙不站最中间,则共有多少种不同的排法? 24.已知()112225113mm mma CAm N ---=-∈,777714-除以19的余数为b,求1bx ⎫⎪⎭展开式的常数项.25.已知在n的展开式中,第6项为常数项. (1)求n ;(2)求展开式中所有的有理项(只需说明第几项是有理项). 26.从1到9的九个数字中取三个偶数四个奇数,试问:(1)能组成多少个没有重复数字的七位数?(2)在(1)中的七位数中三个偶数排在一起的有几个?(3)在(1)中的七位数中,偶数排在一起、奇数也排在一起的有几个? (4)在(1)中任意两偶然都不相邻的七位数有几个? (答题要求:先列式,后计算 , 结果用具体数字表示.)【参考答案】***试卷处理标记,请不要删除一、选择题 1.D 解析:D 【分析】根据题意将10个数字分成三组:即被3除余1的有1,4,7;被3除余2的有2,5,8;被3整除的有3,6,9,0,若要求所得的三位数被3整除,则可以分类讨论:每组自己全排列,每组各选一个,再利用排列与组合的知识求出个数,进而求出答案. 【详解】解:将10个数字分成三组,即被3除余1的有{1,4,7},被3除余2的有{2,5,8},被3整除的有{3,6,9,0}.若要求所得的三位数被3整除,则可以分类讨论:①三个数字均取自第一组{1,4,7}中,或均取自第二组{2,5,8}中,有33212A =个; ②若三个数字均取自第三组{3,6,9,0},则要考虑取出的数字中有无数字0,共有324318A A -=个;③若三组各取一个数字,第三组中不取0,有11133333162C C C A ⋅⋅⋅=个, ④若三组各取一个数字,第三组中取0,有112332236C C A ⋅⋅⋅=个, 这样能被3整除的数共有12+18+162+36228=个. 故选:D. 【点睛】本题考查分类计数原理和排列组合知识,如何分类是关键,属于中档题.2.C解析:C 【分析】先将丙与丁捆绑,形成一个“大元素”与戊进行排列,然后再将甲、乙插空,利用分步乘法计数原理可求得排法种数. 【详解】先将丙与丁捆绑,形成一个“大元素”与戊进行排列,然后再将甲、乙插空,由分步乘法计数原理可知,不同的排法种数为22222324A A A =种. 故选:C. 【点睛】本题考查捆绑法与插空法的综合应用,同时也考查了分步乘法计数原理的应用,考查计算能力,属于中等题.3.D解析:D 【分析】利用捆绑法选择两个球看成整体,再全排列得到答案. 【详解】选择两个球看成整体,共有24C 种取法,再把三个球放入三个盒子中,有33A 种放法,故共有2343C A 种放法. 故选:D. 【点睛】本题考查了排列和组合的应用,意在考查学生的应用能力,利用捆绑法是解题的关键.4.B解析:B 【解析】由间接法得32162420416C C C -⋅=-=,故选B .5.B解析:B 【分析】本题可以通过利用二项展开式的系数关系,采用赋值法将x 分别赋值为1、1-,然后通过运算即可得出结果. 【详解】()22201221nn n x x a a x a x a x ++=++++,令1x =,01223n na a a a ①,令1x =-,01221n a a a a ②,(①+②)02212312nna a a , 故选:B . 【点睛】本题考查二项展开式的相关运算,可通过赋值法进行计算,考查计算能力,考查化归与转化思想,是中档题.6.A解析:A【分析】根据题意,分3步进行讨论:先在4个位置中任选一个安排甲,再安排乙,最后将剩余的2个人,安排在其余的2个位置,分别求出每一步的情况数目,由分步计数原理计算可得答案. 【详解】根据题意,分3步进行讨论:1、先安排甲,在4个位置中任选一个即可,有14C 4=种选法;2、在与甲所选位置不在同一排也不在同一列只有一个位置,安排乙,即1种选法;3、将剩余的2个人,安排在其余的2个位置,有222A =种安排方法; 则这4名同学的站队方法有4128⨯⨯=种; 故选:A . 【点睛】本题主要考查排列、组合的综合应用,注意要优先分析受到限制的元素,属于中档题.7.C解析:C 【分析】根据题意,分清楚有两种情况,利用公式求得结果. 【详解】根据题意,可知有两种情况,一种是有三位同学去参加同一个项目,一种是有两个项目是两位同学参加,所以不同的参加方法种数为22333535332210310661502C C C A A A ⋅⨯⋅+⋅=⨯+⨯=种, 故选:C. 【点睛】该题考查的是有关排列组合的综合题,涉及到的知识点有分类计数加法计数原理,排列组合综合题,属于中档题目.8.C解析:C 【分析】利用等比数列的求和公式,化简得5133450(1)(1)(1)(1)(1)x x x x x x+-+++++++=,再结合二项式定理,即可求解. 【详解】 由题意,可得3485133450(1)(1)1(1)(1)(1)(1)(1)x x x x x x x xx⎡⎤++-+-+⎣⎦++++++==, 所以3450(1)(1)(1)x x x ++++++的展开式中3x 的系数就是51(1)x +的展开式中4x 的系数,即为451C.故选:C.【点睛】本题主要考查二项式定理,以及等比数列的前n项和公式,考查考生分析问题、解决问题的能力、化归与转化能力、运算求解能力.9.C解析:C【分析】分情况进行讨论,先计算“甲乙一起参加除了开车的三项工作之一”有多少种情况,再计算“甲和乙分别承担一份工作,丙、丁、戌三人中有两人承担同一份工作”和“甲或乙与丙、丁、戌三人中的一人承担同一份工作”的情况,相加即得.【详解】由题,分情况讨论,甲乙一起参加除了开车的三项工作之一:133318C A=种;甲乙不同时参加一项工作,又分为两种情况:①甲和乙分别承担一份工作,丙、丁、戌三人中有两人承担同一份工作,有:222 323323236C A A=⨯⨯⨯=种;②甲或乙与丙、丁、戌三人中的一人承担同一份工作:2112332272A C C A=种.由分类计数原理,可得共有183672126++=种.故选:C【点睛】本题考查计数原理,考查学生的逻辑推理能力.10.B解析:B【分析】完成这件事情可分2步进行:第一步将5名医学专家分为3组;第二步将分好的3组分别派到三个医疗点,由分步计数原理计算即可得到答案.【详解】根据已知条件,完成这件事情可分2步进行:第一步:将5名医学专家分为3组①若分为3,1,1的三组,有3510C=种分组方法;②若分为2,2,1的三组,有22532215C CA=种分组方法,故有101525+=种分组方法.第二步:将分好的三组分别派到三个医疗点,甲专家不去A医疗点,可分配到,B C医疗点中的一个,有122C=种分配方法,再将剩余的2组分配到其余的2个医疗点,有222A=种分配方法,则有224⨯=种分配方法.根据分步计数原理,共有254100=⨯种分配方法. 故选:B . 【点睛】本题主要考查排列、组合的应用,同时考查分步计数原理,属于基础题.11.D解析:D 【分析】由二项式定理及其二项展开式通项得:210203110101()()rrr r r r T C x C x x--+==,令2035r -=,解得r 的值,进而求得其系数.【详解】()102203110101rrr r rr T Cx C x x --+⎛⎫== ⎪⎝⎭, 当=5r 时,555610252T C x x ==. 故选:D. 【点睛】本题考查了二项式定理及其二项式展开式的通项,属于基础题.12.D解析:D 【分析】根据题意分析常数项由()2x a +中的某项与511x ⎛⎫- ⎪⎝⎭中的某项项相乘所得,再二项式定理的通项公式求解即可. 【详解】由题可得,()2x a +中含2x 项与511x ⎛⎫- ⎪⎝⎭中含21x 项相乘可得常数项; ()2x a +中含x 项与511x ⎛⎫- ⎪⎝⎭中含1x 项相乘可得常数项; ()2x a +中的常数项与511x ⎛⎫- ⎪⎝⎭中的常数项相乘可得常数项.故()5211x a x ⎛⎫+- ⎪⎝⎭的展开式中常数项为 ()()()2134522122551112111010x C ax C a a a x x ⎛⎫⎛⎫⋅⋅⋅-+⋅⋅⋅-+⋅-=-+- ⎪ ⎪⎝⎭⎝⎭.故22101011090a a a a -+-=-⇒-+=,解得1a =或9a =.故选:D 【点睛】本题主要考查了利用二项式定理,根据常数项求解参数的方法.需要根据题意分析常数项的所有可能组成,属于中档题.二、填空题13.【分析】由题意二项式展开式的通项为结合题意求得进而得到关于的方程即可求解【详解】求得二项式的展开式的通项为当解得此时所以解得故答案为:【点睛】求二项展开式的特定项问题实质时考查通项的特点一般需要建立解析:1-. 【分析】由题意,二项式展开式的通项为9219(1)r r r rr T m C x -+=-⋅⋅,结合题意,求得3r =,进而得到关于m 的方程,即可求解. 【详解】求得二项式9m x x ⎛⎫- ⎪⎝⎭的展开式的通项为992199()(1)r r r r r r rr m T C x m C x x --+=-=-⋅⋅,当923r -=,解得3r =,此时333349(1)T m C x =-⋅⋅,所以3339(1)84m C -⋅⋅=,解得1m =-. 故答案为:1-. 【点睛】求二项展开式的特定项问题,实质时考查通项1C rn r rr n T ab -+=的特点,一般需要建立方程求得r 的值,再将r 的值代入通项求解,同时注意r 的取值范围(0,1,2,,r n =).14.150【分析】分2步分析:先将5名高三教师分成3组分2种情况分类讨论再将分好的三组全排列对应三个学校由分步计数原理计算可得答案;【详解】解:分2步分析:先将5名高三教师分成3组由两种分组方法若分成3解析:150 【分析】分2步分析:先将5名高三教师分成3组,分2种情况分类讨论,再将分好的三组全排列,对应三个学校,由分步计数原理计算可得答案; 【详解】 解:分2步分析:先将5名高三教师分成3组,由两种分组方法,若分成3、1、1的三组,有3510C =种分组方法, 若分成1、2、2的三组,有1225422215C C C A =种分组方法, 则一共有101525+=种分组方法;再将分好的三组全排列,对应三个学校,有336A =种情况, 则有256150⨯=种不同的安排方式; 故答案为:150. 【点睛】(1)解排列组合问题要遵循两个原则:一是按元素(或位置)的性质进行分类;二是按事情发生的过程进行分步.具体地说,解排列组合问题常以元素(或位置)为主体,即先满足特殊元素(或位置),再考虑其他元素(或位置).(2)不同元素的分配问题,往往是先分组再分配.在分组时,通常有三种类型:①不均匀分组;②均匀分组;③部分均匀分组,注意各种分组类型中,不同分组方法的求法.15.0【分析】就是展开式中的系数利用通项公式求解即可【详解】展开式通项为所以故答案为0【点睛】本题主要考查二项展开式定理的通项与系数属于简单题二项展开式定理的问题也是高考命题热点之一关于二项式定理的命题解析:0 【分析】1011,a a 就是21(1)x -展开式中1011,x x 的系数,利用通项公式求解即可.【详解】21(1)x -展开式通项为21121(1)r rr r T C x -+=-, 111111102121(1)a C C =⋅-=- 1010101111212121(1)a C C C =⋅-==所以1111101121210a a C C +=-+=, 故答案为0. 【点睛】本题主要考查二项展开式定理的通项与系数,属于简单题. 二项展开式定理的问题也是高考命题热点之一,关于二项式定理的命题方向比较明确,主要从以下几个方面命题:(1)考查二项展开式的通项公式1C rn r rr n T ab -+=;(可以考查某一项,也可考查某一项的系数)(2)考查各项系数和和各项的二项式系数和;(3)二项展开式定理的应用.16.2940【分析】根据题意有两类分配方案第一类:224三组第二类:233三组分别求得排班种数再利用分类计数原理求解【详解】由8名志愿者根据早中晚三班且每班至少2人分为3组第一类:224三组共有种第二类解析:2940 【分析】根据题意,有两类分配方案,第一类:2,2,4三组,第二类:2,3,3三组,分别求得排班种数,再利用分类计数原理求解. 【详解】由8名志愿者,根据早、中、晚三班,且每班至少2人,分为3组.第一类:2,2,4三组,共有22438643221680C C C A A ⋅=种, 第二类:2,3,3三组,共有23338633221260C C C A A ⋅=种, 所以每人每天必须值一班且只值一班,则开幕式当天不同的排班种数168012602940+=. 故答案为:2940 【点睛】本题主要考查排列组合中的分组分配问题,还考查了分析求解问题的能力,属于中档题.17.192【分析】先将甲乙两人捆绑在一起看成一个人且内部自排再与除丙外的其他人排列最后将丙插空放入保证与乙不相邻即可【详解】第一步:甲乙相邻共有种排法;第二步:将甲乙看成一个人与除丙外的其他人排列共有:解析:192 【分析】先将甲乙两人捆绑在一起看成一个人且内部自排,再与除丙外的其他3人排列,最后将丙插空放入,保证与乙不相邻即可. 【详解】第一步:甲乙相邻,共有222A =种排法;第二步:将甲乙看成一个人,与除丙外的其他3人排列,共有:4424A =种排法; 第三步:将丙插空放入,保证与乙不相邻,共有:144A =种排法; 根据分步计数原理可得,共有2244192⨯⨯=种排法. 故答案为: 192 【点睛】本题主要考查有限制条件的排列问题,属于中档题.解有限制条件的排列问题,可按元素的性质进行分类,按事件发生的连续过程分步,做到标准明确,分步层次清楚,不重不漏,分类标准一旦确定要贯穿于解题过程的始终,同时需掌握有限制条件的排列问题的求解方法.18.144【分析】先排4位同学将教师插入4位同学产生的3个空位中再由乘法原理即可得到答案【详解】先排4位同学共有种不同排法由于教师不能坐在两端也不坐在一起将2位老师插入4位同学产生的3个空位中共种不同排解析:144 【分析】先排4位同学,将教师插入4位同学产生的3个空位中,再由乘法原理即可得到答案. 【详解】先排4位同学共有44A 种不同排法,由于教师不能坐在两端,也不坐在一起,将2位老师插 入4位同学产生的3个空位中,共23A 种不同排法,由乘法原理,共有4243144A A =种不同排故答案为:144 【点睛】本题考查排列的实际应用,涉及到特殊元素分析法,考查学生的逻辑推理能力,是一道中档题.19.1560【分析】分4位同学分得的卡数为1113和1122两种情况讨论即可【详解】分两类:第一类:当4位同学分得的卡数为1113时共有种;第二类:当4位同学分得的卡数为1122时共有种由加法原理知共有解析:1560 【分析】分4位同学分得的卡数为1,1,1,3和1,1,2,2两种情况讨论即可. 【详解】 分两类:第一类:当4位同学分得的卡数为1,1,1,3时,共有3464480C A =种;第二类:当4位同学分得的卡数为1,1,2,2时,共有221146421422221080C C C C A A A =种, 由加法原理,知共有1560种不同分法. 故答案为:1560 【点睛】本题考查排列与组合中的部分均匀分组问题,考查学生逻辑推理能力,数学运算能力,是一道中档题.20.315【分析】根据题意有且只有三个盒子的编号与放入的小球的编号相同再由排列组台及计数原理即可求解【详解】第一步:先确定三个盒子的编号与放入的小球的编号相同共种不同取法;第二步:再将剩下的个小球放入到解析:315 【分析】根据题意,有且只有三个盒子的编号与放入的小球的编号相同,再由排列组台及计数原理,即可求解. 【详解】第一步:先确定三个盒子的编号与放入的小球的编号相同,共3735C =种不同取法; 第二步:再将剩下的4个小球放入到4个盒子中,且小球编号与放入的小球的编号不相同,共()113219C C +=种不同放法;因而有且只有三个盒子的编号与放入的小球的编号相同的不同放法种数为359315⨯=种. 故答案为:315 【点睛】本题考查了排列组合及计数原理,考查理解辨析能力与运算求解能力,属中档题.三、解答题21.(1)8;(2)611120x ⋅. 【分析】(1)由条件利用二项式系数的性质求得n 的值;(2)首先求出二项式展开式的通项,进而得到展开式中二项式系数最大的项. 【详解】(1)由题意知,第二项的二项式系数为1n C ,第三项的二项式系数为2n C ,1236n n C C ∴+=,得2720n n +-=,(9)(8)0n n ∴+-=得8n =或9n =-(舍去).(2)822x ⎫⎪⎭的通项公式为:858218822(1)2kkk k k k k k T C C x x --+⎛⎫=-=- ⎪⎝⎭,又由8n =知第5项的二项式系数最大,此时5611120T x=⋅. 【点睛】本题第一问考查二项式系数的性质,第二问考查二项式系数最大的项,熟记二项式展开式的通项为解题的关键,属于中档题. 22.(1)8n =.(2)4337T x =,2347T x =.【分析】(1)写出展开式通项公式,得前3项系数,由等差数列的性质求出n ;(2)设第k 项系数最大,由第k 项系数不小于第1k -项和第1k +项系数,列不等式组解之可得项数,然后再得项. 【详解】(1)展开式通项公式为2311()2n rrn rrr r r nn T C C x --+==,由题意1022112()22n n n C C C ⨯=+,解得8n =(1n =舍去). (2)由(1)展开式第1r +项系数为81()2r rC ,设第k 项系数最大,则112288118811()()2211()()22k k k k k k k kC C C C ------⎧≥⎪⎪⎨⎪≥⎪⎩,解得34k ≤≤,∴3k =或4,∴系数最大的项为:82242233381()72T C x x -⨯==,82323333481()72T C x x -⨯==.【点睛】本题考查二项式定理,解题关键是掌握二项式展开式通项公式.由通项公式得出前3项系数,从而求得n ,求系数最大的项,一般可设第k 项系数最大,由第k 项系数不小于第1k -项和第1k +项系数,列不等式组解之得项数.23.(1)24(2)12(3)60 【分析】(1)相邻问题利用捆绑法; (2)若男女相间,则用插空法;(3)若男生甲不站两端,女生乙不站最中间,则利用间接法. 【详解】解:(1)利用捆绑法,可得共有22322324A A A =种不同的排法; (2)利用插空法,可得共有232312A A =种不同的排法; (3)利用间接法,可得共有54135423360A A C A -+=种不同的排法. 【点睛】本题考查排列组合及简单的计数问题,涉及间接法和捆绑,插空等方法的应用,属于中档题.24.常数项为240. 【分析】由组合数和排列数的定义可列出不等式组01125022113m mm m≤-≤⎧⎨≤-≤-⎩,求出m 的值,进而求出a 的值.再利用二项式定理,由77777714(1941)14-=⨯+-求出余数b .将a 和b 代入1)b x,在其通项公式中令x 的幂指数等于零,求出常数项. 【详解】 解:由题意得01125022113m m m m≤-≤⎧⎨≤-≤-⎩,解得111375m ≤≤,∵m N ∈,∴2m =,∴72105100a C A =-=, ∵()77777714194114-=⨯+-()()()77760176777777194194...194114C C C =⨯+⨯++⨯+-,∴6b =,∴611b x x ⎫⎛⎫=⎪ ⎪⎭⎝⎭,通项公式(()63662166112rrrr r r r r T C C x x ---+⎛⎫=-=- ⎪⎝⎭,令6302r-=,2r ,故常数项为240. 【点睛】本题考查了排列数和组合数的定义,利用二项式定理解决整除问题,求二项式展开式的指定项问题.属于中档题.25.(1)10;(2)第3项,第6项与第9项为有理项. 【分析】(1)先求出1k T +()233n k k k nC x-=-,解方程1003n -=即得解;(2)由题得1023010k Z k k Z -⎧∈⎪⎪≤≤⎨⎪∈⎪⎩,分析即得解. 【详解】 (1)通项公式为()3313n k k kk k nTC xx --+=-()233n k kk nC x-=-.∵第6项为常数项, ∴5k =时,有203n k-=,即10n =. (2)根据通项公式,由题意得1023010k Z k k Z -⎧∈⎪⎪≤≤⎨⎪∈⎪⎩,令1023k r -=(r Z ∈),则1023k r -=,即352k r =-.∵k Z ∈,∴r 应为偶数.于是r 可取2,0,2-,即k 可取2,5,8.故第3项,第6项与第9项为有理项. 【点睛】本题主要考查二项式定理的通项,考查二项式展开式的常数项和有理项的求法,意在考查学生对这些知识的理解掌握水平.26.(1)100800个;(2)14400个;(3)5760个;(4)28800个. 【分析】从1到9的九个数字中,有奇数1,3,5,7,9共五个,偶数2 ,4, 6, 8共四个.(1)先从四个偶数中取三个,再从五个奇数中取出四个,然后全排列即可得到结果;(2)用捆绑法.将取出三个偶数看作一个元素,然后将该元素与四个奇数全排列,同时其内部自排即可得到结果;(3) 用捆绑法.将取三个偶数捆绑在一起,四个奇数捆绑在一起看成两个元素排列,同时内部分别自排即可得到结果;(4)用插空法.因为三个偶数都不相邻,故只需将取出的四个奇数全排列,然后对偶数插空即可求出结果.【详解】(1)分步完成:第一步在四个偶数中取三个,可有34C种情况;第二步在五个奇数中取四个,可有45C种情况;第三步三个偶数,四个奇数进行排列,可有77A种情况,所以符合题意的七位数有347457100800C C A=个.(2)上述七位数中,三个偶数排在一起的有3453455314400C C A A=.(3)上述七位数中,三个偶数排在一起,四个奇数也排在一起的有34342453425760C C A A A=个.(4)上述七位数中,偶数都不相邻,可先把四个奇数排好,再将三个偶数分别插入5个空档,共有43354528800A C A=个.【点睛】本题主要考查排列组合的综合应用.排列与组合综合问题的常见类型及解题策略:(1)相邻问题捆绑法.在特定条件下,将几个相关元素视为一个元素来考虑,待整个问题排好之后,再考虑它们“内部”的排列.(2)相间问题插空法.先把一般元素排好,然后把特定元素插在它们之间或两端的空当中,它与捆绑法有同等作用.(3)特殊元素(位置)优先安排法.优先考虑问题中的特殊元素或位置,然后再排列其他一般元素或位置.(4)多元问题分类法.将符合条件的排列分为几类,而每一类的排列数较易求出,然后根据分类计数原理求出排列总数.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实用文档 用心整理
千里之行 始于足下
1
《对应计数》配套练习题
一、简答题
1、在5×6的方格棋盘中,取出一个由3个小方格组成的“L”形(如图),一共有多少种不同的方
法?
2、小龙喜欢吃鸭蛋,号称“鸭蛋大王”。现在他手上还有6个鸭蛋,准备吃3天,而且每天至少吃
1个,那么共有多少种不同的吃法?
3、(1)10个相同的苹果分给甲、乙、丙、丁4个人,每人至少分得一个苹果,则有多少种不同的
分法?
(2)将10个相同的球放到4个不同的盒子里,每个盒子至少放2个球,共有多少种不同的方法?
4、小华将8个相同的鸡蛋放到3个不同的盘子,那么总共有多少种不同的放法?
5、在下图中选取3个小方格,使得它们任何两个都没有公共顶点,一共有多少种选法?如果将下图
的小方格列数改为10列,有多少种选法?
实用文档 用心整理
千里之行 始于足下
2
6、以1、2、…、7这个七个数字组成的各位数字不重复、且能被11整除的七位数共有多少个?
二、填空题
1、有一种“上升数”,从左往右的数字依次增大,那么三位的“上升数”共有_____个;五位的“上
升数”共有______。
2、(1)数字之和为10,且由非零数字组成的四位数共有______个;
(2)数字之和为10的四位数共有______个。
(3)数字和为10,且不含数字0的自然数共有______个。
答案部分
一、简答题
1、
【正确答案】:80
【答案解析】:在5×6的棋盘上,内部有4×5=20个交叉点,
所以不同的取法共有:20×4=80(种)。
实用文档 用心整理
千里之行 始于足下
3
【答疑编号10235719】
2、
【正确答案】:10
【答案解析】:
【答疑编号10235715】
3、
【正确答案】:(1)84(2)10
【答案解析】:(1)
我们将10个苹果放成一排,然后用3个隔板插到这10个苹果之间,
然后将第一个隔板前面的苹果给甲,第一个和第二个隔板之间的苹果给乙,
第二个和第三个隔板之间的苹果给丙,第三个隔板后面的苹果给丁。
而10个苹果之间有9个空档可以放隔板,所以这个问题就变成从把3个隔板放到9个地方,
实用文档 用心整理
千里之行 始于足下
4
有多少种不同的排列方法。所以答案为(9×8×7)÷(3×2×1)=84种不同的分法。
【答疑编号10235716】
4、
【正确答案】:21
【答案解析】:
【答疑编号10235714】
5、
【正确答案】:(1)80(2)448
【答案解析】:(1)这三个格不同列,并且不是相邻的列,选法数等于于在1~7中选三个不相邻
的数,有10种选法;
实用文档 用心整理
千里之行 始于足下
5
对于每一列可以选上面的格子,也可以选下面的格子,共有10×2×2×2=80种选法。
(2)
【答疑编号10235720】
6、
【正确答案】:576
【答案解析】:1~7的和是28,这也是七位数中奇数位上的数字和与偶数位上的数字和的总和。
要使七位数能被11整除,则要使奇数位上的数字和与偶数位上的数字和之差是11的倍数。
而这个差肯定是偶数,那么只可能是0或者22。
如果是22,说明两个数字和中较小的一个是(28-22)÷2=3,这不可能。
所以奇数位上的数字和与偶数位上的数字和相等,都是28÷2=14。
要使偶数位上的3个数字的和是14,有四种可能:
14=1+6+7=2+5+7=3+4+7=3+5+6
对于其中每种情形,偶数位上的3个数字有3×2×1=6种排列方法,
奇数位上的4个数字有4×3×2×1=24种排列方法,
由乘法原理,满足条件的七位数有6×24=144个。
由于共有4种情形,所以能被11整除满足题意的七位数一共有144×4=576个。
【答疑编号10235721】
二、填空题
1、
【正确答案】:84个;126个
