求阴影面积的几种常用方法
小升初数学几何求阴影部分面积题带解析
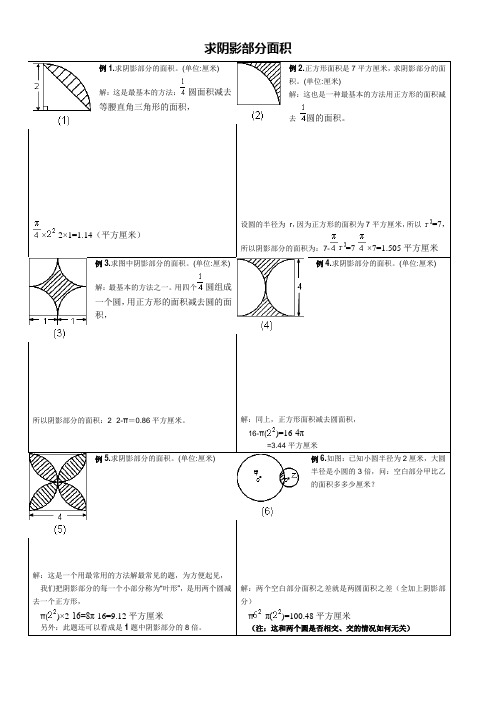
求阴影部分面积例1.求阴影部分的面积。
(单位:厘米)解:这是最基本的方法:圆面积减去等腰直角三角形的面积,×-2×1=1.14(平方厘米)例2.正方形面积是7平方厘米,求阴影部分的面积。
(单位:厘米)解:这也是一种最基本的方法用正方形的面积减去圆的面积。
设圆的半径为r,因为正方形的面积为7平方厘米,所以=7,所以阴影部分的面积为:7-=7-×7=1.505平方厘米例3.求图中阴影部分的面积。
(单位:厘米)解:最基本的方法之一。
用四个圆组成一个圆,用正方形的面积减去圆的面积,所以阴影部分的面积:2×2-π=0.86平方厘米。
例4.求阴影部分的面积。
(单位:厘米)解:同上,正方形面积减去圆面积,16-π()=16-4π=3.44平方厘米例5.求阴影部分的面积。
(单位:厘米)解:这是一个用最常用的方法解最常见的题,为方便起见,我们把阴影部分的每一个小部分称为“叶形”,是用两个圆减去一个正方形,π()×2-16=8π-16=9.12平方厘米另外:此题还可以看成是1题中阴影部分的8倍。
例6.如图:已知小圆半径为2厘米,大圆半径是小圆的3倍,问:空白部分甲比乙的面积多多少厘米?解:两个空白部分面积之差就是两圆面积之差(全加上阴影部分)π-π()=100.48平方厘米(注:这和两个圆是否相交、交的情况如何无关)解:正方形面积可用(对角线长×对角线长÷2,求)正方形面积为:5×5÷2=12.5所以阴影面积为:π÷4-12.5=7.125平方厘米(注:以上几个题都可以直接用图形的差来求,无需割、补、增、减变形)解:右面正方形上部阴影部分的面积,等于左面正方形下部空白部分面积,割补以后为圆,所以阴影部分面积为:π()=3.14平方厘米例9.求阴影部分的面积。
(单位:厘米)解:把右面的正方形平移至左边的正方形部分,则阴影部分合成一个长方形,所以阴影部分面积为:2×3=6平方厘米例10.求阴影部分的面积。
中考求阴影部分面积(供参考)

中考求阴影部分⾯积(供参考)中考求阴影部分⾯积【知识概述】计算平⾯图形的⾯积问题是常见题型,求平⾯阴影部分的⾯积是这类问题的难点。
不规则阴影⾯积常常由三⾓形、四边形、⼸形、扇形和圆、圆弧等基本图形组合⽽成的,在解此类问题时,要注意观察和分析图形,会分解和组合图形。
现介绍⼏种常⽤的⽅法。
⼀、转化法此法就是通过等积变换、平移、旋转、割补等⽅法将不规则的图形转化成⾯积相等的规则图形,再利⽤规则图形的⾯积公式,计算出所求的不规则图形的⾯积。
例1. 如图1,点C、D是以AB为直径的半圆O上的三等分点,AB=12,则图中由弦AC、AD和C D⌒围成的阴影部分图形的⾯积为_________。
⼆、和差法有⼀些图形结构复杂,通过观察,分析出不规则图形的⾯积是由哪些规则图形组合⽽成的,再利⽤这些规则图形的⾯积的和或差来求,从⽽达到化繁为简的⽬的。
三、重叠法就是把所求阴影部分的⾯积问题转化为可求⾯积的规则图形的重叠部分的⽅法。
这类题阴影⼀般是由⼏个图形叠加⽽成。
要准确认清其结构,理顺图形间的⼤⼩关系。
例4. 如图4,正⽅形的边长为a,以各边为直径在正⽅形内作半圆,求所围成阴影部分图形的⾯积。
四、补形法将不规则图形补成特殊图形,利⽤特殊图形的⾯积求出原不规则图形的⾯积。
例5. 如图5,在四边形ABCD中,AB=2,CD=1,∠=?∠=∠=A B D60,90?,求四边形ABCD所在阴影部分的⾯积。
例6. 如图6,在⼀块长为a、宽为b的矩形草地上,有⼀条弯曲的柏油⼩路(⼩路任何地⽅的⽔平宽图2都是c 个单位),求阴影部分草地的⾯积。
六、特殊位置法例7. 如图8,已知两个半圆中长为4的弦AB与直径CD平⾏,且与⼩半圆相切,那么图中阴影部分的⾯积等于_______。
七、代数法将图形按形状、⼤⼩分类,并设其⾯积为未知数,通过建⽴⽅程或⽅程组来解出阴影部分⾯积的⽅法。
例8. 如图10,正⽅形的边长为a,分别以两个对⾓顶点为圆⼼、以a为半径画弧,求图中阴影部分的⾯积。
小升初数学几何热点“求阴影部分面积”专项练习(含解答)

小升初数学几何热点“求阴影部分面积”专项练习求平面图形中阴影部分的面积,是每年小升初考试中的几何热点,思维能力要求高,学生失分率高。
由于阴影部分的图形常常不是以基本几何图形的形状出现,没法直接利用课本中的基本公式来计算,所以比较麻烦。
家长辅导孩子处理这类型的几何题,除了要让孩子熟练地掌握平面图形的概念和面积公式之外,关键还在于懂得如何“巧用方法、妙在变形”。
以下是小学阶段常见的求阴影面积的方法,家长可以让孩子边做边总结方法,逐一攻关,体验解题思维的乐趣。
一、几何图形计算公式1.正方形:周长=边长×4 C=4a面积=边长×边长 S=a×a2.正方体:表面积=棱长×棱长×6 S表=a×a×6体积=棱长×棱长×棱长V=a×a×a3.长方形:周长=(长+宽)×2 C=2(a+b)面积=长×宽 S=ab4.长方体:表面积=(长×宽+长×高+宽×高)×2 S=2(ab+ah+bh)体积=长×宽×高V=abh5.三角形:面积=底×高÷2 s=ah÷26.平行四边形:面积=底×高 s=ah7.梯形:面积=(上底+下底)×高÷2 s=(a+b)×h÷28.圆形:周长=直径×π=2×π×半径 C=πd=2πr面积=半径×半径×π9.圆柱体:侧面积=底面周长×高表面积=侧面积+底面积×2体积=底面积×高10.圆锥体:体积=底面积×高÷3二、解题方法解题要点:1.观察图形的特点,根据图形特点选择合适的方法求解图形的面积。
2.能灵活运用所学过的基本的平面图形的面积求阴影部分的面积。
小升初数学图形求面积方法技巧及阴影面积求法详解总结

求图形的面积是小学数学常考的一种题型。
在数学考试中,很多图形不是以基本图形的形状出现,而是由一些基本图形组合、拼凑成的,它们的面积及周长无法应用公式直接计算。
一般我们称这样的图形为不规则图形。
基本图形我们都有固定的面积和周长公式,直接套用就可以计算。
那么,不规则图形的面积和周长怎么计算呢?这个问题是数学考试中经常难倒孩子的一个难题,特别是小学升学考试中最容易考查这类题型!三角形、长方形、正方形、平行四边形、梯形、菱形、圆和扇形等图形,一般称为基本图形或规则图形。
面积及周长都有相应的公式直接计算,如下表:实际问题中,有些图形不是以基本图形的形状出现,而是由一些基本图形组合、拼凑成的,它们的面积及周长无法应用公式直接计算.一般我们称这样的图形为不规则图形。
那么,不规则图形的面积及周长怎样去计算呢?我们可以针对这些图形通过实施割补、剪拼等方法将它们转化为基本图形的和、差关系,问题就能解决了。
先看三道例题感受一下例1:如右图,甲、乙两图形都是正方形,它们的边长分别是10厘米和12厘米.求阴影部分的面积。
一句话:阴影部分的面积等于甲、乙两个正方形面积之和减去三个“空白”三角形(ABG、BDE、EFG)的面积之和。
例2:如右图,正方形ABCD的边长为6厘米,ABE、ADF与四边形AECF的面积彼此相等,求三角形AEF的面积。
一句话:因为ABE、ADF与四边形AECF的面积彼此相等,都等于正方形ABCD面积的三分之一,也就是12厘米.解:SABE=SADF=S四边形AECF=12在ABE中,因为AB=6.所以BE=4,同理DF=4,因此CE=CF=2,∴ECF的面积为2×2÷2=2。
所以SAEF=S四边形AECF-SECF=12-2=10(平方厘米)。
例3:两块等腰直角三角形的三角板,直角边分别是10厘米和6厘米。
如右图那样重合.求重合部分(阴影部分)的面积。
一句话:阴影部分面积=SABG-SBEF,SABG和SBEF都是等腰三角形总结:对于不规则图形面积的计算问题一般将它转化为若干基本规则图形的组合,分析整体与部分的和、差关系,问题便得到解决。
(完整版)小学求阴影部分面积专题—含答案

(5)【史上最全小学求阴影部分面积专题一含答案】 小学及小升初复习专题-圆与求阴影部分面积----完整答案在最后面目标:通过专题复习,加强学生对于图形面积计算的灵活运用。
并加深对面积和周长概念的理解和区 分。
面积求解大致分为以下几类:1、 从整体图形中减去局部;2、 割补法,将不规则图形通过割补,转化成规则图形。
重难点:观察图形的特点,根据图形特点选择合适的方法求解图形的面积。
能灵活运用所学过的基本 的平面图形的面积求阴影部分的面积。
(4)例1•求阴影部分的面积。
(单位:厘米) 例2.正方形面积是7平方厘米,求阴影部分的面积。
(单位:厘米)(2)例3.求图中阴影部分的面积。
(单位:厘米)例4.求阴影部分的面积。
(单位:厘米)例5.求阴影部分的面积。
(单位:厘米) 例6.如图:已知小圆半径为 2厘米,大圆半径是小圆的 问:空白部分甲比乙的面积多多少即3倍, 厘22㈣厘米)3-10-(M)3(13)—了 —⑴)例8.求阴影部分的面积。
(单位:厘米)例11.求阴影部分的面积。
(单位:厘米) 例13.求阴影部分的面积。
(单位:厘米) 例10.求阴影部分的面积。
(单位:厘米)例12.求阴影部分的面积。
(单位 例14.求阴影部分的面积。
(单位:厘米)例7.求阴影部分的面积。
(单位:厘米)例9.求阴影部分的面积。
(单位:厘米) 3(12)2十“7I* --- 5 —积45(15)扇形,求阴影部分的周长。
BAE C(18)分的面积(佟)(20)(22?(21)例19.正方形边长为2厘米,求阴影部分的面积。
例20.如图,正方形 ABCD 的面积是36平方厘米,求阴影部 例18.如图,在边长为6厘米的等边三角形中挖去三个同样的 例21.图中四个圆的半径都是 1厘米,求阴影部分的面积。
例17.图中圆的半径为5厘米,求阴影部分的面积。
(单位:厘米)例16.求阴影部分的面积。
(单位:厘米)例15.已知直角三角形面积是 12平方厘米,求阴影部分的面 例22.如图,正方形边长为 8厘米,求阴影部分的面积。
六年级容斥原理阴影面积题型

容斥原理在数学中是一种常用的计数方法,通常用于处理具有重复计数的问题。
在六年级的数学课程中,我们也学习了容斥原理的应用,特别是在解决阴影面积的题目时会用到这个原理。
阴影面积题目一般指的是计算由多个图形组成的区域的面积,其中某些部分被其他图形覆盖或重叠而形成阴影。
容斥原理是一种非常有效的解决方法,在这个问题中也能够派上用场。
例如,考虑一个矩形和一个圆形组成的图形区域。
矩形的长为10,宽为6,圆形的半径为4。
我们需要计算这个图形区域的阴影面积。
首先,我们可以计算矩形的面积,即长乘以宽,得到60平方单位。
然后,我们计算圆形的面积,即π乘以半径的平方。
在这个例子中,半径为4,那么圆形的面积为16π平方单位。
接下来,我们需要考虑矩形和圆形的重叠部分。
使用容斥原理,我们可以通过减去重叠部分的面积来避免重复计数。
重叠部分是由矩形和圆形的交集部分组成的,可以通过计算圆心到矩形边界的距离来确定。
在这个例子中,圆心到矩形左边界的距离是6-4=2。
我们知道圆形与矩形的交集是由两个四分之一圆组成的,而每个四分之一圆的面积为1/4乘以π乘以半径的平方。
在这个例子中,半径为4,所以一个四分之一圆的面积为4π/4=π平方单位。
因为重叠部分是由两个四分之一圆组成的,所以重叠部分的面积为2个π平方单位。
最后,我们可以通过应用容斥原理得到阴影面积。
阴影面积等于矩形的面积加上圆形的面积减去重叠部分的面积。
阴影面积 = 矩形面积 + 圆形面积 - 重叠部分面积= 60 + 16π - 2π = 60 + 14π 平方单位最后的结果是一个带有π的阴影面积,如果需要精确的数字,可以用计算器计算π的近似值。
在实际的阴影面积问题中,可能会涉及多个图形的组合,使用容斥原理可以将问题分解成更小的部分,简化计算过程。
通过理解和掌握容斥原理,我们可以更好地解决这类题目。
容斥原理是数学中一个非常重要的概念,它不仅在阴影面积问题中有应用,还可以应用于其他计数问题。
求阴影部分面积的常用方法
专题3:求阴影面积的常用方法通过几条例题,来和大家一起探讨这类问题的解题基本思路和有关技巧。
现介绍几种常用的方法。
一、转化法此法就是通过等积变换、平移、旋转、割补等方法将不规则的图形转化成面积相等的规则图形,再利用规则图形的面积公式,计算出所求的不规则图形的面积。
例1. 如图1,点C 、D 是以AB 为直径的半圆O 上的三等分点,AB=12,则图中由弦AC 、AD 和CD ⌒围成的阴影部分图形的面积为_________。
例2 (2008浙江温州中考试题)如图3,点A 1,A 2,A 3,A 4在射线OA 上,点B 1,B 2,B 3在射线OB 上,且A 1B 1∥A 2B 2∥A 3B 3,A 2B 1∥A 3B 2∥A 4B 3.若△A 2B 1B 2,△A 3B 2B 3的面积分别为1,4,则图中三个阴影三角形面积之和为____________.解析:本题中三个阴影部分均为三角形,但苦于没有现成的底和高,一时无从下手。
如果我们把注意力仅仅集中在三角形面积公式上,是很难一下子找出问题的解决办法的。
不难看出由A 1B 1∥A 2B 2∥A 3B 3,A 2B 1∥A 3B 2∥A 4B 3可以得到△A 2B 1B 2∽△A 3B 2B 3,于是有21413322==B A B A 。
在梯形3322A B B A 中,利用平行线性质可得:21233322=∆∆B B A A B A S S ,于是2322=∆A B A S ,类似地可以求出其余两个三角形面积分别为21,8,从而得解2110。
二、和差法有一些图形结构复杂,通过观察,分析出不规则图形的面积是由哪些规则图形组合而成的,再利用这些规则图形的面积的和或差来求,从而达到化繁为简的目的。
例3. 如图3是一个商标的设计图案,AB=2BC=8,ADE ⌒为14圆,求阴影部分面积。
分析:经观察图3可以分解出以下规则图形:矩形ABCD 、扇形ADE 、Rt EBC ∆。
2019小学六年级数学求阴影面积与周长附答案
小学六年级数学求阴影面积与周长例1.求阴影部分的面积。
(单位:厘米)解:这是最基本的方法:圆面积减去等腰直角三角形的面积,×-2×1=1.14(平方厘米)例2.正方形面积是7平方厘米,求阴影部分的面积。
(单位:厘米)解:这也是一种最基本的方法用正方形的面积减去圆的面积。
设圆的半径为r,因为正方形的面积为7平方厘米,所以=7,所以阴影部分的面积为:7-=7-×7=1.505平方厘米例3.求图中阴影部分的面积。
(单位:厘米)解:最基本的方法之一。
用四个圆组成一个圆,用正方形的面积减去圆的面积,所以阴影部分的面积:2×2-π=0.86平方厘米。
例4.求阴影部分的面积。
(单位:厘米)解:同上,正方形面积减去圆面积,16-π()=16-4π=3.44平方厘米例5.求阴影部分的面积。
(单位:厘米)解:这是一个用最常用的方法解最常见的题,为方便起见,我们把阴影部分的每一个小部分称为“叶形”,是用两个圆减去一个正方形,π()×2-16=8π-16=9.12平方厘米另外:此题还可以看成是1题中阴影部分的8倍。
例6.如图:已知小圆半径为2厘米,大圆半径是小圆的3倍,问:空白部分甲比乙的面积多多少厘米?解:两个空白部分面积之差就是两圆面积之差(全加上阴影部分)π-π()=100.48平方厘米(注:这和两个圆是否相交、交的情况如何无关)例7.求阴影部分的面积。
(单位:厘米)解:正方形面积可用(对角线长×对角线长÷2,求)正方形面积为:5×5÷2=12.5所以阴影面积为:π÷4-12.5=7.125平方厘米(注:以上几个题都可以直接用图形的差来求,无需割、补、增、减变形)例8.求阴影部分的面积。
(单位:厘米)解:右面正方形上部阴影部分的面积,等于左面正方形下部空白部分面积,割补以后为圆,所以阴影部分面积为:π()=3.14平方厘米例9.求阴影部分的面积。
小学六年级求阴影部分面积试题和标准答案附面积公式
求阴影部分面积例1.求阴影部分的面积。
(单位:厘米)解:这是最基本的方法:圆面积减去等腰直角三角形的面积,×-2×1=1.14(平方厘米)例2.正方形面积是7平方厘米,求阴影部分的面积。
(单位:厘米)解:这也是一种最基本的方法用正方形的面积减去圆的面积。
设圆的半径为r,因为正方形的面积为7平方厘米,所以=7,所以阴影部分的面积为:7-=7-×7=1.505平方厘米例3.求图中阴影部分的面积。
(单位:厘米)解:最基本的方法之一。
用四个圆组成一个圆,用正方形的面积减去圆的面积,所以阴影部分的面积:2×2-π=0.86平方厘米。
例4.求阴影部分的面积。
(单位:厘米)解:同上,正方形面积减去圆面积,16-π()=16-4π=3.44平方厘米例5.求阴影部分的面积。
(单位:厘米)解:这是一个用最常用的方法解最常见的题,为方便起见,我们把阴影部分的每一个小部分称为“叶形”,是用两个圆减去一个正方形,π()×2-16=8π-16=9.12平方厘米另外:此题还可以看成是1题中阴影部分的8倍。
例6.如图:已知小圆半径为2厘米,大圆半径是小圆的3倍,问:空白部分甲比乙的面积多多少厘米?解:两个空白部分面积之差就是两圆面积之差(全加上阴影部分)π-π()=100.48平方厘米(注:这和两个圆是否相交、交的情况如何无关)例7.求阴影部分的面积。
(单位:厘米)解:正方形面积可用(对角线长×对角线长÷2,求)正方形面积为:5×5÷2=12.5所以阴影面积为:π÷4-12.5=7.125平方厘米(注:以上几个题都可以直接用图形的差来求,无需割、补、增、减变形)例8.求阴影部分的面积。
(单位:厘米)解:右面正方形上部阴影部分的面积,等于左面正方形下部空白部分面积,割补以后为圆,所以阴影部分面积为:π()=3.14平方厘米例9.求阴影部分的面积。
(完整版)小学求阴影部分面积专题—含答案
【史上最全小学求阴影部分面积专题—含答案】小学及小升初复习专题-圆与求阴影部分面积----完整答案在最后面目标:通过专题复习,加强学生对于图形面积计算的灵活运用。
并加深对面积和周长概念的理解和区分。
面积求解大致分为以下几类:1、从整体图形中减去局部;2、割补法,将不规则图形通过割补,转化成规则图形。
重难点:观察图形的特点,根据图形特点选择合适的方法求解图形的面积。
能灵活运用所学过的基本的平面图形的面积求阴影部分的面积。
例 1.求阴影部分的面积。
例 2.正方形面积是 7 平方厘米,求阴影部分的面积。
(单位:厘米)(单位:厘米)例 4.求阴影部分的面积。
(单位:厘米)例 3.求图中阴影部分的面积。
(单位:厘米)例 5.求阴影部分的面积。
(单位:厘米) 例 6.如图:已知小圆半径为 2 厘米,大圆半径是小圆的 3 倍,问:空白部分甲比乙的面积多多少厘米?例 7.求阴影部分的面积。
(单位:厘米) 例 8.求阴影部分的面积。
(单位:厘米)例 9.求阴影部分的面积。
(单位:厘米) 例 10.求阴影部分的面积。
(单位:厘米)例 11.求阴影部分的面积。
(单位:厘米) 例 12.求阴影部分的面积。
(单位:厘米)例 13.求阴影部分的面积。
(单位:厘米) 例 14.求阴影部分的面积。
(单位:厘米)例 16.求阴影部分的面积。
(单位:厘米) 例 15.已知直角三角形面积是 12 平方厘米,求阴影部分的面积。
例 17.图中圆的半径为 5 厘米,求阴影部分的面积。
(单位:厘米) 例 18.如图,在边长为 6 厘米的等边三角形中挖去三个同样的扇形,求阴影部分的周长。
例 19.正方形边长为 2 厘米,求阴影部分的面积。
例 20.如图,正方形 ABCD 的面积是 36 平方厘米,求阴影部分的面积。
例 21.图中四个圆的半径都是 1 厘米,求阴影部分的面积。
例 22. 如图,正方形边长为 8 厘米,求阴影部分的面积。
例 25.如图,四个扇形的半径相等,求阴影部分的面积。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
未来星培训中心资料
第 1 页 共 3 页 未来星祝你考试成功
求阴影面积的几种常用方法
1、直接用公式法
例1、如图1,在Rt△ABC中,∠A=90°,BC=4,点D是BC的中点,将△ABD绕点A按逆时
针旋转90°,得△AB’D’,那么AD在平面上扫过的区域(图中阴影部分)的面积是( )
A. 4 B. 2 C.π D. 2π
分析:△ABD绕点A按逆时针旋转90°后,形成扇形ADD’,且扇形的圆心角为90°,故可
用扇形的面积公式直接求其面积。
解:∵∠A=90°, 点D是BC的中点,
∴AD=21BC=2,
∴S阴影=S'ADD扇形=3602902=π.
故选C.
2、加减法.
例2、如图2,正方形ABCD的边长为a,那么阴影部分的面积为( )
A. 21πa2 B. 41πa2 C. 81πa2 D. 161πa2
分析:阴影部分的面积可以看作是扇形BCD的面积减去半圆CD的面积。
解:S阴影=SCBD扇形-SCD半圆
=360902a-21π(2a)2
=41πa2-81πa2
=81πa2.
所以本题答案选C.
3、割补法
例3、如图3,以BC为直径,在半径为2且圆心角为90°的扇形内做半圆,交弦AB于点D,
连接CD,则阴影部分的面积是( )
A. π-1 B. π-2 C. 21π-1 D. 21π-2
分析:因为BC为半圆的直径,所以CD⊥AB,CD=BD,所以SCD弓形= SBD弓形,即S阴影=S
CAB扇形
-SADC.
解:∵SCD弓形= SBD弓形
∴S阴影=SCAB扇形-SADC
未来星培训中心资料
第 2 页 共 3 页 未来星祝你考试成功
364423yx22yx
2918929y
x
=3602902-21×2×2
=π-1.
故选A.
4、等积变形法
例4、如图4,已知半圆的直径AB=4cm,点C、D是这个半圆的三等分点,则弦AC、AD和
弧CD围成的的阴影部分的面积为 cm2.
分析:因为C、D是半圆的三等分点,所以能够论证CD∥AB,所以SACD= SOCD,所以S
阴影
=SOCD扇形
解:连接OC、OC、CD
∵C、D是半圆的三等分点,
∴CD∥AB
∴SACD= SOCD(同底等高),
∴S阴影=SOCD扇形=3602602=32π.
5、覆盖法
例5、如图5所示,正方形的边长为a,分别以对角顶点为圆心,边长为半径画弧,则图中
阴影部分的面积是多少?
分析:阴影部分的面积可以看作是两个扇形的重叠部分。
解:S阴影=2SABD扇形-SABCD正方形
=2×360902a-a2
=22a-a2 =(2-1)a2.
6、构造方程法
例6、如图6所示,正方形的边长为6,以边长为直径在正方形内画半圆,则所围成的图形
(阴影部分)的面积为 。
分析:本题虽可以转化为规则图形的面积和差计算阴影
部分面积,但在作图中比较麻烦。这儿的阴影部分和空
白部分都有四部分组成,且形状大小一样。因此可以根据
图形中隐含的数量关系来构造方程求解。
解:设每一部阴影部分面积为x,每一部分的空白
部分面积为y,根据图形得
未来星培训中心资料
第 3 页 共 3 页 未来星祝你考试成功
解得
所以阴影部分面积=4x=4(29-9)=18π-36.
注:此题有多种解答方法,如覆盖法,在此仅以此例说明构造方程法的应用。
练习:
1、如图7,⊙O的半径为10cm,在⊙O中,直径AB与CD垂直,以点B为圆心,BC为半
径的扇形CBD的面积是多少?
2、如图8所示,在Rt△ABC中,∠C=90°,CA=CB=2,分别以A、B、C为圆心,以21AC
为半径画弧,三条弧与边AB所围成的阴影部分的面积是多少?
3、如图9,△ABC 为等腰直角三角形,AC=3,以BC为直径的半圆与斜边AB交于点D,则
图中阴影部分的面积是多少?
4、如图10,A是半径为2的⊙O外的一点,OA=4,AB是⊙O的切线,点B是切点,弦BC
∥OA,连结AC,则图中阴影部分的面积等于多少?
练习答案:1、50πcm2;2、2-2;3、49;4、32π.
