2019年考研数学(二)真题及解析
闽南师范大学802数学综合2018-2019年考研专业课真题试卷

⇒ 2x −1= x − 2 ⇒ x =−1
答题要求: (1)指出解题过程中的错误之处,并分析产生错误的原因; (2)给出正确解法,并简述应采取哪些教学措施避免此类错误发生.
三、简答题(每小题 10 分,共计 30 分)
14.数学思想方法是数学知识的精髓和本质.请简要回答:在数学教学中,教师讲授思想方法需要 注意哪些方面. 15.简述高中数学课堂小结的功能和作用. 16.列举 2011 年版义务教育数学课程标准指出的数学学习内容的核心概念.
两种方式.
7.2017 年版普通高中数学课程标准指出数学学科核心素养包括:
、逻辑推理、数
学建模、直观想象、数学运算和数据分析,这些数学学科核心素养既相互独立、又相互交融,是
一个有机的整体。
8.已知函数 y =(1− x2 )(x2 + ax + b) 的图像关于直线 x = −2 对称,则 a =
,
******************************************************
一、填空(1-8 小题每空 2 分,9-12 小题每空 4 分,共 40 分)
1.由基本初等函数 f1(x) = x 和 f2 (x) = c 经过有限次代数运算所得的初等函数,叫做初等代数函
b=
.
9.函数
y
=
a
与函数(x −1)2
有两个交点,
a
的取值范围是
.
第1页共3页
精都考研()——全国100000考研学子的选择
闽南师范大学2019年考研专业课真题试卷
10.函数 y= (x − 2) 1+ x 的值域是 1− x
考研数学二分类模拟题2019年(21)_真题无答案
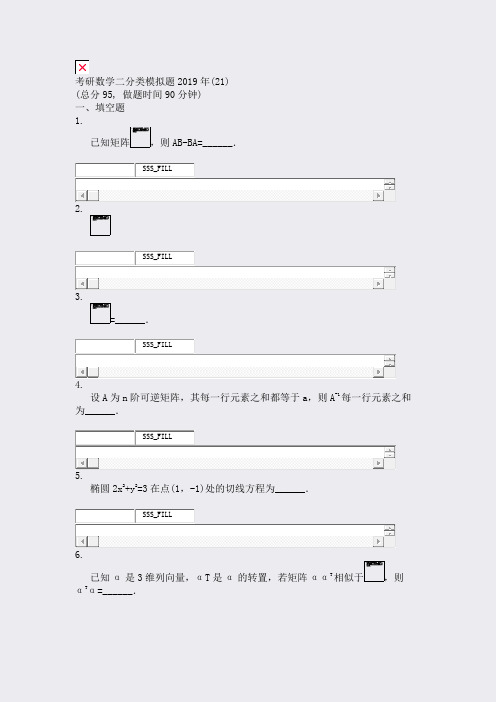
考研数学二分类模拟题2019年(21)(总分95, 做题时间90分钟)一、填空题1.已知矩阵,则AB-BA=______.SSS_FILL2.SSS_FILL3.=______.SSS_FILL4.设A为n阶可逆矩阵,其每一行元素之和都等于a,则A-1每一行元素之和为______.SSS_FILL5.椭圆2x2+y2=3在点(1,-1)处的切线方程为______.SSS_FILL6.已知α是3维列向量,αT是α的转置,若矩阵ααT相似于,则αTα=______.SSS_FILL二、选择题1.设,其中f(x)为连续函数,则等于______ •**.•**(a).•**.D.不存在.SSS_SIMPLE_SINA B C D2.设f(x)可导,则下列结论正确的是______.A.B.C.D.SSS_SIMPLE_SINA B C D3.设,则在x=a处______.•**(x)在x=a处可导且f'(a)≠0•**(a)为f(x)的极大值•**(a)不是f(x)的极值**(x)在x=a处不可导SSS_SIMPLE_SINA B C D4.下列结论正确的是•**=f(x,y)在点(x0,y0)某邻域内两个偏导数存在,则z=f(x,y)在点(x0,y0)处连续.•**=f(x,y)在点(x0,y0)某邻域内连续,则z=f(x,y)在点(x0,y0)处两个偏导数存在.•**=f(x,y)在点(x0,y0)某邻域内两个偏导数存在且有界,则z=f(x,y)在点(x0,y0)处连续.**=f(x,y)在点(x0,y0)某邻域内连续,则z=f(x,y)在点(x0,y0)该邻域内两个偏导数有界.SSS_SIMPLE_SINA B C D5.已知B是3阶非零矩阵,满足AB=0,则______•**=-1时,必有r(B)=1.•**=-1时,必有r(B)=2.•**=1时,必有r(B)=1.**=1时,必有r(B)=2.SSS_SIMPLE_SINA B C D6.微分方程y"-y'-6y=(2x+3)e-2x的特解为______• A.(ax+b)e-2x.•**.C.(ax2+bx)e-2x.**(ax+b)e-2x.SSS_SIMPLE_SINA B C D7.对二元函数z=f(x,y),下列结论正确的是______.•**=f(x,y)可微的充分必要条件是z=f(x,y)有一阶连续的偏导数B.若z=f(x,y)可微,则z=f(x,y)的偏导数连续• C.若z=f(x,y)偏导数连续,则z=f(x,y)一定可微• D.若z=f(x,y)的偏导数不连续,则z=f(x,y)一定不可微SSS_SIMPLE_SINA B C D8.设A=(α1,α2,α3,α4),其中αi是n维列向量(i=1,2,3,4).已知齐次线性方程组Ax=0的基础解系为ξ1=(-2,0,1,0)T,ξ2=(1,0,0,1)T,则______• A.α1,α2线性无关.• B.α1,α3线性无关.• C.α1,α4线性无关.• D.α3,α4线性无关.SSS_SIMPLE_SINA B C D三、解答题1.求极限.SSS_TEXT_QUSTI2.设D={(x,y)|0≤x≤1,0≤y≤1},直线l:x+y=t(t≥0),S(t)为正方形区域D位于l左下方的面积,求SSS_TEXT_QUSTI3.一个半球体状的雪堆,其体积融化的速率与半球面面积S成正比,比例常数K>0.假设在融化过程中雪堆始终保持半球体状,已知半径为r的雪堆在开始融化的3小时内,融化了其体积的,问雪堆全部融化需要多少小时?SSS_TEXT_QUSTI4.设函数f(x)在区间[0,1]上连续,在(0,1)内可导,且试证:(Ⅰ)存在,使f(η)=η;(Ⅱ)对任意实数λ,必存在ξ∈(0,η),使得f'(ξ)-λ[f(ξ)-ξ]=1.SSS_TEXT_QUSTI5.设f(x)二阶连续可导,且f(0)=f'(0)=0,f"(0)≠0,设u(x)为曲线y=f(x)在点(x,f(x))处的切线在x轴上的截距,求SSS_TEXT_QUSTI6.设由sinxy+ln(y-x)=x确定函数y=y(x),求y'(0).SSS_TEXT_QUSTI)的主对角线元素之和,且设二次型,已知该二次型的矩阵A=(aijSSS_TEXT_QUSTI7.求a,b的值;SSS_TEXT_QUSTI8.求正交变换x=Qy将f化为标准形.9.设f(x)二阶连续可导,f(0)=0,f'(0)=1,且[xy(x+y)-f(x)y]dx+[f'(x)+x2y]dy=0为全微分方程,求f(x)及该全微分方程的通解.SSS_TEXT_QUSTI1。
2019年考研数学(三)真题及答案解析(完整版)

【解析】令 un
1 n3
, vn
1n
,故(A)(C)排除。令 un
1 n3
, vn
1n
1 ln n
,故(D)
排除,对于选项(B),由于 vn 条件收敛,则 lim vn 0 ,且 lim unvn lim vn 0 ,
n1 n
n n
n nun n n
根据正项级数判别法 nun 绝对收敛,则 unvn 绝对收敛。综上,故选(B).
(C)3.
(D)4.
【答案】(C)
【解析】 x tan x ~ 1 x3, 故 k 3. 3
(2)已知方程 x5 5x k 0 有 3 个不同的实根,则 k 的取值范围( )
(A) (, 4) (B) (4, ) (C)[4, 4] (D) (4, 4)
【答案】(D)
【解析】令 f x x5 5x k ,则 f x 5x4 5 5 x4 1 5 x2 1 x2 1 ,
则 x 1, f x 0 ; 1 x 1, f x 0 ; x 1, f x 0 ;
又 lim f x , lim f x ,综合单调性知 f 1 0, f 1 0 时才有三个根,
x
x
即 f 1 1 5 k 0, f 1 1 5 k 0, 则 4 k 4 。
n 2 2 3
n n+1 n n+1
(10)
曲线
y
x
sin
x
2
cos
x
2
x
3 2
的拐点坐标为
【答案】
【解析】 y ' sin x x cos x 2sin x x cos x sin x
y '' cos x x sin x cos x x sin x ,令 y '' 0得x 0或x
2019年考研数学一真题及答案解析

2019年全国硕士研究生入学统一考试数学一试题解析一、选择题:1~8小题,每小题4分,共32分,下列每小题给出的四个选项中,只有一项符合题目要求的,请将所选项前的字母填在答题纸...指定位置上.(1)当0x →时,若tan kx x x -与是同阶无穷小,则k =(A )1.(B )2.(C )3.(D )4.【答案】C【解析】33311tan (())~,33x x x x x o x x -=-++-故 3.k =(2)设函数||,0,(),0,x x x f x xlnx x ≤⎧=⎨>⎩则0x =是()f x 的A.可导点,极值点.B.不可导点,极值点.C.可导点,非极值点.D.不可导点,非极值点.【答案】B【解析】.00()(0)lim lim 0,0x x x x f x f x --→→-==-00()(0)ln lim lim ,0x x f x f x x x x +-→→-==-∞-故()f x 不可导.当0x >时,()0;f x <当0x <时,()0.f x <故()f x 在0x =处取极大值.故选(B ).(3)设{}n u 是单调递增的有界数列,则下列级数中收敛的是A.1mn n un=∑. B.11(1)mnn nu =-∑.C.11(1)mn n n uu =+-∑.D.2211()mn n n uu +=-∑【答案】C【解析】举反例:(A )1n n u n -=(B )1n n u n -=(C )1n u n=-(4)设函数2(,)xQ x y y=.如果对上半平面(0)y >内的任意有向光滑封闭曲线C 都有(,)(,)0CP x y dx Q x y dy +=⎰,那么函数(,)P x y 可取为A.23x y y-.B.231x y y-.C.11x y -. D.1x y-【答案】D 【解析】,Q P x y ∂∂=∂∂则21,P y y∂=∂又上半平面含1,x 有零,故(C )错,选(D ).(5)设A 是3阶实对称矩阵,E 是3阶单位矩阵,若22A A E +=,且||4A =,则二次型T x Ax 的规范形为A.222123y y y ++. B.222123y y y +-.C.222123y y y --. D.222123y y y ---【答案】C【解析】22A A E += ,设A 的特征值为λ22λλ∴+=(2)(1)0λλ+-=21λ∴=-或4A = A ∴的特征值为1232,12,1q p λλλ==-=∴==T X Ax ∴的规范形为222123y y y --(6)如图所示,有3张平面两两相交,交线相互平行,它们的方程i123(i=1,2,3)i i i a x a y a z d +++组成的线性方程组的系数矩阵和增广矩阵分别记为,A A ,则A .()2,r()3r A A ==B.()2,r()2r A A ==C.()1,r()2r A A ==D.()1,r()1r A A ==【答案】C【解析】(1)令123,1,2,3i i i i a x a y a z di i π=++==由于123,,πππ无公共交点,则()()r A r A <,故B 、D 排除(2)由(1)分析可知,()2r A ≤,且0A ≠,则1()2r A ≤≤以1π和2π为例,由于11121312122232a x a y a z d a x a y a z d ++=⎧⎨++=⎩的公共解为一条直线则11121321222331a a a r a a a ⎡⎤-=⎢⎥⎣⎦即1112132122232a a a r a a a ⎡⎤=⎢⎥⎣⎦因此111213212223313233() 2.()3a a a r A r a a a r A a a a ⎡⎤⎢⎥===⎢⎥⎢⎥⎣⎦综上A 正确(7)设,A B 为随机事件,则()()P A P B =的充分必要条件是A.()()()P A B P A P B =+ B.()()()P AB P A P B =C.()()P AB P BA = D.()(P AB P AB =【答案】C【解析】()0A P AB ⇔=选项,故A 排除A B ⇔B选项、独立,故B 排除()()()()P A P AB P B P AB ⇔-=-C选项()()P A P B =而,故C 正确()()1()P AB P A B P A B ⇔==- D选项1()()()P A P B P AB =--+1()()P A P B ⇔=+故D 排除(8)设随机变量X 与Y 相互独立,且都服从正态分布2(,)N μσ.则{}1P X Y -<A.与μ无关,而与2σ有关. B.与μ有关,而与2σ无关.C.与2,μσ都有关.D.与2,μσ都无关.【答案】A【解析】,X Y 独立,服从正态分布,则2(,2)z x y N σσ=- (1)(11)(P X Y P Z P -<=-<<=-21=Φ-,故A 正确二、填空题:9-14小题,每小题4分,共24分,请将答案写在答题纸...指定位置上.(9)设函数()f u 可导,(sin sin )z f y x xy =-+,则11cos cos z zx x y y∂∂⋅+⋅=∂∂________【答案】cos cos y x x y+【解析】'(sin sin )(cos )zf y x x y x∂=--+∂'(sin sin )cos zf y x y x y∂=-+∂故11'(sin sin )'(sin sin )cos cos cos cos cos cos z z y x f y x f y x x x y y x yy x x y∂∂⋅+⋅=--++-+∂∂=+(10)微分方程22220yy y --=满足条件(0)1y =的特解y =________【答案】y =【解析】22'2y y y+=2212y dy dx y =+⎰⎰故2ln(2)y x C +=+.由(0)1y =得ln 3C =则2ln(2)ln 3y x +=+.故2ln(2)ln 3y x e e ++=即223x y e +=故y =(11)幂级数0(1)(2)!n nn n ∞=-∑在(0,)+∞内的和函数()S x =________【答案】【解析】20(1)(2)!nn n n ∞=-=∑(12)设∑为曲面22244(0)x y z z ++=≥的上侧,则z=________【答案】323【解析】'22204324sin 3DxyD y dxdy ydxdy d r dr πθθ∑=====⎰⎰⎰⎰⎰⎰(13)设123(,,)A ααα=为三阶矩阵,若12,αα线性无关,且3122ααα=-+。
陕西师范大学考研数学分析真题2019
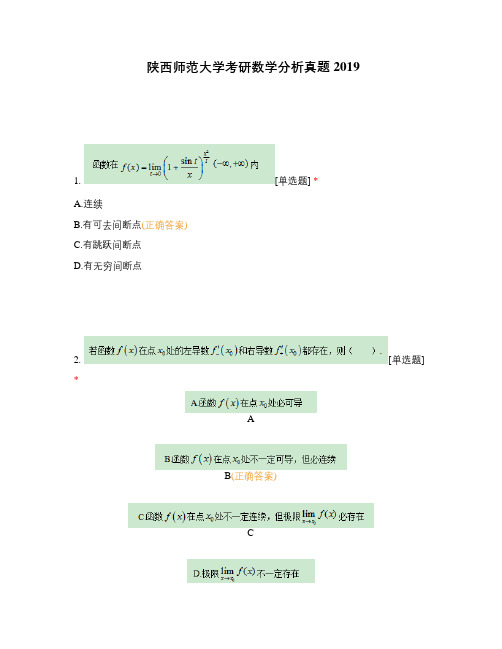
陕西师范大学考研数学分析真题20191. [单选题] *A.连续B.有可去间断点(正确答案)C.有跳跃间断点D.有无穷间断点2. [单选题] *AB(正确答案)CD3. [单选题] *AB(正确答案)CD4. [单选题] *A(正确答案)BCD5. [单选题] *AB(正确答案)CD6. [单选题] *A.①②B.③④C.②④(正确答案)D.①③7.[单选题] *AB(正确答案)CD8.[单选题] *ABCD(正确答案)9. [单选题] *ABCD(正确答案)10.[单选题] *ABCD(正确答案)11.[填空题] *答案若为分数,请用“/”作分数线,示例:三分之一写作1/3_________________________________(答案:-1)12. [填空题] *答案若为分数,请用“/”作分数线,示例:三分之一写作1/3_________________________________(答案:1/12)13.[填空题] *答案若为分数,请用“/”作分数线,示例:三分之一写作1/3;本题的两个答案之间用“,”隔开_________________________________(答案:2,0)14. [填空题] *答案若为分数,请用“/”作分数线,示例:三分之一写作1/3_________________________________(答案:2)15.[填空题] *答案若为分数,请用“/”作分数线,示例:三分之一写作1/3_________________________________(答案:10/3)。
2019考研数一真题及解析

2019年全国硕士研究生入学统一考试数学(一)试题及解析一、选择题:18小题,每小题4分,共32分.下列每题给出的四个选项中,只有一个选项符合题目要求的,请将所选项前的字母填在答题纸...指定位置上. (1)当0x →时,若tan x x -与k x 是同阶无穷小,则k =( )(A) 1(B) 2(C)3(D) 4【答案】C【解析】0x →时,有3tan 3x x x --,故3k =.(2)设函数,0()ln ,0x x x f x x x x ⎧≤=⎨>⎩,则0x =是()f x 的( )(A) 可导点,极值点 (B)不可导点,极值点 (C) 可导点,非极值点(D)不可导点,非极值点【答案】B【解析】由定义可得00()(0)ln (0)lim lim x x f x f x xf x x+++→→-'===-∞; 200()(0)(0)lim lim 0x x f x f x f x x---→→--'===,故(0)f '不存在; 另外直接对()f x 求导有:2,0()ln 1,0x x f x x x -<⎧'=⎨+>⎩,可得0x =是()f x 的极大值点.(3)设{}n u 是单调增加的有界数列,则下列级数中收敛的是( )(A) 1n n un∞=∑(B) 11(1)nn n u ∞=-∑(C) 11(1)nn n u u ∞=+-∑ (D)2211()n n n uu ∞+=-∑【答案】D【解析】由已知可得,{}n u 收敛,不妨设()n u a n →→∞,则有22()n u a n →→∞;对于选项D :部分和22222211111()()nk k n k uu uu a u n ++=-=-→-→∞∑,所以2211()n n n u u ∞+=-∑收敛; 对于选项A :令tan n u arc n =,则111tan 14n n n n u arc n n n n π∞∞∞====≥∑∑∑发散,此时也可排除选项B ; 对于选项C :令1n u n =-,则11111111(1)1111n n n n n n u n n u n n n ∞∞∞∞====+⎛⎫- ⎪+⎛⎫-=-=-=- ⎪ ⎪⎝⎭ ⎪-+⎝⎭∑∑∑∑发散,排除C.(4)设函数2(,)xQ x y y =,如果对上半平面(0y >)内的任意有向光滑封闭曲线C 都有(,)(,)0CP x y dx Q x y dy +=⎰,那么函数(,)P x y 可取为( )(A) 23x y y- (B) 231x y y - (C) 11x y - (D) 1x y-【答案】D【解析】由已知可得,在上半平面(0y >)内积分与路径无关,即只需选择在上半平面(0y >)内有连续偏导数且(,)(,)Q x y P x y x y∂∂=∂∂,而C 选项函数在0x =不连续,故仅有选项D 满足. (5)设A 是3阶实对称矩阵,E 是3阶单位矩阵,若22A A E +=且4A =,则二次型T x Ax 的规范形为( )(A) 222123y y y ++ (B) 222123y y y +-(C) 222123y y y --(D) 222123y y y ---【答案】C【解析】设矩阵A 的特征值为λ,由22A A E +=可得,22λλ+=,解得1λ=,2-,又因为1234A λλλ==,故A 的3个特征值为1,2-,2-,所以二次型T x Ax 的规范形为222123y y y --.(6)如图所示,有3张平面两两相交,交线相互平行,它们的方程123i i i i a x a y a z d ++=(1,2,3i =)组成的线性方程组的系数矩阵和增广矩阵分别记为A ,A ,则( )(A) ()2,()3r A r A == (B) ()2,()2r A r A == (C) ()1,()2r A r A ==(D) ()1,()1r A r A ==【答案】A【解析】由图像可得,3张平面没有公共交点,即()()3r A r A ≠≤,又因为3个平面两两相交,故其中任意两个平面不平行,所以()2r A ≥,答案为A.(7)设,A B 为随机事件,则()()P A P B =的充分必要条件是( ) (A) ()()()P AB P A P B =+(B) ()()()P AB P A P B = (C) ()()P AB P BA =(D) ()()P AB P AB =【答案】C【解析】由减法公式可得:()()()P AB P A P AB =-,()()()P B A P B P AB =-,所以()()P A P B =的充要条件为()()P AB P BA =.(8)设随机变量X 与Y 相互独立,且都服从正态分布2(,)N μσ,则{1}P X Y -<( )(A) 与μ无关,而与2σ有关 (B) 与μ有关,而与2σ无关 (C) 与μ,2σ都有关(D) 与μ,2σ有无关【答案】A【解析】由已知可得,2(0,2)X YN σ-(0,1)N所以{1}{(P X Y P P -<=<=<<=Φ-Φ21=Φ-,所以{1}P X Y -<与μ无关,而与2σ有关. 二、填空题:914小题,每小题4分,共24分.请将答案写在答题纸指定位置上.9.设函数()f u 可导,(sin sin )z f y x xy =-+,则11_______cos cos z z x x y y∂∂⋅+⋅=∂∂ 【答案】cos cos y x x y+ 【解析】(sin sin )(cos )zf y x x y x∂'=--+∂,(sin sin )cos z f y x y x y ∂'=-⋅+∂,故11(sin sin )(sin sin )cos cos cos cos cos cos z z y x y xf y x f y x x x y y x y x y∂∂''⋅+⋅=--++-+=+∂∂. 10.微分方程2220yy y '--=满足条件(0)1y =的特解________y =【答案】【解析】由已知222y y y+'=,所以222y dy dx y =+⎰⎰,即2ln(2)x C y +=+, 因为(0)1y =,所以ln3C =,故2ln(2)ln 3y x +=+, 则223xy e +=,因此y =.11.幂级数0(1)(2)!n nn x n ∞=-∑在(0,)+∞内的和函数()________S x =.【答案】【解析】由泰勒公式可得20(1)cos (2)!n nn x x n ∞=-=∑,故有0(1)(2)!n n n x n ∞=-=∑12.设∑为曲面22244(0)x y z z ++=≥的上侧,则________∑=.【答案】323【解析】由投影法可得:224,02x y y y dxdy ydxdy ∑∑∑+≤≥===⎰⎰⎰⎰220322sin 3d r dr πθθ==⎰⎰. 13.设123(,,)A ααα=为3阶矩阵,若12,αα线性无关,且3122ααα=-+,则线性方程组0Ax =的通解为___________.【答案】(1,2,1),Tx k k R =-∈【解析】由已知可得矩阵()2r A =,故0Ax =的基础解系中含有1个线性无关的解向量,又因为3122ααα=-+,即1231(,,)201ααα⎛⎫⎪-= ⎪ ⎪⎝⎭,故通解为(1,2,1),T x k k R =-∈. 14.设随机变量X 的概率密度为,02()20,xx f x else⎧<<⎪=⎨⎪⎩,()F x 为X 的分布函数,EX 为X 的数学期望,则{()1}P F X EX >-=.【答案】23【解析】由已知可得,224()23x EX xf x dx dx +∞-∞===⎰⎰, 且分布函数20,0()(),0241,2xx xF x f t dt x x -∞<⎧⎪⎪==≤<⎨⎪≤⎪⎩⎰,所以22112{()1}{()}{}{34323X x P F X EX P F X P P X dx >-=>=>=>==. 【法二】易知()(0,1)Y F X U =,所以42{()1}{1}33P F X EX P Y >-=>-=.三、解答题:1523小题,共94分.请将解答写在答题纸指定位置上.解答应写出文字说明、证明过程或演算步骤.15.设函数()y f x =是微分方程22x y xy e -'+=满足条件(0)0y =的特解。
2019考研数学一真题(含答案解析)
2019年考研数学一真题及答案解析一、选择题:1~8小题,每小题4分,共32分,下列每小题给出的四个选项中,只有一项符合题目要求的,请将所选项前的字母填在答题纸...指定位置上.1.当0→x 时,若x x tan -是与kx 是同阶无穷小,则=k2.设函数,0()ln ,0x x x f x x x x ⎧≤⎪=⎨>⎪⎩,则0x =是()f x 的3.设{}n u 是单调增加的有界数列,则下列级数中收敛的是A.1nn u n∞=∑ B.11(1)n n n u ∞=-∑ C.11(1n n n uu ∞=+-∑ D.2211()n n n uu ∞+=-∑(B )的反例,取1n u n=-(C )的反例,取1n u n =-,111n n u u n+-=-,对应的级数发散4.设函数2(,)xQ x y y=,如果对上半平面(0)y >内的任意有向光滑封闭曲线C 都有(,)d (,)d 0CP x y x Q x y y +=⎰ ,那么函数(,)P x y 可取为()A.23x y y - B.231x y y- C.11x y- D.1x y-【分析与解答】答案:D 为了满足条件,一需要函数在积分区域内没有暇点,此题主要指的是没有使得被积函数分母为0的点,注意到上半平面(0)y >时,x 可以取到0,即y 轴正半轴上的点,这些点会使得(C )选项无意义,为(C )选项的暇点,排除(C )选项。
另外为了使闭环积分为0,需要满足(,)(,)Q x y P x y x y ∂∂=∂∂,容易算出2(,)1Q x y x y∂=∂,只有(D )选项满足2(,)1P x y y y∂=∂5.设A 是3阶实对称矩阵,E 是三阶单位矩阵,若E A A 22=+,且4=A ,则二次型Ax x T规范形为A.232221y y y ++ B.232221y y y -+ C.232221y y y -- D.232221y y y ---【分析与解答】答案:C22221,2λλλ+=⇒+=⇒=-A A E ,说明A 的特征值只能在1,2-中选择(这一点很重要,用化零多项式得到的特征值包含A 的所有特征值,有可能会多了假根,但绝对不会漏根),再由于所有特征值之积等于行列式,由于4=A ,可知矩阵A 的特征值必为1,2,2--,特征值两负一正,根据惯性定理,选(C )。
2019年考研数学二评分
2019年考研数学二评分1. 背景介绍2019年考研数学二是中国大陆高校研究生招生考试中的一门科目,是考生申请数学相关专业研究生学位的重要评价标准之一。
这门考试的评分制度直接影响到考生的录取结果,因此对于考生来说,了解2019年考研数学二评分的规则和要求是非常重要的。
2. 评分标准考研数学二的评分标准一般包括两个方面:选择题和主观题。
2.1 选择题评分选择题的评分标准通常是根据考生答案的正确与否来判断,不同的选择题可能存在不同的得分方式,一般有以下几种情况:- 单选题:一般是每题4个选项中只有一个正确答案,答对得4分,答错或不选得0分。
- 多选题:一般是每题4个选项中有多个正确答案,答对得4分,答错或不全选得0分。
- 不定项选择题:一般是每题4个选项中有1个或多个正确答案,考生需自行在答题卷上标记出所有正确选项,答对得4分,答错或不完全选得0分。
选择题的总分一般占整个考试总分的比例较大,一般在60%左右。
2.2 主观题评分主观题的评分一般根据考生答案的完整性、准确性和清晰程度来判断,主观题的评分标准可能包括以下几个方面: - 答案完整性:考生是否回答了所有的问题,并且在回答中没有遗漏关键点。
- 答案准确性:考生的答案是否正确,是否使用了正确的方法和理论进行求解。
- 答案清晰程度:考生的答案是否清晰易懂,是否使用了恰当的数学符号和术语,是否有良好的结构和组织。
主观题的评分一般相对较为主观,评分人员根据自己的判断标准给予分数。
主观题的总分一般占整个考试总分的比例较小,一般在40%左右。
3. 得分统计考研数学二的得分统计通常以百分制进行,最高分为100分。
3.1 总分计算考研数学二的总分计算一般是根据选择题和主观题的得分进行加权平均得到的。
具体的计算方式可能因不同院校或不同年份而有所不同。
3.2 及格分数线考研数学二的及格分数线通常由各个高校根据自身的招生情况和需求来决定,一般分为不同的等级,如优秀、合格等。
2019年考研(数学三)真题试卷(题后含答案及解析)
2019年考研(数学三)真题试卷(题后含答案及解析) 题型有:1. 选择题 2. 填空题 3. 解答题选择题下列每题给出的四个选项中,只有一个选项符合题目要求。
1.当x→0,x—tanx与xk是同阶无穷小,则k=( )A.1B.2C.3D.4正确答案:C解析:因x—tanx~,若要x—tanx与xk是同阶无穷小,则k=3,故选C.2.已知方程x5—5x+k=0有3个不同的实根,则k的取值范围是( )A.(—∞,—4)B.(4,+∞)C.[—4,4]D.(—4,4)正确答案:D解析:设f(x)=x5—5x+k,则f′(x)=5x4—5,令f′(x)=0,得x=±1.由题意知,f(x)=0有3个实根,在(—∞,—1),(—1,1),(1,+∞)上分别具有1个实根,又∵f(—∞)= —∞,f(—1)=4+k,f(1)= —4+k,f(+∞)=+∞∴f(—1)=4+k >0,f(1)= —4+k<0故—4<k<4.3.已知微分方程y″+ay′+by=cex的通解为y=(C1+C2x)e—x+ex,则a,b,c依次为( )A.1,0,1B.1,0,2C.2,1,3D.2,1,4正确答案:D解析:由条件知特征根为λ1=λ2= —1,特征方程为(λ—λ1)(λ—λ2)=λ2+2λ+1=0,故a=2,b=1,而y*=e*为特解,代入得c=4,故选D.4.若绝对收敛,条件收敛,则( )A.C.D.正确答案:B解析:由绝对收敛可知也绝对收敛(因为=0),而当条件收敛时,的敛散性不定.如果令vn=(—1)n及vn=都是条件收敛,而发散,的敛散性是不确定的.则C,D都不正确.再判断的敛散性:由于是绝对收敛的,故选B.5.设A是四阶矩阵,A*是A的伴随矩阵,若线性方程Ax=0的基础解系中只有2个向量,则A*的秩是( )A.0B.1C.2D.3正确答案:A解析:因为Ax=0的基础解系中只有2个向量,∴4—r(A)=2,则r(A)=2∴r(A*)=0,故选A.6.设A是三阶实对称矩阵,E三阶单位矩阵,若A2+A=2E,且|A|=4,则二次型xTAx的规范形为( )A.y12+y22+y32B.y12+y22—y32C.y12—y22—y32D.—y12—y22—y32正确答案:C解析:设λ为A的特征值,由A2+A=2E得λ2+λ=2,解得λ= —2或1,所以A的特征值是1或—2.又∵|A|=4,所以A的三个特征值为1,—2,—2,∴二次型xTAx的规范形为y12—y22—y32,故选C.7.设A,B为随机事件,则P(A)=P(B)充分必要条件是( )A.P(A∪B)=P(A)+P(B)B.P(AB)=P(A)P(B)C.D.P(AB)=正确答案:C解析:=P(A)—P(AB),=P(B)—P(AB),所以P(A)=P(B)故选8.设随机变量X和Y相互独立,且都服从正态分布N(μ,σ2),则P{|X—Y|<1}( )A.与μ无关,而与σ2有关B.与μ有关,而与σ2无关C.与μ,σ2都有关D.与μ,σ2都无关正确答案:A解析:X~Y~N(0,2σ2),所以P{|X—Y|<1}=;故选A.填空题9.= ________.正确答案:解析:10.曲线y=xsinx+2cosx的拐点坐标为________.正确答案:(π,—2)解析:y′=sinx+xcosx—2sinx=xcosx—sinx.y″=cosx—xsinx—cosx= —xsinx,令y″=0,得x=0,x=π.又在x=0的左右两侧,y″<0,故(0,2)不是拐点.因y″′= —sinx—xcosx|x=π≠0,所以拐点为(π,—2).11.已知f(x)=,则∫01x2f(x)dx= ________.正确答案:解析:∫01x2f(x)dx=由已知得f(1)=代入上式得:12.A、B两商品的价格分别表示为PA、PB,设A商品的需求函数QA=500—PA2—PAPB+2PB2,则当PA=10,PB=20时,商品A的需求量对自身价格需求弹性ηAA(ηAA>0)=_________.正确答案:0.4解析:需求函数QA=500—PA2—PAPB+2PB2= —2PA—PB,=0.4.13.已知矩阵,若线性方程组Ax=b有无穷多解,则a= ________.正确答案:1解析:当a=1时,r(A)==2<3,方程组Ax=b有无穷多解,故a=1.14.设连续型随机变量X的概率密度为f(x)=F(X)为X的分布函数,E(X)为X的数学期望,则P{F(X)>E(X)—1}= ________.正确答案:解析:易知Y=F(X)~U(0,1),P{F(X)>E(X)—1}=解答题解答应写出文字说明、证明过程或演算步骤。
2019武汉大学数学专业考研真题(回忆版)
2019武汉⼤学数学专业考研真题(回忆版)数学分析⼀,1)求极限$\lim\limits _{x\rightarrow 0}\left( 1+\sin x\right) ^{\dfrac {1}{x}}$.2)$f(x) =\ln \left(x - \sqrt{1+x^2}\right) $ ,求 $f(0)^{(2k+1)}$,$ k$为⾃然数.3)$f(x,y) = x^yy^x$,求$f(x,y)$的全微分.⼆,计算下⾯积分1)$\int_{-1}^{1} {\dfrac{1+x^2}{1+x^4}}dx$.2)$\iiint _{V} {\dfrac{dxdydz}{(1+x+y+z)^{3}}}$,V={${x+y+z\leq{1}}, x,y,z\geq0$}.3)$\oint_L{\dfrac{xdy-ydx}{x^2+y^2}}$,$L$是不过原点的简单封闭曲线.三,1)判断$\sum_{n=1}^{\infty}\left({\sqrt[n]{n}-1}\right)^2$的敛散.2)若$\sum_1^{\infty}a_n\sin^nx$在[0,$2\pi$]收敛,请问它是否⼀致收敛.四,1)$f(x)$连续可微,$f(0)$不为$0$,其Maclaurin级数(Cauchy余项):$f(x) = f(0)+f^{'}(0)x+\dfrac{f^{(2)}(0)}{2!}x^2+...+\dfrac{f^{(n)} (0)}{n!}x^n+\dfrac{f^{(n+1)}(\theta x)}{n!}\left(1-\theta\right)^nx^{n+1}$,证明:$$\lim_{x\rightarrow0}\theta = 1-\sqrt [n]{\dfrac{1}{n+1}}.$$2)$\{a_n\}$单调递减,$a_n\rightarrow0\left(当n\rightarrow0\right)$,证明:$$\sum_{n=1}^{\infty}a_n收敛\leftrightarrow\sum_{n=1}^{\infty}n\left(a_n-a_{n+1}\right)$$收敛。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2019年考研数学二真题一、选择题 1—8小题.每小题4分,共32分.1.当0x →时,若tan x x -与k x 是同阶无穷小,则k =( ) (A )1 (B )2 (C )3 (D )4 2.曲线3sin 2cos ()22y x x x x ππ=+-<<的拐点是( ) (A )(0,2) (B )(,2)π- (C )(,)22ππ-(D )33(,)22ππ- 3.下列反常积分发散的是 ( ) (A )x xe dx +∞-⎰(B )2x xe dx +∞-⎰(C )20arctan 1x dx x +∞+⎰(D )201xdx x+∞+⎰ 4.已知微分方程xy ay by ce '''++=的通解为12()x xy C C x e e -=++,则,,a b c 依次为( )(A )1,0,1 (B )1,0,2 (C )2,1,3 (D )2,1,45.已知平面区域{(,)|}2D x y x y π=+≤,记1DI =,2DI =⎰⎰,3(1DI dxdy =-⎰⎰ ,则 ( )(A )321I I I << (B )213I I I << (C )123I I I << (D )231I I I << 6.设函数(),()f x g x 的二阶导函数在x a =处连续,则2()()lim0()x af xg x x a →-=-是两条曲线()y f x =,()y g x =在x a =对应的点处相切及曲率相等的 ( )(A )充分不必要条件 (B )充分必要条件 (C )必要不充分条件 (D )既不充分也不必要条件 7. 设A 是四阶矩阵,*A 为其伴随矩阵,若线性方程组0Ax =的基础解系中只有两个向量,则(*)r A =( )(A )0 (B )1 (C )2 (D )38.设A 是三阶实对称矩阵,E 是三阶单位矩阵,若22A A E +=,且4A =,则二次型T x Ax 的规范形是 ( )(A )222123y y y ++ (B )222123y y y +- (C )222123y y y -- (D )222123y y y ---二、填空题(本题共6小题,每小题4分,满分24分. 把答案填在题中横线上) 9.()20lim 2xxx x →+= .10.曲线sin 1cos x t t y t =-⎧⎨=-⎩在32t π=对应点处的切线在y 的截距为 .11.设函数()f u 可导,2y z yf x ⎛⎫= ⎪⎝⎭,则2z zx y x y ∂∂+=∂∂ . 12.曲线ln cos (0)6y x x π=≤≤的弧长为 .13.已知函数21sin ()xt f x xdt t=⎰,则10()f x dx =⎰ .14.已知矩阵1100211132210034A -⎛⎫⎪-- ⎪= ⎪-- ⎪⎝⎭,ij A 表示元素ij a 的代数余子式,则1112A A -= .三、解答题15.(本题满分10分)已知函数2,0()1,0xx xx f x xe x ⎧>⎪=⎨+≤⎪⎩,求()f x ',并求函数()f x 的极值.16.(本题满分10分)求不定积分2236(1)(1)x dx x x x +-++⎰.17.(本题满分10分)设函数()y x是微分方程22x y xy e '-=满足条件(1)y =的特解.(1)求()y x 的表达式;(2)设平面区域{(,)|12,0()}D x y x y y x =≤≤≤≤,求D 绕x 轴旋转一周所形成的旋转体的体积. 18.(本题满分10分)设平面区域2234{(,)|,()}D x y x y x y y =≤+≤,计算二重积分D.19.(本题满分10分)设n 是正整数,记n S 为曲线求曲线sin (0)xy e x x n π-=≤≤与x 轴所形成图形的面积,求n S ,并求lim .n n S →∞20.(本题满分11分)已知函数(,)u x y 满足关系式22222230u u ux y y ∂∂∂-+=∂∂∂.求,a b 的值,使得在变换(,)(,)ax by u x y v x y e +=之下,上述等式可化为函数(,)v x y 的不含一阶偏导数的等式.21.(本题满分11分)已知函数()f x 在[]0,1上具有二阶导数,且(0)0,(1)1f f ==,1()1f x dx =⎰,证明:(1)至少存在一点(0,1)ξ∈,使得()0f ξ'=; (2)至少存在一点(0,1)η∈,使得()2f η''<-.. 22.(本题满分11分)已知向量组Ⅰ:12321111,0,2443a ααα⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪=== ⎪ ⎪ ⎪ ⎪ ⎪ ⎪+⎝⎭⎝⎭⎝⎭;向量组Ⅱ:12321011,2,3313a a a βββ⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪=== ⎪ ⎪ ⎪ ⎪ ⎪ ⎪+-+⎝⎭⎝⎭⎝⎭.若向量组Ⅰ和向量组Ⅱ等价,求常数a 的值,并将3β用123,,ααα线性表示.23.(本题满分11分)已知矩阵22122002A x -⎛⎫ ⎪=- ⎪ ⎪-⎝⎭与21001000B y ⎛⎫⎪=- ⎪ ⎪⎝⎭相似.(1)求,x y 之值;(2)求可逆矩阵P ,使得1P AP B -=.2019年考研数学二真题解析一、选择题 1—8小题.每小题4分,共32分.1.当0x →时,若tan x x -与k x 是同阶无穷小,则k =( )(A )1 (B )2 (C )3 (D )4【答案】(C )【详解】当0x →时,331tan ()3x x x o x =++,所以331tan ()3x x x o x -=-+,所以3k =. 2.曲线3sin 2cos ()22y x x x x ππ=+-<<的拐点是( )(A )(0,2) (B )(,2)π- (C )(,)22ππ- (D )33(,)22ππ-【答案】(D )【详解】sin 2cos y x x x =+,cos sin y x x x '=-,sin y x x ''=-,sin cos y x x x '''=--; 令sin 0y x x ''=-=得120,x x π==,且()0f π'''≠,所以(,2)π-是曲线的拐点; 而对于点(0,0),由于(0)0f '''=,而(4)(0)0f≠,所以不是曲线的拐点.3.下列反常积分发散的是 ( )(A )x xe dx +∞-⎰(B )2x xe dx +∞-⎰(C )20arctan 1x dx x +∞+⎰(D )201xdx x+∞+⎰【答案】(D )【详解】(1)当x →+∞时,2()1x f x x =+是关于1x的一阶无穷小,当然201x dx x +∞+⎰发散; (2)用定义:20201ln(1)|12x dx x x +∞+∞=+=+∞+⎰,当然201x dx x+∞+⎰发散. 4.已知微分方程xy ay by ce '''++=的通解为12()xx y C C x ee -=++,则,,a b c 依次为( )(A )1,0,1 (B )1,0,2 (C )2,1,3 (D )2,1,4 【答案】(D )【详解】(1)由非齐次线性方程的通解可看出121r r ==-是特征方程20r ar b ++=的实根,从而确定2,1a b ==;(2)显然,*xy e =是非齐次方程的特解,代入原方程确定4c =.5.已知平面区域{(,)|}2D x y x y π=+≤,记1DI =,2DI =⎰⎰,3(1DI dxdy =-⎰⎰ ,则 ( )(A )321I I I << (B )213I I I << (C )123I I I << (D )231I I I << 【答案】(A )【详解】(1)显然在区域D 22202x y π⎛⎫≤+≤ ⎪⎝⎭,此时由结论当0x >时sin x x >知道≤12I I >;(2)当0x >时,令()1cos sin f x x x =--,则()sin cos f x x x '=-,()sin cos f x x x ''=+; 令()0f x '=得到在(0,)2π唯一驻点4x π=,且04f π⎛⎫''>⎪⎝⎭,也就是()1cos sin f x x x =--在4x π=取得极小值04f π⎛⎫<⎪⎝⎭,在0,2x x π==同时取得在[0,]2π上的最大值(0)()02f f π==,也就有了结论,当(0,)2x π∈时,1cos sin x x -<,也就得到了32I I <;由(1)、(2)可得到321I I I <<.6.设函数(),()f x g x 的二阶导函数在x a =处连续,则2()()lim0()x af xg x x a →-=-是两条曲线()y f x =,()y g x =在x a =对应的点处相切及曲率相等的 ( )(A )充分不必要条件 (B )充分必要条件 (C )必要不充分条件 (D )既不充分也不必要条件 【答案】(A ) 【详解】充分性:(1)当2()()lim0()x af xg x x a →-=-进,由洛必达法则,2()()1()()10limlim (()())()()()22x ax a f x g x f x g x f a g a f a g a x a x a →→''--''''===-⇒=-- 也就是两条曲线在x a =对应的点处相切; (2)2()()1()()10limlim (()())()()()22x ax a f x g x f x g x f a g a f a g a x a x a →→''--''''''''===-⇒=--由曲率公式k =x a =对应的点处曲率相等.必要性不正确的原因在于,虽然相切能得到()()f a g a ''=,但在相切前提下,曲率相等,只能得到()()f a g a ''''=,不能确定()()f a g a ''''=,当然得不到2()()lim0()x af xg x x a →-=-.7. 设A 是四阶矩阵,*A 为其伴随矩阵,若线性方程组0Ax =的基础解系中只有两个向量,则(*)r A =( )(A )0 (B )1 (C )2 (D )3【答案】(A )【详解】线性方程组0Ax =基础解系中只有两个向量,也就是4()2()213r A r A n -=⇒=<-=, 所以(*)0r A =.8.设A 是三阶实对称矩阵,E 是三阶单位矩阵,若22A A E +=,且4A =,则二次型T x Ax 的规范形是 ( )(A )222123y y y ++ (B )222123y y y +- (C )222123y y y -- (D )222123y y y ---【答案】(C )【详解】假设λ是矩阵A 的特征值,由条件22A A E +=可得220λλ+-=,也就是矩阵A 特征值只可能是1和2-.而1234A λλλ==,所以三个特征值只能是1231,2λλλ===-,根据惯性定理,二次型的规范型为222123y y y --.二、填空题(本题共6小题,每小题4分,满分24分. 把答案填在题中横线上) 9.()20lim 2xxx x →+= .【答案】24e解: ()()02(21)22lim2(1ln 2)20lim 2lim 1214x x x x x x xxx x x x ee e →+-+→→+=++-===10.曲线sin 1cos x t t y t =-⎧⎨=-⎩在32t π=对应点处的切线在y 的截距为 .【答案】322π+ 【详解】32sin ,|11cos t dy t dy dx t dx π===--,所以切线方程为331(1)222y x x ππ=---=-++,在y 的截距为322π+. 11.设函数()f u 可导,2y z yf x ⎛⎫= ⎪⎝⎭,则2z zx y x y ∂∂+=∂∂ . 【答案】22z zy x y yf x y x ⎛⎫∂∂+= ⎪∂∂⎝⎭【详解】3222222,z y y z y y y f f f x x x y x x x ⎛⎫⎛⎫⎛⎫∂∂''=-=+ ⎪ ⎪ ⎪∂∂⎝⎭⎝⎭⎝⎭,22z z y x y yf x y x ⎛⎫∂∂+= ⎪∂∂⎝⎭.12.曲线ln cos (0)6y x x π=≤≤的弧长为 .【答案】1ln 32【详解】sec ds xdx ===66001sec ln(sec tan )|ln 3.2s xdx x x ππ==+=⎰13.已知函数21sin ()xt f x x dt t=⎰,则10()f x dx =⎰ .【答案】1(cos11)4-. 【详解】(1)用定积分的分部积分:2111112000102112201021121220100210sin ()()|()()sin 1sin ()sin 21sin 11|sin sin 22211cos |(cos11)44xx x t f x dx xf x xf x dx x dt dx x x dxtt dt dx x x dxt t x dt x x dx x x dx t x '=-=--=--=--=-==-⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰(2)转换为二重积分:22211111120010000sin sin sin 11()sin (cos11)24x t x t t t f x dx x dt dx xdx dt dt xdx t t dt t t t ⎛⎫==-=-=-=- ⎪⎝⎭⎰⎰⎰⎰⎰⎰⎰⎰14.已知矩阵1100211132210034A -⎛⎫⎪-- ⎪= ⎪-- ⎪⎝⎭,ij A 表示元素ij a 的代数余子式,则1112A A -= . 【答案】4-【详解】111211121314110021110043221034A A A A A A ----=-++==---.三、解答题15.(本题满分10分)已知函数2,0()1,0xx xx f x xe x ⎧>⎪=⎨+≤⎪⎩,求()f x ',并求函数()f x 的极值.【详解】当0x >时,22ln ()xx x f x xe ==,2()2(ln 1)xf x x x '=+;当0x <时,()1xf x xe =+,()(1)xf x x e '=+;在0x =处,22000()(0)12(ln 1)(0)lim lim lim 1x x x x x f x f x x x f x x ++++→→→---'====-∞,所以()f x 在0x =处不可导.综合上述:22(ln 1),0()(1),0x xx x x f x x e x ⎧+>⎪'=⎨+<⎪⎩; 令()0f x '=得到1211,x x e=-=. 当1x <-时,()0f x '<,当10x -<<时,()0f x '>,当10x e <<时,()0f x '<,当1x e>时,()0f x '>; 故11x =-是函数的极小值点,极小值为1(1)1f e --=-;0x =是函数的极大值点,极大值为(0)1f =;21x e=是函数的极小值点,极小值为21()e f e e -=.16.(本题满分10分)求不定积分2236(1)(1)x dx x x x +-++⎰.【详解】22222223623213(1)2ln 1(1)(1)1(1)11132ln 1ln(1)1x x d x x dx dx x x x x x x x x x x x x x x C x ⎛⎫++++=-++=---+ ⎪-++--++-++⎝⎭=---++++-⎰⎰⎰17.(本题满分10分)设函数()y x是微分方程22x y xy e '-=满足条件(1)y =(1)求()y x 的表达式;(2)设平面区域{(,)|12,0()}D x y x y y x =≤≤≤≤,求D 绕x 轴旋转一周所形成的旋转体的体积. 【详解】(1)这是一个一阶线性非齐次微分方程.先求解对应的线性齐次方程0y xy '-=的通解:22x y Ce =,其中C 为任意常数; 再用常数变易法求22x y xy e'-=通解,设22()x y C x e=为其解,代入方程,得2222(),()x x C x e e C x ''==,1()C x C ==,也就是通解为:221)x y C e =+把初始条件(1)y =10C =,从而得到22().x y x xe =(2)旋转体的体积为2222411()()2x x V y x dx xe dx e e πππ===-⎰⎰.18.(本题满分10分)设平面区域2234{(,)|,()}D x y x y x y y =≤+≤,计算二重积分D.【详解】显然积分区域2234{(,)|,()}D x y x y x y y =≤+≤关于y 轴对称,由对称性,显然0D=;233sin 5440441sin sin 2120DDd r dr d ππθππθθθθ====⎰⎰⎰ 19.(本题满分10分)设n 是正整数,记n S 为曲线求曲线sin (0)xy ex x n π-=≤≤与x 轴所形成图形的面积,求n S ,并求lim .n n S →∞【详解】先求曲线与x 轴的交点:令sin 0x e x -=得,0,1,2,x k k n π==L 当2(21)k x k ππ<<+时,sin 0xy e x -=>;当2(22)k x k πππ+<<+时,sin 0x y e x -=<.由不定积分1sin (sin cos )2x xe xdx e x x C --=-++⎰可得 2221sin (1)2k xk k e xdx e e πππππ+---=+⎰,22221sin (1)2k x k k e xdx e e πππππππ+----+=-+⎰所求面积为0sin n x n S e xdx π-=⎰.当n 为奇数时,(21)22221022022002(1)2222(1)20sin sin sin 11(1)(1)2211111(1)(1)(1)22121nnn k k xxx n k k k k nnk k k k n n k n k S exdx e xdx e xdxe e e e e e e e e e e e πππππππππππππππππππππ+++---++==-----==-+-----+--===-=+++-+=+=+=---∑∑⎰⎰⎰∑∑∑同理:(2)22011sin (1)21n xn n e S exdx e eππππ----+==--⎰显然,有21211lim lim 21n n n n e S S e ππ+-→∞→∞+==-.所以11lim 21n n e S e ππ-→∞+=-.20.(本题满分11分)已知函数(,)u x y 满足关系式22222230u u ux y y ∂∂∂-+=∂∂∂.求,a b 的值,使得在变换(,)(,)ax by u x y v x y e +=之下,上述等式可化为函数(,)v x y 的不含一阶偏导数的等式.【详解】在变换(,)(,)ax byu x y v x y e+=之下(,)ax byax by u v e av x y e x x++∂∂=+∂∂,(,),ax by ax by u v e bv x y e y y ++∂∂=+∂∂ 222222(,)ax by ax byax by u v v e a e a v x y e x x x+++∂∂∂=++∂∂∂, 222222(,)ax by ax byax by u v v e b e b v x y e y y y +++∂∂∂=++∂∂∂; 把上述式子代入关系式22222230u u ux y y∂∂∂-+=∂∂∂,得到222222224(34)(223)(,)0v v v va b a b b v x y x y x y∂∂∂∂-++-+-+=∂∂∂∂ 根据要求,显然当30,4a b ==时,可化为函数(,)v x y 的不含一阶偏导数的等式. 21.(本题满分11分)已知函数()f x 在[]0,1上具有二阶导数,且(0)0,(1)1f f ==,1()1f x dx =⎰,证明:(1)至少存在一点(0,1)ξ∈,使得()0f ξ'=; (2)至少存在一点(0,1)η∈,使得()2f η''<-. 证明 (1)令0()()xx f t dt Φ=⎰,则1(0)0,(1)()1f x dx Φ=Φ==⎰,则由于()f x 在[]0,1连续,则()x Φ在[]0,1上可导,且()()x f x 'Φ=,则由拉格朗日中值定理,至少存在一点1(0,1)ξ∈,使得()(1)(0)ξ'Φ=Φ-Φ,也就是1101()()(1)f x dx f f ξ===⎰;对()f x 在()1,1ξ上用罗尔定理 ,则至少存在一点1(,1)(0,1)ξξ∈⊂,使得()0f ξ'=;(2)令2()()F x f x x =+,则显然,()F x 在[]0,1具有二阶导数,且211(0)0,(1)2,()1F F F ξξ===+.对()F x 分别在[][]110,,,1ξξ上用拉格朗日中值定理,至少存在一点11(0,)ηξ∈,使得211111()(0)1()0F F F ξξηξξ-+'==-; 至少存在一点21(,1)ηξ∈,使得1211()(1)()11F F F ξηξξ-'==+-;对()()2F x f x x ''=-在[]12,ηη上用拉格朗日中值定理,则至少存在一点12(,)(0,1)ηηη∈⊂,使得211212111()()()0F F F ηηξηηηηη-''-''==<--,也就是()2f η''<-.22.(本题满分11分)已知向量组Ⅰ:12321111,0,2443a ααα⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪=== ⎪ ⎪ ⎪ ⎪ ⎪ ⎪+⎝⎭⎝⎭⎝⎭;向量组Ⅱ:12321011,2,3313a a a βββ⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪=== ⎪ ⎪ ⎪ ⎪ ⎪ ⎪+-+⎝⎭⎝⎭⎝⎭.若向量组Ⅰ和向量组Ⅱ等价,求常数a 的值,并将3β用123,,ααα线性表示.【详解】向量组Ⅰ和向量组Ⅱ等价的充分必要条件是123123123123(,,)(,,)(,,;,,)r r r αααβββαααβββ==1231232222111101111101(,,;,,)102123011022443313001111a a a a a a a a αααβββ⎛⎫⎛⎫ ⎪ ⎪=→- ⎪ ⎪ ⎪ ⎪++-+----⎝⎭⎝⎭(1)当1a =时,显然, 123123123123(,,)(,,)(,,;,,)2r r r αααβββαααβββ===,两个向量组等价.此时,123311111023(,,;)0112011200000000αααβ⎛⎫⎛⎫ ⎪ ⎪→-→-- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭, 方程组112233x x x αααβ++=的通解为123231210x x x k x -⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪==+- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,也就是3123(23)(2)k k k βααα=-++-+,其中k 为任意常数;(2)当1a ≠时,继续进行初等行变换如下:12312322111101111101(,,;,,)011022011022001111001111a a a a a a αααβββ⎛⎫⎛⎫ ⎪ ⎪→-→- ⎪ ⎪ ⎪ ⎪----+-+⎝⎭⎝⎭显然,当1a ≠-且1a ≠时,123123123(,,)(,,;,,)3r r ααααααβββ==,同时()123101101101,,02202201111101001a a a βββ⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪→→→ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪-+-+⎝⎭⎝⎭⎝⎭,123(,,)3r βββ=,也就是 123123123123(,,)(,,)(,,;,,)2r r r αααβββαααβββ===,两个向量组等价.这时,3β可由123,,ααα线性表示,表示法唯一:3123βααα=-+.23.(本题满分11分)已知矩阵22122002A x -⎛⎫ ⎪=- ⎪ ⎪-⎝⎭与21001000B y ⎛⎫ ⎪=- ⎪ ⎪⎝⎭相似.(1)求,x y 之值;(2)求可逆矩阵P ,使得1P AP B -=.【详解】(1)由矩阵相似的必要条件可知:A B trA trB⎧=⎪⎨=⎪⎩,即2(24)241x y x y --+=-⎧⎨-+=+⎩,解得32x y =⎧⎨=-⎩.(2)解方程组221232(2)(2)(1)0002E A λλλλλλλ+--=--=+-+=+得矩阵A 的三个特征值1232,1,2λλλ==-=-;分别求解线性方程组()0(1,2,3)i E A x i λ-==得到分属三个特征值1232,1,2λλλ==-=-的线性无关的特征向量为:1231112,1,2004ξξξ-⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪=-=-= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭.令()1123111,,212004P ξξξ-⎛⎫ ⎪==-- ⎪ ⎪⎝⎭,则1P 可逆,且11212P AP -⎛⎫ ⎪=- ⎪ ⎪-⎝⎭;同样的方法,可求得属于矩阵B 的三个特征值1232,1,2λλλ==-=-的线性无关的特征向量为:1231100,3,00014ηηη-⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪=== ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭.令()2123110,,030001P ηηη-⎛⎫ ⎪== ⎪ ⎪⎝⎭,则2P 可逆,且12212P BP -⎛⎫ ⎪=- ⎪ ⎪-⎝⎭;由前面111122P AP P BP --=,可知令112111212004P PP --⎛⎫ ⎪==-- ⎪ ⎪⎝⎭,就满足1P AP B -=.。
