2016中考数学第24讲 与圆有关的计算
中考数学总复习 第六单元 圆 第24课时 与圆有关的计算课件

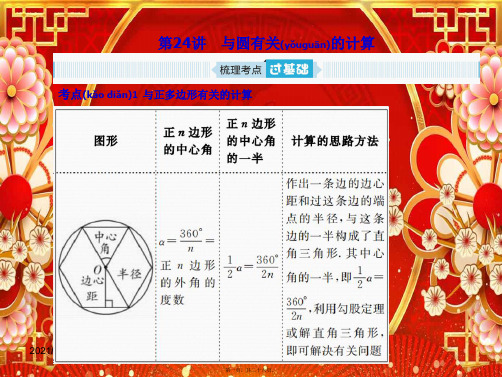
3.以正六边形为例:
图 24-1
(-2)·180°
180°
R·cos
180°
,边长 an=2R·
4.正多边形的一个内角 α=②
;正多边形的边心距(内切圆半径)rn=③
sin
(注:n
为正多边形的边数,R 为外接圆的半径).
12/9/2021
第二页,共二十四页。
课前双基巩固
考点二
弧长和扇形面积(miàn jī)的计算
(2)若∠F=30°,EB=4,求图中阴影部分的面积.(结果保留根号)
图24-10
解:(1)证明:如图,连接 OD.∵四边形 EBOC 是平行四边形,∴OC∥BE,∴∠AOC=∠OBE,∠COD=∠ODB.
∵OB=OD,∴∠OBD=∠ODB,∴∠DOC=∠AOC.
= ,
在△ COD 和△ COA 中, ∠ = ∠,
设☉O 的半径为 x,则 OB=OC=x,∴x+2=2x,解得 x=2.
过点 O 作 OE⊥AC,垂足为点 E,则 AE=CE,
图24-9
1
在 Rt△ OEA 中,OE= OA=1,AE= 2 - 2 = 22 -12 = 3,∴AC=2 3,
2
∴S 阴影=S 扇形 OAC-S△ OAC=
12/9/2021
D,连接 CD 并延长交 AB 的延长线于点 F.
(2)若∠F=30°,EB=4,求图中阴影部分的面积.(结果保留根号)
解: (2)∵∠F=30°,∠ODF=90°,∴∠DOF=∠AOC=∠COD=60°.
图24-10
∵OD=OB,∴△ OBD 是等边三角形,∴∠DBO=60°.∵∠DBO=∠F+∠FDB,∴∠FDB=∠EDC=30°.
中考数学总复习 第一部分 系统复习 成绩基石 第六章 圆 第24讲 与圆有关的计算课件
Image
12/8/2021
第二十六页,共二十六页。
2021/12/8
第二十五页,共二十六页。
内容 总结 (nèiróng)
第24讲 与圆有关的计算。考点2 弧长与扇形面积有关的计算。考点3 与圆锥有关的计算。考点4 阴影部分面 积的计算。1.规则图形:如扇形、圆、特殊四边形等,可直接(zhíjiē)利用公式计算.。命题趋势►近6年考查的热点 知识点是结合圆心角和圆周角之间的关系,直接(zhíjiē)利用弧长公式进行弧长的计算或扇形面积公式进行有关扇形
第24讲 与圆有关(yǒuguān)的计算
考点(kǎo diǎn)1 与正多边形有关的计算
2021/12/8
第一页,共二十六页。
考点2 弧长与扇形面积(miàn jī)有关的计算
2πr
2021/12/8
第二页,共二十六页。
考点3 与圆锥(yuánzhuī)有关的计算
2021/12/8
第三页,共二十六页。
类型5 圆的有关计算(jìsuàn)的探究问题
2021/12/8
第二十页,共二十六页。
2021/12/8
第二十一页,共二十六页。
解:(1)正方形,矩形
(jǔxíng).
2021/12/8
第二十二页,共二十六页。
2021/12/8
第二十三页,共二十六页。
2021/12/8
第二十四页,共二十六页。
第九页,共二十六页。
2021/12/8
第十页,共二十六页。
8
2021/12/8
第十一页,共二十六页。
类型(lèixíng)2 弧长的计算(常考) 15
中考数学复习第六章圆第24节和圆有关的计算正文课件

对课堂上老师讲到的内容自己想不通卡壳的问题,应该在课堂上标出来,下课时,在老师还未离开教室的时候,要主动请老师讲解清楚。如果老师已 经离开教室,也可以向同学请教,及时消除疑难问题。做到当堂知识,当堂解决。
二、补笔记
上课时,如果有些东西没有记下来,不要因为惦记着漏了的笔记而影响记下面的内容,可以在笔记本上留下一定的空间。下课后,再从头到尾阅读一 遍自己写的笔记,既可以起到复习的作用,又可以检查笔记中的遗漏和错误。遗漏之处要补全,错别字要纠正,过于潦草的字要写清楚。同时,将自己 对讲课内容的理解、自己的收获和感想,用自己的话写在笔记本的空白处。这样,可以使笔记变的更加完整、充实。
编后语
常常可见到这样的同学,他们在下课前几分钟就开始看表、收拾课本文具,下课铃一响,就迫不及待地“逃离”教室。实际上,每节课刚下课时的几分 钟是我们对上课内容查漏补缺的好时机。善于学习的同学往往懂得抓好课后的“黄金两分钟”。那么,课后的“黄金时间”可以用来做什么呢?
三、课后“静思2分钟”大有学问
我们还要注意课后的及时思考。利用课间休息时间,在心中快速把刚才上课时刚讲过的一些关键思路理一遍,把老师讲解的题目从题意到解答整个过 程详细审视一遍,这样,不仅可以加深知识的理解和记忆,还可以轻而易举地掌握一些关键的解题技巧。所以,2分钟的课后静思等于同一学科知识的课 后复习30分钟。
2019/5/27
精选最新中小学教学课件Βιβλιοθήκη thankyou!
2019/5/27
精选最新中小学教学课件
中考数学总复习 第六单元 圆 第24课时 与圆有关的计算数学课件

(2)∵∠D=30°,∠OCD=90°,∴∠BOC=60°,OD=2OC,∴∠AOC=120°,∠A=30°.
设☉O 的半径为 x,则 OB=OC=x,∴x+2=2x,解得 x=2.
过点 O 作 OE⊥AC,垂足为点 E,则 AE=CE,
图24-9
1
在 Rt△ OEA 中,OE= OA=1,AE= 2 - 2 = 22 -12 = 3,∴AC=2 3,
图 24-4
A.68π cm2
B.74π cm2
C.84π cm2
D.100π cm2
第七页,共二十四页。
高频考向探究
针对(zhēnduì)训练
1.(1)[2016·云南 6 题] 如果圆柱的侧面展开图是相邻两边长分别为 6,16π 的长方形,那么这个圆柱的体积等于
144 或 384π .
(2)圆心角为 60°,半径为 4 cm 的扇形的弧长为
180
= .
图24-5
3
第十页,共二十四页。
高频考向探究
2.[2018·合肥模拟] 如图 24-5,AB 是☉O 的直径,弦 CD⊥AB,垂足为 P,若 AB=2,AC= 3.
(3)求弓形 CBD 的面积.
3
3
1
(3)∵OC=OA=1,∠BOC=60°,∴CP=OC·sin60°=1× = ,OP=OC·cos60°= ,
[解析]连接 OA,OB.
AB=4,则图中阴影部分的面积是(
∵四边 ABCD 为正方形,∴∠AOB=90°.
)
设 OA=OB=r,则 r2+r2=42.解得:r=2 2,
S 阴影=S☉O-S 正方形 ABCD=π×(2 2)2-4×4
=8π-16.
浙江016年中考数学总复习全程考点训练24与圆有关的计算(含解析)

全程考点训练24 与圆有关的计算一、选择题1.一个圆锥的侧面展开图是半径为6的半圆,则这个圆锥的底面半径为(D ) A .1.5 B .2 C .2.5 D .3【解析】 设圆锥的底面半径是r ,则有2πr =180π×6180,解得r =3.故选D.2.已知正六边形的边心距为3,则它的周长是(B ) A .6 B .12 C .6 3 D .12 3【解析】 sin60°=边心距边长,∴边长=3sin60°=2,∴周长=2×6=12.3.一个圆锥的侧面展开图是半径为R 的半圆,则该圆锥的高是(D ) A .R B.12RC.3RD.32R 【解析】 圆锥的底面周长是πR .设圆锥的底面半径是r ,则2πr =πR ,解得r =12R .由勾股定理,得圆锥的高为R 2-⎝ ⎛⎭⎪⎫12R 2=32R .(第4题)4.如图,PA ,PB 是⊙O 的切线,切点是A ,B ,已知∠P =60°,OA =3,那么∠AOB 所对弧的长度为(D )A .6πB .5πC .3πD .2π【解析】 ∵PA ,PB 为⊙O 的切线, ∴∠PAO =∠PBO =90°,∴∠AOB =180°-∠P =120°,∴l =120π180×3=2π.(第5题)5.如图是某公园的一角,∠AOB =90°,AB ︵所在圆的半径OA 长6 m ,C 是OA 的中点,点D 在AB ︵上,CD ∥OB ,则图中休闲区(阴影部分)的面积是(C )A.⎝⎛⎭⎪⎫10π-923m 2B.⎝⎛⎭⎪⎫π-923m 2 C.⎝⎛⎭⎪⎫6π-923m 2 D .(6π-9 3)m 2【解析】 连结OD .∵AB ︵所在圆的半径OA 的长是6 m ,C 是OA 的中点,∴OC =12OA =12×6=3(m).∵∠AOB =90°,∴CD ⊥OA . 在Rt△OCD 中,∵OD =6,OC =3, ∴CD =OD 2-OC 2=62-32=3 3(m).∵sin∠DOC =CD OD =336=32,∴∠DOC =60°.∴S 阴影=S 扇形AOD -S △DOC =60×π×62360-12×3×3 3=⎝⎛⎭⎪⎫6π-923m 2. 6.如图①所示,一只封闭的圆柱形水桶内盛了半桶水(桶的厚度忽略不计),圆柱形水桶的底面直径与母线长相等,现将该水桶水平放置后如图②所示,设图①,图②中水所形成的几何体的表面积分别为S 1,S 2,则S 1与S 2的大小关系是(B )(第6题)A .S 1≤S 2B .S 1<S 2C .S 1>S 2D .S 1≥S 2 【解析】 设圆柱的底面半径为r .对于图①,水的表面积S 1=2πr 2+2πr ·r =4πr 2; 对于图②,上面的矩形的长是2r ,宽是2r ,则面积是4r 2, 曲面展开后矩形的长是πr ,宽是2r ,则面积是2πr 2, 上、下底面的面积之和是πr 2. 故图②中水的表面积S 2=(4+3π)r 2. 显然S 1<S 2. 二、填空题(第7题)7.如图,在小正方形构成的网格中,半径为1的⊙O 在格点上,则图中阴影部分两个小扇形的面积之和为14π(结果保留π).【解析】 S =14πr 2=14π.(第8题)8.如图,小亮坐在秋千上,秋千的绳长OA 为2 m ,秋千绕点O 旋转了60°,点A 旋转到点A ′处,则AA ′︵的长为23πm(结果保留π).【解析】 lAA ′︵=60π×2180=23π(m).(第9题)9.两块大小一样、斜边为4且含有30°的三角尺按如图所示的方式水平放置.将△CDE 绕点C 按逆时针方向旋转,当点E 恰好落在AB 上时,△CDE 旋转了30度,线段CE 旋转过程中扫过的面积为π3.【解析】 ∵两块三角尺大小一样,斜边为4且含有30°角, ∴CE ′是△ABC 的中线,∴CE ′=BC =BE ′=2, ∴△E ′CB 是等边三角形,∴∠BCE ′=60°, ∴∠ACE ′=90°-60°=30°,∴线段CE 旋转过程中扫过的面积=30π×22360=π3.(第10题)10.如图,在矩形ABCD 中,AB =3,AD =1,将该矩形绕点A 顺时针旋转α得到矩形AB ′C ′D ′,点C ′落在AB 2-π4. 【解析】 在矩形ABCD 中,∵AB =3,BC =AD =1, ∴tan ∠CAB =BCAB=13=33, ∴∠CAB =30°,∴∠BAB ′=30°, ∴S △AB ′C ′=S △ABC =12×1×3=32,S 扇形ABB ′=30π×(3)2360=π4,S 阴影=S △AB ′C ′-S 扇形ABB ′=32-π4. 三、解答题(第11题)11.如图,点D 在⊙O 的直径AB 的延长线上,点C 在⊙O 上,AC =CD ,∠ACD =120°. (1)求证:CD 是⊙O 的切线.(2)若⊙O 的半径为2,求图中阴影部分的面积.(第11题解)【解析】 (1)连结OC ,如解图.∵AC =CD ,∠ACD =120°,∴∠A =∠D =30°. ∵OA =OC , ∴∠2=∠A =30°.∴∠OCD =∠ACD -∠2=90°.∴CD 是⊙O 的切线. (2)∵∠2=∠A =30°,∴∠1=2∠A =60°. ∴S 扇形OBC =60π×22360=2π3.在Rt △OCD 中,∵CD OC=tan ∠1=tan60°,∴CD =2 3. ∴S Rt △OCD =12OC ·CD =12×2×23=2 3.∴图中阴影部分的面积为23-2π3.(第12题)12.如图,圆柱底面半径为2 cm ,高为9π cm ,A ,B 分别是圆柱两底面圆周上的点,且A ,B 在同一母线上.用一根棉线从点A 顺着圆柱侧面绕3圈到点B ,求棉线的最短长度.【解析】 沿AB 剪开,每圈最短为(4π)2+(3π)2=5π(cm),3圈共15π cm.(第13题)13.如图所示为圆柱形大型储油罐固定在U 形槽上的横截面图.已知图中ABCD 为等腰梯形(AB ∥DC ),支点A 与B 相距8 m ,罐底最低点到地面CD 的距离为1 m .设油罐横截面圆心为O ,半径为5 m ,∠D =56°,求U 形槽的横截面(阴影部分)的面积(参考数据:sin 53°≈0.8,tan 56°≈1.5,π≈3,结果保留整数).(第13题解)【解析】 如解图,连结AO ,BO ,过点A 作AE ⊥DC 于点E ,过点O 作ON ⊥DC 于点N ,ON 交⊙O 于点M ,交AB 于点F ,则OF ⊥AB .∵OA =OB =5 m ,AB =8 m ,∴AF =BF =12AB =4 m ,∠AOB =2∠AOF .在Rt△AOF 中,sin∠AOF =AFAO=0.8≈sin 53°,∴∠AOF ≈53°,则∠AOB ≈106°. ∵OF =OA 2-AF 2=3 m ,由题意,得MN =1 m , ∴FN =OM -OF +MN =3 m.∵四边形ABCD 是等腰梯形,AE ⊥DC ,FN ⊥AB , ∴AE =FN =3 m ,DC =AB +2DE . 在Rt△ADE 中,tan 56°=AEDE≈1.5, ∴DE ≈2 m ,DC ≈12 m.∴S 阴影=S 梯形ABCD -(S 扇形OAB -S △OAB )≈12(8+12)×3-⎝ ⎛⎭⎪⎫106360π×52-12×8×3≈20(m 2).(第14题)14.某工艺品由一个底面朝上的圆锥体上方嵌入一颗圆球组成,其横截面如图所示,已知圆锥的母线AB ,AC 和球体相切,且与底座的夹角均为75°,圆锥体底面的周长为20π cm ,求球体的半径(参考数据:sin 15°≈0.26,cos 15°≈0.97,tan 15°≈0.27,结果精确到0.1 cm).【解析】 连结OB ,连结OA 交BC 于点D . ∵圆锥的母线AB ,AC 和球体相切, ∴OB ⊥AB 于点B .∵AB ,AC 与底座夹角均为75°, ∴∠BAO =90°-75°=15°.∵∠BAO +∠ABD =∠ABD +∠OBD =90°, ∴∠OBD =∠BAO =15°.∵圆锥体底面的周长为20π cm , ∴BD =20π÷2π=10,∴OB =BD ÷cos 15°≈10÷0.97≈10.3(cm). 故球体的半径约为10.3 cm.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2016中考数学-----与圆有关的计算
一、选择题(每小题6分,共30分)
1.(2015·义乌)如图,四边形ABCD是⊙O的内接四边形,⊙O的半径为2,∠B=135°,则AC︵的长( )
A.2π B.π C.π2 D.π3
,第1题图) ,第2题图)
2.(2015·自贡)如图,AB是⊙O的直径,弦CD⊥AB,∠CDB=30°,CD=23,则阴影部分图形的面
积为( )
A.4π B.2π C.π D.2π3
3.(2014·金华)一张圆心角为45°的扇形纸板和一张圆形纸板按如图方式分别
剪成一个正方形,边长都为1,则扇形和圆形纸板的面积比是( )
A.5∶4 B.5∶2 C.5∶2 D.5∶2
4.(2015·成都)如图,正六边形ABCDEF内接于⊙O,半径为4,则这个正六边形的边心距OM和BC︵的长
分别为( )
A.2,π3 B.23,π C.3,2π3 D.23,4π3
,第4题图) ,第5题图)
5.(2015·山西百校联考四)如图,一块矩形花池ABCD,AB=23 m,AD=4 m,分别以A,B,C,D
为圆心,2 m长为半径作四条弧交于点E,G,F,H准备在四条弧围成的阴影区种植紫罗兰花,其余区域种植
菊花,则种紫罗兰的区域面积为( )m2.
A.63-43π B.83-43π C.63-83π D.83-83π
二、填空题(每小题6分,共30分)
6.(2015·安徽)如图,点A,B,C在半径为9的⊙O上,AB︵的长为2π,则∠ACB的大小是__ __.
,第6题图) ,第7题图)
7.(2015·酒泉)如图,半圆O的直径AE=4,点B,C,D均在半圆上,若AB=BC,CD=DE,连接OB,
OD,则图中阴影部分的面积为__ __.
8.(2015·宁夏)如图,将正六边形ABCDEF放在直角坐标系中,中心与坐标原点重合,若A点的坐标为(-
1,0),则点C的坐标为__ __.
,第8题图) ,第9题图)
9.(2015·黑龙江)如图,从直径是2米的圆形铁皮上剪出一个圆心角是90°的扇形ABC(A,B,C三点在
⊙O上),将剪下来的扇形围成一个圆锥的侧面,则该圆锥的底面圆的半径是__ __米.
10.(2015·乐山)如图,已知A(2 ,2),B(2 ,1),将△AOB绕着点O逆时针旋转,
使点A旋转到点A′(-2,2 )的位置,则图中阴影部分的面积为__ __.
三、解答题(共40分)
11.(10分)(2013·新疆)如图,已知⊙O的半径为4,CD是⊙O的直径,AC为⊙O的弦,B为CD延长线
上的一点,∠ABC=30°,且AB=AC.
(1)求证:AB为⊙O的切线;
(2)求弦AC的长;
(3)求图中阴影部分的面积.
12.(10分)(2015·山西中考适应性训练)如图,已知⊙O是△ABC的外接圆,AC是直径,∠A=30°,BC
=2,点D是AB的中点,连接DO并延长交⊙O于点P,过点P作PF⊥AC于点F.
(1)求劣弧PC的长;(结果保留π)
(2)求阴影部分的面积.(结果保留π)
13.(10分)(2015·沈阳)如图,四边形ABCD是⊙O的内接四边形,∠ABC=2∠D,连接OA,OB,OC,
AC,OB与AC相交于点E.
(1)求∠OCA的度数;
(2)若∠COB=3∠AOB,OC=23,求图中阴影部分面积.(结果保留π和根号)
