17-19课时教师版
六年级秋季班-第17讲:圆的组合图形的相关练习-教师版

第十三讲 圆的组合图形练习1、三角形的面积 =2⨯底高. 2、等腰直角三角形的面积 =24=直角边的平方斜边的平方. 3、长方形的面积 =⨯长宽. 4、正方形的面积 = 边长的平方 = 2对角线的平方.5、菱形的面积 =2对角线之积.6、梯形的面积 =()2⨯上底+下底高.7、圆的面积 =π⨯半径的平方. 8、扇形的面积 =360π⨯⨯︒圆心角半径的平方.【例1】 如图,以半圆的半径8厘米为直径在半圆内作一个圆,求图中阴影部分的面积.(π取3.14)【难度】★【答案】50.24平方厘米.【解析】2222118432161650.2422S R r πππππππ=-=⨯⨯-⨯=-==平方厘米.【总结】阴影部分的面积等于大半圆的面积减去中间圆的面积.【例2】 如图,正方形的边长是6厘米,则阴影部分的周长是______厘米,面积是______平方厘米.(π取3.14)【难度】★知识精讲习题精炼【答案】61.68;7.74.【解析】3644224422C r ππ=⨯+⨯⨯⨯=+⨯⨯⨯241261.68π=+=厘米; 223664364()3697.742S r πππ=⨯-⨯=-⨯⨯=-=平方厘米.【总结】阴影部分的周长等于正方形的周长加上四个等圆的周长,阴影部分的面积等于正方 形的面积减掉四个等圆的面积.【例3】 如图,正方形的边长为6分米,求阴影部分的面积.(π取3.14) 【难度】★【答案】7.74平方分米.【解析】24566623697.74360S ππ⨯⨯=⨯-⨯=-=平方分米.【总结】阴影部分的面积等于正方形的面积减掉两个扇形的面积.【例4】 如图,求阴影部分的面积.(π取3.14) 【难度】★ 【答案】6.【解析】326S =⨯=阴影.【总结】通过割补法将阴影部分的扇形移到空白部分的扇处,从而阴影部分的面积就是长方 形的面积.【例5】 如图,长方形的宽是8厘米,求阴影部分的面积.(π取3.14) 【难度】★★【答案】50.24平方厘米.【解析】21908168168882360S π⎛⎫⨯⨯=⨯-⨯⨯-⨯- ⎪⎝⎭()6464161650.24ππ=--==平方厘米.【总结】此题中阴影部分的面积等于长方形的面积减去三角形的面积再减去弯角处的空白部 分的面积.【例6】 图中,三个同心圆的半径分别为2、6、10,则图中阴影部分占大圆面积的______%. 【难度】★★22AB【答案】3333%100S S ==阴影总. 【解析】222111106225833444S ππππππ⎛⎫=⨯+⨯-⨯=+= ⎪⎝⎭阴影,210100S ππ=⨯=总,33100S S =阴影总. 【总结】考查阴影部分图形的面积所占的百分比,注意通过割补,将阴影部分的面积移到一 起.【例7】 如图,圆O 的直径为8厘米,则阴影部分的面积是多少平方厘米?(π取3.14) 【难度】★★ 【答案】18.24.和一个半圆的面积的和.故222111482(484)422S πππ=⨯+⨯⨯-⨯⨯⨯+⨯⨯16162(168)163218.24ππππ=+-⨯+=-=平方厘米.【总结】考查阴影部分图形的面积的求法,注意用规则图形的面积去表示阴影部分的面积.【例8】 如图,正方形的边长为2厘米,以圆弧为分界线的A 、B 两部分的面积的差是______平方厘米.(π取3.14)【难度】★★ 【答案】2.28.【解析】由题可得:112222124A B S S +=⨯⨯-⨯⨯=平方厘米;而214522 3.1422 1.570.432360A S =⨯⨯-⨯⨯=-=平方厘米;所以10.430.57B S =-=平方厘米,故0.570.430.14B A S S -=-=平方厘米. 【总结】本题中一方面要区分A 与B 两部分的面积,另一方面要认真观察,进行分析.【例9】 如图,其中四个圆的直径均为4厘米,那么阴影部分的面积为______平方厘米.(π取3.14)G 【难度】★★ 【答案】16.【解析】222(442)16S ππ=⨯+⨯-⨯=平方厘米.【总结】本题中阴影部分的面积等于一个正方形的面积减掉一个圆的面积,解题时要认真分 析.【例10】 如图,扇形AFB 恰为一个圆的14,BCDE 是正方形,边长为3,AFBG 也是正方形,边长为4,求图中阴影部分的面积.(π取3.14)【难度】★★【答案】10.56.【解析】2114744424S π=⨯⨯-⨯-⨯()141644210.56ππ=--=-=()【总结】阴影部分面积等于三角形面积减去左下角空白部分的面积.【例11】 如图,ABC ∆是等腰直角三角形,D 是半圆周的中点,BC 是半圆的直径.已知:AB = BC = 10,求阴影部分的面积.(π取3.14)【难度】★★ 【答案】32.125.【解析】连接BD .因为1105252ABD S ∆=⨯⨯=,21125555424BD S ππ=⨯⨯-⨯⨯=弓所以25252532.12542S π=+-=阴影. 【总结】本题中连接BD 是关键点,这样就可以将阴影部分进行分割,从而进行求解.【例12】 如图,ABC ∆是等腰直角三角形,腰AB 长为4厘米,求阴影部分的面积.(π取3.14) 【难度】★★ 【答案】4平方厘米.【解析】连接BD ,则上面阴影的弓形的面积等于空白弓形的面积,则阴影部分的面积就是直角三角形ABD 的面积,故14242S =⨯⨯=阴影.【总结】本题主要考查通过割补法求阴影部分面积.AABABC DO【例13】 如图,一个大正方形各边都被四等分,分成十六个小正方形,图A 是一个圆,图B 是由三个半圆围成的图形,那么图A 与图B 的周长的大小关系是______,图A 与图B 的面积的大小关系是______.【难度】★★【答案】2B A C C =;A B S S =.【解析】设正方形边长为4,则2A C π=,A S π=,224B C πππ=+=,2122B S πππ=⨯⨯-=, 故2B AC C =;A B S S =.【总结】本题中图A 就是一个圆,图B 是由三个半圆构成的,因此主要考查圆的周长和面 积的运用.【例14】 如图,有半径为5厘米、4厘米、3厘米的三个圆,A 分)的面积与阴影部分的面积相比,哪个大?大多少?【难度】★★ 【答案】相等.【解析】大圆的面积为:2525ππ⨯=;两个内圆的面积分别是:239ππ⨯=;2416ππ⨯=;A 部分的面积为:916ππ+-白色区域面积=25π-白色区域面积; 阴影部分面积为:25π-白色区域面积;所以,两部分面积相等.【总结】半径为5的大圆的面积,减掉半径为3和半径为4的两个小圆的面积的和,再加上 一个A 部分的面积,即为阴影部分面积.【例15】 如图,梯形ABCD 的面积是25平方厘米,求圆环的面积.(π取3.14) 【难度】★★【答案】157平方厘米.【解析】圆环的面积等于大圆面积减小圆面积,即22()OB OC π-;同时,已知梯形的面积又等于两个三角形的面积的差,即:2222111()25222OBA OCD S S S OB OC OB OC ∆∆=-=-=-=梯形,所以圆环的面积为:50157π=平方厘米.【总结】本题综合型较强,亮点在于把圆环面积与三角形面积和梯形的面积结合起来.【例16】 如图是由正方形和半圆形组成的图形,其中P 点为半圆周的中点,Q 点为正方形一边的中点,那么阴影部分的面积是多少平方厘米?(π取3.14)【难度】★★【答案】51.75平方厘米. 【解析】连接PB .ABP BPQ ABCD S S S S S =+--△△阴影正方形半圆21111010 3.145101555222=⨯+⨯⨯-⨯⨯-⨯⨯51.75=平方厘米.【总结】本题主要考查如何将不规则的图形转化成规则图形的组合,从而求出面积.【例17】 如图,直角梯形的面积是54平方厘米,求阴影部分的面积.(π取3.14) 【难度】★★★【答案】11.61平方厘米.【解析】由题意,得圆的半径6r =厘米,所以21355 3.14611.61360S S S =-=-⨯⨯=阴影梯形扇形平方厘米.【总结】本题主要要理解梯形的下底是2个半径长,从而求出阴影部分的面积.【例18】 如图,直径AB 为3厘米的半圆以点A 为圆心逆时针旋转60°,使AB 到达AC的位置,求图中阴影部分的面积.(π取3.14)【难度】★★★【答案】4.71平方厘米.【解析】2603.1434.71360ABC S S ==⨯⨯=阴影扇形平方厘米.【总结】本题主要考查利用割补法将阴影部分转化成一个扇形,从而求出面积.B10【例19】 如图,90AOB ∠=︒,C 为AB 的中点,已知阴影甲的面积为16平方厘米,求阴影乙的面积.(π取3.14)【难度】★★★【答案】16平方厘米.【解析】由图可知:S S S +=甲空半圆,S S S +=乙空扇形,故16S S ==乙甲平方厘米.【总结】本题中要认真观察两个阴影部分之间的关系,进行和差运算之后求出面积.【作业1】 如图,正方形的边长为4厘米,阴影部分的面积是______平方厘米. 【难度】★【答案】5.72平方厘米.【解析】221122(222)4242442S πππππ=⨯-⨯⨯⨯-⨯⨯=-+=+空,故44(24)122 5.72S S S ππ=-=⨯-+=-=正阴影空白平方厘米. 【总结】考查阴影部分的面积的求法.【作业2】 如图,阴影部分的面积是100平方厘米,求圆环的面积. 【难度】★★【答案】100π平方厘米.【解析】设大圆半径为R ,小圆半径为r ,则2222()S S S R r R r πππ=-=-=-圆环小圆大圆,课后作业甲乙COS 空EA BCDFG H又22100S S S R r =-=-=阴影小正方形大正方形, 所以100S π=圆环平方厘米.【总结】本题中要注意正方形的边长就是相应的圆的半径.【作业3】 边长为1的正方形中,分别以边长为直径作3个半圆.求围成的阴影部分的面积. 【难度】★★【答案】12.【解析】方法一:一个半圆面积加上一个正方形面积一半减去两个四分之一 扇形的面积的和,即22111111111()1()()222228282S ππππ⎡⎤=⨯⨯+⨯-⨯⨯=+-=⎢⎥⎣⎦阴影;方法二:下面的半圆拆为两个四分一直扇形拼在上面空白部分,正好与上方阴影部分组 成一个长方形,这个长方形的面积就等于正方形面积的一半. 【总结】本题主要考查利用割补法求阴影部分的面积.【作业4】 如图,长方形的长为5厘米,宽为4厘米,则阴影部分的周长为______厘米,面积是______平方厘米.【难度】★★【答案】16.13;12.185.【解析】9059049(54)(54)216.131801802C πππ⨯⨯⨯⨯=++-+-=+=阴影厘米,2290590441(54)2012.1853603604S πππ⨯⨯⨯⨯=-⨯-=-=扇形平方厘米.【总结】阴影部分的周长是两段弧的长加上两条线段的长,阴影部分的面积等于大扇形的面 积减去长方形的面积再加上小扇形的面积.【作业5】 已知等腰直角三角形ABC ,D 为斜边中点,AC = BC = 2分米,弧DF 、弧DH 分别是以B 、C 为圆心画的弧,求阴影部分的面积.【难度】★★ 【答案】1平方分米.【解析】通过割补法可知,阴影部分的面积的等于正方形的面积,故21(2)12CEDG S S ==⨯=阴影正方形平方分米.E【总结】考查利用割补法求阴影部分的面积.【作业6】 如图,圆的半径都是3厘米,则阴影部分的面积为______平方厘米. 【难度】★★ 【答案】3.87.【解析】三个扇形的圆心角的度数的和为180度,故而将三个扇形面积拼在一起,也就等于去求一个半径为3厘米的圆的面积.三角形面积:166182⨯⨯=,三个扇形的面积:2180393602ππ⨯⨯=,故阴影部分面积为:918 3.872π-=平方厘米.【总结】等腰直角三角形面积减去三个扇形面积既得阴影的部分面积.【作业7】 如图,小正方形的边长4厘米,大正方形边长6厘米,DBE ∆的面积为3.2平方厘米,求阴影部分的面积.【难度】★★★ 【答案】1.38平方厘米.【解析】由图可知: 3.224 1.6BD =⨯÷=厘米,所以 3.6AB =厘米, 所以23.66303.1462360ABC S S S ⨯=-=-⨯⨯△阴影扇形10.89.42 1.38=-=平方厘米.【总结】阴影部分的面积等于三角形ABC 的面积减去小扇形的面积.0.6775=平方米.。
部编版语文五年级上册课时安排
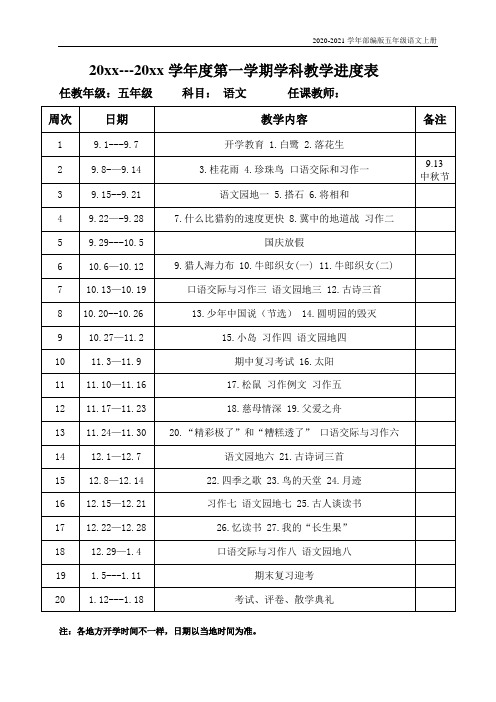
20xx---20xx学年度第一学期学科教学进度表任教年级:五年级科目:语文任课教师:注:各地方开学时间不一样,日期以当地时间为准。
xx小学五年级语文学科集体备课周计划安排表20xx——20xx学年度第一学期2019 — 2020学年度第一学期五年级语文上册教学计划二、学情分析课题:开学第一课教学内容:开学第一课教学目标:1.了解校园安全隐患。
2.掌握安全知识,培养学生“珍爱生命,安全第一”的意识。
3.进行预防灾害,预防突发事情的教育。
教学重点:掌握安全知识,培养学生“珍爱生命,安全第一”的意识。
教学过程:一、校园中存在的安全隐患。
(请学生列举一些现象)1.学生集会、集体活动、课间活动的安全隐患。
2.学生饮食、就餐的安全隐患。
3.学生交通安全隐患。
4.校园隐性伤害的隐患。
二、学生集会、集体活动、课间活动中应该注意的安全事项。
1.上下楼梯要注意什么?①不要因为赶时间而奔跑。
②在人多的地方一定要扶好栏杆。
③整队下楼时要与同学保持一定距离。
④上下楼时不要将手放在兜里。
⑤不要在楼道内弯腰拾东西、系鞋带。
⑥上下楼靠右行。
2.集体活动中要一切行动听指挥,遵守时间,遵守纪律,遵守秩序,语言文明。
3.课间活动应当注意什么?①室外空气新鲜,课间活动应当尽量在室外,但不要远离教室,以免耽误下面的课程。
②活动的强度要适当,不要做剧烈的活动,以保证继续上课时不疲劳、精力集中、精神饱满。
③活动的方式要简便易行,如做做操等。
④活动要注意安全,切忌猛追猛打,要避免发生扭伤、碰伤等危险。
三、学生饮食、就餐的安全注意事项。
不吃过期、腐烂食品,有毒的药物(如杀虫剂、鼠药等)要放在安全的地方。
禁止购买用竹签串起的食物:油反复使用,竹签容易伤人,食品卫生得不到保证,油炸食品有致癌物质。
四、交通安全注意事项。
1.行人靠右走,过马路要走斑马线,注意观察来往车辆,红灯停,绿灯行,遵守交通规则。
2.乘坐公交车注意事项:①车停稳后,方能上下车,上下车时注意秩序,不要拥挤。
最新《九年义务教育英语课程标准(2017版)》试题(附答案)

最新《九年义务教育英语课程标准(2017版)》试题一(答案附后)(满分:100分考试时间90分钟)姓名:得分:一、填空题。
(每空1分,共20分)1.作为全球使用最广泛的语言之一.已经成为国际交往和科技、文化交流的重要工具。
2.义务教育阶段的英语课程具有工具性和的双重性质。
3.就工具性而言,英语课程承担着培养学生素养和发展学生思维能力的任务。
4.就人文性而言,英语课程承担着提高学生素养的任务。
5.学生通过英语课程能够开阔视野,丰富生活经历,形成跨文化意识,增强爱国主义精神,发展创新能力,形成良好的品格和正确世界观、人生观和。
6.工具性和人文性统一的英语课程有利于为学生的发展奠定基础。
7.义务教育阶段英语课程的主要目的是为学生发展能力打基础,为他们继续学习英语和未来发展创造有利条件。
8.义务教育阶段的英语课程应面向全体学生,体现以为主体的思想,在教学目标、教学内容、教过学程、教学评价和教学资源的利用与开发等方面都应考虑全体学生的发展需求。
9.英语学习具有明显的渐进性和特点。
10.基础教育阶段英语课程的目标设为九个级别,体现了英语课程的、渐进性和持续性的特点。
11.现代外语教育注重语言学习的过程,强调语言学习的实践性,主张学生在中接触、体验和理解真实语言,并在此基础上学习和运用语言。
12.英语课程教学倡导体验、实践、参与、探究和合作等方式,让学生逐步掌握语言知识和技能,不断调整情感态度,形成有效的,发展自主学习能力。
13.英语课程评价体系要有利于促进学生综合语言运用能力的发展,采用的评价方式,促进学生的自主学习能力、思维能力、跨文化意识和健康人格的发展。
14.英语课程评价体系应包括形成性评价和终结性评价,日常教学中的评价以为主。
15.着重考查学生的综合语言运用能力,包括语言技能、语言知识、情感态度、学习策略和文化意识等方面。
16.目前我国义务教育阶段的英语课程以小学三年级为起点,以毕业为终点,并与高中阶段的英语课程相衔接。
人教版六年级下册数学教案 1 圆 柱(4课时)

1圆柱第1课时圆柱的认识课时目标导航教学内容圆柱的认识。
(教材第17~19页例1、例2)教学目标1.使学生了解圆柱的特征,认识圆柱的底面及其直径和半径,圆柱的高、侧面及圆柱的展开图。
2.通过观察,认识圆柱并掌握它的特征,建立空间观念。
3.培养学生的观察能力,提高从实物抽象到几何图形的能力。
重点难点重点:理解并掌握圆柱的特征。
难点:明确圆柱沿高展开的侧面展开图是一个长方形(正方形),理解长方形(侧面展开图)的长和宽与圆柱的底面周长和高的关系。
教具准备课件PPT、圆柱模型、硬纸板、剪刀、三角板、牙签盒、罐头盒、木棒。
教学过程一、情景引入同学们,我们做一个“摸一摸”的游戏。
瞧,老师手里有一个魔袋,里面装了几种物体,只要能闭着眼摸出老师想要的物体,就算你过关。
谁愿意来?其他同学作裁判。
请摸出一个长长的、有6个面、8个顶点、12条棱、每个面都是长方形的物体。
长方体是我们已经研究过的立体图形,请再摸出一个直直的、上下一样粗细、能够滚动的物体。
它在数学上叫什么名字?(圆柱)像这样直直的、上下一样粗细、能够滚动的物体,就是我们今天要认识的新朋友——圆柱。
二、学习新课1.初步感知圆柱。
(1)大家找一找我们生活的周围有哪些圆柱形的物体,谁能说一说?举例:茶叶筒、水桶、通风管、木桩、铅笔是圆柱形的……(2)课件展示常见的圆柱形物体。
(3)这些物体有哪些共同的特点?大家也可以拿出自己手中的圆柱形物体看一看,摸一摸。
(4)拿出几个不是圆柱,接近圆柱形的物体,然后问:它们是圆柱吗?为什么?那么什么样的物体才是真正的圆柱?学生回答后,教师强调:圆柱一定是直直的、上下一样粗细。
2.教学例1。
(1)认识圆柱的面。
分组活动,每人拿一个圆柱,摸一摸它的面。
启发学生自主探究圆柱的特征。
①提问:圆柱一共有几个面?用手摸上、下底,看一看有什么特点?再摸一摸侧面,有什么感觉,它是一个什么面?明确:3个面;形状相同,都是圆形,面积相等;曲面。
专题19 三角形内接矩形相似模型(教师版)-中考数学几何模型重点突破讲练

∵四边形 EFGH 是矩形,
∴EH∥BC,
∴△AEH∽△ABC,
∵AM⊥EH,AD⊥BC, ∴ AM EH ,
AD BC 设 EH=3x,则有 EF=2x,AM=AD-EF=2-2x, ∴ 2 2x 3x ,
23 解得: x 1 ,
2 则 EH 3 .
2 故选:C.
2.如图,在 Rt△ABC 中,∠C=90°,放置边长分别为 3,4,x 的三个正方形,则 x 的值为( )
∴S=4t2﹣ 1 ×(6t﹣8)2=﹣14t2+48t﹣32, 2
综上所述,S 与 t 之间的函数关系式为
S=4t2 (0 t 4) 3
.
S=﹣14t
2
48t﹣32
( 4 t 2) 3
(4)如图,当点 E 在△ABC 内部,设 DF 与 PE 交于点 O,
∵四边形 PDEF 是正方形, ∴DF=PE=2PO=2EO,∠DFP=45°, ∴∠DFP=∠ABC=45°, ∴DF∥BC, ∴ PO PF ,
∵AD 是△ABC 的高,四边形 PQRS 是正方形,
∴ SR ∥ BC ,AE 是△ASR 的高, 则 AE=AD-ED=2-x,
∴△ASR∽△ABC,
SR AE , BC AD
x 2 x , 解得: x 6 ,
32
5
6 ∴正方形 PQRS 的边长为 .
5
故选:A.
【例 2】如图,已知三角形铁皮 ABC 的边 BC a cm , BC 边上的高 AM h cm ,要剪出一个正方形铁片
专题 19 三角形内接矩形相似模型
【模型】如图,四边形 DEFG 是△ABC 的内接矩形,EF 在 BC 边上,D、G 分别在 AB、AC 边上,则△ADG
北师大版小学数学二年级上全册教案(共64课时)

课题:加与减第 1、2 课时(总第 1 、2 课时)课题:加与减第 3 课时(总第 3课时)课题:加与减第 4 、5 课时(总第 4-5课时)课题:加与减第 6、7 课时(总第 6-7课时)课题:加与减第 8、9 课时(总第 8-9课时)课题:购物第 1 课时(总第 10课时)课题:购物第 2课时(总第11课时)课题:购物第 3 课时(总第 12课时)课题:数一数与乘法第1课时(总第13课时)课题:数一数与乘法第2课时(总第14课时)课题:数一数与乘法第3课时(总第15课时)课题:数一数与乘法第4课时(总第16课时)课题:数一数与乘法第5课时(总第17课时)课题:数一数与乘法第6、7课时(总第18-19课时)5、看图列算式。
★★★★★★★★★★★★算式是()×()读作()乘()◆◆◆◆◆◆◆◆◆◆算式是()×()读作()乘()7、6×3读作( )乘(),表示()个( )连加6×7读作( ),表示( ) 9×4读作(),表示()第四单元图形的变化课题:图形的变化第1课时(总第20课时)你发现了什么?和大家一起交流一下。
课题:图形的变化第2课时(总第21课时)2、想一想,怎样才能让曹操从华容道逃走?在小组里讨论,试一试。
3、 小组内讨论研究,班级交流。
课题:2~5的乘法口诀第1课时(总第22课时)课题:2~5的乘法口诀第4课时(总第25课时)课题:2~5的乘法口诀第5课时(总第26课时)课题:2~5的乘法口诀第6课时(总第27课时)课题:2~5的乘法口诀第7.8课时(总第28-29课时)课题:2~5的乘法口诀第9、10课时(总第30-31课时)课题:测量第1课时(总第32课时)课题:测量第2课时(总第33课时)课题:测量第3课时(总第34课时)课题:测量第4、5课时(总第35-36课时)课题:分一分与除法第1课时(总第37课时)课题:分一分与除法第2课时(总第38课时)课题:分一分与除法第3课时(总第39课时)课题:分一分与除法第4课时(总第40课时)课题:分一分与除法第5、6课时(总第41-42课时)。
高思导引 四年级第十七讲 数列与数表教师版
第17讲 数列与数表 内容概述 通过观察数列或数表中的已知数据,发现规律并进行填补与计算的问题,注意数表形式的多样性,计算时常常考虑周期性,或进行合理估算. 典型问题 兴趣篇 1.1,1,4,2,7,3,10,1,13,2,16,3,19,1,22,2,25,3,…,100.请观察上面数列的规律,问:(1)这个数列一共有多少项? (2)这个数列所有数的总和是多少? 答案:67;1783 解析:间隔是是等差数列。 2.观察数组(1,2,3),(3,4,5),(5,6,7),(7,8,9)的规律,求: (1)第20组中三个数的和; (2)前20组中所有数的和.
答案:120;1260 解析:(39,40,42),运用等差数列求和公式。
3.一个数列的第一项是l,之后的每一项是这样得到的:如果前一项是一位数,接着的一项就等于前一项的两倍;如果前一项是两位数,接着的一项就等于前一项个位数字的两倍.请问: (1)第100项是多少? (2)前100项的和是多少?
答案:8;975 解析:按规律写:1,2,4,8,16,12,4,8,16,12……四个数为一个周期
4. 如图17-1,方格表中的数是按照一定规律填人的.请观察方格表,并填出“?”处的数. 答案:105 解析:四周数的差是一个等差数列。
5.如图17-2,数阵中的数是按一定规律排列的,请问: (1)100在第几行、第几列? (2)第20行第3列的数是多少? 答案:(1)第25行第6列;(2)79 解析:两行为一个周期。观察除以8的余数与在第几列之间的关系。
6.如图17-3,从4开始的自然数是按某种规律排列的,请问: (1)100在第几行,第几列? (2)第5行第20列的数是多少?
答案:(1)第1第25列;(2)81 解析:两列为一个周期。
7. 如图17-4所示,把偶数2、4、6、8,排成5列.各列从左到右依次为第1列、第2列、第3列、第4列和第5列,请问: (1)100在第几行,第几列? (2)第20行第2列的数是多少?
2021-2022学年度部编版语文八年级下册教学计划及教学进度表模板(三篇)
部编版语文八年级下册教学计划及教学进度表(一)一、指导思想本学期的语文教学工作以语文新课程标准为指导,以学校的工作计划为依据,切实提高自身的业务知识水平和教育教学能力,落实常规工作,扎实基础。
对于八年级学生一方面继续坚持语文基础知识的教学;一方面增加课外阅读量,丰富学生的阅读积累,有的放矢地进行写作训练,口语交际训练,开展综合性学习活动,全面提高学生的语文素养。
使学生的现代文阅读能力、写作能力和口语交际能力得到提高,具有初步的文学鉴赏能力和阅读课外文言文的能力。
掌握语文学习的基本方法,养成自学语文的习惯。
二、学情分析从学生的基础来看,学生的语文成绩和语文素养很不乐观。
学生的口头表达和书面表达能力都不高,自主探究合作的能力也不行,大多学生在以前都是接受式学习,所以,八年级语文教学的道路可谓任重而道远。
本学年按照新课标的理念和要求认真工作,着眼于全面培养学生的语文素养,正确把握语文教育的特点,积极倡导自主、合作、探究的方式,为社会主义建设培养有用的人才。
三、教材分析本册教材为2018年全新改版,共分为六个单元。
本学期记叙类文本增加了科学环保和民俗文化的相关内容;文言文篇幅长度增加,理解难度增大;诗歌单元增加了宋词和元曲。
这些变化,有助于学生思考语文与生活、与科学、与传统文化的联系,扩宽语文学习和运用的领域。
八年级下册四个现代文单元、两个文言文单元,课文的选编主要是从文章的难易程度,以及课程目标这两个方面来考虑的。
第一单元,是以民俗为主题组织单元。
《社戏》记录了鲁迅在归省平桥村的一段童年的回忆;《回延安》节选贺敬之诗选,展示出了浓郁的陕北风情;《安塞腰鼓》刘成章给我们描绘了安塞腰鼓的粗犷豪放、刚健雄浑;《灯笼》吴伯萧为我们抒写了他关于灯笼的一些记忆,从不同方面表达了灯笼对于他乃至民族的重要意义。
第二单元主要由事理说明文构成。
所选的课文涉及物候学、地质学、生态学等领域,体现了求真、严谨的科学精神。
第三单元,是以自然美景,幸福生活,人所向往,奇绝艺人等为内容的古诗文。
【新教材】部编版语文五年级上册课时安排
20xx---20xx学年度第一学期学科教学进度表任教年级:五年级科目:语文任课教师:注:各地方开学时间不一样,日期以当地时间为准。
xx小学五年级语文学科集体备课周计划安排表20xx——20xx学年度第一学期2019 — 2020学年度第一学期五年级语文上册教学计划二、学情分析课题:开学第一课教学内容:开学第一课教学目标:1.了解校园安全隐患。
2.掌握安全知识,培养学生“珍爱生命,安全第一”的意识。
3.进行预防灾害,预防突发事情的教育。
教学重点:掌握安全知识,培养学生“珍爱生命,安全第一”的意识。
教学过程:一、校园中存在的安全隐患。
(请学生列举一些现象)1.学生集会、集体活动、课间活动的安全隐患。
2.学生饮食、就餐的安全隐患。
3.学生交通安全隐患。
4.校园隐性伤害的隐患。
二、学生集会、集体活动、课间活动中应该注意的安全事项。
1.上下楼梯要注意什么?①不要因为赶时间而奔跑。
②在人多的地方一定要扶好栏杆。
③整队下楼时要与同学保持一定距离。
④上下楼时不要将手放在兜里。
⑤不要在楼道内弯腰拾东西、系鞋带。
⑥上下楼靠右行。
2.集体活动中要一切行动听指挥,遵守时间,遵守纪律,遵守秩序,语言文明。
3.课间活动应当注意什么?①室外空气新鲜,课间活动应当尽量在室外,但不要远离教室,以免耽误下面的课程。
②活动的强度要适当,不要做剧烈的活动,以保证继续上课时不疲劳、精力集中、精神饱满。
③活动的方式要简便易行,如做做操等。
④活动要注意安全,切忌猛追猛打,要避免发生扭伤、碰伤等危险。
三、学生饮食、就餐的安全注意事项。
不吃过期、腐烂食品,有毒的药物(如杀虫剂、鼠药等)要放在安全的地方。
禁止购买用竹签串起的食物:油反复使用,竹签容易伤人,食品卫生得不到保证,油炸食品有致癌物质。
四、交通安全注意事项。
1.行人靠右走,过马路要走斑马线,注意观察来往车辆,红灯停,绿灯行,遵守交通规则。
2.乘坐公交车注意事项:①车停稳后,方能上下车,上下车时注意秩序,不要拥挤。
期中考试卷二(考试范围:第16,17,19章)-2021年初中数学八年级下册同步讲练(教师版含解析)
期中考试卷一、选择题(本大题共14个小题,每题2分,共28分,在每个小题的四个选项中只有一项是符合题目要求的)1.(2020·浙江八年级期末)a 的取值范围是()A .1a =B .1a ≥C .1a >D .1a ≠【答案】B【详解】解:由题意可得:a -1≥0,∴a ≥1,故选:B .2.(2020·浙江八年级期末)如图,将一根长度为16cm 、自然伸直的弹性皮筋AB 两端固定在水平的桌面上,然后把皮筋中点C 竖直向上拉升6cm 到点D ,则此时该弹性皮筋被拉长了()A .6cmB .5cmC .4cmD .2cm【答案】C 【详解】解:连接CD ,∵中点C 竖直向上拉升6cm 至D 点,∴CD 是AB 的垂直平分线,∴∠ACD =90°,AC =BC =12AB =8cm ,AD =BD ,在Rt △ACD 中,由勾股定理得:AD cm ),∴BD =10cm ,∴AD +BD =20cm ,∵AB =16cm ,∴该弹性皮筋被拉长了:20-16=4(cm ),故选:C .3.(2021·河北秦皇岛市·八年级期末)下列二次根式中,最简二次根式是()A B C D .【答案】B【详解】解:A A 不符合题意;B 、是最简二次根式,故B 符合题意;C 、62,故C 不符合题意;D a D 不符合题意;故选:B .4.(2021·沙坪坝区·重庆南开中学八年级开学考试)估计+⨯的值应在()A .3和4之间B .4和5之间C .5和6之间D .6和7之间【答案】C【详解】解:3=+,∴23,56,故选:C .5.(2021·北京九年级专题练习)下列计算正确的是()A .-=B .6==C .-==D 5==【答案】D【详解】解:-=,故选项A 错误,不符合题意;选项B B 错误,不符合题意;-==,故选项C 错误,不符合题意;5==,故选项D 正确,符合题意;故选:D .6.(2020·浙江八年级期末)若正比例函数()14y m x =-的图象y 随x 的增大而减小,则m 的取值范围是()A .14m >B .14m <C .0m >D .0m <【答案】A【详解】解:∵正比例函数y =(1-4m )x 的图象y 随x 的增大而减小,∴1-4m <0,解得:m >14,故选:A .7.(2020·广东深圳市·深圳实验学校八年级期末)如图的网格中,每个小正方形的边长为1,A ,B ,C 三点均在格点上,结论错误的是()A .B .∠BAC=90°C .ABC S 10=D .点A 到直线BC 的距离是2【答案】C【详解】解:AB===A 正确,不符合题意;∵AC ==BC 5===,∴22252025AC AB BC +=+==,∴△ACB 是直角三角形,∴∠CAB=90°,故选项B 正确,不符合题意;S △ABC 111442421345222=⨯-⨯⨯-⨯⨯-⨯⨯=,故选项C 错误,符合题意;点A 到直线BC 的距离25AC AB BC ===,故选项D 正确,不符合题意;故选:C .8.(2020·北京海淀区·人大附中七年级期末)三名快递员某天的工作情况如图所示,其中点A 1,A 2,A 3的横、纵坐标分别表示甲、乙、丙三名快递员上午派送快递所用的时间和件数;点B 1,B 2,B 3的横、纵坐标分别表示甲、乙、丙三名快递员下午派送快递所用的时间和件数.有如下四个结论:①上午派送快递所用时间最短的是甲;②下午派送快递件数最多的是丙;③在这一天中派送所用时间最长的是乙;④在这一天中派送快递总件数最多的是乙.上述结论中,所有正确结论的序号是()A .①④B .①③④C .②③D .①②③④【答案】B 【详解】解:从图可知以下信息:上午送时间最短的是甲,①正确;下午送件最多的是乙,②不正确;在这一天中派送所用时间最长的是乙,③正确;在这一天中派送快递总件数最多的是乙,④正确.∴正确结论的序号是①③④.故选:B .9.(2021·陕西九年级零模)无论n 为何值,直线2y x n =-+与3y x =-的交点不可能在第()象限A .一B .二C .三D .四【答案】B【详解】解:∵一次函数y =x -3中,k =1>0,b =-3<0,∴函数图象经过一,三,四象限,∵一次函数2y x n =-+中,k =-2<0,∴函数图象经过二,三,四象限,或者经过一,二,四象限∴无论n 为何实数,直线2y x n =-+与3y x =-的交点不可能在第二象限.故选:B .10.(2020·浙江八年级期末)设b a >,将一次函数y ax b =+与y bx a =+的图象画在同一平面直角坐标系中,则有组a ,b 的取值,使得下列四个备选答案中有一个是正确的,则这个正确的答案是()A.B.C.D.【答案】D【详解】解:A、假设y=ax+b正确,则a<0,b>0,则函数y=bx+a的图象过一、三、四象限,故本选项错误.B、假设y=ax+b正确,则a>0,b>0,则函数y=bx+a的图象应经过一、二、三象限,故本选项错误;C、假设y=ax+b正确,则a<0,b>0,则函数y=bx+a的图象过一、三、四象限,因为函数y=ax+b与y=bx+a 的交点坐标为(1,a+b),由图象可知a≠-b和b>a,两结论矛盾,故本选项错误;D、假设y=ax+b正确,则a>0,b>0,因为b>a,所以函数y=bx+a与y轴的交点在y=ax+b与y轴交点的下方,故本选项正确;故选:D.11.(2021·浙江九年级专题练习)如图,已知图中所有的四边形都是正方形,所有的三角形都是直角三角形.若其中每个直角三角形的最长边与最短边的长度之比均为k,正方形A,B,C,D的面积分别为S1,S2,S3,S4,且S1>S2,S3>S4,则下列结论正确的是()A.S1•S4=k2S2B.S1+S4=S22C.S1•S4=S22D.S1+S4=kS2【答案】C【详解】解:设正方形B的边长为b,正方形D的边长为a,∵其中每个直角三角形的最长边与最短边的长度之比均为k,∴最大正方形的边长为kb,正方形D左侧的正方形的边长为ka,∴最大正方形下方直角三角形的最长边为k2a,∴S1=(kb)2﹣b2,=(k2﹣1)b2,S2=b2,S4=a2,在最大正方形下方的直角三角形中,由勾股定理得:(ka)2+(kb)2=(k2a)2,∴a 2+b 2=k 2a 2,∴b 2=(k 2﹣1)a 2,∴S 1=(k 2﹣1)2a 2,∴S 1•S 4=(k 2﹣1)2a 2•a 2,=[(k 2﹣1)a 2]2,=22S ;故选:C .12.(2021·四川成都市·成都实外八年级期末)如图所示,在平面直角坐标系中,直线124y x =+分别与x 轴,y 轴交于A ,B 两点,以线段OB 为一条边向右侧作矩形OCDB ,且点D 在直线2y x b =-+上,若矩形OCDB 的面积为20,直线124y x =+与直线2y x b =-+交于点P .则P 的坐标为()A .522,33⎛⎫ ⎪⎝⎭B .1731,33⎛⎫ ⎪⎝⎭C .()2,8D .()4,12【答案】A【详解】∵直线y 1=2x +4分别与x 轴,y 轴交于A ,B 两点,∴B (0,4),∴OB =4,∵矩形OCDB 的面积为20,∴OB •OC =20,∴OC =5,∴D (5,4),∵D 在直线y 2=﹣x +b 上,∴4=﹣5+b ,∴b =9,∴直线y 2=﹣x +9,解924y x y x =-+⎧⎨=+⎩,得53223x y ⎧=⎪⎪⎨⎪=⎪⎩,∴P (53,223),故选:A .13.(2021·河北保定师范附属学校八年级期末)甲、乙两车从A 地出发,匀速驶向B 地.甲车以80/km h 的速度行驶1h 后,乙车沿相同路线行驶.乙车先到达B 地并停留1h 后,再以原速按原路返回,直至与甲车相遇.在此过程中,两车之间的距离()y km 与乙车行驶时间(h)x 之间的函数关系如图所示.下列说法:①乙车的速度是120/km h ;②150m =;③点H 的坐标是()7,80;④7.4n =其中说法正确的是()A .①②③④B .①②③C .①②④D .①③④【答案】D 【详解】解:由图象可知,乙出发时,甲乙相距80km ,2小时后,乙车追上甲.则说明乙每小时比甲快40km ,则乙的速度为120km/h .①正确;由图象第2﹣6小时,乙由相遇点到达B ,用时4小时,每小时比甲快40km ,则此时甲乙距离4×40=160km ,则m=160>150,②不正确;当乙在B 地停留1h 时,甲前进80km ,甲乙相距=160-80=80km ,时间=6+1=7小时,则H 点坐标为(7,80),③正确;乙返回时,甲乙相距80km ,到两车相遇用时80÷(120+80)=0.4小时,则n=7+0.4=7.4,④正确.所以正确的有①③④,故选D ,14.(2021·武汉二中广雅中学九年级期末)设12211112a =++,22211123a =++,32211134a =++,……,22111(1)n a n n =+++,其中n为正整数,则+++的值是()A .201920202020B .202020202021C .202020212021D .202120212022【答案】B【详解】解:∵n为正整数,==21 (1) n n n n+++=11(1)n n++;+=(1+112⨯)+(1+123⨯)+(1+134⨯)+…+(1+120202021⨯)=2020+1﹣1111111 2233420202021 +-+-++-=2020+1﹣1 2021=2020 20202021.故选:B.二、填空题(本题共4个小题;每个小题3分,共12分,把正确答案填在横线上) 15.(2020·浙江杭州市·七年级期末)把面积为2平方单位的正方形ABCD按如图所示放置在数轴上,点A所表示的数为,现以点B为圆心,BD长为半径画弧,交数轴于点E,则点E所表示的数是________.【答案】【详解】解:∵正方形ABCD面积为2,∴边长AB =AD ,对角线BD =2,由作图可知:BE =BD =2,∵点A 所表示的数为,即OA∴OB =OA -AB ,∴OE =BE -OB =2-(,∴点E 表示的数为,故答案为:.16.(2020·四川成都市·成都实外八年级月考)如图,四边形ABCD 中,∠C =90°,AD =13,AB =,BC =9,DC =12,则四边形ABCD 的面积为_____.【答案】【详解】解:连接BD ,∵∠C =90°,BC =9,DC =12,∴BD =15BD ====,∵AB 2+AD 2=(22+132=56+169=225=DB 2,∴△ABD 是直角三角形,且∠A =90°,∴四边形ABCD 的面积为:12AB•AD+12CB•CD =12×13+12×9×12=+54,故答案为:+54.17.(2021·四川成都市·成都实外八年级期末)已知5a b +=,3ab =,则的值为________.【答案】3-【详解】解:∵5a b +=,3ab =,∴0a >,0b >,∴-⎛⎫=-+===3=-,故答案为533-.18.(2020·沙坪坝区·重庆一中九年级期中)“以自然之道,养自然之身”,生命在于运动,周末,小靓和小丽先后来到山脚,从山脚出发,沿着同一直线型登山步道进行锻炼,当小靓先匀速前行400米到达途中A 地观景台时,小丽开始从山脚匀速追赶,小靓继续以原速前行.追上后,小靓立即以原速的2倍率先到达山顶,然后立即以提高后的速度原路返回山脚.在上山过程中,小丽一直保持匀速登山,到达山顶后,立即以上山速度的1.5倍原路返回山脚.两人距A 地观景台的距离之和y (米)与小丽从山脚出发的时间t 分钟之间的部分函数关系如图所示,则两人第三次相遇时距A 地观景台________米.【答案】600.【详解】解:设小靓和小丽开始的速度分别为每分钟a 米和每分钟b 米,函数关系图可知,小丽出发第5分钟时,小丽追上了小靓,在这5分钟小丽比小靓多走400米;第11分钟时,小丽到达了山顶,此时y=3360,此时小靓距离山顶(12a-6b)米,距A 地观景台(5a+6b)-(12a-6b)=(12b-7a)米,∴55400(56)(127)3360b a a b b a -=⎧⎨++-=⎩∴120200a b =⎧⎨=⎩∴A 地观景台距离山顶512062001800⨯+⨯=米,第11分钟时小靓距离山顶121206200240⨯-⨯=米,∴小丽下山追上小靓所需时间=240(1.52002120)4÷⨯-⨯=(分钟)此时距离A 地观景台=1800 1.52004600-⨯⨯=,两人第三次相遇时距A 地观景台600米.故答案是:600.三、解答题(本题共8道题,19-21每题6分,22-25每题8分,26题10分,满分60分)19.(2020·甘州中学八年级期中)已知2y +与1x -成正比例,且当3x =时,4y =.(1)求y 与x 之间的函数表达式;(2)当1y =时,求x 的值.【答案】(1)y=3x-5;(2)2【详解】解:(1)设y+2=k(x-1),把x=3,y=4代入得:4+2=k(3-1)解得:k=3,则函数的解析式是:y+2=3(x-1)即y=3x-5;(2)当y=1时,3x-5=1,解得x=2.20.(2021·西安博爱国际学校八年级期末)如图,这是一个供滑板爱好者使用的U 型池的示意图,该U 型池可以看成是长方体去掉一个“半圆柱”而成,中间可供滑行部分的截面是直径为40m π的半圆,其边缘20m ==AB CD ,点E 在CD 上,5m CE =,一滑板爱好者从A 点滑到E 点,则他滑行的最短距离为多少米?(边缘部分的厚度忽略不计)【答案】25米【详解】解:如图是其侧面展开图:AD=π•20π=20,AB=CD=20.DE=CD-CE=20-5=15,在Rt△ADE中,.故他滑行的最短距离约为25米.21.(2020·郑州市·河南省实验中学八年级期中)计算:-;(2)2--.【答案】+2;.【详解】(1)=+2;(2)原式=﹣)﹣)2=)2﹣2﹣(3﹣+2),=18﹣12﹣,=.22.(2020·陕西西安市·八年级期末)如图,ABC的顶点A、B、C都在小正方形的顶点上,按下列要求画图.(1)建立平面直角坐标系,使点A坐标为(1,1),点C坐标为(0,2);(2)作ABC 关于x 轴对称的111A B C △;(3)在x 轴上作一点P ,使PA PC +最小,最小值为______.【答案】(1)见解析;(2)见解析;.【详解】解:(1)如图建立平面直角坐标系;(2)如图,111A B C 即是所求作的图形;(3)如图,连接1AC 与x 交于点P ,连接PA PC 、,1C C 、关于x 轴对称,1PC PC∴=1PA PC PA PC ∴+=+当1P A C 、、三点在同一条直线上时,PA PC +,..23.(2020·苏州市吴江区盛泽第二中学九年级月考)如图所示,在ABC 中,20AB =,12AC =,16BC =,把ABC 折叠,使AB 落在直线AC 上.(1)判断ABC 的形状.(2)求重叠部分(阴影部分)的面积.【答案】(1)直角三角形;(2)36【详解】解:(1)∵20AB =,12AC =,16BC =,则222121620+=,即满足222AB BC AC =+,∴△ABC 是直角三角形;(2)设CD =x ,∵在△ABC 中,AB =20,AC =12,BC =16,把△ABC 折叠,使AB 落在直线AC 上,∴BD =B ′D =16-x ,B ′C =AB -AC =20-12=8,∠DCB ′=90°,∴在Rt △DCB ′中,CD 2+B ′C 2=DB ′2,∴x 2+82=(16-x )2,解得:x =6,∴重叠部分(阴影部分)的面积为:12×6×12=36.24.(2020·浙江八年级期末)已知一次函数()1240y mx m m =-+≠.(1)判断点()2,4是否在该一次函数的图象上,并说明理由;(2)若一次函数26y x =-+,当0m >,试比较函数值1y 与2y 的大小;(3)函数1y 随x 的增大而减小,且与y 轴交于点A ,若点A 到坐标原点的距离小于6,点B ,C 的坐标分别为()0,2-,()2,1.求ABC 面积的取值范围.【答案】(1)点()2,4在该一次函数的图象上,理由见解析;(2)当2x <时,12y y <,当2x >时,12y y >,当2x =时,12y y =;(3)68ABC S △<<【详解】(1)将点()2,4代入到函数解析式,得,4224m m =-+,即44=,∴点()2,4在该一次函数的图象上;(2)两函数联立得,1224264y mx m x y x y =-+=⎧⎧⇒⎨⎨=-+=⎩⎩,∵一次函数26y x =-+,10k =-<,∴该函数单调递减,∵一次函数124y mx m =-+,0k >,∴该函数单调递增,∴当2x <时,12y y <,当2x >时,12y y >,当2x =时,12y y =;(3)设A(0,y ),∵ABC 由A(0,y ),B ()0,2-,C ()2,1三点构成,又∵函数1y 随x 的增大而减小,∴0m <,当0x =时,246y m =-+<,解得,1m >-,∴10m -<<,∴A(0,24m -+),∵B ()0,2-,C ()2,1,∴24226AB m m =-++=-+,∴12262ABC S AB m =⨯=-+△,∵10m -<<,∴6268m -+<<,∴68ABC S △<<.25.(2021·南京外国语学校八年级期中)如图,P 是等边三角形ABC 内的一点,连接PA ,PB ,PC ,以BP 为边作∠PBQ =60°,且BQ =BP ,连接CQ .(1)观察并猜想AP 与CQ 之间的大小关系,并证明你的结论;(2)若∠APB =150°,PB =8,PA =6,连接PQ ,求PC 的长.【答案】(1)AP=CQ ,证明见解析;(2)10.【详解】解:(1)AP =CQ .证明:∵△ABC 为等边三角形,∴∠ABC =60°,AB =CB ,∴∠ABP+∠PBC =60°.又∵∠PBQ =∠PBC+∠CBQ =60°,∴∠ABP =∠CBQ .在△ABP 和△CBQ 中,AB CB ABP CBQ BP BQ =⎧⎪∠=∠⎨⎪=⎩,∴△ABP ≌△CBQ(SAS),∴AP =CQ .(2)连接PQ ,如图所示.∵△ABP ≌△CBQ ,∴∠BQC =∠BPA =150°.∵BP =BQ ,∠PBQ =60°,∴△PBQ 为等边三角形,∴PQ =PB =8,∠BQP =60°,∴∠PQC =90°.在Rt △PQC 中,∠PQC =90°,PQ =8,CQ =AP =6,∴PC 22PQ CQ +=10.26.(2021·辽宁沈阳市·八年级期末)小明同学看到一则材料:甲开汽车,乙骑自行车从P 地出发沿同一条公路匀速前往Q 地、设乙行驶的时间为t (h ).甲乙两人之间的距离为y (km),y 与t 的函数关系如图所示.小明思考后发现了图中的部分信息:乙先出发1h ;甲出发0.5小时与乙相遇.请你帮助小明同学解决以下问题:(1)分别求出线段BC ,CD 所在直线的函数表达式(不需要写出自变量的取值范围);(2)直接写出乙行驶的路程S 乙(km)与时间t (h )的函数表达式是(不需要写出自变量的取值范围);(3)丙骑摩托车从Q 地沿同一条公路匀速前往P 地,若丙与乙同时出发,丙经过1.4h 与甲相遇.①直接写出丙行驶的路程S 丙(km)与时间t (h )的函数表达式是(不需要写出自变量的取值范围);②直接写出甲出发h 后与丙相距10km.【答案】(1)线段BC 所在直线的函数表达式为y=40x -60;线段CD 所在直线的函数表达式为y=-20x +80;(2)S 乙=20t ;(3)①S 丙=40t ;②310或12【详解】解:(1)由图象可知:B(32,0),C(73,1003),D(4,0)设线段BC 所在直线的函数表达式为y=ax +b将点B 和点C 的坐标分别代入,得302100733a b a b ⎧=+⎪⎪⎨⎪=+⎪⎩解得:4060a b =⎧⎨=-⎩∴线段BC 所在直线的函数表达式为y=40x -60;设线段CD 所在直线的函数表达式为y=cx +d将点D 和点C 的坐标分别代入,得04100733c d c d =+⎧⎪⎨=+⎪⎩解得:2080c d =-⎧⎨=⎩∴线段CD 所在直线的函数表达式为y=-20x +80;(2)结合图象可知:点C 表示甲到达终点,由CD 段可知:乙用(4-73)小时,行驶了1003千米∴乙的速度为1003÷(4-73)=20(千米/小时)∴S 乙=20t ;(3)①由图象可得:P 、Q 两地之间的距离为20×4=80(千米)∴甲的速度为80÷(73-1)=60(千米/小时)设丙的速度为v由题意可得()1.4601.4180v +-=解得:v=40∴S 丙=40t故答案为:S 丙=40t ;②设甲出发mh 后与丙相距10km若甲与丙在相遇之前相距10km由题意可得60m +40(m +1)+10=80解得:m =310;若甲与丙在相遇之后相距10km由题意可得60m +40(m +1)-10=80解得:m =12;综上:甲出发310或12h 后与丙相距10km .故答案为:310或12.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
112 第17课时 温度与物态变化 【课标要求】 1.1.2 说出生活环境中常见的温度值。了解液体温度计的工作原理,会用常见温度计测量温度。尝试对环境温度问题发表自己的见解。 例1.观察生活中常见的温度计,了解它们的使用方法和测温范围。 例2.尝试对温室效应、热岛效应等发表自己的见解。 1.1.1 描述固、液和气三种物态的基本特征,列举自然界和生活中不同状态的物质及其应用。 1.1.3 经历物态变化的实验探究过程,知道物质的熔点、凝固点和沸点,了解物态变化过程中的吸热和放热现象,用物态变化的知识说明自然界和生活中的有关现象。 例3.运用物态变化的知识,解释冰熔化、水沸腾等现象。 1.1.4 能用水的三态变化解释自然界中的一些水循环现象。了解我国和当地的水资源状况,有关心环境和节约用水的意识。 活动建议: (1)调查学校和家庭的用水状况,设计一个学校或家庭的节水方案。 (2)调查当地水资源的利用状况,并对当地水资源的利用提出自己的见解。 (3)调查本地农田灌溉的主要方式,了解节水灌溉技术。 【本节考点】 1、 温度和温度计A(会用常见的温度计测量温度) 2、固态、液态和气态的基本特性A 3、物态变化A(实验探究) 4、自然界中的水循环A 【复习导航】 一、温度及温度计: 1.物体的冷热程度叫温度,常用的温度单位是________,国际单位制中采用的是热力学温标,单位是________,简称 ,符号 。热力学温度和摄氏温度之间的换算关系是 。 2.测量——温度计(常用液体温度计) (1)温度计构造:温度计下面有 泡,里盛 等液体;在外面的玻璃管上均匀地刻有刻度。 (2)测温原理:利用 进行工作。 (3)分类及比较: 分类 实验用温度计 寒暑表 体温计 用途 测物体温度 测室温 测体温 量程 -20℃~110℃ -30℃~50℃ 35℃~42℃ 分度值 1℃ 1℃ 0.1℃ 所用液体 水银 煤油(红) 酒精(红) 水银
特殊构造 玻璃泡上方有缩口 使用方法 使用时不能甩,测物体时不能离开物体读数 使用前甩可离开人体读数 (4)常用温度计的使用方法:认清量程和分度值,正确读数。使用前:观察它的 ,判断是否适合待测物体的温度;并认清温度计的 以便准确读数。使用时:温度计的玻璃泡全部浸入被测液体中,不要碰到容器 或容器 ;温度计玻璃泡浸入被测液体中稍候一会儿,待温度计的示数 后再读数;读数时玻璃泡要继续 中,视线与温度计中液 113
柱的上表面 。 二、熔化和凝固 (一)熔化 1.在物理学中,把物质从 变成 叫熔化。 2.固体分为晶体和非晶体。属于晶体物质的有 ;属于非晶体物质的有: 。 3.晶体熔化图象如图17.1所示: 由图像可知,晶体熔化时的特点: 共存, 热量, 温度 。 4.熔点 :晶体 时的温度。 5.晶体熔化的条件:⑴ 熔点。⑵ 继续 。 (二)凝固 1.物质从 变成 的过程称为凝固。 2.晶体熔液在凝固的过程中, 热量,但是温度却保持 。 3. 晶体熔液凝固的条件:(1) ;(2) 。 4. 叫凝固点。同一晶体熔点和凝固点是 。 5.冬季贮菜,人们常在地窖里放几桶水,以防止菜被冻坏,是因为__________________。 三、汽化和液化 (一)汽化 1.在物理学中,把物体从 变成 叫汽化。汽化 热。 2.蒸发:液体在 温度下都能发生的,并且只在液体 发生的 的汽化现象叫蒸发。 影响蒸发快慢的因素:①液体的 ;②液体的 ③液体表面 蒸发 热(吸收外界或自身的热量),具有制冷作用。 3.沸腾:液体在 温度下,在液体 和 同时发生的 的汽化现象叫沸腾。 沸点:液体 时的温度。 沸腾条件:①达到 ;②继续 热。 沸点与气压的关系:一切液体的沸点都是气压减小时 ,气压增大时 。 (二)液化 1.物质从_______变成_______的过程称为液化。液化是_____热的过程。 2.使气体液化的方法有两种: (1)_______________________________,如:_________________________________。 (2)_______________________________,如:_________________________________。 3.生活中的液化现象有________________________________________________;自然界中的液化现象有________________________________________________。 4.100℃的水蒸气比100℃的水烫伤更厉害,原因是_____________________________。 四、升华和凝华 (一)升华 在物理学中,把物质从______直接变成______的过程叫升华。升华______热。 易升华的物质有__________________。生活中升华的例子有__________________。 (二)凝华 1.物质从_________态直接变成________态叫凝华,凝华过程中要_________热。 2.北方秋、冬两季早晨出现霜,窗玻璃上出现冰花等现象,这些是_________现象。 3.生活中的凝华现象有____________________________________;自然界中的凝华现象有
图17.1 114
图18.1 图18.2
____________________________________。 【基础回顾】 1.以下说法中,你认为最符合实际的是 ( ) A. 人体的正常体温为35℃ B. 冰箱冷冻室的温度约为5℃ C. 上海盛夏中午室外温度可达38℃ D. 上海的最低气温可达零下30℃ 2.图18.1中温度计的读数为 ℃,该温度计的测量范围是 ℃。
3.如图18.2所示,用温度计测温度时正确的使用方法是( )
4.填写相应的物态变化及吸、放热情况: 冬天玻璃窗户上的冰花 、需要 热。用铁水浇铸成工件 、需要 热。从游泳池上来感到凉爽 、需要 热。春天水池中的冰融化了 、需要 热。夏天放在衣柜中的樟脑丸不见了 、需要 热。秋天看到草上的露水 、需要 热。 5.实施人工增雨的一种方法是飞机在高空撒干冰(固态二氧化碳),干冰进入云层,很快____成气体,并从周围吸收大量的热,于是高空水蒸气便____成小冰晶或____成小水滴,使云中的冰晶增多,小水滴增大,从而形成降雨。(填物态变化的名称) 6.小丽将一杯常温下的水放入正常工作的冰箱冷冻室中,经过较长时间后,杯中的水发生了物态变化,下面四个图象中能正确反映这杯水的物态变化过程的是( )
7.炎热的夏季,家中的蜡烛、柏油路上的沥青会变软。而冰块熔化时,没有逐渐变软的过程。可见蜡烛,沥青属于_____,而冰属于_____。它们之间的区别是___________________。晶体在熔化过程中,温度___________。在生活中,晶体还有 ,非晶体还有 。 8.【探究名称】影响液体蒸发快慢的因素 【提出问题】液体蒸发快慢跟哪些因素有关? 【猜想与假设】通过观察下图并联系生活实际进行猜想
A B C D 115
猜想一:液体蒸发快慢可能跟液体________的高低、液体________的大小和液体表面空气流动快慢有关。 猜想二:相同条件下,将水和酒精同时擦在手臂上,酒精更容易干,猜想液体蒸发快慢可能还与________有关。 【设计与进行实验】小明同学对其中的一个猜想进行了如下实验:
如图17.2所示,在两块相同的玻璃板上,分别滴一滴质量相等的酒精,通过观察图中情景可知他探究的是酒精蒸发快慢与 是否有关。此实验过程中需控制酒精的 和其表面上方空气流动快慢相同。 【交流与评估】我们知道液体蒸发时要吸热,请你举一个应用蒸发吸热的事例: 。 9.在观察水的沸腾实验中,某小组同学从水温升高到90℃时开始记录数据,以后每隔1 min记录一次水的温度,直到水沸腾5min为止。记录的数据如右表:从数据可知,水沸腾时的温度为 。通过分析实验数据,还可以得出结论: ________________________________________________。 10.在探究“水的沸腾”的实验中,甲、乙两组同学分别使用A、B两套装置(如图17.3)来完成实验。 (1)如图a、b所示的是观察水沸腾实验中出现的两种情景,其中水沸腾时的情景为_____(填a或b)。 (2)甲组观察水沸腾时温度计的示数如图所示,他们所测水的沸点是_____________。他们所选择的装置应是_____(填A或B)。 (3)如果想要节约一些酒精灯的燃料,并适当缩短实验时间,则可行的一种方法是 。 【考点解析】 考点一:温度和温度计 例1.如图中A、B、C、D分别是四位同学“用温度计测水温”的实验操作,其中正确的是( ) 例2.已知酒精、煤油、水银的熔点分别是―117℃、―30℃、―38℃,南极的最低气温可达―89.2℃,t/min 0 1 2 3 4 5 6 7 8 9 10 11 12 t温/℃ 90 91 92 93 94 95 96 97 98 98 98 98 98
图17.3 a b 90 100 ℃
图17.2
