人教版八年级数学下册学练优作业课件:第十八章检测卷
(最新)部编人教版数学八年级下册《第十八章 单元检测试题》(含答案)

第十八章检测题(时间:120分钟满分:120分)一、选择题(每小题3分,共30分)1.若平行四边形中两个内角的度数比为1∶3,则其中较小的内角是( B)A.30° B.45° C.60° D.75°2.(2019·株洲)如图,已知四边形ABCD是平行四边形,对角线AC,BD相交于点O,E是BC的中点,以下说法错误的是( D)A.OE=12DC B.OA=OC C.∠BOE=∠OBA D.∠OBE=∠OCE,第2题图) ,第3题图),第6题图)3.如图,矩形ABCD的对角线AC=8 cm,∠AOD=120°,则AB的长为( D)A. 3 cm B.2 cm C.2 3 cm D.4 cm4.已知四边形ABCD是平行四边形,下列结论中不正确的是( D)A.当AB=BC时,它是菱形 B.当AC⊥BD时,它是菱形C.当∠ABC=90°时,它是矩形 D.当AC=BD时,它是正方形5.若顺次连接四边形各边中点所得的四边形是菱形,则该四边形一定是( C)A.矩形 B.一组对边相等,另一组对边平行的四边形C.对角线相等的四边形 D.对角线互相垂直的四边形6.如图,已知点E是菱形ABCD的边BC上一点,且∠DAE=∠B=80°,那么∠CDE的度数为( C)A .20° B.25° C.30° D.35°7.(2019·菏泽)在▱ABCD 中,AB =3,BC =4,当▱ABCD 的面积最大时,下结论正确的有( B )①AC =5;②∠A +∠C =180°;③AC ⊥BD ;④AC =BD . A .①②③ B.①②④ C.②③④ D.①③④8.如图,把矩形ABCD 沿EF 翻折,点B 恰好落在AD 边的B′处,若AE =2,DE =6,∠EFB′=60°,则矩形ABCD 的面积是( D )A .12B .24C .12 3D .16 3,第8题图) ,第9题图),第10题图)9.如图,正方形ABCD 的边长为4,点E 在对角线BD 上,且∠BAE=22.5°,EF⊥AB,垂足为F ,则EF 的长为( C )A .1 B. 2 C .4-2 2 D .32-410.如图,在矩形ABCD 中,点E 是AD 的中点,∠EBC 的平分线交CD 于点F ,将△DEF 沿EF 折叠,点D 恰好落在BE 上点M 处,延长BC ,EF 交于点N ,有下列四个结论:①DF=CF ;②BF⊥EN;③△BEN 是等边三角形;④S △BEF =3S △DEF ,其中正确的结论是( B )A .①②③ B.①②④ C.②③④ D.①②③④ 二、填空题(每小题3分,共24分)11.如图,在▱ABCD 中,AB =5,AC =6,当BD =__8__时,四边形ABCD 是菱形.,第11题图) ,第12题图),第14题图)12.(2019·江西)如图,在▱ABCD 中,∠C=40°,过点D 作CB 的垂线,交AB 于点E ,交CB 的延长线于点F ,则∠BEF 的度数为__50°__.13.在四边形ABCD 中,AD∥BC,分别添加下列条件之一:①AB∥CD;②AB =CD ;③∠A=∠C;④∠B=∠C.能使四边形ABCD 为平行四边形的条件的序号是__①或③__.14.如图,∠ACB=90°,D 为AB 中点,连接DC 并延长到点E ,使CE =14CD ,过点B 作BF∥DE 交AE 的延长线于点F ,若BF =10,则AB 的长为__8__.15.如图,四边形ABCD 是正方形,延长AB 到点E ,使AE =AC ,则∠BCE 的度数是__22.5__度.,第15题图) ,第16题图),第17题图) ,第18题图)16.如图,在四边形ABCD 中,对角线AC⊥BD,垂足为点O ,E ,F ,G ,H 分别为边AD ,AB ,BC ,CD 的中点,若AC =8,BD =6,则四边形EFGH 的面积为__12__.17.已知菱形ABCD 的两条对角线长分别为6和8,M ,N 分别是边BC ,CD 的中点,P 是对角线BD 上一点,则PM +PN 的最小值是__5__.18.(2019·天津)如图,在正方形ABCD 中,点E ,N ,P ,G 分别在边AB ,BC ,CD ,DA 上,点M ,F ,Q 都在对角线BD 上,且四边形MNPQ 和AEFG 均为正方形,则S 正方形MNPQ S 正方形AEFG 的值等于__89__.三、解答题(共66分)19.(8分)如图,点E,F分别是锐角∠A两边上的点,AE=AF,分别以点E,F为圆心,以AE的长为半径画弧,两弧相交于点D,连接DE,DF.(1)请你判断所画四边形的形状,并说明理由;(2)连接EF,若AE=8 cm,∠A=60°,求线段EF的长.解:(1)菱形,理由:根据题意得AE=AF=ED=DF,∴四边形AEDF是菱形(2)∵AE=AF,∠A=60°,∴△EAF是等边三角形,∴EF=AE=8 cm20.(8分)(2019·宿迁)如图,已知BD是△ABC的角平分线,点E,F分别在边AB,BC上,ED∥BC,EF∥AC.求证:BE=CF.解:∵ED∥BC,EF∥AC,∴四边形EFCD是平行四边形,∴DE=CF,∵BD平分∠ABC,∴∠EBD=∠DBC,∵DE∥BC,∴∠EDB=∠DBC,∴∠EBD=∠EDB,∴EB=ED,∴EB=CF21.(9分)(2019·南通)如图,将▱ABCD 的边AB 延长到点E ,使BE =AB ,连接DE ,交边BC 于点F.(1)求证:△BEF≌△CDF;(2)连接BD ,CE ,若∠BFD=2∠A,求证:四边形BECD 是矩形.解:(1)∵四边形ABCD 是平行四边形,∴AB =CD ,AB ∥CD.∵BE =AB ,∴BE =CD.∵AB ∥CD ,∴∠BEF =∠CDF ,∠EBF =∠DCF ,∴△BEF ≌△CDF (ASA ) (2)∵四边形ABCD 是平行四边形,∴AB ∥CD ,AB =CD ,∠A =∠DCB ,∵AB =BE ,∴CD =EB ,∴四边形BECD 是平行四边形,∴BF =CF ,EF =DF ,∵∠BFD =2∠A ,∴∠BFD =2∠DCF ,∴∠DCF =∠FDC ,∴DF =CF ,∴DE =BC ,∴四边形BECD 是矩形22.(9分)如图,在▱ABCD 中,E ,F 两点在对角线BD 上,BE =DF.(1)求证:AE =CF ;(2)当四边形AECF 为矩形时,请求出BD -ACBE的值.解:(1)由SAS 证△ABE ≌△CDF 即可 (2)连接CE ,AF ,AC.∵四边形AECF 是矩形,∴AC =EF ,∴BD -AC BE =BD -EF BE =BE +DF BE =2BEBE=223.(10分)如图,在矩形ABCD 中,M ,N 分别是边AD ,BC 的中点,E ,F 分别是线段BM ,CM 的中点.(1)求证:△ABM≌△DCM;(2)填空:当AB∶AD=__1∶2__时,四边形MENF 是正方形,并说明理由.解:(1)由SAS 可证 (2)理由:∵AB ∶AD =1∶2,∴AB =12AD ,∵AM =12AD ,∴AB =AM ,∴∠ABM =∠AMB ,∵∠A =90°,∴∠AMB =45°,∵△ABM ≌△DCM ,∴BM =CM ,∠DMC =∠AMB =45°,∴∠BMC =90°,∵E ,F ,N 分别是BM ,CM ,BC 的中点,∴EN ∥CM ,FN ∥BM ,EM =MF ,∴四边形MENF 是菱形,∵∠BMC =90°,∴菱形MENF 是正方形24.(10分)(2019·遵义)如图,在Rt △ABC 中,∠BAC=90°,D 是BC 的中点,E 是AD 的中点,过点A 作AF∥BC 交BE 的延长线于点F.(1)求证:△AEF≌△DEB; (2)求证:四边形ADCF 是菱形;(3)若AC =4,AB =5,求菱形ADCF 的面积.解:(1)由AAS 易证△AFE ≌△DBE (2)由(1)知,△AEF ≌△DEB ,则AF =DB ,∵DB =DC ,∴AF =CD ,∵AF ∥BC ,∴四边形ADCF 是平行四边形,∵∠BAC =90°,D 是BC 的中点,∴AD =DC =12BC ,∴四边形ADCF 是菱形 (3)连接DF ,由(2)知AF 綊BD ,∴四边形ABDF 是平行四边形,∴DF =AB =5,∴S 菱形ADCF =12AC·DF =12×4×5=1025.(12分)如图,在正方形ABCD 中,AC 是对角线,今有较大的直角三角板,一边始终经过点B ,直角顶点P 在射线AC 上移动,另一边交DC 于点Q.(1)如图①,当点Q 在DC 边上时,猜想并写出PB 与PQ 所满足的数量关系,并加以证明;(2)如图②,当点Q 落在DC 的延长线上时,猜想并写出PB 与PQ 满足的数量关系,并证明你的猜想.解:(1)PB =PQ.证明:连接PD ,∵四边形ABCD 是正方形,∴∠ACB =∠ACD ,∠BCD =90°,BC =CD ,又∵PC =PC ,∴△DCP ≌△BCP (SAS ),∴PD =PB ,∠PBC =∠PDC ,∵∠PBC +∠PQC =180°,∠PQD +∠PQC =180°,∴∠PBC =∠PQD ,∴∠PDC =∠PQD ,∴PQ =PD ,∴PB =PQ (2)PB =PQ.证明:连接PD ,同(1)可证△DCP ≌△BCP ,∴PD =PB ,∠PBC =∠PDC ,∵∠PBC =∠Q ,∴∠PDC =∠Q ,∴PD =PQ ,∴PB =PQ。
人教新版八年级下册数学《第18章 平行四边形》单元测试卷和答案详解(PDF可打印)

人教新版八年级下册《第18章平行四边形》单元测试卷(1)一、单选题1.如图,△ABC中,D,E分别上边AB,AC的中点,若DE=3,则BC=()A.B.9C.6D.52.如图,正方形ABCD中,以对角线AC为一边作菱形AEFC,则∠FAB等于()A.22.5°B.45°C.30°D.135°3.已知:如图,在平行四边形ABCD中,AB=4,AD=7,∠ABC的平分线交AD于点E,交CD的延长线于点F,则DF的长为()A.6B.5C.4D.34.如图,矩形ABCD的两条对角线相交于点O,∠AOD=60°,AD=2,则AC的长是()A.2B.4C.D.5.如图,在平行四边形ABCD中,以A为圆心,AB为半径画弧,交AD于F,再分别以B、F为圆心,大于BF的长为半径画弧,两弧相交于点G,若BF=6,AB=5,则AE的长为()A.11B.6C.8D.106.如图,在锐角△ABC中,延长BC到点D,点O是AC边上的一个动点,过点O作直线MN∥BC,MN分别交∠ACB、∠ACD的平分线于E,F两点,连接AE、AF,在下列结论中:①OE=OF;②CE=CF;③若CE=12,CF=5,则OC的长为6;④当AO=CO时,四边形AECF是矩形.其中正确的是()A.①④B.①②C.①②③D.②③④7.如图,在边长为1的小正方形组成的网格中,点A,B,C都在格点上,若将线段AB沿BC方向平移,使点B与点C重合,则线段AB扫过的面积为()A.11B.10C.9D.88.在平行四边形ABCD中,∠A+∠C=160°,则∠B的度数是()A.130°B.120°C.100°D.90°9.如图,正方形ABCD边长为2,点P是线段CD边上的动点(与点C,D不重合),∠PBQ=45°,过点A作AE∥BP,交BQ于点E,则下列结论正确的是()A.BP•BE=2B.BP•BE=4C.=D.=10.如图,在△ABC中,∠ACB=90°,点D为AB的中点,若CD=5,AC=8,则BC的长为()A.3B.4C.5D.611.下面四个标志属于中心对称的是()A.B.C.D.12.矩形ABCD中,对角线AC,BD相交于点O,∠AOB=60°,AB=6cm,则BD的长()A.6cm B.8cm C.10cm D.12cm二、填空题13.如图,在△ABC中,AD⊥BC于点D,点E,F分别是AB,AC边的中点,请你在△ABC 中添加一个条件:,使得四边形AEDF是菱形.14.如图,DE∥AC交AB于点E,DF∥AB交AC于F,∠1=∠2,四边形AEDF的形状是.15.如图,在Rt△ACB中,AC=BC=8,O为AB的中点,以O为直角顶点作等腰直角三角形OEF,与边AC,BC相交于点M,N.有下列结论:①AM=CN;②CM+CN=8;③S四边形OMCN=6;④当M是AC的中点时,OM=ON.其中正确结论的序号是.16.如图,在平面直角坐标系中有一边长为1的正方形OABC,边OA,OC分别在x轴,y 轴上,如果以对角线OB为边作第二个正方形OBB1C1,再以对角线OB1为边作第三个正方形OB1B2C2,照此规律作下去,则点B2019的坐标为.17.如图,四个小正方形的边长都是1,若以O为圆心,OG为半径作弧分别交AB、DC于点E、F,则图中阴影部分的面积为.18.如图:点E、F分别是菱形ABCD的边BC、CD上的点,且∠EAF=∠D=60°,∠FAD =45°,则∠CFE=度.19.如图,矩形ABCD中,点A坐标是(﹣1,0),点C的坐标是(2,4),则BD的长是.20.在平面直角坐标系中,四边形AOBC是菱形,若点A的坐标是(3,4),则菱形的周长为,点C的坐标是.三、解答题21.如图,在△ABC中,点D,E分别是AB,AC的中点,F是BC延长线上的一点,且CF =BC.试猜想DE与CF有怎样的数量关系,并说明理由.22.如图,∠MON=90°,正方形ABCD的顶点A、B分别在OM、ON上,AB=13,OB =5,E为AC上一点,且∠EBC=∠CBN,直线DE与ON交于点F.(1)求证:BE=DE;(2)判断DF与ON的位置关系,并说明理由;(3)△BEF的周长为.23.盈盈同学要证明命题“两组对边分别相等的四边形是平行四边形”是正确的,她先用尺规作出了如图1的四边形ABCD,并写出了如下不完整的已知和求证.已知:如图1,在四边形ABCD中,BC=AD,.求证:.(1)填空,补全已知和求证;(2)按盈盈的想法写出证明;(3)用文字叙述所证命题的逆命题为.24.已知:如图,在平行四边形ABCD中,点E是边AD上一点,分别连接BE,CE,若点F,G,H分别是EC,BC,BE的中点.(1)求证:四边形EFGH是平行四边形;(2)设四边形EFGH的面积为S1,四边形ABCD的面积为S2,请直接写出S1:S2的值.25.如图,AC为正方形ABCD的对角线,E为AC上一点,且AB=AE,EF⊥AC,交BC 于F,试说明EC=EF=BF.26.已知,如图,△ABC中,∠A=90°,D是AC上一点,且∠ADB=2∠C,P是BC上任一点,PE⊥BD于E,PF⊥AC于F.(1)求证:CD=BD;(2)写出线段AB,PF和PE之间数量关系,并证明你的结论.27.如图,△ABC中,D、E分别是AB、AC的中点,延长DE至点F,使EF=DE,连接CF,证明:四边形DBCF是平行四边形.28.如图,在四边形纸片ABCD中,∠B=∠D=90°,点E,F分别在边BC,CD上,将AB,AD分别沿AE,AF折叠,点B,D恰好都和点G重合,∠EAF=45°.(1)求证:四边形ABCD是正方形;(2)若EC=FC=1,求AB的长度.29.如图,△ABC是边长为6的等边三角形,P是AC边上一动点,由A向C运动(与A,C不重合),Q是CB延长线上一点,由B向CB延长线方向运动(Q不与B重合),连接PQ交AB于D,过P作PE⊥AB于E.若两点同时出发,以相同的速度每秒1个单位运动,运动时间为t.(1)当∠PQC=30°时,求t的值;(2)求证:PD=DQ;(3)当P,Q在运动过程中线段ED的长是否发生变化?如果不变,求出线段ED的长;如果变化请说明理由.人教新版八年级下册《第18章平行四边形》单元测试卷(1)参考答案与试题解析一、单选题1.如图,△ABC中,D,E分别上边AB,AC的中点,若DE=3,则BC=()A.B.9C.6D.5【考点】三角形中位线定理.【分析】由已知条件得出DE是△ABC的中位线,根据三角形中位线定理即可得出BC=2DE.【解答】解:∵D,E分别上边AB,AC的中点,∴DE是△ABC的中位线,∴BC=2DE=6;故选:C.2.如图,正方形ABCD中,以对角线AC为一边作菱形AEFC,则∠FAB等于()A.22.5°B.45°C.30°D.135°【考点】正方形的性质;菱形的性质.【分析】根据正方形的性质求出∠CAB=45°,再根据菱形的性质∠FAB=∠CAB,即可解决问题.【解答】解:∵四边形ABCD是正方形,∴∠CAB=∠DAB=×90°=45°,∵四边形AEFC是菱形,∴∠FAB=∠CAE=×45°=22.5°,故选:A.3.已知:如图,在平行四边形ABCD中,AB=4,AD=7,∠ABC的平分线交AD于点E,交CD的延长线于点F,则DF的长为()A.6B.5C.4D.3【考点】平行四边形的性质.【分析】平行四边形的对边相等且平行,利用平行四边形的性质以及平行线的基本性质求解.【解答】解:∵平行四边形ABCD∴AB∥CD∴∠ABE=∠CFE∵∠ABC的平分线交AD于点E∴∠ABE=∠CBF∴∠CBF=∠CFB∴CF=CB=7∴DF=CF﹣CD=7﹣4=3故选:D.4.如图,矩形ABCD的两条对角线相交于点O,∠AOD=60°,AD=2,则AC的长是()A.2B.4C.D.【考点】矩形的性质;等边三角形的判定与性质.【分析】根据矩形的对角线互相平分且相等可得OC=OD,再根据三角形的一个外角等于与它不相邻的两个内角的和求出∠OCD=30°,然后根据直角三角形30°角所对的直角边等于斜边的一半解答.【解答】解:在矩形ABCD中,OC=OD,∴∠OCD=∠ODC,∵∠AOD=60°,∴∠OCD=∠AOD=×60°=30°,又∵∠ADC=90°,∴AC=2AD=2×2=4.故选:B.5.如图,在平行四边形ABCD中,以A为圆心,AB为半径画弧,交AD于F,再分别以B、F为圆心,大于BF的长为半径画弧,两弧相交于点G,若BF=6,AB=5,则AE的长为()A.11B.6C.8D.10【考点】平行四边形的性质.【分析】连接EF,根据题意得出AE垂直平分BF,AF=AB=5,得出OB=OF=3,∠BAE=∠FAE,由勾股定理求出OA,再证出BE=AB=AF,得出四边形ABEF是平行四边形,由平行四边形的性质得出OA=OE=AE,即可得出结果.【解答】解:连接EF,如图所示:根据题意得:AE垂直平分BF,AF=AB=5,∴∠AOF=90°,OB=OF=3,∠BAE=∠FAE,∴OA==4,∵四边形ABCD是平行四边形,∴AD∥BC,∴∠FAE=∠AEB,∴∠BAE=∠AEB,∴BE=AB=AF,∴四边形ABEF是平行四边形,∴OA=OE=AE,∴AE=2OA=8;故选:C.6.如图,在锐角△ABC中,延长BC到点D,点O是AC边上的一个动点,过点O作直线MN∥BC,MN分别交∠ACB、∠ACD的平分线于E,F两点,连接AE、AF,在下列结论中:①OE=OF;②CE=CF;③若CE=12,CF=5,则OC的长为6;④当AO=CO时,四边形AECF是矩形.其中正确的是()A.①④B.①②C.①②③D.②③④【考点】矩形的判定.【分析】①只要证明OC=OE,OC=OF即可.②首先证明∠ECF=90°,若EC=CF,则∠OFC=45°,显然不可能,故②错误,③利用勾股定理可得EF=13,推出OC=6.5,故③错误.④根据矩形的判定方法即可证明.【解答】解:∵MN∥CB,∴∠OEC=∠BCE,∠OFC=∠ACF∵∠ACE=∠BCE,∠ACF=∠DCF,∴∠OEC=∠OCE,∠OFC=∠OCF,∴OC=OE=OF,故①正确,∵∠BCD=180°,∴∠ECF=90°,若EC=CF,则∠OFC=45°,显然不可能,故②错误,∵∠ECF=90°,EC=12,CF=5,∴EF==13,∴OC=EF=6.5,故③错误,∴OE=OF,OA=OC,∴四边形AECF是平行四边形,∵∠ECF=90°,∴四边形AECF是矩形.故选:A.7.如图,在边长为1的小正方形组成的网格中,点A,B,C都在格点上,若将线段AB沿BC方向平移,使点B与点C重合,则线段AB扫过的面积为()A.11B.10C.9D.8【考点】坐标与图形变化﹣平移.【分析】观察图象可知线段AB扫过的图形是正方形,求出正方形的边长即可解决问题.【解答】解:由题意,AB==.线段AB扫过的图形是正方形ABCD,所以线段AB扫过的面积=()2=10.故选:B.8.在平行四边形ABCD中,∠A+∠C=160°,则∠B的度数是()A.130°B.120°C.100°D.90°【考点】平行四边形的性质.【分析】直接利用平行四边形的对角相等,邻角互补即可得出答案.【解答】解:如图所示:∵四边形ABCD是平行四边形,∴∠A=∠C,∠A+∠B=180°,∵∠A+∠C=160°,∴∠A=∠C=80°,∴∠B的度数是:100°.故选:C.9.如图,正方形ABCD边长为2,点P是线段CD边上的动点(与点C,D不重合),∠PBQ =45°,过点A作AE∥BP,交BQ于点E,则下列结论正确的是()A.BP•BE=2B.BP•BE=4C.=D.=【考点】正方形的性质.=S△ABP=S正方形ABCD=2即可解决问【分析】连接AP,作EM⊥PB于M,根据S△PBE题.【解答】解:如图,连接AP,作EM⊥PB于M.∵AE∥PB,=S△ABP=S正方形ABCD=2,∴S△PBE∴•PB•EM=2,∵∠EBM=45°,∠EMB=90°,∴EM=BE,∴•PB•BE=2,∴PB•BE=4.故选:B.10.如图,在△ABC中,∠ACB=90°,点D为AB的中点,若CD=5,AC=8,则BC的长为()A.3B.4C.5D.6【考点】直角三角形斜边上的中线.【分析】依据直角三角形的斜边上中线的性质,即可得到AB的长,再根据勾股定理,即可得到BC的长.【解答】解:∵△ABC中,∠ACB=90°,点D为AB的中点,∴AB=2CD=2×5=10,∴Rt△ABC中,BC===6,故选:D.11.下面四个标志属于中心对称的是()A.B.C.D.【考点】中心对称图形.【分析】根据中心对称图形的概念对各选项分析判断后利用排除法求解.【解答】解:A、是中心对称图形,故本选项正确;B、不是中心对称图形,故本选项错误;C、不是中心对称图形,故本选项错误;D、不是中心对称图形,故本选项错误.故选:A.12.矩形ABCD中,对角线AC,BD相交于点O,∠AOB=60°,AB=6cm,则BD的长()A.6cm B.8cm C.10cm D.12cm【考点】矩形的性质.【分析】由矩形的性质得出OA=OB,再由已知条件得出△AOB是等边三角形,得出OB =AB=6cm,即可得出BD的长.【解答】解:如图所示:∵四边形ABCD是矩形,∴OA=OC=AC,OB=OD=BD,AC=BD,∴OA=OB,∵∠AOB=60°,∴△AOB是等边三角形,∴OB=AB=6cm,∴BD=2OB=12cm;故选:D.二、填空题13.如图,在△ABC中,AD⊥BC于点D,点E,F分别是AB,AC边的中点,请你在△ABC 中添加一个条件:AB=AC(答案不唯一),使得四边形AEDF是菱形.【考点】菱形的判定;直角三角形斜边上的中线.【分析】由直角三角形斜边上的中线性质得出DE=AB=AE,DF=AC=AF,由AB =AC,得出DE=DF=AE=AF,即可得出结论.【解答】解:添加条件:AB=AC.理由如下:∵AD⊥BC,点E,F分别是AB,AC边的中点,∴DE=AB=AE,DF=AC=AF,∵AB=AC,∴DE=DF=AE=AF,∴四边形AEDF是菱形;故答案为:AB=AC(答案不唯一).14.如图,DE∥AC交AB于点E,DF∥AB交AC于F,∠1=∠2,四边形AEDF的形状是菱形.【考点】菱形的判定.【分析】先证明四边形AEDF是平行四边形,再证明邻边相等即可得出四边形AEDF是菱形.【解答】解:∵DE∥AC,DF∥AB,∴四边形AEDF是平行四边形,∠2=∠ADE,∵∠1=∠2,∴∠1=∠ADE,∴AE=DE,∴四边形AEDF是菱形,故答案为:菱形.15.如图,在Rt△ACB中,AC=BC=8,O为AB的中点,以O为直角顶点作等腰直角三角形OEF,与边AC,BC相交于点M,N.有下列结论:①AM=CN;②CM+CN=8;③S四边形OMCN=6;④当M是AC的中点时,OM=ON.其中正确结论的序号是①②④.【考点】全等三角形的判定与性质;等腰直角三角形;三角形中位线定理.=S△CON,【分析】由“ASA”可证△AOM≌△CON,可得AM=CN,OM=ON,S△AOM 即可求解.【解答】解:连接OC,∵在Rt△ACB中,AC=BC=8,O为AB的中点,∴AO=BO=CO,∠ACO=∠BCO=∠A=∠B=45°,CO⊥AB,∴∠AOM+∠MOC=90°,且∠MOC+∠NOC=90°,∴∠AOM=∠NOC,且AO=CO,∠A=∠BCO,∴△AOM≌△CON(ASA)=S△CON,∴AM=CN,OM=ON,S△AOM∴AC=AM+CM=CM+CN=8故①②④符合题意,=S△OMC+S△ONC=S△OMC+S△AOM=S△AOC=S△ACB,∵S四边形OMCN=××8×8=16,∴S四边形OMCN故③不符合题意;故答案为:①②④.16.如图,在平面直角坐标系中有一边长为1的正方形OABC,边OA,OC分别在x轴,y 轴上,如果以对角线OB为边作第二个正方形OBB1C1,再以对角线OB1为边作第三个正方形OB1B2C2,照此规律作下去,则点B2019的坐标为(0,﹣21010).【考点】规律型:点的坐标.【分析】首先求出B1、B2、B3、B4、B5、B6、B7、B8、B9的坐标,找出这些坐标的之间的规律,然后根据规律计算出点B2019的坐标.【解答】解:∵正方形OABC边长为1,∴OB=,∵正方形OBB1C1是正方形OABC的对角线OB为边,∴OB1=2,∴B1点坐标为(2,0),同理可知OB2=2,B2点坐标为(2,﹣2),同理可知OB3=4,B3点坐标为(0,﹣4),B4点坐标为(﹣4,﹣4),B5点坐标为(﹣8,0),B6(﹣8,8),B7(0,16)B8(16,16),B9(32,0),由规律可以发现,每经过8次作图后,点的坐标符号与第一次坐标符号相同,每次正方形的边长变为原来的倍,∵2019÷8=252…3,∴B2019的横坐标,与点B3的相同为0,横纵坐标都是负值,∴B2013的坐标为(0,﹣21010).故答案为:(0,﹣21010).17.如图,四个小正方形的边长都是1,若以O为圆心,OG为半径作弧分别交AB、DC于点E、F,则图中阴影部分的面积为.【考点】扇形面积的计算.【分析】先根据OD=OF得出∠DOF=60°,同理可得出∠AOE=60°,进而得出∠EOF的度数,根据扇形的面积公式即可得出结论.【解答】解:∵OD=1,OF=OG=2,∴cos∠DOF==,∴∠DOF=60°.同理,∠AOE=60°,∴∠EOF=180°﹣60°﹣60°=60°,∴图中阴影部分的面积==.故答案为:.18.如图:点E、F分别是菱形ABCD的边BC、CD上的点,且∠EAF=∠D=60°,∠FAD =45°,则∠CFE=45度.【考点】菱形的性质;等边三角形的判定.【分析】首先证明△ABE≌△ACF,然后推出AE=AF,证明△AEF是等边三角形,最后可求出∠AFD,∠CFE的度数.【解答】解:连接AC,∵菱形ABCD,∴AB=BC,∠B=∠D=60°,∴△ABC为等边三角形,∠BCD=120°∴AB=AC,∠ACF=∠BCD=60°,∴∠B=∠ACF,∵△ABC为等边三角形,∴∠BAC=60°,即∠BAE+∠EAC=60°,又∠EAF=60°,即∠CAF+∠EAC=60°,∴∠BAE=∠CAF,在△ABE与△ACF中∴△ABE≌△ACF(ASA),∴AE=AF,又∠EAF=∠D=60°,则△AEF是等边三角形,∴∠AFE=60°,又∠AFD=180°﹣45°﹣60°=75°,则∠CFE=180°﹣75°﹣60°=45°.故答案为:45.19.如图,矩形ABCD中,点A坐标是(﹣1,0),点C的坐标是(2,4),则BD的长是5.【考点】矩形的性质;坐标与图形性质.【分析】利用矩形的性质得出BD=AC,求得线段AC的长即可得出BD的长.【解答】解:连接AC、BD,如图:∵四边形ABCD是矩形,∴BD=AC,∵点A的坐标是(﹣1,0),点C的坐标是(2,4),∴AC==5,∴BD=AC=5,故答案为5.20.在平面直角坐标系中,四边形AOBC是菱形,若点A的坐标是(3,4),则菱形的周长为20,点C的坐标是(8,3).【考点】菱形的性质;坐标与图形性质.【分析】过A作AE⊥x轴于点E,根据勾股定理可求出OA的长,进而可求出菱形的周长,再由菱形的性质可得AO=AC=BO=BC=5,即可求出点C的坐标.【解答】解:过A作AE⊥x轴于点E,∵点A的坐标是(3,4),∴OE=3,AE=4.∴AO==5,∵四边形AOBC是菱形,∴AO=AC=BO=BC=5,∴菱形的周长=4AB=20,点C的坐标是(8,3),故答案为:20,(8,3).三、解答题21.如图,在△ABC中,点D,E分别是AB,AC的中点,F是BC延长线上的一点,且CF =BC.试猜想DE与CF有怎样的数量关系,并说明理由.【考点】三角形中位线定理.【分析】根据三角形中位线定理得到DE=BC,等量代换,得到答案.【解答】解:DE=CF,理由如下:∵点D,E分别是AB,AC的中点,∴DE=BC,∵CF=BC,∴DE=CF.22.如图,∠MON=90°,正方形ABCD的顶点A、B分别在OM、ON上,AB=13,OB=5,E为AC上一点,且∠EBC=∠CBN,直线DE与ON交于点F.(1)求证:BE=DE;(2)判断DF与ON的位置关系,并说明理由;(3)△BEF的周长为24.【考点】正方形的性质;全等三角形的判定与性质.【分析】(1)利用正方形的性质,即可得到△BCE≌△DCE(SAS),根据全等三角形的性质即可得到BE=DE.(2)依据∠EDC=∠CBN,∠EDC+∠1=90°,∠1=∠2,即可得出∠2+∠CBN=90°,进而得到DF⊥ON;(3)过C作CG⊥ON于G,过D作DH⊥CG于H,则∠CGB=∠AOB=90°,四边形DFGH是矩形,利用全等三角形的对应边相等,即可得到DF=HG=17,GF=DH=5,BF=BG﹣GF=7,进而得出△BEF的周长.【解答】解:(1)∵四边形ABCD正方形,∴CA平分∠BCD,BC=DC,∴∠BCE=∠DCE=45°,∵CE=CE,∴△BCE≌△DCE(SAS),∴BE=DE.(2)DF⊥ON,理由如下:∵△BCE≌△DCE,∴∠EBC=∠EDC,∵∠EBC=∠CBN,∴∠EDC=∠CBN,∵∠EDC+∠1=90°,∠1=∠2,∴∠2+∠CBN=90°,∴∠EFB=90°,即DF⊥ON;(3)如图所示,过C作CG⊥ON于G,过D作DH⊥CG于H,则∠CGB=∠AOB=90°,四边形DFGH是矩形,又∵∠ABC=90°,∴∠ABO+∠BAO=90°=∠ABO+∠CBG,∴∠BAO=∠CBG,又∵AB=BC,∴△ABO≌△BCG(AAS),∴BG=AO==12,CG=BO=5,同理可得△CDH≌△BCG,∴DH=CG=5,CH=BG=12,∴HG=5+12=17,∴DF=HG=17,GF=DH=5,∴BF=BG﹣GF=12﹣5=7,∴△BEF的周长=BF+EF+BE=BF+EF+DE=BF+DF=7+17=24,故答案为:24.23.盈盈同学要证明命题“两组对边分别相等的四边形是平行四边形”是正确的,她先用尺规作出了如图1的四边形ABCD,并写出了如下不完整的已知和求证.已知:如图1,在四边形ABCD中,BC=AD,AB=CD.求证:四边形ABCD是平行四边形.(1)填空,补全已知和求证;(2)按盈盈的想法写出证明;(3)用文字叙述所证命题的逆命题为平行四边形两组对边分别相等.【考点】作图—复杂作图;平行四边形的判定.【分析】(1)命题的题设为“两组对边分别相等的四边形”,结论是“是平行四边形”,根据题设可得已知:在四边形ABCD中,BC=AD,AB=CD,求证:四边形ABCD是平行四边形;(2)连接BD,利用SSS定理证明△ABD≌△CDB可得∠ADB=∠DBC,∠ABD=∠CDB,进而可得AB∥CD,AD∥CB,根据两组对边分别平行的四边形是平行四边形可得四边形ABCD是平行四边形;(3)把命题“两组对边分别相等的四边形是平行四边形”的题设和结论对换可得平行四边形两组对边分别相等.【解答】解:(1)已知:如图1,在四边形ABCD中,BC=AD,AB=CD求证:四边形ABCD是平行四边形.(2)证明:如图1,连接BD,在△ABD和△CDB中,,∴△ABD≌△CDB(SSS),∴∠ADB=∠DBC,∠ABD=∠CDB,∴AB∥CD,AD∥CB,∴四边形ABCD是平行四边形;(3)用文字叙述所证命题的逆命题为:平行四边形两组对边分别相等.故答案为:平行四边形两组对边分别相等.24.已知:如图,在平行四边形ABCD中,点E是边AD上一点,分别连接BE,CE,若点F,G,H分别是EC,BC,BE的中点.(1)求证:四边形EFGH是平行四边形;(2)设四边形EFGH的面积为S1,四边形ABCD的面积为S2,请直接写出S1:S2的值.【考点】平行四边形的判定与性质;三角形中位线定理.【分析】(1)由中位线定理可得出结论;=S△GFC,S△GEH=S△GHB,S1=S△BCE;可得出答案.(2)连接GE,则S△GEF【解答】(1)证明:∵点F,G,H分别是EC,BC,BE的中点,∴GF∥BE,且GF=BE=HE,∴四边形EFGH是平行四边形;(2)解:∵点F,H分别是EC,BE的中点,连接GE;=S△GFC,S△GEH=S△GHB,则S△GEF∴S1=S△BCE;又S2=2S△BCE,∴S1:S2=1:4.25.如图,AC为正方形ABCD的对角线,E为AC上一点,且AB=AE,EF⊥AC,交BC 于F,试说明EC=EF=BF.【考点】正方形的性质;全等三角形的判定与性质.【分析】通过△AEF≌△ABF,可以求证FE=FB,然后证得△CEF为等腰直角三角形即可.【解答】解:在Rt△AEF和Rt△ABF中,,∴Rt△AEF≌Rt△ABF(HL),∴FE=FB.∵正方形ABCD,∴∠ACB=∠BCD=45°,在Rt△CEF中,∵∠ACB=45°,∴∠CFE=45°,∴∠ACB=∠CFE,∴EC=EF,∴FB=EC=EF.26.已知,如图,△ABC中,∠A=90°,D是AC上一点,且∠ADB=2∠C,P是BC上任一点,PE⊥BD于E,PF⊥AC于F.(1)求证:CD=BD;(2)写出线段AB,PF和PE之间数量关系,并证明你的结论.【考点】全等三角形的判定与性质.【分析】(1)根据三角形的一个外角等于与它不相邻的两个内角的和可得∠ADB=∠C+∠DBC,然后求出∠C=∠DBC,再根据等角对等边可得CD=BD;(2)连接PD,利用△BCD的面积列式求解即可得到PE+PF=AB.【解答】证明:(1)在△BCD中,∠ADB=∠C+∠DBC,∵∠ADB=2∠C,∴∠C=∠DBC,∴CD=BD;(2)连接PD,=BD•PE+CD•PF=CD•AB,则S△BCD∵CD=BD,∴PE+PF=AB.27.如图,△ABC中,D、E分别是AB、AC的中点,延长DE至点F,使EF=DE,连接CF,证明:四边形DBCF是平行四边形.【考点】平行四边形的判定;三角形中位线定理.【分析】只要证明DF=BC,DF∥BC,即可解决问题;【解答】证明:∵D、E分别是AB、AC的中点,∴DE=BC,DE∥BC,又EF=DE,∴DF=DE+EF=BC,∴四边形DBCF是平行四边形.28.如图,在四边形纸片ABCD中,∠B=∠D=90°,点E,F分别在边BC,CD上,将AB,AD分别沿AE,AF折叠,点B,D恰好都和点G重合,∠EAF=45°.(1)求证:四边形ABCD是正方形;(2)若EC=FC=1,求AB的长度.【考点】翻折变换(折叠问题);正方形的判定与性质.【分析】(1)根据邻边相等的矩形是正方形证明即可.(2)解直角三角形求出EC,EG,FG即可解决问题.【解答】(1)证明:由题意得,∠BAE=∠EAG,∠DAF=∠FAG,∴∠BAD=2∠EAF=90°,∴四边形ABCD是矩形,∵AB=AG,AD=AG,∴AB=AD,∴四边形ABCD是正方形.(2)解:∵EC=FC=1,∴BE=DF,∴EF=,∵EF=BE+DF,∴BE=DF=EF=,∴AB=BC=BE+EC=+1.29.如图,△ABC是边长为6的等边三角形,P是AC边上一动点,由A向C运动(与A,C不重合),Q是CB延长线上一点,由B向CB延长线方向运动(Q不与B重合),连接PQ交AB于D,过P作PE⊥AB于E.若两点同时出发,以相同的速度每秒1个单位运动,运动时间为t.(1)当∠PQC=30°时,求t的值;(2)求证:PD=DQ;(3)当P,Q在运动过程中线段ED的长是否发生变化?如果不变,求出线段ED的长;如果变化请说明理由.【考点】三角形综合题.【分析】(1)先判断出∠QPC是直角,再利用含30°的直角三角形的性质得出QC=2PC,建立方程求解决即可;(2)作QF⊥AB交AB的延长线于点F,证明△BQF≌△APE(AAS),得出QF=PE,证明△PDE≌△QDF(AAS),由全等三角形的性质得出PD=QD;(3)连接QE,PF,利用等边三角形的性质信平行四边形的性质可得出答案.【解答】(1)解:∵△ABC是边长为6的等边三角形,∴∠ACB=60°,∵∠PQC=30°,∴∠QPC=90°,∵P、Q每秒运动1个单位,运动时间为t,设AP=t,则PC=6﹣t,QB=t,∴QC=QB+BC=6+t,在Rt△QCP中,∠PQC=30°,∴PC=QC,即,解得t=2;(2)证明:如图,作QF⊥AB交AB的延长线于点F,由点P、Q做匀速运动且速度相同,可知AP=BQ,在△BQF和△APE中,∵∠F=∠AEP=90°,∠FBQ=∠ABC=60°=∠A,BQ=AP,∴△BQF≌△APE(AAS),∴QF=PE,在△PDE和△QDF中,∵∠PDE=∠QDF,∠PED=∠F=90°,PE=QF,∴△PDE≌△QDF(AAS),∴PD=QD;(3)解:当点P、Q运动时,线段ED的长度不会改变,ED=3,理由如下:如图,连接QE,PF,∵PE⊥AB,QF⊥AB,∴PE∥QF,又∵PE=QF(已证),∴四边形PEQF是平行四边形,∵△BQF≌△APE(已证),∴BF=AE,∴AB=EB+AE=BE+BF=EF,又∵△PDE≌△QDF(已证),∴ED=DF=EF=AB,∵等边△ABC的边长为6,∴ED=AB=3,故当点P、Q运动时,线段ED的长度不会改变.。
人教版-八年级数学下册----第十八章--平行四边形-单元检测卷(含答案)
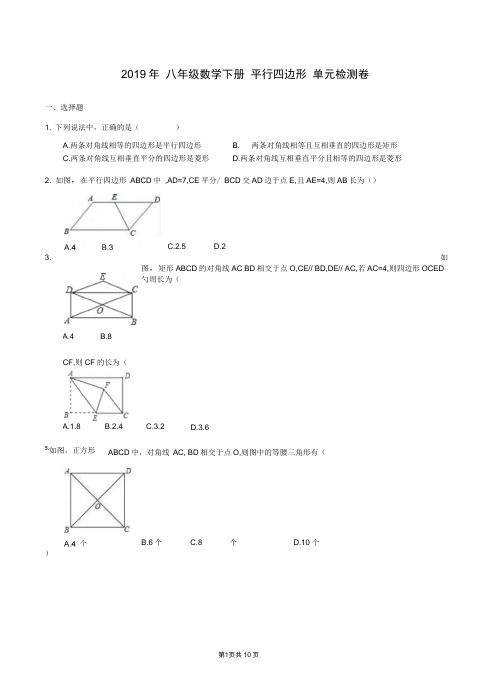
2019年 八年级数学下册 平行四边形 单元检测卷一、选择题1. 下列说法中,正确的是( )A.两条对角线相等的四边形是平行四边形B. 两条对角线相等且互相垂直的四边形是矩形C.两条对角线互相垂直平分的四边形是菱形D.两条对角线互相垂直平分且相等的四边形是菱形2. 如图,在平行四边形 ABCD 中 ,AD=7,CE 平分/ BCD 交AD 边于点E,且AE=4,则AB 长为()3.如图,矩形ABCD 的对角线AC BD 相交于点O,CE// BD,DE// AC,若AC=4,则四边形OCED勺周长为() D.2C.3.2D.3.6 5.如图,正方形 ABCD 中,对角线 AC, BD 相交于点O,则图中的等腰三角形有(C.8 个D.10 个C.2.5 A.4B.8CF,则CF 的长为(A.1.8B.2.4 B.6个C.10D.124. 如图,在矩形ABCD中,AB=4,BC=6,点E为BC的中点,将△ ABE沿AE折叠,使点B落在矩形F处,连接内点6.如图,正方形ABCD勺边长为8,在各边上顺次截取AE=BF=CG=DH=5则四边形EFGH勺面积是(7. 对角线相等且互相平分的四边形是(A.30B.34C.36D.40 A. 一般四边形 B. 平行四边形 C. 矩形 D. 菱形8.如图,在平面直角坐标系中,以 0(0, 0), A (1, 1) , B (3, 0)为顶点,构造平行四边形,下列各点中不能作为平行四边形顶点坐标的是(B • (4, 1)C . (- 2, 1) 9.四个点A , B , C,D 在同一平面内,从① AB// CD ②AB=CD ③AC 丄BD ④AD=?BC ⑤AD// BC 这5个条件中任选三个,能使四边形ABCD 是菱形的选法有( )•A.1种B.2C.3D.410.如图,正方形ABCD 的面积为1,则以相邻两边中点连线 EF 为边正方形EFGH 的周长为() B.2C. +1D.2 +1 11.如图,正方形ABCD 的边长为 9,将正方形折叠,使顶点D 落在BC 边上的点E 处,折痕为GH.C.5D.6A. (- 3, 1)A. A.3B.4 CH 的长是(12.如图,?ABCD的对角线AC BD交于点O,AE平分/ BAD交BC于点E,且/ ADC=60 ,2AB=BC,连接0E•下列结论:①/ CAD=30 :②S ABC=AB?AC;③OB=AB④40E=BC成立个数有()A.1个B.2 个C.3 个D.4 个二、填空题13・如图,在△ ABC中,点D E分别是边AB AC的中点,已知DE=6cm贝U BC= _______ cm.14.___________________________________________________________________________________ 如图,在?ABCD中,对角线AC BD相交于点0.如果AC=8,BD=14,AB=x,那么x取值范围是_________________15.如图,在四边形ABCD中, E、F、G H分别是AB BD CD AC的中点,要使四边形EFGH是菱形,四边16.如图,将矩形纸片ABC[折叠,使边AB CB均落在对角线BDk,得折痕BE、BF,则/ EBF=317.如图,设四边形ABCD是边长为1的正方形,以正方形ABCD的对角线AC为边作第二个正方形ACEF再以第二个正方形的对角线AE为边作第三个正方形AEGH如此下去…,记正方形ABCD的边长a i=1, 依上述方法所作的正方形的边长依次为a2, a s, a4,…,贝U a n= _______ .18.矩形纸片ABC中,AB=3cm BC=4cm现将纸片折叠压平,使A与C重合,设折痕为EF,则重叠部分△ 的面积等于 ________________ .19.图①,图②,图③都是4X 4的正方形网格,每个小正方形的顶点称为格点,每个小正方形的边长均为图①,图②中已画出线段AB,在图③中已画出点 A.按下列要求画图:(1) 在图①中,以格点为顶点,AE为一边画一个等腰三角形;(2) 在图②中,以格点为顶点,AB为一边画一个正方形;(3) 在图③中,以点A为一个顶点,另外三个顶点也在格点上,画一个面积最大的正方形.图①图②圍③AEF3 E C三、作图题1 .在H A B四、解答题如图,将?ABCD 沿 CE 折叠,使点 D 落在BC 边上的F 处,点E 在AB 上.如图,在平行四边形 ABC 中,BE 、CE 分别平分/ ABG / BCD,E 在ADh , BE=12cm,CE=5cm 求平行四边形 ABCD如图,正方形 ABCD 中,以对角线 BD 为边作菱形 BDFE 使B , C, E 三点在同一直线上,连接 BF ,交CD 与点G.20. 21. 22. (1)求证:四边形 ABFE 为平行四边形;(1)求证:CG=CE23・如图,在四边形 ABC 中,/ ABC=90 ,AC=AD,M,N 分别为AC,AD 的中点,连接 BM,MN,BN.(1) 求证:BM=MN;(2) / BAD=60 ,AC 平分/ BAD,AC=2,求 BN 的长。
人教版初中八年级下册数学第十八章单元检测卷2附答案解析

第十八章卷(2)一、选择题1.如图,已知四边形ABCD是平行四边形,下列结论中不正确的是()时,它是菱形⊥BD时,它是菱形B.当ACA.当AB=BC时,它是正方形AC=BDD.当.当∠ABC=90°时,它是矩形C).下列命题中正确的是(2对C.对角线互相平分的四边形是菱形B.对角线互相平分且相等的四边形是菱A..对角线互相垂直平分的四边形是菱形角线互相垂直的四边形是菱形D、、GE、F.3如图,某花木场有一块等腰梯形ABCD的空地,其各边的中点分别是场地,则需篱笆得总长,现想利用篱笆围成四边形EFGHH,测得对角线AC=10m)度是(10 mD..B.30 m C20 m A.40 m,则该梯形的面BD=6BD⊥,且AC=10,ABCD4.在梯形中,AD∥BC,对角线AC)积是(60D.15 30 B.C..ARPAP、分别是上的点,分别是R、PDC、BCE、F中,.如图,已知矩形5ABCD)那么下列结论成立的是RCBBCP的中点,当在上从向移动而不动时,(的长不改变EFC.线段B.线段EF的长逐渐减小A.线段EF的长逐渐增大的长不能确定.线段EFD,那么另一腰的,这腰与一底所成的角为30°6.已知一个直角梯形,一腰长为6)长是(9D.C.6 A.1.5 B.3个洞,则纸片展开.如图所示,将一张正方形纸片对折两次,然后在上面打37)后是(..C DA.B..用两个全等的直角三角形拼下列图形:①矩形;②菱形;③正方形;④平行8)四边形;⑤等腰三角形;⑥等腰梯形.其中一定能拼成的图形是(.②⑤⑥D.①④⑤A.①②③ B C.①②⑤二、填空题度.则∠BDC=70°中,如图,在平行四边形ABCDDB=DC,∠,AE ⊥于E,DAE=.9是平行四边形,AECFBDABCD在、.如图,点10EF?的对角线上,要使四边形..还需添加一个条件(只需写出一个结论,不必考虑所有情况).如图所示,工人师傅做铝合金窗框分下面三个步骤进行:11.,EF=GH先截出两对符合规格的铝合金窗料(如图①所示),使AB=CD(1).,根据的数学道理是(2)摆放成如图②的四边形,则这时窗框的形状是,调整窗框的边框,当直角尺的两条直角将直尺紧靠窗框的一个角(如图③)(3),根据的数学道理边与窗框无缝隙时(如图④,说明窗框合格,这时窗框是.是,重合)不与A、C,AC=2,BD=5P是AC上一动点(P中,12.如图,菱形ABCD)的,则图中阴影部分(即多边形BCPFEBAD∥CD交于FPFABPE∥BC交于E,.面积为,若再补充一个条件OBDABCD13.如图所示,菱形中,对角线AC,相交于点(只填一个条件即可,答案不.成为正方形,则这个条件是能使菱形ABCD唯一)14.等腰梯形两底之差为12cm,高为6cm,则其锐角底角为度.15.若矩形的对角线长为8cm,两条对角线的一个交角为60°,则该矩形的面积2.cm为三、解答题16.已知:如图,在梯形ABCD中,AD∥BC,CD=10cm,∠B=45度,∠C=30度,AD=5cm.求:(1)AB的长;(2)梯形ABCD的面积.48cm.:的度数比为12,周长是.如图,在菱形17ABCD中,∠A与∠B两条对角线的长度;(1)求:菱形的面积.(2).求证:DE=BFAC上的两点,且AE=CF.是中,.18如图,在平行四边形ABCDE、F上,BCFEDCAFDEABBCADABCD19.如图,在梯形中,∥,∥,∥,、两点在边是平行四边形.AEFD且四边形.有何等量关系,请说明理由;与BC(1)AD是矩形.时,求证:平行四边形AEFD(2)当AB=DC∥CEO,于点ABD,交AC于点的垂直平分线.如图,△20ABC中,ACMN交的形状,说明理由.ADCE、AECD.请判断四边形于AB交MNE,连接答案1.如图,已知四边形ABCD是平行四边形,下列结论中不正确的是()时,它.当∠ABC=90°BDAC⊥时,它是菱形CA.当AB=BC时,它是菱形B.当时,它是正方形.当AC=BD是矩形D正方形的判定;平行四边形的性质;菱形的判定;矩形的判定.【考点】选择题.【专题】根据邻边相等的平行四边形是菱形;根据所给条件可以证出邻边相等;【分析】根据对角线相等的平行四边形是矩形.根据有一个角是直角的平行四边形是矩形;是平行、根据邻边相等的平行四边形是菱形可知:四边形ABCD【解答】解:A选项正确;A时,它是菱形,故四边形,当AB=BC222,+BD,∴AB=BOAOBO=ODB、∵四边形ABCD是平行四边形,∴,∵AC⊥222选项正确;是菱形,故BABCD,∴AB=ADAD=DO,∴四边形+AO选项正确;、有一个角是直角的平行四边形是矩形,故CC时,它是矩形,不是正方、根据对角线相等的平行四边形是矩形可知当AC=BDD 选项错误;形,故D选项;D综上所述,符合题意是.D故选菱形的判定和平行四边形的性质、【点评】此题主要考查学生对正方形的判定、矩形的判定的理解和掌握,此题涉及到的知识点较多,学生答题时容易出错.)2.下列命题中正确的是(对..对角线互相平分且相等的四边形是菱C.A对角线互相平分的四边形是菱形B.对角线互相垂直平分的四边形是菱形角线互相垂直的四边形是菱形D菱形的判定.【考点】选择题.【专题】对角线互相垂直平分的四边形是菱形.【分析】解:根据菱形的判定,知对角线互相垂直平分的四边形是菱形,【解答】A、B、C错误,D正确.故选D.【点评】本题考查菱形的判定方法.3.如图,某花木场有一块等腰梯形ABCD的空地,其各边的中点分别是E、F、G、H,测得对角线AC=10m,现想利用篱笆围成四边形EFGH场地,则需篱笆得总长度是()10 m..20 m D40 m B.30 m C.A三角形中位线定理.【考点】选择题.【专题】,BDEF=GH=AC,EH=GF=【分析】据等腰梯形的性质和三角形的中位线定理有的周长,即需篱笆的周长=4EF=2AC,进而可得出四边形EFGH可知四边形EFGH得总长.解:如图,连接BD,【解答】各边中点,H、G、是等腰梯形ABCDF∵E、,BD,∴EF=GH=ACEH=GF=,∵等腰梯形ABCD,∴BD=AC.的周长=4EF=2AC=20mEFGH∴四边形.故选CEFGH得出四边形此题主要考查了等腰梯形的性质和三角形中位线定理,【点评】.的周长与AC的关系是解题的关键,难度一般.4.在梯形ABCD中,AD∥BC,对角线AC⊥BD,且AC=10,BD=6,则该梯形的面积是()60.D.15 C.A.30 B根据边的关系判定平行四边形.【考点】选择题.【专题】÷×6【分析】根据对角线互相垂直的四边形的面积公式,得该梯形的面积是10.2=30EBC延长线于∥AC交DE【解答】解:如图,作BC∥∵AD为平行四边形ADEC∴四边形DCA,∠CDE=∠∴CE=AD,AC⊥BD∵,AC⊥DE∴为直角三角形,∴△BDE,S=S∴EBDABCD△梯,÷2=30×∴S=DE?BD=AC?BD=106ABCD梯.故选A对角线互相垂直的四边形的面积等于根据三角形的面积公式可以导出:【点评】两条对角线乘积的一半.RP、APEDC、P分别是、BC上的点,、F分别是RABCD5.如图,已知矩形中,)不动时,移动而向上从在当的中点,PBCBCR那么下列结论成立的是(的长不改变.线段EF.线段EF的长逐渐减小CA.线段EF的长逐渐增大B的长不能确定.线段EF D三角形中位线定理.【考点】选择题.【专题】不变.不变.根据中位线定理,EFR不动,所以AR【分析】因为.【解答】解:连接AR的中点,AP、RP因为E、F分别是的中位线,为△APR则EF,为定值.AR所以EF=的长不改变.EF所以线段.故选C不变,则对应的【点评】本题考查了三角形的中位线定理,只要三角形的边AR 中位线的长度就不变.,那么另一腰的6,这腰与一底所成的角为30°6.已知一个直角梯形,一腰长为)长是(96C.D..A.1.5 B3【考点】根据边的关系判定平行四边形.选择题.【专题】的直角三角形,根据直角三30°作梯形的另一高,则得一个矩形和一个【分析】.,即是所对的直角边是斜边的一半,得另一腰是已知腰的330°角形中,,BC⊥DE解:作【解答】.,∥BC∵AD为平行四边形,ABED∴四边形,AB=DE∴,C=30°又∠.∴DE=DC=3.故选B的直角三角注意:直角梯形中常见的辅助线即作另一高.熟练运用30°【点评】形的性质.个洞,则纸片展开.如图所示,将一张正方形纸片对折两次,然后在上面打37)(.D.C..A B正方形的性质.【考点】选择题.【专题】结合空间思维,分析折叠的过程及打孔的位置,易知展开的形状.【分析】在平行于斜当正方形纸片两次沿对角线对折成为一直角三角形时,【解答】解:个洞.边的位置上打3个洞,则直角顶点处完好,且有12即原正方形中间无损,.D故选错误的主要原因是空间观念以及转化【点评】本题主要考查学生抽象思维能力,的能力不强,缺乏逻辑推理能力,需要在平时生活中多加培养..用两个全等的直角三角形拼下列图形:①矩形;②菱形;③正方形;④平行8)四边形;⑤等腰三角形;⑥等腰梯形.其中一定能拼成的图形是(A.①②③B.①④⑤C.①②⑤D.②⑤⑥【考点】菱形的判定;等腰三角形的判定;平行四边形的判定;矩形的判定;正方形的判定;等腰梯形的判定.【专题】选择题.【分析】根据菱形、正方形、梯形、矩形、平行四边形、等腰三角形的性质判断.【解答】解:由于菱形和正方形中都四边相等的特点,而直角三角形中不一定有两边相等,故两个全等的直角三角形不能拼成菱形和正方形;由于等腰梯形有两边不等,故也不能.矩形,平行四边形,等腰三角形可以拼成.如图:.故选B本题考查了三角形的拼接图形的特点.以及特殊四边形的性质.【点评】度.则∠DAE=AE⊥BD于E,DB=DC9.如图,在平行四边形ABCD中,,∠C=70°,平行四边形的性质.【考点】填空题.【专题】ADB=推出∠又由AD∥BCDBC=由DB=DC,∠C=70°可以得到∠∠C=70°,【分析】.,由此可以求出∠,而∠AED=90°DAE∠DBC=∠C=70°,DB=DC,∠C=70°【解答】解:∵,∠C=70°∴∠DBC=,BD,AE⊥BC∵AD∥,AED=90°C=70°ADB=∴∠∠DBC=∠,∠.﹣70=20°DAE=90∴∠.故答案为:20°【点评】主要考查了平行四边形的基本性质,并利用性质解题.平行四边形基本性质:①平行四边形两组对边分别平行;②平行四边形的两组对边分别相等;③平行四边形的两组对角分别相等;④平行四边形的对角线互相平分.10.如图,点E、F在?ABCD的对角线BD上,要使四边形AECF是平行四边形,还需添加一个条件.(只需写出一个结论,不必考虑所有情况).平行四边形的判定与性质.【考点】填空题.【专题】也是平行四边形,则要证四边形的两组对边相等,或两使四边形【分析】AECF.组对边分别平行,可添加条件DF=BE.理由如下:解:需要添加的条件可以是:DF=BE【解答】是平行四边形,∵四边形ABCD,BC=AD∥BC,∴AD,ADFCBE=∠∴∠中,与△ADFBCE在△,,(SAS)≌△∴△ADFBCE,CDFCE=AF∴,同理,△ABE≌△,∴CF=AE是平行四边形.∴四边形AECF此题属于开放【点评】此题主要考查了平行四边形的判定以及矩形的判定方法,题熟练掌握各判定定理是解题的关键..如图所示,工人师傅做铝合金窗框分下面三个步骤进行:11.,EF=GH先截出两对符合规格的铝合金窗料(如图①所示),使AB=CD(1).,根据的数学道理是(2)摆放成如图②的四边形,则这时窗框的形状是,调整窗框的边框,当直角尺的两条直角将直尺紧靠窗框的一个角(如图③)(3),根据的数学道理边与窗框无缝隙时(如图④,说明窗框合格,这时窗框是.是【考点】平行四边形的判定;矩形的判定.填空题.【专题】此题主要考查平行四边形,矩形的判定问题,掌握其判定定理,即可作【分析】答.解:平行四边形;两组对边分别相等的四边形是平行四边形;【解答】矩形;由一个角是直角的平行四边形是矩形.熟练掌握平行四边形及矩形的判定.【点评】,重合)AP不与、CACBD=5ABCD12.如图,菱形中,AC=2,,P是上一动点()的,则图中阴影部分(即多边形AD于FBCPFEB交∥,于交∥PEBCABEPFCD.面积为【考点】菱形的性质.【专题】填空题.【分析】根据菱形性质得出AC⊥BD,求出△ABC的面积,求出△AEF的面积和△PEF的面积相等,得出阴影部分的面积等于三角形ABC的面积,即可得出答案.【解答】解:∵四边形ABCD是菱形,,BO=OD=BD=2.5AC⊥BD,∴,BO=2.5×AC×∴△ABC的面积是,DC,AB∥∵AD∥BC,PF∥CD又∵PE∥BC,,∥ADAB∴PF∥,PE是平行四边形,∴四边形AEPF的面积相等,的面积和△PEF∴△AEF.2.5∴阴影部分的面积等于△ABC的面积是.2.5故答案为:平行四边形的性质和判定等知三角形的面积,【点评】本题考查了菱形的性质,识点的应用.,若再补充一个条件相交于点OBD13.如图所示,菱形ABCD中,对角线AC,(只填一个条件即可,答案不.能使菱形ABCD成为正方形,则这个条件是唯一)正方形的判定;菱形的性质.【考点】填空题.【专题】根据菱形的性质及正方形的判定来添加合适的条件.【分析】有一【解答】解:要使菱形成为正方形,只要菱形满足以下条件之一即可,(1)对角线相等.个内角是直角(2).即∠BAD=90°或AC=BD故答案为:∠BAD=90°或AC=BD.【点评】本题比较容易,考查特殊四边形的判定.14.等腰梯形两底之差为12cm,高为6cm,则其锐角底角为度.【考点】根据边的关系判定平行四边形.【专题】填空题.【分析】先作图,过点D作DE∥AB,四边形ABED是平行四边形,根据题意得CE=12cm,△CDE是等腰三角形,从而得出DF=CF=6cm,则锐角底角为45°.【解答】解:过点D作DE∥AB,∵AD∥BC,∴四边形ABED是平行四边形,∴AB=DE,∵AB=CD,∴DE=CD,∴△CDE是等腰三角形,又DF⊥CE,,=6cm﹣AD)CE=∴EF=CF=(BC,∵高DF=6cm,∴DF=CF=6cm.,∴∠DCF=45°而∠DFC=90°还考查了等【点评】本题考查了梯形中辅助线的作法:平移一腰得出两底之差,腰三角形的性质.,则该矩形的面积,两条对角线的一个交角为60°.若矩形的对角线长为158cm2.为cm矩形的性质.【考点】填空题.【专题】根据矩形的性质,画出图形求解.【分析】【解答】解:∵ABCD为矩形∴OA=OC=OB=OD∵一个角是60°cm∴BC=OB===∴根据勾股定理2.=cm∴面积=BC?CD=4×.故答案为本题考查的知识点有:矩形的性质、勾股定理.【点评】度,∠C=30,如图,在梯形ABCD中,AD∥BCCD=10cm,∠B=45度,已知:16.的面积.梯形AD=5cm.求:(1)AB的长;(2)ABCD.矩形的判定定理2【考点】解答题.【专题】角所对的直角边等于斜边的一半可E,根据30°BCD【分析】(1)过点作DE⊥于然后根据等腰直角三角形斜边等CD得DE=,再判断△ABH是等腰直角三角形,倍解答;于直角边的的长,再求出,BCHE=AD是矩形,先判定四边形(2)AHED根据矩形对边相等求出然后根据梯形的面积公式列式进行计算即可得解.,E于BC⊥DE作D如图,过点(1)解:【解答】.,CD=10cmC=30°,∵∠,10=5cm∴DE=CD=×,AH=DE=5cmBC于H,则A过作AH⊥,B=45°∵∠是等腰直角三角形,ABH∴△;AH=5cm∴AB=都是梯形的高线,、DE(2)∵AH是矩形,AHED∴四边形,HE=AD=5cm∴,=CE==5cm又∵BH=AH=5cm,,)(=10+5cm++∴BC=BH+HECE=5+555105=的面积(+.(5)×=+)cm+∴梯形ABCD角所对的直角边等于斜边的一【点评】30°本题考查了梯形的性质,直角三角形熟记性质并作出辅勾股定理的应用,等腰直角三角形的判定与性质,半的性质,助线是解题的关键.21BAABCD17.如图,在菱形中,∠与∠的度数比为:,周长是.48cm两条对角线的长度;(1)求:菱形的面积.(2)菱形的性质.【考点】解答题.【专题】【分析】在菱形ABCD中,∠A与∠B互补,即∠A+∠B=180°,因为∠A与∠B的度数比为1:2,就可求出∠A=60°,∠B=120°,根据菱形的性质得到∠BDA=120°,根据勾股定理得到×=12cm,则△ABD是正三角形,所以BD=AB=48×=60°的值;然后根据菱形的面积公式求解.AC,BD连接【解答】解:(1),2的度数比为1:BA+∠B=180°,∠A与∠互补,即∠∵∠A与∠B.B=120°∴∠A=60°,∠.BDA=120°×=60°∴∠是正三角形.∴△ABD.=12cm∴BD=AB=48×.cmAC=2×=12AC=12,∴cm.BD=12cm212=×=72cm×12=(2)S×两条对角线的乘积ABCD菱形本题考查的是菱形的面积求法及菱形性质的综合.【点评】.求证:AE=CF上的两点,F是AC且.DE=BF、中,在平行四边形.18如图,ABCDE平行四边形的性质.【考点】解答题.【专题】,再由已知条件,可得△BCF∠,∠AD=CB由平行四边形的性质得【分析】DAE=,进而得出结论.≌△ADECBF【解答】证明:在平行四边形ABCD中,则AD=CB,∠DAE=∠BCF,又AE=CF,∴△ADE≌△CBF(SAS),∴DE=BF.【点评】本题主要考查平行四边形的性质及全等三角形的判定问题,应熟练掌握.19.如图,在梯形ABCD中,AD∥BC,AB∥DE,AF∥DC,E、F两点在边BC上,且四边形AEFD是平行四边形.有何等量关系,请说明理由;与BC(1)AD是矩形.AEFD当AB=DC时,求证:平行四边形(2)平行四边形的性质;矩形的判定.【考点】解答题.【专题】都是平行AFCDABED和四边形【分析】(1)由题中所给平行线,不难得出四边形所,三个平行四边形都共有一条边AD四边形,而四边形AEFD也是平行四边形,的结论.BCAD=以可得出AF=DE根据矩形的判定和定义,对角线相等的平行四边形是矩形.只要证明(2)即可得出结论..解:AD=BC【解答】(1)理由如下:,DC∥ABDE,AF∥∥∵ADBC,都是平行四边形.∴四边形ABED和四边形AFCD,AD=BE,AD=FC∴是平行四边形,AEFD又∵四边形.∴AD=EF.∴AD=BE=EF=FC.AD=∴BC(2)证明:∵四边形ABED和四边形AFCD都是平行四边形,∴DE=AB,AF=DC.∵AB=DC,∴DE=AF.又∵四边形AEFD是平行四边形,∴平行四边形AEFD是矩形.【点评】本题考查了梯形、平行四边形的性质和矩形的判定,是一道集众多四边形于一体的小综合题,难度中等稍偏上的考题.有的学生往往因为基础知识不扎实,做到一半就做不下去了,建议老师平时教学中,重视一题多变,适当地变式联系,可以触类旁通.20.如图,△ABC中,AC的垂直平分线MN交AB于点D,交AC于点O,CE∥AB交MN于E,连接AE、CD.请判断四边形ADCE的形状,说明理由.菱形的判定;线段垂直平分线的性质.【考点】解答题.【专题】,根据中垂线的性质中垂线上的点线段两个端点的距离相等可得出【分析】AE=CE,从CEO≌△AB,可证得△ADO∠OA=OC∠AOD=EOC=90°,再结合CE∥,AD=CD,OD=OE而根据由一组对边平行且相等知,四边形ADCE是平行四边形,结合可证得为菱形.AOD=90°OA=OC,∠是菱形.ADCE【解答】四边形的垂直平分线,是AC证明:∵MN,∠AOD=EOC=90°,∴AE=CE,AD=CDOA=OC,∠,AB∵CE∥,∠∴∠DAO=ECO∴△ADO≌△CEO.(ASA)∴AD=CE,OD=OE,∵OD=OE,OA=OC,∴四边形ADCE是平行四边形又∵∠AOD=90°,∴?ADCE是菱形.【点评】本题考查了菱形的判定及线段垂直平分线的性质,利用了:中垂线的性质;全等三角形的判定和性质;平行四边形和菱形的判定.。
人教版八年级下册数学第十八章单元同步检测试题(含答案)

人教版八年级下册数学第十八章单元同步检测试题(含答案)一、选择题1.已知AB∥CD,AD∥BC,则四边形ABCD是()A.平行四边形B.矩形C.菱形D.正方形2.已知菱形ABCD的对角线AC、BD的长分别为10cm、24cm,则这个菱形的周长为()A.13cm B.26cm C.48cm D.52cm3.如图,矩形ABCD中,对角线AC,BD相交于点O,下列结论不一定成立的是()A.∠ABC=90°B.AC=BD C.AB=CD D.OA=AB4.如图,在▱ABCD中,AE平分∠BAD,交CD边于E,AD=6,EC=4,则AB的长为()A.1B.6C.10D.125.如图,平行四边形ABCD的对角线AC,BD交于点O,顺次连接四边形ABCD各边中点得到一个新的四边形,如果添加下列四个条件中的一个条件:①AC⊥BD,②△ABO与△CBO周长相等;③∠DAO=∠CBO;④∠DAO=∠BAO,可以使这个新的四边形成为矩形,那么这样的条件个数是()A.1个B.2个C.3个D.4个6.如图,在正方形ABCD的边BC的延长线上取一点E,使CE=AC,连接AE交CD于F,则∠AFC 等于()A.112.5°B.120°C.135°D.145°7.如图,在▱ABCD中,AB=6,BC=10,AC的垂直平分线交AD于点E,连接CE,则△CDE的周长为()A.8B.10C.12D.168.如图,在矩形ABCD中,AB=4,BC=6,点E为BC的中点,将△ABE沿AE折叠,使点B落在矩形内点F处,连接CF,则CF的长为()A.B.C.D.9.如图,在菱形ABCD中,∠D=135°,AD=3,CE=2,点P是线段AC上一动点,点F是线段AB上一动点,则PE+PF的最小值()A.2B.3C.2D.10.如图,正方形ABCD中,点E、F、G分别为边AB、BC、AD上的中点,连接AF、DE交于点M,连接GM、CG,CG与DE交于点N,则结论①GM⊥CM;②CD=DM;③四边形AGCF是平行四边形;④∠CMD=∠AGM中,正确的有()个.A.1B.2C.3D.4二、填空题11.平行四边形ABCD中,AB、BC、CD的长度分别为2x+1,3x,x+4,则平行四边形ABCD的周长为.12.四边形ABCD中,AD∥BC,且AD=BC,当∠A=时,四边形ABCD是矩形.13.已知:正方形ABCD的边长等于8cm,那么边AB的中点M到对角线BD的距离等于cm.14.如图,直线l是矩形ABCD的一条对称轴,点P是直线l上一点,且使得△P AB和△PBC均为等腰三角形,则满足条件的点P共有个.15.如图,菱形ABCD和菱形ECGF的边长分别为3和4,∠A=120°,则图中阴影部分的面积.16.如图,点A、B、C在同一直线上,且AB=AC,点D、E分别是AB、BC的中点,分别以AB,DE,BC为边,在AC同侧作三个正方形,得到三个平行四边形(阴影部分)的面积分别记作S1、S2、S3,若S1=,则S2+S3=.三、解答题17.如图,在平行四边形ABCD中,O是其对角线AC的中点,EF过点O,求证:BE=DF.18.已知:如图,E,F为▱ABCD的对角线BD上的两点,请你添加一个条件,使得AE=CF.(1)你添加的条件是;(2)根据你添加的条件和题目的已知条件,证明AE=CF.19.如图,在▱ABCD中,DE平分∠ADB,交AB于点E,BF平分∠CBD,交CD于点F.(1)求证:DE=BF;(2)若AD=BD,求证:四边形DEBF是矩形.20.如图,在四边形ABCD中,AD=BC,若将AB沿AD方向平移,则AB与CD完全重合.(1)四边形ABCD是平行四边形吗?请说明理由;(2)若∠A=120°,求∠B,∠C的度数.21.已知:如图,在菱形ABCD中,点E,O,F分别为AB,AC,AD的中点,连接CE,CF,OE,OF.(1)求证:△BCE≌△DCF;(2)当AB与BC满足什么关系时,四边形AEOF是正方形?请说明理由.22.如图,已知正方形ABCD,点E是AB上的一点,连接CE,以CE为一边,在CE的上方作正方形CEFG,连接DG.求证:(1)△CBE≌△CDG;(2)AB=AE+DG.23.如图,在△ABC中,∠ABC=90°,AC的垂直平分线分别与AC,BC及AB的延长线相交于点D,E,F.点O是EF中点,连接BO并延长到G,且GO=BO,连接EG,FG.(1)试判断四边形EBFG的形状,说明理由;(2)求证:BD⊥BG;(3)当AB=BE=1时,求EF的长.24.如图,四边形AOBC是正方形,点C的坐标是(4,0).(Ⅰ)正方形AOBC的边长为,点A的坐标是.(Ⅱ)将正方形AOBC绕点O顺时针旋转45°,点A,B,C旋转后的对应点为A′,B′,C′,求点A′的坐标及旋转后的正方形与原正方形的重叠部分的面积;(Ⅲ)动点P从点O出发,沿折线OACB方向以1个单位/秒的速度匀速运动,同时,另一动点Q从点O出发,沿折线OBCA方向以2个单位/秒的速度匀速运动,运动时间为t秒,当它们相遇时同时停止运动,当△OPQ为等腰三角形时,求出t的值(直接写出结果即可).参考答案一、选择题1.已知AB∥CD,AD∥BC,则四边形ABCD是()A.平行四边形B.矩形C.菱形D.正方形【解答】解:∵AB∥CD,AD∥BC,∴四边形ABCD是平行四边形.故选:A.2.已知菱形ABCD的对角线AC、BD的长分别为10cm、24cm,则这个菱形的周长为()A.13cm B.26cm C.48cm D.52cm【解答】解:设对角线AC,BD相交于O∵四边形ABCD是菱形∴AC⊥BD,AO=CO=5,BO=DO=12∴AB==13∴菱形ABCD的周长=13×4=52故选:D.3.如图,矩形ABCD中,对角线AC,BD相交于点O,下列结论不一定成立的是()A.∠ABC=90°B.AC=BD C.AB=CD D.OA=AB【解答】解:∵四边形ABCD是矩形,∴∠ABC=90°,AC=BD,AB=CD,故A、B、C正确,故选:D.4.如图,在▱ABCD中,AE平分∠BAD,交CD边于E,AD=6,EC=4,则AB的长为()A.1B.6C.10D.12【解答】解:∵四边形ABCD是平行四边形,∴BA∥CD,AB=CD,∴∠DEA=∠EAB,∵AE平分∠DAB,∴∠DAE=∠EAB,∴∠DAE=∠DEA,∴DE=AD=6,∴CD=CE+DE=6+4=10,∴AB=CD=10.故选:C.5.如图,平行四边形ABCD的对角线AC,BD交于点O,顺次连接四边形ABCD各边中点得到一个新的四边形,如果添加下列四个条件中的一个条件:①AC⊥BD,②△ABO与△CBO周长相等;③∠DAO=∠CBO;④∠DAO=∠BAO,可以使这个新的四边形成为矩形,那么这样的条件个数是()A.1个B.2个C.3个D.4个【解答】解:顺次连接四边形的中点,得到的四边形形状和四边形的对角线位置、数量关系有关,利用三角形中位线性质可得:当对角线垂直时,所得新四边形是矩形.①∵AC⊥BD,∴新的四边形成为矩形,符合条件;②∵四边形ABCD是平行四边形,∴AO=OC,BO=DO.∵△ABO与△CBO周长相等,∴AB=BC.根据等腰三角形的性质可知BO⊥AC,∴BD⊥AC.所以新的四边形成为矩形,符合条件;③∵四边形ABCD是平行四边形,∴∠CBO=∠ADO.∵∠DAO=∠CBO,∴∠ADO=∠DAO.∴AO=OD.∴AC=BD,∴四边形ABCD是矩形,连接各边中点得到的新四边形是菱形,不符合条件;④∵∠DAO=∠BAO,BO=DO,∴AO⊥BD,即平行四边形ABCD的对角线互相垂直,∴新四边形是矩形.符合条件.所以①②④符合条件.故选:C.6.如图,在正方形ABCD的边BC的延长线上取一点E,使CE=AC,连接AE交CD于F,则∠AFC 等于()A.112.5°B.120°C.135°D.145°【解答】解:∵四边形ABCD为正方形,∴∠BCD=90°,∴∠DCE=90°,又∵AC是正方形ABCD的对角线,∴∠ACF=45°,∴∠ACE=∠DCE+∠ACF=135°,∵CE=CA,∴∠F AC=∠E=(180°﹣135°)=22.5°∴∠AFD=∠F AC+∠ACF=22.5°+45°=67.5°,∴∠AFC=180°﹣67.5°=112.5°,故选:A.7.如图,在▱ABCD中,AB=6,BC=10,AC的垂直平分线交AD于点E,连接CE,则△CDE的周长为()A.8B.10C.12D.16【解答】解:∵四边形ABCD是平行四边形,∴AD=BC=10,CD=AB=6,∵AC的垂直平分线交AD于点E,∴AE=CE,则CD+DE+CE=CD+DE+AE=CD+AD=16,即△CDE的周长为16,故选:D.8.如图,在矩形ABCD中,AB=4,BC=6,点E为BC的中点,将△ABE沿AE折叠,使点B落在矩形内点F处,连接CF,则CF的长为()A.B.C.D.【解答】解:连接BF,∵BC=6,点E为BC的中点,∴BE=3,又∵AB=4,∴AE==5,由折叠知,BF⊥AE(对应点的连线必垂直于对称轴)∴BH==,则BF=,∵FE=BE=EC,∴∠BFC=90°,∴CF==.故选:D.9.如图,在菱形ABCD中,∠D=135°,AD=3,CE=2,点P是线段AC上一动点,点F是线段AB上一动点,则PE+PF的最小值()A.2B.3C.2D.【解答】解:作点E关于AC的对称点点G,连接PG、PE,则PE=PG,CE=CG=2,连接BG,过点B作BH⊥CD于H,则∠BCH=∠CBH=45°,∴Rt△BHC中,BH=CH=BC=3,∴HG=3﹣2=1,∴Rt△BHG中,BG==,∵当点F与点B重合时,PE+PF=PG+PB=BG(最短),∴PE+PF的最小值是.故选:D.10.如图,正方形ABCD中,点E、F、G分别为边AB、BC、AD上的中点,连接AF、DE交于点M,连接GM、CG,CG与DE交于点N,则结论①GM⊥CM;②CD=DM;③四边形AGCF是平行四边形;④∠CMD=∠AGM中,正确的有()个.A.1B.2C.3D.4【解答】解:∵AG∥FC且AG=FC,∴四边形AGCF为平行四边形,故③正确;∴∠GAF=∠FCG=∠DGC,∠AMN=∠GND在△ADE和△BAF中,∵,∴△ADE≌△BAF(SAS),∴∠ADE=∠BAF,∵∠ADE+∠AEM=90°∴∠EAM+∠AEM=90°∴∠AME=90°∴∠GND=90°∴∠DE⊥AF,DE⊥CG.∵G点为AD中点,∴GN为△ADM的中位线,即CG为DM的垂直平分线,∴GM=GD,CD=CM;在△GDC和△GMC中,∵,∴△GDC≌△GMC(SSS),∴∠CDG=∠CMG=90°,∠MGC=∠DGC,∴GM⊥CM,故①正确;∵∠CDG=∠CMG=90°,∴G、D、C、M四点共圆,∴∠AGM=∠DCM,∵CD=CM,∴∠CMD=∠CDM,在Rt△AMD中,∠AMD=90°,∴DM<AD,∴DM<CD,∴∠DMC≠∠DCM,∴∠CMD≠∠AGM,故②④均错误.故选:B.二、填空题11.平行四边形ABCD中,AB、BC、CD的长度分别为2x+1,3x,x+4,则平行四边形ABCD的周长为32.【解答】解:∵平行四边形的对边相等,∴2x+1=x+4解得:x=3,即得AB=7、BC=9、CD=7、DA=9,∴平行四边形ABCD的周长是:AB+BC+CD+DA=32,故答案为:32.12.四边形ABCD中,AD∥BC,且AD=BC,当∠A=90°时,四边形ABCD是矩形.【解答】解:当∠A=90°时,四边形ABCD是矩形,理由如下:∵AD∥BC,且AD=BC,∴四边形ABCD是平行四边形,又∵∠A=90°,∴平行四边形ABCD是矩形,故答案为:90°.13.已知:正方形ABCD的边长等于8cm,那么边AB的中点M到对角线BD的距离等于2cm.【解答】解:如图,过点M作MF⊥BD于F,∵四边形ABCD是正方形,∴AB=BC=8cm,∠ABD=45°,∵MF⊥BD,∴△MBF是等腰直角三角形,∴BM=MF,∵M是AB的中点,∴MB=4cm,∴MF==2cm,故答案为:2.14.如图,直线l是矩形ABCD的一条对称轴,点P是直线l上一点,且使得△P AB和△PBC均为等腰三角形,则满足条件的点P共有5个.【解答】解:如图,作AB或DC的垂直平分线交l于P,如图,在l上作点P,使P A=AB,PD=DC,同理,在l上作点P,使PC=DC,AB=PB,如图,在长方形外l上作点P,使AB=AP,DC=PD,同理,在长方形外l上作点P,使AP=AB,PD=DC,故答案为5.15.如图,菱形ABCD和菱形ECGF的边长分别为3和4,∠A=120°,则图中阴影部分的面积.【解答】解:作BM⊥FG于M,交EC于N,如图,∵四边形ABCD和四边形CGFE为菱形,∴BC=CD=3,CG=GF=4,AB∥CE∥GF,∴∠ABC=∠BCD=∠CGF=120°,∴∠BCN=∠BGM=60°,∵BM⊥GF,∴BN⊥EC,在Rt△BCN中,∵∠NBC=30°,∴CN=BC=,BN=CN=,在Rt△BMG中,GM=BG=,BM=GM=,∴MN=BM﹣BN=﹣=2,∴S阴影部分=S△BCD+S梯形CDFG﹣S△BGF=×3×+×(3+4)×2﹣×4×=.另一种解法:连接CF,如图,∵四边形ABCD和四边形CGFE为菱形,∠A=120°,∴∠DBC=∠FCG=30°,∴BD∥CF,∴S△FDB=S△CDB=S菱形ABCD=•2••32=.故答案为.16.如图,点A、B、C在同一直线上,且AB=AC,点D、E分别是AB、BC的中点,分别以AB,DE,BC为边,在AC同侧作三个正方形,得到三个平行四边形(阴影部分)的面积分别记作S1、S2、S3,若S1=,则S2+S3=.【解答】解:设BE=x,则EC=x,AD=BD=2x,∵四边形ABGF是正方形,∴∠ABF=45°,∴△BDH是等腰直角三角形,∴BD=DH=2x,∴S1=DH•AD=,即2x•2x=,,∵BD=2x,BE=x,∴S2=MH•BD=(3x﹣2x)•2x=2x2,S3=EN•BE=x•x=x2,∴S2+S3=2x2+x2=3x2=,故答案为:.三、解答题17.如图,在平行四边形ABCD中,O是其对角线AC的中点,EF过点O,求证:BE=DF.【解答】证明:∵四边形ABCD是平行四边形,∴CD=AB,CD∥AB,∴∠DCA=∠BAC,∵CO=AO,∴△COF≌△AOE(ASA),∴AE=CF.∵CD=AB,∴BE=DF.18.已知:如图,E,F为▱ABCD的对角线BD上的两点,请你添加一个条件,使得AE=CF.(1)你添加的条件是DF=BE(答案不唯一);(2)根据你添加的条件和题目的已知条件,证明AE=CF.【解答】(1)解:添加DF=BE,故答案为:DF=BE(答案不唯一);(2)证明:∵DF=BE,∴DE=BF,∵四边形ABCD是平行四边形,∴AD=BC,AD∥BC,∴∠ADE=∠CBF,在△ADE和△CBF中,,∴△ADE≌△CBF(SAS),∴AE=CF.19.如图,在▱ABCD中,DE平分∠ADB,交AB于点E,BF平分∠CBD,交CD于点F.(1)求证:DE=BF;(2)若AD=BD,求证:四边形DEBF是矩形.【解答】(1)证明:∵四边形ABCD是平行四边形,∴AD∥BC,AB∥CD,∴∠ADB=∠CBD,∵DE平分∠ADB,BF平分∠CBD,∴∠EDB=∠ADB,∠DBF=∠CBD,∴∠EDB=∠DBF,∴DE∥BF,又∵AB∥CD,∴四边形DEBF是平行四边形.∴DE=BF.(2)∵AD=BD,DE平分∠ADB,∴DE⊥AB,又∵四边形DEBF是平行四边形,∴四边形DEBF是矩形.20.如图,在四边形ABCD中,AD=BC,若将AB沿AD方向平移,则AB与CD完全重合.(1)四边形ABCD是平行四边形吗?请说明理由;(2)若∠A=120°,求∠B,∠C的度数.【解答】(1)解:四边形ABCD是平行四边形,理由如下:∵将AB沿AD方向平移,则AB与CD完全重合,∴AB∥CD,AB=CD,∴四边形ABCD是平行四边形;(2)解:∵四边形ABCD是平行四边形,∠A=120°,∴∠B=60°,∠C=120°.21.已知:如图,在菱形ABCD中,点E,O,F分别为AB,AC,AD的中点,连接CE,CF,OE,OF.(1)求证:△BCE≌△DCF;(2)当AB与BC满足什么关系时,四边形AEOF是正方形?请说明理由.【解答】(1)证明:∵四边形ABCD是菱形,∴∠B=∠D,AB=BC=DC=AD,∵点E,O,F分别为AB,AC,AD的中点,∴AE=BE=DF=AF,OF=DC,OE=BC,OE∥BC,在△BCE和△DCF中,,∴△BCE≌△DCF(SAS);(2)解:当AB⊥BC时,四边形AEOF是正方形,理由如下:由(1)得:AE=OE=OF=AF,∴四边形AEOF是菱形,∵AB⊥BC,OE∥BC,∴OE⊥AB,∴∠AEO=90°,∴四边形AEOF是正方形.22.如图,已知正方形ABCD,点E是AB上的一点,连接CE,以CE为一边,在CE的上方作正方形CEFG,连接DG.求证:(1)△CBE≌△CDG;(2)AB=AE+DG.【解答】证明:(1)∵四边形ABCD和四边形CEFG均是正方形,∴CB=CD,CE=CG,∠BCD=∠ECG=90°,∴∠BCE=∠DCG,∴△CBE≌△CDG(SAS);(2)由(1)知,△CBE≌△CDG,∴BE=DG.∵AB=AE+EB,∴AB=AE+DG.23.如图,在△ABC中,∠ABC=90°,AC的垂直平分线分别与AC,BC及AB的延长线相交于点D,E,F.点O是EF中点,连接BO并延长到G,且GO=BO,连接EG,FG.(1)试判断四边形EBFG的形状,说明理由;(2)求证:BD⊥BG;(3)当AB=BE=1时,求EF的长.【解答】(1)解:四边形EBFG是矩形,理由如下:∵OE=OF,OB=OG,∴四边形EBFG是平行四边形,∵∠ABC=90°,∴∠FBC=90°,∴平行四边形EBFG是矩形;(2)证明:∵DF是AC的垂直平分线,∴AD=DC,在Rt△ABC中,AD=DC,∴BD=AC=CD,∴∠DBC=∠C,∵∠CDE=90°,∴∠CED+∠C=90°,∵四边形EBFG是矩形,∴OE=OB,∴∠OBE=∠OEB,∵∠CED=∠OEB,∴∠DBE+∠OBE=90°,即∠DBG=90°,∴BD⊥BG;(3)解:连接AE,∵DF是AC的垂直平分线,∴EA=EC,在Rt△ABE中,AE==,∴BC=BE+EC=1+,∵∠CDE=∠FBE=90°,∠CED=∠FEB,∴∠C=∠BFE,在△ABC和△EBF中,,∴△ABC≌△EBF(AAS)∴BF=BC=1+,在Rt△EBF中,EF==.24.如图,四边形AOBC是正方形,点C的坐标是(4,0).(Ⅰ)正方形AOBC的边长为4,点A的坐标是(2,2).(Ⅱ)将正方形AOBC绕点O顺时针旋转45°,点A,B,C旋转后的对应点为A′,B′,C′,求点A′的坐标及旋转后的正方形与原正方形的重叠部分的面积;(Ⅲ)动点P从点O出发,沿折线OACB方向以1个单位/秒的速度匀速运动,同时,另一动点Q从点O出发,沿折线OBCA方向以2个单位/秒的速度匀速运动,运动时间为t秒,当它们相遇时同时停止运动,当△OPQ为等腰三角形时,求出t的值(直接写出结果即可).【解答】解:(Ⅰ)如图,连接AB,交OC于点E,∵四边形AOBC是正方形∴AO=AC=OB=BC,AB⊥OC,OE=EC,AE=BE,∵点C的坐标是(4,0).∴OC=4∴OE=EC=2∵OA2+AC2=OC2=32,∴OA=4∴AE==2∴正方形边长为4,点A坐标为(2,2)故答案为:4,(2,2)(Ⅱ)如图,∵旋转45°,∠AOC=45°∴点A'落在OC上,∴OA=OA'=4,∠OA'C'=∠A=90°∴点A'(4,0),A'C=OC﹣OA'=4﹣4∵∠OCB=45°,∴∠A'PC=∠A'CP=45°∴A'C=A'P=4﹣4∴S重叠部分=S△OBC﹣S△A'PC=8﹣×(4)2=16﹣16(Ⅲ)∵t=4时,点P与A重合,点Q与C重合,且△OAC是等腰三角形∴当t=4时,△OPQ为等腰三角形当点P在OA上,点Q在OB上时,OP=t,OQ=2t,则直角三角形OPQ不是等腰三角形;当点P在OA上,点Q在BC上时,∵△OPQ是等腰三角形∴点Q在OP的垂直平分线上,∴2t﹣4=∴t=当点P在AC上时,点Q在AC上时,OP≠OQ≠PQ∴△OPQ不是等腰三角形.∴当t=4或时,△OPQ为等腰三角形.。
最新人教版八年级下册数学第十八章达标测试卷

第十八章达标测试卷一、选择题(本题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合要求的)1.如图,菱形ABCD中,∠D=150°,则∠1=()A.30°B.25°C.20°D.15°(第1题)(第2题)(第4题)2.如图,▱ABCD中,对角线AC,BD交于点O,点E是BC的中点.若OE=3 cm,则AB 的长为()A.12 cm B.9 cm C.6 cm D.3 cm3.下列四组条件中,不能判定四边形ABCD是平行四边形的是()A.AB=DC,AD=BC B.AB∥DC,AD∥BCC.AB∥DC,AD=BC D.AB∥DC,AB=DC4.如图,在Rt△ABC中,∠B=90°,BC=12,AB=5,则斜边上的中线BO长是() A.2.5 B.4 C.6 D.6.55.如图,在菱形ABCD中,∠B=60°,AB=4,则以AC为一边的正方形ACEF的周长为() A.14 B.15 C.16 D.17(第5题)(第7题)(第8题)6.下列说法中,正确的个数有()①对顶角相等;②两直线平行,同旁内角相等;③对角线互相垂直的四边形为菱形;④对角线互相垂直平分且相等的四边形为正方形.A.1个B.2个C.3个D.4个7.如图,已知在菱形ABCD中,对角线AC与BD交于点O,∠BAD=120°,AC=4,则该菱形的面积是()A.16 3 B.16 C.8 3 D.88.将五个边长都为2 cm的正方形按如图所示方式摆放,点A,B,C,D分别是四个正方形的中心,则图中四块阴影部分面积的和为()A.2 cm2B.4 cm2C.6 cm2D.8 cm29.如图,在矩形ABCD中,AD=3AB,点G,H分别在AD,BC上,连接BG,DH,且BG∥DH,若四边形BHDG为菱形,则AGAD=()A.45 B.35 C.49 D.38 (第9题)(第10题)(第11题)10.如图,在正方形纸片ABCD中,对角线AC,BD交于点O,折叠纸片使得AD落在BD上,点A恰好与BD上的点F重合.展开后,折痕DE分别交AB,AC于E,G,连接FG,EF,下列结论:①∠AGD=112.5°;②AD∶AE=2∶1;③S△AGD=S△OGD;④四边形AEFG 是菱形;⑤BE=2OG,其中正确结论的个数是()A.2 B.3 C.4 D.5二、填空题(本题共6小题,每小题3分,共18分)11.如图,▱ABCD中,AC,BD相交于点O,若AD=6,AC+BD=16,则△BOC的周长为________.12.如图,四边形ABCD是对角线互相垂直的四边形,且OB=OD,请你添加一个适当的条件:____________,使四边形ABCD成为菱形(只需添加一个即可).(第12题)(第14题)(第16题)13.若以A(-0.5,0),B(2,0),C(0,1)三点为顶点画平行四边形,则第四个顶点不可能在第________象限.14.如图,BD为正方形ABCD的对角线,BE平分∠DBC,交DC于点E,延长BC到点F,使CF=CE,连接DF.若CE=1 cm,则BF=__________.15.矩形ABCD中,AB=3,AD=4,P是AD上一动点,PE⊥AC于E,PF⊥BD于F,则PE +PF的值为________.16.如图,在边长为1的菱形ABCD中,∠DAB=60°.连接对角线AC,以AC为边作第二个菱形ACEF,使∠F AC=60°.连接AE,再以AE为边作第三个菱形AEGH,使∠HAE=60°,…,按此规律所作的第n个菱形的边长是________.三、解答题(本题共6小题,共52分.解答应写出文字说明、证明过程或演算步骤)17.(8分)如图,在▱ABCD中,点E,F分别在边CB,AD的延长线上,且BE=DF,EF分别与AB,CD交于点G,H.求证:AG=CH.18.(8分)如图,正方形ABCD中,E是BC上的一点,连接AE,过B点作BH⊥AE,垂足为点H,延长BH交CD于点F,连接AF.(1)求证:AE=BF;(2)若正方形的边长是5,BE=2,求AF的长.19.(8分)如图,▱ABCD的对角线AC与BD相交于点E,点G为AD的中点,连接CG,CG 的延长线交BA的延长线于点F,连接FD.(1)求证:AB=AF;(2)若AG=AB,∠BCD=120°,判断四边形ACDF的形状,并证明你的结论.20.(8分)如图,在四边形ABCD中,AB∥DC,AB=AD,对角线AC,BD交于点O,AC平分∠BAD,过点C作CE⊥AB交AB的延长线于点E,连接OE.(1)求证:四边形ABCD是菱形;(2)若AE=5,OE=3,求线段CE的长.21.(10分)如图,在△ABC中,AB=AC,AD为∠BAC的平分线,AN为△ABC的外角∠CAM 的平分线,CE⊥AN,垂足为E.(1)求证:四边形ADCE是矩形;(2)连接DE,试判断四边形ABDE的形状,并说明理由;(3)△ABC再添加一个什么条件时,可使四边形ADCE是正方形,并证明你的结论.22.(10分)我们给出如下定义:顺次连接任意一个四边形各边中点所得的四边形叫做中点四边形.(1)如图①,在四边形ABCD中,点E,F,G,H分别为边AB,BC,CD,DA的中点,求证:中点四边形EFGH是平行四边形;(2)如图②,点P是四边形ABCD内一点,且满足P A=PB,PC=PD,∠APB=∠CPD,点E,F,G,H分别为边AB,BC,CD,DA的中点,判断中点四边形EFGH的形状,并说明理由;(3)若改变(2)中的条件,使∠APB=∠CPD=90°,其他条件不变,直接写出中点四边形EFGH的形状(不必证明).答案一、1.D 2.C 3.C 4.D 5.C 6.B7.C 8.B9.C 点拨:在矩形ABCD 中,AD =3AB ,设AB =1,则AD =3.若四边形BHDG 为菱形,则BG =GD ,设BG =GD =x ,则AG =3-x .在Rt △ABG 中,1+()3-x 2=x 2 ,解得x =53,所以AG AD =3-533=49.10.B 点拨:∵四边形ABCD 是正方形,∴∠GAD =∠ADO = 45°,由折叠的性质可得,∠ADG =12∠ADO = 22.5°,∴∠AGD =180°-45°-22.5°=112.5°,故①正确;由折叠的性质可得AE =EF ,∠EFD =∠EAD =90°,∴AE =EF <BE ,∴AE <12AB ,∴易得AD AE >2,故②错误;由折叠的性质可得AG =FG .∵∠AOB = 90°,∴AG =FG >OG ,又∵△AGD 与△OGD 同高,∴S △AGD >S △OGD ,故③错误;∵∠EFD =∠AOF =90°,∴EF ∥AC ,∴∠FEG =∠AGE .∵由折叠的性质得∠AGE =∠FGE ,∴∠FEG=∠FGE,∴EF=GF,∴AE=EF=GF=AG,∴四边形AEFG是菱形,故④正确;∵四边形AEFG是菱形,∴AE∥GF.∴∠OGF=∠OAB=45°.∵∠AOB=90°,∴∠OFG=∠OGF=45°,∴OG=OF,∴GF=OG2+OF2=2OG,∴EF=2OG.同理可得BE=2EF,∴BE=2×2OG=2OG,故⑤正确.故选B.二、11.1412.OA=OC(答案不唯一)13.三14.(2+2)cm点拨:过点E作EG⊥BD于点G.∵BE平分∠DBC,∠EGB=∠BCE=90°,∴EG=EC=1 cm.易知△DEG为等腰直角三角形,∴DE=2EG=2cm.∴CD=(1+2)cm,∴BC=(1+2)cm.又∵CF =CE =1 cm ,∴BF =(2+2)cm.15.125 点拨:设AC 与BD 交于点O ,连接PO ,过D 作DG ⊥AC 于G ,由△AOD 的面积=△AOP 的面积+△POD 的面积,可得PE +PF =DG ,易得PE +PF =125.16.(3)n -1 点拨:连接DB 与AC 相交于M .∵四边形ABCD 是菱形,∴AD =AB ,AC ⊥DB .∵∠DAB =60°,∴△ADB 是等边三角形.∴DB =AD =1.∴DM =12.∴AM =32.∴AC = 3.同理可得AE =3AC =(3)2,AG =3AE =3 3=(3)3,…,按此规律所作的第n 个菱形的边长为(3)n -1.三、17.证明:∵四边形ABCD 是平行四边形,∴AD =BC ,AD ∥BC ,∠A =∠C .∴∠F =∠E .∵BE =DF ,∴AD +DF =CB +BE ,即AF =CE .在△AGF 和△CHE 中,⎩⎨⎧∠A =∠C ,AF =CE ,∠F =∠E ,∴△AGF ≌△CHE (ASA).∴AG =CH .18.(1)证明:∵四边形ABCD 是正方形,∴AB =BC ,∠ABE =∠BCF =90°.∴∠BAE +∠AEB =90°.∵BH ⊥AE ,∴∠BHE =90°.∴∠AEB +∠EBH =90°.∴∠BAE =∠EBH .在△ABE 和△BCF 中,⎩⎨⎧∠BAE =∠CBF ,AB =BC ,∠ABE =∠BCF ,∴△ABE ≌△BCF (ASA).∴AE =BF .(2)解:由(1)得△ABE ≌△BCF ,∴BE =CF .∵正方形的边长是5,BE =2,∴DF =CD -CF =CD -BE =5-2=3.在Rt △ADF 中,由勾股定理得AF =AD 2+DF 2=52+32=34.19.(1)证明:∵四边形ABCD 是平行四边形,∴BF ∥CD ,AB =CD .∴∠AFC =∠DCG .∵易得GA =GD ,∠AGF =∠DGC ,∴△AGF ≌△DGC (AAS).∴AF =CD .∴AB =AF .(2)解:四边形ACDF 是矩形.证明:∵由(1)得AF =CD ,AF ∥CD ,∴四边形ACDF 是平行四边形.∵四边形ABCD 是平行四边形,∴∠BAD=∠BCD=120°.∴∠F AG=60°.∵AB=AG=AF,∴△AGF是等边三角形.∴AG=GF.∵△AGF≌△DGC,∴FG=CG.又∵AG=GD,∴AD=CF.∴四边形ACDF是矩形.20.(1)证明:∵AB∥CD,∴∠OAB=∠DCA.∵AC平分∠BAD,∴∠OAB=∠DAC,∴∠DCA=∠DAC,∴CD=AD.∵AB=AD,∴AB=CD.又∵AB∥CD,∴四边形ABCD是平行四边形,∵AD=AB,∴四边形ABCD是菱形.(2)解:由(1)知四边形ABCD是菱形,∴AO=CO,∵CE⊥AB,∴∠AEC=90°,∴AC=2OE=6.在Rt△ACE中,CE=AC2-AE2=11.21.(1)证明:在△ABC中,∵AB=AC,AD为∠BAC的平分线,∴AD⊥BC,∠BAD=∠CAD=12∠BAC,∴∠ADC=90°.∵AN为△ABC的外角∠CAM的平分线,∴∠MAN=∠CAN=12∠CAM,∴∠DAE=∠DAC+∠CAN=12∠BAC+12∠CAM=12×180°=90°.∵CE⊥AN,∴∠AEC=90°,∴四边形ADCE是矩形.(2)解:四边形ABDE是平行四边形.理由:由(1)知,四边形ADCE是矩形,则AE=CD,AE∥CD.∵AB=AC,AD为∠BAC的平分线,∴BD=CD,∴AE=BD.又∵AE∥BD,∴四边形ABDE是平行四边形.(3)解:当∠BAC=90°时,四边形ADCE是正方形.证明:∵∠BAC=90°,AB=AC,AD为∠BAC的平分线,∴AD=CD=BD.又∵四边形ADCE是矩形,∴四边形ADCE是正方形.22.(1)证明:如图①,连接BD.∵点E,H分别为边AB,DA的中点,∴EH∥BD,EH=12BD.∵点F,G分别为边BC,CD的中点,∴FG∥BD,FG=12BD.∴EH∥FG,EH=FG.∴中点四边形EFGH是平行四边形.(2)解:中点四边形EFGH 是菱形.理由:如图②,连接AC ,BD .∵∠APB =∠CPD ,∴∠APB +∠APD =∠CPD +∠APD ,即∠BPD =∠APC .在△APC 和△BPD 中,⎩⎨⎧P A =PB ,∠APC =∠BPD ,PC =PD ,∴△APC ≌△BPD (SAS).∴AC =BD .∵点E ,F ,G 分别为边AB ,BC ,CD 的中点,∴EF =12AC ,FG =12BD .∴EF =FG .又由(1)中结论知中点四边形EFGH 是平行四边形, ∴中点四边形EFGH 是菱形.(3)解:中点四边形EFGH 是正方形.。
人教版八年级数学下册第十八章测试题(附答案)
人教版八年级数学下册第十八章测试题(附答案)姓名:__________ 班级:__________考号:__________一、单选题(共12题;共24分)1.若菱形的周长是40,则它的边长为()A. 20B. 10C. 15D. 252.下列叙述,错误的是( )A. 对角线互相垂直且相等的平行四边形是正方形B. 对角线互相垂直平分的四边形是菱形C. 对角线互相平分的四边形是平行四边形D. 对角线相等的四边形是矩形3.如图,四边形ABCD是正方形,点E、F在AC上(除端点外),且AF=CE,下列结论不一定成立的是()A. △ADF≌△CBEB. 四边形BEDF是平行四边形C. BF DED. AE=AD4.在下列所给出的4个图形中,对角线一定互相垂直的是()A. 长方形B. 平行四边形C. 菱形D. 直角梯形5.如图,正方形ABCD的对角线AC、BD相交于点O,OA=3,则此正方形的面积为()A. 3B. 12C. 18D. 366.如图,直线AB∥CD,P是AB上的动点,当点P的位置变化时,三角形PCD的面积将()A. 变大B. 变小C. 不变D. 变大变小要看点P向左还是向右移动7.顺次连接四边形ABCD各边中点,得到四边形EFGH,要使四边形EFGH是菱形,应添加的条件是()A. AD∥BCB. AC=BDC. AC⊥BDD. AD=AB8.菱形ABCD的对角线AC=5,BD=10,则该菱形的面积为()A. 50B. 25C.D. 12.59.如图,△ABC的中线BD、CE交于点O,连接OA,点G,F分别为OC,OB的中点,BC=4,AO=3,则四边形DEFG的周长为()A. 6B. 7C. 8D. 1210.下列对正方形的描述错误的是()A. 正方形的四个角都是直角B. 正方形的对角线互相垂直C. 邻边相等的矩形是正方形D. 对角线相等的平行四边形是正方形11.在下列条件中,不能确定四边形ABCD为平行四边形的是()A. ∠A=∠C,∠B=∠DB. ∠A=∠B=∠C=90°C. ∠A+∠B=180°,∠B+∠C=180°D. ∠A+∠B=180°,∠C+∠D=180°12.在平面直角坐标系中,正方形A1B1C1D1、D1E1E2B2、A2B2C2D2、D2E3E4B3、A3B3C3D3…按如图所示的方式放置,其中点B1在y轴上,点C1、E1、E2、C2、E3、E4、C3…在x轴上,已知正方形A1B1C1D1的边长为1,∠B1C1O=60°,B1C1∥B2C2∥B3C3…则正方形A2015B2015C2015D2015的边长是()A. B. C. D.二、填空题(共8题;共9分)13.如图,正方形ABCD的边长为1,以对角线AC为边作第二个正方形,再以对角线AE为边作第三个正方形AEGH,如此下去,第n个正方形的边长为________14.在平行四边形ABCD中,已知∠A﹣∠B=60°,则∠C=________.15.平行四边形ABCD中,AE平分∠BAD交BC与点E,且将BC分成4cm和6cm两部分,则平行四边形ABCD 的周长为________.16.如图,四边形ABCD的两条对角线AC、BD的长分别为5cm、4cm,点A1,B1,C1,D1是四边形ABCD各边上的中点,则四边形A1B1C1D1的周长为________cm.17.在Rt△ABC中,∠ACB=90°,若CA=8,BC=6,点D、E分别是AC、AB的中点.则DE=________,CE=________.18.如图,正方形ABCD的边长为2,点E为边BC的中点,点P在对角线BD上移动,则PE+PC的最小值是________.19.如图,矩形ABCD被分成四部分,其中△ABE、△ECF、△ADF的面积分别为2、3、4,则△AEF的面积为________.20.如图,在四边形ABCD中,已知AB=BC=CD,∠BAD和∠CDA均为锐角,点F是对角线BD上的一点,EF∥AB交AD于点E,FG∥BC交DC于点G,四边形EFGP是平行四边形,给出如下结论:①四边形EFGP是菱形;②△PED为等腰三角形;③若∠ABD=90°,则△EFP≌△GPD;④若四边形FPDG也是平行四边形,则BC∥AD且∠CDA=60°.其中正确的结论的序号是________(把所有正确结论的序号都填在横线上).三、解答题(共4题;共20分)21.如图,延长矩形ABCD的边BC至点E,使CE=BD,连接AE,如果∠ADB=60°,求∠E的度数.22.如图,已知△ABC中,BE、CF分别是AC、AB边上的高,D是BC的中点,求证:DE=DF.23.已知正方形ABCD,P为射线AB上的一点,以BP为边作正方形BPEF,使点F在线段CB的延长线上,连接EA,EC.(Ⅰ)如图1,若点P在线段AB的延长线上,求证:EA=EC;(Ⅱ)如图2,若点P在线段AB的中点,连接AC,判断△ACE的形状,并说明理由;(Ⅲ)如图3,若点P在线段AB上,连接AC,当EP平分∠AEC时,设AB=a,BP=b,求a:b及∠AEC的度数.24.阅读材料,解决问题:明明家准备装修房子,房子的部分平面图如图1所示.为了增大房子的使用空间,爸爸想把现在两间卧室之间的非承重墙打掉,之后在打掉的位置做一排衣柜.爸爸说:“我想测量一下非承重墙的厚度,从而知道打掉这堵墙后可以腾出多少空间.我手里有的工具是教学用量角器、大刻度尺,明明,你帮助爸爸看看应该怎样测量.”“这堵墙的厚度处处相等吗?”明明说.爸爸说:“这个没问题,当年收房的时候我就考察过.”“那我就可以在地面上直接进行测量了.我再问您,每个房间中地面和墙的交线都是垂直或平行的吗?”明明说.爸爸回答:“是的”.“那就简单了.我们俩先测出客厅的东西向宽度,再测出每个卧室的东西向宽度,用客厅的宽度减去两个卧室的宽度就是中间这堵非承重墙的厚度.”明明说.爸爸说:“那不行,客厅和卧室的家具摆得满满的,东西向宽度勉强测到也不准确.你能不能在不借助测量房间宽度或房间内其它家具的前提下,设计一个通过测量和计算得到非承重墙厚度的方案.”请你利用学到的三角形或四边形的知识帮助明明解决此问题.要求:(1)在图2中画出测量时用到的示意图,图形要规范;(2)简要叙述测量过程;(3)写出测量的依据.四、综合题(共4题;共47分)25.已知直线a,b,a平行于b,过直线a上任意两点A,B分别向直线b作垂线,交直线b于点C,D.(1)线段AC,BD所在的直线有怎样的位置关系?(2)比较线段AC,BD的长短.26.如图,已知正七边形ABCDEFG,请仅用无刻度的直尺,分别按下列要求画图.(1)在图1中,画出一个以AB为边的平行四边形;(2)在图2中,画出一个以AF为边的菱形.27.如图1,△ABD和△BDC都是边长为1的等边三角形。
八年级数学下册人教版第十八章平行四边形测试卷(含答案).docx
第十八章平行四边形测试题-、选择题(每小题3分,共24分)1.下列命题中正确的是()A.平行四边形的对角线和等 B.矩形的对角线互和垂直C.菱形的对角线互和垂直且平分 D.四边形的对角线相等2.在平行I丿U边形ABCD中,已知AD=5cm, AB=3 cm, AE平分ZBAD交BC边于点E,贝UEC等于()A. 1.5 cm B・ 2 cm C. 2.5 cm D・ 3 cm3.如图1,在菱形ABCD中,对角线AC, BD交于点O, ZBAD=120°, AC=4,则该菱形的面积是( )A. 16^3B. 16C. 8A/3D. 84.要测量一个门框是否是矩形,下列方法中正确的是()A.测量对角线是否平分B.测量上下边是否和等C.测量一组对角是直角D.测量三个角是直角5.如图2,将正方形纸片ABCD折叠,使边AB, CB均落在对角线BD上,得折痕BE, BF,贝HZEBF的大小为()A. 15°B. 30°C. 45°D. 60°6.已知下列四个命题:①对角线互相垂H平分的四边形是正方形;②对角线互相垂直且相等的四边形是菱形;③对角线互相平分口相筹的四边形是矩形;④对角线互相平分、相等冃垂宜的四边形是正方形.其中真命题的个数是()A. 1B. 2C. 3D. 47.如图3,把-•个长方形纸片对折两次,然后剪下一个角,为了得到一个内角为12()啲菱形,剪口与第二次折痕所成角的度数应为()A. 15。
或30。
B. 30。
或45。
C. 45。
或60。
D. 30。
或60。
8.如图4,菱形纸片ABCD中,ZA=60°,折叠菱形纸片ABCD,使点C落在DP (P为AB屮点)所在的直线上,得到经过点D的折痕DE,则ZDEC的大小为()A. 78°B. 75°C. 60°D. 45°二、填空题(每小题4分,共32分)9.在矩形ABCD中,对角线AC, BD相交于点O,若ZAOB=6()°,AC=1(),贝ljAB= ______10.点A, B, C是同-•平面内不在同一条直线上的三点,点D是平面内任意一点.若A, B,C, D四点恰能构成一个平行四边形,则在这个平面内符合这样条件的点D有_______ 个.11.已知止方形ABCD,以CD为边作等边三角形CDE,则ZAED的度数是________ .12.如图5,在正方形ABCD中,E是AB上一点,BE=2, AE=3BE, P是AC上一•动点,贝'JPB+PE的最小值是____ . 图3图4图5图613.如图6,在OABCD中,AE丄BC于点E, AF1CD于点F.若AE=4, AF=6, 口ABCD的周长为40,贝I JS^ABCD为________ •14. 如图7,在矩形ABCD 中,0是两对角线的交点,AE 丄BD,垂足为E.若OD=2OE, AE= 则DE 的长为15•如图8,四边形ABCD 是对角线互相垂岂的四边形,X ・OB=OD,请你添加一个适当的条 件: ________ ,使ABCD 为菱形(只需添加一个即可).16. 如图9, 0为四边形ABCD 的对角线AC, BD 的交点,EF 过点O 且与边AD, BC 分别交于 点E, F.若BF=DE, AD 〃BC,则图中的平行四边形分别是 ____________ .三、解答题(共64分)17. (12分)在口ABCD 中,ZA 比ZB 小30。
人教版初中数学八年级下学期第十八章测试卷(含答案)
初中数学人教版八年级下学期第十八章测试卷一、单选题(共6题;共12分)1. ( 2分) 在四边形ABCD中,∠A:∠B:∠C:∠D的比例依次如下,其中能使四边形ABCD是平行四边形的是( )A. 1:2:3:4B. 2:2:3:3C. 2:3:3:2D. 2:3:2:32. ( 2分) 如图,已知△ABC与△CDA关于点O成中心对称,过点O任作直线EF分别交AD,BC于点E,F,则下则结论:①点E和点F,点B和点D是关于中心O的对称点;②直线BD必经过点O;③四边形ABCD是中心对称图形;④四边形DEOC与四边形BFOA的面积必相等;⑤△AOE与△COF成中心对称.其中正确的个数为()A. 2B. 3C. 4D. 53. ( 2分) 如图,在等腰梯形ABCD中,AD∥BC,AD=5,AB=6,BC=8,且AB∥DE,则△DEC的周长是().A. 3B. 12C. 15D. 194. ( 2分) 如图,矩形A BCD的对角线AC,BD相交于点O,CE//BD,DE//AC.若AC=4,则四边形CODE的周长是( ).A. 4B. 6C. 8D. 105. ( 2分) 如图,菱形ABCD中,边CD的中垂线交对角线BD于点E,交CD于点F,连结AE.若∠ABC=50°,则∠AEB的度数为()A. 30°B. 40°C. 50°D. 60°6. ( 2分) 已知平行四边形ABCD中,对角线AC、BD相交于O.则下列说法准确的是()A. 当OA=OC时,平行四边形ABCD为矩形B. 当AB=AD时,平行四边形ABCD为正方形C. 当∠ABC=90°时,平行四边形ABCD为菱形D. 当AC⊥BD时,平行四边形ABCD为菱形二、填空题(共2题;共2分)7. ( 1分) 在四边形ABCD中,对角线AC,BD相交于点O,若OA=OC,要使四边形ABCD成为平行四边形,则可添加的条件为________(填一个即可)8. ( 1分) 如图,菱形中,对角线AC,BD交于点O,E为AD边中点,菱形ABCD的周长为28,则OE的长等于________.三、解答题(共1题;共5分)9. ( 5分) 如图,D,E分别是△A BC的边AB,AC的中点,点O是OA BC内部任意一点,连接OB,0C,点G,F分别是OB ,OC的中点,顺次连接点D,G,F,E.求证:四边形DGFE是平行四边形.四、综合题(共3题;共26分)10. ( 6分) 如图,在菱形ABCD中,对角线AC,BD交于点O,过点A作AE⊥BC于点E,延长BC至F,使CF=BE,连接DF.(1)求证:四边形AEFD是矩形;(2)若AC=10,∠ABC=60°,则矩形AEFD的面积是________.11. ( 10分) 如图,在正方形ABCD中,点E是BC的中点,连接DE,过点A作AG⊥ED交DE于点F,交CD于点G.(1)证明:△ADG≌△DCE;(2)连接BF,证明:AB=FB.12. ( 10分) 如图,AC是矩形ABCD的对角线,过AC的中点O作EF⊥AC,交BC于点E,交AD于点F,连接AE,CF.(1)求证:四边形AECF是菱形;(2)若AB=2,BC=4,求四边形AECF的面积.答案解析部分一、单选题1.【答案】D【考点】平行四边形的判定【解析】【解答】A、由∠A:∠B:∠C:∠D=1:2:3:4,没有角相等,不能判定四边形是平行四边形,故A 错误;B、由∠A:∠B:∠C:∠D=2:2:3:3,没有角相等,不能判定四边形是平行四边形,故A错误;C、、由∠A:∠B:∠C:∠D=2:2:3:3,虽然有两组角相等,但它们是邻角,不能判定四边形是平行四边形,故C错误;D、、由∠A:∠B:∠C:∠D=2:3:2:3,两组对角分别相等,能判定四边形是平行四边形,故D正确.故选D.【分析】两组对角分别相等的四边形是平行四边形,据此逐一判断即可.2.【答案】D【考点】平行四边形的判定与性质【解析】【解答】△ABC与△CDA关于点O对称,则AB=CD、AD=BC,所以四边形ABCD是平行四边形,因此点O就是▱ABCD的对称中心,则有:(1)点E和点F;B和D是关于中心O的对称点,符合题意;(2)直线BD必经过点O,符合题意;(3)四边形ABCD是中心对称图形,符合题意;(4)四边形DEOC 与四边形BFOA的面积必相等,符合题意;(5)△AOE与△COF成中心对称,符合题意;其中正确的个数为5个,故答案为:D.【分析】由于△ABC与△CDA关于点O对称,那么可得到AB=CD、AD=BC,即四边形ABCD是平行四边形,由于平行四边形是中心对称图形,且对称中心是对角线交点,可根据上述特点对各结论进行判断.3.【答案】C【考点】平行四边形的判定与性质【解析】【解答】∵AD∥BC,AB∥DE,∴ABED是平行四边形,∴DE=CD=AB=6,EB=AD=5,∴EC=8-5=3,则△DEC的周长=DE+DC+EC=6+6+3=15.故答案为:C【分析】根据两组对边分别平行可证四边形ABED是平行四边形,从而可得DE=CD=AB=6,EB=AD=5,继而求出CE的长,利用△DEC的周长=DE+DC+EC计算即可.4.【答案】C【考点】菱形的判定与性质,矩形的性质【解析】【解答】解:∵CE//BD,DE//AC,∴四边形CODE是平行四边形,在矩形A BCD中,AC =4,∴OD=OC=12AC=2,∴四边形CODE是菱形,∴四边形CODE的周长:4OC=8.故选:C.【分析】利用两组对边分别平行可证四边形CODE是平行四边形,根据矩形的性质可得OC=OD=12AC=2,利用一组邻边相等的平行四边形可证四边形CODE是菱形,利用菱形的性质即可求出结论.5.【答案】C【考点】菱形的性质【解析】【解答】如图,连接CE.∵四边形ABCD是菱形,∴AB=BC,∠ABD=∠DBC=12∠ABC=25 °,AB∥CD,∴∠BDC=∠ABD=25 °,∵点E在线段CD的中垂线上,∴EC=ED,∴∠ECD=∠EDC=25 °,∴∠BEC=∠ECD+∠EDC=50°.在△ABE与△CBE中,{AB=CB∠ABE=∠CBEBE=BE,∴△ABE≌△CBE(SAS),∴∠AEB=∠CEB =50 °.故答案为:C.【分析】连接CE.根据菱形的性质以及平行线的性质可得AB=BC,∠ABD=∠DBC,∠BDC=∠ABD=25 °,利用线段中垂线的性质得出EC=ED,那么∠ECD=∠EDC=25 °,点F垂直平分DC∠BEC=∠ECD +∠EDC=50 °.利用SAS证明△ABE≌△CBE,即可得出∠AEB=∠CEB=50 °.6.【答案】D【考点】菱形的判定,矩形的判定,正方形的判定【解析】【解答】∵平行四边形对角线互相平分,∴OA=OC而对角线相等的平行四边形是矩形,∴OA=OC不能判定平行四边形ABCD为矩形,故A错误;∵邻边相等的平行四边形是菱形,∴当AB=AD时,平行四边形ABCD是菱形,故B错误;∵有一个角是直角的平行四边形是矩形∴当∠ABC=90°时,平行四边形ABCD为矩形,故C错误;∵对角线互相垂直的平行四边形是菱形∴当AC⊥BD时,平行四边形ABCD为菱形,故D正确.故答案为:D.【分析】A. 根据平行四边形的性质和对角线相等的平行四边形是矩形进行判断;B. 根据邻边相等的平行四边形是菱形进行判断;C. 根据有一个角是直角的平行四边形是矩形进行判断;D. 根据对角线互相垂直的平行四边形是菱形进行判断.二、填空题7.【答案】答案不唯一如:OB=OD等【考点】平行四边形的判定【解析】【解答】解:条件:OB=OD.∵OA=OC,OB=OD,∴四边形ABCD是平行四边形.故答案为:OB=OD.【分析】根据对角线互相平分的四边形是平行四边形进行解答即可.8.【答案】3.5【考点】直角三角形斜边上的中线,菱形的性质【解析】【解答】∵四边形ABCD是菱形,∴AC⊥BD,AD=1×28=7,4∵E为AD的中点,∴OE=1AD=3.5.2故答案为:3.5.【分析】由于菱形的四边相等,对角线互相垂直,可得AD的长,AC⊥BD,结合E是AD的中点,则由直角三角形斜边的中线等于斜边的一半可知OE的长.三、解答题9.【答案】解:证明:如图,连接OA,∵D、E分别是AB和AC的中点,∴DE∥BC,DE=1BC,2BC,同理GF∥BC,GH=12∴DE∥GF,DE=GF,∴四边形DGFE是平行四边形.【考点】三角形中位线定理,平行四边形的判定【解析】【分析】由三角形的中位线定理可得DE平行等于BC的一半,GF平行等于BC的一半,因此可得DE和GH平行且相等,则四边形DGFE是平行四边形.四、综合题10.【答案】(1)证明:∵四边形ABCD是菱形,∴AD∥BC,AD=BC,∵CF=BE,∴BC=EF,∴AD∥EF,AD=EF,∴四边形AEFD是平行四边形,∵AE⊥BC,∴∠AEF=90°,∴平行四边形AEFD是矩形(2)50√3【考点】菱形的性质,矩形的判定与性质【解析】【解答】(2)∵AB=CD,BE=CF,∠AEB=∠DFC=90°,∴Rt△ABE≌Rt△DCF (HL),∴矩形AEFD的面积=菱形ABCD的面积,∵∠ABC=60°,∴△ABC是等边三角形,∵AC=10,∴AO=1AC=5,AB=10,BO=5 √3,2∴矩形AEFD的面积=菱形ABCD的面积=1×10×10 √3=50 √3,2故答案为:50 √3.【分析】(1)根据菱形的性质得到AD∥BC且AD=BC,等量代换得到BC=EF,推出四边形AEFD是平行四边形,根据矩形的判定定理即可得到结论;(2)根据全等三角形的判定定理得到Rt△ABE≌Rt△DCF (HL),求得矩形AEFD的面积=菱形ABCD的面积,根据等腰三角形的性质得到结论.11.【答案】(1)证明:∵四边形ABCD是正方形,∴∠ADG=∠C=90°,AD=DC,又∵AG⊥DE,∴∠DAG+∠ADF=90°=∠CDE+∠ADF,∴∠DAG=∠CDE,∴△ADG≌△DCE(ASA);(2)解:如图所示,延长DE交AB的延长线于H,∵E是BC的中点,∴BE=CE,又∵∠C=∠HBE=90°,∠DEC=∠HEB,∴△DCE≌△HBE(ASA),∴BH=DC=AB,即B是AH的中点,又∵∠AFH=90°,∴Rt△AFH中,BF=1AH=AB.2【考点】正方形的性质【解析】【分析】(1)利用正方形的性质可得∠ADG=∠C=90°,AD=DC,再利用AG⊥DE得DAG+∠ADF 90°=∠CDE+∠ADF,则有∠DAG=∠CDE,从而可证△ADG≌△DCE;(2)延长DE交AB的延长线于H,易得△DCE≌△HBE,利用全等三角形的对应边相等可得DH=DC=AB,然后利用直角三角形斜边上的中线等于是斜边的一半证得BF=1AH=AB,故得证。
人教版八年级下册数学达标检测卷—第十八章 平行四边形(含答案)
人教版八年级下册数学达标检测卷 【检测内容:第十八章 平行四边形 满分:120分】
一、选择题(每小题3分,共30分) 1. 如图,在矩形ABCD中,对角线AC,BD交于点O.若∠AOB=60°,AC=6 cm,则AB的长是( )
A.3 cm B.6 cm C.10 cm D.12 cm 2. 如图,在▱ABCD中,∠ADC的平分线交边AB于点E,连接CE.若∠ADE=25°,∠BCE=15°,则∠BEC的度数为( )
A.115° B.120° C.125° D.130° 3. 如图,在3×3的正方形网格中,以线段AB为对角线作平行四边形,使另外两个顶点也在格点上,则这样的平行四边形最多可以画( )
A.2个 B.3个 C.4个 D.5个 4. 如图,O为四边形ABCD内任意一点,E,F,G,H分别为OA,OB,OC,OD的中点,则四边形EFGH的周长为( )
A.9 B.12 C.18 D.不能确定 5. 如图,在▱ABCD中,E,F分别是AD,BC边的中点,G,H是对角线BD上的两点,且BG=DH,则下列结论不正确的是( )
A.GF=EH B.GF⊥FH C.EF与AC互相平分 D.EG=FH 6. 小敏不慎将一块平行四边形玻璃打碎成如图的四块,为了能在商店配到一块与原来相同的平行四边形玻璃,她带了两块碎玻璃,其编号应该是( )
A.①② B.②③ C.③④ D.①④ 7. 如图,在△ABC中,BD平分∠ABC,AF⊥BD于点E,交BC于点F,G是AC的中点.若BC=10,AB=7,则EG的长为( )
A.1.5 B.2 C.2.5 D.3.5 8. 如图,将▱ABCD对角线的交点与平面直角坐标系的原点重合,已知点B(12,-1)和C(2,1),则点D和点A的坐标分别是( )
A.(-12,1)和(-2,-1) B.(2,-1)和(-12,-1) C.(-2,1)和(12,1) D.(-1,-2)和(-1,12) 9. 如图,D,E分别是AB,AC的中点,BE是∠ABC的平分线,对于下列结论:①BC=2DE;②DE∥BC;③BD=DE;④BE⊥AC.其中正确的结论是( ) A.①② B.①②③ C.①②④ D.①②③④ 10. 如图,△ABC是等边三角形,P是三角形内一点,PD∥AB,PE∥BC,PF∥AC.若△ABC的周长为18,则PD+PE+PF=( )
