专题二-勾股定理 最短路径问题
勾股定理最短路径问题-解析版--初中数学专题训练

利用勾股定理求最短路径问题【考法导图】解题技巧:把几何体适当展开成平面图形,再利用“两点之间线段最短”,或点到直线“垂线段最短”等性质来解决问题。
1◎类型1台阶中的最值问题1(2017秋·山东济南·八年级济南外国语学校校考期中)如图,是一个三级台阶,它的每一级的长,宽和高分别等于5cm,3cm和1cm,A和B是这个台阶的两个相对的端点,A点上有一只蚂蚁,想到B点去吃可口的食物,请你想一想,这只蚂蚁从A点出发,沿着台阶面爬到B点,最短线路是()A.12B.13C.14D.15【答案】B【分析】将台阶展开,根据勾股定理即可求解.【详解】将台阶展开,如下图,因为AC=3×3+1×3=12,BC=5,所以AB2=AC2+BC2=169,所以AB=13(cm),所以蚂蚁爬行的最短线路为13cm.故选B.【点睛】本题考查了勾股定理的应用,掌握勾股定理是解题的关键.2(2023·全国·九年级专题练习)一个三级台阶,它的每一级的长宽和高分别为20、3、2,A和B是这个台阶两个相对的端点,A点有一只蚂蚁,想到B点去吃可口的食物,则蚂蚁沿着台阶面爬到B点最短路程为()A.481B.25C.30D.35【答案】B【分析】先将图形平面展开,再用勾股定理根据两点之间线段最短进行解答.【详解】如图所示,∵三级台阶平面展开图为长方形,长为20,宽为(2+3)×3,∴蚂蚁沿台阶面爬行到B点最短路程是此长方形的对角线长AB.由勾股定理得:AB2=202+2+3×32=252,解得:AB=25.故选:B.【点睛】本题考查了平面展开-最短路径问题以及勾股定理的应用,用到台阶的平面展开图,只要根据题意判断出长方形的长和宽即可解答.3(2020·山东淄博·统考一模)地面上铺设了长为20cm,宽为10cm的地砖,长方形地毯的位置如图所示.那么地毯的长度最接近多少?()A.50cmB.100cmC.150cmD.200cm【答案】C【分析】根据等腰直角三角形的性质即可得到结论.【详解】解:观察图像可知,地毯长可以看做是10个等腰直角三角形的斜边长度之和,则斜边=102+102=102,∴长方形地毯的长为:10×102=1002≈141.4cm,故选C.【点睛】本题考查了生活中的平移现象,等腰直角三角形的性质,正确的识别图形是解题的关键.4(2023春·八年级课时练习)如图是楼梯的一部分,若AD=2,BE=1,AE=3,一只蚂蚁在A处发现C处有一块糖,则这只蚂蚁吃到糖所走的最短路程为()A.5B.3C.13D.25【答案】D【分析】此类题目只需要将其展开便可直观的得出解题思路.将台阶展开得到的是一个矩形,蚂蚁要从A点到C点的最短距离,便是矩形的对角线,利用勾股定理即可解出答案.【详解】解:将台阶展开,如图,因为DC=AE+BE=3+1=4,AD=2,所以AC2=DC2+AD2=20,所以AC=25,故选:D.【点睛】本题考查了平面展开-最短路径问题,用到台阶的平面展开图,根据题意判断出长方形的长和宽是解题的关键.2◎类型2正方体中的最值问题1(2023·江苏常州·校考一模)如图,是一个棱长为1的正方体纸盒,若一只蚂蚁要沿着正方体纸盒的表面,从顶点A爬到顶点B去觅食,则需要爬行的最短路程是()A.3B.2C.5D.3【答案】C【分析】根据正方体展开图的特点,将正方体展开,然后利用勾股定理求解即可.【详解】解:如图所示,将正方体展开,则AC=2,BC=1,∠ACB=90°,∴由勾股定理得AB=AC2+BC2=5,∴需要爬行的最短路程是5,故选C.【点睛】本题主要考查了勾股定理的实际应用,正确将正方体展开,利用勾股定理进行求解是解题的关键.2(2023秋·陕西西安·八年级统考期末)如图,正方体盒子的棱长为2,M为EH的中点,现有一只蚂蚁位于点B处,它想沿正方体的表面爬行到点M处获取食物,则蚂蚁需爬行的最短路程为()A.10B.213C.13D.25【答案】C【详解】先把图中展开,根据两点间线段距离最短,再根据勾股定理求出BM的长即可;【解答】解:如图,连接BM,则线段BM的长就是蚂蚁需爬行的最短路程,∵正方体的棱长为2,M是EH的中点,∴∠Q=90°,MQ=2,BQ=1+2=3,由勾股定理得BM=22+32=13,故选:C.【点睛】本题考查两点间线段距离最短及勾股定理,解题的关键是理解最短路线.3(2022秋·广东佛山·八年级校考阶段练习)如图,正方体的棱长为2cm,点B为一条棱的中点.蚂蚁在正方体表面爬行,从点A爬到点B的最短路程是()A.10cmB.4cmC.17cmD.5cm【答案】C【分析】正方体侧面展开为长方形,确定蚂蚁的起点和终点,根据两点之间线段最短,根据勾股定理可求出路径长,【详解】解:如图,它运动的最短路程AB=(2+2)2+222=17(cm),故选:C.【点睛】本题考查平面展开最短路径问题,掌握两点之间线段最短,找到起点终点,根据勾股定理求出是解题的关键.4(2023春·北京大兴·八年级北京市第八中学大兴分校校考阶段练习)如图,正方体盒子的棱长为2,M为BC的中点,则一只蚂蚁从A点沿盒子的表面爬行到M点的最短距离为()A.23B.13C.14D.17【答案】B【分析】先利用展开图确定最短路线,再利用勾股定理求解即可.【详解】解:如图,蚂蚁沿路线AM爬行时距离最短;∵正方体盒子棱长为2,M为BC的中点,∴AD=2,MD=3,∴AM=22+32=13,故选:B.【点睛】本题考查了蚂蚁爬行的最短路径为题,涉及到了正方形的性质、正方体的展开图、勾股定理、两点之间线段最短等知识,解题关键是牢记相关概念与灵活应用.3◎类型3长方体中的最值问题1(2023春·全国·八年级专题练习)如图所示,有一个长、宽各2米,高为3米的无盖长方体纸盒放在桌面上,一只昆虫从顶点A要爬到顶点B,那么这只昆虫爬行的最短路程为()A.3米B.4米C.5米D.6米【答案】C【分析】分别画出三个路径的示意图,利用勾股定理求出路程,再从中找出最短路程即可.【详解】解:由题意,有以下三个路径:①如图,路径一:则这只昆虫爬行的路程为22+(2+3)2=29(米);②如图,路径二:则这只昆虫爬行的路程为32+(2+2)2=5(米);③如图,路径三:则这只昆虫爬行的路程为22+(3+2)2=29(米);因为29>5,所以这只昆虫爬行的最短路程为5米,故选:C.【点睛】本题考查了勾股定理的应用,正确画出三个路径的示意图是解题关键.2(2022秋·陕西西安·八年级校考阶段练习)如图,一只蚂蚁从长为4cm,宽为3cm,高为5cm的长方体纸箱的A点沿纸箱表面爬到B点,那么它所爬行的最短路线的长是()A.12cmB.74cmC.80cmD.90cm【答案】B【分析】先将图形展开,再根据两点之间线段最短,再由勾股定理求解即可.【详解】解:将长方体展开,如图1所示,连接A、B,根据两点之间线段最短,AB=(3+4)2+52=74 cm;如图2所示,(3+5)2+42=45cm,如图3所示,32+(5+4)2=310cm,∵74<45<310,∴蚂蚁所行的最短路线为74cm.【点睛】本题考查最短路径问题,将长方体展开,根据两点之间线段最短,运用勾股定理是解题.3(2023春·全国·八年级专题练习)如图,正四棱柱的底面边长为4cm,侧棱长为6cm,一只蚂蚁从点A 出发,沿棱柱外表面到C′点处吃食物,那么它需要爬行的最短路径的长是()A.229cmB.14cmC.(213+4)cmD.10cm【答案】D【分析】把正四棱柱展开为平面图形,分两种情形求出路径,比较即可解答.【详解】解:把正四棱柱展开为平面图形,分两种情形:如图1中,AC =AB2+BC 2=42+102=116=229,如图2中,AC =AC2+CC 2=82+62=10,∵10<229,∴爬行的最短路径是10cm.故选:D【点睛】本题考查平面展开-最短路径问题,涉及了勾股定理的应用,解题的关键是将问题进行转化,然后根据勾股定理求解.4(2022秋·江苏·八年级专题练习)如图,长方体的长、宽、高分别是6、3、5,一只蚂蚁要从点A爬行到点B,则爬行的最短距离是()A.130B.126C.10D.86【答案】C【分析】做此题要把这个长方体中蚂蚁所走的路线放到一个平面内,在平面内线段最短,根据勾股定理即可计算.【详解】解:第一种情况:把我们所看到的前面和上面组成一个平面,则这个长方形的长和宽分别是8和6,则所走的最短线段是82+62=10;第二种情况:把我们看到的左面与上面组成一个长方形,则这个长方形的长和宽分别是11和3,所以走的最短线段是112+32=130;第三种情况:把我们所看到的前面和右面组成一个长方形,则这个长方形的长和宽分别是9和5,所以走的最短线段是92+52=106;∵10<106<130,三种情况比较而言,第一种情况最短,最短路程=10,故选:C .【点睛】本题考查了平面展开---最短路径问题,解题的关键是将图形展开,转化为直角三角形利用勾股定理解答.4◎类型4圆柱(锥)中的最值问题1(2023春·全国·八年级专题练习)如图,圆柱的底面半径为6πcm ,AC 是底面圆的直径,点P 是BC 上一点,且PC =4cm ,一只蚂蚁从A 点出发沿着圆柱体的表面爬行到点P 的最短距离是()A.45cmB.213cmC.56cmD.10cm【答案】B【分析】把圆柱侧面展开后,连接AP .由已知可求得圆柱底面圆的周长,从而可求得周长的一半,由勾股定理即可计算出AP 的长.【详解】侧面展开图如图所示:∵圆柱的底面半径为6cm,π∴圆柱的底面周长为12cm,∴AC′=6cm.在Rt△ACP中,AP=42+62=213(cm).故选:B.【点睛】本题考查了勾股定理的应用,关键是把圆柱展开,即把空间问题转化为平面问题来解决,体现了转化思想.2(2022春·全国·八年级假期作业)如图,圆柱形玻璃杯高为12cm、底面周长为18cm,在杯内离杯底4cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4cm与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最短距离为( )cm.A.15B.20C.18D.30【答案】A【分析】把圆柱沿蚂蚁所在的高剪开并展开在一个平面内,得到一个矩形,作A点关于DF的对称点B,分别连接BD、BC,过点C作CE⊥DH于点E,则BC就是蚂蚁到达蜂蜜的最短距离,根据勾股定理即可求得BC的长.【详解】把圆柱沿蚂蚁所在的高剪开并展开在一个平面内,得到一个矩形,作A点关于DF的对称点B,分别连接BD、BC,过点C作CE⊥DH于点E,如图所示:则DB=AD=4cm,由题意及辅助线作法知,M与N分别为GH与DF的中点,且四边形CMHE为长方形,∴CE=MH=9cm,EH=CM=4cm,∴DE=DH-EH=12-4=8cm,∴BE=DE+DB=8+4=12cm,在Rt△BEC中,由勾股定理得:BC=BE2+CE2=122+92=15cm,即蚂蚁到达蜂蜜的最短距离为15cm,故选;:A.【点睛】本题考查了勾股定理,两点间线段最短,关键是把空间问题转化为平面问题解决,这是数学上一种重要的转化思想.3(2022秋·全国·八年级专题练习)如图,有一个圆柱形玻璃杯,高为10cm,底而周长为12cm,在圆柱的下底面的内壁A处有一只蚂蚁,它想吃到在杯内离杯上沿2cm的点E处的一滴蜂蜜,求蚂蚁到达蜂蜜的最短距离()A.261cmB.234cmC.413cmD.10cm【答案】D【分析】根据题意画出图形,然后根据勾股定理,即可求解.【详解】解:如图,根据题意得:BC=10cm,AB=12×12=6cm,CE=2cm,∴BE=BC-CE=8cm,在Rt△ABE中,由勾股定理得:AC=AB2+BE2=62+82=10cm,即蚂蚁到达蜂蜜的最短距离10cm.故选:D.【点睛】本题主要考查了勾股定理的应用,明确题意,画出图形是解题的关键.4(2019·全国·八年级专题练习)如图,一个圆柱形油罐,油罐的底面周长12m,高5m,要从点A环绕油罐建梯子,正好到达点A的正上方的点B,则梯子最短需要()A.12mB.13mC.17mD.20m【答案】B【分析】先把圆柱的侧面展开得到一个长方形,利用勾股定理求出AB的长即可得到答案.【详解】解:将圆柱形油罐的侧面展开如图所示,由题意可知,在△ABC中,∠C=90°,BC=5m,AC=12m,∴由勾股定理可得:AB=AC2+BC2=52+122=169=13m,∴梯子最短需要13m.故选B.【点睛】本题主要考查了勾股定理的应用,本题的解题要点是:将圆柱的侧面展开,结合题意就可将问题转化到Rt△ABC中,这样就可利用“勾股定理”求出AB的长度,从而得到梯子的最短长度.。
17.1.4 勾股定理最短路径问题

a b c .
2 2 2
2 2
a
C
2 2 2
c
b
2
A
a c b
b c a
c a b
二、解决问题
• 问题1. 有一个圆柱,它的高等于12厘米,底面半径等 于3厘米,在圆柱下底面上的A点有一只蚂蚁,它想从点 A爬到点B ,蚂蚁沿着圆柱侧面爬行的最短路程是多少 ?
O B
A
O'
二、解决问题
A B
• 问题2.如图是一个三级台阶,它的每一级的长、宽和 高分别为20dm、3dm、2dm,A和B是这个台阶两个相对 的端点,A点有一只蚂蚁,想到B点去吃可口的食物, 则蚂蚁沿着台阶面爬到B点最短路程是多少?
展开图: 20 A 3 A 20 2 3
2
3 2 3 C
2 B
B
二、解决问题
• 问题 3. 如图,长方体的长为 15cm ,宽为 10cm ,高为 20cm ,点B 离点 C 5cm, 一只蚂蚁如果要沿着长方体的 表面从点 A爬到点B,需要爬行的最短距离是多少?
二、解决问题
• 归纳小结:
• 曲面上的最短路径问题,一般均可通过展开曲面 从而转化成平面上的最短路径问题,我们要通过勾股 定理来求出未知线段,需要构造直角三角形。所以在 剪开圆柱侧面时,要沿垂直于底面的线剪,这样就得
到了长方形,利用直角来构造直角三角形。
O
O B B
A
O'
A O'
C
A
二、解决问题
最短路程是蚂蚁沿圆柱侧面爬行的15曲面上的最短路径问题一般均可通过展开曲面从而转化成平面上的最短路径问题我们要通过勾股定理来求出未知线段需要构造直角三角形
2019八年级数学下册第十七章勾股定理小专题(二)利用勾股定理解决最短路径问题练习新人教版
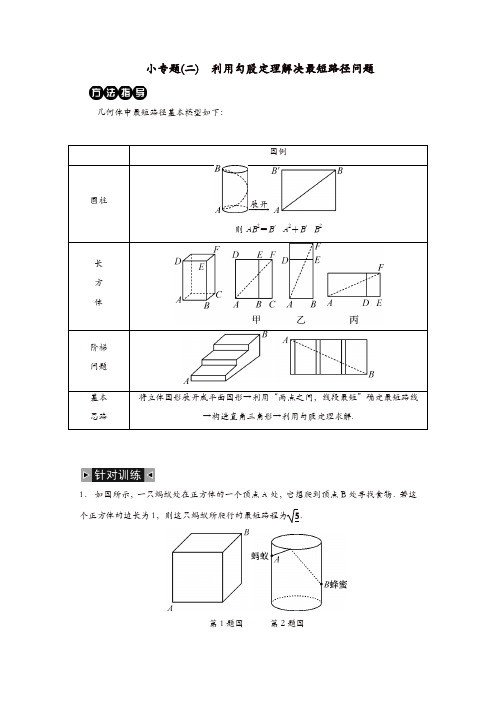
小专题(二) 利用勾股定理解决最短路径问题
几何体中最短路径基本模型如下:
――→展开
则
AB
2=
B ′A 2+B ′B 2
将立体图形展开成平面图形→利用“两点之间,线段最短”确定最短路线
1. 如图所示,一只蚂蚁处在正方体的一个顶点A 处,它想爬到顶点B 处寻找食物.若这个正方体的边长为1
第1题图 第2题图
2.(2018·黄冈)如图,圆柱形玻璃杯高为14 cm,底面周长为32 cm,在杯内壁离杯底5 cm 的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿3 cm与蜂蜜相对的点A处,则蚂蚁从外壁A处到内壁B处的最短距离为20cm.(杯壁厚度不计)
3.如图,在一个长为2 m,宽为1 m的长方形草地上,放着一根长方体的木块,它的棱和草地宽AD平行且棱长大于AD,木块从正面看是边长为0.2 m的正方形,一只蚂蚁从点A处到达点C处需要走的最短路程是2.60m(精确到0.01 m).。
勾股定理中的四类最短路径模型(学生版)--初中数学

勾股定理中的四类最短路径模型勾股定理中的最短路线问题通常是以“两点之间,线段最短”为基本原理推出的。
人们在生产、生活实践中,常常遇到带有某种限制条件的最近路线即最短路线问题。
对于数学中的最短路线问题可以分为两大类:第一类为在同一平面内;第二类为空间几何体中的最短路线问题,对于平面内的最短路线问题可先画出方案图,然后确定最短距离及路径图。
对于几何题内问题的关键是将立体图形转化为平面问题求解,然后构造直角三角形,利用勾股定理求解。
模型1.圆柱中的最短路径模型【模型解读】圆柱体中最短路径基本模型如下:计算跟圆柱有关的最短路径问题时,要注意圆柱的侧面展开图为矩形,利用两点之间线段最短结合勾股定理进行求解,注意展开后两个端点的位置,有时候需要用底面圆的周长进行计算,有时候需要用底面圆周长的一半进行计算。
注意:1)运用勾股定理计算最短路径时,按照展开-定点-连线-勾股定理的步骤进行计算;2)缠绕类题型可以求出一圈的最短长度后乘以圈数。
【最值原理】两点之间线段最短。
1(2023·广东·八年级期中)如图,一个底面圆周长为24cm,高为9cm的圆柱体,一只蚂蚁从距离上边缘4cm的点A沿侧面爬行到相对的底面上的点B所经过的最短路线长为()A.413cmB.15cmC.14cmD.13cm【答案】D【分析】将圆柱体展开,利用勾股定理进行求解即可.【详解】解:将圆柱体的侧面展开,连接AB,如图所示:由于圆柱体的底面周长为24cm,则BD=24×12=12cm,又因为AD=9-4=5cm,所以AB=122+52=13(cm),即蚂蚁沿表面从点A到点B所经过的最短路线长为13cm.故选:D.【点睛】本题考查勾股定理的应用-最短路径问题.解题的关键是将立体图形展开为平面图形,利用勾股定理进行求解.2(2023·重庆·八年级期末)如图,圆柱形玻璃杯高14cm,底面周长为18cm,在外侧距下底处1cm有一只蜘蛛,与蜘蛛相对的圆柱形容器的上端距开口处1cm的外侧点处有一只苍蝇,蜘蛛捕到苍蝇的最短路线长是cm.【答案】15【分析】展开后连接SF,求出SF的长就是捕获苍蝇的蜘蛛所走的最短路径,过S作SE⊥CD于E,求出SE、EF,根据勾股定理求出SF即可.【详解】解:如图展开后连接SF,求出SF的长就是捕获苍蝇的蜘蛛所走的最短路径,过S作SE⊥CD于E,则SE=BC=12×18=9(cm),EF=14-1-1=12(cm),在Rt△FES中,由勾股定理得:SF=SE2+EF2=92+122=15(cm),故答案为15.【点睛】本题考查勾股定理、平面展开-最短路线问题,关键是构造直角三角形,题目比较典型,难度适中.3(2023春·山东济宁·八年级校考期中)春节期间,某广场用彩灯带装饰了所有圆柱形柱子.为了美观,每根柱子的彩灯带需要从A点沿柱子表面缠绕两周到其正上方的B点,如图所示,若每根柱子的底面周长均为2米,高均为3米,则每根柱子所用彩灯带的最短长度为米.【答案】5【分析】要求彩带的长,需将圆柱的侧面展开,进而根据“两点之间线段最短”得出结果,在求线段长时,借助于勾股定理.【详解】解:将圆柱表面切开展开呈长方形,则彩灯带长为2个长方形的对角线长,∵圆柱高3米,底面周长2米,∴AC2=22+1.52=6.25,∴AC=2.5,∴每根柱子所用彩灯带的最短长度为5m.故答案为5.【点睛】本题考查了平面展开-最短路线问题,勾股定理的应用.圆柱的侧面展开图是一个矩形,此矩形的长等于圆柱底面周长,高等于圆柱的高,本题就是把圆柱的侧面展开成矩形,“化曲面为平面”,用勾股定理解决.1.(2023·湖北十堰·统考一模)如图,这是一个供滑板爱好者使用的U形池,该U形池可以看作是一个长方体去掉一个“半圆柱”而成,中间可供滑行部分的截面是弧长为12m的半圆,其边缘AB= CD=20m(边缘的宽度忽略不计),点E在CD上,CE=4m.一滑板爱好者从A点滑到E点,则他滑行的最短距离为()A.28mB.24mC.20mD.18m【答案】C【分析】滑行的距离最短,即是沿着AE的线段滑行,我们可将半圆展开为矩形来研究,展开后,A、D、E 三点构成直角三角形,AE为斜边,AD和DE为直角边,写出AD和DE的长,根据题意,由勾股定理即可得出AE的距离.【解析】解:将半圆面展开可得:AD =12米,DE =DC -CE =AB -CE =16米,在Rt △ADE 中,AE =122+162=20(米).即滑行的最短距离为20米.故选:C .【点睛】本题考查了平面展开-最短路径问题,U 型池的侧面展开图是一个矩形,此矩形的宽是半圆的弧长,矩形的长等于AB =CD =20m .本题就是把U 型池的侧面展开成矩形,“化曲面为平面”,用勾股定理解决.2.(2023春·四川德阳·八年级校考期中)如图,圆柱底面半径为2πcm ,高为9cm ,点A ,B 分别是圆柱两底面圆周上的点,且A ,B 在同一条竖直直线上,用一根棉线从A 点顺着圆柱侧面绕3圈到B 点,则这根棉线的长度最短为cm .【答案】15【分析】要求圆柱体中两点之间的最短路径,最直接的作法,就是将圆柱体展开,然后利用两点之间线段最短解答.【解析】解:圆柱体的展开图如图所示:用一棉线从A 顺着圆柱侧面绕3圈到B 的运动最短路线是:AC →CD →DB ;即在圆柱体的展开图长方形中,将长方形平均分成3个小长方形,A 沿着3个长方形的对角线运动到B的路线最短;∵圆柱底面半径为2πcm ∴长方形的宽即是圆柱体的底面周长:2π×2π=4cm ;又∵圆柱高为9cm ,∴小长方形的一条边长是3cm ;根据勾股定理求得AC =CD =DB =32+42=5(cm );∴AC +CD +DB =15(cm );故答案为:15.【点睛】本题主要考查了平面展开--路径最短问题.圆柱的侧面展开图是一个长方形,此长方形的宽等于圆柱底面周长,长方形的长等于圆柱的高.本题就是把圆柱的侧面展开成长方形,“化曲面为平面”,用勾股定理解决.3.(2022·山东青岛·八年级期末)如图,一个圆桶,底面直径为16cm,高为18cm,则一只小虫从下底点A处爬到上底B处再回到A处,则小虫所爬的最短路径长是( )(π取3)A.60cmB.40cmC.30cmD.20cm【答案】A【分析】先将圆柱的侧面展开为一矩形,而矩形的长就是底面周长的一半,高就是圆柱的高,再根据勾股定理就可以求出其值.【解析】解:展开圆柱的侧面如图,根据两点之间线段最短就可以得知AB最短.由题意,得AC=3×16÷2=24,在Rt△ABC中,由勾股定理,得AB=AC2+BC2=242+182=30cm.∵一只小虫从下底点A处爬到上底B处再回到A处,∴最短路径长为60cm.故选:A.【点睛】本题考查了圆柱侧面展开图的运用,两点之间线段最短的运用,勾股定理的运用.在解答时将圆柱的侧面展开是关键.模型2.长方体中的最短路径模型【模型解读】长方体中最短路径基本模型如下:计算跟长方体有关的最短路径问题时,要熟悉长方体的侧面展开图,利用两点之间线段最短结合勾股定理进行求解,注意长方体展开图的多种情况和分类讨论。
勾股定理应用之最短路径问题

圆柱侧面两点最短路径问题
如图所示,圆柱体的底面周长为18cm ,高AC为12cm ,一只蚂蚁从A点出发,
沿着圆柱的侧面爬行到点B,试求出爬行的最短路程。
为什么这 样走最短?
C
B
我怎么走 会最近呢?
A
D
圆柱侧面两点最短路径问题 如图所示,圆柱体的底面周长为18cm ,高AC为12cm ,一只蚂蚁从A点出发,
我怎么走 会最近呢?
A
8
B
2 4
长方体中的最值问题 如图,长方体的长、宽、高分别为4、2、8。现有一蚂蚁从顶点A出发,沿
长方体表面到达顶点B,蚂蚁走的路程最短为多少厘米?
A
8
4
B 2 B1
A
4
8
B
B2 2A
8
B
2
4
B3
长方体中的最值问题 如图,长方体的长、宽、高分别为4、2、8。现有一蚂蚁从顶点A出发,沿
沿着圆柱的侧面爬行到点B,试求出爬行的最短路程。
C
B
C
③②
B
①
④
A
A
D
由以上4种路线,可知路线①最短(两点之间线段最短)
圆柱侧面两点最短路径问题 如图所示,圆柱体的底面周长为18cm ,高AC为12cm ,一只蚂蚁从A点出发,
沿着圆柱的侧面爬行到点B,试求出爬行的最短路程。
解: 如图,将圆柱体展开,
线路是多少?
AA203源自232 B
3
2 B
台阶中的最值问题
如图是一个三级台阶,它的每一级的长、宽和高分别等于20cm,3cm和2cm,
请你想一想,一只蚂蚁从A点出发,沿着台阶面爬到B点去吃可口的食物,最短
线路是多少?
勾股定理在最短路径问题中的应用

『勾股定理在最短路径问题中的应用』一、引言在数学和实际生活中,勾股定理是一个被广泛应用的基本定理,它不仅仅是一个几何定理,还在诸多领域中有着重要的应用,其中就包括最短路径问题。
本文将探讨勾股定理在最短路径问题中的应用,从而帮助我们更深入地理解这一数学原理在实际生活中的作用。
二、最短路径问题概述最短路径问题是指在图中找到两个顶点之间的最短路径,通常以距离或权重来衡量路径的长度。
这个问题在现实生活中有着广泛的应用,比如在网络传输中寻找最短路径可以提高传输效率,在交通规划中寻找最短路径可以节省时间和成本等等。
寻找最短路径是一个被广泛关注的问题。
三、勾股定理在最短路径问题中的应用1. 从原理上来看,勾股定理可以帮助我们计算两点之间的直线距离,这在寻找最短路径时是至关重要的。
通过勾股定理,我们可以准确地计算出两点之间的距离,从而找到最短路径。
2. 勾股定理还可以帮助我们理解和推导其他寻找最短路径的算法,比如迪杰斯特拉算法和弗洛伊德算法。
这些算法都是建立在对距离的准确计算基础上的,而勾股定理为我们提供了这样的基础知识。
3. 在实际的地图导航中,勾股定理也被广泛应用。
通过勾股定理,地图导航可以准确计算出最短路径,并为我们提供最优的导航方案,从而节省时间和成本。
四、结论和回顾通过本文的探讨,我们更加深入地了解了勾股定理在最短路径问题中的重要应用。
勾股定理不仅仅是一个单纯的数学定理,它还在实际生活中发挥着重要作用,特别是在寻找最短路径这样的实际问题中。
我们应该重视和深入理解勾股定理这一基础数学原理,从而更好地应用它解决现实生活中的问题。
五、个人观点在我看来,数学定理和实际问题之间的联系总是让人感到惊讶和敬畏。
勾股定理作为一个古老的数学定理,竟然在现代的最短路径问题中发挥着如此重要的作用,这让我对数学的普适性有了更深刻的理解。
我相信,随着数学和现实生活的更加深入的结合,我们将能够更好地解决各种实际问题,提高生活质量和效率。
《利用勾股定理的运用——最短路径问题》教学PPT课件【初中数学】公开课
A●
●C
(2)如图,圆柱形玻璃杯,高为12cm,底面 圆的周长为 18cm,在杯子内壁离杯底4cm的 点C处有一滴蜂蜜, 此时一只蚂蚁正好在杯 子外壁,距离杯子上沿4cm 与蜂蜜相对的点 A处,则蚂蚁到达蜂蜜的最短距离为多少 ?
AC2 AB22 B2C22 52 22 29 25
答:森迪爬行的最短路径长为5厘米。
2 C2
B2
拓展探究
如果森迪是从长、宽、高 分别为4、2、 8的长方体 的顶点A出发,沿长方体侧 面到达顶点C,它爬行的最 短路径长为多少呢?
A● 4
8
8
B1 4 2
B3
C
●
2 C1
C3
2 C2
C
体的侧面延A点
聪明的同学们,你能帮帮它吗?
BC
B
r 33 9
所在的母线展开。
r BC= =3x3=9 A
12
AC=12
A
在Rt △ ABC中,根据勾股定理得:
AB 122 92 144 81 225 15
答:森迪爬行的最短路径长是15 厘米。
练一练
1、如果他来到的是高为5厘米,底面半径为1厘米的圆柱体的A处, 离顶部1厘米B处的面包,它沿圆柱体的表面怎样爬行才能很快地吃 包?它爬行的最短路径长是多少呢?(π的值取3 )
C● B
A
当森迪从圆柱体上爬下来时, 还是有点饿,它准备继续向前爬 行,寻找食物……
例题讲解 森迪爬呀爬,他来到了单位长度为1的 正方体A处,嗅到了放置在B处的食物, 这次它沿着怎样的路线爬行才能很快 地吃到食物呢?爬行的最短路径长又 A● 是多少呢?
人教版数学八年级下册17.1.3勾股定理的应用-最短路径问题(教案)
1.理论介绍:首先,我们要了解勾股定理的基本概念。勾股定理是指在直角三角形中,斜边的平方等于两个直角边的平方和。它在解决最短路径问题中起着关键作用。
2.案例分ห้องสมุดไป่ตู้:接下来,我们来看一个具体的案例。这个案例展示了如何将实际的最短路径问题转化为直角三角形问题,并运用勾股定理求解。
4.练习相关习题,巩固所学知识。
二、核心素养目标
本节课旨在培养学生以下核心素养:
1.数学抽象:通过实际问题,让学生抽象出直角三角形中的最短路径问题,理解勾股定理的数学本质;
2.逻辑推理:引导学生运用勾股定理进行逻辑推理,解决实际最短路径问题,提高解决问题的能力;
3.数学建模:培养学生将现实问题转化为数学模型的能力,通过构建直角三角形模型,求解最短路径;
-难点二:在多个可能的直角三角形中,如何选择正确的三角形进行计算。教师应通过实例演示,如何根据问题的具体条件,选择合适的三角形进行求解。
-难点三:计算过程中的精度要求。在求解过程中,学生可能会因为计算错误导致最终结果不准确,教师需要强调精确计算的重要性,并提供相应的练习来加强学生的计算能力。
-教学方法:
五、教学反思
在今天的教学中,我尝试通过生活中的实际例子引入勾股定理的最短路径问题,希望以此激发学生的兴趣。在理论讲解环节,我发现学生们对勾股定理的概念已经有了初步的了解,但在具体应用上还存在一定的难度。我通过案例分析、图示和实验操作等多种方式,尽量让学生在直观上理解并掌握如何将实际问题转化为直角三角形问题。
3.成果分享:每个小组将选择一名代表来分享他们的讨论成果。这些成果将被记录在黑板上或投影仪上,以便全班都能看到。
(五)总结回顾(用时5分钟)
今天的学习,我们了解了勾股定理在解决最短路径问题中的基本概念、重要性和应用。同时,我们也通过实践活动和小组讨论加深了对这一知识点的理解。我希望大家能够掌握这些知识点,并在日常生活中灵活运用。最后,如果有任何疑问或不明白的地方,请随时向我提问。
2016年秋八年级数学上册1勾股定理专题训练(二)利用勾股定理解决最短路径问题(新版)北师大版
1 专题训练(二) 利用勾股定理解决最短路径问题 1.如图,一圆柱体的底面周长为24 cm,高AB为5 cm,BC是直径,一只蚂蚁从点A出发沿着圆柱体的表面爬行到点C的最短路程是( )
A.6 cm B.12 cm C.13 cm D.16 cm 2.如图,长方体的长为15,宽为10,高为20,点B离点C的距离为5,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是( )
A.521 B.25 C.105+5 D.35 3.如图,长方体的底面边长分别为2 cm和4 cm,高为5 cm,若一只蚂蚁从点P开始经过4个侧面爬行一圈达到点Q,则蚂蚁爬行的最短路径长为多少?
4.(青岛中考改编)如图,圆柱形玻璃杯,高为12 cm,底面周长为18 cm,在杯内离杯底3 cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4 cm与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最短距离的平方是多少?
5.如图,一个长方体形状的木柜放在墙角处(与墙面和地面均没有缝隙),有一只蚂蚁从柜角A处沿着木柜表面爬2
到柜角C1处. (1)请你画出蚂蚁能够最快到达目的地的可能路径;
(2)当AB=4,BC=4,CC1=5时,求蚂蚁爬过的最短路径的长. 参考答案 1.C 2.B 3.如图是长方体的展开图,连接PQ,则PQ即为蚂蚁爬行的最短路程.易知PP′=12 cm,QP′=5 cm.由勾股定理,得PQ2=PP′2+P′Q2=122+52=169.所以PQ=13 cm.所以蚂蚁爬行的最短路径长为13 cm.
4.如图,将杯子侧面展开,作A关于EF的对称点A′,连接A′C即为最短距离.A′C2=A′D2+CD2=92+132=250(cm2).
5.(1)如图,木柜的表面展开图是两个长方形ABC′1D1和ACC1A1.蚂蚁能够最快到达目的地的可能路径有如图所示的AC′1和AC1两种.(2)蚂蚁沿着木柜表面经线段A1B1到C′1,爬过的路径的长l1=42+(4+5)2=97.蚂蚁沿着木柜表面经线段BB1到C1,爬过的路径的长l2=(4+4)2+52=89.∵l1>l2,∴最短路径的长是89.
勾股定理中的最短路径问题
勾股定理中的最短路径问题1. 勾股定理的基础1.1 勾股定理的来历哎,你知道吗?勾股定理这玩意儿可真是数学界的明星!想想看,两个直角边的平方和,等于斜边的平方,简直就像是数学的秘密武器。
古希腊的数学家毕达哥拉斯可是大名鼎鼎,他的这个定理为我们揭开了许多几何谜团。
不过,咱们可不能把它当成死板的公式,生活中处处都有它的影子。
1.2 勾股定理的应用想象一下,你和朋友在公园里散步,结果你们发现了一条小径。
这条小径绕来绕去,走得可费劲了,但其实你们只需要沿着一条直线走到目的地。
这个时候,勾股定理就像你的导航,告诉你怎么走最省事。
无论是爬山、越野,还是走街串巷,最短路径的问题无处不在,真是“走一步算一步”的好帮手。
2. 最短路径的趣味探讨2.1 最短路径的魅力说到最短路径,简直可以用“行走在正确的道路上”来形容。
想象一下,你在迷宫里游荡,四周都是墙壁,脑袋都要炸了。
这个时候,找到那条直达出口的路,那种心里一亮的感觉,真的是无与伦比!而勾股定理就像你的秘密武器,让你用最少的步数找到最佳出口,真是“智者千虑,必有一失”,谁都想少走弯路嘛!2.2 日常生活中的最短路径不过,最短路径可不仅限于数学题。
比如说,假设你要去隔壁的超市,走着走着,突然发现原来有一条小巷子可以穿过去,走起来省时又省力,心里那个爽啊,简直像捡到了一分钱。
生活中总是有这样的小发现,就像勾股定理教给我们的道理——有时候,直接一点,反而是最好的选择。
3. 总结与思考3.1 勾股定理的哲理勾股定理不仅是个数学公式,它其实还给我们带来了一些人生的哲理。
我们常常在生活中绕来绕去,寻找看似完美的路径,但实际上,简单的直线才是最有效的。
有时候,想太多反而让我们迷失方向,真的是“越想越糊涂”。
所以,咱们在面对选择时,别忘了用勾股定理的思维,寻找那条最短、最简单的路。
3.2 实际应用的启示最终,勾股定理和最短路径的问题不仅仅是数学的事,更是生活的智慧。
我们在每一次选择中,都可以尝试运用这种思维,尽量少走弯路,快速达到目标。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专题二-勾股定理最短路径问题
1.长方体的长、宽、高分别为6cm、4cm、2cm。
一只蚂蚁从点A出发,沿长方体表面到达B处。
求所走的最短路径长,答案为10cm。
2.一个棱长为1的正方体纸箱,一只蚂蚁从A点沿纸箱表面爬到B点。
求它所爬行的最短路线的长,答案为√
3.
3.一个底面圆周长为12cm、高为8cm的圆柱,一只蚂蚁从点A爬到点B处吃食。
求要爬行的最短路程,答案为4√10.
4.一个三级台阶,每一级的长宽高分别为20cm、3cm、2cm。
A和B是这个台阶两个相对的端点,A点有一只蚂蚁,想到B点去吃可口的食物。
蚂蚁沿着台阶面爬到B点的最短路程为29cm。
5.从A点(圆柱底面一点)环绕圆柱形侧面,建梯子到A 点正上方的B点。
若圆柱底面周长为12m,XXX为5m,求所建梯子最短需7m。
6.一个底面周长为16cm、高为11cm的圆柱形玻璃杯,离杯底3cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4cm与蜂蜜相对的点A处。
求蚂蚁到达蜂蜜的最短
距离为√170.。
