2016年深圳市中考一模数学试卷
2016届深圳中考数学模拟考试

最大最全最精的教育资源网
一、
选择
题(本题满分36分)
二、填空题 (本题满分12分)
三、解答题(共52分)
17.(本题5分)计算:︒+---+--45tan 28)2011()2
1
(301π 解:原式=
13. ; 14. ; 15. ; 16. ;
19.(本题7分)
(1)证明: (2)解: 1 2
3 4 5 6 10 11 12
7 8 9
18.(本题5分)解方程:x x x -=+-+41
143
解:
2016届深圳中考模拟考试数学试卷—答题卡 学校: 班级: 姓名: 注意事项:
1. 选择题作答必须用2B 铅笔,修改时用橡皮擦干净。
解答题作答必须用黑色墨迹签字笔或钢笔填写,答
题不得超出答题框。
2. 保持卡面清洁,不要折叠,不要弄破。
3. 在每页考生信息框中填写姓名及考生号。
4. 采用网上阅卷的务必要在右侧填涂考生号。
考 生 号
最大最全最精的教育资源网
23.(本题10分) (1)解:
(2)解:
22.(本题8分) (1)证明:
(2)解:
(3)解:
请不要在此区域答题或书写!
A B
C
D
E
R G
F P
图7-1
y
P
A
M
B
C
O
E
F 图8-1
x。
【深圳】2016-2017广东省深圳市福田区初三一模数学

2017年九年级教学质量检测试卷数 学 第一部分 选择题一、选择题(本部分共12小题,每小题3分,共36分.每小题给出的4个选项,其中只有一个是正确的.) 1.2016年深圳市生产总值同比增和工9%,记作9%+,而尼日利亚国内生产总值同比下降2.24%,应记作 A .2.24% B . 2.24%-C .2.24D . 2.24-【答案】B【解析】下降是增长的相反意义的量。
故下降2.24%记作 2.24%-。
2.很多美味的食物,它们的包装盒也很漂亮,观察banana boat 、可爱多冰激凌、芒果原浆以及玫瑰饴的包装盒,从正面看、从上面看分别得到的平面图形是长方形、圆的是A .B .C .D .【答案】C【解析】A .从正面看是梯形,不符合。
B .从正面看是三角形,不符合。
C .从正面看是长方形,从上面看是圆,符合题意。
D .从正面看是长方形,从上面看是长方形,不符合。
3.2016年6月21日,京东宣布与沃尔玛达成深度战略合作,京东向沃尔玛发行近1.45亿股A 类普通股,而京东则获得1号店第三方平台1号商场的主要资产。
1.45亿用科学记数法表示为 A .101.4510⨯ B .90.14510⨯C .81.4510⨯D .714.510⨯【答案】C【解析】1.45亿8145000000 1.4510==⨯。
4.下列计算正确的是 A .321x x -= B .326()a a -=-C .623x x x ÷=D .325x x x ⋅=【答案】D【解析】A .32x x x -=,选项错误。
B .326()a a -=,选项错误。
C .624x x x ÷=,选项错误。
D .325x x x ⋅=,选项正确。
5.下表是全国7个城市2017年3月份某日空气质量指数(AQI )的统计结果:该日空气质量指数的中位数是 A .49 B .62C .241D .97【答案】B【解析】7个AQI 从小到大依次为25、49、49、62、72、185、241,故中位数为62。
2016年深圳市中考数学试题及答案解析
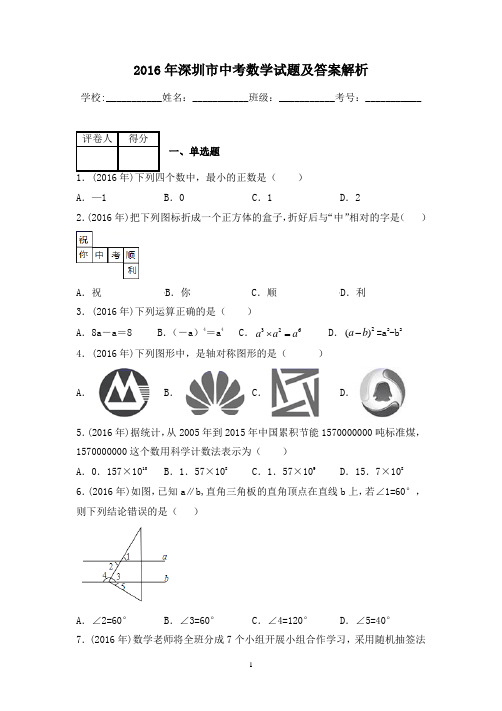
2016年深圳市中考数学试题及答案解析学校:___________姓名:___________班级:___________考号:___________一、单选题 ) A .—1B .0C .1D .22.(2016年)把下列图标折成一个正方体的盒子,折好后与“中”相对的字是( )A .祝B .你C .顺D .利 3.(2016年)下列运算正确的是( )A .8a -a =8B .(-a )4=a 4C .326a a a ⨯=D .2()a b -=a 2-b 2 4.(2016年)下列图形中,是轴对称图形的是( )A .B .C .D .5.(2016年)据统计,从2005年到2015年中国累积节能1570000000吨标准煤,1570000000这个数用科学计数法表示为( ) A .0.157×1010 B .1.57×108C .1.57×109D .15.7×1086.(2016年)如图,已知a ∥b,直角三角板的直角顶点在直线b 上,若∠1=60°,则下列结论错误的是( )A .∠2=60°B .∠3=60°C .∠4=120°D .∠5=40°7.(2016年)数学老师将全班分成7个小组开展小组合作学习,采用随机抽签法确定一个小组进行展示活动.则第3小组被抽到的概率是()A.B.C.D.8.(2016年)下列命题正确是()A.一组对边平行,另一组对边相等的四边形是平行四边形B.两边及一角对应相等的两个三角形全等C.16的平方根是4D.一组数据2,0,1,6,6的中位数和众数分别是2和69.(2016年)施工队要铺设一段全长2000米,的管道,因在中考期间需停工两天,实际每天施工需比原来计划多50米,才能按时完成任务,求原计划每天施工多少米。
设原计划每天施工x米,则根据题意所列方程正确的是()A. B.C. D.10.(2016年)给出一种运算:对于函数,规定。
广东省深圳市2016年十七校联考中考数学模拟试卷及参考答案

,每回收1吨塑料类垃圾可获得0.7吨二级原料.假设该城市每月产生
的生活垃圾为5 000吨,且全部分类处理,那么每月回收的塑料类垃圾可以获得多少吨二级原料? 19. 如图1,在△OAB中,∠OAB=90°,∠AOB=30°,OB=8.以OB为边,在△OAB外作等边△OBC,D是OB的中点
,连接AD并延长交OC于E.
.
15. 如图,△AOB与△ACD均为正三角形,且顶点B、D均在双曲线y= (x>0)上,点A、C在x轴上,连接BC交AD 于点P,则△OBP的面积=________.
三、解答题
16. 计算:﹣22+ +(3﹣π)0﹣|﹣3|
17. 先化简(
)+(1﹣ ),然后从﹣ <x< 范围内选取一个合适的整数作为x的值代入求值.
18. 垃圾的分类处理与回收利用,可以减少污染,节省资源.某城市环保部门为了提高宣传实效,抽样调查了部分居民
小区一段时间内生活垃圾的分类情况,其相关信息如下:
根据图表解答下列问题:
(1) 请将条形统计图补充完整; (2) 在抽样数据中,产生的有害垃圾共吨; (3) 调查发现,在可回收物中塑料类垃圾占
15. 16.
17. 18. 19.
20.
21.
22.
A.
B.
C . +1 D .
二、填空题
12. 因式分解:x3y﹣xy=________. 13. 小亮与小明一起玩“石头、剪刀、布”的游戏,两同学同时出“剪刀”的概率是________. 14. “五一”国际劳动节,广场中央摆放着一个正六边形的鲜花图案,如图所示,已知第一层摆黄色花,第二层摆红色花 ,第三层是紫色花,第四层摆黄色花…由里向外依次按黄、红、紫的颜色摆放,那么第10层应摆________盆________花
2016年广东省深圳市中考数学试卷(学生版)

2016年广东省深圳市中考数学试卷一、单项选择题:本大题共12小题,每小题3分,共36分1.(3分)下列四个数中,最小的正数是()A.﹣1B.0C.1D.22.(3分)把下列图标折成一个正方体的盒子,折好后与“中”相对的字是()A.祝B.你C.顺D.利3.(3分)下列运算正确的是()A.8a﹣a=8B.(﹣a)4=a4C.a3•a2=a6D.(a﹣b)2=a2﹣b24.(3分)下列图形中,是轴对称图形的是()A.B.C.D.5.(3分)据统计,从2005年到2015年中国累积节能1570000000吨标准煤,1570000000这个数用科学记数法表示为()A.0.157×1010B.1.57×108C.1.57×109D.15.7×108 6.(3分)如图,已知a∥b,直角三角板的直角顶点在直线b上,若∠1=60°,则下列结论错误的是()A.∠2=60°B.∠3=60°C.∠4=120°D.∠5=40°7.(3分)数学老师将全班分成7个小组开展小组合作学习,采用随机抽签确定一个小组进行展示活动,则第3个小组被抽到的概率是()A.B.C.D.8.(3分)下列命题正确的是()A.一组对边平行,另一组对边相等的四边形是平行四边形B.两边及其一角相等的两个三角形全等C.16的平方根是4D.一组数据2,0,1,6,6的中位数和众数分别是2和69.(3分)施工队要铺设一段全长2000米的管道,因在中考期间需停工两天,实际每天施工需比原计划多50米,才能按时完成任务,求原计划每天施工多少米.设原计划每天施工x米,则根据题意所列方程正确的是()A.2B.2C.2D.210.(3分)给出一种运算:对于函数y=x n,规定y′=nx n﹣1.例如:若函数y=x4,则有y′=4x3.已知函数y=x3,则方程y′=12的解是()A.x1=4,x2=﹣4B.x1=2,x2=﹣2C.x1=x2=0D.x1=2,x2=﹣211.(3分)如图,在扇形AOB中∠AOB=90°,正方形CDEF的顶点C是的中点,点D 在OB上,点E在OB的延长线上,当正方形CDEF的边长为2时,则阴影部分的面积为()A.2π﹣4B.4π﹣8C.2π﹣8D.4π﹣412.(3分)如图,CB=CA,∠ACB=90°,点D在边BC上(与B、C不重合),四边形ADEF为正方形,过点F作FG⊥CA,交CA的延长线于点G,连接FB,交DE于点Q,给出以下结论:①AC=FG;②S△F AB:S四边形CBFG=1:2;③∠ABC=∠ABF;④AD2=FQ•AC,其中正确的结论的个数是()A.1B.2C.3D.4二、填空题:本大题共4小题,每小题3分,共12分13.(3分)分解因式:a2b+2ab2+b3=.14.(3分)已知一组数据x1,x2,x3,x4的平均数是5,则数据x1+3,x2+3,x3+3,x4+3的平均数是.15.(3分)如图,在▱ABCD中,AB=3,BC=5,以点B的圆心,以任意长为半径作弧,分别交BA、BC于点P、Q,再分别以P、Q为圆心,以大于PQ的长为半径作弧,两弧在∠ABC内交于点M,连接BM并延长交AD于点E,则DE的长为.16.(3分)如图,四边形ABCO是平行四边形,OA=2,AB=6,点C在x轴的负半轴上,将▱ABCO绕点A逆时针旋转得到▱ADEF,AD经过点O,点F恰好落在x轴的正半轴上,若点D在反比例函数y(x<0)的图象上,则k的值为.三、解答题:本大题共7小题,其中17题5分,18题6分,19题7分,20题8分,共52分17.(5分)计算:|﹣2|﹣2cos60°+()﹣1﹣(π)0.18.(6分)解不等式组:.19.(7分)深圳市政府计划投资1.4万亿元实施东进战略.为了解深圳市民对东进战略的关注情况.某校数学兴趣小组随机采访部分深圳市民,对采访情况制作了统计图表的一部分如下:关注情况频数频率A.高度关注m0.1B.一般关注1000.5C.不关注30nD.不知道500.25(1)根据上述统计图可得此次采访的人数为人,m=,n=;(2)根据以上信息补全条形统计图;(3)根据上述采访结果,请估计在15000名深圳市民中,高度关注东进战略的深圳市民约有人.20.(8分)某兴趣小组借助无人飞机航拍校园.如图,无人飞机从A处水平飞行至B处需8秒,在地面C处同一方向上分别测得A处的仰角为75°,B处的仰角为30°.已知无人飞机的飞行速度为4米/秒,求这架无人飞机的飞行高度.(结果保留根号)21.(8分)荔枝是深圳的特色水果,小明的妈妈先购买了2千克桂味和3千克糯米糍,共花费90元;后又购买了1千克桂味和2千克糯米糍,共花费55元.(每次两种荔枝的售价都不变)(1)求桂味和糯米糍的售价分别是每千克多少元;(2)如果还需购买两种荔枝共12千克,要求糯米糍的数量不少于桂味数量的2倍,请设计一种购买方案,使所需总费用最低.22.(9分)如图,已知⊙O的半径为2,AB为直径,CD为弦.AB与CD交于点M,将沿CD翻折后,点A与圆心O重合,延长OA至P,使AP=OA,连接PC(1)求CD的长;(2)求证:PC是⊙O的切线;(3)点G为的中点,在PC延长线上有一动点Q,连接QG交AB于点E.交于点F(F与B、C不重合).问GE•GF是否为定值?如果是,求出该定值;如果不是,请说明理由.23.(9分)如图,抛物线y=ax2+2x﹣3与x轴交于A、B两点,且B(1,0)(1)求抛物线的解析式和点A的坐标;(2)如图1,点P是直线y=x上的动点,当直线y=x平分∠APB时,求点P的坐标;(3)如图2,已知直线y x分别与x轴、y轴交于C、F两点,点Q是直线CF 下方的抛物线上的一个动点,过点Q作y轴的平行线,交直线CF于点D,点E在线段CD的延长线上,连接QE.问:以QD为腰的等腰△QDE的面积是否存在最大值?若存在,请求出这个最大值;若不存在,请说明理由.。
深圳2016中考模拟01(含答案)

2016届深圳中考数学模拟题(1)一、选择题(本题共有 12小题,每小题3分,共36分,每小题有四个选项,其中只有一个是正确的) 1. -1的倒数是()4A 、 -4 2.如图是五个相同的小正方体搭成的几何体,这几个几何体的主视图是( 召AB B 田C 由D fc 3.下列计算正确的是(4.下列图形中既是轴对称图形又是中心对称图形的是( 7. 某商人在一次买卖中均以 120元卖出两件衣服,一件赚 25% 一件赔25%在这次交易中,该商人 () 8.某班级第一小组 7名同学积极捐出自己的零花钱支持地震灾区,他们捐款的数额分别是(单位:元)50, 20, 50, 30, 25, 50, 55,这组数据的众数和中位数分别是()A 、50 元,20 元B 50 元,40 元C 50 元,50 元29. 如图,观察二次函数 y=ax +bx+c 的图象,下列结论:2①a+b+c > 0,②2a+b > 0,③b - 4ac >0,④ac > 0.其中正确的是(A 、①②D -1 4)3 2 5 A 、2a +a =3a2 2 B ( 3a ) =6a 2C 、( a+b ) =a +b2 3 5D 2a ?a =2a5.据测算,世博会召开时,上海使用清洁能源可减少二氧化碳排放约 表示为()16万吨,将16万吨用科学记数法3 . A 、1.6 X 10 吨4 . B 1.6 X 10 吨5 . C 1.6 X 10 吨 6 .D 1.6 X 10 吨6.如图 ,AB// CD / ABE=60,/ D=5C °,则/E 的度数为( )A 、 40° B、30°C 、20° D 10°A 、赚16元 C 不赚不赔 D 无法确定C ②③D ③④??-8?? 5< 3 10. 如图,正六边形ABCDEF 内接于O 0,半径为4,则这个正六边形的边心距 0M 和厂的长分别为()11. 如图,在?ABCD 中,用直尺和圆规作/ BAD 的平分线 AG 交BC 于点E.若BF=6,AB=5则AE 的长为()A 、4B 6C 8D 1012. 如图,G, E 分别是正方形 ABCD 勺边AB, BC 的点,且 AG=CE AE1EF, AE=EF 现有如下结论:第二部分非选择题二、填空题(本题共有 4小题,每小题3分,共12分) 13. 因式分解:a 3- 4a= ________ .14. 从-3、1、- 2这三个数中任取两个不同的数,积为正数的概率是 _______________15. 用同样大小的黑色五角星按图所示的方式摆图案,按照这样的规律摆下去,第99个图案需要的黑色16. 如图,△ ABC 的内心在x 轴上,点B 的坐标是k点A 的坐标是(-3, b ),反比例函数y=-( x v 0)的图象经过点 A 则k= _______________________________________________________ A 2, 3C 、乜,等B 2v3,n1①BE=GE ②厶 AGE^A ECF ③/FCD=45 ;④厶GBEo ^ ECH 其中,正确的结论有()C 3个D 4个11题图 12五角星**W ** * *个.丄* W 喰翡WWW * W ** *★ A * ** ★ *17. 计算:v 16+ (- 1)20131 -2-(2) + (n- 3)-4(??+ 1) 18.解不等式组{< 7??+10并写出它的所有非负整数解. D(2, 0),点C 的坐标是(0, - 2),X三、解答题(本题共7小题,其中第17题6分,第18题6分,第19题7分,第20题8分,第21题8分,第22题8分,第23题9分,共52 分)??-8 ?? 5<321.某开发商要建一批住房,经调查了解,若甲、乙两队分别单独完成,则乙队完成的天数是甲队的 倍;若甲、乙两队合作,则需 120天完成.19. 丹东是个美丽的旅游城市,吸引了很多外地游客,某旅行社对今年五月接待的外地游客来丹东旅游的 首选景点做了一次抽样调查,根据收集到的数据, 绘制成如下统计图(不完整),请根据图中提供的 信息,完成下列问题:(1) 此次共调查了 _____________ 人 (2)请将两幅统计图补充完整.(3) “凤凰山”部分的圆心角是 __________ 度。
深圳市2016年初中毕业生学业考试数学模拟试卷(1).
深圳市2016年初中毕业生学业考试数学试卷模拟试题(一)说明:1.全卷分二部分,第一部分为选择题,第二部分为非选择题,共4页。
考试时间90分钟,满分100分。
2.考生必须在答题卡上按规定作答;答题卡必须保持清洁,不能折叠。
3.答题前,请将姓名.考生号.考场等用规定的笔填涂在答题卡指定的位置上(将条形码粘贴好)。
4.本卷选择题1—12,每小题选出答案后,用2B铅笔将答题卡选择题答题区内对应题目的答案标号涂黑;非选择题13—23,答案(含作辅助线)必须用规定的笔,按作答题目序号,写在答...某机构对30万人的调查显示,沉迷于手机上网的初中生大约占第7题图..第二部分非选择题填空题(本题共4小题,每小题3分,共12分)913.=18.若a 是正整数,且a 满足⎪⎩⎪⎨⎧>--<-02a 312a 1,试解分式方程11x x a ax 3=++-19.我市某中学今年年初开学后打算招聘一名数学教师,对三名前来应聘的数学教师A 、B 、C 进行了考核,他们的笔试成绩和说课成绩(单位:分)分别用了两种方式进行了统计,如表一和图一:(1)请将表一和图一中的空缺部分补充完整. (2)应聘的最后一个程序是由该校的24名数学教师进行投票,三位应聘人的得票情况如图二(没有弃权票,该校的每位教师只能选一位应聘教师),请计算每人的得票数(得票数可是整数哟).(3)若每票计1分,该校将笔试、说课、得票三项测试得分按3:4:4的比例确定个人成绩,请计算三位应聘人的最后成绩,并根据成绩判断谁能应聘成功.20.作图与证明 (1)作图题:如图1,在网格图中做出将四边形ABCD 向左平移3格,再向上平移2格得到的四边形A ′B ′C ′D ′. (2)证明题:已知:如图2,在△ABC 中,BE=EC ,过点E 作ED ∥BA 交AC 与点G ,且AD ∥BC ,连接AE 、CD .求证:四边形AECD 是平行四边形.图一 图二21.某商场试销一种成本为每件60元的服装,规定试销期间销售单价不低于成本单价,且获利不得高于40%.经试销发现,销售量y (件)与销售单价x (元)符合一次函数y=kx+b ,且x=80时,y=40;x=70时,y=50.(1)求一次函数y=kx+b 的表达式;(2)若该商场获得利润为W 元,试写出利润W 与销售单价x 之间的关系式;销售单价定为多少元时,商场可获得最大利润,最大利润是多少元?22.已知⊙O 的半径为4,BC 为⊙O 的弦,060=∠OBC ,P 是射线AO 上的一动点,连结CP . (1)当点P 运动到如图1所示的位置时,34=∆PBC S ,求证:CP 是⊙O 的切线;(2)如图2,当点P 在直径AB 上运动时,CP 的延长线与⊙O 相交于点Q ,试问PB 为何值时,CBQ ∆是等腰三角形?23.抛物线y=ax 2+bx +c(a≠0)的顶点为D (1,4),交x 轴于A 、B 两点,且经过点C (2,3) (1)求抛物线的解析式,(2)如图13,M 为线段O 、B 之间一动点,N 为y 轴正半轴上一动点,是否存在使M 、C 、D 、N 四点围成的四边形周长最小.若存在,求出这个最小值及M 、N 的坐标;若不存在,请说明理由, (3) 若P 是y 轴上的点,Q 是抛物线上的点,求:以P 、 Q 、 A 、B 为顶点构成平行四边形的点Q 的坐标.图1图2参考答案及评分意见第二部分 非选择题填空题(本题共4小题,每小题3分,共12分)解答题(本题共7小题,其中第17题6分,第18题6分,第19题7分,第20题7分,第21题8分,第22题9分,第23题9分,共52分) 17.解: 原式=1134+++ ………………1+2+1+1分=9. ………………………6分 (注:运算的第一步正确一项给1分.)18.解:∵⎪⎩⎪⎨⎧>--<-)()(20 (2)a 31 1......2a 1∴由(1)得,a>1∴由(2)得,a<3∴1<a<3………………………………………………… ....1分 ∵a 是正整数,∴a=2.…………………………………………………….2分 将a=2代入分式方程得11x x22x 3=++-………………3分 去分母,方程两边同时乘以()()1x 22x +-得()()()()1x 22x 22x x 1x 3+-=-++……………………..4分整理得:-5x =………………………………………..…..5分 经检验,原分式方程的解是-5x =.…………………....6分19.解:(1)90,注:每个正确答案1分.(2)24×33.3%=7.992,24×41.7%=10.008,24×25%=6…………………..3分 根据实际意义可得,A 得8票,B 得10票,C 得6票.……………………4分 (3)因为3+4+4=10,由题可得,A 的最后成绩为:7.6310481049010385=⨯+⨯+⨯B 的最后成绩为:5.64104101048010395=⨯+⨯+⨯(对两个或以下,得1分)C 的最后成绩为:4.6310461048510390=⨯+⨯+⨯……………6分∵63.4<63.7<64.5∴B 能应聘成功.………………………………………………………..………7分 20.(1)解:如图所示:………………………3分(2)证明:∵ED ∥BA ,且AD ∥BC ,∴四边形BEDA 是平行四边形, ………………………4分 ∴AD=BE , ………………………5分 ∵BE=EC ,∴AD=EC , ………………………6分 ∵AD ∥BC ,∴四边形AECD 是平行四边形. ………………………7分图一21.解:(1)60≤x ≤60(1+40%),∴60≤x ≤84, ………………………1分 由题得:解之得:k=﹣1,b=120, ………………………2分∴一次函数的解析式为y=﹣x+120(60≤x ≤84). ………………………3分 (2)销售额:xy=x (﹣x+120)元;成本:60y=60(﹣x+120).………………………4分 ∴W=xy ﹣60y ,=x (﹣x+120)﹣60(﹣x+120), =(x ﹣60)(﹣x+120),=﹣x 2+180x ﹣7200,=﹣(x ﹣90)2+900, ………………………6分∴W=﹣(x ﹣90)2+900,(60≤x ≤84),当x=84时,W 取得最大值,最大值是:﹣(84﹣90)2+900=864(元).………………7分 即销售价定为每件84元时,可获得最大利润,最大利润是864元.………………………8分22.解:(1)∵060=∠OBC ,OC OB =,∴OBC ∆是等边三角形.∴060=∠COB . ·······································1分 ∵CP 与⊙O 相切, ∴090=∠OCP .∴003090=∠-=∠COP CPO …………2分 又∵⊙O 的半径为4,∴4==OC OB .∴82==OC OP . ∴448=-=-=OB OP PB . ························3分 (2)①过点C 作1CP OB ⊥,垂足为1P ,延长1CP 交⊙O 于1Q , ∵AB ⊙O 是的直径, ∴⋂⋂=1BQ BC ,∴1BQ BC =,…………4分 ∴1CBQ △是等腰三角形.…………5分由(1)可知OBC ∆是等边三角形,∴011P B BC cos 6042=∙=⨯=2 .…………6分 ②解:过O 作BC OD ⊥,垂足为D ,延长DO 交⊙O 于2Q ,2CQ 与AB 交于2P , ∵O 是圆心, ∴2DQ 是BC 的垂直平分线. ∴22BQ CQ = ∴2CBQ ∆是等腰三角形. …………7分∵060=∠COB ,∴023021=∠=∠COB B CQ .∵2DQ 平分22,OQ OC B CQ =∠,∴02215=∠=∠OCQ O CQ .∵OBC ∆是等边三角形,1CP OB ⊥, ∴013021=∠=∠OCB OCP . ∴0002112P CP PCO OCQ 301545∠=∠+∠=+=. ∴12CPP △是等腰直角三角形. ·········································································· 8分∴121PP CP ==∴2321212+=+=B P P P B P . ······································································ 9分 23.23.(本小题满分9分)解:(1)设抛物线的表达式为:4)1(2+-=x a y将C (2,3)代入,解得:a=-1∴抛物线的表达式为:322++-=x x y ……(2分)(2)作D (1,4)关于y 轴对称点G (-1,4),C (2,3)关于x 轴对称点H (2,-3),∵CD 是一个定值,∴要使四边形MCDN 的周长最小, 只要使DN +MN +MC 最小即可 由图形的对称性,可知,DN +MN +MC =GN +NM +HM只有当GH 为一条直线段时,GN +NM +HM可求得: CD 2=,GH 58=∴四边形MCDN 的周长最小为582+ ……(6(3)若AB 为平行四边形的边, ∵AB=4, AB ∥PQ 且AB =PQ, ①当点Q 在y 轴的右侧时,4=Q x ,又∵点Q 在抛物线上, ∴5-=Q y ,∴)5,4(1-Q ………7分②当点Q 在y 轴的左侧时,4-=Q x ,又∵点Q 在抛物线上, ∴21-=Q y ,∴2Q (4,21)--……8分若AB 为平行四边形的对角线,如图,过Q 作QF ⊥x 轴,垂足为F ,∵四边形PAQB 为平行四边形, ∴QFA POB ∆≅∆,∴AF=OB=1 ∴Q x 2=,又∵点Q 在抛物线上,∴Q y 3=,∴3Q (2,3) …………9综上:符合要求的点Q 的坐标为:)5,4(1-Q ,2Q (4,21)--,3Q (2,3)(注:(3)没有求解过程只直接给出结果且三个点坐标全对可给1分 其它解法只要合理,参照给分.)GDE。
2016届广东深圳十七校联考中考模拟数学试卷(带解析)
绝密★启用前2016届广东深圳十七校联考中考模拟数学试卷(带解析)试卷副标题考试范围:xxx ;考试时间:119分钟;命题人:xxx学校:___________姓名:___________班级:___________考号:___________注意事项.1.答题前填写好自己的姓名、班级、考号等信息 2.请将答案正确填写在答题卡上第I 卷(选择题)一、选择题(题型注释)1、如图,在直角梯形ABCD 中,DC ∥AB ,∠DAB=90°,AC ⊥BC ,AC=BC ,∠ABC的平分线分别交AD 、AC 于点E ,F ,则的值是( )A .B .C .D .【答案】C 【解析】试题分析:作FG ⊥AB 于点G ,由AE ∥FG ,得出,求出Rt △BGF ≌Rt △BCF ,再由AB=BC 求解==.试卷第2页,共20页故选:C .考点:1、平行线分线段成比例,2、全等三角形及角平分线2、如图是二次函数y=ax 2+bx+c 过点A (﹣3,0),对称轴为x=﹣1.给出四个结论:①b 2>4ac ,②2a+b=0;③a ﹣b+c=0;④5a <b .其中正确结论是( )A .②④B .①④C .②③D .①③【答案】B 【解析】试题分析:∵抛物线与x 轴有两个交点, ∴△>0,即b 2﹣4ac >0, ∴b 2>4ac ,故①正确. ∵对称轴x=﹣1,∴-=﹣1,∴b=2a ,∴2a ﹣b=0,故②错误, ∵x=﹣1时,y >0, ∴a ﹣b+c >0,故③错误, ∵b=2a ,a <O ,∴5a <2a ,即5a <b ,故④正确, 故选B .考点:二次函数的图象与系数的关系3、如图,直线AB 与⊙O 相切于点A ,⊙O 的半径为2,若∠OBA=30°,则AB 的长为( )A .4B .4C .2D .2【答案】C 【解析】试题分析:由切线的性质得∠OAB=90°,利用锐角三角函数的定义,由∠OBA=30°,OA=2,可得AB=.故选C .考点:1、切线的性质,2、锐角三角函数4、四个命题:①三角形的一条中线能将三角形分成面积相等的两部分;②有两边和其中一边的对角分别相等的两个三角形全等;③点P (1,2)关于原点的对称点坐标为(﹣1,﹣2);④对角线互相垂直的四边形是菱形,其中正确的是( ) A .①②B .①③C .②③D .③④【答案】B 【解析】试题分析:①三角形的一条中线能将三角形分成面积相等的两部分,正确; ②有两边和其中一边的对角对应相等的两个三角形全等,错误; ③点P (1,2)关于原点的对称点坐标为(﹣1,﹣2),正确; ④对角线互相垂直的平行四边形才是菱形,故错误. 综上所述,正确的是①③.试卷第4页,共20页故选B . 考点:真假命题5、下列不等式变形正确的是( ) A .由a >b ,得a ﹣2<b ﹣2 B .由a >b ,得|a|>|b| C .由a >b ,得﹣2a <﹣2bD .由a >b ,得a 2>b 2【答案】C 【解析】试题分析:根据不等式两边加(或减)同一个数(或式子),不等号的方向不变;等式两边乘(或除以)同一个正数,不等号的方向不变;不等式两边乘(或除以)同一个负数,不等号的方向改变,可得:A 、等式的两边都减2,不等号的方向不变,故A 错误;B 、如a=2,b=﹣3,a >b ,得|a|<|b|,故B 错误;C 、不等式的两边都乘以﹣2,不等号的方向改变,故C 正确;D 、如a=2,b=﹣3,a >b ,得a 2>b 2,故D 错误. 故选:C .考点:不等式的基本性质6、阳光公司销售一种进价为21元的电子产品,按标价的九折销售,仍可获利20%,则这种电子产品的标价为( ) A .26元B .27元C .28元D .29元【答案】C 【解析】试题分析:根据题意,设电子产品的标价为x 元,按照等量关系“标价×0.9﹣进价=进价×20%”,列出一元一次方程得:0.9x ﹣21=21×20%解得:x=28所以这种电子产品的标价为28元. 故选C .考点:一元一次方程的应用7、为了解某班学生每天使用零花钱的情况,小红随机调查了15名同学,结果如下表:则这15名同学每天使用零花钱的众数和中位数分别是( ) A .3,3 B .2,3 C .2,2 D .3,5【答案】B 【解析】试题分析:由小红随机调查了15名同学,根据表格数据可以知道中位数在第三组,即中位数为3.再由2出现了5次,它的次数最多,所以众数为2. 故选B .考点:1、中位数,2、众数8、一个几何体的三视图如图所示,这个几何体是( )A .棱柱B .圆柱C .圆锥D .球【答案】B 【解析】试题分析:由于主视图和左视图为长方形可得此几何体为柱体,由俯视图为圆可得为圆柱体. 故选B .考点:三视图来判断几何体9、下列图形中,既是轴对称图形又是中心对称图形的是( )A .B .C .D .【答案】D 【解析】试题分析:依据轴对称图形的定义和中心对称图形的定义可知: A 、是轴对称图形,但不是中心对称图形,故A 错误; B 、是中心对称图形,不是轴对称图形,故B 错误; C 、是轴对称图形,不是中心对称图形,故C 错误; D 、既是轴对称图形,也是中心对称图形,故D 正确.试卷第6页,共20页故选:D .考点:轴对称图形和中心对称图形 10、下列计算正确的是( ) A .a 3•a 4=a 12B .(a 3)4=a 7C .(a 2b )3=a 6b 3D .a 3÷a 4=a (a≠0)【答案】C 【解析】试题分析:A 、根据同底数幂的乘法,应为a 3`·a 4=a 7,故本选项错误; B 、根据幂的乘方的性质,应为(a 3)4=a 12,故本选项错误; C 、根据积的乘方的性质,可知每个因式都分别乘方,正确;D 、根据同底数幂的除法和负整指数幂的性质,应为a 3÷a 4=(a≠0),故本选项错误. 故选C .考点:1、同底数幂的乘法,2、积的乘方和幂的乘方11、2015年初,一列CRH5型高速车组进行了“300000公里正线运营考核”标志着中国高速快车从“中国制造”到“中国创造”的飞跃,将300000用科学记数法表示为( ) A .3×106B .3×105C .0.3×106D .30×104【答案】B 【解析】试题分析:科学记数法的表示形式为a×10n 的形式,其中1≤|a|<10,n 为整数.确定n 的值时,要看把原数变成a 时,小数点移动了多少位,n 的绝对值与小数点移动的位数相同.当原数绝对值>1时,n 是正数;当原数的绝对值<1时,n 是负数.将300000用科学记数法表示为:3×105. 故选:B . 考点:科学记数法12、的倒数是( )A .﹣2B .2C .D .【答案】A试题分析:根据乘积为1的两个数互为倒数,可得的倒数是﹣2. 故选:A.考点:倒数试卷第8页,共20页第II 卷(非选择题)二、填空题(题型注释)13、如图,△AOB 与△ACD 均为正三角形,且顶点B 、D 均在双曲线y=(x >0)上,点A 、C 在x 轴上,连接BC 交AD 于点P ,则△OBP 的面积= .【答案】4 【解析】试题分析:设等边△AOB 的边长为a ,等边△ACD 的边长为b ,由等边三角形的性质找出点B 的坐标(a ,a ),点D 的坐标为(a+b ,b ),过点B 作BE ⊥x 轴于点E ,过点P 作PF ⊥x 轴于点F ,由等边三角形的性质可找出∠BOA=60°=∠PAC ,从而得出BO ∥PA ,根据平行线的性质即可得出,再由BE ⊥x 轴,PF ⊥x 轴得出BE ∥PF ,由此得出,根据比例关系找出线段PF 的长度,通过分割三角形以及三角形的面积公式找出=,由点B 的坐标结合反比例函数图象上点的坐标特征即可得出.考点:1、等边三角形的性质,2、反比例函数图象上点的坐标特征,3、三角形的面积公式,4、平行线的性质14、“五一”国际劳动节,广场中央摆放着一个正六边形的鲜花图案,如图所示,已知第一层摆黄色花,第二层摆红色花,第三层是紫色花,第四层摆黄色花…由里向外依次按黄、红、紫的颜色摆放,那么第10层应摆 盆 花.【答案】60盆黄花 【解析】试题分析:根据题意发现:颜色是黄、红、紫三个一循环;花盆个数是逐层加6盆鲜花.第10层是10÷3=3…1,应摆放黄花;第一层是2×6﹣6=6盆花;第二层是3×6﹣6=12盆花;依此类推,第10层是11×6﹣6=60盆花. 考点:规律探索15、小亮与小明一起玩“石头、剪刀、布”的游戏,两同学同时出“剪刀”的概率是 .【答案】【解析】试题分析:画树状图得:∵共有9种等可能的结果,两同学同时出“剪刀”的有1种情况,∴两同学同时出“剪刀”的概率是:.考点:用列表法或画树状图法求概率 16、因式分解:x 3y ﹣xy= .【答案】xy (x+1)(x ﹣1)试卷第10页,共20页【解析】试题分析:首先提取公因式xy ,再运用平方差公式进行二次分解. x 3y ﹣xy ,=xy (x 2﹣1)=xy (x+1)(x ﹣1). 考点:因式分解三、计算题(题型注释)17、计算:﹣22++(3﹣π)0﹣|﹣3|【答案】-4 【解析】试题分析:分别进行乘方、二次根式、零指数幂和绝对值的化简等运算,然后合并求解. 试题解析:﹣22++(3﹣π)0﹣|﹣3|=﹣4+2+1﹣3 =﹣4考点:实数的运算四、解答题(题型注释)18、抛物线y=ax 2+bx+4A (1,﹣1),B (5,﹣1),与y 轴交于点C .(1)求抛物线的函数表达式;(2)如图1,连接CB ,若点P 在直线BC 上方的抛物线上,△BCP 的面积为15,求点P 的坐标;(3)如图2,⊙O 1过点A 、B 、C 三点,AE 为直径,点M 为弧ACE 上的一动点(不试卷第11页,共20页与点A ,E 重合),∠MBN 为直角,边BN 与ME 的延长线交于N ,求线段BN 长度的最大值.【答案】(1)y=x 2﹣6x+4;(2)(6,4)或(﹣1,11)(3)【解析】试题分析:(1)将点A 、B 的坐标代入抛物线的解析式,得到关于a 、b 的方程,从而可求得a 、b 的值;(2)设点P 的坐标为P (m ,m 2﹣6m+4),根据=15,由,得到关于m 的方程求得m 的值,从而可求得点P 的坐标;(3)首先证明△EAB ∽△NMB ,从而可得到NB=,当MB 为圆的直径时,NB 有最大值.试题解析:(1)将点A 、B 的坐标代入抛物线的解析式得:,解得:.∴抛物线得解析式为y=x 2﹣6x+4; (2)如图所示:设点P 的坐标为P (m ,m 2﹣6m+4)∵S △CBP =15,即:S △CBP=S 梯形CEDP ﹣S △CEB ﹣S △PBD ,∴m (5+m 2﹣6m+4+1)﹣×5×5﹣(m ﹣5)(m 2﹣6m+5)=15,化简得:m 2﹣5m ﹣6=0, 解得:m=6,或m=﹣1,试卷第12页,共20页∴点P 的坐标为(6,4)或(﹣1,11), (3)连接AB 、EB ,∵AE 是圆的直径, ∴∠ABE=90°, ∴∠ABE=∠MBN , 又∵∠EAB=∠EMB , ∴△EAB ∽△NMB ,∵A (1,﹣1),B (5,﹣1), ∴点O 1的横坐标为3,将x=0代入抛物线的解析式得:y=4, ∴点C 的坐标为(0,4), 设点O 1的坐标为(3,m ), ∵O 1C=O 1A , ∴=,解得:m=2,∴点O 1的坐标为(3,2), ∴O 1A=, 在Rt △ABE 中,由勾股定理得:BE===6,∴点E 的坐标为(5,5), ∴AB=4,BE=6, ∵△EAB ∽△NMB ,∴,试卷第13页,共20页∴,∴NB=BM ,∴当MB 为直径时,MB 最大,此时NB 最大, ∴MB=AE=2,∴NB=×2=3.考点:1、二次函数的综合应用,2、相似三角形的判定和性质,3、勾股定理,4、圆周角定理19、如图,已知AB 是⊙O 的直径,直线CD 与⊙O 相切于点C ,AD ⊥CD 于点D .(1)求证:AC 平分∠DAB ;(2)若点E 为的中点,AD=,AC=8,求AB 和CE 的长.【答案】(1)证明见解析(2)AB=10,CE=7【解析】试题分析:(1)首先连接OC ,由直线CD 与⊙O 相切于点C ,AD ⊥CD ,易证得OC ∥AD ,继而可得AC 平分∠DAB ;(2)首先连接BC ,OE ,过点A 作AF ⊥CE 于点F ,可证得△ADC ∽△ACB ,△ACB ∽△AFE ,△ACF 是等腰直角三角形,然后由相似三角形的对应边成比例以及勾股定理,即可求得答案. 试题解析:(1)连接OC , ∵直线CD 与⊙O 相切于点C , ∴OC ⊥CD , ∵AD ⊥CD ,试卷第14页,共20页∴OC ∥AD , ∴∠DAC=∠OCA , ∵OA=OC , ∴∠OCA=∠OAC , ∴∠OAC=∠DAC , 即AC 平分∠DAB ;(2)连接BC ,OE ,过点A 作AF ⊥EC 于点F , ∵AB 是⊙O 的直径, ∴∠ACB=90°, ∴∠ACB=∠ADC , ∵∠DAC=∠BAC , ∴△ADC ∽△ACB ,∴,即,解得:AB=10, ∴BC==6,∵点E 为的中点,∴∠AOE=90°,∴OE=OA=AB=5,∴AE==5,∵∠AEF=∠B (同弧所对圆周角相等),∠AFE=∠ACB=90°, ∴△ACB ∽△AFE ,∴,∴, ∴AF=4,EF=3,试卷第15页,共20页∵∠ACF=∠AOE=45°,∴△ACF 是等腰直角三角形, ∴CF=AF=4,∴CE=CF+EF=7.考点:1、切线的性质,2、相似三角形的判定与性质,3、勾股定理,4、等腰直角三角形性质20、山地自行车越来越受到中学生的喜爱,各种品牌相继投放市场,某车行经营的A 型车去年销售总额为5万元,今年每辆销售价比去年降低400元,若卖出的数量相同,销售总额将比去年减少20%.(1)今年A 型车每辆售价多少元?(列方程解答)(2)该车行计划今年新进一批A 型车和B 型车共60辆,A 型车的进货价为每辆1100元,销售价与(1)相同;B 型车的进货价为每辆1400元,销售价为每辆2000元,且B 型车的进货数量不超过A 型车数量的两倍,应如何进货才能使这批车获利最多?【答案】(1)1600(2)当新进A 型车20辆,B 型车40辆时,这批车获利最大 【解析】试题分析:(1)设今年A 型车每辆售价x 元,则去年售价每辆为(x+400)元,由卖出的数量相同建立方程求出其解即可;(2)设今年新进A 型车a 辆,则B 型车(60﹣a )辆,获利y 元,由条件表示出y 与a 之间的关系式,由a 的取值范围就可以求出y 的最大值.试题解析:(1)设今年A 型车每辆售价x 元,则去年售价每辆为(x+400)元,由题意,得解得:x=1600,试卷第16页,共20页经检验,x=1600是元方程的根; 答:今年A 型车每辆售价1600元;(2)设今年新进A 型车a 辆,则B 型车(60﹣a )辆,获利y 元,由题意,得 y=(1600﹣1100)a+(2000﹣1400)(60﹣a ), y=﹣100a+36000,∵B 型车的进货数量不超过A 型车数量的两倍, ∴60﹣a≤2a , ∴a≥20. ∵k=﹣100<0, ∴y 随a 的增大而减小. ∴a=20时,y 最大=34000元. ∴B 型车的数量为:60﹣20=40辆.∴当新进A 型车20辆,B 型车40辆时,这批车获利最大. 考点:列分式方程解实际问题21、如图1,在△OAB 中,∠OAB=90°,∠AOB=30°,OB=8.以OB 为边,在△OAB 外作等边△OBC ,D 是OB 的中点,连接AD 并延长交OC 于E .(1)求证:四边形ABCE 是平行四边形;(2)如图2,将图1中的四边形ABCO 折叠,使点C 与点A 重合,折痕为FG ,求OG 的长.【答案】(1)证明见解析(2)1 【解析】试题分析:(1)首先根据直角三角形中斜边上的中线等于斜边的一半可得DO=DA ,再根据等边对等角可得∠DAO=∠DOA=30°,进而算出∠AEO=60°,再证明BC ∥AE ,CO ∥AB ,进而证出四边形ABCE 是平行四边形;(2)设OG=x ,由折叠可得:AG=GC=8﹣x ,再利用三角函数可计算出AO ,再利用勾股定理计算出OG 的长即可.试卷第17页,共20页试题解析:(1)∵Rt △OAB 中,D 为OB 的中点,∴AD=OB ,OD=BD=OB∴DO=DA ,∴∠DAO=∠DOA=30°,∠EOA=90°, ∴∠AEO=60°,又∵△OBC 为等边三角形, ∴∠BCO=∠AEO=60°, ∴BC ∥AE ,∵∠BAO=∠COA=90°, ∴CO ∥AB ,∴四边形ABCE 是平行四边形;(2)设OG=x ,由折叠可得:AG=GC=8﹣x , 在Rt △ABO 中,∵∠OAB=90°,∠AOB=30°,BO=8,∴AO=BOcos30°=8×=4,在Rt △OAG 中,OG 2+OA 2=AG 2, x 2+(4)2=(8﹣x )2,解得:x=1, ∴OG=1.考点:1、平行四边形的判定与性质,2、勾股定理的应用,3、图形的翻折变换 22、垃圾的分类处理与回收利用,可以减少污染,节省资源.某城市环保部门为了提高宣传实效,抽样调查了部分居民小区一段时间内生活垃圾的分类情况,其相关信息如下:试卷第18页,共20页根据图表解答下列问题: (1)请将条形统计图补充完整;(2)在抽样数据中,产生的有害垃圾共 吨;(3)调查发现,在可回收物中塑料类垃圾占,每回收1吨塑料类垃圾可获得0.7吨二级原料.假设该城市每月产生的生活垃圾为5 000吨,且全部分类处理,那么每月回收的塑料类垃圾可以获得多少吨二级原料?【答案】(1)图形见解析(2)3(3)378 【解析】试题分析:(1)根据D 类垃圾量和所占的百分比即可求得垃圾总数,然后乘以其所占的百分比即可求得每个小组的频数从而补全统计图; (2)求得C 组所占的百分比,即可求得C 组的垃圾总量; (3)首先求得可回收垃圾量,然后求得塑料颗粒料即可. 试题解析:(1)观察统计图知:D 类垃圾有5吨,占10%, ∴垃圾总量为5÷10%=50吨, 故B 类垃圾共有50×30%=15吨, 故统计表为:试卷第19页,共20页(2)∵C 组所占的百分比为:1﹣10%﹣30%﹣54%=6%, ∴有害垃圾为:50×6%=3吨;(3)5000×54%××0.7=378(吨),答:每月回收的塑料类垃圾可以获得378吨二级原料. 考点:条形统计图的应用23、先化简,然后从﹣<x <范围内选取一个合适的整数作为x 的值代入求值.【答案】,-3【解析】试题分析:先根据分式混合运算的法则把原式进行化简,再选取合适的x 的值代入进行计算即可.试题解析:====,试卷第20页,共20页当x=时,原式==-3.考点:分式的化简求值。
【深圳】2016-2017广东省深圳市福田区初三下学期17校一模数学
2016-2017学年度第二学期初三联考数学第一部分选择题(本部分共12小题,每小题3分,共36分,每小题给出的四个选项,只有一项是正确的)1.13-的倒数是().A .13-B .13C .3-D .32.人民网北京1月24日电(记者杨迪)财政部23日公布了2016年财政收支数据.全国一般公共预算收入159600亿元,将159600亿元用科学记数法表示为().A .51.59610⨯元B .131.59610⨯元C .1315.9610⨯元D .60.159610⨯元3.下列四个图案中,具有一个共有的性质.那么下面四个数中,满足上述共有性质的一个是(). A .228B .707C .808D .6094.下列运算正确的是().A .88a a -=B .44()a a -=C .326a a a ⋅=D .222()a b a b -=-5.如图,现分别旋转两个标准的转盘,则转盘所转到的两个数字之积为奇数的概率是().A .13B .35C .12D .166.一家服装店将某种服装按进价提高50%后标价,又以八折销售,售价为360元,则每件服装的进价是().A .168元B .300元C .60元D .400元7.定义:点(,)A x y 为平面直角坐标系内的点,若满足x y =,则把点A 叫做“平衡点”.例如:(1,1)M ,(2,2)N --都是“平衡点”.当13x -≤≤时,直线2y x m =+上有“平衡点”,则m 的取值范围是(). A .01m ≤≤B .10m -≤≤C .33m -≤≤D .31m -≤≤8.如图,直线m n ∥,ABC △的顶点B ,C 分别在直线n ,m 上,且90ACB ∠=︒,若140∠=︒,则2∠的度数为(). A .140︒B .130︒C .120︒D .110︒9.如图,已知ABC △()AB BC AC <<,用尺规在AC 上确定一点P ,使PB PC AC +=,则下列选项中,一定符合要求的作图痕迹是().A .B .C .D .10.如图,ABC △是等边三角形,点P 是三角形内的任意一点,PD AB ∥,PE BC ∥,PF AC ∥,若ABC△的周长为36,则PD PE PF ++=().A .12B .8C .4D .311.如图,在矩形ABCD 中,2AB =,点E 在边AD 上,45ABE ∠=︒,BE DE =,连接BD ,点P 在线段DE 上,过点P 作PQ BD ∥交BE 于点Q ,连接QD .设PD x =,PQD △的面积为y ,则能表示y 与x 函数关系的图象大致是().12nm C BAAB CACCPFE DCBAA .B .C .D .12.如图,如图,平行四边形ABCD 中,AE 平分BAD ∠,交BC 于E ,DE AE ⊥,下列结论:①DE 平分ADC ∠;②E 是BC 的中点;③2AD CD =;④四边形ADCE 的面积与ABE △的面积比是3:1,其中正确的结论的个数有().A .4B .3C .2D .1第二部分非选择题填空题(本题共4小题,每小题3分,共12分) 13.分解因式:228x -=__________.14.若213m x y 与62n x y 是同类项,则m n +=____________.15.如图,在平面直角坐标系中,A 、B 两点分别在x 轴和y 轴上,1OA =,OB AB ,过AB 中点1C 分别作x 轴和y 轴的垂线,垂足分别是点1A 、1B ,连接11A B ,再过11A B 中点2C 作x 轴和y 轴的垂线,照此规律依次作下去,则点n C 的坐标为__________.Q ABCDE PEDCBA16.如图,一次函数y kx b =+的图象l 与坐标轴分别交于点E 、F ,与双曲线4(0)y x x=-<交于点(1,)P n -,且F 是PE 的中点.直线x a =与l 交于点A ,与双曲线交于点B (不同于A ),P A P B =,则a =__________. 解答题(本题共7小题,其中第17小题5分,第18小题6分,第19小题7分,第20小题8分,第21小题8分,第22小题9分,第23小题9分,共52分).17.计算:2012sin60(π4)2-⎛⎫---+︒+- ⎪⎝⎭18.先化简,再求值:2211221x x x x x +⎛⎫÷- ⎪---⎝⎭,其中1.19.我市某中学决定在学生中开展丢沙包、打篮球、跳大绳和踢毽球四种项目的活动,为了解学生对四种项目的喜欢情况,随机调查了该校m 名学生最喜欢的一种项目(每名学生必选且只能选择四种活动项目的一种),并将调查结果绘制成如下的不完整的统计图表:学生最喜欢的活动项目的人数统计表 学生最喜欢的活动项目的人数条形统计图根据图表中提供的信息,解答下列问题:百分比学生数(名)20%40% p %10%40n 6020踢键球跳大绳打篮球丢沙包项目丢沙包打篮球跳大绳踢键球(1)m =__________,n =__________,P =__________. (2)请根据以上信息直接补全条形统计图.(3)根据抽样调查结果,请你估计该校2000名学生中有多少名学生最喜欢跳大绳.20.如图,在矩形ABCD 中,AE 平分BAD ∠,交BC 于E ,过E 做EF AD ⊥于F ,连接BF 交AE 于P ,连接PD .(1)求证:四边形ABEF 是正方形.(2)如果6AB =,8AD =,求tan ADP ∠的值.21.深圳市某校对初三综合素质测评中的审美与艺术进行考核,规定如下:考核综合评价得分由测试成绩(满分100分)和平时成绩(满分100分)两部分组成,其中测试成绩占80%,平时成绩占20%,并且当综合评价得分大于或等于80分时,该生综合评价为A 等.(1)小明同学的测试成绩和平时成绩两项得分之和为185分,而综合评价得分为91分,则小明同学测试成绩和平时成绩各得多少分?(2)某同学测试成绩为70分,他的综合评价得分有可能达到A 等吗?为什么?(3)如果一个同学综合评价要达到A 等,他的测试成绩至少要多少分?22.如图,已知AB 是⊙O 的直径,点C 在⊙O 上,过点C 的直线与AB 的延长线交于点P ,AC PC =,2COB PCB ∠=∠.(1)求证:PC 是⊙O 的切线.(2)求证:12BC AB =. (3)点M 是弧AB 的中点,CM 交AB 于点N ,若8AB =,求MN MC ⋅的值.23.如图,平面直角坐标系中,抛物线23y ax bx =++与x 轴的两个交点分别为(3,0)A -,(1,0)B ,与y 轴交点为D ,对称轴与抛物交于点C ,与x 轴负半轴交于点H .CDFPEBAAPM(1)求抛物线的表达式.(2)点E ,F 分别是抛物线对称轴CH 上的两个动点(点E 在点F 上方),且1EF ,求使四边形BDEF的周长最小时的点E ,F 坐标及最小值.(3)如图,点P 为对称轴左侧,x 轴上方的抛物线上的点,PQ AC ⊥交AC 于点Q ,是否存在这样的点P使PCQ △与ACH △相似,若存在请求出点P 的坐标,若不存在请说明理由.。
深圳2016中考模拟02
2016届深圳中考数学模拟题(2)一.选择题(每小题3分,共36分)1.下列式子结果为负数的是()A.(﹣3)0 B.﹣|﹣3| C.(﹣3)2D.(﹣3)﹣22.下列计算正确的是()A.(2a2)3=8a B.()2=9 C.3﹣=3 D.﹣a8÷a4=﹣a43.下面调查中,适合采用普查的是()A.调查全国中学生心理健康现状B.调查你所在的班级同学的身高情况C.调查我市食品合格情况D.调查南京市电视台《今日生活》收视率4.如图,在方格纸中选择标有序号①②③④的一个小正方形涂黑,使它与图中阴影部分组成的新图形为中心对称图形,该小正方形的序号是()A.①B.②C.③D.④5. 化简111aa a+--的结果为()A.-1B.1C.11aa+-D.11aa+-6.已知是二元一次方程组的解,则a﹣b的值为()A.﹣1 B.1 C.2 D.37.如图,△ABC的顶点都是正方形网格中的格点,sin∠ABC等()A.B.C.D.8.小朱要到距家1500米的学校上学,一天,小朱出发10分钟后,小朱的爸爸立即去追小朱,且在距离学校60米的地方追上了他.已知爸爸比小朱的速度快100米/分,求小朱的速度.若设小朱速度是x米/分,则根据题意所列方程正确的是()A.1440144010100x x-=-B.1440144010100x x=++C.1440144010100x x=+-D.1440144010100x x-=+9.如图,在△ABC中,点D,E,F分别在边AB,AC,BC上,且DE∥BC,EF∥AB.若AD=2BD,则的值为()A.B.C.D.10.已知二次函数y =a (x -1)2-c 的图象如图2所示,则一次函数y =ax +c 的大致图象可能是( )11.如图,在△ABC 中,∠A=90°,AB=AC=2,点O 是边BC 的中点,半圆O 与△ABC 相切于点D 、E ,则阴影部分的面积等( )A .1﹣B .C .1﹣D .12.如图,直线y=﹣x+2与x 轴、y 轴分别交于A 、B 两点,把△AOB 沿直线AB 翻折后得到△AO ′B ,则点O ′的坐标是( ) A .(,3)B . (,)C.(2,2)D.(2,4)二.填空题(每小题3分,共12分)13.若点P (a ,a ﹣2)在第四象限,则a 的取值范围是 . 14.分解因式:4x 3﹣4x 2y+xy 2= .15.如图,在正方形ABCD 中,E 是AB 上一点,BE =2,AE =3BE , P 是AC 上一动点,则PB +PE 的最小值是________. 16.反比例函数y =xk(x >0)的图像如图,点B 在图像上,连接OB 并延长到点A ,使AB =2OB ,过点A 作AC ∥y 轴,交y =xk(x >0)的图像于点C ,连接OC ,S △AOC =5,则k = .ABDCPE三、解答题(6+6+8+8+7+8+9=52分)17.计算:﹣2cos30°+()﹣2﹣|1﹣|.18.解不等式组:,并求它的整数解的和.19.我省教育厅下发了《在全省中小学幼儿园广泛深入开展节约教育的通知》,通知中要求各学校全面持续开展“光盘行动”.某市教育局督导检查组为了调查学生对“节约教育”内容的了解程度(程度分为:“A—了解很多”,“B—了解较多,“C—了解较少”,“D—不了解”),对本市一所中学的学生进行了抽样调查,我们将这次调查的结果绘制了以下两幅统计图.根据以上信息,解答下列问题:(1)本次抽样调查了_______名学生.(2)补全第二幅统计图.(3)若该中学共有1800名学生,请你估计这所中学的所有学生中,对“节约教育”内容“了解较多”的有多少名?20.如图,点A、B、C分别是⊙O上的点,∠B=60°,CD是⊙O的直径,P是CD延长线上的点,且AP=AC.(1)求证:AP是⊙O的切线;(2)若AC=3,求PD的长.21. 甲、乙两个工程队共同承担一项筑路任务,甲队单独施工完成此项任务比乙队单独施工完成此项任务多用l0天。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2016年广东省深圳市中考一模数学
一、选择题(共12小题;共60分)
1. 下列是的相反数是
A. B. C. D.
2. 一张坐凳的形状如图所示,以箭头所指的方向为主视方向,则它的左视图可以是
A. B.
C. D.
3. 某机构对万人的调查显示,沉迷于手机上网的初中生大约占,则这部分沉迷于手机上网的
初中生人数,可用科学记数法表示为
A. B. C. D.
4. 下列计算正确的是
A. B.
C. D.
5. 下列数据是2013年3月7日6点公布的中国六大城市的空气污染指数情况:
则这组数据的中位数和众数分别是
A. 和
B. 和
C. 和
D. 和
6. 一个盒子中有个红球,个白球,这些球除颜色外都相同,从中随机摸出一个球,记下颜色后
放回,再从中随机摸出一个球,则两次摸到红球的概率为
A. B. C. D.
7. 如图,直线与双曲线交于、两点,则当线段的长度取最小值时,
的值为
A. B. C. D.
8. 在中,,,,则
A. B. C. D.
9. 如图,将绕点逆时针旋转一定角度,得到.若,,且
,的度数为
A. B. C. D.
10. 下列命题是真命题的有
①方程的解是;
②连接矩形各边中点的四边形是菱形;
③如果将抛物线向右平移个单位,那么所得新抛物线的表达式为;
④若反比例函数的图象上有两点,则.
A. 个
B. 个
C. 个
D. 个
11. 如图,正六边形中,,点是的中点,连接,则的长为
A. B. C. D.
12. 若二次函数的图象与轴有两个交点,坐标分别为,,
且,图象上有一点在轴下方,则下列判断正确的是
A. B.
C. D.
二、填空题(共4小题;共20分)
13. .
14. 因式分解.
15. 如图中,,点在边上,,若,则的度数
为.
16. 观察下列图形中点的个数,若按其规律再画下去,可以得到第个图形中所有点的个数
为(用含的代数式表示).
三、解答题(共7小题;共91分)
17. 计算:.
18. 若是正整数,且满足试解分式方程.
19. 我市某中学今年年初开学后打算招聘一名数学教师,对三名前来应聘的数学教师、、进
行了考核,他们的笔试成绩和说课成绩(单位:分)分别用了两种方式进行了统计,如表一和图一:
表一
(1)请将表一和图一中的空缺部分补充完整.
(2)应聘的最后一个程序是由该校的名数学教师进行投票,三位应聘人的得票情况如图二(没有弃权票,该校的每位教师只能选一位应聘教师),请计算每人的得票数(得票数可是整数哟).
(3)若每票计分,该校将笔试、说课、得票三项测试得分按的比例确定个人成绩,请计算三位应聘人的最后成绩,并根据成绩判断谁能应聘成功.
20. 作图与证明
(1)作图题:
如图1,在网格图中做出将四边形向左平移格,再向上平移格得到的四边形.
(2)证明题:
已知:如图2,在中,,过点作交与点,且,连接、.
求证:四边形是平行四边形.
21. 某商场试销一种成本为每件元的服装,规定试销期间销售单价不低于成本单价,且获利不得
高于.经试销发现,销售量(件)与销售单价(元)符合一次函数,且时,;时,.
(1)求一次函数的表达式;
(2)若该商场获得利润为元,试写出利润与销售单价之间的关系式;销售单价定为多少元时,商场可获得最大利润,最大利润是多少元?
22. 已知的半径为,为的弦,,是射线上的一动点,连接.
(1)当点运动到如图1所示的位置时,,求证:是的切线;
(2)如图2,当点在直径上运动时,的延长线与相交于点,试问为何值时,是等腰三角形?
23. 抛物线的顶点为,交轴于、两点,且经过点.
(1)求抛物线的解析式;
(2)如图1,为线段、之间一动点,为轴正半轴上一动点,是否存在使、、、四点围成的四边形周长最小.若存在,求出这个最小值及、的坐标;若不存在,请说明理由;
(3)若是轴上的点,是抛物线上的点,求:以、、、为顶点构成平行四边形的点的坐标.
答案
第一部分
1. A
2. C
3. D
4. C
5. A
6. D
7. C 【解析】根据反比例函数的对称性可知,要使线段的长度取最小值,则直线
经过原点,
.
解得.
8. B 9. C 【解析】根据旋转的性质知,,.
如图,设于点.
则,
在中,,
在中,∠,即的度数为.
10. B
11. A 【解析】提示:, .
由题意可知: .
.
,
.
12. D 【解析】A、二次函数()的图象与轴有两个交点无法确定的正负情况,故本选项错误;
B、,
,故本选项错误;
C、若,则,
若,则或,故本选项错误;
D、若,则,,
所以 .
,
若,则与同号,
.
综上所述正确,故本选项正确.
第二部分
13.
14.
15.
16.
【解析】图1点的个数:;
图2点的个数:;
图3点的个数:;
依此类推,可知第个图形中所有点的个数为 . 第三部分
17. 原式
18.
由①得,
由②得,
.
是正整数,
.
将代入分式方程得
去分母,方程两边同时乘以得
整理得:
经检验,是原分式方程的解.
.
19. (1);
(2),,.根据实际意义可得,得票,得票,得票.
(3)因为,
由题可得,的最后成绩为:
的最后成绩为:
的最后成绩为:
,
能应聘成功.
20. (1)如图所示:
(2),且,
四边形是平行四边形,
.
,
.
,
四边形是平行四边形.
21. (1),
∴,
由题得:
解之得:
∴一次函数的解析式为
(2)销售额:元;成本:.
∴,
当时,取得最大值,最大值是:
元
即销售价定为每件元时,可获得最大利润,最大利润是元.22. (1)连接,过点作,垂足为.
,,
是等边三角形.
.
,,
.
,
,即 .
,,
.
是的切线
(2)①过点作,垂足为,延长交于 .
是是的直径,
,
,
是等腰三角形.
由(1)可知是等边三角形,
.
②过作,垂足为,延长交于,与交于 .
是圆心,
是的垂直平分线.
是等腰三角形.
,
.
平分,,
.
是等边三角形,,
.
.
是等腰直角三角形.
.
.
23. (1)设抛物线的表达式为: .
将代入,解得: .
抛物线的表达式为: .
(2)作关于轴对称点,
关于轴对称点,
是一个定值,
要使四边形的周长最小,
只要使最小即可.
由图形的对称性,可知,
只有当为一条直线段时,最小,
可求得:,
四边形的周长最小为.
(3)若为平行四边形的边,
,且,以为顶点的四边形构成平行四边形,①当点在轴的右侧时,,
又点在抛物线上,
,
②当点在轴的左侧时,,
又点在抛物线上,
,
若为平行四边形的对角线,如图,过作轴,垂足为,
四边形为平行四边形,
.
.
.
又点在抛物线上,
.
.
综上:符合要求的点的坐标为:,,.。
