2017高考必考知识点总结:数学平方差公式大盘点_知识点总结
平方差公式课件PPT

$(a+b-c)^2 = a^2 + b^2 - c^2 + 2ab - 2bc$
$(a-b+c)^2 = a^2 - b^2 + c^2 + 2(ab)c$
平方差公式的其他变种形式
$(a+b)^3 = (a+b)(a^2 - ab + b^2)$ $(a-b)^3 = (a-b)(a^2 + ab + b^2)$
平方差公式课件
目录
CONTENTS
• 平方差公式的基本概念 • 平方差公式的推导过程 • 平方差公式的证明 • 平方差公式的应用举例 • 平方差公式的变种 • 总结与回顾
01 平方差公式的基本概念
平方差公式的定义
总结词
平方差公式是数学中一个重要的恒等 式,用于表示两个数的平方差与这两 个数之间的关系。
$(a+b+c)^3 = (a+b+c)(a^2 - ab + b^2 - ac + bc - c^2)$
06 总结与回顾
本节课的重点回顾
01
02
03
04
平方差公式的形式和结 构
平方差公式的推导过程
平方差公式的应用范围 和条件
平方差公式的代数表示 和几何意义
本节课的难点解析
01
02
03
04
如何理解和记忆平方差公式的 形式和结构
目标
证明该公式成立
证明的步骤
01
02
03
步骤1
展开左侧,得到 $(a+b)(a-b) = a^2 b^2 + ab - ab$
步骤2
合并同类项,得到 $(a+b)(a-b) = a^2 b^2$
平方差公式和平方和公式

平方差公式和平方和公式平方差公式和平方和公式是学习数学中非常重要的两个公式,它们在解决各种数学问题以及实际应用中起着重要的作用。
本文将为大家详细介绍这两个公式的含义、推导以及具体应用,希望能够帮助大家更好地理解和应用这两个公式。
首先,我们来介绍一下平方差公式。
平方差公式是指两个数的平方差等于这两个数的和乘以差的公式。
表达式如下:a^2 - b^2 = (a + b) * (a - b)平方差公式的推导可以通过因式分解来得到。
假设我们已知一个二次差分式 a^2 - b^2,我们通过因式分解把它变成一个乘法式。
我们先观察一下(a + b)(a - b)这个式子,根据分配律展开可以得到a^2 - b^2。
这就是平方差公式的基本推导过程。
接下来,我们来介绍一下平方和公式。
平方和公式是指两个数的平方和等于这两个数的和的平方加上两个数的乘积的公式。
表达式如下:(a + b)^2 = a^2 + b^2 + 2ab平方和公式的推导可以通过多项式的展开和整理得到。
如果我们展开(a + b)^2,得到 a^2 + 2ab + b^2,然后再与原式进行比较,我们可以发现它们是相等的。
因此,我们得到了平方和公式。
这两个公式在数学中具有广泛的应用。
平方差公式常用于解决代数中的因式分解问题。
例如,当我们要因式分解一个二次差分式时,我们可以利用平方差公式将其化简为一个乘法式,进而更容易进行后续的计算和分析。
而平方和公式则常用于解决关于平方和的问题。
例如,在计算一个数列的平方和时,如果数列之间存在某种关系,我们可以使用平方和公式来简化计算过程。
此外,平方和公式也常用于推导各种数学恒等式和证明中。
除了数学领域的应用,这两个公式还在实际生活中发挥着重要作用。
例如,在物理学中,平方差公式可以用于计算物体的运动速度和加速度,解决动态问题。
而平方和公式在统计学中也有广泛的应用,用于计算方差和标准差等统计指标。
总之,平方差公式和平方和公式是数学中重要的公式,它们在解决各种问题和应用中起到了至关重要的作用。
14.2.1 平方差公式

(2)你能将红色部分拼成一个完整的长方形图案吗?
你拼出的长方形的面积是___(_a_+__b_)_(_a__-_b_)______
例1:运用平方差公式计算
⑴ (3x+2)(3x-2)
平方差公式:(a+b)(a-b)=a2-b2
⑵ (b+2a)(2a-b)
两数和 两数差 两数平方差
证明:(a+b)(a-b)
(多项式乘法法则) (合并同类项)
平方差公式: (a+差的积, 等于这两个数的平方差。
特征分析:
(a+b)(a-b)=a2-b2
a
b
a
b b
如图:在边长为a的大正方形的一角剪去一个边 长为b的小正方形。
14.2.1
平方差公式
(1) (x+1)(x−1) ==xx22−−1 12 (2) (m+2)(m−2) ==mm2−24−22
(3) (2x+1)(2x−1 ) == 4(x22x−)21− 12 观察 & 发现
观察上述算式及其运算结果,你发现了什么规律?
大胆猜想
(a+b) (a-b) =a²-b²
⑶ (-x+2y)(-x-2y)
书上108页练习1.
下面各式的计算对不对?如果不对, 应当怎样改正?
(1) (x+2)(x-2) = x2-2
(2) (-3a-2) (3a-2) = 9a2 -4
1.用两种方法计算: (-3a-2) (3a-2) = 9a2 -4
例2:计 算:
(1) 998×1002
1.计算: 综 合 拓 展
平方差公式(基础)知识讲解

平方差公式(基础) 知识讲解【学习目标】1. 能运用平方差公式把简单的多项式进行因式分解.2. 会综合运用提公因式法和平方差公式把多项式分解因式;3.发展综合运用知识的能力和逆向思维的习惯.【要点梳理】要点一、公式法——平方差公式两个数的平方差等于这两个数的和与这两个数的差的积,即:()()22a b a b a b -=+-要点诠释:(1)逆用乘法公式将特殊的多项式分解因式.(2)平方差公式的特点:左边是两个数(整式)的平方,且符号相反,右边是两个数(整式)的和与这两个数(整式)的差的积.(3)套用公式时要注意字母a 和b 的广泛意义,a 、b 可以是字母,也可以是单项式或多项式.要点二、因式分解步骤(1)如果多项式的各项有公因式,先提取公因式;(2)如果各项没有公因式那就尝试用公式法;(3)如用上述方法也不能分解,那么就得选择分组或其它方法来分解(以后会学到). 要点三、因式分解注意事项(1)因式分解的对象是多项式;(2)最终把多项式化成乘积形式;(3)结果要彻底,即分解到不能再分解为止.【典型例题】类型一、公式法——平方差公式1、(2016•富顺县校级模拟)下列各式能用平方差公式分解因式的有( )①x 2+y 2;②x 2﹣y 2;③﹣x 2﹣y 2;④﹣x 2+y 2;⑤﹣x 2+2xy ﹣y 2.A .1个B .2个C .3个D .4个【思路点拨】能够运用平方差公式分解因式的多项式必须是二项式,两项都能写成平方的形式,且符号相反,进而可得答案.【答案与解析】解:下列各式能用平方差公式分解因式的有;②x 2﹣y 2;④﹣x 2+y 2;,共2个,故选:B .【总结升华】能否运用平方差公式分解因式,应紧紧抓住平方差公式的特点进行判断.分别从项数、符号、平方项等方面来判断.2、分解因式:(1)229a b -; (2)22251x y -; (3)22168194a b -+; (4)214m -+. 【思路点拨】本题都符合平方差公式的特点,可以分别写成两数(式)平方差的形式,然后运用平方差公式进行因式分解.【答案与解析】解:(1)22229(3)(3)(3)a b a b a b a b -=-=+-.(2)2222251(5)1(51)(51)x y xy xy xy -=-=+-. (3)2222168194949494232323a b b a b a b a ⎛⎫⎛⎫⎛⎫⎛⎫-+=-=+- ⎪ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭. (4)22214(2)1(21)(21)m m m m -+=-=+-.【总结升华】(1)可以利用加法的交换律把负平方项交换放在后面.(2)“1”是平方项,可以写成“21”.(3)一定要把两项写成22a b -的形式,再套用平方差公式. 举一反三:【变式1】分解因式:(1)212516m -;(2)22(2)16(1)x x -++-. 【答案】 解:(1)212516m -22111555444m m m ⎛⎫⎛⎫⎛⎫=-=+- ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭. (2)22(2)16(1)x x -++-2216(1)(2)x x =--+ [4(1)(2)][4(1)(2)]x x x x =-++--+(36)(52)3(2)(52)x x x x =--=--.【变式2】(2015春•泗阳县期末)下列各式能用平方差公式计算的是( )A.(2a+b )(2b ﹣a )B.(﹣x+1)(﹣x ﹣1)C.(a+b )(a ﹣2b )D.(2x ﹣1)(﹣2x+1) 【答案】B .类型二、平方差公式的应用3、(2015春•开江县期末)计算20152﹣2014×2016的结果是( )A.﹣2B.﹣1C.0D.1【思路点拨】原式变形后,利用平方差公式计算即可得到结果.【答案】D ;【解析】解:原式=20152﹣(2015﹣1)×(2015+1)=20152﹣(20152﹣1)=20152﹣20152+1=1, 故选D.【总结升华】此题考查了平方差公式,熟练掌握平方差公式是解本题的关键.举一反三:【变式1】如图,在边长为a 的正方形中挖掉一个边长为b 的小正方形)(b a >,把余下的部分剪成一个矩形,通过计算两个图形(阴影部分)的面积,验证了一个等式是( )A.()()22a b a b a b -=+-B. ()2222a b a ab b +=++ C. ()2222a b a ab b -=-+ D. ()()2222a b a b a ab b +-=+-【答案】A ;【变式2】用简便方法计算:(1)2199919982000-⨯;(2)2253566465⨯-⨯.【答案】解:(1)原式()()219991999119991=--+ 221999199911=-+=(2)原式()226535456=⨯- ()()65354655354656100070420000=⨯+-=⨯⨯=4、已知大正方形的周长比小正方形的周长长96厘米,它们的面积相差960平方厘米.求两个正方形的边长.【答案与解析】解:设大正方形的边长为a ,则小正方形的边长为(a -24).依题可列22(24)960a a --=.运用平方差公式:[a +(a -24)][ a -(a -24)]=960.24(2a -24)=960.解得a =32.a -24=32-24=8.答:它们的边长分别为32厘米,8厘米.【总结升华】无论在哪一方面应用因式分解,都须仔细观察,是有公因式还是符合公式,切忌不能盲目乱用,这样应用起来才能达到真正意义上的化简,不然反而走向误区,就是说不要为用因式分解而用,要因题用,能用则用,不能用千万别用,千万别硬套.。
平方差公式和完全平方公式
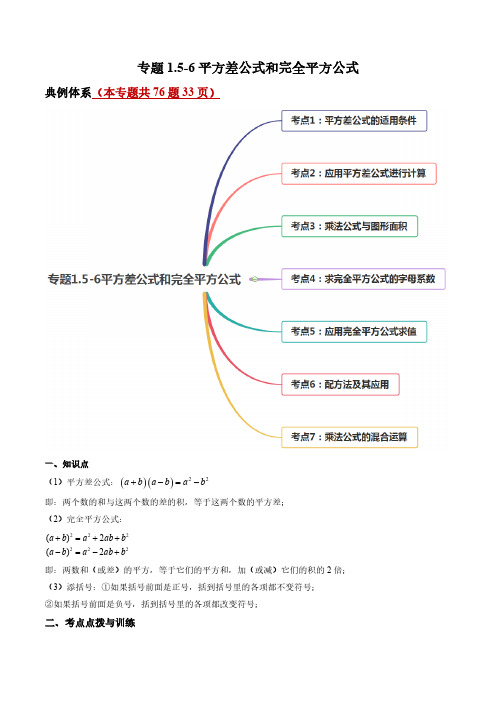
专题1.5-6平方差公式和完全平方公式典例体系(本专题共76题33页)一、知识点(1)平方差公式:()()22a b a b a b +-=-即:两个数的和与这两个数的差的积,等于这两个数的平方差;(2)完全平方公式:222222()2()2a b a ab b a b a ab b +=++-=-+即:两数和(或差)的平方,等于它们的平方和,加(或减)它们的积的2倍;(3)添括号:①如果括号前面是正号,括到括号里的各项都不变符号;②如果括号前面是负号,括到括号里的各项都改变符号;二、考点点拨与训练考点1:平方差公式的适用条件典例:(2020·山西左权·期末)下列各式能用平方差公式计算的是( )A .(a+b)(a-2b)B .(x+2y)(x-2y)C .(-a+2b)(a-2b)D .(-2m-n )(2m+n )【答案】B【解析】A :()()2a b a b +-无法化为()()a b a b +-形式的式子,故其不能用平方差公式计算;B :()()22x y x y +-符合平方差公式的形式,故其可以用平方差公式计算;C :()()22a b a b -+-无法化为()()a b a b +-形式的式子,故其不能用平方差公式计算;D :()()22m n m n --+无法化为()()a b a b +-形式的式子,故其不能用平方差公式计算;故选:B.方法或规律点拨本题主要考查了平方差公式,熟练掌握相关公式是解题关键.巩固练习1.(2019·河北南宫·期末)下列各式不能运用平方差公式计算的是( )A .(2)(2)a b a b -+B .(5)(5)a a -+--C .(21)(12)x x --+D .(2)(2)x y x y ---【答案】C 【解析】解:C 、两项都是相同的项,不能运用平方差公式;A 、B 、D 中均存在相同和相反的项,故选:C .2.(2020·河南舞钢·期中)下列各式中,不能运用平方差公式计算的是( )A .()()m n m n ---B .()()11mn mn -++C .()()m n m n -+-D .23)(3)(2m m -+【答案】C【解析】∵()()m n m n ---=()()m n m n --+=()2222m nmn -=-+-,∴A 不符合题意,∵()()11mn mn -++=()221mn -=221m n -,∴B 不符合题意,∵()()m n m n -+-=()()()2m n m n m n ---=--∴C 符合题意,∵23)(3)(2m m -+=222(2)349m m -=-,∴D 不符合题意.故选C .3.(2020·江苏梁溪·期末)下列各式中,不能用平方差公式计算的是( )A .(2)(2)x a x a +-B .(12)(12)a a --+C .(5)(5)b c c b +-D .(2)(2)x y x y +-+【答案】B【解析】解:A 、能用平方差公式进行计算,故本选项不符合题意;B 、(1-2a )(-1+2a )=-(1-2a )2,不能用平方差公式进行计算,故本选项符合题意;C 、能用平方差公式进行计算,故本选项不符合题意;D 、能用平方差公式进行计算,故本选项不符合题意;故选:B .4.(2020·安徽临泉·期末)能用平方差公式计算的是( )A .()()x y x y -+-B .()()x y x y -++C .()2(1)x x +-D .()23(32)x x +-【答案】B【解析】解:A .不能用平方差公式计算,该项不符合题意;B .可以用平方差公式计算,该项符合题意;C .不能用平方差公式计算,该项不符合题意;D .不能用平方差公式计算,该项不符合题意;故选:B .5.(2020·达州市通川区第八中学期中)下列各式不能用平方差公式计算的是( )A .()(+)x y x y --B .()(+)x y x y ---C .()()ab c ab c +-D .(0.3)(0.3)x y y x ---【答案】A【解析】A. 含x 、y 的项都符号相反,不能用平方差公式计算;B. 含x 的项符号相同,含y 的项符号相反,能用平方差公式计算;C. 含y 的项符号相同,含x 的项符号相反,能用平方差公式计算;D. 含y 的项符号相同,含x 的项符号相反,能用平方差公式计算.故选:A.6.(2020·沈阳市第一二七中学期中)下列各多项式相乘:①(-2ab+5x )(5x+2ab);②(ax -y)(-ax-y);③(-ab-c)(ab-c);④(m+n)(-m-n).其中可以用平方差公式的有 ()A .4个B .3个C .2个D .1个【答案】B【解析】解:①(-2ab+5x )(5x+2ab)= (5x -2ab )(5x+2ab),符合平方差公式,故①正确;②(ax -y)(-ax-y) =- (ax -y)( ax+y),符合平方差公式,故②正确;③(-ab-c)(ab-c)=- (a+-c)(ab-c) ,符合平方差公式,故③正确;④(m+n)(-m-n)=- (m+n)(m+n),不符合平方差公式,故④错误.正确的有①②③.故选B.7.(2020·西藏日喀则·期末)下列乘法运算中不能用平方差公式计算的是( )A .(x+1)(x ﹣1)B .(x+1)(﹣x+1)C .(﹣x+1)(﹣x ﹣1)D .(x+1)(﹣x ﹣1)【答案】D【解析】解:选项A :(x+1)(x-1)=x 2-1,故选项A 可用平方差公式计算,不符合题意,选项B :(x+1)(-x+1)=1-x 2,故选项B 可用平方差公式计算,不符合题意,选项C :(-x+1)(-x-1)=x 2-1,故选项C 可用平方差公式计算,不符合题意,选项D :(x+1)(-x-1)=-(x+1)2,故选项D 不可用平方差公式计算,符合题意,故选:D .考点2:应用平方差公式进行计算典例:(2020·上海市静安区实验中学初一课时练习)1122xy xy æöæö÷çç---=÷çç÷ççèøè______.【答案】2214x y -【解析】()2222111*********xy xy xy xy xy x y æöæöæöæöæö÷ççççç---=-+--=--=-÷ççççç÷çççççèøèøèøèøèø方法或规律点拨本题考查了平方差公式,运用平方差公式计算时,关键要找相同项和相反项,其结果是相同项的平方减去相反项的平方.巩固练习1.(2020·聊城市茌平区教育和体育局教研室期末)若245a a +=,则代数式2(2)(1)(1)a a a a +-+-的值为( )A .1B .2C .4D .6【答案】D【解析】解:2(2)(1)(1)a a a a +-+-22241a a a =+-+241,a a =++245a a +=Q ,\ 上式51 6.=+=故选D .2.(2020·湖南涟源·初一期末)计算()()2323a b a b -+的正确结果是( )A .2249a b +B .2249a b -C .224129a ab b ++D .224129a ab b -+【答案】B【解析】()()2323a b a b -+2249a b =-.故选:B .3.(2020·绍兴市文澜中学期中)若2210m n -=,且4m n -=,则m n +=_____【答案】2.5【解析】∵2210m n -=,4m n -=,∴m n +=(22m n -)÷(m n -)= 2.54.(2020·河南洛宁·月考)计算:(4(4´=__________.【答案】9【解析】根据平方差公式可得(4(4´=2241679-=-=,故答案为9.5.(2020·山东中区·初一期末)若5a b +=,3a b -=,则22a b -=_____.【答案】15【解析】解:∵5a b +=,3a b -=,∴22a b -()()a b a b =+-53=´15=故答案为156.(2020·上海市静安区实验中学初一课时练习)44q q p p æöæö÷÷çç---+=÷÷çç÷÷ççèøèø________.【答案】2216q p -【解析】解:22224444416q q q q q q p p p p p p æöæöæöæöæö÷÷÷÷÷ççççç---+=---+=--=-÷÷÷÷÷ççççç÷÷÷÷÷çççççèøèøèøèøèø故答案为:2216q p -.7.(2020·吉林延边·初二期末)计算:+-=____________.【答案】4【解析】解:+-22=-4=,故答案为:4.8.(2020·上海市静安区实验中学初一课时练习)()()()()()224488a b a b a ba b a b -++++【答案】1616a b -【解析】解:原式=22224488(-)()()()a b a b a b a b +++=444488(-)()()a b a b a b ++=8888(-)()a b a b +=1616-a b .考点3:乘法公式与图形面积典例:(2020·北京通州·初一期中)将边长为a 的正方形的左上角剪掉一个边长为b 的正方形(如图1),将剩下部分按照虚线分割成①和②两部分,将①和②两部分拼成一个长方形(如图2).(1)设图1中阴影部分的面积为S ₁,图2中阴影部分的面积为S ₂,请用含a .b 的式子表示:S ₁= ,S ₂= ;(不必化简)(2)以上结果可以验证的乘法公式是 .(3)利用(2)中得到的公式,计算;20202﹣2019×2021.【答案】(1)a 2﹣b 2,(a +b )(a ﹣b );(2)(a +b )(a ﹣b )=a 2﹣b 2;(3)1.【解析】解:(1)根据图形以及正方形和长方形的面积计算公式可得:S ₁=a 2﹣b 2,S ₂=(a +b )(a ﹣b )故答案为:a 2﹣b 2,(a +b )(a ﹣b );(2)以上结果可以验证的乘法公式是a 2﹣b 2=(a +b )(a ﹣b ).故答案为:(a +b )(a ﹣b )=a 2﹣b 2.(3)20202﹣2019×2021=20202﹣(2020﹣1)×(2020+1)=20202﹣(20202﹣1)=20202﹣20202+1=1.方法或规律点拨本题考查了平方差公式的几何背景及其在简算中的应用,数形结合并明确平方差公式的形式是解题的关键.巩固练习1.(2020·沈阳市第一二七中学期中)如图,它由两块相同的直角梯形拼成,由此可以验证的算式为( )A .22()()a b a b a b -=+-B .222()2a b a ab b +=++C .222()2a b a ab b -=-+D .22(1)(1)a b -=+【答案】A【解析】如图,拼成的等腰梯形如下:上图阴影的面积s =a 2−b 2,下图等腰梯形的面积s =2(a +b )(a−b )÷2=(a +b )(a−b ),两面积相等所以等式成立a 2−b 2=(a +b )(a−b ).这是平方差公式.故选:A .2.(2020·福建省惠安科山中学月考)如下图所示,在边长为a 的正方形中,剪去一个边长为b 的小正方形(a b >),将余下部分拼成一个梯形,根据两个图形阴影部分面积的关系,可以得到一个关于a 、b 的恒等式为( )A .222()2a b a ab b -=-+B .222()2a b a ab b +=++C .22()()a b a b a b -=+-D .2()a ab a a b +=+【答案】C【解析】解:正方形中,S 阴影=a 2-b 2;梯形中,S 阴影=12(2a+2b )(a-b )=(a+b )(a-b );故所得恒等式为:a 2-b 2=(a+b )(a-b ).故选:C .3.(2020·广东禅城·期末)在边长为a 的正方形中挖掉一个边长为 b 的小正方形(a >b 〉)把余下的部分剪拼成一个矩形,通过计算图形(阴影部分)的面积,验证了一个等式,则这个等式是( )A .2()a ab a a b -=-B .()2222a b a ab b +=++C .()2222a b a ab b -=-+D .()22()a b a b a b -=+-【答案】D【解析】解:左图的阴影部分的面积为(a +b )(a−b ),右图的阴影部分的面积为a 2−b 2,因此有为a 2−b 2=(a +b )(a−b ),故选:D .4.(2018·河南汝阳·初二期末)图(1)是一个长为2a ,宽为2b (a >b )的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图(2)那样拼成一个正方形,则中间空的部分的面积是A. abB.()2a b +C. ()2a b -D. 22a b -【答案】C【解析】由题意可得,正方形的边长为a b +,故正方形的面积为()2a b +。
平方差公式和完全平方公式

平方差公式和完全平方公式在数学中,平方差公式和完全平方公式是两个重要的公式,它们在代数中的运用频繁,能够帮助我们简化计算和解决问题。
本文将介绍这两个公式的定义、应用以及推导过程。
一、平方差公式平方差公式是指两个数的平方差等于它们的积与和的差。
具体表达如下:a^2 - b^2 = (a + b)(a - b)其中,a、b为任意实数。
平方差公式的应用可以帮助我们快速计算平方差,以及解决一些与平方差相关的问题。
例如,考虑以下例子:例1:计算 16^2 - 9^2 的值。
根据平方差公式,我们可以将该式转化为 (16 + 9)(16 - 9)。
进一步计算可得= 25 × 7= 175因此,16^2 - 9^2 的值为 175。
平方差公式也可以用于因式分解和方程求解等问题。
通过将平方差公式进行变形,可以将复杂的表达式进行简化。
二、完全平方公式完全平方公式是指一个二次多项式能够被写成两个平方项的和的形式。
具体表达如下:(a ± b)^2 = a^2 ± 2ab + b^2其中,a、b为任意实数。
完全平方公式的应用范围广泛,涉及到二次函数、方程、因式分解等等。
以下是一些例子:例2:将 x^2 - 6x + 9 表示为完全平方形式。
我们可以观察到该式可以写成 (x - 3)^2 的形式,其中 a = x,b = -3。
这样,我们就可以利用完全平方公式进行简化和计算。
例3:解方程 x^2 + 6x + 9 = 0同样地,我们可以将该方程改写为 (x + 3)^2 = 0 的形式。
根据完全平方公式,这意味着 x + 3 = 0 或 x = -3。
因此,方程的解为 x = -3。
总结:平方差公式和完全平方公式在代数中起到了重要的作用,能够帮助我们简化计算和解决问题。
我们可以通过灵活运用这两个公式来化简表达式、因式分解、解方程等。
熟练掌握平方差公式和完全平方公式,对理解和应用代数知识都有很大帮助。
平方差和完全平方公式
一、同步知识梳理知识点1:平方差公式是指22(a b)(a b)a b +-=-就是说,两个数的和与这两个数的差的积等于这两个数的平方差。
【注意】 a,b 仅仅是一个符号,它们可以表示数,也可以表示式子(单项式、多项式等),只是它们的和与差的积,一定等于它们的平方差。
知识点2:完全平方公式:222(a b)a 2b ab +=++ 222(a b)a 2b ab -=-+两数和(或差)的平方,等于它们的平方和,加(或减)它们的积的2倍.这两个公式叫做(乘法的)完全平方公式。
二、同步题型分析题型1:平方差公式例1、下列可以用平方差公式计算的是( )A 、(x -y ) (x + y )B 、(x -y ) (y -x )C 、(x -y )(-y + x )D 、(x -y )(-x + y )例2、下列各式中,运算结果是22169b a -的是( )A 、)43)(43(b a b a --+-B 、)34)(34(a b a b --+-C 、)34)(34(a b a b -+D 、)83)(23(b a b a -+例3、若2422549))(________57(y x y x -=--,括号内应填代数式 ( )A 、y x 572+B 、y x 572--C 、y x 572+-D 、y x 572-(5) 例4、计算⑴)5)(5(33m n n m -+ ⑵ )2.02)(22.0(x y y x -+(3) 22)2()2(a b b a --+ (4))49)(23)(23(22b a b a b a ++-(5)(2x -1) (2x + 1)-2(x -2) (x + 2)例5、用简便方法计算(1) 3259931600⨯ (2))12)(12)(12)(12)(12(16842+++++题型2:完全平方公式例1、2)2(n m +-的运算结果是 ( )A 、2244n mn m ++B 、2244n mn m +--B 、C 、2244n mn m +-D 、2242n mn m +-例2、运算结果为22(1)96a ab b --的是 ( )A 、22)1(x +-B 、22)1(x +C 、22)1(x --D 、2)1(x -例3、已知2264b Nab a +-是一个完全平方式,则N 等于 ( )A 、8B 、±8C 、±16D 、±32例4、填空⑴ (x + y)2=_________________,(x -y)2=______________________;⑵______________________)2(_________,__________)3(22=+-=-b a b a 解:22(1)x 2xy y ++ 22x 2xy y -+(2) 2244a ab b -+例5、用简便方法计算⑴ 982 ⑵ 20032 ⑶ 13.42-2×13.4 + 3.42例6、已知3)()1(2-=+-+y x x x ,求xy y x -+222的值三、课堂达标检测1.计算题:(y +x )(x -y )=______;(x +y )(-y +x )=______;(-x -y )(-x +y )=______;(-y +x )(-x -y )=______;2.直接写出结果:(1)(2x +5y )(2x -5y )=________; (2)(x -ab )(x +ab )=______;(3)(3m +2n )2=________;(4)( )2=m2+8m +16;3.在括号中填上适当的整式:(1)(m -n )( )=n2-m2; (2)(-1-3x )( )=1-9x2.4.多项式x2-8x +k 是一个完全平方式,则k =______.5.-+=+222)1(1x x x x ______=2)1(xx -+______. 6.下列各多项式相乘,可以用平方差公式的有( )①(-2ab +5x )(5x +2ab ) ②(ax -y )(-ax -y )③(-ab -c )(ab -c ) ④(m +n )(-m -n )A .4个B .3个C .2个D .1个7.下列计算正确的是( ) A .(5-m )(5+m )=m2-25B .(1-3m )(1+3m )=1-3m2C .(-4-3n )(-4+3n )=-9n2+16D .(2ab -n )(2ab +n )=2a2b2-n2 8.下列等式能够成立的是( )A .(a -b )2=(-a -b )2B .(x -y )2=x2-y2C .(m -n )2=(n -m )2D .(x -y )(x +y )=(-x -y )(x -y ) 9.若9x2+4y2=(3x +2y )2+M ,则 M 为( ) A .6xy B .-6xyC .12xyD .-12xy 10.如图2-1所示的图形面积由以下哪个公式表示( )A .a2-b2=a (a -b )+b (a -b )B .(a -b )2=a2-2ab +b2C .(a +b )2=a2+2ab +b2D .a2-b2=a (a +b )-b (a +b )图2-111.(xn -2)(xn +2)12.(3x +0.5)(0.5-3x )13.用适当的方法计算.(1)1.02 ×0.98(2)13111321⨯(3)2)2140( (4)20052-4010×2006+2006214.当a =1,b =-2时,求)212]()21()21[(2222b a b a b a --++的值.一、 能力培养综合题1、已知22610340m n m n +-++=,求m+n 的值综合题2、若a +b =17,ab =60,求(a -b )2和a 2+b 2的值.综合题3、已知x≠1,计算(1+x )(1-x )=1-2x ,(1-x )(1+x+2x )=1-3x ,(1-x )(•1+x+2x +3x )=1-4x ,(1)观察以上各式并猜想:(1-x )(1+x+2x +…+n x )=______.(n 为正整数)(2)根据你的猜想计算:①(1-2)(1+2+22+32+42+52)=______.②2+22+32+…+2n =______(n 为正整数).③(x -1)(9998972...x x x x x +++++ +1)=_______.(3)通过以上规律请你进行下面的探索:①(a -b )(a+b )=_______.②22(a b)(a b b )a -++=______.③ 3223(a b)(a b b b )a a -+++=______.二、 能力点评例题中涉及到了完全平方公式的变形,要注意总结与运用,还有规律探讨题的方法。
平方差公式和完全平方公式
平方差公式和完全平方公式平方差公式是数学中一条重要的公式,也是学习平方差的基础。
它可以帮助我们快速计算两个数的平方差,而不必一个一个去计算。
完全平方公式是数学中求解一元二次方程的方法之一,它可以帮助我们快速找到方程的解。
下面将详细介绍这两个公式。
一、平方差公式设两个数分别为a和b,它们的平方差可以表示为(a+b)(a-b)。
我们可以通过拆分(a+b)(a-b)来计算平方差。
拆分后得到的是一个差式,可以简化计算。
例如,计算25的平方差时,我们可以使用平方差公式:(25+5)(25-5)=30×20=600。
同样地,计算8的平方差时,使用平方差公式:(8+2)(8-2)=10×6=60。
通过平方差公式,我们可以快速准确地计算两个数的平方差。
二、完全平方公式完全平方公式是一种用来求解一元二次方程的方法。
一元二次方程的一般形式为ax^2 + bx + c = 0,其中a、b、c为已知常数,而x为未知数。
完全平方公式是由求解一元二次方程的根的公式推导而来。
若一元二次方程ax^2 + bx + c = 0有实数根,那么根可以表示为一个平方数。
利用完全平方公式,可以直接找到方程的解。
完全平方公式的表达式为:x = (-b ± √(b^2-4ac)) / (2a)利用完全平方公式,我们可以求解一元二次方程的根。
例如,对于方程x^2-2x-3=0,我们可以直接套用完全平方公式:x=(-(-2)±√((-2)^2-4×1×(-3)))/(2×1)化简得:x=(2±√(4+12))/2即:x=(2±√16)/2化简得:x=(2±4)/2分别计算得到两个根:x1=(2+4)/2=6/2=3x2=(2-4)/2=-2/2=-1通过完全平方公式,我们可以直接得到方程的根。
总结:平方差公式和完全平方公式是数学中重要的计算工具,它们可以帮助我们快速计算平方差和求解一元二次方程。
数学公式大全完全平方差
数学公式大全完全平方差这一期我们开始学习乘法公式的第二个基本公式——完全平方公式。
我们先来一起看一下这一期的知识点吧!知识点1. 完全平方公式两个数和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的两倍.即: (a+b)^ 2 = a ^2+2ab+b ^2 ,\ \ \ \ \ \ \ (a−b) ^2 = a^ 2 −2ab+b ^2 .这两个公式叫做(乘法的)完全平方公式.证明方法1(代数证法):多项式乘多项式。
(a+b) (a+b) =a^2+ab+ab-b^2=a^2+2ab+b^2(a-b) (a-b) =a^2-ab-ab-b^2=a^2-2ab+b^22. 完全平方公式的几何意义证明方法如下:第二个公式的几何图证法如下:完全平方公式的识别方法相对来说比平方差容易,但是依然需要观察其特点。
如下:① (a+b) (b-a) 不是完全平方公式② (a+b) (-a-b) 是完全平方公式③ (a-b) (-b-a) 不是完全平方公式④ (a-b) (-a+b) 是完全平方公式这里有一个总结可以判断平方差公式,需要大家记住。
「总结」能用完全平方公式化简的式子中,括号内两项符号要么都不变,要么都改变。
完全平方公式口诀:首平方,尾平方,二倍乘积放中央。
同号相加,异号相减。
我们一起来看看今天的例题吧!例1:(1)计算: (4m+n) ^2 .(2)计算:( −4y− \frac1 4 )^2 .极简分析:利用公式直接计算即可,记得给系数平方。
解:(1) (4m+n) ^2=(4m)^2+2\cdot4m\cdotn+n^2=16m^2+8mn+n^2(2)\begin{eqnarray} \label{eq} &&( −4y− \frac1 4 )^2 \nonumber \\ ~&=&(-4y)^2+2\cdot (-4y)\cdot (− \frac1 4 )+(− \frac1 4 )^2\nonumber \\ ~&=&16y^2+2y+\frac1{16} \nonumber \\ \end{eqnarray}总结:第(2)问中, -4y 和 -\frac14 同号,所以是二倍乘积那一项是相加的形式。
第三讲-平方差完全平方公式
平方差公式、完全平方公式一、知识目标:熟练掌握平方差公式和完全平方公式。
二、知识梳理:1. 平方差公式1).平方差公式:两数和与这两数差的积,等于它们的平方差,即。
2). 结构特征:①公式左边是两个二项式相乘,两个二项式中第一项相同,第二项互为相反数;②公式右边是两项的平方差,即相同项的平方与相反项的平方之差。
2.完全平方公式1).完全平方公式:两数和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的2倍,即;2).结构特征:①公式左边是二项式的完全平方;②公式右边共有三项,是二项式中二项的平方和,再加上或减去这两项乘积的2倍三、经典例题:例一、计算:(1)2001×1999 (2)998×1002(3)(a-b)(a+b)(4)(-a+b)(-a-b)(5)(a-b)(-a-b)(6)(a+b)(-a+b)练习1、计算:(1)(4b2-a)((-2b)2+a)(2)(3a+2b)(3a-2b)(3)(a5-b2)(a5+b2)(4)(a-b)(a+b)(a2+b2)2 (5))2)(1(2)1(22+--+a a a a(6))2)(2()2)(2(22x x x x x x -+++-例二、计算:(1)(-a-b )2(2)(b-a )2(3)(-a-b )2 +(-a+b )2(4)(b-a )2+4ab练习2、计算:(1)(4m+n )2(2)(y-12)2(3)22(1)(1)ab ab +--(4)(2x-y )2-4(x-y )(x+2y )例三、(1)若2212,6,x y x y x y -=+=-则=练习3、(2)已知63)122)(122(=-+++b a b a ,则=+b a ____________例四、(1)已知2,4==+xy y x ,则2)(y x -=练习4、(2)已知3)(,7)(22=-=+b a b a ,求=+22b a ________,=ab ________例五、22)()(c b a c b a +--++练习5、()()()()()42212122224++---+-x x x x x x例六、已知0132=+-x x ,求221x x +和441x x +的值。
