20181122小学奥数练习卷(知识点:相似三角形)含答案解析
三角形相似测试题及答案

三角形相似测试题及答案1. 已知三角形ABC和三角形DEF相似,且AB/DE = 2/3,求AC/DF的比值。
答案:AC/DF = 2/3。
2. 若三角形ABC与三角形DEF相似,且∠A = ∠D,∠B = ∠E,那么∠C与∠F的关系是什么?答案:∠C = ∠F。
3. 在一个三角形中,如果两个角的度数分别为50度和60度,那么第三个角的度数是多少?答案:第三个角的度数是70度。
4. 一个三角形的三边长分别为3cm,4cm,5cm,另一个三角形的三边长分别为6cm,8cm,10cm,这两个三角形是否相似?答案:这两个三角形相似,因为它们的边长比相等,即3/6 = 4/8 = 5/10 = 1/2。
5. 已知三角形ABC与三角形DEF相似,且AB = 6cm,DE = 9cm,那么AC与DF的比值是多少?答案:AC/DF = AB/DE = 6/9 = 2/3。
6. 如果一个三角形的两边长分别为8cm和15cm,且这两个边的夹角为90度,那么这个三角形的第三边长是多少?答案:根据勾股定理,第三边长为17cm。
7. 两个相似三角形的对应高的比为3:4,那么它们的周长比是多少?答案:周长比也是3:4。
8. 一个三角形的三个内角的度数分别为30度,60度,90度,那么这个三角形与另一个三角形相似,其三个内角的度数分别为15度,30度,45度,这两个三角形是否相似?答案:这两个三角形不相似,因为它们的内角不相等。
9. 已知三角形ABC与三角形DEF相似,且BC = 2cm,EF = 4cm,那么AB与DE的比值是多少?答案:AB/DE = BC/EF = 2/4 = 1/2。
10. 一个三角形的三边长分别为2cm,3cm,4cm,另一个三角形的三边长分别为4cm,6cm,8cm,这两个三角形是否相似?答案:这两个三角形相似,因为它们的边长比相等,即2/4 = 3/6 = 4/8 = 1/2。
相似三角形基础练习题(附解题答案)

相似三角形基础练习题一.选择题(共27小题)1.如图,在△ABC中,DE∥BC,若=,则=()A.B.C.D.2.如图,已知直线a∥b∥c,直线m交直线a,b,c于点A,B,C,直线n交直线a,b,c于点D,E,F,若=,则=()A.B.C.D.13.如图,在△ABC中,点D在AB上,BD=2AD,DE∥BC交AC于E,则下列结论不正确的是()A.BC=3DE B.=C.△ADE∽△ABC D.S△ADE=S△ABC4.如图,直线l1∥l2∥l3,一等腰直角三角形ABC的三个顶点A,B,C分别在l1,l2,l3上,∠ACB=90°,AC交l2于点D,已知l1与l2的距离为1,l2与l3的距离为3,则的值为()A.B.C.D.5.如果两个相似三角形的面积比是1:4,那么它们的周长比是()A.1:16 B.1:4 C.1:6 D.1:26.已知△ABC∽△DEF,若△ABC与△DEF的相似比为,则△ABC与△DEF对应中线的比为()A.B.C.D.7.若△ABC∽△DEF,相似比为1:3,则△ABC与△DEF的面积比为()A.1:9 B.1:3 C.1:2 D.1:8.已知△ABC∽△DEF,且相似比为2:3,则△ABC与△DEF的对应高之比为()A.2:3 B.3:2 C.4:9 D.9:49.如图,在直角坐标系xOy中,A(﹣4,0),B(0,2),连结AB并延长到C,连结CO,若△COB∽△CAO,则点C的坐标为()A.(1,)B.(,)C.(,2)D.(,2)10.如图,M是Rt△ABC 的斜边BC上一点(M不与B、C重合),过点M作直线截△ABC,所得的三角形与△ABC相似,这样的直线共有()A.0条B.2条C.3条D.无数条11.如果一个直角三角形的两条边长分别是6和8,另一个与它相似的直角三角形边长分别是3、4及x,那么x的值()A.只有1个B.可以有2个C.可以有3个D.有无数个12.在四边形ABCD中,∠B=90°,AC=4,AB∥CD,DH垂直平分AC,点H为垂足.设AB=x,AD=y,则y关于x的函数关系用图象大致可以表示为()A.B.C.D.13.如图,△ABC中,∠A=78°,AB=4,AC=6.将△ABC沿图示中的虚线剪开,剪下的阴影三角形与原三角形不相似的是()A.B.C.D.14.如图,在△ABC中,中线BE,CD相交于点O,连接DE,下列结论:①=;②=;③=;④=其中正确的个数有()A.1个B.2个C.3个D.4个15.如图,在△ABC中,BF平分∠ABC,AF⊥BF于点F,D为AB的中点,连接DF延长交AC于点E.若AB=10,BC=16,则线段EF的长为()A.2 B.3 C.4 D.516.如图,正方形ABCD的边长为2,BE=CE,MN=1,线段MN的两端点在CD、AD上滑动,当DM为()时,△ABE与以D、M、N为顶点的三角形相似.A.B.C.或D.或17.阳光通过窗口AB照射到室内,在地面上留下2.7米的亮区DE(如图所示),已知亮区到窗口下的墙角的距离EC=8.7米,窗口高AB=1.8米,则窗口底边离地面的高BC为()A.4米B.3.8米C.3.6米D.3.4米18.已知,如图所示的一张三角形纸片ABC,边AB的长为20cm,AB边上的高为25cm,在三角形纸片ABC中从下往上依次裁剪去宽为4cm的矩形纸条,若剪得的其中一张纸条是正方形,那么这张正方形纸条是()A.第4张B.第5张C.第6张D.第7张19.如图,数学兴趣小组的小颖想测量教学楼前的一棵树的树高,下午课外活动时她测得一根长为1m的竹竿的影长是0.8m,但当她马上测量树高时,发现树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上(如图),他先测得留在墙壁上的影高为 1.2m,又测得地面的影长为2.6m,请你帮她算一下,树高是()A.3.25m B.4.25m C.4.45m D.4.75m20.为了测量校园水平地面上一棵不可攀的树的高度,学校数学兴趣小组做了如下的探索:根据光的反射定律,利用一面镜子和一根皮尺,设计如下图所示的测量方案:把一面很小的镜子水平放置在离树底(B)8.4米的点E处,然后沿着直线BE后退到点D,这时恰好在镜子里看到树梢顶点A,再用皮尺量得DE=3.2米,观察者目高CD=1.6米,则树(AB )的高度约为()A.4.2米B.4.8米C.6.4米D.16.8米21.如图,将一张三角形纸片沿虚线剪成甲、乙、丙三块,其中甲、丙为梯形,乙为三角形.根据图中标示的边长数据,比较甲、乙、丙的面积大小,下列判断正确的是()A.乙>丙>甲B.丙>乙>甲C.甲>丙>乙D.无法判断22.下列说法:①凡正方形都相似;②凡等腰三角形都相似;③凡等腰直角三角形都相似;④有一个底角相等的两个等腰三角形相似;⑤两个相似多边形的面积比为4:9,则周长的比为16:81中,正确的个数有()个.A.1 B.2 C.3 D.423.如图,已知矩形ABCD中,AB=2,在BC上取一点E,沿AE将△ABE向上折叠,使B点落在AD上的F点处,若四边形EFDC与矩形ABCD相似,则AD=()A.B.+1 C.4 D.224.如图,取一张长为a,宽为b的长方形纸片,将它对折两次后得到一张小长方形纸片,若要使小长方形与原长方形相似,则原长方形纸片的边a、b应满足的条件是()A.a= b B.a=2b C.a=2 b D.a=4b25.彼此相似的矩形A1B1C1D1,A2B2C2D2,A3B3C3D3,…,按如图所示的方式放置.点A1,A2,A3,…,和点C1,C2,C3,…,分别在直线y=kx+b(k>0)和x轴上,已知点B1、B2的坐标分别为(1,2),(3,4),则Bn的坐标是()A.(2n﹣1,2n)B.(2n﹣,2n)C.(2n﹣1﹣,2n﹣1)D.(2n﹣1﹣1,2n﹣1)26.如图,以点O为位似中心,将△ABC缩小后得到△A′B′C′,已知OB=3OB′,则△A′B′C′与△ABC的面积比为()A.1:3 B.1:4 C.1:5 D.1:927.如图,在平面直角坐标中,正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且相似比为,点A,B,E在x轴上,若正方形BEFG的边长为6,则C点坐标为()A.(3,2)B.(3,1)C.(2,2)D.(4,2)二.解答题(共3小题)28.如图,已知AD是△ABC的外角∠EAC的平分线,交BC的延长线于点D,延长DA 交△ABC的外接圆于点F,连接FB,FC.(1)求证:∠FBC=∠FCB;(2)已知FA•FD=12,若AB是△ABC外接圆的直径,FA=2,求CD的长.29.如图,在△ABC中,点D,E分别在边AB,AC上,∠AED=∠B,射线AG分别交线段DE,BC于点F,G,且.(1)求证:△ADF∽△ACG;(2)若,求的值.30.尤秀同学遇到了这样一个问题:如图1所示,已知AF,BE是△ABC的中线,且AF⊥BE,垂足为P,设BC=a,AC=b,AB=c.求证:a2+b2=5c2该同学仔细分析后,得到如下解题思路:先连接EF,利用EF为△ABC的中位线得到△EPF∽△BPA,故,设PF=m,PE=n,用m,n把PA,PB分别表示出来,再在Rt△APE,Rt△BPF中利用勾股定理计算,消去m,n即可得证(1)请你根据以上解题思路帮尤秀同学写出证明过程.(2)利用题中的结论,解答下列问题:在边长为3的菱形ABCD中,O为对角线AC,BD的交点,E,F分别为线段AO,DO的中点,连接BE,CF并延长交于点M,BM,CM分别交AD于点G,H,如图2所示,求MG2+MH2的值.相似三角形基础练习题参考答案与试题解析一.选择题(共27小题)1.(2016•兰州)如图,在△ABC中,DE∥BC,若=,则=()A.B.C.D.故选C.2.(2016•杭州)如图,已知直线a∥b∥c,直线m交直线a,b,c于点A,B,C,直线n 交直线a,b,c于点D,E,F,若=,则=()A.B.C.D.1故选B.3.(2016•黔西南州)如图,在△ABC中,点D在AB上,BD=2AD,DE∥BC交AC于E ,则下列结论不正确的是()A.BC=3DE B.=C.△ADE∽△ABC D.S△ADE=S△ABC故选:D.4.(2016•淄博)如图,直线l1∥l2∥l3,一等腰直角三角形ABC的三个顶点A,B,C分别在l1,l2,l3上,∠ACB=90°,AC交l2于点D,已知l1与l2的距离为1,l2与l3的距离为3,则的值为()A.B.C.D.【解答】解:如图,作BF⊥l3,AE⊥l3,∵∠ACB=90°,∴∠BCF+∠ACE=90°,∵∠BCF+∠CFB=90°,∴∠ACE=∠CBF,在△ACE和△CBF中,∴△ACE≌△CBF,∴CE=BF=3,CF=AE=4,∵l1与l2的距离为1,l2与l3的距离为3,∴AG=1,BG=EF=CF+CE=7∴AB==5,∵l2∥l3,∴=∴DG=CE=,∴BD=BG﹣DG=7﹣=,∴=.故选A.5.(2016•临夏州)如果两个相似三角形的面积比是1:4,那么它们的周长比是()A.1:16 B.1:4 C.1:6 D.1:2故选:D.6.(2016•兰州)已知△ABC∽△DEF,若△ABC与△DEF的相似比为,则△ABC与△DEF对应中线的比为()A.B.C.D.故选:A.7.(2016•如皋市校级二模)若△ABC∽△DEF,相似比为1:3,则△ABC与△DEF的面积比为()A.1:9 B.1:3 C.1:2 D.1:故选:A.8.(2016•重庆模拟)已知△ABC∽△DEF,且相似比为2:3,则△ABC与△DEF的对应高之比为()A.2:3 B.3:2 C.4:9 D.9:4【解答】解:∵△ABC∽△DEF,且相似比为2:3,∴△ABC与△DEF的对应高之比为2:3,故选:A.9.(2016•嘉善县模拟)如图,在直角坐标系xOy中,A(﹣4,0),B(0,2),连结AB并延长到C,连结CO,若△COB∽△CAO,则点C的坐标为()A.(1,)B.(,)C.(,2)D.(,2)【解答】解:∵A(﹣4,0),B(0,2),∴OA=4,OB=2,∵△COB∽△CAO,∴====,∴CO=2CB,AC=2CO,∴AC=4CB,∴=,过点C作CD⊥y轴于点D,∵AO⊥y轴,∴AO∥CD,∴△AOB∽△CDB,∴===,∴CD=AO=,BD=OB=,∴OD=OB+BD=2+=,∴点C的坐标为(,).故选B.10.(2016春•房山区期末)如图,M是Rt△ABC 的斜边BC上一点(M不与B、C重合),过点M作直线截△ABC,所得的三角形与△ABC相似,这样的直线共有()A.0条B.2条C.3条D.无数条【解答】解:∵截得的三角形与△ABC相似,∴过点M作AB的垂线,或作AC的垂线,或作BC的垂线,所得三角形满足题意.∴过点M作直线l共有三条,故选:C.11.(2015•武汉校级自主招生)如果一个直角三角形的两条边长分别是6和8,另一个与它相似的直角三角形边长分别是3、4及x,那么x的值()A.只有1个B.可以有2个C.可以有3个D.有无数个【解答】解:∵一个直角三角形的两条边长分别是6和8,另一个与它相似的直角三角形的边长分别是3和4及x,∴x可能是斜边或4是斜边,∴x=5或.∴x的值可以有2个.故选:B.12.(2016•金华)在四边形ABCD中,∠B=90°,AC=4,AB∥CD,DH垂直平分AC,点H为垂足.设AB=x,AD=y,则y关于x的函数关系用图象大致可以表示为()A.B.C.D.【解答】解:∵DH垂直平分AC,∴DA=DC,AH=HC=2,∴∠DAC=∠DCH,∵CD∥AB,∴∠DCA=∠BAC,∴∠DAN=∠BAC,∵∠DHA=∠B=90°,∴△DAH∽△CAB,∴=,∴=,∴y=,∵AB<AC,∴x<4,∴图象是D.故选D.13.(2016•河北)如图,△ABC中,∠A=78°,AB=4,AC=6.将△ABC沿图示中的虚线剪开,剪下的阴影三角形与原三角形不相似的是()A.B.C.D.【解答】解:A、阴影部分的三角形与原三角形有两个角相等,故两三角形相似,故本选项错误;B、阴影部分的三角形与原三角形有两个角相等,故两三角形相似,故本选项错误;C、两三角形的对应边不成比例,故两三角形不相似,故本选项正确;D、两三角形对应边成比例且夹角相等,故两三角形相似,故本选项错误.故选C.14.(2016•咸宁)如图,在△ABC中,中线BE,CD相交于点O,连接DE,下列结论:①=;②=;③=;④=其中正确的个数有()A.1个B.2个C.3个D.4个【解答】解:∵BE、CD是△ABC的中线,即D、E是AB和AC的中点,∴DE是△ABC的中位线,∴DE=BC,即=,DE∥BC,∴△DOE∽△COB,∴=()2=()2=,===,故①正确,②错误,③正确;设△ABC的BC边上的高AF,则S△ABC=BC•AF,S△ACD=S△ABC=BC•AF,∵△ODE中,DE=BC,DE边上的高是×AF=AF,∴S△ODE=×BC×AF=BC•AF,∴==,故④错误.故正确的是①③.故选B.15.(2016•达州)如图,在△ABC中,BF平分∠ABC,AF⊥BF于点F,D为AB的中点,连接DF延长交AC于点E.若AB=10,BC=16,则线段EF的长为()A.2 B.3 C.4 D.5【解答】解:∵AF⊥BF,∴∠AFB=90°,∵AB=10,D为AB中点,∴DF=AB=AD=BD=5,∴∠ABF=∠BFD,又∵BF平分∠ABC,∴∠ABF=∠CBF,∴∠CBF=∠DFB,∴DE∥BC,∴△ADE∽△ABC,∴=,即,解得:DE=8,∴EF=DE﹣DF=3,故选:B.16.(2016•富顺县校级一模)如图,正方形ABCD的边长为2,BE=CE,MN=1,线段MN 的两端点在CD、AD上滑动,当DM为()时,△ABE与以D、M、N为顶点的三角形相似.A.B.C.或D.或【解答】解:∵四边形ABCD是正方形,∴AB=BC,∵BE=CE,∴AB=2BE,又∵△ABE与以D、M、N为顶点的三角形相似,∴①DM与AB是对应边时,DM=2DN∴DM2+DN2=MN2=1∴DM2+DM2=1,解得DM=;②DM与BE是对应边时,DM=DN,∴DM2+DN2=MN2=1,即DM2+4DM2=1,解得DM=.∴DM为或时,△ABE与以D、M、N为顶点的三角形相似.故选C.17.(2016•河西区模拟)阳光通过窗口AB照射到室内,在地面上留下2.7米的亮区DE(如图所示),已知亮区到窗口下的墙角的距离EC=8.7米,窗口高AB=1.8米,则窗口底边离地面的高BC为()A.4米B.3.8米C.3.6米D.3.4米【解答】解:连接AE、BD,∵光是沿直线传播的,∴AE∥BD,∴△BCD∽△ACE,∴=即=解得:BC=4.故选A.18.(2016春•威海期末)已知,如图所示的一张三角形纸片ABC,边AB的长为20cm,AB边上的高为25cm,在三角形纸片ABC中从下往上依次裁剪去宽为4cm的矩形纸条,若剪得的其中一张纸条是正方形,那么这张正方形纸条是()A.第4张B.第5张C.第6张D.第7张【解答】解:已知剪得的纸条中有一张是正方形,则正方形中平行于底边的边是3,所以根据相似三角形的性质可设从顶点到这个正方形的线段为x,则=,解得x=5,所以另一段长为25﹣5=20,因为20÷4=5,所以是第5张.故选:B.19.(2015•聊城模拟)如图,数学兴趣小组的小颖想测量教学楼前的一棵树的树高,下午课外活动时她测得一根长为1m的竹竿的影长是0.8m,但当她马上测量树高时,发现树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上(如图),他先测得留在墙壁上的影高为1.2m,又测得地面的影长为2.6m,请你帮她算一下,树高是()A.3.25m B.4.25m C.4.45m D.4.75m【解答】解:如图,设BD是BC在地面的影子,树高为x,根据竹竿的高与其影子的比值和树高与其影子的比值相同得而CB=1.2,∴BD=0.96,∴树在地面的实际影子长是0.96+2.6=3.56,再竹竿的高与其影子的比值和树高与其影子的比值相同得,∴x=4.45,∴树高是4.45m.故选C.20.(2015•兰州二模)为了测量校园水平地面上一棵不可攀的树的高度,学校数学兴趣小组做了如下的探索:根据光的反射定律,利用一面镜子和一根皮尺,设计如下图所示的测量方案:把一面很小的镜子水平放置在离树底(B)8.4米的点E处,然后沿着直线BE后退到点D,这时恰好在镜子里看到树梢顶点A,再用皮尺量得DE=3.2米,观察者目高CD=1.6米,则树(AB)的高度约为()A.4.2米B.4.8米C.6.4米D.16.8米【解答】解:过点E作EF⊥BD于点E,则∠1=∠2,∵∠DEF=∠BEF=90°,∴∠DEC=∠AEB,∵CD⊥BD,AB⊥BD,∴∠CDE=∠ABE=90°,∴△CDE∽△ABE,∴=,∵DE=3.2米,CD=1.6米,EB=8.4米,∴=,解得AB=4.2(米).故选A.21.(2015•海曙区模拟)如图,将一张三角形纸片沿虚线剪成甲、乙、丙三块,其中甲、丙为梯形,乙为三角形.根据图中标示的边长数据,比较甲、乙、丙的面积大小,下列判断正确的是()A.乙>丙>甲B.丙>乙>甲C.甲>丙>乙D.无法判断【解答】解:如图:过点B作BH⊥GF于点H,则S乙=AB•AC,∵AC∥DE,∴△ABC∽△DBE,∴==,∵BC=7,CE=3,∴DE=AC,DB=AB,∴AD=BD﹣BA=AB,∴S丙=(AC+DE)•AD=AB•AC,∵AD∥GF,BH⊥GF,AC⊥AB,∴BH∥AC,∴四边形BDFH是矩形,∴BH=DF,FH=BD=AB,∴△GBH∽△BCA,∴==,∵GB=2,BC=7,∴GH=AB,BH AC,∴DF=AC,GF=GH+FH=AB,∴S甲=(BD+GF)•DF=AB•AC,∴甲<乙<丙.故选:B.22.(2016秋•陕西校级月考)下列说法:①凡正方形都相似;②凡等腰三角形都相似;③凡等腰直角三角形都相似;④有一个底角相等的两个等腰三角形相似;⑤两个相似多边形的面积比为4:9,则周长的比为16:81中,正确的个数有()个.A.1 B.2 C.3 D.4【解答】解:①正方形四个角都是直角,四条边都相等,所以对应成比例,所以都相似,正确;②等腰三角形的两底角相等,而与另一个等腰三角形的两个底角不一定相等,所以不一定相似,本选项错误;③等腰直角三角形都有一个直角,且另两角都是45°的锐角,所以都相似,正确;④有一个底角相等的两个等腰三角形相似,正确;⑤两个相似多边形的面积比为4:9,则周长的比应为2:3,本选项错误.所以①③④三项正确.故选C.23.(2016春•重庆校级月考)如图,已知矩形ABCD中,AB=2,在BC上取一点E,沿AE 将△ABE向上折叠,使B点落在AD上的F点处,若四边形EFDC与矩形ABCD相似,则AD=()A.B.+1 C.4 D.2【解答】解:∵沿AE将△ABE向上折叠,使B点落在AD上的F点,∴四边形ABEF是正方形,∵AB=2,设AD=x,则FD=x﹣2,FE=2,∵四边形EFDC与矩形ABCD相似,∴,,解得x1=1+,x2=1﹣(负值舍去),经检验x1=1+是原方程的解.故选B24.(2015秋•宁波期末)如图,取一张长为a,宽为b的长方形纸片,将它对折两次后得到一张小长方形纸片,若要使小长方形与原长方形相似,则原长方形纸片的边a、b应满足的条件是()A.a= b B.a=2b C.a=2 b D.a=4b【解答】解:对折两次后的小长方形的长为b,宽为a,∵小长方形与原长方形相似,∴=,∴a=2b.故选B.25.(2014•杭州模拟)彼此相似的矩形A1B1C1D1,A2B2C2D2,A3B3C3D3,…,按如图所示的方式放置.点A1,A2,A3,…,和点C1,C2,C3,…,分别在直线y=kx+b(k>0)和x轴上,已知点B1、B2的坐标分别为(1,2),(3,4),则Bn的坐标是()A.(2n﹣1,2n)B.(2n﹣,2n)C.(2n﹣1﹣,2n﹣1)D.(2n﹣1﹣1,2n﹣1)【解答】解:∵B1(1,2),∴相似矩形的长是宽的2倍,∵点B1、B2的坐标分别为(1,2),(3,4),∴A1(0,2),A2(1,4),∵点A1,A2在直线y=kx+b上,∴,解得,∴y=2x+2,∵点A3在直线y=2x+2上,∴y=2×3+2=8,∴点A3的坐标为(3,8),∴点B3的横坐标为3+×8=7,∴点B3(7,8),…,B n的坐标为(2n﹣1,2n).故选A.26.(2016•十堰)如图,以点O为位似中心,将△ABC缩小后得到△A′B′C′,已知OB=3OB′,则△A′B′C′与△ABC的面积比为()A.1:3 B.1:4 C.1:5 D.1:9【解答】解:∵OB=3OB′,∴,∵以点O为位似中心,将△ABC缩小后得到△A′B′C′,∴△A′B′C′∽△ABC,∴=.∴=,故选D27.(2016•烟台)如图,在平面直角坐标中,正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且相似比为,点A,B,E在x轴上,若正方形BEFG的边长为6,则C点坐标为()A.(3,2)B.(3,1)C.(2,2)D.(4,2)【解答】解:∵正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且相似比为,∴=,∵BG=6,∴AD=BC=2,∵AD∥BG,∴△OAD∽△OBG,∴=,∴=,解得:OA=1,∴OB=3,∴C点坐标为:(3,2),故选:A.二.解答题(共3小题)28.(2016•呼和浩特)如图,已知AD是△ABC的外角∠EAC的平分线,交BC的延长线于点D,延长DA交△ABC的外接圆于点F,连接FB,FC.(1)求证:∠FBC=∠FCB;(2)已知FA•FD=12,若AB是△ABC外接圆的直径,FA=2,求CD的长.【解答】(1)证明:∵四边形AFBC内接于圆,∴∠FBC+∠FAC=180°,∵∠CAD+∠FAC=180°,∴∠FBC=∠CAD,∵AD是△ABC的外角∠EAC的平分线,∴∠EAD=∠CAD,∵∠EAD=∠FAB,∴∠FAB=∠CAD,又∵∠FAB=∠FCB,∴∠FBC=∠FCB;(2)解:由(1)得:∠FBC=∠FCB,又∵∠FCB=∠FAB,∴∠FAB=∠FBC,∵∠BFA=∠BFD,∴△AFB∽△BFD,∴,∴BF2=FA•FD=12,∴BF=2,∵FA=2,∴FD=6,AD=4,∵AB为圆的直径,∴∠BFA=∠BCA=90°,∴tan∠FBA===,∴∠FBA=30°,又∵∠FDB=∠FBA=30°,∴CD=AD•cos30°=4×=2.29.(2016•杭州)如图,在△ABC中,点D,E分别在边AB,AC上,∠AED=∠B,射线AG分别交线段DE,BC于点F,G,且.(1)求证:△ADF∽△ACG;(2)若,求的值.【解答】(1)证明:∵∠AED=∠B,∠DAE=∠DAE,∴∠ADF=∠C,∵=,∴△ADF∽△ACG.(2)解:∵△ADF∽△ACG,∴=,又∵=,∴=,∴=1.30.(2016•邵阳)尤秀同学遇到了这样一个问题:如图1所示,已知AF,BE是△ABC的中线,且AF⊥BE,垂足为P,设BC=a,AC=b,AB=c.求证:a2+b2=5c2该同学仔细分析后,得到如下解题思路:先连接EF,利用EF为△ABC的中位线得到△EPF∽△BPA,故,设PF=m,PE=n,用m,n把PA,PB分别表示出来,再在Rt△APE,Rt△BPF中利用勾股定理计算,消去m,n即可得证(1)请你根据以上解题思路帮尤秀同学写出证明过程.(2)利用题中的结论,解答下列问题:在边长为3的菱形ABCD中,O为对角线AC,BD的交点,E,F分别为线段AO,DO的中点,连接BE,CF并延长交于点M,BM,CM分别交AD于点G,H,如图2所示,求MG2+MH2的值.【解答】解:(1)设PF=m,PE=n,连结EF,如图1,∵AF,BE是△ABC的中线,∴EF为△ABC的中位线,AE=b,BF=a,∴EF∥AB,EF=c,∴△EFP∽△BPA,∴,即==,∴PB=2n,PA=2m,在Rt△AEP中,∵PE2+PA2=AE2,∴n2+4m2=b2①,在Rt△AEP中,∵PF2+PB2=BF2,∴m2+4n2=a2②,①+②得5(n2+m2)=(a2+b2),在Rt△EFP中,∵PE2+PF2=EF2,∴n2+m2=EF2=c2,∴5•c2=(a2+b2),∴a2+b2=5c2;(2)∵四边形ABCD为菱形,∴BD⊥AC,∵E,F分别为线段AO,DO的中点,由(1)的结论得MB2+MC2=5BC2=5×32=45,∵AG∥BC,∴△AEG∽△CEB,∴==,∴AG=1,同理可得DH=1,∴GH=1,∴GH∥BC,∴===,∴MB=3GM,MC=3MH,∴9MG2+9MH2=45,∴MG2+MH2=5.。
20181122小学奥数练习卷(知识点:周期性问题)含答案解析

小学奥数练习卷(知识点:周期性问题)注意事项:1.答题前填写好自己的姓名、班级、考号等信息2.请将答案正确填写在答题卡上第Ⅰ卷(选择题)一.选择题(共2小题)1.将某数的3倍减5,计算出答案:将这个答案的3倍减5,计算出答案;…;这样反复4次,最后得出的结果是1177,那么原数是()A.14B.15C.16D.172.将“OPQRST”连续写下去可得到:“OPQRSTOPQRST…”,从左至右第2015个字母应该是()A.S B.Q C.O D.T第Ⅱ卷(非选择题)二.填空题(共42小题)3.某班40名学生全都面向前方,从前向后站成一列,按照1、2、3、4、1、2、3、4、…的顺序循环报数,每人报一次数,报到3的同学向后转.之后,如果相邻两个学生面对面,他们就会握一次手,然后同时向后转,一直到不再有学生面对面.那么,整个过程中,全班同学一共握手了次.4.算式(367367+762762)×123123的得数的尾数是.5.2017年3月19日是星期日,据此推算,2017年9月1日是星期.6.2015年6月1日是星期一,那么,2017年10月1日是星期.7.一串珠子,按照3颗黑色、2颗白色、1颗红色;3颗黑色、2颗白色、1颗红色…的顺序不断这样排下去.问第2017颗珠子的颜色是色.8.6月7日,中午11时30分,董事长陈某报警,在自家车库被绑架,犯罪嫌疑人勒索100万后驾车逃离现场.6月9日凌晨1时30分,四名犯罪嫌疑人全部落网,警方只用小时就破了案.9.分数化成小数后,小数点后前448位数字的和是.10.把假分数化为小数后,整数部分都是1,小数点后第2017位上的数字是2,到a的值是.11.每个月的周一、周二、周三、周四、周五、周六、周日都有4天或5天,某月,周三比其他日期恰好都多一天,这个月28日是星期.12.在中国古代的历法中,甲、乙、丙、丁、戊、己、庚、辛、壬、癸被称为“十天干”,子、丑、寅、卯、辰、已、午、未、申、酉、戌、亥叫作“十二地支,;十天干和十二地支进行循环组合:甲子、乙丑、丙寅.一直到癸亥,共得到60个组合,称为六十甲子.如此周而复始用来纪年的方法,称为甲子纪年法在甲子纪年中,以“丑”结尾的年份除了“乙丑”外,还有.13.每个月的周一、周二、周三、周四、周五、周六、周日都有4天或5天.某个月,周六、周日恰好有5天,而每个工作日都是4天,这个月1日是星期.14.如果某年某月的日期中,第一天与最后一天都是星期二,那么这个月是月,这一年有天.15.按顺时针方向不断取如图中的12个数字,可组成不超过1000的循环小数x,如23.067823,678.30678等,若将x的所有数字从左至右依次相加,在加完某个循环节的所有数字之后,得到2017,则x=.16.在表中,8位于第3行第2列,2017位于第a行第b列,则a﹣b=.17.将10、11、12、13、…除以3的余数依次排列起来,得到一个数列.这个余数数列的第50个数是.18.在一条马路边按红、黄、蓝、绿四种颜色的顺序插了30面彩旗,最后一面是色的彩旗,红色的彩旗一共插了面.19.5个小朋发围成一圈,按照下面的方法给他们发糖果,首先给第一个小朋友,然后逆时针隔1个人发给另一个小朋发,然后逆时针隔2个人发给另一个小朋发,接着隔3个人发糖,然后是隔4个人发,隔5个人发….一共发了2016块糖,那么第一个小朋友一共得到了块糖.20.小明通过2、0、1、6这四个数构造了一个数列(不断地将2、0、1、6这四个数字按照这个顺序加在数后面):2、20、201、2016、20162、201620、2016201、20162016、201620162、…,这个数列中,质数有个.21.将算式20÷(6+1)的计算结果写成循环小数,那么在小数点后第2016位数字是.22.如图是2016年4月份的日历,根据这个日历提供的信息,可以算出如2015年4月4日是星期.(填1~7、星期日请填7)23.将化成小数,小数部分从左到右第2016个数字是.24.中国北京在2015年7月31日获得了2022年第24届冬季奥林匹克运动会的主办权.预定该届冬奥会的开幕时间为2022年2月4日,星期.(今天是2016年3月12日,星期六)25.中国古代采用天干(甲乙丙丁戊己庚辛壬癸)地支(子丑寅卯辰巳午未申酉戌亥)纪年法,如公元1984年是甲子年,公元1983年就是癸亥年;公元的2015年是乙末年,公元2016年就是丙申年,根换这种算法,唐朝元年(公元618年)应为年.26.循环小数0.01小数点后第2016位数字是.27.王老师在一个特殊的学校上课,他每上3天课可以休息一天,已知本学期他第一次休息在星期二,那么他第五次休息是星期(填数字1﹣7).28.七名同学在老师的指导下玩击鼓传花游戏,老师每敲一下,同学就将花传给顺时针方向下一位同学,例如1号传给2号.2号传给3号,…,7号传给1号,那么,当老师敲第50下,同学完成第50次传递后,花在号手中.29.有一颗神奇的树上长了60个果子,第一天会有1个果子掉落,从第二天起,每天掉落的果子数量比前一天多1个.但如果某天树上的果子数量少于这一天本应该掉落的数量时,那么这一天它又重新从掉落1个果子开始,按原规律进行新的一轮.如此继续,那么第天树上的果子会掉光.30.王华每星期二、六学书法,已知2016年的元旦是星期五,那么在2016年8月,王华学书法的天数是.31.“阳光空气都市报阳光空气都市报阳光空气都市报…”按这样一直排列下去,第41个字是.32.冬至又称“冬节”“贺冬”,是华夏二十四节气之一,与二十四节气中的“夏至”节气相对.2014年的“冬至”是12月22日星期一,那么2015年“冬至”(也在12月22日)是星期.33.乘积0.3×0.25的小数点后第2015位数是.34.冬至又称“冬节”、“贺冬,是华夏二十四节气之一,与”二十四节气中的“夏至”节气相对,如果2014年12月22日是“冬至”,这一天恰好是星期一,那么2015年的“夏至”(6月22日)是星期.35.课外活动课上,有四个同学A、B、C、D围成一圈进行报数游戏:A报“1”,B报“2”,C报“3”,D报“4”,A报“5”,B报“6”,…,这样循环下去,每个同学报的数比前一个同学报的数多1,那么报“54”的是;报“201”的是.36.在一根绳子上依次穿入5颗红珠、4颗白珠、3颗黄珠和2颗蓝珠,并按照此方式不断重复,如果从头开始一共穿了2014颗珠子,那么第2014颗珠子的颜色是色.37.2015年1月1日是星期四,那么2015年6月1日是星期.38.如表,将从1开始的自然数按照一定的规律排列起来,那么第3行第51列的数是.39.如图是挨在一起的大、中、小三个圆,半径分别为9cm,3cm,1cm;中圆顺时针向下沿着大圆内侧滚动;小圆逆时针向上沿着中圆内侧滚动,速度都是沿着圆周方向每秒1厘米.如果小圆上固定着一个箭头,那么中圆滚动一周回到出发点的过程中,箭头的旋转角度(小圆绕着自身中心)是度.40.乐乐发现某个月的星期二比星期一多一天,星期三比星期四多一天,那么这个月一共有天.41.2015年4月1日是星期三,2015年6月1日儿童节是星期.42.一根绳子对折,对折,再对折,然后从对折后的种间剪开.这根绳子一共被剪成了段.43.甲、乙二人从同一天开始工作,公司规定:甲每工作3天后休息1天,乙每工作7天后连续休息3天,则在开始的前1000天中,甲、乙同一天休息的日子有天.44.循环小数0.04285.的小数部分的前2015位数字之和是.三.解答题(共6小题)45.一本历史书共有2640页,张强每小时阅读16页.第一日到第十日,每日读5小时;第十一日到第二十日,每日读6小时;第二十一日到最后一日的前一日,每日读7小时.经过若干日全部读完.问:最后一日是第几日?最后一日读了几小时?46.小袋鼠甲和乙在如图的区域中跳动,甲按ABCDEFGHIABC…的顺序循环跳动,乙按照ABDEGHABD…的顺序跳动,如果开始时两只袋鼠都从A出发,并且这算是第一次他们同跳到了一起,问经过2017跳跃,他们一共跳到了一起多少次?47.从1开始依次把自然数一一写下去得:1 2 3 4 5 6 7 8 9 10 11 12 13…从左向右数,数到第12个数字起将开始第一次出现三个连排的1.数到第几个数字起将开始出现五个连排的1.48.2012位同学排成一列依次报数.若某位同学报的是一位数,后面的同学就报这个数的2倍;若某位同学报的是两位数,后面的同学就报其个位数字与5的和.已知第一位同学报1.(1)那么第2012位同学所报的数是多少?(2)到了第100位同学,他却把前面那位同学报的数加上了另一个一位自然数,其他人都没有注意到,仍然按以前的规则继续报数,直到最后一位同学报的数是5.那么第100位同学所报的数是把前一位同学报的数加上了多少?49.有158个小朋友排成一排,从左边第一个人起(第一个人发一个苹果),每隔1人发一个苹果,又从右边第一个人起(第一个人发一个香蕉),每隔2人发一个香蕉,求没有得到水果的小朋友的人数.50.某一年共有53个星期五和53个星期六,那么这一年3月1日是星期几?参考答案与试题解析一.选择题(共2小题)1.将某数的3倍减5,计算出答案:将这个答案的3倍减5,计算出答案;…;这样反复4次,最后得出的结果是1177,那么原数是()A.14B.15C.16D.17【分析】从最后的结果往前逆推,结果是1177,这是一个数的3倍减5得到的,这个数应该是(1177+5)÷3=394,这是经过3次后的结果;以此类推便可求出原数.【解答】解:第四次计算后的结果为1177,第三次计算后的结果为:(1177+5)÷3=394,第二次计算后的结果为:(394+5)÷3=133,第一次计算后的结果为(133+5)÷3=46,原数为:(46+5)÷3═17.故选:D.【点评】本题需要逆着思考,从最后的结果向前根据数量关系,求出上一步的结果,一步步的推,进而求解.2.将“OPQRST”连续写下去可得到:“OPQRSTOPQRST…”,从左至右第2015个字母应该是()A.S B.Q C.O D.T【分析】根据题干分析可得,这组图形的排列规律是:6个字母一个循环周期,分别按照OPQRST的顺序依次循环排列,由此求出第2015个字母是第几个周期的第几个即可解答.【解答】解:2015÷6=335…5,所以第2015个字母是第336周期的第5个字母,是S;故选:A.【点评】解决这类问题往往是把重复出现的部分看成一组,先找出排列的周期性规律,再根据规律求解.二.填空题(共42小题)3.某班40名学生全都面向前方,从前向后站成一列,按照1、2、3、4、1、2、3、4、…的顺序循环报数,每人报一次数,报到3的同学向后转.之后,如果相邻两个学生面对面,他们就会握一次手,然后同时向后转,一直到不再有学生面对面.那么,整个过程中,全班同学一共握手了145次.【分析】根据题意可知编号是3的学生向后转后,就会和编号是4的学生面对面,就要握40÷4=10(次);第二轮编号是4的学生和编号是1的学生握手,一共要握10﹣1=9(次);依此类推,据此解答即可.【解答】解:根据题意可知编号是3的学生向后转后,就会和编号是4的学生面对面,就要握40÷4=10(次);第二轮编号是4的学生和编号是1的学生握手,一共要握10﹣1=9(次);10+(9+8+7+6+5+4+3+2+1)×3=145(次)答:整个过程中,全班同学一共握手了145次.【点评】本题的关键是利用周期进行解题.4.算式(367367+762762)×123123的得数的尾数是9.【分析】分别找出个位数字7、2、3的连乘积的个位数的循环周期:如7的连乘积,积的尾数以7,9,3,1,循环出现,周期为4,因为367÷4=913,所以,367367的尾数为3;如此类推,…即可解决问题.【解答】解:(1)7的连乘积,尾数(个位数字)以7,9,3,1循环出现,周期为4;因为367÷4=91…3,所以,367367的尾数为3.(2)2的连乘积,尾数以2,4,8,6循环出现,周期为4;因为762÷4=190…2,所以,762762的尾数为4.(3)3的连乘积,尾数以3,9,7,1循环出现,周期为4;123÷4=30…3,所以,123123的尾数为7.(4)综上所述,(367367+762762)×123123的尾数就是(3+4)×7的尾数,(3+4)×7=49,答:得数的尾数是9.故答案为:9.【点评】此题考查了利用个位数字为7,2,3的连乘积的积的尾数的规律进行解决问题的方法.5.2017年3月19日是星期日,据此推算,2017年9月1日是星期五.【分析】先求3月19日到9月1日经过了多少天,再求这些天里有几周,还余几天,再根据余数判断.【解答】解:3月19日到3月31日共:31﹣19=12(天)4、6月30天,5、7、8月31天,一共:30×2+31×3+12+1=60+93+13=166(天)166÷7=23(周)…5(天)所以3月19日是星期日,9月1日是星期五.答:2017年9月1日是星期五.故答案为:五.【点评】解决这类问题先求出经过的天数,再求经过的天数里有几周还余几天,再根据余数推算.6.2015年6月1日是星期一,那么,2017年10月1日是星期日.【分析】2016年,是闰年,先求出2015年的6月1日到2017的6月1日的天数,一共是366+365=731天,再求出6月1日到10月1日经过的时间,一共是30+31+31+30=122天,然后相加,再找到天数与7相除的商的余数,即可作出判断.【解答】解:366+365+30+31+31+30=853(天)则853÷7=121(星期)…6(天)1+6=7,即星期日,答:2017年10月1日是星期日.故答案为:日.【点评】考查了日期和时间的推算,由于每个星期是7天一循环,可以运用这个规律进行解答.7.一串珠子,按照3颗黑色、2颗白色、1颗红色;3颗黑色、2颗白色、1颗红色…的顺序不断这样排下去.问第2017颗珠子的颜色是黑色.【分析】因为“按3颗黑色、2颗白色、1颗红色”的顺序进行排列,可得每6个珠子为一个循环,所以计算出第2017颗珠子里面有几个6,即可求出第2017颗珠子是什么颜色.【解答】解:1+2+3=62017÷6=336…1,所以第2017颗珠子是第337个循环的第1个,是黑色的.答:第2017颗珠子的颜色是黑色.故答案为:黑.【点评】本题考查了事物的间隔排列规律.求出这些珠子排列的周期规律是解决此类问题的关键.8.6月7日,中午11时30分,董事长陈某报警,在自家车库被绑架,犯罪嫌疑人勒索100万后驾车逃离现场.6月9日凌晨1时30分,四名犯罪嫌疑人全部落网,警方只用38小时就破了案.【分析】首先应知道1日=24小时,为了便于计算,先计算6月7日中午11时30分,到9日11时30分,经过了2天48小时;然后减去多算的小时数即可.【解答】解:6月7日,中午11时30分到9日11时30分,共是:24×2=48(小时);多算了:11时30分﹣1时30分=10(小时);6月7日,中午11时30分到6月9日凌晨1时30分,共计:48﹣10=38(小时).答:警方只用38小时就破了案.故答案为:38.【点评】此题考查了学生对时间单位之间的换算方法,知道1日=24小时,注意:结束时刻﹣起始时刻=经过时间.9.分数化成小数后,小数点后前448位数字的和是2017.【分析】先把化成小数,再看它的循环节,然后再用448除以循环节的位数,再根据商和余数,进行判定有几个循环周期,据此再求出数字的和即可.【解答】解:=0.2857,它的循环节是6位数,每个周期的数字和是4+2+8+5+7+1=27448÷6=74…4,所以前448位数字的和:27×74+4+2+8+5=2017;答:小数点后前448位数字的和是2017.故答案为:2017【点评】做这类题先把分数化为小数,(一般为循环小数),找出它的循环周期及循环的数列,再根据有余数的除法解答.10.把假分数化为小数后,整数部分都是1,小数点后第2017位上的数字是2,到a的值是9.【分析】由是假分数且化为小数后整数部分是1得出a=8或9、10、11、12、13,将各分数化为小数得出所有小数部分均6位数为一个周期循环,由2017÷6=336…1知小数点后第2017位上的数字与循环周期的第1个数字相同,据此可得答案.【解答】解:因为是假分数,且化为小数后整数部分是1,所以a=8或9、10、11、12、13,若a=8,则==1=1.142857 142857…;若a=9,则==1=1.285714 285714…;若a=10,则==1=1.428571 428571…;若a=11,则==1=1.571428 571428…;若a=12,则==1=1.714285 714285…;若a=13,则==1=1.857142 857142…;由以上可知,所有小数部分均6位数为一个周期循环,而2017÷6=336…1,所以小数点后第2017位上的数字与循环周期的第1个数字相同,所以a=9,故答案为:9.【点评】本题主要考查周期性问题,根据假分数的定义求得a的可能取值及各分数的小数部分循环的规律是解题的关键.11.每个月的周一、周二、周三、周四、周五、周六、周日都有4天或5天,某月,周三比其他日期恰好都多一天,这个月28日是星期二.【分析】首先分析这个月一个有多少天,周三比其他都多一天说明这个月是4个星期多一天共29天,继续分析即可求解.【解答】解:依题意可知:周三比其他都多一天说明这个月是4个星期多一天共29天,最后一天是星期三,那么28日就是星期二.故答案为:二【点评】本题考查对周期问题的理解和运用,关键问题是找到这个月的天数,问题解决.12.在中国古代的历法中,甲、乙、丙、丁、戊、己、庚、辛、壬、癸被称为“十天干”,子、丑、寅、卯、辰、已、午、未、申、酉、戌、亥叫作“十二地支,;十天干和十二地支进行循环组合:甲子、乙丑、丙寅.一直到癸亥,共得到60个组合,称为六十甲子.如此周而复始用来纪年的方法,称为甲子纪年法在甲子纪年中,以“丑”结尾的年份除了“乙丑”外,还有丁丑,己丑,辛丑,癸丑.【分析】首先分析题中的丑经过12年出现一次,共60年出现5次.枚举法即可.【解答】解:依题意可知:第一个是乙丑,丑出现时经过12+2=14年.24+2=26年,36+2=38年,48+2=50年.经过14,26,38,50年对应的天干是丁,己,辛,癸.故答案为:丁丑,己丑,辛丑,癸丑【点评】本题考查对周期问题的理解和掌握,关键是找到对应的数字.问题解决.13.每个月的周一、周二、周三、周四、周五、周六、周日都有4天或5天.某个月,周六、周日恰好有5天,而每个工作日都是4天,这个月1日是星期六.【分析】分析天数可知共30天.继续分析即可求解.【解答】解:依题意可知:该月周一至周五都是4天,周六周日是5天,这个月共有30天.说明开始的第一天是周六,最后一天是周日.故答案为:六【点评】本题考查对周期问题的理解和运用,关键问题是找到天数和开始时间,问题解决.14.如果某年某月的日期中,第一天与最后一天都是星期二,那么这个月是2月,这一年有366天.【分析】首先分析这个日期的天数是4个星期多一天,根据平年和闰年的时间计算即可.【解答】解:依题意可知:第一天是星期二,最后一天也是星期二证明这个月是4个星期多一天共29天,只能是星期二,这一年是闰年共366天.故答案为:29,366【点评】本题考查对周期性问题的理解和运用,关键是分析出这个月的天数,可知是29天,问题解决.15.按顺时针方向不断取如图中的12个数字,可组成不超过1000的循环小数x,如23.067823,678.30678等,若将x的所有数字从左至右依次相加,在加完某个循环节的所有数字之后,得到2017,则x=78.3067.【分析】首先分析数字的周期发现数字周期为6,7,8,2,3,0.找到对应组数和余数即可.【解答】解:依题意可知:按照顺时针方向观察可发现,不管起始数字是几,循环小数的循环节均由6,7,8,2,3,0这六个数字组成.因2017÷(6+7+8+2+3+0)=77(组)…15.15=7+8,因此x=78.3067故答案为:78.3067【点评】本题考查对周期问题的理解和运用,关键问题是找到数字和的周期数字.问题解决.16.在表中,8位于第3行第2列,2017位于第a行第b列,则a﹣b=672.【分析】首先分析数字规律的周期为9.对应计算即可解题.【解答】解:依题意可知:周期为9.2017÷9=224…1.a=224×3+1=673;b=1.a﹣b=672.故答案为:672【点评】本题考查对周期性的理解和运用,关键是分析周期的规律,问题解决.17.将10、11、12、13、…除以3的余数依次排列起来,得到一个数列.这个余数数列的第50个数是2.【分析】通过计算可知,余数是以1、2、0这三个数为一个周期进行循环,由此解答即可.【解答】解:通过计算可知,余数是以1、2、0这三个数为一个周期进行循环50÷3=16 (2)即这个余数数列的第50个数是2.【点评】本题的关键是找到余数的规律.18.在一条马路边按红、黄、蓝、绿四种颜色的顺序插了30面彩旗,最后一面是黄色的彩旗,红色的彩旗一共插了8面.【分析】彩旗的颜色以红、黄、蓝、绿四种颜色为一个周期进行循环,周期长度是4,用彩旗的总数30除以周期长度,余数是1就是红色,余数是2就是黄色,余数是3就是蓝色,正好整除就是绿色的,据此解答即可.【解答】30÷4=7…2,最后一面是黄色,红色的有7+1=8(面).答:最后一面是黄色的彩旗,红色的彩旗一共有8面.【点评】解答本题就是用总数量除以周期长度,看有几个周期和余数分别是多少,从而确定最后一面彩旗的颜色和红色彩旗的数量.19.5个小朋发围成一圈,按照下面的方法给他们发糖果,首先给第一个小朋友,然后逆时针隔1个人发给另一个小朋发,然后逆时针隔2个人发给另一个小朋发,接着隔3个人发糖,然后是隔4个人发,隔5个人发….一共发了2016块糖,那么第一个小朋友一共得到了807块糖.【分析】首先分析枚举法找到数字长度周期,再计算有多少组即可求解.【解答】解:依题意可知:发糖的顺序是1,3,1,5,5,1,3,1,5,5,1,发现周期规律为13155共5个数字.2016÷5=403…1.每一组都有2个1,共有403×2+1=807(个).故答案为:807【点评】本题考查对周期问题的理解和运用,关键是找到周期长度和余数的关系,问题解决.20.小明通过2、0、1、6这四个数构造了一个数列(不断地将2、0、1、6这四个数字按照这个顺序加在数后面):2、20、201、2016、20162、201620、2016201、20162016、201620162、…,这个数列中,质数有1个.【分析】根据质数的概念:一个大于1的自然数,除了1和它本身外,不能被其他自然数整除,换句话说就是该数除了1和它本身以外不再有其他的因数,为质数,例如:2、3、5、7、11、13、17、19…按照这个定义,研究数构造了一个数列数字的规律,可以将数列分为:偶数2、个位数是0和偶数的、个位是1的,其中个位数是0和偶数的都不是质数,所以除了2,只需要研究个位数是1的,综合分析这些数字特点,列出综合表达式,即可求解.【解答】解:这个数列中的数按照周期个位分别是2、0、1、6;也就是说除了个位是1的,其余都是偶数,而偶数中也有2是质数,其余偶数均不是质数;再考虑以1结尾的奇数,如:201、2016201…这些数的数字和为:(2+0+1+6)×k+2+0+1=9k+3(其中k=0,1,2…),所以,这些数一定是3的倍数,所以,这些数不是质数;所以,只有1个质数,即数2.故答案为:1.【点评】主要在理解质数定义的基础上,主要查找个位数是1的数字特点即可.21.将算式20÷(6+1)的计算结果写成循环小数,那么在小数点后第2016位数字是2.【分析】求出20÷7的商的循环节,用2016除以循环节的位数,余数是几,就是循环节第几位上的数,据此可解答.【解答】解:20÷(6+1)=2.5714,循环节为6位数,2016÷6=336;没有余数,所以第2016位上的数字就和循环节的第6位上的数字相同,是2.故答案为:2.【点评】此题考查小数除法的计算法则和数字问题,关键是看循环节是几位数,进而进行求解.22.如图是2016年4月份的日历,根据这个日历提供的信息,可以算出如2015年4月4日是星期6.(填1~7、星期日请填7)【分析】按规律“平年后推1天,闰年往后推2天”,来求解.【解答】由周期规律“平年后推1天,闰年往后推2天”,可知2015年4月到2016年4月,刚好包括2月29日,所以,应该往前推2天,即星期六.故:填6.【点评】周期规律是:“平年后推1天,闰年往后推2天”,依此可以推出答案.23.将化成小数,小数部分从左到右第2016个数字是5.【分析】首先找到循环小数的循环节,用2016除以循环节找余数即可.【解答】解:依题意可知:=.2016÷3=672.那么第2016个数字就是5.故答案为:5【点评】本题考查对周期问题的理解和运用,关键是找到周期和余数,问题解决.24.中国北京在2015年7月31日获得了2022年第24届冬季奥林匹克运动会的主办权.预定该届冬奥会的开幕时间为2022年2月4日,星期五.(今天是2016年3月12日,星期六)【分析】首先分析2016年的3月12日到2022年的3月13日是星期几,然后再根据3月12向前推理出2月4日即可.【解答】解:依题意可知:平年365天是52个星期多1天.润年是52个星期多2天.2016年3月12到2022年3月12日经过了5个平年1个闰年,向后推的天数为1+1+1+1+1+2=7.恰好为星期六.那么2022年的2月4日到2022年的3月12日.经过24+12=36天.36÷7=5…1.从星期六前推前天.说明2022年的2月4日是星期五.故答案为:五【点评】本题考查对周期问题的理解和运用,关键问题是找到时间差,周期看余数即可,问题解决.25.中国古代采用天干(甲乙丙丁戊己庚辛壬癸)地支(子丑寅卯辰巳午未申酉戌亥)纪年法,如公元1984年是甲子年,公元1983年就是癸亥年;公元的2015年是乙末年,公元2016年就是丙申年,根换这种算法,唐朝元年(公元618年)应为戊寅年.【分析】首先分析天干和地支的最小公倍数,一个周期为60年,时间从公元1984年向前推到公元618年,找到余数即可.【解答】解:依题意可知:天干有甲乙丙丁戊己庚辛壬癸共10个,地支有子丑寅卯辰巳午未申酉戌亥共12个.两次比较10和12的最小公倍数为60.故从一个甲子到下一个甲子共60年.天干:(1984﹣618)÷10=136…6.倒着数癸,壬,辛,庚,己,戊,所以是“戊”;地支:(1984﹣618)÷12=113…10到这数为亥,戌,酉,申,未,午,巳,辰,卯,寅.所以是“寅”.故答案为:戊寅【点评】本题考查对周期问题的理解和运用,关键问题是找到周期同时找到余数,注意是倒推问题解决.26.循环小数0.01小数点后第2016位数字是6.。
相似三角形练习题及答案
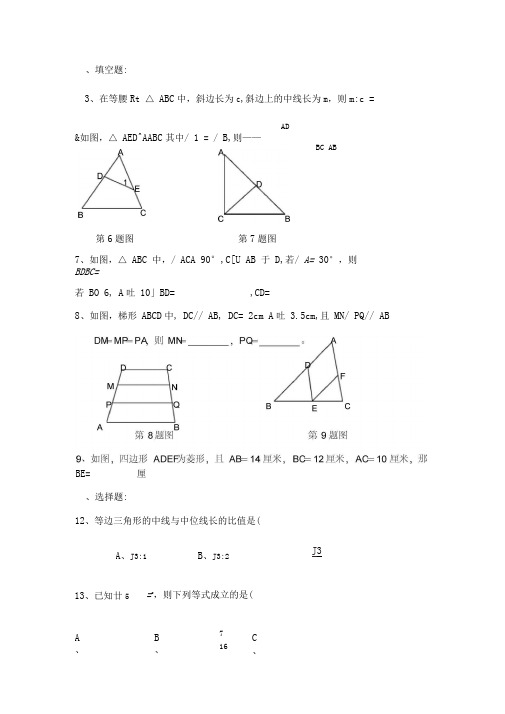
、填空题:3、在等腰Rt △ ABC中,斜边长为c,斜边上的中线长为m,则m:c =AD&如图,△ AED^AABC其中/ 1 = / B,则——7、如图,△ ABC 中,/ ACA 90°,C[U AB 于D,若/ A= 30°,则BDBC=、选择题:12、等边三角形的中线与中位线长的比值是(A、J3:1B、J3:2 J 313、已知廿5 =z,则下列等式成立的是(A 、B、716C、BC AB若BO 6, A吐10」BD= ,CD=第6题图第7题图8、如图,梯形ABCD中, DC// AB, DC= 2cm A吐3.5cm,且MN/ PQ// AB厘BE=14、已知直角三角形三边分别为a,a+b,a+2b , (a>0,b>0),则a:b=()15、AABC 中, A 吐12, BCh 18,CAh24,另一个和它相似的三角形最长的一边 是36,则最短的一边是()16、已知a,b,c 是^ABC 的三条边,对应高分别为h a ,h b ,h c ,且a:b:c = 4:5:6 ,那么h a : h b : h c 等于()17、一个三角形三边长之比为4:5:6,三边中点连线组成的三角形的周长为 30cm 则原三角形最大边长为( )A 1: 3B 、1: 4C 、2: 1D 3: 1A 27B 、12C 、18D 20A 4: 5: 615B 、 6: 5: 4C 、15: 12: 10D 10: 12:A 、44厘米B 、40厘米C 36厘米D 24厘个20、如图,在平行四边形 ABCC 中,E 为BC 边上的点,若BE ECh4: 5, AE 交 BD于F ,则BF: FD 等于()A 4: 5B 、3: 5 21、C 、4: 9D 3: 8解答题:已知(X —y ) y =2:3, 求 3x —2y 如图,在Rt △ ABC 中, CD 为斜边AB 上的高,且 AO6厘米,AD= 4厘米, 22、求AB 与BC 的长24、如图,Rt A ABC 中斜边 AB 上一点 M MNL AB交AC 于N,若AMh 3厘米,AB AO5: 4,求MN 的长。
小学奥数-几何五大模型(相似模型)分解
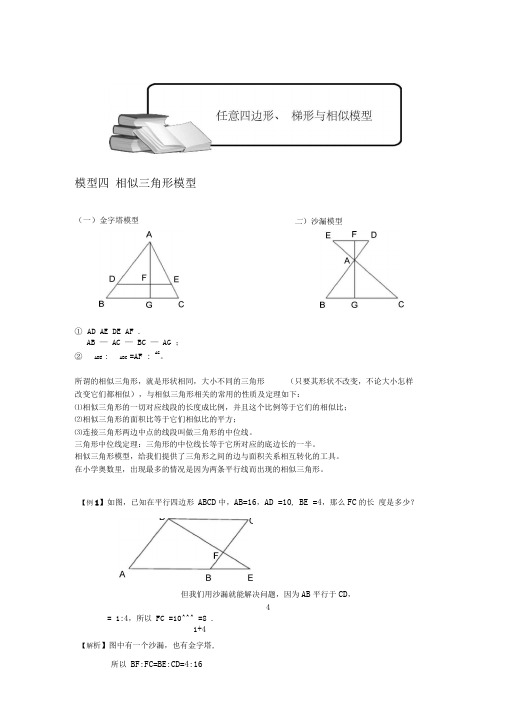
模型四 相似三角形模型(一)金字塔模型① AD AE DE AF .AB — AC — BC — AG ;②ADE :ABC=AF : AG。
所谓的相似三角形,就是形状相同,大小不同的三角形(只要其形状不改变,不论大小怎样改变它们都相似),与相似三角形相关的常用的性质及定理如下:⑴相似三角形的一切对应线段的长度成比例,并且这个比例等于它们的相似比; ⑵相似三角形的面积比等于它们相似比的平方; ⑶连接三角形两边中点的线段叫做三角形的中位线。
三角形中位线定理:三角形的中位线长等于它所对应的底边长的一半。
相似三角形模型,给我们提供了三角形之间的边与面积关系相互转化的工具。
在小学奥数里,出现最多的情况是因为两条平行线而出现的相似三角形。
【例1】如图,已知在平行四边形 ABCD 中,AB=16,AD =10, BE =4,那么FC 的长 度是多少?但我们用沙漏就能解决问题,因为AB 平行于CD ,4= 1:4,所以 FC =10^^^ =8 .1+4二)沙漏模型【解析】图中有一个沙漏,也有金字塔,进而有S四边形DEGF=3份 ,S 四边形FGCB =5份,所以ADE: S 四边形DEGF : S 四边形 FGCB =1: 3: 5如图,测量小玻璃管口径的量具 ABC , AB 的长为15厘米,AC 被分为60等份。
如果小玻璃管口 DE 正好对着量具上20等份处(DE 平行AB ),那么小玻璃管口径 DE 是多大?有一个金字塔模型, 所以DE:AB=DC:AC , DE :15 =40:60,所以DE=10厘米。
如图,DE 平行 BC ,若 AD: DB =2:3,那么 S AADE : S AECB =【解析】根据金 字塔 模 型 AD : AB = AE : AC = DE :BC =2: (2+3) =2:5,S A ADE: SA ABC =22 :52=4: 25 ,设SA ADE —4份则SA ABC=25 份,SABEC= 25 X 5 = 3份,所以& A D :SA毛 C 4【例4】如图,A ABC 中,DE , 贝U S A ADE : &边形DEGF :S四边形FGCB【解析】设S AADE =1份,根据面积比等于相似比的平方,所以SA ADE : SA AFG =AD: AF —1: 4,SA ADE : SA ABC =AD: AB =1: 9 ,因此S A AFG =4 份,S A ABC =9 份,【例2】 【解析】 【例3】FG ,BC 互相平行, AD = DF = FB ,2已知△ ABC 中,DE 平行 BC ,若 AD : DB =2:3,且 S 弟形DBCE 比 $△ ADE 大 8.5 cm2求 SA ABC 。
相似三角形经典大题解析(含答案)

相似三角形经典大题解析1.如图,已知一个三角形纸片ABC ,BC 边的长为8,BC 边上的高为6,B ∠和C ∠都为锐角,M 为AB 一动点(点M 与点A B 、不重合),过点M 作MN BC ∥,交AC 于点N ,在AMN △中,设MN 的长为x ,MN 上的高为h . (1)请你用含x 的代数式表示h .(2)将AMN △沿MN 折叠,使AMN △落在四边形BCNM 所在平面,设点A 落在平面的点为1A ,1A MN △与四边形BCNM 重叠部分的面积为y ,当x 为何值时,y 最大,最大值为多少?【答案】解:(1)MN BC ∥AMN ABC ∴△∽△ 68h x ∴= 34x h ∴=(2)1AMN A MN △≌△1A MN ∴△的边MN 上的高为h ,①当点1A 落在四边形BCNM 内或BC 边上时,1A MN y S =△=211332248MN h x x x ==··(04x <≤) ②当1A 落在四边形BCNM 外时,如下图(48)x <<,设1A EF △的边EF 上的高为1h , 则132662h h x =-=- 11EF MNA EF A MN ∴∥△∽△11AMN ABC A EF ABC ∴△∽△△∽△1216A EF S h S ⎛⎫= ⎪⎝⎭△△ABC168242ABC S =⨯⨯=△ 22363224122462EFx S x x ⎛⎫- ⎪∴==⨯=-+ ⎪⎪⎝⎭1△A 1122233912241224828A MN A EF y S S x x x x x ⎛⎫=-=--+=-+- ⎪⎝⎭△△所以 291224(48)8y x x x =-+-<<综上所述:当04x <≤时,238y x =,取4x =,6y =最大 当48x <<时,2912248y x x =-+-, 取163x =,8y =最大 86>∴当163x =时,y 最大,8y =最大M NCBEFAA 12.如图,抛物线经过(40)(10)(02)A B C -,,,,,三点.(1)求出抛物线的解析式;(2)P 是抛物线上一动点,过P 作PM x ⊥轴,垂足为M ,是否存在P 点,使得以A ,P ,M 为顶点的三角形与OAC △相似?若存在,请求出符合条件的点P 的坐标;若不存在,请说明理由;【答案】解:(1)该抛物线过点(02)C -,,∴可设该抛物线的解析式为22y ax bx =+-. 将(40)A ,,(10)B ,代入,得1642020a b a b .+-=⎧⎨+-=⎩,解得1252a b .⎧=-⎪⎪⎨⎪=⎪⎩,∴此抛物线的解析式为215222y x x =-+-.(2)存在.如图,设P 点的横坐标为m , 则P 点的纵坐标为215222m m -+-, 当14m <<时,4AM m =-,215222PM m m =-+-.又90COA PMA ∠=∠=°,∴①当21AM AO PM OC ==时,APM ACO △∽△,即21542222m m m ⎛⎫-=-+- ⎪⎝⎭.解得1224m m ==,(舍去),(21)P ∴,. ②当12AM OC PM OA ==时,APM CAO △∽△,即2152(4)222m m m -=-+-. 解得14m =,25m =(均不合题意,舍去)∴当14m <<时,(21)P ,. 类似地可求出当4m >时,(52)P -,. 当1m <时,(314)P --,.综上所述,符合条件的点P 为(21),或(52)-,或(314)--,.3.如图,已知直线128:33l y x =+与直线2:216l y x =-+相交于点C l l 12,、分别交x 轴于A B 、两点.矩形DEFG 的顶点D E 、分别在直线12l l 、上,顶点F G 、都在x 轴上,且点G 与点B 重合.(1)求ABC △的面积;(2)求矩形DEFG 的边DE 与EF 的长;(3)若矩形DEFG 从原点出发,沿x 轴的反方向以每秒1个单位长度的速度平移,设移动时间为(012)t t ≤≤秒,矩形DEFG 与ABC △重叠部分的面积为S ,求S 关于t 的函数关系式,并写出相应的t 的取值范围.【答案】(1)解:由28033x +=,得4x A =-∴.点坐标为()40-,.由2160x -+=,得8x B =∴.点坐标为()80,.∴()8412AB =--=.由2833216y x y x ⎧=+⎪⎨⎪=-+⎩,.解得56x y =⎧⎨=⎩,.∴C 点的坐标为()56,. ∴111263622ABC C S AB y ==⨯⨯=△·. (2)解:∵点D 在1l 上且2888833D B D x x y ==∴=⨯+=,. ∴D 点坐标为()88,.又∵点E 在2l 上且821684E D E E y y x x ==∴-+=∴=,.. ∴E 点坐标为()48,. ∴8448OE EF =-==,.(3)解法一:①当03t <≤时,如图1,矩形DEFG 与ABC △重叠部分为五边形CHFGR (0t =时,为四边形CHFG ).过C 作CM AB ⊥于M ,则R t R t R G B C M B△∽△.∴BG RG BM CM =,即36t RG=,∴2RG t =. Rt Rt AFH AMC △∽△,∴()()11236288223ABC BRG AFH S S S S t t t t =--=-⨯⨯--⨯-△△△.即241644333S t t =-++.当83<≤t 时,如图2,为梯形面积,∵G (8-t,0)∴GR=32838)8(32t t -=+-,∴38038]32838)4(32[421+-=-++-⨯=t t t s当128<≤t 时,如图3,为三角形面积,4883)12)(328(212+-=--=t t t t s(图3)(图1)(图2)4.如图,矩形ABCD 中,3AD =厘米,AB a =厘米(3a >).动点M N ,同时从B 点出发,分别沿B A →,B C →运动,速度是1厘米/秒.过M 作直线垂直于AB ,分别交AN ,CD 于P Q ,.当点N 到达终点C 时,点M 也随之停止运动.设运动时间为t 秒. (1)若4a =厘米,1t =秒,则PM =______厘米;(2)若5a =厘米,求时间t ,使PNB PAD △∽△,并求出它们的相似比;(3)若在运动过程中,存在某时刻使梯形PMBN 与梯形PQDA 的面积相等,求a 的取值范围;(4)是否存在这样的矩形:在运动过程中,存在某时刻使梯形PMBN ,梯形PQDA ,梯形PQCN 的面积都相等?若存在,求a 的值;若不存在,请说明理由.【答案】解: (1)4PM =,(2)2t =,使PNB PAD △∽△,相似比为3:2 (3)PM AB CB AB AMP ABC ∠=∠⊥,⊥,,AMP ABC △∽△,PM AM BN AB ∴=即()PM a t t a t PM t a a--==,,(1)3t a QM a-∴=-当梯形PMBN 与梯形PQDA 的面积相等,即()()22QP AD DQ MP BN BM++=()33(1)()22t a t t a a t t ta a -⎛⎫⎛⎫-+--+ ⎪ ⎪⎝⎭⎝⎭==化简得66a t a =+,3t ≤,636aa∴+≤,则636a a ∴<≤,≤, (4)36a <≤时梯形PMBN 与梯形PQDA 的面积相等∴梯形PQCN 的面积与梯形PMBN 的面积相等即可,则CN PM =()3t a t t a ∴-=-,把66a t a=+代入,解之得a =±a = 所以,存在a ,当a =PMBN 与梯形PQDA 的面积、梯形PQCN 的面积相等.N5.如图,已知△ABC 是边长为6cm 的等边三角形,动点P 、Q 同时从A 、B 两点出发,分别沿AB 、BC 匀速运动,其中点P 运动的速度是1cm/s ,点Q 运动的速度是2cm/s ,当点Q 到达点C 时,P 、Q 两点都停止运动,设运动时间为t (s ),解答下列问题: (1)当t =2时,判断△BPQ 的形状,并说明理由; (2)设△BPQ 的面积为S (cm 2),求S 与t 的函数关系式;(3)作QR //BA 交AC 于点R ,连结PR ,当t 为何值时,△APR ∽△PRQ ?【答案】 解:(1)△BPQ 是等边三角形,当t=2时,AP=2×1=2,BQ=2×2=4,所以BP=AB-AP=6-2=4,所以BQ=BP.又因为∠B=600,所以△BPQ 是等边三角形. (2)过Q 作QE ⊥AB,垂足为E,由QB=2y,得QE=2t ·sin600=3t,由AP=t,得PB=6-t,所以S △BPQ=21×BP ×QE=21(6-t)×3t=-23t 2+33t ; (3)因为Q R ∥BA,所以∠QRC=∠A=600,∠RQC=∠B=600,又因为∠C=600, 所以△QRC 是等边三角形,所以QR=RC=QC=6-2t.因为BE=BQ ·cos600=21×2t=t, 所以EP=AB-AP-BE=6-t-t=6-2t,所以EP ∥QR,EP=QR,所以四边形EPRQ 是平行四边形, 所以PR=EQ=3t,又因为∠PEQ=900,所以∠APR=∠PRQ=900.因为△APR ~△PRQ,所以∠QPR=∠A=600,所以tan600=PR QR ,即3326=-tt,所以t=56, 所以当t=56时, △APR ~△PRQ6.在直角梯形OABC中,CB∥OA,∠CO A=90º,CB=3,OA=6,BA=35.分别以OA、OC边所在直线为x轴、y轴建立如图1所示的平面直角坐标系.(1)求点B的坐标;(2)已知D、E分别为线段OC、OB上的点,OD=5,OE=2E B,直线DE交x轴于点F.求直线DE的解析式;(3)点M是(2)中直线DE上的一个动点,在x轴上方的平面内是否存在另一个点N.使以O、D、M、N为顶点的四边形是菱形?若存在,请求出点N的坐标;若不存在,请说明理由.图7-2AD O BC 21MN图7-1AD B MN1 2D 2MO.7.在图15-1至图15-3中,直线MN 与线段AB 相交 于点O ,∠1 = ∠2 = 45°.(1)如图15-1,若AO = OB ,请写出AO 与BD的数量关系和位置关系;(2)将图15-1中的MN 绕点O 顺时针旋转得到图15-2,其中AO = OB . 求证:AC = BD ,AC ⊥ BD ;(3)将图15-2中的OB 拉长为AO 的k 倍得到图15-3,求ACBD的值.【答案】 解:(1)AO = BD ,AO ⊥BD ;(2)证明:如图4,过点B 作BE ∥CA 交DO 于E ,∴∠ACO = ∠BEO .又∵AO = OB ,∠AOC = ∠BOE , ∴△AOC ≌ △BOE .∴AC = BE . 又∵∠1 = 45°, ∴∠ACO = ∠BEO = 135°. ∴∠DEB = 45°.∵∠2 = 45°,∴BE = BD ,∠EBD = 90°.∴AC = BD . 延长AC 交DB 的延长线于F ,如图4.∵BE ∥AC ,∴∠AFD = 90°.∴AC ⊥BD .(3)如图5,过点B 作BE ∥CA 交DO 于E ,∴∠BEO = ∠ACO .又∵∠BOE = ∠AOC , ∴△BOE ∽ △AOC .∴AOBOAC BE =. 又∵OB = kAO ,由(2)的方法易得 BE = BD .∴k ACBD=. 10.如图,已知过A (2,4)分别作x 轴、y 轴的垂线,垂足分别为M 、N ,若点P 从O 点出发,沿OM 作匀速运动,1分钟可到达M 点,点Q 从M 点出发,沿MA 作匀速运动,1分钟可到达A 点。
经典《相似三角形》练习题-附答案(汇编)
相似三角形(二)一.选择题(共30小题)1.若,则=()A.B.C.D.2.如图,小明作出了边长为1的第1个正△A1B1C1,算出了正△A1B1C1的面积.然后分别取△A1B1C1三边的中点A2、B2、C2,作出了第2个正△A2B2C2,算出了正△A2B2C2的面积.用同样的方法,作出了第3个正△A3B3C3,算出了正△A3B3C3的面积…,由此可得,第10个正△A10B10C10的面积是()A.B.C.D.3.如图,在Rt△ABC中,AB=AC,D、E是斜边BC上两点,且∠DAE=45°,将△ADC绕点A顺时针旋转90°后,得到△AFB,连接EF,下列结论中正确的个数有①∠EAF=45°;②△ABE∽△ACD;③AE平分∠CAF;④BE2+DC2=DE2()A.1个B.2个C.3个D.4个4.如图,在▱ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE,垂足为G,BG=,则△CEF的周长为()A.8 B.9.5 C.10 D.11.55.如图,设M、N分别是直角梯形ABCD两腰AD、CB的中点,DE上AB于点E,将△ADE沿DE翻折,M与N恰好重合,则AE:BE等于()A.2:1 B.1:2 C.3:2 D.2:36.在中华经典美文阅读中,小明同学发现自己的一本书的宽与长之比为黄金比.已知这本书的长为20cm,则它的宽约为()A.12.36cm B.13.6cm C.32.36cm D.7.64cm7.如图,等边△ABC的边长为3,P为BC上一点,且BP=1,D为AC上一点,若∠APD=60°,则CD的长为()A.B.C.D.8.图(1)、图(2)、图(3)分别表示甲、乙、丙三人由A地到B地的路线图.已知:甲的路线为:A⇒C⇒B.乙的路线为:A⇒D⇒E⇒F⇒B,其中E为AB的中点.丙的路线为:A⇒I⇒J⇒K⇒B,其中J在AB上,且AJ>JB.若符号⇒表示「直线前进」,则根据图(1)、图(2)、图(3)的数据,判断三人行进路线长度的大小关系为何()A.甲=乙=丙B.甲<乙<丙C.乙<丙<甲D.丙<乙<甲9.下列命题中不成立的是()A.矩形的对角线相等B.一组对边平行,另一组对边相等的四边形一定是平行四边形C.两个相似三角形面积的比等于其相似比的平方D.三边对应相等的两个三角形全等10.如图,平行四边形ABCD中,F是BC延长线上一点,AF交BD于O,与DC交于点E,则图中相似三角形共有()对(全等除外).A.3 B.4 C.5 D.611.如图,已知AB∥CD∥EF,那么下列结论正确的是()A.B.C.D.12.如图,△ABC中,A,B两个顶点在x轴的上方,点C的坐标是(﹣1,0).以点C为位似中心,在x轴的下方作△ABC的位似图形,并把△ABC的边长放大到原来的2倍,记所得的像是△A′B′C.设点B的对应点B′的横坐标是a,则点B的横坐标是()A.B.C.D.13.如图,在平行四边形ABCD中,E是AB的中点,CE和BD交于点O,设△OCD的面积为m,△OEB的面积为,则下列结论中正确的是()A.m=5 B.m=4C.m=3D.m=1014.若△ABC∽△DEF,△ABC与△DEF的相似比为1:2,则△ABC与△DEF的周长比为()A.1:4 B.1:2 C.2:1 D.1:15.如图,丁轩同学在晚上由路灯AC走向路灯BD,当他走到点P时,发现身后他影子的顶部刚好接触到路灯AC的底部,当他向前再步行20m到达Q点时,发现身前他影子的顶部刚好接触到路灯BD的底部,已知丁轩同学的身高是1.5m,两个路灯的高度都是9m,则两路灯之间的距离是()A.24m B.25m C.28m D.30m16.在△ABC中,BC=10,B1、C1分别是图①中AB、AC的中点,在图②中,B1,B2,C1,C2分别是AB,AC的三等分点,在图③中B1,B2…B9;C1,C2…C9分别是AB、AC的10等分点,B1C1+B2C2+…+B9C9的值是()A.30 B.45 C.55 D.6017.如图,点A,B分别在射线OM,ON上,C,D分别是线段OA和OB上的点,以OC,OD为邻边作平行四边形OCED,下面给出三种作法的条件:①取OC=OA,OD=OB;②取OC=OA,OD=OB;③取OC=OA,OD=OB.能使点E落在阴影区域内的作法有()A.①B.①②C.①②③D.②③18.如图所示,给出下列条件:①∠B=∠ACD;②∠ADC=∠ACB;③;④AC2=AD•AB.其中单独能够判定△ABC∽△ACD的个数为()A.1 B.2 C.3 D.419.如图,□ABCD中,E为AD的中点.已知△DEF的面积为S,则△DCF的面积为()A.S B.2S C.3S D.4S20.如图,在Rt△ABC内有边长分别为a,b,c的三个正方形,则a,b,c满足的关系式是()A.b=a+c B.b=ac C.b2=a2+c2D.b=2a=2c21.如图,已知D、E分别是△ABC的AB,AC边上的点,DE∥BC,且S△ADE:S四边形DBCE=1:8,那么AE:AC等于()A.1:9 B.1:3 C.1:8 D.1:222.以OA为斜边作等腰直角三角形OAB,再以OB为斜边在△OAB外侧作等腰直角三角形OBC,如此继续,得到8个等腰直角三角形(如图),则图中△OAB与△OHI的面积比值是()A.32 B.64 C.128 D.25623.已知△ABC∽△DEF,相似比为3:1,且△ABC的周长为18,则△DEF的周长为()A.2 B.3 C.6 D.5424.如图,△ABC是等边三角形,被一平行于BC的矩形所截,AB被截成三等分,则图中阴影部分的面积是△ABC的面积的()A.B.C.D.25.小刚身高1.7m,测得他站立在阳光下的影子长为0.85m,紧接着他把手臂竖直举起,测得影子长为1.1m,那么小刚举起的手臂超出头顶()A.0.5m B.0.55m C.0.6m D.2.2m26.如图,直角梯形ABCD中,∠BCD=90°,AD∥BC,BC=CD,E为梯形内一点,且∠BEC=90°,将△BEC绕C点旋转90°使BC与DC重合,得到△DCF,连EF交CD于M.已知BC=5,CF=3,则DM:MC的值为()A.5:3 B.3:5 C.4:3 D.3:427.平面直角坐标中,已知点O(0,0),A(0,2),B(1,0),点P是反比例函数y=﹣图象上的一个动点,过点P作PQ⊥x轴,垂足为Q.若以点O、P、Q为顶点的三角形与△OAB相似,则相应的点P共有()A.1个B.2个C.3个D.4个28.在平面坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2),延长CB交x轴于点A1,作正方形A1B1C1C,延长C1B1交x轴于点A2,作正方形A2B2C2C1,…按这样的规律进行下去,第2012个正方形的面积为()A.B.C.D.29.如图,△ABD中,EF∥BD交AB于点E、交AD于点F,AC交EF于点G、交BD于点C,S△AEG=S四边形EBCG,则的值为()A.B.C.D.30.如图,每个小正方形边长均为1,则下列图中的三角形(阴影部分)与左图中△ABC相似的是()A.B.C.D.2013年6月xy861的初中数学组卷参考答案与试题解析一.选择题(共30小题)1.(2010•漳州)若,则=().解:∵2.(2010•铜仁地区)如图,小明作出了边长为1的第1个正△A1B1C1,算出了正△A1B1C1的面积.然后分别取△A1B1C1三边的中点A2、B2、C2,作出了第2个正△A2B2C2,算出了正△A2B2C2的面积.用同样的方法,作出了第3个正△A3B3C3,算出了正△A3B3C3的面积…,由此可得,第10个正△A10B10C10的面积是().的面积是()的面积是则面积的比是的面积是×;的面积的比也是,面积是()的面积的比是个三角形的面积是(的面积是3.(2010•江津区)如图,在Rt△ABC中,AB=AC,D、E是斜边BC上两点,且∠DAE=45°,将△ADC绕点A顺时针旋转90°后,得到△AFB,连接EF,下列结论中正确的个数有①∠EAF=45°;②△ABE∽△ACD;③AE平分∠CAF;④BE2+DC2=DE2()4.(2010•衡阳)如图,在▱ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE,垂足为G,BG=,则△CEF的周长为(),可得BG=5.(2010•鞍山)如图,设M、N分别是直角梯形ABCD两腰AD、CB的中点,DE上AB于点E,将△ADE 沿DE翻折,M与N恰好重合,则AE:BE等于()MF=6.(2009•浙江)在中华经典美文阅读中,小明同学发现自己的一本书的宽与长之比为黄金比.已知这本书金分割,他们的比值(7.(2009•烟台)如图,等边△ABC的边长为3,P为BC上一点,且BP=1,D为AC上一点,若∠APD=60°,则CD的长为().=,即=,CD=9.(2009•台湾)图(1)、图(2)、图(3)分别表示甲、乙、丙三人由A地到B地的路线图.已知:甲的路线为:A⇒C⇒B.乙的路线为:A⇒D⇒E⇒F⇒B,其中E为AB的中点.丙的路线为:A⇒I⇒J⇒K⇒B,其中J在AB上,且AJ>JB.若符号⇒表示「直线前进」,则根据图(1)、图(2)、图(3)的数据,判断三人行进路线长度的大小关系为何()AB AC图三与图一中,三个三角形相似,所以,==,∴==10.(2009•沈阳)如图,平行四边形ABCD中,F是BC延长线上一点,AF交BD于O,与DC交于点E,则图中相似三角形共有()对(全等除外).11.(2009•上海)如图,已知AB∥CD∥EF,那么下列结论正确的是().12.(2009•衢州)如图,△ABC中,A,B两个顶点在x轴的上方,点C的坐标是(﹣1,0).以点C为位似中心,在x轴的下方作△ABC的位似图形,并把△ABC的边长放大到原来的2倍,记所得的像是△A′B′C.设点B的对应点B′的横坐标是a,则点B 的横坐标是().(点的横坐标是﹣(1=DC=DO=13.(2009•庆阳)如图,在平行四边形ABCD中,E是AB的中点,CE和BD交于点O,设△OCD的面积为m,△OEB的面积为,则下列结论中正确的是()14.(2009•綦江县)若△ABC∽△DEF,△ABC与△DEF的相似比为1:2,则△ABC与△DEF的周长比为15.(2009•兰州)如图,丁轩同学在晚上由路灯AC走向路灯BD,当他走到点P时,发现身后他影子的顶部刚好接触到路灯AC的底部,当他向前再步行20m到达Q点时,发现身前他影子的顶部刚好接触到路灯BD的底部,已知丁轩同学的身高是1.5m,两个路灯的高度都是9m,则两路灯之间的距离是()解:由两三角形相似可知,=16.(2009•江津区)在△ABC中,BC=10,B1、C1分别是图①中AB、AC的中点,在图②中,B1,B2,C1,C2分别是AB,AC的三等分点,在图③中B1,B2…B9;C1,C2…C9分别是AB、AC的10等分点,B1C1+B2C2+…+B9C9的值是()BC BC×=4517.(2009•贺州)如图,点A,B分别在射线OM,ON上,C,D分别是线段OA和OB上的点,以OC,OD为邻边作平行四边形OCED,下面给出三种作法的条件:①取OC=OA,OD=OB;②取OC=OA,OD=OB;③取OC=OA,OD=OB.能使点E落在阴影区域内的作法有()OC=OB,,=,OC=AC=CE=b CE=OD=bOC=OB,OD==,OC=b相矛盾,错误.同理18.(2009•滨州)如图所示,给出下列条件:①∠B=∠ACD;②∠ADC=∠ACB;③;④AC2=AD•AB.其中单独能够判定△ABC∽△ACD的个数为()19.(2008•永春县)如图,□ABCD中,E为AD的中点.已知△DEF的面积为S,则△DCF的面积为()AD=20.(2008•烟台)如图,在Rt△ABC内有边长分别为a,b,c的三个正方形,则a,b,c满足的关系式是()==21.(2008•湘潭)如图,已知D、E分别是△ABC的AB,AC边上的点,DE∥BC,且S△ADE:S四边形DBCE=1:8,那么AE:AC等于()22.(2008•温州)以OA为斜边作等腰直角三角形OAB,再以OB为斜边在△OAB外侧作等腰直角三角形OBC,如此继续,得到8个等腰直角三角形(如图),则图中△OAB与△OHI的面积比值是()24.(2008•茂名)如图,△ABC是等边三角形,被一平行于BC的矩形所截,AB被截成三等分,则图中阴影部分的面积是△ABC的面积的().,S S=25.(2008•南京)小刚身高1.7m,测得他站立在阳光下的影子长为0.85m,紧接着他把手臂竖直举起,测得根据同一时刻物高与影长成比例,得26.(2008•荆州)如图,直角梯形ABCD中,∠BCD=90°,AD∥BC,BC=CD,E为梯形内一点,且∠BEC=90°,将△BEC绕C点旋转90°使BC与DC重合,得到△DCF,连EF交CD于M.已知BC=5,CF=3,则DM:MC的值为()=427.(2011•徐州)平面直角坐标中,已知点O(0,0),A(0,2),B(1,0),点P是反比例函数y=﹣图象上的一个动点,过点P作PQ⊥x轴,垂足为Q.若以点O、P、Q为顶点的三角形与△OAB相似,则相应时,则±为(,﹣)或(﹣,,)或(,﹣)28.(2012•鄂州)在平面坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2),延长CB交x轴于点A1,作正方形A1B1C1C,延长C1B1交x轴于点A2,作正方形A2B2C2C1,…按这样的规律进行下去,第2012个正方形的面积为().),AB=AD=BC=,==B=B=)=,=×===()))(29.(2012•呼伦贝尔)如图,△ABD中,EF∥BD交AB于点E、交AD于点F,AC交EF于点G、交BD于点C,S△AEG=S四边形EBCG,则的值为().=;==.S=(平行线截线段成比例)=(相似三角形面积的比等于相似比的平方)=;==.30.(2008•黄石)如图,每个小正方形边长均为1,则下列图中的三角形(阴影部分)与左图中△ABC相似的是().分别为、。
(完整版)相似三角形经典解答题难题含答案个人精心整理,推荐文档
一、相似三角形中的动点问题1.如图,在Rt △ABC 中,∠ACB=90°,AC=3,BC=4,过点B 作射线BB1∥AC .动点D 从点A 出发沿射线AC 方向以每秒5个单位的速度运动,同时动点E 从点C 沿射线AC 方向以每秒3个单位的速度运动.过点D 作DH ⊥AB 于H,过点E作EF⊥AC交射线BB1于F,G 是EF 中点,连接DG .设点D 运动的时间为t 秒.(1)当t 为何值时,AD=AB ,并求出此时DE 的长度;(2)当△DEG 与△ACB 相似时,求t 的值.2.如图,在△ABC 中,ABC =90°,AB=6m ,BC=8m ,动点P 以2m/s 的速度从A 点出发,沿AC 向点C 移动.同时,动点Q 以1m/s 的速度从C 点出发,沿CB 向点B 移动.当其中有一点到达终点时,它们都停止移动.设移动的时间为t 秒.(1)①当t=2.5s 时,求△CPQ 的面积;②求△CPQ 的面积S (平方米)关于时间t (秒)的函数解析式;(2)在P ,Q 移动的过程中,当△CPQ 为等腰三角形时,求出t 的值.3.如图1,在Rt △ABC 中,ACB =90°,AC =6,BC =8,点D 在边AB 上运动,DE 平分CDB 交边BC 于点E ,EM ⊥BD ,垂足为M ,EN ⊥CD ,垂足为N .(1)当AD =CD 时,求证:DE ∥AC ;(2)探究:AD 为何值时,△BME 与△CNE 相似?4.如图所示,在△ABC 中,BA =BC =20cm ,AC =30cm ,点P 从A 点出发,沿着AB 以每秒4cm 的速度向B 点运动;同时点Q 从C 点出发,沿CA 以每秒3cm 的速度向A 点运动,当P 点到达B 点时,Q 点随之停止运动.设运动的时间为x .(1)当x 为何值时,PQ ∥BC ?(2)△APQ 与△CQB 能否相似?若能,求出AP 的长;若不能说明理由.5.如图,在矩形ABCD 中,AB=12cm ,BC=6cm ,点P 沿AB 边从A 开始向点B 以2cm/s 的速度移动;点Q 沿DA 边从点D 开始向点A 以1cm/s 的速度移动.如果P 、Q 同时出发,用t (s )表示移动的时间(0<t <6)。
经典相似三角形练习题(附答案)
相似三角形一.解答题(共30小题)1.如图,在AABC 中,DE〃BC. EF〃AB,求证:AADE^AEFC.2.如图,梯形ABCD中,AB〃CD,点F在BC上,连DF与AB的延长线交于点G.(1)求证:ACDF^ABGF;(2)当点F是BC的中点时,过F作EF〃CD交AD于点E,若AB二6cm, EF二4cm,求CD的长.3.如图,点D, E在BC上,且FD〃AB, FE〃AC・求证:△ABC S AFDE.4.如图,已知E是矩形ABCD的边CD上一点,BF丄AE于F,试说明:AABF^AEAD.5.已知:如图①所示,在AABC 和Z\ADE 中,AB二AC, AD二AE, ZBAC=ZDAE,且点B,A, D在一条直线上,连接BE, CD, M, N分别为BE, CD的中点(1)求证:①BE二CD:②ZkAMN是等腰三角形:(2)任图①的基础上,将AADE绕点A按顺时针方向旋转180° ,英他条件不变,得到图②所示的图形.请直接写出(1)中的两个结论是否仍然成立:(3)在(2)的条件下,请你在图②中延长ED交线段BC于点P.求证:APBD^AAMN.c田①D图②6.如图,E是口ABCD的边BA延长线上一点,连接EC,交AD于点F・在不添加辅助线的情况下,请你写出图中所有的相似三角形,并任选一对相似三角形给予证明.7.如图,在4X3的正方形方格中,ZkABC和Z\DEF 的顶点都在边长为1的小正方形的顶点上.(1)填空:ZABC二 __ ° , BC二 _ —(2)判断AABC与ADEC是否相似,并证明你的结论.8.如图,已知矩形ABCD的边长AB=3cm, BC=6cm.某一时刻,动点H从A点出发沿AB方向以lcm/s的速度向B点匀速运动;同时,动点N从D点出发沿DA方向以2cm/s的速度向A点匀速运动,问:⑴经过多少时间,/的而积等于矩形ABCD而积的寺的值;若不存在•请说明理由.(2)是否存在时刻t,使以A, M, N为顶点的三角形与AACD相似?若存在,求t9.如图,在梯形ABCD中,若AB〃DC, AD二BC,对角线BD、AC把梯形分成了四个小三角形.(1)列岀从这四个小三角形中任选两个三角形的所有可能情况,并求出选取到的两个三角形是相似三角形的概率是多少;(注意:全等看成相似的特例)(2)请你任选一组相似三角形,并给出证明.-4 B 10.如图ZUBC 中,D 为AC 上一点,CD二2DA, ZBAC=45° , ZBDC=60° , CE丄BD 于E,连接AE・(1)写出图中所有相等的线段,并加以证明;(2)图中有无相似三角形?若有,请写出一对:若没有,请说明理由;(3)求ZkBEC与ZkBEA的面积之比.11.如图,t^AABC中,AB=AC=a, H为底边BC上的任意一点,过点M分别作AB、ACA 的平行线交AC于P,交AB于Q.(1)求四边形AQMP的周长;(2)写出图中的两对相似三角形(不需证明);(3)M位于BC的什么位豊时,四边形AQMP为菱形并证明你的结论.12.已知:P是正方形ABCD的边BC上的点,且BP二3PC, M是CD的中点,试说明:AADM^AMCP.13・如图,已知梯形ABCD 中,AD〃BC, AD二2, AB二BC二8, CD二10・(1)求梯形ABCD的而积S;(2)动点P从点B出发,以lcm/s的速度,沿B=>A=>D=>C方向,向点C运动:动点Q从点C出发,以lcm/s的速度,沿C=D=A方向,向点A运动,过点Q作QE丄BC 于点E.若P、Q两点同时出发,当英中一点到达目的地时整个运动随之结束,设运动时间为t秒•问:①当点P在B=>A上运动时,是否存在这样的使得直线PQ将梯形ABCD的周长平分?若存在,请求出t的值;若不存在,请说明理由:②在运动过程中,是否存在这样的t,使得以P、A、D为顶点的三角形与ACQE相似?若存在,请求岀所有符合条件的t的值;若不存在,请说明理由:③在运动过程中,是否存在这样的t,使得以P、D、Q为顶点的三角形恰好是以DQ 为一腰的等腰三角形?若存在,请求出所有符合条件的t的值;若不存在,请说明理由.14・已知矩形ABCD,长BC 二12cm,宽AB=8cm> P 、Q 分别是AB 、BC 上运动的两点・若 P 自点A 岀发,以lcm/s 的速度沿AB 方向运动,同时,Q 自点B 岀发以2cm/s 的速度 沿BC 方向运动,问经过几秒,以P 、B 、Q 为顶点的三角形与ABDC 相似?15.如图,在△ABC 中,AB 二10cm, BC 二20cm,点P 从点A 开始沿AB 边向B 点以2cm/s 的速度移动,点Q 从点B 开始沿BC 边向点C 以4cm/s 的速度移动,如果P 、Q 分別从 A. B 同时出发,问经过几秒钟,r 16.如图,ZACB 二ZADC 二90° , AC=V&, AD 二2•问当AB 的长为多少时,这两个直角 三角形相似.17.已知,如图.在边长为a 的正方形ABCD 中,M 是AD 的中点,能否在边AB 上找 一点N (不含A. B ),使得ZkCDM 与ZkMAN 相似? 若能,请给出证明,若不能,请说明理由.18.如图在2XABC 中,ZC 二90。
相似试题及答案
相似试题及答案1. 题目:请解释什么是相似三角形,并给出它们的判定条件。
答案:相似三角形是指两个三角形的对应角相等,对应边成比例的三角形。
判定条件包括:- AA准则:两个三角形的两组对应角相等,则这两个三角形相似。
- SAS准则:两个三角形的两组对应边成比例且夹角相等,则这两个三角形相似。
- SSS准则:两个三角形的三组对应边成比例,则这两个三角形相似。
2. 题目:在相似三角形中,如果一个三角形的边长是另一个三角形边长的两倍,那么它们的面积比是多少?答案:如果一个三角形的边长是另一个三角形边长的两倍,那么它们的面积比是4:1。
3. 题目:给定两个相似三角形ABC和DEF,其中AB/DE = 3/2,求AC/DF的比例。
答案:由于三角形ABC和DEF是相似的,所以它们的对应边成比例。
因此,AC/DF = AB/DE = 3/2。
4. 题目:在相似三角形中,如果一个三角形的面积是另一个三角形面积的9倍,那么它们的边长比是多少?答案:如果一个三角形的面积是另一个三角形面积的9倍,那么它们的边长比是3:1。
5. 题目:解释相似三角形的性质,并给出一个例子。
答案:相似三角形的性质包括:- 对应角相等。
- 对应边成比例。
- 对应高的比等于相似比。
- 对应中线、角平分线、垂直平分线的比等于相似比。
- 周长的比等于相似比。
- 面积的比等于相似比的平方。
例子:如果三角形ABC与三角形DEF相似,且AB/DE = 2/3,则AC/DF = 2/3,BC/EF = 2/3,且三角形ABC的面积是三角形DEF面积的4/9。
6. 题目:在相似三角形中,如果一个三角形的周长是另一个三角形周长的3倍,那么它们的相似比是多少?答案:如果一个三角形的周长是另一个三角形周长的3倍,那么它们的相似比是3:1。
7. 题目:在相似三角形中,如果一个三角形的边长是另一个三角形边长的1/2,那么它们的面积比是多少?答案:如果一个三角形的边长是另一个三角形边长的1/2,那么它们的面积比是1/4。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
小学奥数练习卷(知识点:相似三角形)题号一二三总分得分注意事项:1.答题前填写好自己的姓名、班级、考号等信息2.请将答案正确填写在答题卡上第Ⅰ卷(选择题)评卷人得分一.选择题(共3小题)1.在面积为360的正方形ABCD中,E是AD中点,H是FG中点,且DF=CG,那么三角形AGH的面积是()A.70B.72C.75D.902.如图,△ABC中,DE、FC、BC互相平行,AD=DF=FB,则S△ADE:S四边形DEGF:S =()四边形FGCBA.1:2:3B.1:4:9C.2:5:8D.1:3:5 3.如图,四边形FBCE为长方形,四边形ABCD为边长为1的正方形.若AX长n,则AF长()A.2(1﹣n)B.C.D.E.2n第Ⅰ卷(非选择题)评卷人得分二.填空题(共32小题)4.如图,正方形ABCD的边长为4,正方形CEFG的边长为12,D、C、E三点在一条直线上,联结DF,作GI∥DF与DA的延长线交于点I.作IH⊥DF与DF 交于点H.则IH的长度为.5.如图,在长方形ABCD中,AB=30,阴影部分面积是120,那么,CF=.6.如图,在三角形ABC中,AF=2BF,CE=3AE,CD=4BD.连接CF交DE于P点,求的值.7.如图,在直角三角形ABC中,点F在AB上且AF=2FB,四边形EBCD是平行四边形,那么FD:EF为.8.如图,在直角形△ABC中,角C=90°,AC=2,BC=1,D在AC上.将△ADB沿直线BD翻折后,点A落在点E处.如果AD⊥ED,则△ABE的面积为.9.如图,ABCD是长边为6的正方形,ADGH是一个梯形,点E、F分别是AD、GH的中点,HF=6,EF=4,EF⊥GH.联结HE并延长交CD于点I,作IJ⊥HA,则IJ=.10.如图,在圆O中,AB为直径,C为圆内一点.作AD平行BC与CO的延长线交于D点.延长OD至E点,使得DE=2CO.联结AE、BE、BD,延长BD交AE于点F,则AF:FE=.11.如图,A是长方形宽的中点,B位于长方形长边的三分之一处,长方形的面积是阴影部分面积的倍.12.如图,P、Q分别是正方形ABCD的边AD和对角线AC上的点,且AP:PD=1:3,AQ:QC=4:1,如果正方形ABCD的面积为100,那么三角形PBQ的面积是.13.如图,正方形与阴影长方形的边分别平行,正方形边长为10,阴影长方形的面积为6,那么图中四边形ABCD的面积是.14.如图,长方形ABCD的长BC=15cm.宽AB=6cm.在AD上有一点E,使得DE=2AE.长方形ABCD的对角线交点为O.连接BE并延长交CD的延长线于点F,连接OF与AD相交于点G.则阴影部分的面积为cm2.15.如图,ABCD是直角梯形,AB=4,AD=5,DE=3,那么梯形ABCD的面积是.16.如图,两个等腰直角三角形重叠在一起,阴影部分为重合部分,阴影部分的面积是平方厘米.17.如图所示,四边形ABCD与四边形CPMN都是平行四边形,若三角形DFP与三角形AEF的面积分别是22和36,则三角形BNE的面积为.18.三个正方形如图放置,中心都重合,它们的边长依次是1cm、3cm、5cm,图中阴影部分的面积是cm2.19.如图1,等腰直角三角形DEF的斜边在等腰直角三角形ABC的斜边上,连结AE、AD、AF,于是整个图形被分成五块小三角形,图2中已标出其中三块的面积,那么△ABC的面积是.20.在梯形ABCD中,上底长4厘米,下底长8厘米,S△COD=9平方厘米,梯形ABCD面积是.21.如图中,三角形ABC面积为48平方厘米,AD=2.5DB,CF=FD,阴影部分的面积总和比空白部分的面积总和少平方厘米.22.正方形ABCD与等腰直角三角形BEF叠放在一起(如图),M、N点为正方形的边的中点.阴影部分的面积是14cm2,三角形BEF的面积是cm2.23.如图,有两条线段BG和EF把一个边长15分米的正方形分成两个高相等(AF=FD)的直角梯形与一个直角三角形,已知两个梯形面积的差是18平方分米,图中线段CG的长是分米.24.图中AC:CD=5:1,S△ADE:S△ABC=4:5,那么AE:EB=.25.如图,长方形ABCD的面积是40平方厘米,E、F、G、H分别为AC、AH、DH、BC的中点.三角形EFG的面积是平方厘米.26.将一个三角形的三条边同时扩大相同的倍数,如图,得到的新三角形的面积变为原三角形面积的9倍,则新三角形的周长是原三角形的周长的倍.27.如图,将一个三角形(有阴影)的两条边分别延长2倍,得到一个大三角形,这个大三角形的面积是原三角形面积的倍.28.如图,在平行四边形ABCD中,AB=16,AD=10,BE=4,则FC=.29.图中,四边形FMCG和FDHG都是梯形.D为BC的中点,BE=BA,MF=MA,△ABC的面积为1.那么梯形FDHG的面积是.30.在如图中,AE:EC=1:2,CD:DB=1:4,BF:FA=1:3,△ABC的面积S=1,那么四边形AFHG的面积为.31.如图所示,E是矩形ABCD的边BC的中点,BD与AE的交点为F,那么三角形FAB的面积与矩形ABCD的面积之比为.32.图中,三角形ABC的面积是60cm2,已知AF:FC=2:3,E为BC边的中点,那么阴影部分的面积是cm2.33.如图,梯形ABCD中,BO=3OD,三角形ABO的面积为12平方厘米,则梯形ABCD的面积为平方厘米.34.如图,长方形ABCD的面积为120平方厘米,BE=3AE,BF=2FC,则S△AEG=.35.如图,ABCD是正方形,其面积为50平方厘米,3AE=AB,求△GCD的面积评卷人得分三.解答题(共15小题)36.如图所示,正方形ABCD的边长是20,E、F、G分别是AD、BC、CD的中点,连接AF、AG、FG、BE、EC,这些线段相交于H、N、M、P点,请问:(1)△GCF的面积是多少?(2)△CPF的面积是多少?(3)五边形HFPMN的面积是多少?37.将一张长方形纸片依如图所示之方式折叠,使得纸片的一个顶点落在一条短边的中点上.若阴影部分的两个三角形是完全相同的三角形(三条边相等ao=do;oe=ob;ac=db,三个角相等,面积相等),且未折叠前的长方形纸片短边长度是12 厘米.那么,BF的长度是多少厘米.38.边长分别为8cm和6cm 的两个正方形ABCD与BEFG如图并排放在一起.连接DE交BC于P,则图中阴影部分APEG的面积是多少?39.图中D是△ABC的BC上的一点,且BD:CD=2:1,过D点作DF∥AC交AB 于E,延长DE到F,使FE:ED=2:1,如果△CDF的面积是42平方厘米,则△ABC的面积是平方厘米.40.如图,ABCD是一个长方形,从G、F、E引出的小横线都平行于AB.若AD=12,则AG等于多少?41.如图是由边长分别为5厘米和4厘米的两个正方形拼成,图中阴影部分的面积是多少平方厘米?42.图中正方形的边长为8厘米,CE为20厘米,梯形BCDF的面积是多少平方厘米?43.在一个直角三角形纸片上剪一块正方形,并使正方形的面积尽可能大,正方形的面积是多少?44.长方形ABCD的面积是2011平方厘米.梯形AFGE的顶点F在BC上,D是腰EG的中点.试求梯形AFGE的面积.45.如图,梯形ABCD的上底AD长12厘米,高BD长18厘米,BE=2DE,则下底BC长厘米.46.如图所示,在梯形ABCD中,AB∥CD,对角线AC,BD相交于点O.已知AB=5,CD=3,且梯形ABCD的面积为4,求三角形OAB的面积.47.如图,在梯形ABCD中,三角形AOB的面积是13平方厘米,线段OB的长度是OD的2倍.△BOC的面积是多少平方厘米?48.如图,正方形ABCD的边长为4,是BC边的中点的,F是DC边上的点且DF= DC,AE与BF相交于G点.求△ABG的面积.49.如图,在△ABC中,AB=11cm,AC=9cm.首先,在BC边上,取点H使么∠BHA=90°;然后在BC边上,在H与C之间取点D,使么BAD=60°;这样,∠DAC是∠HAD的2倍.请问,这时BH的长度是CH长度的几倍?50.如图,在长方形ABCD的外侧取点E,将各顶点用直线连接,AD和EB的交点是F.当三角形EAF是18cm2;四边形FBCD是50cm2;三角形EDC是8cm2时,求三角形EFD的面积.请写出答案及思考过程.参考答案与试题解析一.选择题(共3小题)1.在面积为360的正方形ABCD中,E是AD中点,H是FG中点,且DF=CG,那么三角形AGH的面积是()A.70B.72C.75D.90【分析】连结EG,EF,设正方形边长为1份,GC=DF=x份.由风筝模型知,故列出方程:S△EGC :S△ECF=GH:HF=1:1,x×1=(1﹣x)×,即可求得DF的值,连AF,阴影部分的面积可用正方形的面积减去空白部分的小三角形的面积得到.【解答】解:根据分析,连结EG,EF,设正方形边长为1份,GC=DF=x份.由风筝模型知,故列出方程:S△EGC :S△ECF=GH:HF=1:1,x×1=(1﹣x)×,解得:x=.连结AF,∵;;,∴S△AGF =1﹣S△ABG﹣S△GCF﹣S△ADF=,∴=70.故选:A.【点评】本题考查了相似三角形,突破点是:利用风筝模型,列出关系式,再求解,根据各三角形的面积最后求出阴影部分的面积.2.如图,△ABC中,DE、FC、BC互相平行,AD=DF=FB,则S△ADE:S四边形DEGF:S四边形FGCB=()A.1:2:3B.1:4:9C.2:5:8D.1:3:5【分析】因为DE∥FC,AD=DF,所以S△ADE :S△AFG=1:4,S△ADE=S△AFG,S四边形DEGF=S△AFG,FG∥BC,AD=DF=FB,S△AFG:S△ABC=4:9,所以S△ABC=S△AFG,S四边形FGCB=S△AFG,再求比即可.【解答】解:因为DE∥FC,AD=DF,所以S△ADE :S△AFG=1:4,S△ADE=S△AFG,S四边形DEGF=S△AFG,FG∥BC,AD=DF=FB,S△AFG:S△ABC=4:9,所以S△ABC =S△AFG,S四边形FGCB=S△AFG,S△ADE:S四边形DEGF:S四边形FGCB=S△AFG:S△AFG:=S△AFG,=::=1:3:5.故选:D.【点评】本题考查了相似三角形的性质,关键是用S△ADE 表示出S四边形DEGF和S四边形FGCB.3.如图,四边形FBCE为长方形,四边形ABCD为边长为1的正方形.若AX长n,则AF长()A.2(1﹣n)B.C.D.E.2n【分析】分析:要求AF的长,可以根据△AFX与△BCF相似,得到相应的线段的比值,继而得到答案.【解答】解:因为四边形FBCE为长方形,四边形ABCD为边长为1的正方形,所以AX∥BC,所以△AFX∽△FBC,所以,即:,所以FA=.故选:B.【点评】本题主要考查了利用三角形的相似求线段的长度,解题的关键在于如何判定两三角形相似,并找出相应的对应边.二.填空题(共32小题)4.如图,正方形ABCD的边长为4,正方形CEFG的边长为12,D、C、E三点在一条直线上,联结DF,作GI∥DF与DA的延长线交于点I.作IH⊥DF与DF 交于点H.则IH的长度为7.2.【分析】过G作GJ⊥DF,垂足为J.根据勾股定理、相似三角形的判定与性质,求出GJ,证明IH=GJ,即可得出结论.【解答】解:过G作GJ⊥DF,垂足为J.在直角△DEF中,∠E=90°,EF=12,DE=4+12=16,由勾股定理得DF=20,因为∠E=90°,所以∠EDF+∠EFD=90°,因为∠EFG=∠JFG+∠EFD=90°,所以∠EDF=∠JFG,在△DEF和△FJG中,,所以△DEF∽△FJG,所以,所以,所以GJ=7.2,因为GI∥DF,IH⊥DF,GJ⊥DF,所以IH=GJ,所以IH=7.2.故答案为7.2.【点评】本题考查勾股定理、相似三角形的判定与性质,考查学生的计算能力,正确运用勾股定理、相似三角形的判定与性质是关键.5.如图,在长方形ABCD中,AB=30,阴影部分面积是120,那么,CF=8.【分析】按题意,可以利用阴影部分的面积求得BF和CE的乘积,而由BF:FC=AB:CE,从而可以求得FC和AB的乘积,再利用线段之比,求得CF的长.【解答】解:根据分析,阴影部分的面积=×BF×CE=120⇒BF×CE=240,又∵BF:FC=AB:CE∴BF×CE=FC×AB=240,又∵AB=30∴FC=240÷30=8,故答案是:8.【点评】本题考查了剪切和拼接,突破点是:利用阴影部分的面积和线段的比例关系求得CF的长.6.如图,在三角形ABC中,AF=2BF,CE=3AE,CD=4BD.连接CF交DE于P点,求的值.【分析】连接EF,DF,则根据风筝模型,有:S△EFC :S△FDC=EP:PD,只要求出S△EFC 和S△FDC的比即可求出EP:PD,从已知的线段之间的比例关系,可以算出面积之比,可以求得△EFC和△FDC分别与△ABC的面积比,从而最后求得EP:PD的值.【解答】解:根据分析,如图,连接EF,DF,则根据风筝模型,有:S△EFC :S△FDC=EP:PD又∵AF=2BF∴S△AFC :S△BFC=AF:BF=2:1⇒,;同理:CE=3AE⇒S△EFC :S△AEF=EC:AE=3:1⇒=;CD=4BD⇒S△CDF:S△BDF=CD:BD=4:1⇒=故:EP:PD=S△EFC :S△FDC=.故答案是:.【点评】本题考查了相似三角形和风筝模型,突破点是:利用风筝模型列出线段比和面积比的关系式,再求解.7.如图,在直角三角形ABC中,点F在AB上且AF=2FB,四边形EBCD是平行四边形,那么FD:EF为2:1.【分析】因为AF=2FB,所以AF:FB=2:1,因为四边形EBCD是平行四边形,所以BE∥AC,所以△ADF∽△BEF,所以FD:EF=AF:FB=2:1,据此解答即可.【解答】解:因为AF=2FB,所以AF:FB=2:1,因为四边形EBCD是平行四边形,所以BE∥AC,则∠ADF=∠BEF,∠EFB=∠DFA,所以△ADF∽△BEF,所以FD:EF=AF:FB=2:1,故答案为:2:1.【点评】本题考查了相似三角形的性质,关键是根据BE∥AC,得出△ADF∽△BEF.8.如图,在直角形△ABC中,角C=90°,AC=2,BC=1,D在AC上.将△ADB沿直线BD翻折后,点A落在点E处.如果AD⊥ED,则△ABE的面积为.【分析】先根据勾股定理计算出AB=,根据折叠的性质得BE=BA=,DA=DE,由于AD⊥ED得BC∥DE,可得△BCD是等腰直角三角形,CD=1,AD=1,继而求得△ABE的面积.【解答】解:由勾股定理得:AB=,∵△ADB沿直线BD翻折后,点A落在点E处,∴△ABD≌△BDE,∴BE=BA=,∠BDA=∠BDE=135°,又∵AD⊥ED,∴BC∥DE,所以△BCD是等腰直角三角形∴BC=CD=1,所以S=,△BDE同理可得:,所以△ABE的面积是.故答案为:.【点评】本题考查了折叠问题:折叠前后两图形全等,即对应线段相等;对应角相等性质的综合应用.9.如图,ABCD是长边为6的正方形,ADGH是一个梯形,点E、F分别是AD、GH的中点,HF=6,EF=4,EF⊥GH.联结HE并延长交CD于点I,作IJ⊥HA,则IJ= 3.6.【分析】如下图所示作辅助线,过点E作EN⊥HJ于点N,延长BA,交EH于点O,交HG于点M,则AM⊥HF,AM⊥AD,因此AM=EF=4;由点E、F分别是AD、GH的中点,可知AE=HM=3,又HM∥AE,所以四边形AEMH是平行四边形,则OA=AM=×4=2,由△OAE≌△IDE,可得DI=AO=2;在RT△AMH 中,由勾股定理可得AH=5;同理可得HE=2,EI=,于是可以求得HI=HE+EI=3;由S△HAE=AE•EF=AH×EN,可以求得EN的长;由∠ENJ=∠J=90°,∠NHE=∠JHI,可得△HNE∽△HJI,由相似三角形的对应边成比例即可求得IJ的长.【解答】解:如图作辅助线,由分析可知,AM⊥HF,AM⊥AD,则AM=EF=4;因为点E、F分别是AD、GH的中点,所以AE=HM=3,又HM∥AE,所以四边形AEMH是平行四边形,所以OA=AM=×4=2.因为AE=DE,∠AEO=∠DEI,∠OAE=∠IDE=90°,所以△OAE≌△IDE,所以DI=AO=2;在RT△AMH中,由勾股定理可得AH==5,同理可得:HE=2,EI=,所以HI=HE+EI=3;=AE•EF=AH×EN可得:×3×4=×5×EN,由S△HAE解之得,EN=2.4;因为∠ENJ=∠J=90°,∠NHE=∠JHI,所以△HNE∽△HJI,所以=,所以=,解得IJ=3.6.故答案为:3.6.【点评】本题较难,辅助线很关键;用到平行四边形的判定以及性质,三角形的全等及相似,勾股定理等知识.10.如图,在圆O中,AB为直径,C为圆内一点.作AD平行BC与CO的延长线交于D点.延长OD至E点,使得DE=2CO.联结AE、BE、BD,延长BD交AE于点F,则AF:FE=1.【分析】如图,连接AC.根据比例模型可知AC∥DF,可得==1,由此即可解决问题.【解答】解:如图,连接AC.∵AD∥BC,OA=OB,∴==1,∴CO=OD,∵OA=OB,OC=OD,∴AC∥BF,∴=,∵DE=2OC=CD,∴=1,∴AF:EF=1,故答案为1.【点评】本题考查比例模型,圆的有关知识,解题的关键是灵活运用比例模型的知识解决问题.11.如图,A是长方形宽的中点,B位于长方形长边的三分之一处,长方形的面积是阴影部分面积的3倍.【分析】分析:如下图,设长方形CDFE边长为3x,宽为2y,则BD=2x,CD=2y,则可计算矩形CDFE的面积、三角形CBF的面积、三角形CBA的面积,根据三角形CBF的面积、三角形CBA的面积即可计算阴影部分的面积,根据计算得数值比较可以计算长方形的面积是阴影部分面积的几倍.【解答】解:设FD=3x,CD=2y,∴FB=x,CA=y,则矩形ABCD的面积=6xy,△FBC的面积是,△CBA的面积是,阴影部分的面积为xy+xy=2xy,所以长方形的面积是阴影部分面积的3倍,故答案为:3.【点评】本题考查了当高一定的时候,三角形的面积与底成正比例这一性质的灵活应用.12.如图,P、Q分别是正方形ABCD的边AD和对角线AC上的点,且AP:PD=1:3,AQ:QC=4:1,如果正方形ABCD的面积为100,那么三角形PBQ的面积是37.5.【分析】连接DQ,作△DQP的高QE.分别求出△ABP、△BCQ、△DCQ、△DPQ 的面积,然后用正方形的面积减去它们的和即可.【解答】解:连接DQ,作△DQP的高QE.正方形ABCD 的面积为100,所以它的边长是10.因为AP :PD=1:3,所以AP=2.5;DP=7.5.S △ABP =10×2.5÷2=12.5.AQ :QC=4:1,所以S △CQB =S △ABC =S 正方形ABCD =×100=10.同理,S △DCQ =10.EQ ⊥AD ,所以EQ :DC=AQ :AC=4:5,EQ=×10=8,S △OQD =7.5×8÷2=30.S △PBQ =S 正方形ABCD ﹣S △ABP ﹣S △CQB ﹣S △DCQ ﹣S △OQD =100﹣12.5﹣10﹣10﹣30=37.5.【点评】根据边的比求出四个三角形的面积是关键.求三角形PQD 是面积时,根据平行线分线段成比例原理,求出高EQ 是关键.13.如图,正方形与阴影长方形的边分别平行,正方形边长为10,阴影长方形的面积为6,那么图中四边形ABCD 的面积是 53 .【分析】分析:要求四边形ABCD 的面积在这里可以采用整体思想来求,在大正方形里面共有5个矩形,其中除去阴影部分的面积,四个矩形的面积为10×10﹣6=94,每个三角形的面积分别是所在矩形面积的一半,继而可求得答案.【解答】解:(10×10﹣6)÷2+6=94÷2+6=47+6=53答:四边形ABCD的面积是53.故答案为:53.【点评】本题主要采用了整体思想的运用,在平常的解题中,我们要注意平行四边形的对角线分成的两个三角形面积相等这样一个性质的运用.14.如图,长方形ABCD的长BC=15cm.宽AB=6cm.在AD上有一点E,使得DE=2AE.长方形ABCD的对角线交点为O.连接BE并延长交CD的延长线于点F,连接OF与AD相交于点G.则阴影部分的面积为6cm2.【分析】DE=2AE可知:DE=BC,延长GO交BC与M点;ED∥BC可知:△FED ∽△FBC,FD=FC;△FGD∽△FMC,GD=MC;△AOG≌△COM,AG=MC,再由AG+GD=15厘米进行代换求出AG的长度,进而求出EG的长度,再从O 点做出△EOG的高,这个高的长度是长方形ABCD宽的一半,进而根据三角形的面积公式求出△EOG的面积.【解答】解:如图:延长GD交BC于M点,做△EOG的高ON;DE=2AE,那么AE=AD=15×=5(厘米);DE=AD=BC;因为ED∥BC,所以∠FED=∠FBC;∠FDE=∠FBC,又因为:△FED∽△FBC,所以:ED=BC,FD=FC;同理:因为GD∥MC,△FGD∽△FMC,GD=MC;因为∠DAC=∠ACB,AO=CO,∠AOG=∠MOC,所以△AOG≌△COM,那么:AG=MC;GD=AG,AG+GD=15,AG+AG=15,AG=9(厘米);所以:EG=AG﹣AE=9﹣5=4(厘米);ON=AB=×6=3(厘米);S△EOG=×4×3=6(平方厘米);答:阴影部分的面积是6平方厘米.故答案为:6.【点评】本题根据相似三角形边之间的比例关系以及全等三角形边之间的关系,求出EG的长度,再求出EG边上高的长度,根据三角形的面积公式求解即可.15.如图,ABCD是直角梯形,AB=4,AD=5,DE=3,那么梯形ABCD的面积是40.【分析】如图所示,三角形ADC 和三角形BDC 等底等高,则二者的面积相等,它们都减去公共部分(三角形ODC ),剩余部分的面积仍然相等,即三角形AOD 和三角形BOC 的面积相等,于是即可求出三角形OBC 的面积,进而得出三角形AOB 的面积,因为等高不等底的三角形的面积比就等于对应底的比,也就能求出AO 与OC (BO 与OD )的比,从而即可求出三角形ODC 的面积,问题即可得解.【解答】解:S △AOD =S △BOC =5×3÷2=7.5,S △AOB =4×5÷2﹣7.5=10﹣7.5=2.5;所以AO :OC=BO :OD=2.5:7.5=1:3,所以S △ODC =7.5×3=22.5,所以梯形的面积为:10+7.5+22.5=10+30=40.答:梯形ABCD 的面积是 40.故答案为:40.【点评】解答此题的主要依据是:等底等高的三角形的面积相等,等高不等底的三角形的面积比就等于对应底的比.16.如图,两个等腰直角三角形重叠在一起,阴影部分为重合部分,阴影部分的面积是21.5平方厘米.【分析】利用等腰直角三角形的特点,计算出其面积.阴影部分的面积比较容易算出.【解答】解:因为是两个等腰直角三角形叠放在一起,所以△BGF,△BDH,△CFI都是等腰直角三角形.因为BF=12 厘米;所以BF 边上的高就是6厘米;所以S△BFG=12×6×=36 平方厘米;S△ICF=2×2÷2=2平方厘米;因为BD=BF﹣DF=12﹣7=5厘米;所以DH=5厘米;S△BDH=5×5×=12.5平方厘米;所以阴影部分的面积是36﹣2﹣12.5=21.5 平方厘米.【点评】此题考查了等腰直角三角形的特殊性质,底边上的中线,高线,顶角平分线三线合一以及在面积计算中的综合运用.17.如图所示,四边形ABCD与四边形CPMN都是平行四边形,若三角形DFP与三角形AEF的面积分别是22和36,则三角形BNE的面积为14.【分析】如下图所示,连接AM,由等底等高的三角形的面积相等,有S△DAP =S△DAM,所以S△DAP﹣S△DAF=S△DAM﹣S△DAF,即S△PDF=S△MAF=22,同理可得,S△BNE=S △MAE,所以S△BNE =S△MAE=S△EAF﹣S△MAF=36﹣22=14,据此解决即可.【解答】解:如上图所示:因为S△DAP =S△DAM,所以S△DAP ﹣S△DAF=S△DAM﹣S△DAF,即S△PDF =S△MAF=22.同理可得,S△BNE =S△MAE,所以S△BNE =S△MAE=S△EAF﹣S△MAF=36﹣22=14.答:三角形BNE的面积为14.故答案为:14.【点评】本题解决的关键是能作出辅助线,利用等底等高的三角形的面积相等解决.18.三个正方形如图放置,中心都重合,它们的边长依次是1cm、3cm、5cm,图中阴影部分的面积是17cm2.【分析】求阴影部分的面积就相当于求大正方形的面积减去另外两个正方形的面积差;据此解答.【解答】解:5×5﹣(3×3﹣1×1),=25﹣8,=17(平方厘米);答:图中阴影部分的面积是17cm2.故答案为:17.【点评】本题关键是观察得出:阴影部分的面积=大正方形的面积﹣(中正方形的面积﹣小正方形的面积).19.如图1,等腰直角三角形DEF的斜边在等腰直角三角形ABC的斜边上,连结AE、AD、AF,于是整个图形被分成五块小三角形,图2中已标出其中三块的面积,那么△ABC的面积是36.【分析】根据燕尾定理,求得三角形的面积比与边长比,然后再利用等腰直角三角形的性质,求得中间的小等腰直角三角形与大的等腰直角三角形的面积比,即可求得大的三角形的面积.【解答】解:根据分析,如图(1)延长AD交BC于G.如图(2)根据燕尾定理,得到:S△DEG:S△DFG=2:3=0.4:0.6;如图(3)得:GD:GA=0.4:(2+0.4)=0.4:2.4=1:6,∵ED∥BA,∴EG:GB=1:6,同理FG:GC=1:6,∴,故:S△ABC =36×S△DEF=36×1=36,故答案是:36.【点评】本题考查了相似三角形和燕尾定理,本题突破点是:利用燕尾定理求得三角形的面积比与边长比.20.在梯形ABCD中,上底长4厘米,下底长8厘米,S△COD=9平方厘米,梯形ABCD面积是40.5平方厘米.【分析】三角形AOD相似于BOC,再依据“上底长4厘米,下底长8厘米,S=9△COD 平方厘米”,即可代入公式计算.【解答】解:AD=4,BC=8,因为△AOD∽△BOC,所以OD:OB=1:2,则S△DOC:S△BOC=1:2,因为S△DOC=S△BOA=9平方厘米,所以S△BOC=18平方厘米;S△AOD=S△AOB=9÷2=4.5(平方厘米),SABCD=4.5+9+9+18=40.5(平方厘米);答:梯形的面积是40.5平方厘米.故此题应填40.5平方厘米.【点评】此题主要考查梯形的面积公式及相似三角形的特点,将题目数据代入公式及可以求出.21.如图中,三角形ABC面积为48平方厘米,AD=2.5DB,CF=FD,阴影部分的面积总和比空白部分的面积总和少8平方厘米.【分析】AD=2.5DB,则AD:DB=5:2此题应根据梅涅劳斯定理,得到××=1,得到=,设S△CEF=7X,则S△AEF=5X,S△EDC=12X,S△BED=S△ABE=30X.再由图中三角形ABC的面积是48平方厘米,解决问题.【解答】解:AD=2.5DB,则AD:DB=5:2,根据梅涅劳斯定理,得到××=1,得到=, 设S △BEF =7X ,则S △CEF =5X ,因为CF=DF ,所以S △EDC =7X +5X=12X ,又因为AD :DB=5:2,则三角形ADF 的面积:三角形BDF 的面积=5:2, 所以S △AFD =S △AFC =12X ×5÷2=30X所以可得:5X +7X +12X +30X +30X=4884X=48X=则阴影部分的面积比空白处的面积少:12X +7X +30X ﹣30X ﹣5X=14X=14×=8(平方厘米)答:阴影部分的面积总和比空白部分的面积总和少 8平方厘米.故答案为:8.【点评】掌握梅涅劳斯定理,是解答此题的关键.22.正方形ABCD 与等腰直角三角形BEF 叠放在一起(如图),M 、N 点为正方形的边的中点.阴影部分的面积是14cm 2,三角形BEF 的面积是 18 cm 2.【分析】因为M 、N 是中点,故我们可以将该图形进行分割,所得图形如图形中的三角形面积都相等,阴影部分由7个三角形组成,且其面积为14平方厘米,故一个三角形的面积为2平方厘米,那么三角形BEF 的面积是18平方厘米.【解答】解:如图,作出辅助线后,可知每个小三角形的面积为:14÷7=2,所以大三角形的面积为:14÷7×9=18(平方厘米).故答案为:18.【点评】此题较难,应结合题意,根据图形进行分析,将该图形进行分割后,使所得图形如图形中的三角形面积都相等.23.如图,有两条线段BG和EF把一个边长15分米的正方形分成两个高相等(AF=FD)的直角梯形与一个直角三角形,已知两个梯形面积的差是18平方分米,图中线段CG的长是4分米.【分析】过E点做BC的平行线,交AB于H,交DC于I.已知两个梯形的面积差为15,所以△HBE+△GIE=15,即HB×HE÷2+IG×IE÷2=15,再根据HE=IE=,即可求出CG.【解答】解:如图,过E点做BC的平行线,交AB于H,交DC于I.因为S梯形ABEF﹣S梯形GDEF=15平方分米,所以△HBE+△GIE=15平方分米,所以HB×HE÷2+IG×IE÷2=15因为HE=IE=所以(HB+IG)×=30所以GC×=30所以GC=4答:线段CG的长是4分米.故答案为:4.【点评】此题解答的关键通过作辅助线,运用转化的数学思想,解决问题.24.图中AC:CD=5:1,S△ADE:S△ABC=4:5,那么AE:EB=2:1.【分析】如图,从B点向AC做垂线BF,它是三角形ABC的高,从E向AC做垂线EG,它是三角形ADE的高,根据三角形的面积公式分别表示出三角形ABC 和三角形ADE的面积,再根据这两个三角形的面积比,得出EG与BF的比,然后根据三角形AEG与三角形ABF相似,得出它们的相似比,从而得出AE 与AB的比,进而求出AE与EB的比.【解答】解:如图,做三角形ABC的高BF,以及三角形ADE的高EG;因为AC:CD=5:1所以AD:AC=6:5,AC=AD;S△ADE=EG×ADS△ABC=BF×AC=BF×AD,又S△ADE :S△ABC=4:5,所以:(EG×AD):(BF×AD)=4:5EG:BF=4:55EG=BFEG=BF,所以:EG:BF=2:3,因为:EG⊥AC,BF⊥AC,所以EG∥BE,△AGE∽△AFB,所以AE:AB=EG:BF=2:3那么AE:EB=2:(3﹣2)=2:1.故答案为:2:1.【点评】解答此题的关键是结合题意,利用三角形的面积公式,得出对应高的比,再由相似三角形的性质,得出对应边的比相等.25.如图,长方形ABCD的面积是40平方厘米,E、F、G、H分别为AC、AH、DH、BC的中点.三角形EFG的面积是5平方厘米.【分析】如图:连接BF、CG,因为E、F、G、H分别为AD、AH、DH、BC的中点.这样把长方形ABCD平均分成8份,阴影部分占,根据一个数乘分数的意义,用乘法解答.【解答】解:因为E、F、G、H分别为AD、AH、DH、BC的中点.所以AE=ED,BH=HC,EF=FB,DG=GH,所以三角形EFG的面积占长方形ABCD面积的,40×(平方厘米),答:三角形EFG的面积是5平方厘米.故答案为:5.【点评】求出阴影部分的面积占长方形面积的几分之几是解答关键,根据一个数乘分数的意义,用乘法解答.26.将一个三角形的三条边同时扩大相同的倍数,如图,得到的新三角形的面积变为原三角形面积的9倍,则新三角形的周长是原三角形的周长的3倍.【分析】根据题干分析可得,原三角形与新三角形相似三角形,相似比是1:3.根据相似三角形的性质可得:相似三角形的面积的比等于相似比的平方,相似三角形的周长的比等于相似比.由此即可得出答案.【解答】解:根据题干可得原三角形与新三角形相似,相似比是1:3,由相似三角形的性质可得:周长的比等于相似比,即:原三角形周长:新三角形周长=1:3答:新三角形的周长是原三角形的周长的3倍.故答案为:3.【点评】此题考查了相似三角形的相似比与它们周长的比以及面积的比的性质.27.如图,将一个三角形(有阴影)的两条边分别延长2倍,得到一个大三角形,这个大三角形的面积是原三角形面积的9倍.【分析】因大三角形的两条边分别被三等分,根据:如果三角形的高相等,则高所在边的长度比就等于面积比,可以求得结果.【解答】解:分别连接由b边延长得到的等分点与对应的顶点,则得到三个一b 为底边的三个面积相等的三角形,又因最左边的面积与阴影的面积比是3:1,所以阴影的面积与大三角形的面积比是1:9,则这个大三角形的面积是原三角形面积的9倍.故此题应填:9.【点评】此题主要考查等底等高的三角形面积相等.28.如图,在平行四边形ABCD中,AB=16,AD=10,BE=4,则FC=8.【分析】因为四边形ABCD是平行四边形,所以AB∥CD,所以可得三角形BEF 和三角形CDF相似,则对应线段成比例:BE:CD=BF:FC,据此设FC为x,则BF就是10﹣x,根据线段比例式可得:4:16=(10﹣x):x,据此解比例求出x的值即可.【解答】解:AB∥CD,所以可得三角形BEF和三角形CDF相似,则对应线段成比例:BE:CD=BF:FC,设FC为x,则BF就是10﹣x,根据线段比例式可得:4:16=(10﹣x):x,4x=16(10﹣x),4x=160﹣16x,20x=160,x=8,答:FC=8.故答案为:8.。
