力矩 刚体定轴转动定律
合集下载
§3-2定轴转动定理

i
刚体内力是刚体内各质元间的相互作用力, 可以证明:刚体内各质元间每一对内力的内力 矩之和为零。 讨论 1)力经过转轴,力矩恒为零。 2)合力为零,合力矩不一定为零. 太原理工大学物理系
3)合力矩为零,合力不一定为零
例:将两个半径不同的圆盘 同心地粘在一起,两个圆盘 的半径分别为r1、r2,圆盘 上绕有绳子,如图。 如果
太原理工大学物理系
设外力作用于P点, F 的方向 与轴既不垂直也不平行,将力分解 为垂直于转轴和平行于转轴两个 分量
力对原点o´的力矩
M RF
一、力对转轴的力矩
z
F //
F
F
R
o'
P
力矩在z轴方向的分量
M
z
xF y yF x
x
y
太原理工大学物理系
写成矢量式 M z k r F 平行于转动轴的分力 只能引 起轴的变形, 对转动无贡献。
三、转动惯量 转动惯量 J
m r
i
2
i i
由刚体的各质元相对于固定转轴的分布所 决定的,与刚体的运动及所受外力无关。 对于质量连续分布的刚体
J
m
r
2
dm
其中r为质元dm到转轴的垂直距离。
太原理工大学物理系
对质量线分布的刚体: d m d l
质量线密度
对质量面分布的刚体: d m
太原理工大学物理系
f
/ r
当不计滑轮质量及摩擦阻力矩
即令m=0、Mf=0时,有
T1 T 2
2 m1m 2 m 2 m1
g
a
m 2 m1 m 2 m1
g
阿特伍德机是一种可用来测量重力加速 度g的简单装置。
刚体内力是刚体内各质元间的相互作用力, 可以证明:刚体内各质元间每一对内力的内力 矩之和为零。 讨论 1)力经过转轴,力矩恒为零。 2)合力为零,合力矩不一定为零. 太原理工大学物理系
3)合力矩为零,合力不一定为零
例:将两个半径不同的圆盘 同心地粘在一起,两个圆盘 的半径分别为r1、r2,圆盘 上绕有绳子,如图。 如果
太原理工大学物理系
设外力作用于P点, F 的方向 与轴既不垂直也不平行,将力分解 为垂直于转轴和平行于转轴两个 分量
力对原点o´的力矩
M RF
一、力对转轴的力矩
z
F //
F
F
R
o'
P
力矩在z轴方向的分量
M
z
xF y yF x
x
y
太原理工大学物理系
写成矢量式 M z k r F 平行于转动轴的分力 只能引 起轴的变形, 对转动无贡献。
三、转动惯量 转动惯量 J
m r
i
2
i i
由刚体的各质元相对于固定转轴的分布所 决定的,与刚体的运动及所受外力无关。 对于质量连续分布的刚体
J
m
r
2
dm
其中r为质元dm到转轴的垂直距离。
太原理工大学物理系
对质量线分布的刚体: d m d l
质量线密度
对质量面分布的刚体: d m
太原理工大学物理系
f
/ r
当不计滑轮质量及摩擦阻力矩
即令m=0、Mf=0时,有
T1 T 2
2 m1m 2 m 2 m1
g
a
m 2 m1 m 2 m1
g
阿特伍德机是一种可用来测量重力加速 度g的简单装置。
3.3刚体定轴转动中的功与能

−1 1
解:以 ω 和 ω 分别表示冲孔前后的飞轮的角速度
1 2
ω = (1 − 0 .2 )ω = 0.8ω
2 1
2
2
2πn ω = = 8πrad ⋅ s 60
1 1
−1
1
1 1 1 由转动动能定理 A = Jω − Jω = Jω (0 .8 − 1) 2 2 2 1 又 J = mr A = −5 .45 × 10 J 2
课后习题 3-8
θ1
θ2
二、刚体的转动动能和重力势能
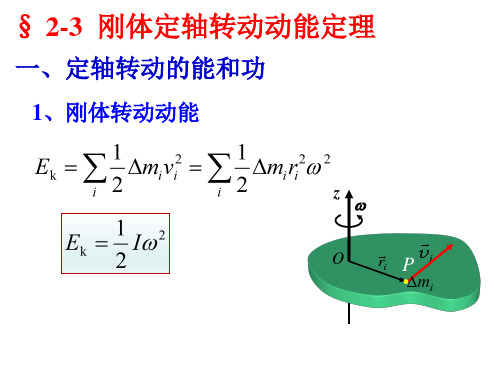
1.绕定轴转动刚体的动能 绕定轴转动刚体的动能 绕定轴转动刚体的
∆ ,∆ ,⋅⋅⋅,∆ ,⋅⋅⋅,∆ m m m m r r r r r, r ,⋅⋅⋅, r ⋅⋅⋅, r r r r r v ,v ,⋅⋅⋅,v ,⋅⋅⋅,v
1 2 i
1 2 i, N
N
Q = rω v 1 E= ∆ v m 2
2 2 2
1 1
2
3
质量M的圆盘滑轮可绕通过盘心的水平轴转 例3-7半径R质量 的圆盘滑轮可绕通过盘心的水平轴转 半径 质量 滑轮上绕有轻绳,绳的一端悬挂质量为m的物体 的物体。 动,滑轮上绕有轻绳,绳的一端悬挂质量为 的物体。 当物体从静止下降距离h时 物体速度是多少? 当物体从静止下降距离 时,物体速度是多少? 以滑轮、 解:以滑轮、物体和地球组成系统为研究对 由于只有保守力做功,故机械能守恒。 象。由于只有保守力做功,故机械能守恒。 设终态时重力势能为零 初态:动能为零,重力势能为mgh 初态:动能为零,重力势能为 末态: 末态:动能包括滑轮转动动能和物体平动动能 由机械能守恒
i i
i i i
2
1
2
i
N
解:以 ω 和 ω 分别表示冲孔前后的飞轮的角速度
1 2
ω = (1 − 0 .2 )ω = 0.8ω
2 1
2
2
2πn ω = = 8πrad ⋅ s 60
1 1
−1
1
1 1 1 由转动动能定理 A = Jω − Jω = Jω (0 .8 − 1) 2 2 2 1 又 J = mr A = −5 .45 × 10 J 2
课后习题 3-8
θ1
θ2
二、刚体的转动动能和重力势能
1.绕定轴转动刚体的动能 绕定轴转动刚体的动能 绕定轴转动刚体的
∆ ,∆ ,⋅⋅⋅,∆ ,⋅⋅⋅,∆ m m m m r r r r r, r ,⋅⋅⋅, r ⋅⋅⋅, r r r r r v ,v ,⋅⋅⋅,v ,⋅⋅⋅,v
1 2 i
1 2 i, N
N
Q = rω v 1 E= ∆ v m 2
2 2 2
1 1
2
3
质量M的圆盘滑轮可绕通过盘心的水平轴转 例3-7半径R质量 的圆盘滑轮可绕通过盘心的水平轴转 半径 质量 滑轮上绕有轻绳,绳的一端悬挂质量为m的物体 的物体。 动,滑轮上绕有轻绳,绳的一端悬挂质量为 的物体。 当物体从静止下降距离h时 物体速度是多少? 当物体从静止下降距离 时,物体速度是多少? 以滑轮、 解:以滑轮、物体和地球组成系统为研究对 由于只有保守力做功,故机械能守恒。 象。由于只有保守力做功,故机械能守恒。 设终态时重力势能为零 初态:动能为零,重力势能为mgh 初态:动能为零,重力势能为 末态: 末态:动能包括滑轮转动动能和物体平动动能 由机械能守恒
i i
i i i
2
1
2
i
N
第三章 刚体的定轴转动

令
m r
i 1
n
2
i i
=J
1 2 Ek Jω 2
转动动能
ω 对应 v
J 对应 m
1 2 Ek mv 2
质点的动能
二 转动惯量 ( moment of inertia ) 质量 质点惯性大小的量度
J 与 m 对应
转动惯量 刚体转动惯性大小的量度
n
J mi ri
i 1
2
体分布
dm =ρdV dm =σdS dm =λdl
面分布 线分布
J r dm
2 m
单位:
kg · 2 m
说明: J r 2dm
m
1. J 与刚体的质量有关; 2. 质量一定,与质量的分布有关;
3. 与轴的位置有关。因此叫作绕轴的
转动惯量。
转动惯量的计算
例1 质量为m,半径为 r 的均匀细圆环, 对通过其中心并垂直环面的转轴的转动惯量。 解: 根据转动惯量的定义求解。
3. 题 3-2,3-8,3-9。
§3-1
刚体的定轴转动
刚体 ( rigid body ) :在任何情况下,其形状和大 小都不发生任何变化的物体 刚体是一种理想模型
一 刚体的运动 刚体的运动
{ 转动
平动
平动 ( translation ) 刚体运动时,其上任意两点的连线 , 在运动过程中始终保持其方向不变 。 刚体的平动遵从质点运动的规律
ω ω0 αt
1 2 θ θ0 ω0t αt 2 2 2 ω ω0 2α(θ θ0 )
切向加速度 ( tangential acceleration )
dv at dt d (rω) dt dω r dt
m r
i 1
n
2
i i
=J
1 2 Ek Jω 2
转动动能
ω 对应 v
J 对应 m
1 2 Ek mv 2
质点的动能
二 转动惯量 ( moment of inertia ) 质量 质点惯性大小的量度
J 与 m 对应
转动惯量 刚体转动惯性大小的量度
n
J mi ri
i 1
2
体分布
dm =ρdV dm =σdS dm =λdl
面分布 线分布
J r dm
2 m
单位:
kg · 2 m
说明: J r 2dm
m
1. J 与刚体的质量有关; 2. 质量一定,与质量的分布有关;
3. 与轴的位置有关。因此叫作绕轴的
转动惯量。
转动惯量的计算
例1 质量为m,半径为 r 的均匀细圆环, 对通过其中心并垂直环面的转轴的转动惯量。 解: 根据转动惯量的定义求解。
3. 题 3-2,3-8,3-9。
§3-1
刚体的定轴转动
刚体 ( rigid body ) :在任何情况下,其形状和大 小都不发生任何变化的物体 刚体是一种理想模型
一 刚体的运动 刚体的运动
{ 转动
平动
平动 ( translation ) 刚体运动时,其上任意两点的连线 , 在运动过程中始终保持其方向不变 。 刚体的平动遵从质点运动的规律
ω ω0 αt
1 2 θ θ0 ω0t αt 2 2 2 ω ω0 2α(θ θ0 )
切向加速度 ( tangential acceleration )
dv at dt d (rω) dt dω r dt
刚体绕定轴转动定律和角动量定理的表达式

刚体绕定轴转动定律和角动量定理的表达式
刚体绕定轴转动定律:
Mz=Jβ,其中Mz表示对于某定轴的合外力矩,J表示刚体绕给定轴的转动惯量,β表示角加速度。
刚体定轴转动定律是指刚体所受的对于某定轴的合外力矩等于刚体对此定轴的转动惯量与刚体在此合外力矩作用下所获得的角加速度的乘积。
角动量定理的表达式:
角动量守恒定律是物理学的普遍定律之一,反映质点和质点系围绕一点或一轴运动的普遍规律;反映不受外力作用或所受诸外力对某定点(或定轴)的合力矩始终等于零的质点和质点系围绕该点(或轴)运动的普遍规律。
角动量守恒定律是对于质点,角动量定理可表述为质点对固定点的角动量对时间的微商,等于作用于该质点上的力对该点的力矩。
角动量L=转动惯量J*角速度ω
所以角动量守恒表达为J1ω1=J2ω2。
刚体定轴转动定律

R
例题8:
普通物理学教案
如图所示,滑轮半径为r 。 (设绳与滑 轮间无相对滑动)①若m2与桌面间的摩擦系 数为μ,求系统的加速度a 及张力 T1 与 T2; ②若桌面光滑,再求。 解:方法1 按隔离法 力和力矩分析、 建坐标
m2 g
m
T
2
2
J
0
1
Tm 2 g m a 2 2
T r T r J 1 2
线分布
面分布
体分布
只有对于几何形状规则、质量连续且均匀分布的 刚体才能用积分计算出刚体的转动惯量。
例题1 :
普通物理学教案
如图套两个质点的细杆长l , 杆绕空端 转动,分析整个系统绕 o 点的转动惯量。将 两质点换位再作计算。
2 解: 由 J mr i i i
l 2 2 3 2 J 2 m ( ) m l m l 1 2 2
J1 J2
例题3 :
普通物理学教案
求质量为m 、半径为R 的均匀圆环的转 动惯量。轴与圆环平面垂直并通过圆心。 解: 取质量元
d m d x
2 J Rd m
O
R
dm
R2 dm
mR2
例题4 :
普通物理学教案
求质量为m 、半径为R 均匀圆盘的转动 惯量。轴与盘平面垂直并通过盘心。 解: 这样的一个圆盘可以视 为半径不等的有宽度的 dr 圆环拼接而成。 r 任取其中一环 d m 2 r d r R 利用前例环的转动惯量结果 2 3 d J rd m 2 rd r R 1 3 rd r R 4 J dJ 2 0 2 m 1 2 J mR 2 R 2
与牛顿定律比较: M J 或
定轴转动动能定理
只有保守力做功时,含刚体的物体机械能守恒。
例 一质量为m ,长为 l 的均质细杆,转轴在O点, 距A端 l/3 。今使棒从静止开始由水平位置绕O点转 动,求:垂直位置时的角速度。
解:设水平位置为重力势能零点
初末机械能相同:
A
C
B
0 0 1 I2 1 mgl
O
2
6
1 1 ml22 1 mgl
29
6
返回 退出
作业:2.16、2.19、2.20
返回 退出
O
(1)水平位置
方向:
返回 退出
(2)解1:转动定律
A
C
B
O
返回 退出
(2)解2:转动动能定理
A
C
B
O
返回 退出
三、定轴转动刚体的机械能守恒
1、刚体的重力势能
以地面为势能零点,刚体和
z
地球系统的重力势能:
i O
刚体的重力势能: 与质量集中于质心处的质点重力势能相同
2、定轴转动刚体的机械能守恒
dt
二、定轴转动的动能定理
刚体定轴转动的动能定理:总外力矩对刚体所做的功 等于刚体转动动能的增量。
讨论
子细 弹绳 击质 入量 沙不 袋计
o
v
角动量相对于转轴
以子弹和沙袋为系统 动量守恒; 角动量守恒; 机械能不守恒 .
子o
弹 击 入 杆
v
角动量相对于转轴
以子弹和杆为系统 动量不守恒; 角动量守恒; 机械能不守恒.
角动量相对于转轴
o'
圆 锥 摆
T
m oR
p v
圆锥摆系统 动量不守恒; 角动量守恒; 机械能守恒.
力矩的功转动动能动能定理
4
第四章 刚体的转动
7
物理学
第五版
五
4-4 力矩的功 刚体绕定轴转动的动能定理
刚体的重力势能
mi yi
Ep
i
mi gyi mg i m
mgyc
六 刚体(质点系)的功能原理
W ex Wnicn (Ek Ep ) (Ek0 Ep0)
第四章 刚体的转动
8
物理学
第五版
4-4 力矩的功 刚体绕定轴转动的动能定理
0
3
第四章 刚体的转动
6
物理学
第五版
4-4 力矩的功 刚体绕定轴转动的动能定理
(2) 由转动定律求 ,(唱片J=mR2/2)
M 4g(作匀加速转动)
由
0
t
J 3R 可求得 t
3R 4g
(3) 由 2 02 2 的时间内,转过的角度为
可得在 0
3 2R
到
t
8g
驱动力矩做的功为 W M 1 mR2 2
1 2
J12
——刚体绕定轴转动的动能定理
比较
W
F
dr
1 2
mv22
1 2
mv12
第四章 刚体的转动
3
物理学
第五版
4-4 力矩的功 刚体绕定轴转动的动能定理
例1 留声机的转盘绕通过盘心垂直盘 面的轴以角速率 ω 作匀速转动.放上唱片 后,唱片将在摩擦力作用下随转盘一起转
动.设唱片的半径为R,质量为m,它与转
第四章 刚体的转动
10
物理学
第五版
4-4 力矩的功 刚体绕定轴转动的动能定理
一 力矩作功
dW F dr Ftds
Ftrd
第四章 刚体的转动
7
物理学
第五版
五
4-4 力矩的功 刚体绕定轴转动的动能定理
刚体的重力势能
mi yi
Ep
i
mi gyi mg i m
mgyc
六 刚体(质点系)的功能原理
W ex Wnicn (Ek Ep ) (Ek0 Ep0)
第四章 刚体的转动
8
物理学
第五版
4-4 力矩的功 刚体绕定轴转动的动能定理
0
3
第四章 刚体的转动
6
物理学
第五版
4-4 力矩的功 刚体绕定轴转动的动能定理
(2) 由转动定律求 ,(唱片J=mR2/2)
M 4g(作匀加速转动)
由
0
t
J 3R 可求得 t
3R 4g
(3) 由 2 02 2 的时间内,转过的角度为
可得在 0
3 2R
到
t
8g
驱动力矩做的功为 W M 1 mR2 2
1 2
J12
——刚体绕定轴转动的动能定理
比较
W
F
dr
1 2
mv22
1 2
mv12
第四章 刚体的转动
3
物理学
第五版
4-4 力矩的功 刚体绕定轴转动的动能定理
例1 留声机的转盘绕通过盘心垂直盘 面的轴以角速率 ω 作匀速转动.放上唱片 后,唱片将在摩擦力作用下随转盘一起转
动.设唱片的半径为R,质量为m,它与转
第四章 刚体的转动
10
物理学
第五版
4-4 力矩的功 刚体绕定轴转动的动能定理
一 力矩作功
dW F dr Ftds
Ftrd
[理学]第5章 刚体的定轴转动_OK
J 2
x 2dm l x2dx 1 ml 2
0
3
o
dx
dm
17 x
图(2)
记住几个典型的转动惯量:
*圆环(通过中心轴)………………… J = mR2
*圆盘、圆柱(通过中心轴)………… J 1 mR2 2
*细棒(端点垂直轴)…………………J A
1 3
m L2
*细棒(质心垂直轴)…………………J c
滑轮的角速度.
解:两重物加速度大小a相同,滑轮角加速度为
隔离物体分析力方向如图
由牛顿第二定律: m1g-T1=m1a T2-m2g=m2a
转动定律: (T1-T2)r=Jb 且有: a=rb
T1 T1 a m1 m1g
r T2
m2 T2 a
m2g
解方程组得:
m1 m2 gr m1 m2 r 2 J
转动平面: 取垂直于转轴 的平面为参考系, 称转动平面。,
转轴
Z 转动方向
vi
Δmi
转动平面
P
o θ
x
op r
2.定轴转动的角量描述
1.角位置θ
6
2.角位移
3.角速度: d 角速度是矢量 。dt
单位:rad/s
Zω 转动方向
v
方向与转动方向成 右手螺旋法则。
P点线速度 v r
P
o θ 转动平面 op r
第五章 刚体的定轴转动
转轴
1
一、力矩
复习
M rF
1. 大小:M = rFsinθ
2.方向:由右手螺旋定则确定。
Z F// F
O r F⊥ p
注意:上式中F指的是与转轴垂直平面(转动平面)上的力,
第二节 刚体定轴转动的动力学方程
刚体定轴转动的动力学方程z
F//
1. 力矩
F
力F 对z 轴的力矩 力F 在垂直于轴的平面内
M z Fd F r sin Fτr
力不在垂直于轴的平面内
dr
θ
F
P Fn
FF
M z Fd Frsin Fτr
若力 F F 也作用在P点上.
则力矩大小相等,效果不同.
力对定轴 力矩的矢量形式 M Z r F
GC F’T2 FT2
求 两物体的线加速度和水平、竖直两段绳索的张力
mB B
解 以mA , mB , m C为研究对象, 受力分析
物体 mA: FT1 mAaA
物体 mB :mB g FT 2 mBaB
滑轮
mC
:FT2R
FT1R
J
1 2
mC R2
aA aB a
FT1 FT1 FT 2 FT2
J dJ R 1(r2 dx) r2 02
R R2 x2 2 dx 2 mR2
2 R
5
x
r
dx x o
R
dJ 1 dm r2 2
转动定律的应用举例
基本方法和步骤
分析力,确 定外力矩
列出转动定律和牛 顿定律方程
列出线量和角量 之间的关系式
求解联 立方程
例 一轻绳绕在半径 r =20 cm 的飞轮边缘,在绳端施以F=98 N
a R
GB
a mBg
mA
mB
1 2
mC
FT1
mA
mAmB g
mB
1 2
mC
FT
2
mA
mA
1 2
mC
mB
mB g
F//
1. 力矩
F
力F 对z 轴的力矩 力F 在垂直于轴的平面内
M z Fd F r sin Fτr
力不在垂直于轴的平面内
dr
θ
F
P Fn
FF
M z Fd Frsin Fτr
若力 F F 也作用在P点上.
则力矩大小相等,效果不同.
力对定轴 力矩的矢量形式 M Z r F
GC F’T2 FT2
求 两物体的线加速度和水平、竖直两段绳索的张力
mB B
解 以mA , mB , m C为研究对象, 受力分析
物体 mA: FT1 mAaA
物体 mB :mB g FT 2 mBaB
滑轮
mC
:FT2R
FT1R
J
1 2
mC R2
aA aB a
FT1 FT1 FT 2 FT2
J dJ R 1(r2 dx) r2 02
R R2 x2 2 dx 2 mR2
2 R
5
x
r
dx x o
R
dJ 1 dm r2 2
转动定律的应用举例
基本方法和步骤
分析力,确 定外力矩
列出转动定律和牛 顿定律方程
列出线量和角量 之间的关系式
求解联 立方程
例 一轻绳绕在半径 r =20 cm 的飞轮边缘,在绳端施以F=98 N
a R
GB
a mBg
mA
mB
1 2
mC
FT1
mA
mAmB g
mB
1 2
mC
FT
2
mA
mA
1 2
mC
mB
mB g
08 刚体定轴转动的动能定理和转动定律
3-1 刚体定轴转动的动能定理和转动定律
n
定义转动惯量 J miri2 i1
对质量连续分布的刚体,任取质量元dm,其到轴的距离为 r,则转动惯量
J r2dm 单位:kg ·m2(千克·米2)
dm:质量元
dmdl :线密度 dmdS :面密度
dmdV :体密度
3-1 刚体定轴转动的动能定理和转动定律
刚体定轴转动的动能定理
W12M d1 2J2 21 2J12
合外力矩对绕定轴转动的刚体所作的功等于刚体转动动能 的增量.
注意
1. 如果刚体在运动过程中还有势能的变化,可用质点组的功能
原理和机械能转换与守恒定律讨论. 总之,刚体作为特殊的质
点组,它服从质点组的功能转换关系.
2. 刚体的定轴转动的动能应用 Ek
m1(2m2
1 2
m)g
m1
m2
1 2
m
,
FT 2
m2
(2m1
1 2
m)
g
m1
m2
1 2
m
决定刚体转动惯量的因素 ⑴与刚体的密度有关(即与m有关); ⑵与刚体的几何形状有关(即与m的分布有关); ⑶与刚体的转轴位置有关。
3-1 刚体定轴转动的动能定理和转动定律
求质量为m、长为l的均匀细长棒,对通过棒中心和过端点 并与棒垂直的两轴的转动惯量.
O
Or
l 2 O´ dr l 2
O´ dr l
M
1.力矩
动 点平P面刚, 且的体在交绕转点O动z,轴平力旋面F 转内作,,用Or 为在轴刚为与体由上转点
O 到力的作用点 P 的位矢.
O
M zr*
dP
F
F对转轴z的力矩 M Fsrin Fd
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
定轴转动定律
此处e是盘的厚度。 此处 是盘的厚度。圆盘所受阻力矩就是 是盘的厚度
M τ = ∫ r µ dmg = µ g ∫ r ρ red θ dr = µ g ρ e ∫0 d θ ∫0 r dr 2 3 = µ gρ eπ R 3 2 2,代入得 因m=ρeπR M τ = µ mgR 3
a=
(m2 − m1 )g − M r / r (m2 − m1 )g − M τ / r
J m2 + m1 + 2 r =
1 m2 + m1 + m 2 而 1 m1 2m2 + m g − M τ / r 2 T1 = m1 ( g + a ) = 1 m2 + m1 + m 2 1 m2 2m1 + m g+M τ / r 2 T2 = m1 ( g-a ) = 1 m2 + m1 + m 2
定轴转动定律
例题4 一半径为R 质量为m匀质圆盘 匀质圆盘, 例题4-6 一半径为R,质量为 匀质圆盘,平放在 粗糙的水平桌面上。 粗糙的水平桌面上 。 设盘与桌面间摩擦系数为 µ , 令圆盘最初以角速度 ω0 绕通过中心且垂直盘面的轴 旋转,问它经过多少时间才停止转动? 旋转,问它经过多少时间才停止转动?
F sin ϕi + fi sin θi = ∆miaiτ = ∆miri β i
定轴转动定律
用 r 乘以上式左右两端: i 乘以上式左右两端:
F ri sin ϕi + firi sin θ i
2 i = ∆m r i i
β
设刚体由N 个点构成, 设刚体由 个点构成,对每个质点可写出上述 类似方程, 类似方程,将N 个方程左右相加,得: 个方程左右相加,
R 2 2π
根据定轴转动定律,阻力矩使圆盘减速, 根据定轴转动定律,阻力矩使圆盘减速,即 获得负的角加速度. 获得负dω − µ mgR = J α = mR 3 2 dt
设圆盘经过时间t停止转动, 设圆盘经过时间t停止转动,则有
2 1 0 t − µ g ∫0 dt = R ∫ω 0 d ω 3 2
i=1
∑Firi sin ϕi + ∑ firi sin θi = ∑
i=1 i=1
N
N
N
2 (∆mi ri )
β
根据内力性质(每一对内力等值、反向、 根据内力性质(每一对内力等值、反向、共 对同一轴力矩之代数和为零) 线,对同一轴力矩之代数和为零),得:
i= 1
∑ firi sin θi = 0
N
由此求得
3 R t= ω0 4 µg
定轴转动定律
2 1 2 dω − µ mgR = J α = mR 3 2 dt
设圆盘经过时间t停止转动, 设圆盘经过时间t停止转动,则有
2 1 0 t − µ g ∫0 dt = R ∫ω 0 d ω 3 2
由此求得
3 R t= ω0 4 µg
用线的距离,称为力臂 用线的距离,称为力臂。
r F 1
r F
r F 2
r (3) F 对转轴的力矩为零, 1 对转轴的力矩为零,
在定轴转动中不予考虑。 在定轴转动中不予考虑。
转动 平面
r r
(4)在转轴方向确定后,力对 在转轴方向确定后, 转轴的力矩方向可用+ 号表示。 转轴的力矩方向可用+、-号表示。
上题中的装置叫阿特伍德机, 上题中的装置叫阿特伍德机 , 是一种可用来测 量重力加速度g的简单装置。因为在已知m 量重力加速度g的简单装置。因为在已知 1、 m2 、 r和J的情况下,能通过实验测出物体1和2的加速度 , 的情况下, 的加速度a, 和 的情况下 能通过实验测出物体1 再通过加速度把g算出来。在实验中可使两物体的m 再通过加速度把g算出来。在实验中可使两物体的 1 和 m2 相近, 从而使它们的加速度a和速度 都较小, 相近 , 从而使它们的加速度 和速度v都较小 , 和速度 都较小 这样就能角精确地测出a来 这样就能角精确地测出 来。
dω M = Jβ = J dt
刚体定轴 转动定律
定轴转动定律
dω M = Jβ = J dt
讨论: 讨论:
(1) M 一定,J ) 一定, 惯性大小的量度; 惯性大小的量度;
β
转动惯量是转动
的符号: (2)M 的符号:使刚体向规定的转动正方向加速 的力矩为正; 的力矩为正; (3)J 和质量分布有关; 和质量分布有关; 和转轴有关, (4)J 和转轴有关,同一个物体对不同转轴的转 动惯量不同。 动惯量不同。
ω
dθ r dr R e
由于摩擦力不是集中作用于一点, 解 由于摩擦力不是集中作用于一点,而是分布在 整个圆盘与桌子的接触面上, 整个圆盘与桌子的接触面上,力矩的计算要用积分 在图中,把圆盘分成许多环形质元, 法。在图中,把圆盘分成许多环形质元,每个质元 的质量dm=ρrdθdre,所受到的阻力矩是 µdmg 。 的质量 ,所受到的阻力矩是r
定轴转动定律
得到: 得到:
i=1
∑Firi sin ϕi = ∑
i=1
N
N
2 (∆mi ri )
β
上式左端为刚体所受外力的合外力矩, 上式左端为刚体所受外力的合外力矩,以M 表 右端求和符号内的量与转动状态无关, 示;右端求和符号内的量与转动状态无关,称为刚 表示。 体转动惯量,以J 表示。于是得到 体转动惯量,
§4-3 力矩 刚体定轴转动定律 1. 力矩
r r r r 点的力矩: F 对O 点的力矩:M = r × F
Z
r M
转 动 平 面
M = rF sin α r F
r M
MZ
α r
r
r r M沿Z 轴分量为 F对Z 轴力矩 MZ
r F
r O r A
力矩
力不在转动平面内
r r r M = r× F r r r = r ×(F1 + F2 ) r r r r = r × F + r × F2 1 r r r × F1 只能引起轴的
定轴转动定律
a (m2 − m1 )g − M τ / r α= = r m + m + 1 m r 2 1 2
当不计滑轮质量及摩擦阻力矩即令m= 当不计滑轮质量及摩擦阻力矩即令 =0、Mτ=0时,有
2m1m2 T1 = T2 = g m2 + m1
m2 − m1 a= g m2 + m1
变形, 对转动无贡献。 变形 对转动无贡献 注 (1)在定轴动问题中 如不加说明, ,如不加说明,所指的力矩 是指力在转动平面内的分力 对转轴的力矩。 对转轴的力矩。
r F 1
转动 平面
r F
r F 2
r r
力矩
(2 )
MZ = rF si α = F d 2 n 2
d = r sin α是转轴到力作
G2 − T2 = m2 a T2′r − T1′r − M τ = Jα
是滑轮的角加速度, 是物体的加速度 是物体的加速度。 式中α是滑轮的角加速度,a是物体的加速度。滑轮 边缘上的切向加速度和物体的加速度相等, 边缘上的切向加速度和物体的加速度相等,即
a = rα
从以上各式即可解得
定轴转动定律
定轴转动定律
2. 刚体定轴转动定律
对刚体中任一质量元 ∆m i
O’
ω
r 外力 Fi -外力
r fi -内力
O
r ri
∆mi
r fi
θi ϕ i
r F i
应用牛顿第二定律,可得: 应用牛顿第二定律,可得:
r r r Fi + fi = ∆mai i
采用自然坐标系,上式切向分量式为: 采用自然坐标系,上式切向分量式为:
定轴转动定律
例题4 一轻绳跨过一定滑轮,滑轮视为圆盘, 例题4-5 一轻绳跨过一定滑轮,滑轮视为圆盘,绳的 的物体1 两端分别悬有质量为m1和m2的物体1和2,m1< m2 如图 所示。 设滑轮的质量为m 半径为r, 所示 。 设滑轮的质量为 , 半径为 , 所受的摩擦阻力 矩为m。绳与滑轮之间无相对滑动。 矩为 。 绳与滑轮之间无相对滑动 。 试求物体的加速度 和绳的张力。 和绳的张力。 解:滑轮具有一定的转动惯 量。在转动中受到阻力矩 T T 的作用, 的作用,两边的张力不再 ′ 1 T 2 T′ 相等,设物体1 相等,设物体1这边绳的张 1 2 ’(T ’= T ) , 力为T1、 T1 1 1 a m
1
a
a m
2
物体2 物体2这边的张力为
m G m
2 1
T2、 T2’(T2’= T2)
1
G
2
定轴转动定律
物体1向上运动,物体2向下运动, 因m2>m1,物体1向上运动,物体2向下运动,滑轮以 顺时针方向旋转, 的指向如图所示。 顺时针方向旋转,Mr的指向如图所示。可列出下列方 程
T1 − G1 = m1a
