热传导方程基本解
一维热传导方程 解析解

一维热传导方程解析解标题:热传导方程与温度的变化在日常生活中,我们经常会遇到各种物体的温度变化现象。
而这些温度变化可以通过一维热传导方程来描述。
热传导方程是一个非常重要的方程,它可以帮助我们理解物体内部温度的分布和变化规律。
假设我们有一根长度为L的金属棒,两端分别与温度为T1和T2的热源相接触。
我们想要知道金属棒的中间位置温度随时间的变化情况。
这时,我们可以使用一维热传导方程来描述这个问题。
热传导方程的数学形式是这样的:∂u/∂t = α * ∂²u/∂x²其中,u代表温度,t代表时间,x代表位置,α代表热扩散系数。
这个方程告诉我们,温度随时间的变化率等于热扩散系数乘以温度在空间上的二阶导数。
通过求解这个方程,我们可以得到金属棒中间位置温度随时间的变化规律。
解析解的具体形式会根据初始条件和边界条件的不同而有所变化,但总体上可以分为几个阶段。
在金属棒刚与热源接触的时候,中间位置的温度会迅速上升,接近热源的温度。
然后,随着时间的推移,温度会逐渐向两端传播,金属棒的整体温度会趋于平稳。
在这个过程中,金属棒中间位置的温度会随着时间的增加而不断增加,直到达到一个稳定的值。
而金属棒两端的温度则会保持恒定,不随时间变化。
通过热传导方程的解析解,我们可以更好地理解温度的变化规律。
这对于很多实际问题的解决都非常有帮助,比如热工学、材料科学等领域。
一维热传导方程是描述物体温度变化的重要工具。
通过求解这个方程,我们可以得到温度随时间和位置的变化规律,从而更好地理解和解决实际问题。
通过研究热传导方程,我们可以为人类的生活和科学研究提供更多的帮助和指导。
傅里叶热传导定律导热微分方程

傅里叶热传导定律导热微分方程傅里叶热传导定律导热微分方程:探索热传导的奥秘1、引言:了解傅里叶热传导定律热传导是我们日常生活中重要的现象之一,在多个领域都有广泛应用,包括工程、物理、化学和生物等。
傅里叶热传导定律是描述物体内部温度分布的重要方程,通过导热微分方程可以更深入地理解温度传导现象。
2、基础知识:热传导和傅里叶热传导定律热传导是指热量从高温区域向低温区域传递的过程。
傅里叶热传导定律则是一组描述热传导的微分方程,最常用的是一维传热情况下的傅里叶热传导定律。
3、傅里叶热传导定律的一维形式在一维情况下,傅里叶热传导定律可以表示为:(1) ∂T/∂t = α ∂²T/∂x²其中,T是温度,t是时间,x是空间坐标,α是传热系数。
这个方程描述了温度随时间和空间变化的关系,可以帮助我们理解物体内部的温度分布情况。
4、解析解和数值解:探索温度变化的方法傅里叶热传导定律的导热微分方程是一个偏微分方程,可以通过解析解或数值解来获取温度的变化情况。
解析解适用于简单的几何形状和边界条件,而数值解则可以应用于更为复杂的情况。
5、实际应用:傅里叶热传导定律的物理意义傅里叶热传导定律的物理意义是描述热量如何在物体内部传递和分布的过程。
通过研究傅里叶热传导定律,我们可以探索不同物质和结构的热传导行为,进而优化材料的热性能、设计更高效的散热系统。
6、个人观点和理解:热传导与现代科技的关系热传导作为能量传递的重要方式之一,在现代科技发展中扮演着重要角色。
通过研究傅里叶热传导定律,我们可以更好地理解材料的热传导行为,从而开发出更高效的散热材料和散热系统,提高设备的效能,推动科技的发展。
7、总结回顾:深入理解热传导的奥秘在本文中,我们深入探讨了傅里叶热传导定律导热微分方程,从基础知识到实际应用,对热传导现象进行了全面评估。
傅里叶热传导定律导热微分方程可以帮助我们理解温度传导的机制和规律,为现代科技的发展提供了重要的理论支持,同时也为我们研究和优化热传导过程提供了有效工具。
热传导方程的求解及其应用

热传导方程的求解及其应用热传导是指物质内部由高温区向低温区传递热量的过程,是自然界中十分普遍的现象。
为了更好地理解和研究这一过程,我们需要借助数学模型来描述和求解热传导过程,其中最常用的数学模型就是热传导方程。
一、热传导方程的数学模型热传导方程是描述物质内部温度变化随时间和空间的变化而变化的偏微分方程。
它可以描述均质物质内部的热量传递,以及介质中的温度变化。
热传导方程的数学表示式如下:$$ \frac{\partial u}{\partial t}=\alpha \nabla^2 u $$其中,$u$表示物质内部温度的分布,$t$表示时间,$\alpha$表示热扩散系数,$\nabla^2$表示拉普拉斯算子,表示温度分布的曲率。
二、热传导方程的求解方法热传导方程是一个偏微分方程,需要借助一定的数学方法才能求解。
下面简要介绍两种常见的求解方法:1.分离变量法分离变量法是求解偏微分方程的常见方法之一。
对于热传导方程,我们通常采用分离变量法将其转化为两个方程:$$ \frac{1}{\alpha}\frac{\partial u}{\partial t}= \nabla^2 u $$设$u(x,t)=f(x)g(t)$,代入上式得:$$ \frac{1}{\alpha}\frac{g'(t)}{g(t)}= \frac{f''(x)}{f(x)}=\lambda $$其中,$\lambda$为待定常数,$f(x)$和$g(t)$分别为$x$和$t$的函数。
将上述两个方程分别求解,可以得到形如下面的解:$$ u(x,t)=\sum_{n=1}^{\infty}c_nexp(-\lambda_n\alphat)sin(\frac{n\pi x}{L}) $$其中,$\lambda_n$为常数,$L$为问题的区间长度。
2.有限差分法有限差分法是一种常见的数值求解方法,可以用来求解各种偏微分方程,包括热传导方程。
大学物理-热传导方程的定解问题

在各向同性的介质中,热流强度 q 与温度的负梯度成正比, 即
(k:热传导系数)
|q|:单位时间垂直通过等温面单位面积的热量,即 q 的方向:等温面的法线方向 (由高温指向低温) 定律的物理意义:q 正比于温度的下降率 单位时间内流入 / 流出 V 的热量为
单位时间内热源在 V 中释放 / 吸收的热量为
单位时间内,V 中介质温度升高/降低所需/放出的热量为
能量守恒定律:Q3 = Q1 + Q2 则 由 V 的任意性,得到
若介质均匀,即 k 为常量,有来自定义:,因此得到
当 V 内无热源,即 f = 0,故有
二、扩散方程 1. 扩散现象:当空间各点浓度分布不均匀时,就有粒子
从高浓度处流向低浓度处。(浓度:单位体 积中的粒子数) 2. 方程的推导 设:空间中任一小体积 V,其边界面为 S
粒子源强度:F (x, y, z, t) ——单位时间,单位体积 内产生的粒子数
求:空间各点粒子浓度 u(x, y, z, t) 的方程 V 内粒子数增加的来源:扩散 + 粒子源
扩散浓度:N ——单位时间通过垂直于 v (粒子定向运动速 度) 的单位面积的粒子数 N=uv,方向:v 的方向
对于扩散现象,有斐克定律: 扩散强度与浓度的负梯度成正比,即 D:扩散系数
扩散导致 V 内粒子增加的数量:
粒子源 V 粒子增加的数量: 内粒子数总的增加数:
因粒子数守恒,有 由 V 的任意性,得到 若 D 为常量,且设 D = a2,则
若 V 内无粒子源,即 F = 0,因而
总结:热传导:热量的传递;扩散:粒子的运动,两 者物理本质不同,但满足同一微分方程。
热传导方程求解-分离变量法
牛曼外问题
拉普拉斯方程的狄氏内问题
Q(x, y, z)
拉普拉斯方程的基本解
• 1 三维空间的拉氏方程基本解
将三维空间拉氏方程用球坐标系表示
z
r M(x, y,z)
z
1 r2
r
(r2
u ) r
1
r2 sin
(sin
u )
r2
1
sin2
2u
2
0
A xo
xy
P
y
求其球对称解 u u(r)(解只与r有关,与角度无关)
0
n 0,1, 2,....
X
n
(
x)
sin
2n 2a
1
x
n 0,1, 2....
ux (0, y) u(a, y) 0 u(x, 0) (x) u(x,b) (x)
X (x) X (x) 0
X (0)
X (a)
0
n
(2n 1 2a
)2
0
n 0,1, 2,....
ux (0, y) ux (a, y) 0 u(x,0) (x) u(x,b) (x)
内容回忆
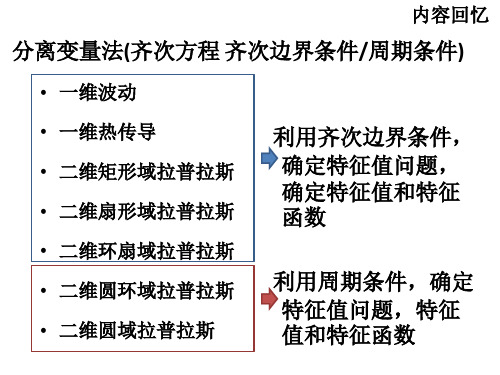
分离变量法(齐次方程 齐次边界条件/周期条件)
• 一维波动
• 一维热传导 • 二维矩形域拉普拉斯 • 二维扇形域拉普拉斯
利用齐次边界条件,
确定特征值问题, 确定特征值和特征 函数
• 二维环扇域拉普拉斯 • 二维圆环域拉普拉斯 • 二维圆域拉普拉斯
利用周期条件,确定
特征值问题,特征 值和特征函数
X (x) X (x) 0
X (0) X (l) 0
n
( n l
)2
0
热学方程热传导方程的解析解

热学方程热传导方程的解析解在热学中,热传导方程是一个重要的方程,用于描述热量在物体中的传导过程。
热传导方程的解析解是指能够用解析表达式准确描述热传导过程的解。
热传导方程一般形式为:$$\frac{{\partial T}}{{\partial t}} = a \cdot \nabla^2 T$$其中,$\frac{{\partial T}}{{\partial t}}$表示温度$T$随时间$t$的变化率,$a$是热扩散系数,$\nabla^2 T$表示温度$T$的拉普拉斯算子。
为了求解热传导方程的解析解,我们需要考虑不同情况下的边界条件和初始条件。
1. 一维热传导方程的解析解首先,考虑一维情况下的热传导方程。
假设热传导发生在长度为$L$的直杆上,且直杆的两端保持温度固定,即边界条件为$T(0, t) = T_1$和$T(L, t) = T_2$,其中$T_1$和$T_2$为已知常数。
对于这种情况,可以使用分离变量法来求解热传导方程。
假设解为$T(x, t) = X(x) \cdot T(t)$,将其代入热传导方程得到两个常微分方程:$$\frac{{1}}{{aX}} \frac{{d^2X}}{{dx^2}} = \frac{{1}}{{T}}\frac{{dT}}{{dt}} = -\lambda^2$$其中,$\lambda$为常数。
将得到的两个方程进行求解,可以得到解析解为:$$T(x, t) = \sum_{n=1}^{\infty} C_n \cdot e^{-a \lambda_n^2 t} \cdot\sin(\lambda_n x)$$其中,$C_n$为系数,和边界条件相关。
对于给定的边界条件$T(0, t) = T_1$和$T(L, t) = T_2$,可以确定系数$C_n$的值。
2. 二维热传导方程的解析解接下来,考虑二维情况下的热传导方程。
假设热传导发生在一个矩形区域内,且边界上的温度已知。
热传递方程
热传递方程(最新版)目录1.热传递方程的定义与概念2.热传递方程的基本形式3.热传递方程的求解方法4.热传递方程的应用领域正文热传递方程是描述热量在物体间传递过程的数学方程,它是热力学领域的基本方程之一。
热传递过程是热力学系统中常见的现象,如散热、热传导和热辐射等。
热传递方程在工程、物理和化学等领域具有广泛的应用。
热传递方程的基本形式包括以下三种:1.热传导方程:描述在稳态条件下,物体内部热量沿着温度梯度传递的过程。
热传导方程为:T=α(T),其中,T 表示温度,α表示热扩散系数,T 表示温度梯度。
2.热扩散方程:描述在非稳态条件下,物体内部热量沿着温度梯度传递的过程。
热扩散方程为:T/t=α(T),其中,t 表示时间。
3.热辐射方程:描述物体表面与外界之间热量传递的过程。
热辐射方程为:Q=εσA(T^4-T0^4),其中,Q 表示热辐射强度,ε表示表面发射率,σ表示斯特藩 - 玻尔兹曼常数,A 表示表面积,T 表示物体温度,T0 表示环境温度。
求解热传递方程的方法有很多,如分离变量法、有限元法、有限体积法等。
这些方法可以有效地解决各种复杂的热传递问题。
热传递方程在许多领域都有广泛的应用,例如:1.电子器件散热:在设计电子器件时,需要考虑器件在工作过程中产生的热量如何有效地传递出去,以保证器件的正常工作和使用寿命。
2.建筑节能:在建筑设计中,合理地利用热传递方程可以降低建筑物的能耗,提高能源利用效率。
3.工业热处理:在金属加工、铸造等过程中,需要对材料进行加热或冷却处理,热传递方程可以为这些过程提供理论依据。
总之,热传递方程是描述热量传递过程的重要数学工具,它在工程、物理和化学等领域具有广泛的应用价值。
热学中的热传导问题及计算练习
热学中的热传导问题及计算练习热学是物理学中的一个重要分支,研究物体热平衡、热传导、热辐射等现象。
热传导问题是热学中的一个基本概念,指的是热量在物体中的传递过程。
在本文中,我们将探讨热传导问题,并进行一些计算练习。
一、热传导的基本原理热传导是指物体内部或不同物体之间由于温度差异而引起的热量传递现象。
热能会从高温区域自动流向低温区域,直到温度达到均衡。
这个过程可以用热传导方程描述:q = -kA(dT/dx)其中,q是单位时间内通过物体的热量,k是材料的热导率,A是传热截面积,dT是温度差,dx是传热距离。
二、热传导的应用1. 热传导在工程领域中的应用热传导在工程领域中有广泛的应用,比如在建筑设计中,需要考虑墙体、屋顶等材料的热传导性能,以确保室内温度的稳定性。
此外,在电子设备中,散热器的设计也需要考虑材料的热传导性质,以保持设备的正常工作。
2. 热传导在自然界中的应用自然界中的很多现象也与热传导有关。
例如,地球上的温度分布不均匀就是因为热量的传导引起的,导致地球表面出现了不同的气候区域。
同时,在生物体内也存在热传导现象,人体通过皮肤散发热量,保持体温的稳定。
三、热传导计算练习1. 热传导计算实例一现有一个长为2.5m、宽为1.8m、厚度为0.15m的木质板材,其热导率为0.15 W/(m·K),一侧温度为200℃,另一侧温度为80℃,求在平衡状态下,单位时间内通过板材的热量。
解:根据热传导方程,我们可以计算出温度差:dT = 200℃ - 80℃ = 120℃板材的传热截面积可以计算如下:A = 2.5m × 1.8m = 4.5m²传热距离为板材的厚度:dx = 0.15m将上述数值代入热传导方程,可计算出单位时间内通过板材的热量:q = -0.15 W/(m·K) × 4.5m² × (120℃/0.15m)2. 热传导计算实例二现有两个金属棒,棒A的热导率为100 W/(m·K),长度为1.2m,棒B的热导率为50 W/(m·K),长度为0.8m。
热传导偏微分方程
热传导偏微分方程热传导偏微分方程是描述热传导现象的数学模型。
热传导是指物质内部热量的传递过程,当一个物体的一部分受热时,热量会通过热传导方式从高温区域向低温区域传递,直到达到热平衡。
热传导偏微分方程可以用来描述热量在空间和时间上的分布。
假设热传导过程在一个一维材料中进行,我们可以使用一维热传导方程来描述这个过程。
一维热传导方程的形式如下:∂u/∂t = α (∂²u/∂x²)其中,u是温度关于时间和位置的函数,t是时间,x是位置,α是热扩散系数。
这个方程表示温度随时间的变化率等于热扩散系数乘以温度在空间上的二阶导数。
通过求解这个偏微分方程,我们可以得到热传导过程中温度的分布情况。
为了求解这个方程,我们需要给定适当的边界条件和初始条件。
边界条件可以是材料的两端保持恒定温度,也可以是一端保持恒定温度,另一端保持绝热。
初始条件是指在初始时刻材料各点的温度分布情况。
热传导偏微分方程的解可以通过数值方法或解析方法求得。
数值方法包括有限差分法、有限元法等,通过离散化空间和时间,将偏微分方程转化为代数方程组进行求解。
解析方法则利用数学分析技巧,直接求解偏微分方程。
热传导偏微分方程不仅可以用来研究材料中的热传导现象,还可以应用于其他领域。
例如,在工程中可以用来分析热传导引起的温度变化对结构的影响;在地球科学中可以用来研究地球内部温度分布的演化;在物理学中可以用来研究热传导对电子、声波等的影响。
热传导偏微分方程是描述热传导现象的重要数学模型。
通过求解这个方程,我们可以了解热传导过程中温度的分布情况,进而研究其对材料性质和结构的影响。
热传导偏微分方程的应用广泛,不仅在材料科学领域有重要意义,也在其他领域发挥着重要作用。
波动方程与热传导方程的解法
波动方程与热传导方程的解法波动方程与热传导方程是物理学中常见的偏微分方程,它们描述了波动和热传导的过程。
在实际问题中,解这两个方程可以帮助我们了解和预测物理现象,例如声波传播、电磁波传播和热量传导等。
本文将介绍波动方程和热传导方程的解法及其应用。
一、波动方程的解法波动方程描述了波的传播和干涉。
通常表示为:∂²u/∂t² = v²∇²u其中,u代表波的振幅,t代表时间,v代表波速,∇²u是u的拉普拉斯算子。
1. 分离变量法分离变量法是求解偏微分方程的常用方法。
对于波动方程,我们可以假设u(x, t)的解为u(x, t) = X(x)T(t),其中X(x)和T(t)是仅与x和t相关的函数。
将u(x, t)的表达式带入波动方程,我们可以得到两个关于X(x)和T(t)的普通微分方程。
通过求解这两个方程,我们可以得到波动方程的解。
2. 傅里叶变换法傅里叶变换法也是求解偏微分方程的重要方法。
通过将波动方程进行傅里叶变换,我们可以将其变换为关于频率和空间变量的代数方程,进而求解得到波动方程的解。
二、热传导方程的解法热传导方程描述了热量在物质中的传导过程。
通常表示为:∂u/∂t = α∇²u其中,u代表温度分布,t代表时间,α代表热扩散系数,∇²u是u 的拉普拉斯算子。
1. 分离变量法与波动方程类似,热传导方程也可以通过分离变量法求解。
我们可以假设u(x, t)的解为u(x, t) = X(x)T(t),其中X(x)和T(t)是只与x和t有关的函数。
将u(x, t)的表达式带入热传导方程,我们可以得到两个关于X(x)和T(t)的普通微分方程。
通过求解这两个方程,我们可以得到热传导方程的解。
2. 球坐标系或柱坐标系下的解法对于具有球对称性或柱对称性的问题,我们可以将热传导方程转换为径向方程和角向方程,并通过求解这些方程得到热传导方程的解。
三、波动方程和热传导方程的应用波动方程和热传导方程广泛应用于物理学、工程学和其他领域中。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
热传导方程基本解
热传导方程是一个有用的数学模型来描述物体的温度的分布,它的解决方案能
够被用来计算热传导现象,这在热传导实验之中是非常重要的。
这篇文章将会介绍热传导方程的基本解,这对于互联网行业的用户以及其他学科专业的研究者而言,都具有很大的用处。
热传导方程基本解有两个,即位置解,也称为解析解,另一个是折衷解决方案,有时也被称为数值解。
位置解是一种精确的计算方法,可以将方程的未知变量准确求解出来。
这种精确计算方法是建立在裂缝分析基础上的,特点是参数准确,曲线平滑,可以作出任何指定的恒温线。
折衷解决方案,也称为数值解,也可以有效地求解热传导方程。
但这种方法比
上述位置解法更加容易。
它可以利用数值算法在简单的分割块之间拟合曲线,数值算法不需要非常准确,并且它可以在较短的时间内计算出来,得出的温度分布不是很精确,但仍然可以提供足够的可靠结果。
热传导方程的基本解很重要,它可以帮助互联网行业的用户和学科专业的研究
者更好地理解和解决热传导问题。
它也为研究者构建和验证数学模型提供了一种重要的参考依据,可以更迅速地进行研究。
总之,热传导方程的基本解是一个重要的数学概念,对于互联网行业而言,更可以提升灵活性和提高效率。
