八年级数学下学期测试题第十四周双休日作业试题
八年级数学下学期测试题第二周双休日作业试题

HY 中学2021-2021学年八年级数学下学期测试题〔第二周双休日作业〕班级 姓名 学号一.选择题1.以下四个图案中,既是轴对称图形又是中心对称图形的图案是 ( )2.:如图,在平行四边形ABCD 中,4=AB ,7=AD ,∠ABC 的平分线交AD 于点E ,交CD 的延长线于点F ,那么DF 的长为 〔 〕 A .6 B . 5 C .4 D . 3形ABCD 中,AB =3,AD =2,=150B ∠︒,那3.如图,平行四边么平行四边形ABCD 的面积为 〔 〕 A. 2 B. 3 C. 33 D. 64.如图,在□ABCD 中,CE AB ⊥,E 为垂足.假如125A =∠,那么BCE =∠〔 〕A .25B .30C .35D .555.如图,一张纸片□ABCD ,90B ∠>︒,点E 是AB 的中点,点G 是BC 上的一个动点,沿EG 将纸片折叠,使点B 落在纸片上的点F 处,连结AF ,那么以下各角中与BEG ∠不.一定..相等的是〔 〕 A. ∠FEG B. ∠EAF C.∠AEF D. ∠EFA 6.如图,P 为平行四边形ABCD 的对称中心,以P 为圆心作圆,过P 的任意直线与圆相交于点M ,N .那么线段BM ,DN 的大小关系是 〔 〕A. BMDN B. BM第6题 第7题7.如图,在平行四边形ABCD 中,AD =5,AB =3,AE 平分∠BAD 交BC 边于点E ,那么线段BE ,EC 的长度分别为〔 〕A .2和3B .3和2C .4和1D .1和48. 菱形的周长为40cm,两条对角线之比3:4,那么菱形面积为 〔 〕 A.12 B.24C.48D.969.菱形具有而矩形不一定具有的性质是 ( ) A .内角和等于3600B .对角相等C .对边平行且相等D .对角线互相垂直 10.如图,P 是矩形ABCD 的边AD 上一个动点,矩形的两条边AB 、BC 的长分别为3和4,那么点P 到矩形的两条对角线AC 和BD 的间隔 之和是 ( ) A .125 B .65 C .245D .不确定 11.四边形ABCD 是平行四边形,以下结论不正确的选项是 ( ) A .当AB =BC 时,它是菱形 B .当AC ⊥BD 时,它是菱形 C .当∠ABC =90°时,它是矩形 D .当AC =BD 时,它是正方形12. 如图,正方形ABCD 的面积为12,△ABE 是等边三角形,点E 在正方形ABCD 内,在对角线AC 上有一点P ,使PD +PE 的和最小,那么这个最小值为 ( ) A .12 B .24 C .3 D .613.□ABCD 中,∠C =∠B+∠D ,那么∠A =_______度.ABCDEEDCBA14.在□ABCD 中,对角线AC 、BD 相交于点O ,△AOD 的周长比△AOB 的周长小3 cm .假设AD =5 cm ,那么□ABCD 的周长为______cm .15 在矩形ABCD 中,AB =3 cm ,BC =4 cm ,点A 到对角线BD 的间隔 为 . 16. 一个菱形的两条对角线长分别为6 cm 、8cm ,那么这个菱形的面积S 为 . 17.平行四边形ABCD 中,AB=3,BC=4,∠A 、∠D 的平分线交BC 于E 、F ,那么EF= 。
八年级数学下学期测试题第六周双休日作业试题

卜人入州八九几市潮王学校HY 二零二零—二零二壹八年级数学下学期测试题〔第六周双休日作业〕班级学号111x -=〔〕A .x ≥1B .x ≥-1C .-1≤x ≤1D .x ≥1或者x ≤-12.假设│a -2│+244b b ++=0〔〕A .4B .2C .-2D .13.以下各式的计算中,不正确的选项是〔〕A =〔-2〕×〔-4〕=8B ===2a 2C ===5D 5==== 4.在以下各式中,是最简二次根式的是〔〕A B D5(0)x y <<得〔〕A .))((y x y x -+±B .y 2-x 2C .x 2-y 2D .以上答案都不对6.设3a =-,1ab =,那么a 、b 大小关系是〔〕 A .a =b B .a >b C .a <b D .a >-b7.化简)12(2-÷的结果是〔〕 A .122-B .22- C .21-D .22+8.a xx =+1,那么x x 1+的值是〔〕 A .22-a B .2a C .42-a D .不确定9.能使75n 开得尽方,n 的最小正整数为〔〕 A .1 B .3C .5D .9 10.函数1y x =+中的x 范围为;函数11y x =+中的x 范围为; 函数11y x =+中的x 范围为;函数1x y x+=中的x 范围为. 11.计算:36÷=_______,605=________,8×〔-26〕=________, 223-=________,777-=________,1a ab b ab ÷=________. 12.a ,b 在数轴上的位置如图,那么()22a b a --的化简的结果为_______. 13.当y =22x x -+-+3时,那么x y =_______.14.x 为奇数,且6699x x x x --=--,那么221x x ++的算术平方根为______.15.:312311=+;413412=+;514513=+;……你发现了什么规律? 请用含n 〔n 是正整数〕的式子来表示:.16.把1x x-中根号外的因式移人根号内,所得的结果是. 17.计算:〔1〕123121335÷⨯〔2〕)2()()(a x ab bx x a a b x ⋅-⋅-⋅- 18.直角三角形的两条直角边的长分别为2、22,求它的周长和斜边上的高.19.如图,在ABCD 中,AC 与BD 相交于点O ,那么以下结论不一定成立的是〔〕A .BO DO =B .CD AB =C .BAD BCD ∠=∠ D .AC BD =20.双曲线21k y x-=的在各象限内的图像y 随x 增大而增大,那么k 的取值范围是〔〕 A .12k >B .12k <C .12k =D .不存在 21.菱形具有而矩形不一定具有的性质是〔〕A .对角线相等B .对角线互相平分C .对边平行且相等D .对角线互相垂直 〔第19题〕〔第24题〕26题〕 22.点()123123A y B y C y -,、,、,都在双曲线 ()0k y k x=>上,那么y 1、y 2、y 3〔〕A .312y y y << B .123y y y <<C .213y y y <<D .321y y y <<〔第28题〕 23.矩形的两条对角线的夹角为60°,这个矩形两邻边的比是A .1:1B .1:2C .2:3D .1:3〔〕24.如图,过□ABCD 的对角线BD 上一点M 分别作平行四边形两边的平行线EF 与GH ,那么图中的□AEMG 的面积S 1与□HCFM 的面积S 2的大小关系是〔〕A.12S S >B.12S S <C.12S S =D.122S S =25.顺次连接四边形四边中点所组成的四边形是菱形,那么原四边形为〔〕A .对角线垂直B .矩形C .对角线相等D .菱形26.如图,在四边形ABCD 中,R 、P 分别是边BC 、CD 上的点,E 、F 分别是AP 、RP 的中点,当点P 在CD 上从点C 向点D 挪动而点R 不动时,结论成立的是〔〕A .线段EF 的长逐渐增大B .线段EF 的长逐渐减小C .线段EF 的长不变D .线段EF 的长与点P 的位置有关27.2y +与3x -成反比例,假设2x =时,3y =-,那么当0x =时,y =.28.如图,双曲线经过直角三角形OAB 斜边OB 的中点D ,与直角边AB 相交于点C .假设△OBC 的面积为3,那么k =.29.菱形ABCD 的周长为40,一条对角线长为12,那么它的面积是________.30.如图,反比例函数1k y x=与一次函数2y mx b =+交于A(1,3),B(n ,-1) (1) 求反比例函数与一次函数的解析式.(2)根据图象答复:①当x <-3时,写出y 1的取值范围;OC B D②当y 1≥y 2时,写出x 的取值范围;(3)连结AO ,BO ,求△AOB 的面积.31.如图,在△ABC 中,AD 是边BC 上的中线,过点A 作AE ∥BC ,过点D 作DE ∥AB ,DE 与AC 、AE 分别交于点O 、E ,连接EC .(1)求证:AD =EC ;(2)当∠BAC =90°时,试说明四边形ADCE 是菱形.32.如图,坐标系中有Rt △ABC ,∠A =90°,AB =AC ,A(-2,0)、B(0,1)、C (a ,b).(1)直接填空:a =,b =;(2)将△ABC 沿x 轴的正方向平移,在第一象限内B 、C 两点的对应点B'、C'正好落在某反比例函数图象上.恳求出这个反比例函数和此时的直线B'C'的解析式.33.如图,直线l :333+-=x y 交x 轴于点A ,交y 轴于点B ,将△AOB 沿直线l 翻折,点O 的对应点C 恰好落在双曲线上.(1)求双曲线;(2)将△ABC 绕AC 的中点旋转180°得到△PCA ,请判断点P 是否在此双曲线上,并说理.。
第14周——2023-2024学年人教版数学八年级上册周周练(含答案)

第十四周——2023-2024学年人教版数学八年级上册周周练考查范围:15.3 1.下列关于x的方程:,,,中,分式方程的个数为( )A.1B.2C.3D.42.某工厂计划生产300个零件,由于采用新技术,实际每天生产零件的数量是原计划的2倍,因此提前5天完成任务.设原计划每天生产零件x个,根据题意,所列方程正确的是( )A. B. C. D.3.小明解分式方程的过程下.去分母,得.①去括号,得.②移项,合并同类项,得.③化系数为1,得.④以上步骤中,开始出错的一步是( )A.①B.②C.③D.④4.解分式方程,去分母得( )A. B.C. D.5.若关于x的方程的解为正数,则m的取值范围为( )A. B.且 C. D.且6.《九章算术》之“均输篇”中记载了中国古代的“运粟之法”:今有一批公粮,需运往距出发地420km的储粮站,若运输这批公粮比原计划每日多行10km,则提前1日到达储粮站.设运输这批公粮原计划每日行x km,则根据题意可列出的方程是( ).A. B.C. D.7.若关于x的分式方程的解为正数,则m的取值范围为( )A. B.C.且D.且8.中世纪意大利数学家斐波那契(1175年﹣1250年),编写的《计算之书》记载一道数学题,译文如下:一组人平分90枚硬币,每人分得若干,若再加上6人,平分120枚硬币,则第二次每人所得与第一次相同.求第二次分硬币的人数.设第一次分硬币的人数为x人,则可列方程为( )A. B.C. D.9.若是分式方程10.若分式方程无解,则m的值是_______.11.若关于x方程的解是,则a的值为______.12.一项工程,若由甲、乙两公司合作18天可以完成,共需付施工费144000元,若甲、乙两公司单独完成此项工程,乙公司所用时间是甲公司的1.5倍,已知乙公司每天的施工费比甲公司每天的施工费少2000元.(1)求甲、乙两公司单独完成此项工程,各需多少天?(2)若由一个公司单独完成这项工程,哪个公司的施工费较少?答案以及解析1.答案:C解析:判定方程是分式方程的关键:方程里含有分母,且分母里含有未知数.只有方程的分母里不含未知数,不是分式方程,所以分式方程的个数是3.2.答案:C解析:根据“实际每天生产零件的数量是原计划的2倍,提前5天完成任务”可以列出分式方程.由题意可得,故选C.3.答案:B解析:,去分母,得,去括号,得,移项,得,合并同类项,得,以上步骤中,开始出错的一步是②.故选:B4.答案:A解析:,去分母,得,故选:A.5.答案:B解析:解方程得,,该方程的解是正数,且,,且,且.故选:B.6.答案:A解析:由题意可得,,故选:A.7.答案:D解析:原式去分母的,解得,方程的解为正数,,且,m的取值范围为且,故选:D.8.答案:D解析:第一次分硬币的人数为x人,设第二次分硬币的人数为人,第二次每人所得与第一次相同,列出分式方程:,故选D.9.答案: 5解析:因为是分式方程的根,所以.解得.10.答案:3解析:方程两边都乘以得,,分式方程无解,方程有增根,,解得,,解得.故答案为:3.11.答案:4解析:关于x方程的解是,,,故答案为:4.12.答案:(1)甲公司单独完成需要30天,乙公司单独完成需要45天;(2)乙公司施工费用较少;解析:(1)设甲公司单独完成此项工程需x天,则乙公司单独完成需要1.5x天,由题意,得,解得:,经检验是原方程的解,则,答:甲公司单独完成需要30天,乙公司单独完成需要45天;(2)设乙公司每天的施工费用为y元,则甲公司每天的施工费用为元,由题意,得,解得,则(元),乙公司施工费为:,甲公司施工费为:,答:乙公司施工费用较少.。
八年级数学下学期测试题第十五周双休日作业试题

HY 中学2021-2021学年八年级数学下学期测试题〔第十五周双休日作业〕制卷人:打自企; 成别使; 而都那。
审核人:众闪壹; 春壹阑; 各厅……日期:2022年二月八日。
班级_______学号_____ 姓名 1.以下各组数中,能构成直角三角形的一组是〔 〕 A .2,2,5 B .1,3,2 C .4,5,6 D .6,8,122.以下各选项的图形中,不是..轴对称图形的是〔 〕A B C D3.点P 〔m +3,m +1〕在x 轴上,那么点P 坐标为〔 〕A .〔0,-2〕B .〔2,0〕C .〔4,0〕D .〔0,-4〕 4.以下函数中,是一次函数的有〔 〕个.①y =x ; ②x y 3=;③65+=x y ;④32y x =-;⑤23x y =. A .1 B .2C .3D .4 5.假设点〔-3,错误!未找到引用源。
〕,〔-2,错误!未找到引用源。
〕都在一次函数错误!未找到引用源。
223y x =-+的图象上,那么错误!未找到引用源。
、错误!未找到引用源。
的大小关系是〔 〕A .错误!未找到引用源。
B .错误!未找到引用源。
C .错误!未找到引用源。
D .不能比拟6. 81的平方根是 ;算术平方根.....是 . 7.等腰三角形的两边长分别是5和7,那么其周长等于 ;8.点A 〔a ,-5〕与点B 〔-4,b 〕关于y 轴对称,那么a +b= ; 9.一次函数y=x+b 的图像经过一、三、四象限,那么b 的值可以是 〔填一个即可〕; 么原直线10. 假设将一直线向上平移5个单位后所得直线的表达式为24y x =-,那的表达式是 ;11.点A 〔3,4〕先向左平移5个单位,再向下平移2个单位得到点B ,那么点B 的坐标为 .12.如图,在△ABC 中,AB=AC=13,BC=10,D 是AB 的中点,过点D 作DE ⊥AC 于点E ,那么DE 的长是13.如下图,在△ABC 中,∠B=40°,将△ABC 绕点A 逆时针旋转至在△ADE 处,使点B 落在BC 的延长线上的D 点处,那么∠BDE= 度.14.如图,函数y=x+b 和y=ax+3的图象交点为P ,那么不等式x+b >ax+3的解集为15.直角△ABC 的周长为6+23,其中一条直角边的长为23,那么另一条直角边的长为 .16.假设一次函数y =(m -3)x +(m -1)的图像经过原点,那么m = .17.对于一次函数23y x =--,当x 满足 条件时,图象在x 轴下方.18.如图,在Rt △ABC 中,AB=10,∠BAC=45°,∠BAC 的平分线交BC 于点D ,E 、F 分别是线段AD 和AB 上的动点,那么BE+EF 的最小值19.计算:(1)222b a ab a b a b b a +--+- (2)265222x x x x -⎛⎫÷-- ⎪--⎝⎭++〔502(π+--+ 〔6〕30274)21(23-+++--解方程:〔1〕2(21)9x += 〔2〕38(1)27x -=(3)1132422x x +=-- (4)214111x x x +-=--20.先化简:2344111x x x x x -+⎛⎫-+÷ ⎪++⎝⎭,然后从一1≤x ≤2中选一个适宜的整数作为x 的值代入求值.21.假设x 、y 是实数,且12,求11y y --的值.22.等腰三角形的周长为30 cm .〔1〕假设底边长为x cm ,腰长为y cm ,写出y 与x 的函数关系式;并写出自变量的取值范围 〔2〕假设腰长为x cm ,底边长为y cm ,写出y 与x 的函数关系式.并写出自变量的取值范围23.关于x 的分式方程21a x +-=1的解是非负数,求a 的取值范围.第24题②第24题①24.如图,每个小正方形的边长都是1.①在图中画出一个面积是2的直角三角形,并用字母标示顶点;②在图中画出一个面积是2的正方形,并用字母标示顶点.25.A 、B 两所在一条东西走向公路的同旁,以公路所在直线为x 轴建立如下图的平面直角坐标系,且点A 的坐标是〔2,2〕,点B 的坐标是〔7,3〕.〔1〕一辆汽车由西向东行驶,在行驶过程中是否存在一点C ,使C 点到A 、B 两校的间隔 相等,假如有?请用尺规作图找出该点,保存作图痕迹,不求该点坐标.〔2〕假设在公路边建一游乐场P ,使游乐场到两校间隔 之和最小,通过作图在图中找出建游乐场P 的位置,并求出它的坐标.26. Rt △ACD 中,∠ADC=900 AD=2,CD=1, 点B 在AD 的延长线上,BD=1,连接BC ,(1)求BC 的长(2)动点P 从点A 出发,向终点B 运动,速度为1个单位/秒,运动时间是为t 秒。
八年级数学下学期测试题第七周双休日作业试题

卜人入州八九几市潮王学校HY 二零二零—二零二壹八年级数学下学期测试题〔第七周双休日作业〕班级学号1.以下各等式成立的是()A 2B 25-C .6=D x2.以下运算错误的选项是()A 5=B 236=C =.(22=3.以下是同类二次根式的一组是()A -0)x ≥D .4.假设a >0()A ..D 5.假设a =b =,那么a +b +ab 的值是()A .1+.1-.-5D .36的被开方数一样,那么a 的值是()A .54-B .54C .-1D .1720m -=成立,那么m 的取值范围是()A .m>2B .m ≥2C .m<2D .m ≤28.设-,b=2--2,那么a 、b 、c 的大小关系是()A .a>b>cB .a>c>bC .c>b>aD .b>c>a9.+2,-2的值是()A .3B .4C .5D .6 10.把223x y -在实数范围内分解因式为:________.110,=那么2=________.12.ab的小数局部,那么2a +b 的值是_______.13.假设化简|1-x|-2x -5,那么x 的取值范围是.14是同类二次根式,那么b =_______.15.1x x +=那么1x x-的值是________. 16.先观察以下等式,再答复以下问题:5141==⨯+:11251==⨯+:19361==⨯+:…将猜想到的规律用含自然数n(n ≥1)的代数式表示出来是__________________. 17.计算:;⎛⎛÷ ⎝⎝(x>0,y>0) 18.计算:--2-1)(5-〔3⎛- ⎝〔4〕5x (x >0,y >0).19.:实数a ,b 在数轴上的位置如下列图,a b -1.如图,过y 轴正半轴上的任意一点P ,作x 轴的平行线,分别与反比例函数y =-4x 和y =2x的图像交于点A和点a bB .假设点C 是x 轴上的任意一点,连接AC 、BC ,那么△ABC 的面积为()A .3 B .4 C .5D .62.如图,菱形OABC 的顶点C 的坐标为(3,4),顶点A 在x 轴的正半轴上.反比例函数y =k x(x>0)的图像经过顶点B ,那么k 的值是()A .12B .20C .24D .32 3.函数y =1x 与y =x -2的图像交点的横坐标分别为a 、b ,那么11a b的值是_______. 4.在平面直角坐标系中,将直线y =x 向上平移1个单位长度得到直线l ,直线l 与反比例函数y =kx的图像的一个交点为A(a ,2),那么k 的值是_______. 5.如图,直线y =k 1x +b 与双曲线y =2k x 交于A 、B 两点,其横坐标分别为1和5,那么不等式k 1x<2kx+b 的解集是_______.6.如图,反比例函数y =4x(x>0)的图像上,有点P 1、P 2、P 3、P 4,它们的横坐标依次为1、2、3、4.分别过这些点作x 轴与y 轴的垂线,图中所构成的阴影局部的面积从左到右依次为S 1、S 2、S 3,那么S 1+S 2+S 3=_______. 7.如图,在直角坐标系中,矩形OABC 的顶点O 与坐标原点重合,A 、C 分别在坐标轴上.点B 的坐标为(4,2),直线y =-12x +3交AB 、BC 分别于点M .N ,反比例函数y =k x的图像经过点M 、N . (1)求反比例函数的解析式,(2)假设点P 在y 轴上,且△OPM 的面积与四边形BMON 的面积相等,求点P 的坐标.8.近年来,我国煤矿平安事故频频发生,其中危害最大的是瓦斯,其主要成分是CO .在一次矿难事件的调查中发现:从零时起,井内空气中CO 的浓度到达4mg/L ,此后浓度呈直线型增加,在第7小时到达最高值46mg/L ,发生爆炸;爆炸后,空气中的CO 浓度成反比例下降,如图,根据题中相关信息答复以下问题: (1)求爆炸前后空气中CO 浓度y 与时间是x 的函数关系式,并写出相应的自变量取值范围;(2)当空气中的CO 浓度到达34mg/L 时,井下3 km 的矿工接到自动HY 信号,这时他们至少要以多少km/h 的速度撤第1题 第2题 第5题 第6题离才能在爆炸前逃生?(3)矿工只有在空气中的CO浓度降到4mg/L及以下时,才能回到矿井开展消费自救,求矿工至少在爆炸后多少小时才能下井?9.用洗衣粉洗衣物时,漂洗的次数与衣物中洗衣粉的残留量近似地满足反比例函数关系.小红和小敏用同一种洗衣粉各自洗一件同样的衣服,漂洗时,小红每次用一盆水〔约10升〕,小敏每次用半盆水〔约5升〕.假设她们都用了5克洗衣粉,第一次漂洗后,小红的衣服中残留的洗衣粉还有,小敏的衣服中残留的洗衣粉还有2克.(1)分别求出小红和小敏各自衣服中洗衣粉的残留量y与漂洗次数x之间的函数表达式;(2)当洗衣粉的残留量降至时,便视为衣服漂洗干净.从节约用水的角度来看,你认为谁的漂洗方法值得提倡?为什么?。
2021年八年级(下)数学学科双休日练习题(第15周)
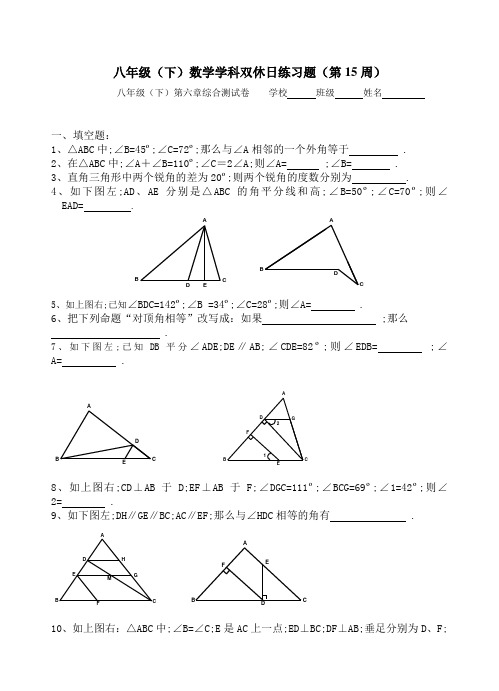
八年级(下)数学学科双休日练习题(第15周)八年级(下)第六章综合测试卷 学校 班级 姓名一、填空题:1、△ABC 中;∠B=45º;∠C=72º;那么与∠A 相邻的一个外角等于 .2、在△ABC 中;∠A +∠B=110º;∠C =2∠A;则∠A= ;∠B= .3、直角三角形中两个锐角的差为20º;则两个锐角的度数分别为 .4、如下图左;AD 、AE 分别是△ABC 的角平分线和高;∠B=50º;∠C=70º;则∠EAD= .ED CBADCBA5、如上图右;已知∠BDC=142º;∠B =34º;∠C=28º;则∠A= .6、把下列命题“对顶角相等”改写成:如果 ;那么 .7、如下图左;已知DB 平分∠ADE;DE ∥AB;∠CDE=82º;则∠EDB= ;∠A= .EDCBAGFEDCBA218、如上图右;CD ⊥AB 于D;EF ⊥AB 于F;∠DGC=111º;∠BCG=69º;∠1=42º;则∠2= .9、如下图左;DH ∥GE ∥BC;AC ∥EF;那么与∠HDC 相等的角有 .MHGFED CBAFEDCBA10、如上图右:△ABC 中;∠B=∠C;E 是AC 上一点;ED ⊥BC;DF ⊥AB;垂足分别为D 、F;若∠AED=140º;则∠C= ∠A= ∠BDF= .11、△ABC 中;BP 平分∠B;CP 平分∠C;若∠A=60º;则∠BPC= . 二、选择题12、满足下列条件的△ABC 中;不是直角三角形的是( ) A 、∠B+∠A=∠C B 、∠A :∠B :∠C=2:3:5 C 、∠A=2∠B=3∠C D 、一个外角等于和它相邻的一个内角 13、如图;∠ACB=90º;CD ⊥AB;垂足为D;下列结论错误的是( )A 、图中有三个直角三角形B 、B 、∠1=∠2C 、∠1和∠B 都是∠A 的余角D 、∠2=∠A14、三角形的一个外角是锐角;则此三角形的形状是( )A 、锐角三角形B 、钝角三角形C 、直角三角形D 、无法确定 15、如下图左:∠A+∠B+∠C+∠D+∠E+∠F 等于( ) A 、180º B 、360º C 、540º D 、720ºF ECB A16、锐角三角形中;最大角α的取值范围是( )A 、0º<α<90ºB 、60º<α<90ºC 、60º<α<180ºD 、60º≤α<90º 17、下列命题中的真命题是( )A 、锐角大于它的余角B 、锐角大于它的补角C 、钝角大于它的补角D 、锐角与钝角之和等于平角18、已知下列命题:①相等的角是对顶角;②互补的角就是平角;③互补的两个角一定是一个锐角;另一个为钝角;④平行于同一条直线的两直线平行;⑤邻补角的平分线互相垂直.其中;正确命题的个数为( )A 、0B 、1个C 、2个D 、3个19、如上图右:AB ∥CD;直线HE ⊥MN 交MN 于E;∠1=130º;则∠2等于( ) A 、50º B 、40º C 、30º D 、60º 20、如图;如果AB ∥CD;则角α、β、γ之间的关系式为( )A 、α+β+γ=360ºB 、α-β+γ=180ºC 、α+β+γ=180º 21DC B A αγβEDCBAD 、α+β-γ=180º三、解答题21、如图;BC ⊥ED;垂足为O;∠A=27º;∠D=20º;求∠ACB 与∠B 的度数.EODCBA22、如图:∠A=65º ;∠ABD=∠DCE=30º;且CE 平分∠ACB,求∠BEC.EDCB A23、如图:(1) 画△ABC 的外角∠BCD;再画∠BCD 的平分线CE. (2) 若∠A=∠B;请完成下面的证明:已知:△ABC 中;∠A=∠B;CE 是外角∠BCD 的平分线 求证:CE ∥AB24、看图填空: (1) 如下图左;∠A +∠D =180º(已知)∴ ∥ ( ) ∴∠1= ( ) ∵∠1=65º(已知)∴∠C =65º( )(2) 如上图右;已知;∠ADC =∠ABC;BE 、DF 分别平分∠ABC 、∠ADC;且∠1=∠2;求证:∠A=∠C.证明:∵BE 、DF 分别平分∠ABC 、∠ADC (已知)∴ ∠1=21∠ABC;∠3=21∠ADC ( )∵∠ABC =∠ADC (已知)1DCBACBA∴21∠ABC =21∠ADC ( ) ∴∠1=∠3( ) ∵∠1=∠2(已知)∴∠2=∠3( ) ∴( )∥( )( )∴∠A +∠ =180º ;∠C +∠ =180º( ) ∴∠A =∠C ( )25、如图:已知CB ⊥AB;CE 平分∠BCD;DE 平分∠ADC;∠1+∠2=90º 求证:AB ∥CD26、如图;已知:AC ∥DE;DC ∥EF;CD 平分∠BCA求证:EF 平分∠BED.27、如图;已知:CF ⊥AB 于F;ED ⊥AB 于D;∠1=∠2; 求证:FG ∥BC21EDCB A54321ADFCEB。
八年级数学下学期测试题第十三周双休日作业试题
HY中学2021-2021学年八年级数学下学期测试题〔第十三周双休日作业〕创作人:历恰面日期:2020年1月1日班级姓名学号一、选择题(本大题一一共10小题,每一小题3分,一共30分)( ) 1.以下命题:①长度相等的弧是等弧;②同弧所对的圆周角相等;③相等的圆心角所对的弦相等;④半圆是弧,弧是半圆.其中真命题一共有A.0个 B.1个 C.2个 D.3个( ) 2.如图,∠BOD的度数为A.750 B.800 C.1350 D.1500( ) 3.如图,AB、CD是⊙O的两条直径,∠AOC=500,过点A作AE∥CD交⊙O 于点 E,那么弧AE的度数为 A.650 B.700 C.750 D.800( ) 4.如图,⊙O的直径为10,弦AB的长为8,M是弦AB上的动点,那么OM的长的取值范围是A. 3≤OM≤5 B.4≤OM≤5 C.3<OM<5 D.4<OM<5 ( ) 5.点P在⊙O内,OP=2 cm,假设⊙O的半径是3 cm,那么过点P的最短的弦的长度为 A.1 cm B.2 cm C5cm D.56( ).如图,AB是⊙O的直径,直线EF切⊙O于点B,C、D是⊙O上的点,且弦AD=CD,∠CBE=400,那么∠BCD的度数为 A.1100 B.1150 C.1200 D.1350NM BAE D BC A( ) 7.如图,⊙O 的弦AB 垂直平分半径OC ,假设AB =6,那么⊙O 的半径为A. 2B.2 2C.22 D.62( )8.在圆柱形油槽内装有一些油。
截面如图,油面宽AB 为6分米,假如再注入一些油 后,油面AB 上升1分米,油面宽变为8分米,圆柱形油槽直径MN 为A.6分米B.8分米C.10分米D.12分米( )9.一个圆形人工湖如下图,弦AB 是湖上的一座桥,桥AB 长100m ,测得圆周角45ACB ∠=︒,那么这个人工湖的直径AD 为〔 〕A. 502mB.1002mC.1502mD. 2002m ( )10.如图,小华同学设计了一个圆直径的测量器,标有刻度的尺子OA 、OB 在O 点钉在一起,并使它们保持垂直,在测直径时,把O点靠在圆周上,读得刻度OE=8,OF=6,那么圆的直径为〔 〕A. 12个 B. 10 C.4D. 15二、填空题 第11题 第13题AOBCDO DB C11.如图,,,A B C 是O 上的三点,30BAC ︒∠=,那么BOC ∠= 度.12.如图,点A 、B 、C 在⊙O 上,AO ∥BC ,∠OAC=150,那么∠AOB 的度数是______0. 13.如图,⊙O 的两条弦AB 、CD 互相垂直,垂足为E ,且AB =CD ,CE =1,ED =3,那么⊙O 的半径是 .14.圆中一弦把垂直于它的直径分为2 cm 和6 cm 两局部,这条弦长为__________. 15.如图,⊙O 的弦CD 与直径AB 相交,假设∠BAD=50°,那么∠ACD= 16.如图,⊙O 的直径AB 与弦CD 相交于点E ,假设AE =5,BE =1,42CD =,那么∠AED= .第15题 第16题 第17题第18题17.如图,AB 是⊙O 的直径,点C ,D 都在⊙O 上,连结CA ,CB ,DC ,DB .∠D =30°,BC =3,那么AB 的长是 .18.如图,OB 是⊙O 的半径,点C 、D 在⊙O 上,∠DCB=27°,那么∠OBD= 度. 19.如图,点D 为边AC 上一点,点O 为边AB 上一点,AD =DO .以O 为圆心,OD 长为半径作半圆,交AC 于另一点E ,交AB 于点F ,G ,连接EF .假设∠BAC =22º,那么∠EFG =_____.三、解答题20.如图,在⊙O中,弦AB=CD,请问弦AD与弦CB的大小关系如何?为什么?21.⊙O的半径为12 cm,弦AB=16 cm.(1)求圆心O到弦AB的间隔;(2)假如弦AB的两个端点在圆周上滑动,那么弦AB中点形成什么样的图形?22.某居民小区一处圆柱形的输水管道破裂,维修人员为更换管道,需确定管道圆形截面的半径,以下图是程度放量的破裂管道有水局部的截面.(1)请你补全这个输水管道的圆形截面;(2)假设这个输水管道有水局部的水面宽AB=16 cm,水面最深地方的高度为4 cm,求这个圆形截面的半径.23. 如图7,在△ABC中,∠ACB=90°,∠B=36°,以C为圆心,CA为半径的圆交AB于AD DE点D,交BC于点E.求、的度数.24. 如图,AB是⊙O的弦,AB长为8,P是⊙O上一个动点〔不与A、B重合〕,过点O作OC⊥AP 于点C,OD⊥PB于点D,求CD的长?,BF和AD交于点E说明AE与25. 如图,BC为⊙O的直径,AD⊥BC,垂足为D,AB AFBE的大小关系,并证明这一结论.26.如图,AB是⊙O的直径,AC是⊙O的弦,以OA为直径的⊙D与AC相交于点E.(1)试断定线段OE与线段BC的关系,并说明理由;(2)假设F为BC边上的中点,试断定四边形OFCE的形状.27.如图,AB 是⊙O 的直径,BC 是弦,OD ⊥BC 于E ,交BC ⌒ 于D .〔1〕请写出四个不同类型....的正确结论; 〔2〕假设BC = 8,ED = 2,求⊙O 的半径.O E DCBA。
八年级数学下学期测试题第十三周双休日作业试题
HY中学2021-2021学年八年级数学下学期测试题〔第十三周双休日作业〕班级姓名学号一、选择题(本大题一一共10小题,每一小题3分,一共30分)( ) 1.以下命题:①长度相等的弧是等弧;②同弧所对的圆周角相等;③相等的圆心角所对的弦相等;④半圆是弧,弧是半圆.其中真命题一共有A.0个 B.1个 C.2个 D.3个( ) 2.如图,∠BOD的度数为A.750 B.800 C.1350 D.1500( ) 3.如图,AB、CD是⊙O的两条直径,∠AOC=500,过点A作AE∥CD交⊙O 于点 E,那么弧AE的度数为 A.650 B.700 C.750 D.800( ) 4.如图,⊙O的直径为10,弦AB的长为8,M是弦AB上的动点,那么OM的长的取值范围是A. 3≤OM≤5 B.4≤OM≤5 C.3<OM<5 D.4<OM<5 ( ) 5.点P在⊙O内,OP=2 cm,假设⊙O的半径是3 cm,那么过点P的最短的弦的长度为 A.1 cm B.2 cm C5cm D.56( ).如图,AB是⊙O的直径,直线EF切⊙O于点B,C、D是⊙O上的点,且弦AD=CD,∠CBE=400,那么∠BCD的度数为 A.1100 B.1150 C.1200 D.1350( ) 7.如图,⊙O的弦AB垂直平分半径OC,假设AB=6,那么⊙O的半径为NM BAE D BC AA. 2B.2 2C.22 D.62( )8.在圆柱形油槽内装有一些油。
截面如图,油面宽AB 为6分米,假如再注入一些油 后,油面AB 上升1分米,油面宽变为8分米,圆柱形油槽直径MN 为A.6分米B.8分米C.10分米D.12分米( )9.一个圆形人工湖如下图,弦AB 是湖上的一座桥,桥AB 长100m ,测得圆周角45ACB ∠=︒,那么这个人工湖的直径AD 为〔 〕A. 502mB.1002mC.1502mD. 2002m ( )10.如图,小华同学设计了一个圆直径的测量器,标有刻度的尺子OA 、OB 在O 点钉在一起,并使它们保持垂直,在测直径时,把O点靠在圆周上,读得刻度OE=8,OF=6,那么圆的直径为〔 〕A. 12个 B. 10 C.4D. 15二、填空题 第11题 第13题 11.如图,,,A B C 是O 上的三点,30BAC ︒∠=,那么BOC ∠= 度.12.如图,点A 、B 、C 在⊙O 上,AO ∥BC ,∠OAC=150,那么∠AOB 的度数是______0.AOBCDO DB C13.如图,⊙O 的两条弦AB 、CD 互相垂直,垂足为E ,且AB =CD ,CE =1,ED =3,那么⊙O 的半径是 .14.圆中一弦把垂直于它的直径分为2 cm 和6 cm 两局部,这条弦长为__________. 15.如图,⊙O 的弦CD 与直径AB 相交,假设∠BAD=50°,那么∠ACD= 16.如图,⊙O 的直径AB 与弦CD 相交于点E ,假设AE =5,BE =1,42CD ,那么∠AED= .第15题 第16题 第17题第18题17.如图,AB 是⊙O 的直径,点C ,D 都在⊙O 上,连结CA ,CB ,DC ,DB .∠D =30°,BC =3,那么AB 的长是 .18.如图,OB 是⊙O 的半径,点C 、D 在⊙O 上,∠DCB=27°,那么∠OBD= 度. 19.如图,点D 为边AC 上一点,点O 为边AB 上一点,AD =DO .以O 为圆心,OD 长为半径作半圆,交AC 于另一点E ,交AB 于点F ,G ,连接EF .假设∠BAC =22º,那么∠EFG =_____.三、解答题20.如图,在⊙O中,弦AB=CD,请问弦AD与弦CB的大小关系如何?为什么?21.⊙O的半径为12 cm,弦AB=16 cm.(1)求圆心O到弦AB的间隔;(2)假如弦AB的两个端点在圆周上滑动,那么弦AB中点形成什么样的图形?22.某居民小区一处圆柱形的输水管道破裂,维修人员为更换管道,需确定管道圆形截面的半径,以下图是程度放量的破裂管道有水局部的截面.(1)请你补全这个输水管道的圆形截面;(2)假设这个输水管道有水局部的水面宽AB=16 cm,水面最深地方的高度为4 cm,求这个圆形截面的半径.23. 如图7,在△ABC中,∠ACB=90°,∠B=36°,以C为圆心,CA为半径的圆交AB于AD DE点D,交BC于点E.求、的度数.24. 如图,AB是⊙O的弦,AB长为8,P是⊙O上一个动点〔不与A、B重合〕,过点O作OC⊥AP 于点C,OD⊥PB于点D,求CD的长?,BF和AD交于点E说明AE与25. 如图,BC为⊙O的直径,AD⊥BC,垂足为D,AB AFBE的大小关系,并证明这一结论.26.如图,AB是⊙O的直径,AC是⊙O的弦,以OA为直径的⊙D与AC相交于点E.(1)试断定线段OE与线段BC的关系,并说明理由;(2)假设F为BC边上的中点,试断定四边形OFCE的形状.27.如图,AB 是⊙O 的直径,BC 是弦,OD ⊥BC 于E ,交BC ⌒ 于D .〔1〕请写出四个不同类型....的正确结论; 〔2〕假设BC = 8,ED = 2,求⊙O 的半径.励志赠言经典语录精选句;挥动**,放飞梦想。
八年级数学下学期测试题2第十六周双休日作业试题
卜人入州八九几市潮王学校HY 二零二零—二零二壹八年级数学下学期测试题2班级学号1.二次根式()22-可化简成〔〕 A .-2 B .4 C .2 D .22.要使分式11x +有意义,x 的取值范围是〔〕 A .x ≠1 B .x ≠-1 C .x ≠0 D .x>-13.以下函数中,y 是x 的反比例函数的是〔〕A .y =-2xB .y =-1xC .y =x +3D .y =23x - 4.a ,b 都是正数,化简b a 28,正确的结果是〔〕 A .b a 8B .b a 222C .b a 22D .22ab5.如图,一场暴雨过后,垂直于地面的一棵树在距地面1米处折断,树尖B 恰好碰到地面, 经测量AB =2米,那么树高为〔〕A .5米B .3米C .()51+)米D .3米 6.一次函数y=-4x+8的图象不经过的象限是〔〕A .第一象限B .第二象限C .第三象限D .第四象限7.一等腰三角形底边长为10 cm ,腰长为13 cm ,那么腰上的高为〔〕A .12cmB .6013cmC .12013cmD .135cm 8.一次函数y 1=kx+b 与y 2=x+a 的图象如图,那么以下结论:①k<0;②a>0;③当x<3时,y 1<y 2.其中正确的个数是〔〕A .0个B .1个C .2个D .3个9.如图,点A 、B 、C 、在一次函数2y x m =-+的图象上,它们的横坐标依次为—1、1、2,分别过这些点作x 轴与y 轴的垂线,那么图中阴影C局部的面积之和是〔〕A .1B .3C .3(1)m -D .3(2)2m - 10.地球与月球的间隔大约为384000km ,将384000准确到万位,并用科学记数法表示. 11.点P 〔m ,m-2〕在第四象限内,那么m 取值范围是_.12.假设|x -3|+〔y +33〕2=0,那么2013()xy =__.13.△ABC 的三边分别为2、x 、5,化简22)7()3(-+-x x 的值是_.14.假设直线y x a y x b =-+=+和直线相交于点〔m ,8〕,那么a b +=.15.直角三角形的周长是56cm ,斜边上的中线为,那么这个直角三角形的面积__.16.(1)填空:①1233⨯=, ②123a a ⨯=(a ≥0),(2)化简:③25=, ④32ba =(a>0,b ≥0).17.小明根据某个一次函数关系式填写上了下面的这张表,其中有一格不慎被墨迹遮住了,想想看,表中空格原来填的数是___. 18.如图,一次函数223y x =-+的图象分别与x 轴、y 轴交于点A 、B ,以线段AB 为边在第一象限内作等腰R t△ABC,∠BAC=90°,假设点P 在x 轴上且它到B 、C 两点的间隔之和最小,那么P 点坐标是. 19.在平面直角坐标系xOy 中,点A 1,A 2,A 3,…和B 1,B 2,B 3,…分别在直线y kx b =+和x 轴上.△OA 1B 1,△B 1A 2B 2,△B 2A 3B 3,…都是等腰直角三角形,假设A 1〔1,1〕,A 2〔23,27〕,那么点A n 的纵坐标是______.20.如图,四边形OABC 为正方形,边长为6,点A 、C 分别在x 轴、y 轴的正半轴上,点D 在OA 上,且点D 的坐标为(2,0),点P 是OB 上的一个动点,那么PD +PA 的最小值是.yxy=kx+O B 3 B 2 B 1 A 3 A 2A 121.计算:()2962034x x x x ⎛⎫-+> ⎪ ⎪⎝⎭()2421110,0346y x y x y x y x ⎛⎫⎛⎫⨯-÷->> ⎪ ⎪ ⎪⎝⎭⎝⎭22.解分式方程:22124x x x +=--23.先化简,再求值:21111a a a a -⎛⎫-÷ ⎪++⎝⎭,其中a =2+3. 24.x =3+22,y =3-22,求以下各式的值:(1)22x y xy +;(2)x y y x+ 25.实数a 、b 、c 在数轴上的位置如下列图,且a b =,化简:()222a a b c a c ++---. 24.如图,把长方形纸片ABCD 沿EF 折叠后,使得点D 与点B 重合,点C 落在点C ′的位置上.(1)折叠后,DC 的对应线段是,CF 的对应线段是;(2)假设AB=8,DE=10,求CF 的长度.25.直线l 1:y=3x -3和直线2362l y x =-+:相交于点A . (1)求点A 的坐标;(2)假设l 1与x 轴交于点B ,l 2与x 轴交于点C ,求△ABC 的面积;(3)假设点D 与点A 、B 、C 能构成平行四边形,请直接写出点D 的坐标.26.小明用12元买软面笔记本,小丽用21元买硬面笔记本。
八年级数学下学期测试题第五周双休日作业试题
卜人入州八九几市潮王学校HY 二零二零—二零二壹八年级数学下学期测试题〔第五周双休日作业〕班级学号1.可以找到一点,使该点到各边间隔都相等的图形为〔〕 ①平行四边形②菱形③矩形④正方形 A .①与②B.②与③C.②与④D.③与④2.矩形、菱形、正方形都具有的性质是() A .每一条对角线平分一组对角B .对角线相等 C .对角线互相平分D .对角线互相垂直3..在菱形ABCD 中,对角线AC 、BD 相交于点O ,E 为AB 的中点,且OE=a ,那么菱形 ABCD 的周长为A .16aB .12aC .8aD .4a()4.如图,E 、F 分别是正方形ABCD 的边CD 、AD 上的点,且CE=DF ,AE 、BF 相交于 点O ,以下结论:①AE=BF ;②AE ⊥BF ;③AO=OE ;④S △AOB =S 四边OEDF ,其中错误的 有A .1个B .2个C .3个D .4个〔〕5.如图,直线AB 交y 轴于点C ,与双曲线1y x=(k <0)交于A 、B 两点,P 是线段AB 上的点(不与A 、B 重合),Q 为线段BC 上的点(不与B 、C 重合),过点A 、P 、Q 分别向x 轴作垂线,垂足分别为D 、E 、F ,连结OA 、OP 、OQ ,设△AOD 的面积为S 1、△POE 的面积为S 2、△QOF 的面积为S 3,那么有〔〕 A .S 1<S 2<S 3B .S 3<S 1<S 2 C .S 3<S 2<S 1D .S 1、S 2、S 3相等6.如图,点A 是一次函数y =的图象与反比例函数ky x=的图象在第一象限内的交点,AB ⊥x 轴于点B ,点C 在x 轴的负半轴上,且OA=OC ,△AOB ,那么AC 的长为A B ..D .4〔〕3k y x-=图象的每一支曲线上,y 都随x 的增大而减小,那么k 的取值范围是〔〕A .k >3B .k >0 C .k <3D .k <0PFEDCBA8、在反比例函数y=x2的图象中,阴影局部的面积不等于2的是〔〕9.假设函数122--=m x m y 是反比例函数,那么=m 〔〕A 、0B 、-2C 、±2D 、210.假设一个平行四边形的对角线长分别为8和6,那么这个平行四边形的边长m 的取值范围是__________. 11.在菱形ABCD 中,∠A=60°,对角线BD=8,那么菱形ABCD 的周长等于________.12.方形ABCD 中,P 为AB 的中点,BE ⊥PD 的延长线于点E,连结AE 、BE 、FA ⊥AE 交DP 于点F ,连结BF,FC.以下结论:①△ABE ≌△ADF ;②FB=AB ;③CF ⊥DP ;④FC=EF 其中正确的选项是13.如图,A 、B 是双曲线y=kx (k>0)上的点,A 、B 两点的横坐标分别是a 、2a ,线段AB 的延长线交x 轴于点C ,假设AOCS=6.那么k=__________.14.如图,假设点A 在反比例函数(0)ky k x=≠的图象上,AM x ⊥轴于点M ,AMO △的面积为4,那么k=.15.如图,点A(m ,0),B(0,n),直线AB 与反比例函数m y x=的图象交于C 、D 两点.假设S △AOD =S △COD =S △COB ,那么n 的值是16.假设m <-1,那么以下函数:①x my =;②y=-mx+1;③y=mx;④y=(m+1)x 中,y 随x 增大而增大的是___________〔填序号〕。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
〔第5题〕〔第6题〕
A
B
C
O
O
B
A
C
D
H
卜人入州八九几市潮王学校HY二零二零—
二零二壹八年级数学下学期测试题〔第十四
周双休日作业〕
班级学号
一.填空题
1.如图,△ABC内接于⊙O,BC是⊙O的直径,MN与⊙O相切,切点为A,假设∠MAB=30°,那么∠B=_______.
2.如图,∠APB=30°,圆心在边PB上的⊙O的半径为1cm,OP=3cm,假设⊙O沿BP方向挪动,那么当
⊙O与PA相切时,圆心O挪动的间隔为_______cm.
3.假设⊙O的半径为8,圆心O到直线l的间隔为4,那么直线l与⊙O的位置关系是.
4.如图,点O是△ABC的内切圆的圆心,假设∠BAC=80°,那么∠BOC等于.
5.如图,弦CD垂直于⊙O直径AB,垂足为H,且CD=22,BD=3,那么AB长为.
6.如图,半径为R的圆内接正三角形的边长是,面积是.
7.如图,在△ABC中,AB=2,AC=2,假设以点A为圆心,1为半径的
圆与边BC相切于点D,那么∠BAC的度数是_______.
8.⊙O半径OA=6,∠AOB=90°,那么∠AOB所对的弧AB的长为.
9.直角三角形两直角边为6和8,那么这个三角形外接圆半径为,内切圆半径为.
10.如图,△ABC的两边切内切圆于D、E,∠B=40°,∠C=80°,P是内切圆上异于D、E的一个动点,那
么∠DPE的度数是.
11.如图,AB是半圆O的直径,∠BAC=32°,D为的中点,∠DAC=_____°.
12.如图,PA、PB是⊙O是切线,A、B为切点,AC是⊙O的直径,假设∠BAC=25°,那么∠P=°_______.
13.如图,假设AB、AC分别切⊙O于点B、C,延长OB到点D使BD=OB,连接AD,∠DAC=72°,那么∠
A
D
E
B
C
〔第10题〕
ADO等于.
14.以下说法正确的选项是()
15.如图,PA、PB切⊙O于A、B,OP交AB于C,那么图中能用字母表示的直角一共有()个A.3B.4 C.6D.5
(15)(16)〔17〕〔18〕
16.如图,圆心角∠AOB为100°,那么∠ACB的度数是()
A.80°B.130°C.120°D.100°
17.如图,O是正方形ABCD的对角线BD上一点,⊙O边AB,BC都相切,点E,F分别在边AD,DC上.现将
△DEF沿着EF对折,折痕EF与⊙O相切,此时点D恰好落在圆心O处.假设DE=2,那么正方形ABCD的
边长是()A.3 B.4 C.22 D.
22
18.如图,正方形ABCD的顶点A、C分别在y轴、x轴上,以ABA的坐标为(0,8),那么圆心M的坐标为
()A.(-4,5)B.(-5,4)C.(5,-4)D.(4,-5)
19.如图,在△ABC中,AB=6,AC=8,BC=10,假设D,E分别是AC,AB的中点,
那么以DE为直径的圆与BC的位置关系是()
A.相交 B.相切
C.相离 D.无法确定
20.⊙O的半径为2,假设直线l上有一点P满足PO=2,那么直线l与⊙O的位置关系是()
A.相切B.相离C.相离或者相切D.相切或者相交
21.如图,AB为⊙O的直径,C为⊙O外一点,过点C作⊙O的切线,切点为B,连
接AC交⊙O于点D,∠C=38°,假设点E在AB右侧的半圆周上运动〔不与点A,
B重合〕,那么∠AED的大小是()
A.19° B.38°C.52° D.76°
22.如图,AB、AC切⊙O于点B、C,AO交⊙O于点D,过点D作⊙O的切线分别交AB、
AC于点E、F,假设OB=6,AO=10,那么△AEF的周长是()
A.10 B.12 C.14 D.16
23.△ABC外切于⊙O,
(1)假设AB=8,BC=6,AC=4,求AD、BE、CF的长度。
(2)假设C△ABC=36,S△ABC=18,求内切圆的半径的长度。
24.如图,PA、PB是⊙O的两条切线,切点分别为点A、B,假设直径AC=12,∠P=60o,
求弦AB的长.
25.如图:△ABC中,∠C=900,点O在BC上,以OC为半径的半圆切AB于点E,交BC于点D,假设BE=4,BD
=2,求⊙O的半径和边AC的长.
26.如图,AB是⊙O的直径,AC是弦,∠BAC的平分线AD交⊙O于点D,DE⊥AC,交AC的延
长线于点E,OE交AD于点F.求证:DE是⊙O的切线;
27.如图,△ABC内接于⊙O,OC和AB相交于点E,点D在OC的延长线上,且∠B=∠D=∠BAC=30°.
(1)试判断直线AD与⊙O的位置关系,并说明理由;
(2)假设AB=63,求⊙O的半径.
28.如图,⊙O是Rt△ABC的外接圆,∠ABC=90°,P是圆外一点,PA切⊙O于
点A,且PA=PB.
(1)试说明:PB是⊙O的切线;
(2)PA=3,30BAC,求⊙O的半径.
29.如图,⊙O内切于Rt△ABC,∠BOC=105°,∠ACB=90°,AB=20 cm.求
BC、AC的长.
30.如图,四边形ABCD的边AB、BC、CD、DA和⊙O分别相切于点E、F、G、H,试探究这个四边形ABCD的
F
E D C B A O B
A
C
E
O
D
F
D
E
o
B
C
A
